Abstract
The structural protein elastin endows large arteries with unique biological functionality and mechanical integrity, hence its disorganization, fragmentation, or degradation can have important consequences on the progression and treatment of vascular diseases. There is, therefore, a need in arterial mechanics to move from materially uniform, phenomenological, constitutive relations for the wall to those that account for separate contributions of the primary structural constituents: elastin, fibrillar collagens, smooth muscle, and amorphous matrix. In this paper, we employ a recently proposed constrained mixture model of the arterial wall and show that prestretched elastin contributes significantly to both the retraction of arteries that is observed upon transection and the opening angle that follows the introduction of a radial cut in an unloaded segment. We also show that the transmural distributions of elastin and collagen, compressive stiffness of collagen, and smooth muscle tone play complementary roles. Axial prestresses and residual stresses in arteries contribute to the homeostatic state of stress in vivo as well as adaptations to perturbed loads, disease, or injury. Understanding better the development of and changes in wall stress due to individual extracellular matrix constituents thus promises to provide considerable clinically important insight into arterial health and disease.
Keywords: vascular development, tortuosity, elastin, adaptation, aging, aneurysms, hypertension, Marfan Syndrome
INTRODUCTION
Observations in the 1960s revealed that many arteries experience little to no axial deformation during the cardiac cycle (e.g., Patel and Fry 1966; Tickner and Sacks 1967); soon thereafter it was suggested that this constancy of length is biomechanically favorable (Cox 1975; van Loon et al. 1977). Observations also revealed that arteries retract when transected, thus suggesting the existence of an axial prestretch that defines the favorable length in vivo. Dobrin et al. (1975) showed that this axial prestretch (or “longitudinal traction”) increases nearly linearly with age during postnatal development and suggested that it can be “attributed to stretching of the vessels by growth and to changes in connective tissue composition.” Subsequent studies by Dobrin et al. (1990), using elastase and collagenase to selectively remove structural components from the wall, demonstrated that nearly all axial prestretch in healthy arteries is due to the presence of intramural elastin, not collagen.
Findings in the 1960s revealed further that there exists “some degree of stress even when there is no distending pressure” in an artery (Bergel 1960). Independent observations by Fung (1983) and Vaishnav and Vossoughi (1983) confirmed the existence of residual stresses in arteries, which appear to arise from nonuniform growth and remodeling processes during development and can change in response to disease or injury in maturity (Fung 1991). Experiments by Greenwald et al. (1997), using elastase, collagenase, and rapid freezing to selectively remove the three dominant structural constituents from the wall, showed that these residual stresses depend primarily on intramural elastin, not collagen or smooth muscle. Related to this finding, Zeller and Skalak (1998) suggested that the net residual stresses in an excised artery likely depend on different residual stresses within individual constituents, with elastin having a residual tension and collagen a residual compression. Indeed, this suggestion is consistent with current thinking that elastin is deposited and cross-linked during the perinatal period and its half-life is normally on the order of the lifespan of the organism, thus causing it to undergo extensive elastic deformations during normal biological growth (Davis 1995) that are only partially relieved in the mature artery upon excision. On the other hand, collagen turns over continuously and is likely deposited at a preferred deposition stretch independent of the current state of the artery in maturity (Humphrey and Rajagopal 2002, Tomasek et al. 2002), thus yielding a more modest collagen prestretch.
The existence of residual stress in an intact but traction-free excised arterial segment suggests a net compressive (primarily circumferential) stress in the inner wall and a net tensile (primarily circumferential) stress in the outer wall, which is captured easily by both standard stress analyses (e.g., Chuong and Fung 1986) and computational models of arterial growth (e.g., Taber and Humphrey 2001). Such models are based on materially uniform, phenomenological, constitutive relations, however, and thus have not been capable of assessing the potential roles of individual constituents or how they are formed or reorganized during development or maturity. The goal of this paper, therefore, is to employ a recently proposed materially nonuniform, structurally motivated, constrained mixture model of the arterial wall to study the means by which elastin plays such an important role in the development of axial prestress and residual stress in the normal arterial wall, two key factors in mechanical homeostasis. By prestress, we mean stress in a body under a normal state of loading in the absence of what might be thought of as additional, perturbing loads. By residual stress, we mean stresses that exist independent of applied loads, which must self-equilibrate by definition1. We submit further that the constrained mixture model employed herein can be used to build residual stresses into patient-specific computational models without the need to define clinically unattainable spatially and temporally changing opened configurations (cf. Delfino et al. 1997; Alastrue et al. 2007), a feature that could be particularly advantageous in modeling complex arterial geometries and diseased states.
METHODS
Theoretical Framework
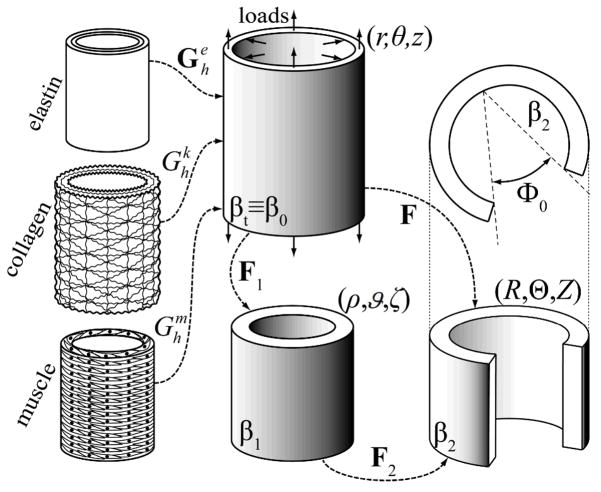
It proves convenient to study salient aspects of arterial wall mechanics using the semi-inverse approach of finite elasticity. In contrast to usual formulations, which use the “stress-free” configuration as a reference, we use the current, stressed configuration as a computational reference (cf. Zhou and Lu 2008). Two reasons motivate this choice. First, most investigators prescribe the stress-free reference configuration (e.g., via an opening angle and radii) based on empirical observations and then seek consequences of this reference on the in vivo state of stress. In contrast, we seek to determine consequences of material nonuniformity and nonhomogeneity on both the in vivo state of stress and the residual stress related opening of cut segments. Second, our work is motivated by the desire to model growth and remodeling processes mathematically, which necessarily occur in the in vivo, stressed state. Hence, for illustrative purposes, we prescribe the kinematics for an idealized axisymmetric artery via two successive motions (Figure 1): mappings of material points from a physiologically-relevant in vivo configuration βt (with coordinates r,θ, z ) associated with the finite extension and inflation of an intact cylindrical segment at time t to an intact but traction-free excised configuration β1(with coordinates ρ,ϑ,ζ) and finally to a nearly stress-free, radially-cut configuration β ( R,Θ, Z ). These mappings are given by:
| (1)1 |
| (1)2 |
whereby deformation gradients for these motions are
Figure 1.
Schema of the constrained mixture model of an arterial segment consisting of elastin, multiple families of collagen fibers, and smooth muscle. Shown, too, are the in vivo configuration, βt, which is taken as a reference β0 for the kinematics, a traction-free excised configuration, β1, and a radially-cut, nearly stress-free configuration β2. The deformation gradients are denoted by Fi and Φ0 is the opening angle in β2
| (2) |
with Φo and Λ the residual stress related opening angle and axial stretch, respectively, and λ the additional axial stretch related primarily to the in vivo “prestretch” (note: one can think of these deformation gradients as inverses of the usual tensors referred to the stress-free configuration; cf. Humphrey 2002). The total deformation gradient is thus computed via F=F2F1 and incompressibility is assumed to hold during transient motions, but not overall growth and remodeling, hence det F=1 herein. Assuming quasi-static motions (Humphrey and Na 2002), the Cauchy stress t associated with either the first (F=F1 with F2=I ) or the total ( F=F2F1) motion can be computed via
| (3) |
where p is a Lagrange multiplier that enforces incompressibility, W is the net strain energy function for the passive behavior of the wall, and tact accounts for smooth muscle activity. Consistent with an early, insightful paper by Brankov et al. (1975) as well as the more recent work by Valentin et al. (2008), we employ a rule-of-mixtures constitutive relation for the passive response, namely
| (4) |
where ϕi are mass fractions for each structurally significant constituent and Wi are individual strain energy functions (i = e for amorphous elastin, i = 1,2,3,4 for four oriented families of collagen fibers, and i = m for circumferentially oriented passive smooth muscle; note that we neglect any possible load carrying capability of fibroblasts and migratory/synthetic smooth muscle cells). Moreover, Fe, λk, and λm represent the elastin deformation gradient, collagen fiber stretch, and smooth muscle stretch, respectively. These quantities are defined with respect to individual stress-free configurations (see Figure 1) and are detailed below. The active smooth muscle contribution, assumed consistent with a predominantly circumferential orientation, is given by (cf. Nevo and Lanir 1989; Rachev and Hayashi 1999)
| (5) |
where TM, λM, λ o are the maximum (mass averaged) stress, the stretch at which active force generation is maximal, and the stretch at which active force generation is minimal (zero), respectively. Clearly, therefore, the active stress depends on a constrictor concentration C (i.e., its dose response curve) and the muscle fiber stretch (i.e., its active length-tension curve). Henceforth, we focus on the basilar artery, one of the primary arteries that supplies blood to the brain.
Recall the key observation that elastin is produced primarily during the perinatal period and is normally stable thereafter (Davis 1995; Langille 1996), thus it undergoes large multiaxial stretches as the artery enlarges to the adult configurationβ0≡βt. On the other hand, collagen and smooth muscle turn over continuously throughout life (Langille 1996) and we assume that they are deposited at a preferred stretch during maturity. These assumptions result in higher “prestretches” in elastin (the product of both deposition and development-induced stretches) than in collagen fibers and smooth muscle in maturity. That is, the different timing of deposition and values of deposition stretches for each constituent play particularly important roles because the associated prestretches can thereby vary transmurally, which together with the changing mass fractions of the constituents can strongly influence the unloaded length (i.e., net axial prestress) and the opening angle (i.e., net residual stress) of the vessel. To study this mathematically, consider the following.
Equilibrium of the in vivo configuration β0, in both local and global (integral) forms, requires
| (6) |
and
| (7) |
where ri and ra denote inner (intimal) and outer (adventitial) radii in β0 (associated with the deformation F=I ) and P and f are the in vivo luminal pressure and axial force, respectively. Herein, the in vivo configuration was assumed to correspond to a mean transmural pressure and basal muscular tone in the basilar artery (cf. Valentin et al. 2008). To ensure radial equilibrium at the prescribed in vivo luminal pressure, equation (7)1 was solved for the adventitial radius r; equation (7)2 was solved similarly for the in vivo axial force. In this way, the material parameters, intimal radius, and luminal pressure were kept the same in all the simulations regardless of the assumed distributions of constituent prestretches and mass fractions (with slight variations in outer radius maintaining radial equilibrium). The variation in computed ra for the wide range of cases simulated below was less than 0.1% of the reference value (i.e. 1.6 mm; see Table 1 for the definition of the reference case).
Table 1.
Parameter values used for the normal rabbit basilar artery (from Valentin et al. 2008, based in part on data from Wicker et al. 2008).
| Prestretches and elastic parameters |
| Ce = 237.65kPa, |
| Mass fractions (dry weight) |
| ϕe = 0.02, ϕc = 0.22 ϕm= 0.76 |
| Parameters governing active stress generation |
| TM =150MPa × ϕm λm λ0= 0.4, Cbasal= 0.68 |
| In vivo geometry |
| ri = 1.42 mm, ra ≈ 1.60mm** |
uniform elastin prestretches for the reference case used if not specified otherwise
slightly dependent on the distribution of constituents mass fraction and prestretch, this reference value corresponds to uniform distribution of constituents and .
Equilibrium of the unloaded configuration β 1similarly requires
| (8) |
and
| (9) |
where ρ i and ρ a denote inner (intimal) and outer (adventitial) radii in β1 (associated with the deformation F=F1). The two global equations can be solved to determine the inner radius ρi and the net in vivo axial prestretch λ for prescribed material properties and distributions of constituent prestretches and mass fractions, with zero transmural pressure and axial force.
Finally equilibrium of the excised, radially-cut configuration can be satisfied via (cf. Taber and Humphrey 2001)
| (10) |
and
| (11) |
where Ri and Ra denote inner (intimal) and outer (adventitial) radii in β2 (associated with the deformation F=F2F1). Note that the additional global equilibrium equation enforces zero applied moments on the radially-cut section. The three global equations can be solved for the inner radius Ri, the net in vivo axial prestretch Λλ, given λ from above, and the residual stress related opening angle Φ0, all for the prescribed material properties and distributions of constituent prestretches and mass fractions, again with zero transmural pressure and axial force.
Simulation Strategy
For illustrative purposes, let the mechanical behavior of the elastin-dominated amorphous matrix be described by a neo-Hookean strain energy function (Dorrington and McCrum 1977; Holzapfel et al. 2000)
| (12) |
where c1 is a material parameter (Table 1) and (with i = r, θ, z ) are principal stretches for elastin, whose deformation gradient is given by (cf. equation 4). Hence, Fe=Ge in the in vivo configuration, again emphasizing that the in vivo elastin “prestretch” Ge results from both its actual deposition stretch (in development) and subsequent stretches due to development/maturation of the whole vessel (Dobrin et al. 1975; Davis 1995). Similarly, let the behavior of the passive smooth muscle and collagen fibers be described by exponential forms (Nevo and Lanir 1989; Valentin et al. 2008),
| (13) |
| (14) |
where are material parameters (Table 1). For simplicity, and due to the lack of data, behaviors of collagen and smooth muscle are assumed to be the same in compression but different in tension. Most other investigators assume that fibrillar collagen cannot resist compression, which would be true of isolated fibers but not those embedded within the arterial wall and supported by many other constituents, including abundant proteoglycans. It is for this reason that we assume a bimodular behavior of fibrillar collagen herein, consistent with observations of Zeller and Skalak (1998) that collagen can be in compression in an unloaded configuration.
Recall that each structurally significant constituent, elastin (e), collagen fiber family k (=1,2,3,4), and smooth muscle (m), can possess a unique natural (i.e., stress free) configuration. That is, individual constituents need not be unstressed when the overall tissue is unstressed (i.e., when t=0 ) as recognized by Brankov et al. (1975) and Zeller and Skalak (1998), among others. It can be shown (Baek et al., 2006) that constituent-level stretches for collagen and smooth muscle (i.e.,λk, λm ) can be related to tissue-level stretches (e.g., λr, λ θ, λ z) via homeostatic “deposition stretches” (e.g., ), as, for example, for collagen
| (15) |
where denotes the angle between the axial direction of the vessel and the collagen fiber direction in a common reference configuration. The four families of parallel collagen fibers are assumed to be oriented axially, circumferentially, and diagonally (Wicker et al. 2008). Results are similar for smooth muscle, but simpler for it is assumed to be oriented in the circumferential direction alone.
Integrating equations (7), (9) and (11) by parts, to write the Cauchy stresses in terms of extra (i.e., deformation dependent) rather than total (including reaction terms) components, and transforming the integrands to the reference configuration that is, integration over r rather than eitherρ in equations (9) or R in equations (11) – simplifies numerical analysis (Taber and Humphrey 2001). These equations were solved using a Newton-Raphson method to determine the yet unknown values (i.e., ra and f in β0,λ and ρ i in β1, and Φo, Λλ, and Ri in β2), with the requisite derivatives estimated via a forward Euler finite difference scheme. The in vivo state corresponding to the case of a uniform distribution of constituent mass fractions and prestretches (see Table 1 for the reference case) was assumed as the initial guess in the solution of equation (7)1 for the other cases discussed below. Similarly, the computed in vivo configuration β 0 was assumed as the initial guess for the solution of equations (9) whereas the intact unloaded configuration β 1 was assumed as the initial guess for the solution of equations (11). An analysis of the sensitivity of the solutions to these initial guesses revealed that the computations were not influenced by the choice of the initial guess in most cases. In the few cases that we found multiple solutions, only one proved physically admissible (i.e., positive values of the inner radius and axial stretch and opening angle smaller than 180°, noting that the present model cannot simulate an inversion of the arterial ring corresponding to an opening angle Φ0 >180°). Table 1 lists illustrative values of the requisite parameters used in the simulations.
RESULTS
Elastin degradation
A loss of functional elastin was expected to relieve some of the residual stress and to increase the unloaded length, thus reducing the opening angle and decreasing the axial prestretch (Greenwald et al. 1997; Fonck at al. 2006). Degradation was simulated numerically by reducing the elastin stiffness coefficient c1 by 30, 60, or 90%. Consider first the case of uniformly distributed constituents with the “prestretch” for elastin being isotropic in the plane (θ, z) and isochoric (as in Table 1), thus rendering the artery materially homogeneous albeit not materially uniform. Note that overall volume was preserved despite the reduction in functional elastin, which thereby only affected the structural behavior of the mixture. In other words, the elastin was not removed from the vessel wall, it merely lost its ability to bear mechanical load. This assumption may reflect fragmentation that occurs in aging or Marfan syndrome.
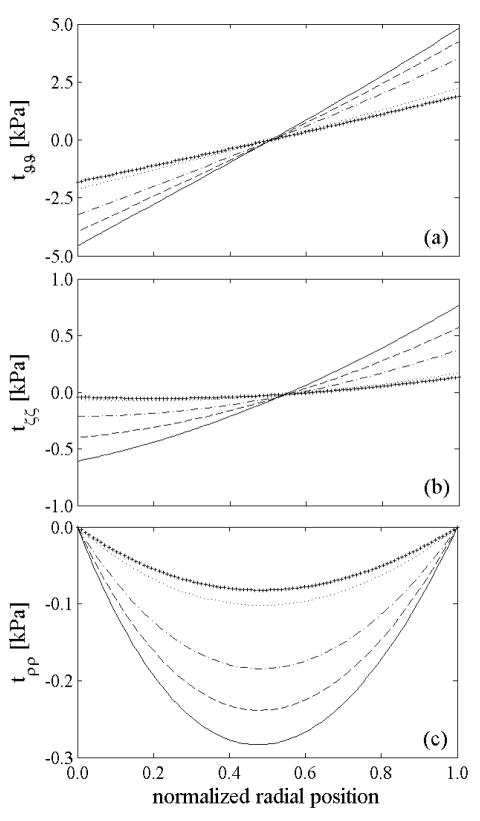
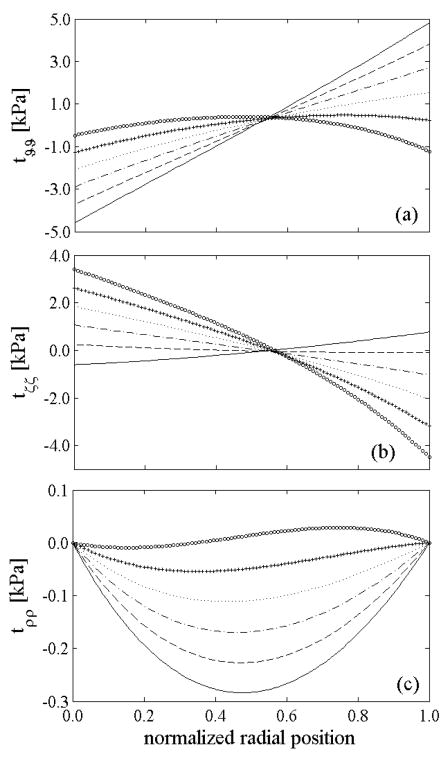
Simulations showed that axial stretch λ and opening angle Φ0 both decreased monotonically and substantially with increased degradation of elastin (Table 2), consistent with clinical and experimental observations. The associated increase in the unloaded length is explained easily because the overall unloaded configuration results from a trade-off between the highly stretched elastin, which is always in tension and thus trying to recoil, and the collagen and smooth muscle, which are in tension in vivo but compressed in the unloaded configuration β1 (cf. Zeller and Skalak, 1998). As more elastin degrades, the less it is able to compress the other constituents of the mixture, and the unloaded configuration of the vessel will approach the in vivo configuration. A similar explanation can be given for the reduction in the opening angle; degradation of elastin reduces radial recoil of the vessel upon unloading (Table 2), hence reducing overall circumferential compression of the inner wall, with compressive and tensile stresses balancing to maintain equilibrium. This phenomenon is evident in panel (a) of Figure 2, which further shows a continued reduction of all components of stress in the unloaded configuration as more elastin degrades, even though the qualitative distribution of the residual stresses is similar regardless of the amount of degraded elastin.
Table 2.
Intact and radially-cut unloaded configurations for different percents of elastin degradation. Both the axial retraction and the opening angle decrease with increased elastin degradation. Values of 0% degradation (i.e., normalcy) are similar to measured values for the normal rabbit basilar artery (cf. Wicker et al. 2008 and unpublished results by H. P. Hutchens).
| Intact, unloaded | Radially-cut, unloaded | ||||
|---|---|---|---|---|---|
| Elastin Degradation | ρi(mm) | λ | Ri (mm) | Λ | Φ0 |
| 0% | 1.0768 | 1.3783 | 2.4296 | 1.0095 | 94.45° |
| 30% | 1.0916 | 1.3493 | 2.3613 | 1.0111 | 91,19° |
| 60% | 1.1107 | 1.2879 | 2.2372 | 1.0130 | 85.39° |
| 90% | 1.1403 | 1.1185 | 1.9249 | 1.0118 | 69.15° |
Figure 2.
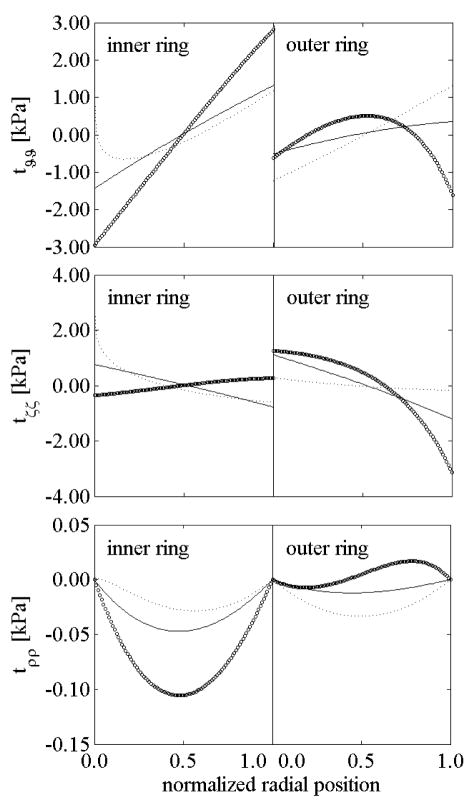
Computed residual stresses in the intact, unloaded configuration β 1 given uniform prestretches for elastin, but different levels of elastin degradation: 0% (solid), 30% (dashed), 60% (dash-dotted), 90% (dotted) and 100% (+). The lower values of overall (mixture) residual stresses in cases of lost of elastin are consistent with lower opening angles (Table 1). In all cases, however, note the overall compressive residual stresses in the inner wall and tensile residual stresses in the outer wall as originally computed by Chuong and Fung (1986). Note that the normalized radial position goes from the intima (0.0) to the adventitia (1.0).
Introducing a radial cut relieved all of the residual stresses regardless of the amount of degraded elastin because the material behavior remained homogeneous (cf. Taber and Humphrey 2001). Nevertheless, because of the different constituent prestretches and assumption of constrained motions, individual constituents remained residually stressed after the radial cut, despite the overall vessel being stress free (cf. Zeller and Skalak 1998). As reported in Table 2, the axial stretch decreased slightly from the intact to the radially-cut configuration as expected (Kang and Humphrey 1991), with greater reductions for higher percentages of elastin degradation.
Uniform versus linear distributions of elastin prestretches through the thickness
Whereas the initial simulations considered uniform “prestretches” for elastin ( , which account for both deposition stretches in development and subsequent stretch during normal growth), we now consider nonuniform distributions. Recall, therefore, that elastin is produced primarily during the late prenatal and early postnatal periods, starting in the inner layer of the wall and moving to successively outer layers, and it is very stable (Davis 1995; Langille 1996). Hence, it is reasonable to assume that elastin deposited earlier (inner layers) experiences higher prestretches in the final in vivo configuration since it “remembers” a smaller original configuration and is stretched more during arterial enlargement. That is, outer layers of elastin are deposited within configurations that are slightly closer to the adult one, thus their prestretches in the final in vivo configuration should be smaller compared to those in the inner layers. We now examine potential consequences of radial gradients in elastin prestretch.
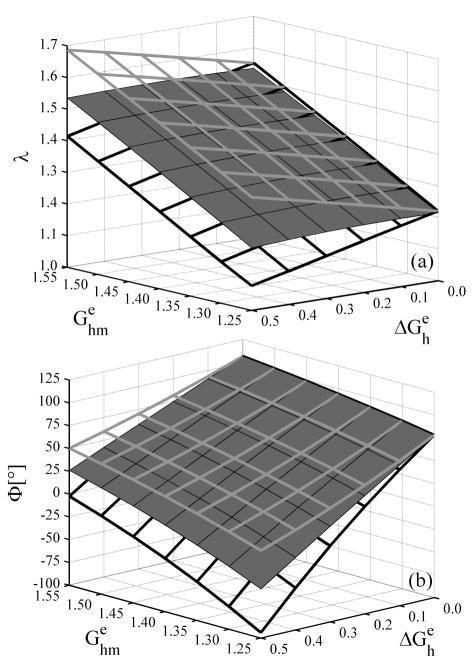
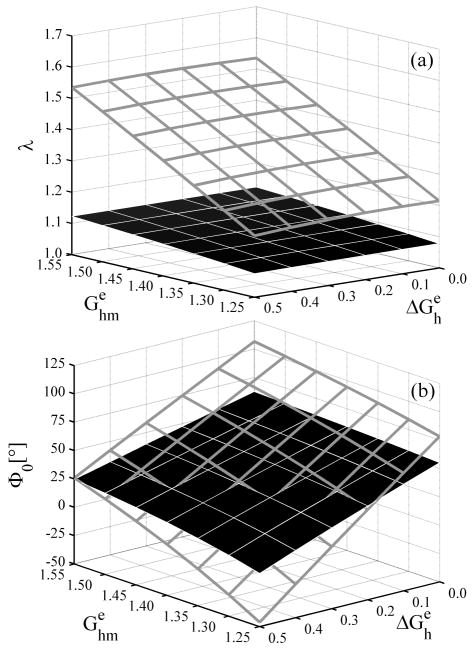
Given this hypothesis, we compared a uniform versus a linear distribution of elastin prestretches for different mean values or for differences between the highest prestretch at the inner wall and the lowest one at the outer wall (i.e., ). Figure 3 shows the predicted overall axial prestretch and opening angle as a function of assumed values for both and for the intact vessel (solid surfaces) as well as for inner (gray frame) and outer (black frame) rings obtained via a circumferential cut at the mid-wall in the in vivo configuration (cf. Vossoughi et al. 1993). As is evident from Figure 3(a), the unloaded length decreased with increases in the mean value of elastin prestretches but was nearly insensitive to transmural differences . Again this result is explained easily by noting that the unloaded length is dictated by an equilibrium between compression of collagen and smooth muscle and tension in the elastin; increasing the mean elastin prestretch shifted the equilibrium towards a greater compression of collagen and muscle and thus towards a shorter unloaded length. Figure 3(a) also shows that the unloaded axial length varied nearly linearly with the mean elastin prestretch within the range of simulated distributions. The unloaded length for the inner and outer rings increased and decreased, respectively, with because the mean elastin prestretch increased in the inner and decreased in the outer ring when the magnitude of the distribution increased.
Figure 3.
(a) Overall axial stretch from the intact, unloaded configuration and (b) opening angle due to a radial cut, each for elastin prestretches distributed linearly through the thickness. Solid surfaces are for the intact vessel whereas gray and black framed surfaces show results for inner and outer rings, respectively.
Figure 3(b) shows that the opening angle depended strongly on both the mean value and the transmural distribution of elastin prestretches, but it was more sensitive to the latter. The change in the opening angle, as noticed for the unloaded length, was also nearly a linear function of both and . For (i.e., a homogeneous material), both the whole vessel and each ring obtained from the circumferential cut opened to the same angle because the unloaded radially-cut, configuration was stress free and the circumferential cut had no further effect. For nonuniform prestretches ( ), however, the inner (outer) ring experienced larger (smaller) opening angles because the mean prestretch was higher (lower) than in the intact vessel; this is consistent with reports by Vossoughi et al. (1993) and Greenwald et al. (1997).
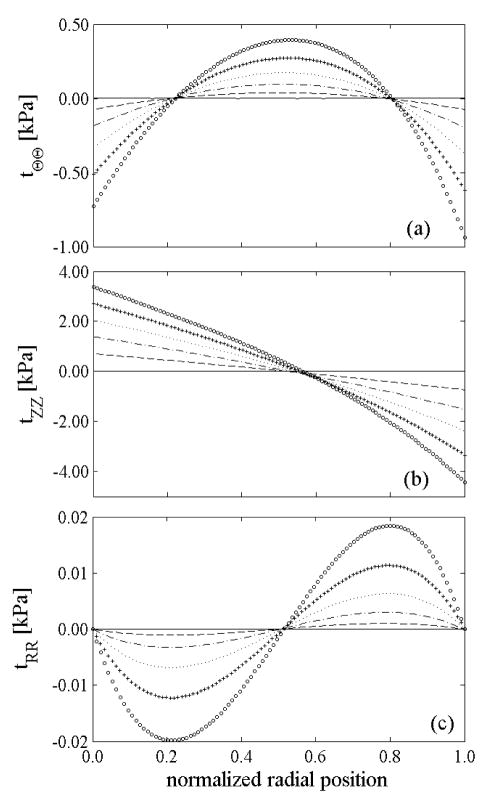
As is evident from Figure 4(a), larger opening angles for a whole vessel having greater mean elastin prestretches can be explained by the increased circumferential residual stress in the intact unloaded configuration, which leads to a larger opening moment – see equation (11c). Figure 4 also shows that increasing the mean elastin prestretches increased the residual stresses in the unloaded configuration, but these residual stresses were not influenced qualitatively by the value of . In contrast, Figure 5 shows that the magnitude of the transmural distribution in prestretch influenced the transmural distribution of the residual stresses qualitatively. Comparison of Figures 4 and 5 shows that variations in influence the residual stresses in the intact unloaded configuration much more than .
Figure 4.
Residual stresses in the intact, unloaded configuration β 1of the whole vessel for uniformly distributed prestretch of elastin: (dashed), (solid), and (dotted).
Figure 5.
Residual stresses in the intact, unloaded configuration β 1of the whole vessel for a fixed mean elastin prestretch , but different linear transmural distribution in prestretches: (solid), (dashed), (dash-dotted), (dotted), (+) and (○).
Consistent with the unloaded configuration depending mainly on the mean prestretch of elastin, not its transmural distribution, increasing led to less compression of inner layers and less tension in outer layers, and thus a strong reduction of the opening angle. For high values of , the opening moment actually changed sign (Figure 5(a)) and the vessel closed on itself after introducing the radial cut (Figure 3(b)). Uniform distributions of prestretches never led to negative opening angles, yet such results have been observed in arteries (Fung 1993).
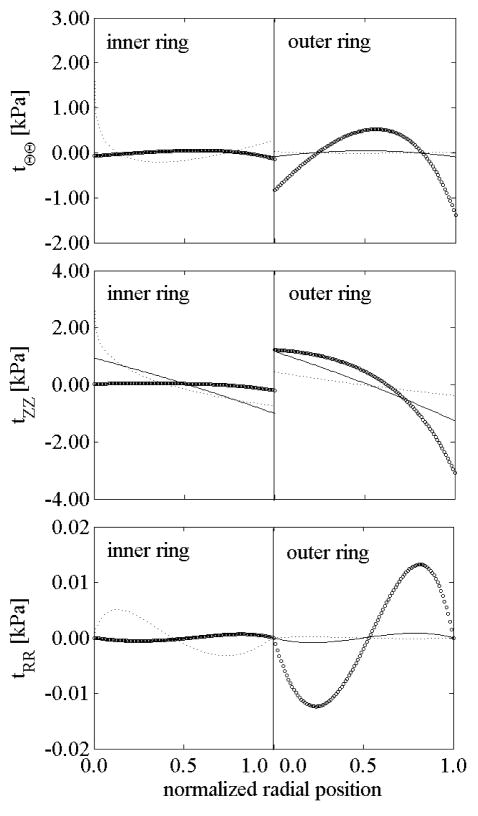
Figure 6 shows that introducing a single radial cut was sufficient to release all residual stresses only if the material was homogeneous, otherwise the vessel was not stress free in the radially-cut, unloaded configuration. Indeed, the residual stresses increased with greater material inhomogeneity (i.e. ): the axial component of the residual stress became higher (and could cause a warping edge effect) and the vessel was under higher radial compression in its inner region.
Figure 6.
Residual stresses in the radially-cut configuration β 2 for fixed mean elastin prestretch but different linear transmural distributions in prestretches: (solid), (dashed), (dash-dotted), (dotted), (+) and (○).
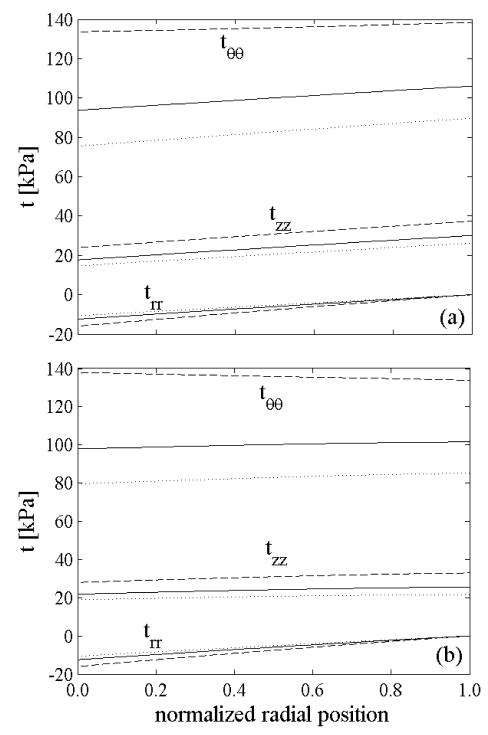
We found that variations in the mean prestretch caused only a slight (few kPa) vertical shift in the circumferential and axial stress in the in vivo configuration (not shown), but increasing led to a more uniform distribution of the stresses through the thickness (Figure 7): the ratio between maximum and average circumferential stress was 1.06 for a uniform distribution of elastin prestretch ( ) but only 1.01 for a nonuniform distribution ( ). For comparison, Chuong and Fung (1986) reported values of 1.42 for a residually stressed artery and 6.5 for a non-residually stressed one. Our simulations showed that all components of stress increased slightly from the intima to the adventitia at a pressure of 93 mmHg and basal smooth muscle tone. This result is similar to reports in Stalhand et al. (2004) and Masson et al. (2008), but not Chuong and Fung (1986) who ignored possible smooth muscle activation.
Figure 7.
Transmural distribution of stresses in the in vivo configuration at diastole (80 mmHg – dotted lines), mean pressure (93 mmHg – solid lines), and systole (120 mmHg dashed lines) at basal smooth muscle tone for: a) uniform distribution of elastin prestretches ( and ), b) nonuniform distribution of elastin prestretches ( and ).
Nonlinear distribution of elastin prestretches through the thickness
The assumption of a linear distribution of elastin prestretches through the wall implies that the “rate of deposition” is somehow synchronized with arterial development. To study different hypotheses for the rate of deposition of elastin, we considered the following distributions of prestretch in the axial and circumferential directions
| (16) |
where K is a parameter governing the “deposition rate”. K>1 models consequences of a higher rate of deposition in early stages of development such that all inner layers experience similar elastin prestretches in maturity (Figure 8). K<1 models a slower rate in early development such that the inner layers experience a strong gradient in elastin prestretch while the outer layers vary less. K=1 recovers the linear distribution. We studied potential consequences of the rate of deposition by fixing the prestretches in the intima ( ) and adventitia ( ) and varying the rate parameter K. A circumferential cut was also introduced at the mid-wall to study the effect of nonuniform distributions of elastin prestretch on the unloaded configuration, opening angle, and residual stresses for inner and the outer rings.
Figure 8.
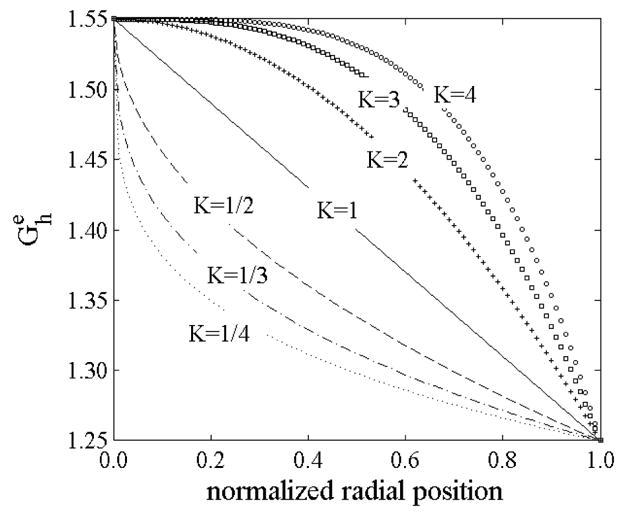
Transmural distributions of elastin prestretches (axial and circumferential) for different “rates of elastin deposition” during development for and as given by equation 16.
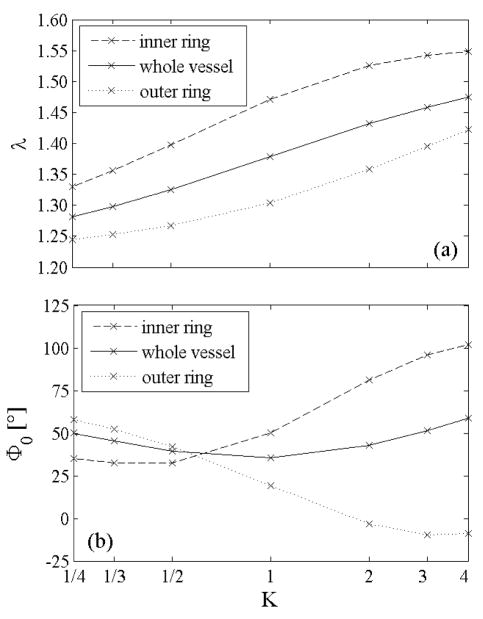
The net unloaded axial stretch and the opening of the two rings obtained from both circumferential and radial cuts are shown in Figure 9 as a function of K. The unloaded length decreased monotonically with K for the whole vessel and both rings. This is consistent with our other findings because increasing K leads to an increased mean prestretch and thus an increased retraction upon unloading. Moreover, the order λin<λ <λ out was preserved regardless of the value of K because the mean elastin prestretch was higher in the inner ring than in the whole vessel and it was higher in the whole vessel than in the outer ring.
Figure 9.
(a) Overall axial stretch and (b) opening angle as function of the “rate of elastin deposition” parameter K. A value of K=1 represents the case of a linear distribution of elastin prestretch.
Figure 9(b) shows that the opening angle for the intact vessel was smallest for K=1 and those for the inner and outer rings differed most when K≥1. For K>1 the inner layers had a high mean elastin prestretch and a low transmural distribution; both of these features led, consistent with the aforementioned observations for linearly distributed prestretches, to larger opening angles compared to the whole vessel. In contrast, the outer layers experienced a large transmural variation of prestretch with radial position, which led to a negative opening angle (such angles have been reported for different arteries; Fung 1993). For K<1 the high level of inhomogeneity within the inner ring overwhelmed the effect of mean elastin prestretch, thus the inner ring opened less than the whole vessel while the small inhomogeneity in the outer layer dominated the effect of the small mean prestretch and its opening angle was larger compared to the whole vessel. The opening angles for both inner and outer rings reinforce the finding, shown in Figure 3, that the distribution of elastin prestretch dominates the effect of the mean value. K≥1 are the most realistic results, predicting higher opening angles for the inner ring compared to the outer ring (cf. Vossoughi et al. 1993). Moreover, considering that most layers of elastin are deposited and cross-linked during early development, the distribution of elastin prestretches given by K≥1 could be the most representative.
Figures 10 and 11 show residual stresses in intact and radially-cut configurations for the two rings following a circumferential cut. The axial stress changed little after the radial cut for both the inner and outer rings (compare Figures 10(b) and 11(b)), and remained the higher component of residual stress in the open configuration, especially for cases of nonlinearly distributed elastin prestretches. The circumferential residual stress in the open configuration remained high in the inner ring for K<1 and in the outer ring for K>1. This is explained by the higher nonlinear behavior being confined to the inner ring for K<1 and to the outer ring for K>1.
Figure 10.
Residual stresses in the intact, unloaded configuration for both inner and outer rings for different values of the “rate of elastin deposition”: K=1 (solid), K=1/4 (dotted), and K=4 (○).
Figure 11.
Residual stresses in the radially-cut, unloaded configuration for both inner and outer rings: K=1 (solid), K=1/4 (dotted) and K=4 (○).
Effect of collagen compressive behavior
In the mechanical framework assumed here, both the unloaded length and the opening angle result from a trade-off between the tensile behavior of elastin, which experiences the highest in vivo prestretches, and the compressive stiffness of collagen and smooth muscle. Since arteries contain fibrillar collagen (type I and III), it is reasonable to assume that the fibers can buckle in compression, thus giving the fibrillar network a lower net compressive than tensile stiffness. The presence of proteoglycans and water in the interstitial spaces may augment to the compressive stiffness of fibrillar collagen, however, much like an Euler column with lateral supports. For these reasons we modeled collagen as bimodular in all previous simulations, assuming that it behaves like smooth muscle in compression (equation (14)).
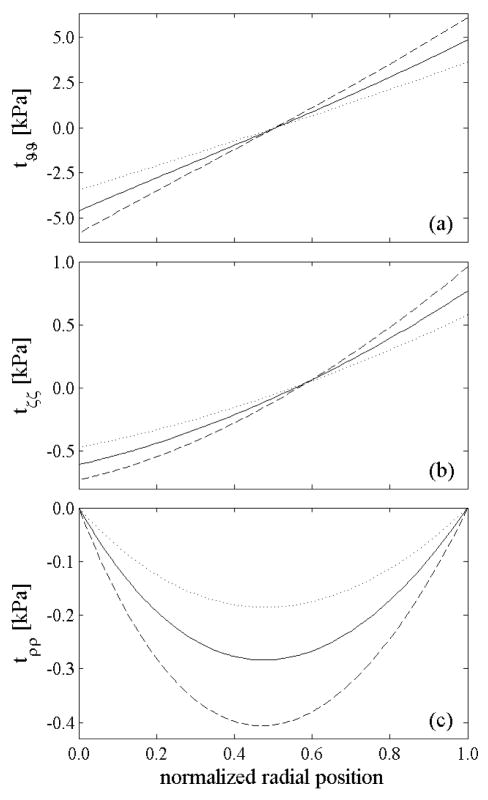
To assess the importance of the compressive behavior of collagen, we repeated the numerical experiments of Figure 3 without assuming a bimodular behavior, thus the collagen fibers were stiffer in compression than in the previous simulations. Figure 12(a) reveals that an increased compressive stiffness of collagen reduced the in vivo axial stretch and drastically reduced its sensitivity to the distribution of elastin prestretch. These results are intuitive because an increased compressive stiffness of collagen would reduce its compression by recoiling elastin, regardless of the magnitude of elastin prestretch. Figure 12(b) shows that, for a similar reason, the sensitivity of the opening angle to the distribution of elastin prestretches also decreased with an increase in collagen compressive stiffness.
Figure 12.
The shaded surfaces represent (a) the axial stretch from the intact, unloaded configuration and (b) the opening angle, each for linearly distributed elastin prestretches through the thickness and non-bimodular behavior of the collagen. Compare with results for bimodular collagen, (framed surfaces here) reported as shaded surfaces in Figure 3. The in vivo axial prestretch and opening angle have the same qualitative behavior in these two cases, but are more sensitive to the distribution of elastin prestretches when the collagen is more compliant in compression (i.e., bimodular).
Pressure-radius behavior
It has long been thought that the pressure-radius behavior, at basal tone, is influenced by elastin at low luminal pressures and primarily by collagen fibers and smooth muscle at physiological pressure (cf Burton 1954). Simulations (not shown) showed that only the mean value of elastin prestretch, not its distribution, had only a slight effect on the pressure-radius response at low pressures.
Brief Summary
Based on results presented thus far, it appears that a nonuniform distribution of elastin prestretch, with and K ≥1, is the most realistic – it yields a nearly uniform stress distribution through the thickness at any pressure during the cardiac cycle (see Figure 7(b)) and it gives a larger opening angle for the inner ring than the outer ring following a circumferential cut (Figure 9(b)). Moreover this type of distribution could find its explanation in the developmental process as discussed earlier. For these reasons we assume , and K=3 (see the curve in Figure 8) with bimodular collagen in the remaining simulations.
Effect of smooth muscle tone
All prior computations for both the intact and the radially-cut unloaded configurations were performed with no smooth muscle tone (i.e., passive). Nevertheless, muscle tone can influence the opening angle because it modifies the distributions of both in vivo and residual stresses. Figure 13 shows that an increased smooth muscle tone increased the opening angle, consistent with data for rat aorta reported by Matsumoto et al. (1996) and Fridez (2000) as well as with simulations in Rachev and Hayashi (1999). Moreover, our simulations showed that the opening angle of the inner (outer) ring is more (less) sensitive to smooth muscle contraction than that for the whole vessel.
Figure 13.
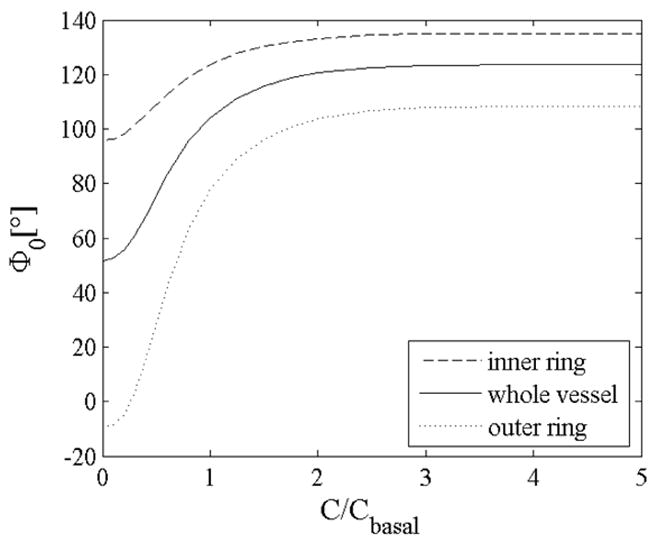
Opening angle as a function of the normalized constrictor concentration for , K=3, and bimodular collagen behavior.
Aging
Feldman and Glagov (1971) reported that transmural gradients of elastin and collagen mass fractions reverse with age in human aorta. In particular, the amount of elastin decreases and that of collagen increases from the intima to the adventitia in young individuals; conversely, in aging the amount of intimal elastin decreases while that of collagen increases and adventitial elastin increases while collagen decreases, all without significantly changing total scleroprotein through the wall (i.e., the sum of elastin plus collagen was reported to be nearly uniform and not a function of age). Later studies on human aortas (Saini et al. 1995) and rat aortas (Badrek-Amoudi et al. 1996) showed further that there is an increase in the opening angle with age.
We simulated effects of the redistribution of collagen and elastin in the wall, as reported in Feldman and Glagov (1971), by assuming the linear distributions depicted in Figure 14 while keeping uniform the total mass fraction of the scleroprotein (ϕe (r)+ ϕc (r)=0.24∀r∈ [ri, ra]). The simulations confirmed that a gradual reversal in the gradients of elastin and collagen (as in aging) causes a monotonic increase in opening angle. Moreover, as evident in Table 3, a transmural redistribution of collagen and elastin overwhelmed the effects of elastin fragmentation that reduced the opening angle (see Table 2). Results in Table 3 also show that differences in opening angle between inner and outer rings decreased with elastin degradation, thus suggesting that the presence of elastin is a key factor in the different opening angles in the two rings obtained by a circumferential cut.
Figure 14.
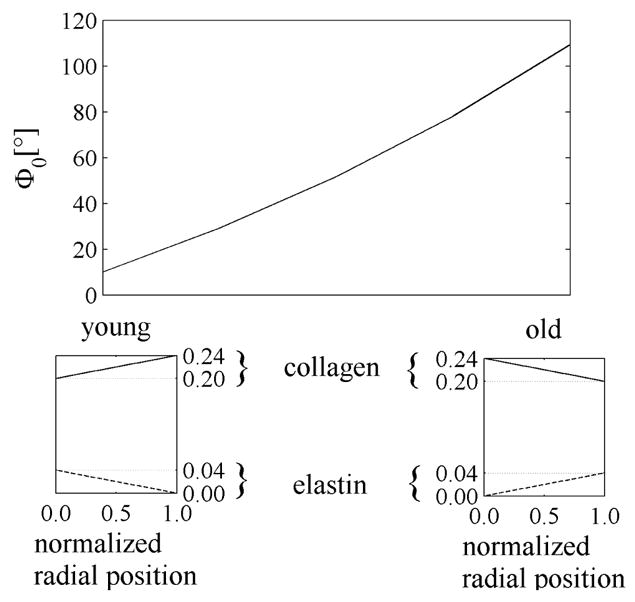
Effect of one aspect of aging on the opening angle with , K=3, and bimodular collagen behavior. Linear distributions of collagen and elastin mass fractions were assumed here in qualitative agreement with Feldman and Glagov (1971). Young: ϕe(ri)=0.04, ϕe(ra) =0, ϕc(ri)=0.2, and ϕc(ra)=0.24. Old: ϕe(ri)=0, ϕe(ra)=0.04, ϕc(r i)=0.24, and ϕc(ra)=0.2.
Table 3.
Comparison of the opening angle between young-type and old-type distributions of constituents (according to Feldman and Glagov, 1971) for different levels of elastin degradation due to aging or other pathologies.
| Φ0vessel | Φ0 inner ring | Φ0outer ring | |
|---|---|---|---|
|
ϕc (ri) =0.20, ϕc (ra) =0.24, ϕe (ri) =0.04, ϕe (ra) =0.00 (i. e., young with 0% elastin degradation) |
10.08° | 45.39° | −38.08° |
|
ϕc (ri) =0.24, ϕc (ra) =0.20, ϕe (ri) =0.00, ϕe (ra) =0.02 (i. e., old with 50% elastin degradation) |
106.07° | 151.89° | 42.41° |
|
ϕc (ri) =0.24, ϕc (ra) =0.20, ϕe (ri) =0.00, ϕe (ra) =0.01 (i. e., old with 75% elastin degradation) |
95.84° | 116.46° | 63.40° |
|
ϕc (ri) =0.24, ϕc (ra) =0.20, ϕe (ri) =0.00, ϕe (ra) =0.00 (i. e., old with 100% elastin degradation) |
62.88° | 62.79° | 62.97° |
DISCUSSION
Elastin and collagen both accumulate within the arterial wall during development, but the rate of elastin synthesis is particularly high during the late prenatal and early postnatal periods and essentially nonexistent thereafter (Gerrity and Cliff 1975, Mathieux and Weiss 2005). Moreover, in contrast with collagen, which has a normal half-life on the order of 70 days (Langille, 1996), elastin is exceptionally stable biologically with a normal half-life of years to decades depending on the species (Davis 1995, Mathieux and Weiss 2005, Arribas et al. 2006). This remarkable stability appears to result from the alternating hydrophobic and lysine-based cross-linking domains of tropoelastin (i.e., the elastin monomer), with ~90% of the possible domains typically cross-linked via the action of lysyl oxidases (Wagenseil and Mecham 2007). Indeed, the unique cross-links within vascular elastin (e. g., desmosine and isodesmosine based) appear to contribute further to the extreme extensibility and elasticity of elastin. Hence, as suggested by Davis (1995), “the [highly stable] elastic laminae stretch as the vessel grows in diameter” from development to maturity, thus resulting in a highly prestretched, materially nonuniform tissue. Of particular importance in this regard, “The elastin fibre keeps its elastic properties up to extensions of about 140%, with an elastic modulus in the range of 0.4 MPa” (Faury, 2001).
In a paper titled “What Are the Residual Stresses Doing in Our Blood Vessels,” Fung (1991) suggested that “an implication of the residual stresses in arteries is to make the stress distribution more uniform in the vessel wall in normal condition.” Not only have subsequent findings supported this conclusion (see Rachev and Greenwald 2003; Holzapfel and Ogden, 2006), predictions of nearly uniform equibiaxial stresses in vivo (cf. Humphrey and Na 2002) suggest the existence of a homeostatic state that arteries achieve during normal development and which they try to maintain via growth and remodeling processes when perturbed from normal. Although Fung suggested that the existence of residual stresses (e.g., revealed by an opening angle) resulted from nonuniform growth and remodeling, he merely concluded that “We would like to find a higher principle from which this hypothesis can be delivered. I believe such higher principle is the stress-growth law”.
Motivated by our prior development of constrained mixture models of stress-mediated vascular growth and remodeling (Humphrey and Rajagopal 2003, Gleason et al. 2004, Baek at al. 2006, Valentin et al. 2008), we adopted a rule of mixtures approach herein to study the origin of residual stress and axial prestress (note: Brankov et al. (1975) proposed the use of rule-of-mixture models for arteries many years ago). The present results support Fung’s suspicion that residual stress results from nonuniform growth and remodeling. Yet, our results further suggest the importance of temporal and spatial differences in the deposition of individual constituents and, hence, differences between the in vivo prestretches of elastic fibers, which are highly elastic and stable, and collagen/smooth muscle, which turnover continually. Because contributions to wall mechanics by elastin are defined early in development, subsequent fragmentation or degradation of elastin as well as changes in collagen mass fraction, orientation, or cross-linking will change the axial prestress and residual stress, even in an artery (e.g., basilar) that has little elastin initially (cf. Briones et al. 2003). In other words, despite the longstanding thought that elastin mainly contributes to arterial mechanics at low (non-physiologic) pressure (cf. Burton 1954), its unique properties highly elastic, biologically stable, and deposition primarily during early development render it fundamental to establishing the in vivo homeostatic state in maturity and thereby playing a vital role in any compensatory adaptation to perturbed mechanical loading.
Numerical results herein support the hypothesis that elastin is cross-linked soon after deposition in development (Davis 1995), hence outer layers of elastin likely experience less circumferential prestretch in maturity than do the inner layers. Results showing up to a 30% reduction in the opening angle Φo with loss of elastin in the basilar artery (Table 2) are also consistent qualitatively with experimental and theoretical results for rat aorta (Greenwald et al. 1997; Alford et al. 2008) and experimental results for rabbit carotid arteries (Fonck et al. 2006), both of which have higher elastin to collagen ratios than basilar arteries. Effects of different constituent prestretches are thus expected to be at least as important in extracranial arteries, indeed likely more so.
For small radial gradients in elastin prestretch, computed residual stresses in the intact unloaded configuration (Figures 4 and 5) were qualitatively comparable to those reported in Chuong and Fung (1986) and many others since (e.g., Taber and Humphrey 2001; Guillou and Ogden 2006), all of whom employed phenomenological constitutive relations. The predicted axial retraction from the intact, unloaded configuration to the radially-cut, unloaded configuration was about 1%, consistent with a reinterpretation of the Chuong and Fung data by Kang and Humphrey (1991). The present results also confirm those in Taber and Humphrey (2001) that the radially-cut, unloaded configuration is completely stress-free only if the material is homogeneous (Figure 6); for non-uniform distributions, the radially-cut configuration was still residually stressed and the rings obtained by the introduction of a circumferential cut manifested different opening angles (Figure 3(b)). Moreover, we showed (Figure 7(b)) that a distribution of elastin prestretches that decreases from the intima to the adventitia helps render the in vivo distribution of stress more uniform through the thickness for all values of physiological pressure during the cardiac cycle, perhaps enhancing the performance of the artery as a load-bearing thick-walled structure as well as its mechanobiological responses (cf. Fung 1983, Rachev and Greenwald 2003).
Because the rate of elastin deposition is higher during development, distributions of elastin prestretch obtained from equation (16) for K≥1 are likely more realistic than those obtained for K<1 (see Figure 8); when K≥1, the opening angle of the inner ring is greater than the opening angle of the whole vessel, which in turn is higher than the one for the outer ring in agreement with prior results (e.g., Vossoughi et al. 1993, Greenwald et al. 1997, Stergiopulos et al. 2001).
Although the compressive behavior of the arterial wall is critical to all discussions of residual stress (which must self-equilibrate and thereby exhibit both compressive and tensile stresses), there has been surprisingly little attention to this aspect of the mechanics. Chuong and Fung (1984) studied the compressive behavior in the radial direction, but there are no data on circumferential or axial behaviors. Our consideration of the behavior of individual constituents further emphasizes the need for information on the compressive behavior of smooth muscle and collagen fibers in particular. Because these constituents are embedded in a “ground substance” matrix, which is known to contribute significantly to compressive behavior, it is not surprising that Azeloglu et al. (2008) found that transmural distributions of proteoglycans are also important regulators of residual stress. Consistent with this finding, our results suggest that the compressive mechanical behavior of proteoglycan-supported collagen plays a particularly important role in determining the unloaded length of the artery: the in vivo axial prestretch λ decreased and became dramatically less sensitive to the transmural distribution of elastin prestretch when the collagen was stiffer in compression (Figure 12(a)). Moreover, the sensitivity of the opening angle to the distribution of elastin prestretches decreased with increases in the compressive stiffness of collagen (Figure 12(b)). When muscle activity was included in the unloaded, radially-cut configuration, the model predicted changes with increases of constrictor concentration in qualitative agreement with results reported in Matsumoto et al. (1996) and Fridez (2000). Finally, the simulations showed that a gradual, age-related reversal of radial gradients in elastin and collagen (Feldman and Glagov 1971) could explain, in part, the observed increases in opening angle with age found by Saini et al. (1995) and Badrek-Amoudi et al. (1996) in human and rat aortas, respectively. Aging is, of course, a very complex process, involving among other things fragmentation and calcification of elastin and changes in collagen cross-linking. There is, therefore, a pressing need to understand better the contributions of the many constituents within the arterial wall, and how they change over time, that affect axial prestress and residual stress and thereby the overall homeostatic state of stress.
Whereas Fung (1991) focused on the question “What are the residual stresses doing in our blood vessels?” and appropriately answered that they tend to homogenize the transmural distribution of stress, we focused more on the question “How do residual stresses arise in arteries?” Based on the present results, we submit that axial prestresses and residual stresses arise in arteries largely due to the deposition of remarkably stable, highly elastic, elastin during development and the continual turnover of collagen and smooth muscle at consistent, preferred stretches within an important ground substance matrix. That is, residual stresses arise due to the different natural configurations of individual constituents (Humphrey and Rajagopal 2002), and they can be influenced greatly by transmural gradients therein as well as changes in the relative mass fractions and degrees of cross-linking. There is obviously a need to account for other complexities, including differences in medial and adventitial composition (Holzapfel et al. 2007) as well as the effects of specific microfibrils (e.g., fibrillins and fibulins) within the elastic fibers, the different types of collagens (e.g., I versus III), and the different proteoglycans (e.g., bigylcan versus decorin). Nevertheless, our results, based on a simple constrained mixture model, qualitatively recover most of the accepted observations in the literature and thereby provide further motivation to formulate mixture models of arterial growth and remodeling in diverse cases important to studies of clinical and basic science. Moreover, because residual stresses arise naturally using this constrained mixture model, such constitutive relations promise to simplify the inclusion of residual stresses, and their changes with disease, within finite element models of complex arterial geometries without needing to define evolving opened-up configurations at each axial position (cf. Delfino et al. 1997; Alastrue et al. 2007), the residual stress field itself (van Dyke and Hoger 2002), or the existence of a homeostatic in vivo stress (Zhou and Lu 2008) that need not be maintained during growth and remodeling (Valentin et al. 2008). There is, therefore, great promise, but also considerable need, to develop finite element based 3-D constrained mixture models of the arterial wall in health and disease.
Acknowledgments
This work was supported, in part, by NIH grants HL-64372, HL-80415, and HL-86418.
Footnotes
This work is dedicated to Prof. Dr. Y.C. Fung in celebration of his 90th birthday.
One can think of a tensed guitar string as prestressed and an isolated inverted rubber tube as residually stressed.
References
- Alastrue V, Pena E, Martinez MA, Doblare M. Assessing the use of the “opening angle method” to enforce residual stresses in patient-specific arteries. Annl Biomed Engr. 2007;35:1821–1837. doi: 10.1007/s10439-007-9352-4. [DOI] [PubMed] [Google Scholar]
- Alford PW, Humphrey JD, Taber LA. Growth and remodeling in a thick-walled artery model: effects of spatial variations in wall constituents. Biomech Model Mechanobiol. 2008;7:245–262. doi: 10.1007/s10237-007-0101-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arribas SM, Hinek A, Gonzalez MC. Elastic fibres and vascular structure in hypertension. Pharmacol Therapeu. 2006;111:771–791. doi: 10.1016/j.pharmthera.2005.12.003. [DOI] [PubMed] [Google Scholar]
- Azeloglu EU, Albro MB, Thimmappa VA, Ateshian GA, Costa KD. Heterogeneous transmural proteoglycan distribution provides a mechanism for regulating residual stresses in the aorta. Am J Physiol. 2008;294:H1197–1205. doi: 10.1152/ajpheart.01027.2007. [DOI] [PubMed] [Google Scholar]
- Badrek-Amoudi A, Patel CK, Kane TPC, Greenwald SE. The effect of age on residual strain in the rat aorta. J Biomech Engr. 1996;118:189–192. doi: 10.1115/1.2796029. [DOI] [PubMed] [Google Scholar]
- Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurism. J Biomech Engr. 2006;128:142–149. doi: 10.1115/1.2132374. [DOI] [PubMed] [Google Scholar]
- Bergel DH. PhD Thesis. University of London; UK: 1960. The visco-elastic properties of the arterial wall. [Google Scholar]
- Brankov G, Rachev A, Stoychev S. Mechanics of Biological Solids. Bulgaria: 1975. A composite model of large blood vessels; pp. 71–78. [Google Scholar]
- Briones AM, Gonzalez JM, Somoza B, Giraldo J, Daly CJ, Vila E, Gonzalez MC, McGrath JC, Arribas SM. Role of elastin in spontaneously hypertensive rat small mesenteric artery remodeling. J Physiol. 2003;552:185–195. doi: 10.1113/jphysiol.2003.046904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burton AC. Relation of structure to function of the tissues of the wall of blood vessels. Physiol Rev. 1954;34:619–642. doi: 10.1152/physrev.1954.34.4.619. [DOI] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC. Compressibility and constitutive equation of arterial wall in radial compression experiments. J Biomech. 1984;17:35–40. doi: 10.1016/0021-9290(84)90077-0. [DOI] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC. On residual stress in artery. J Biomech Engr. 1986;108:189–192. doi: 10.1115/1.3138600. [DOI] [PubMed] [Google Scholar]
- Cox RH. Anisotropic properties of the canine carotid artery in vitro. J Biomech. 1975;8:293–300. doi: 10.1016/0021-9290(75)90081-0. [DOI] [PubMed] [Google Scholar]
- Davis EC. Elastic lamina growth in the developing mouse aorta. J Histochem Cytochem. 1995;43:1115–1123. doi: 10.1177/43.11.7560894. [DOI] [PubMed] [Google Scholar]
- Delfino 1997
- Dobrin PB, Canfield T, Sinha S. Development of longitudinal retraction of carotid arteries in neonatal dogs. Experientia. 1975;31:1295–1296. doi: 10.1007/BF01945788. [DOI] [PubMed] [Google Scholar]
- Dobrin PB, Schwarcz TH, Mrkvicka R. Longitudinal retractive force in pressurized dog and human arteries. J Surg Res. 1990;48:116–120. doi: 10.1016/0022-4804(90)90202-d. [DOI] [PubMed] [Google Scholar]
- Dorrington KL, McCrum NG. Elastin as rubber. Biopolymers. 1977;16:1201–1222. doi: 10.1002/bip.1977.360160604. [DOI] [PubMed] [Google Scholar]
- Faury G. Function-structure relationship of elastic arteries in evolution: from microfibrils to elastin and elastic fibres. Pathol Biol. 2001;49:310–325. doi: 10.1016/s0369-8114(01)00147-x. [DOI] [PubMed] [Google Scholar]
- Feldman SA, Glagov S. Transmural collagen and elastin in human aortas: reversal with age. Atherosclerosis. 1971;13:385–394. doi: 10.1016/0021-9150(71)90081-5. [DOI] [PubMed] [Google Scholar]
- Fonck E, Prod’hom G, Roy S, Augsburger L, Rufenacht AD, Stergiopulos N. Effect of elastin degradation on carotid wall mechanics as assessed by a constituent-based biomechanical model. Am J Physiol. 2006;292:H2754–2763. doi: 10.1152/ajpheart.01108.2006. [DOI] [PubMed] [Google Scholar]
- Fridez P. PhD. Swiss Federal Institute of Technology; 2000. The role of vascular smooth muscle in biomechanical adaptation of the arterial wall to induced hypertension. [Google Scholar]
- Fung YC. What principle governs the stress distribution in Living organism? In: Fung YC, Fukada E, Wang JJ, editors. Biomechanics in China, Japan and USA. Science Press; Beijing: 1983. pp. 1–13. [Google Scholar]
- Fung YC. What are residual stresses doing in our blood vessels? Annl Biomed Engr. 1991;19:237–249. doi: 10.1007/BF02584301. [DOI] [PubMed] [Google Scholar]
- Fung YC. Biomechanics: Motion, Flow, Stress, and Growth. Springer-Verlag; NY: 1993. [Google Scholar]
- Gerrity RG, Cliff WJ. The aortic tunica media of the developing rat. I. Quantitative stereological and biochemical analysis. Lab Invest. 1975;32:585–600. [PubMed] [Google Scholar]
- Gleason RL, Taber LA, Humphrey JD. A 2-D model of flow-induced alterations in the geometry, structure, and properties of carotid arteries. J Biomech Engr. 2004;126:371–381. doi: 10.1115/1.1762899. [DOI] [PubMed] [Google Scholar]
- Greenwald SE, Moore JE, Rachev A, Kane TPC, Meister J-J. Experimental investigation of the distribution of residual strains in the artery wall. J Biomech Engr. 1997;119:438–444. doi: 10.1115/1.2798291. [DOI] [PubMed] [Google Scholar]
- Guillou A, Ogden RW. Growth of soft biological tissue and residual stress development. In: Holzapfel GA, Ogden RW, editors. Mechanics of Biological Tissue. Springer; Berlin: 2006. [Google Scholar]
- Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast. 2000;61:1–48. [Google Scholar]
- Holzapfel GA, Ogden RW. Mechanics of Biological Tissues. Springer; Berlin: 2006. [Google Scholar]
- Holzapfel GA, Sommer G, Auer M, Regitnig P, Ogden RW. Layer-specific residual deformations of human aortas with non-atherosclerotic intimal thickening. Ann Biomed Engr. 2007;35:530–545. doi: 10.1007/s10439-006-9252-z. [DOI] [PubMed] [Google Scholar]
- Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues and Organs. Springer-Verlag; NY: 2002. [Google Scholar]
- Humphrey JD, Na S. Elastodynamics and Arterial Wall Stress. Ann Biomed Engr. 2002;30:509–523. doi: 10.1114/1.1467676. [DOI] [PubMed] [Google Scholar]
- Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Math Model Meth Appl Sc. 2002;12:407–430. doi: 10.1002/zamm.201700302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey JD, Rajagopal KR. A constrained mixture model for arterial adaptations to a sustained step change in blood flow. Biomech Model Mechanobiol. 2003;2:109–126. doi: 10.1007/s10237-003-0033-4. [DOI] [PubMed] [Google Scholar]
- Kang T, Humphrey JD. Finite deformation of an inverted artery. In: Vanderby R, editor. 1991 ASME Advances in Bioengineering. New York: 1991. [Google Scholar]
- Langille BL. Arterial remodeling: relation to hemodynamics. Can J Physiol Pharmacol. 1996;74:834–841. [PubMed] [Google Scholar]
- Masson I, Boutouyrie P, Laurent S, Humphrey JD, Zidi M. Characterization of arterial wall mechanical behavior and stress from human clinical data. J Biomech. 2008;41:2618–2627. doi: 10.1016/j.jbiomech.2008.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto T, Tsuchida M, Sato M. Change in intramural strain distribution in rat aorta due to smooth muscle contraction and relaxation. Am J Physiol. 1996;271:H1711–1716. doi: 10.1152/ajpheart.1996.271.4.H1711. [DOI] [PubMed] [Google Scholar]
- Mithieux SM, Weiss AS. Elastin. Adv Protein Chem. 2005;70:437–461. doi: 10.1016/S0065-3233(05)70013-9. [DOI] [PubMed] [Google Scholar]
- Nevo E, Lanir Y. Strucutural finite deformation model of the left ventricle during diastole and systole. J Biomech Engr. 1989;111:342–349. doi: 10.1115/1.3168389. [DOI] [PubMed] [Google Scholar]
- Patel DJ, Fry DL. Longitudinal tethering of arteries in dogs. Circ Res. 1966;19:1011–1021. doi: 10.1161/01.res.19.6.1011. [DOI] [PubMed] [Google Scholar]
- Rachev A, Greenwald SE. Residual strains in conduit arteries. J Biomech. 2003;36:661–670. doi: 10.1016/s0021-9290(02)00444-x. [DOI] [PubMed] [Google Scholar]
- Rachev A, Hayashi K. Theoretical study of the effects of vascular smooth muscle contraction on strain and stress distributions in arteries. Annl Biomed Engr. 1999;27:459–468. doi: 10.1114/1.191. [DOI] [PubMed] [Google Scholar]
- Saini A, Berry CL, Greenwald SE. The effect of age and sex on residual stress in the aorta. J Vasc Res. 1995;32:398–405. doi: 10.1159/000159115. [DOI] [PubMed] [Google Scholar]
- Stalhand J, Klarbrang A, Karlsson M. Towards in vivo aorta material identification and stress estimation. Biomech Model Mechanobiol. 2004;2:169–186. doi: 10.1007/s10237-003-0038-z. [DOI] [PubMed] [Google Scholar]
- Stergiopulos N, Vulliemoz S, Rachev A, Meister JJ, Greenwald SE. Assessing the homogeneity of the elastic properties and composition of the pig aortic media. J Vasc Res. 2001;38:237–246. doi: 10.1159/000051052. [DOI] [PubMed] [Google Scholar]
- Taber LA, Humphrey JD. Stress-modulated growth, residual stress, and vascular heterogeneity. J Biomech Engr. 2001;123:528–535. doi: 10.1115/1.1412451. [DOI] [PubMed] [Google Scholar]
- Tickner EG, Sacks AH. A theory for the static elastic behavior of blood vessels. Biorheology. 1967;4:151–168. doi: 10.3233/bir-1967-4402. [DOI] [PubMed] [Google Scholar]
- Tomasek JJ, Gabbiani G, Hinz B, Chaponnier C, Brown RA. Myofibroblasts and mechano-regulation of connective tissue remodeling. Nature Rev. 2002;3:349–363. doi: 10.1038/nrm809. [DOI] [PubMed] [Google Scholar]
- Vaishnav RN, Vossoughi J. Estimation of residual strain in aortic segment. In: Hall CW, editor. Biomedical Engineering II, Recent developments. Pergamon Press; NY: 1983. pp. 330–333. [Google Scholar]
- Valentín A, Cardamone L, Baek S, Humphrey JD. Complementary vasoactivity and matrix remodeling in arterial adaptations to altered flow and pressure. J Roy Soc Interface. 2008 doi: 10.1098/rsif.2008.0254. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dyke TJ, Hoger A. A new method for predicting the opening angle for soft tissues. J Biomech Engr. 2002;124:347–354. doi: 10.1115/1.1487881. [DOI] [PubMed] [Google Scholar]
- Van Loon P, Klip W, Bradley EL. Length-force and volume-pressure relationships in arteries. Biorheology. 1977;14:181–201. [PubMed] [Google Scholar]
- Vossoughi J, Hedjazi H, Borris FSI. Intimal residual stress and strain in large arteries. ASME Bioengineering Conference; New York: ASME; 1993. pp. 434–437. [Google Scholar]
- Wagenseil JE, Mecham RP. New insights into elastic fiber assembly. Birth Defects Res. 2007;81:229–240. doi: 10.1002/bdrc.20111. [DOI] [PubMed] [Google Scholar]
- Wicker BK, Hutchens HP, Wu Q, Yeh AT, Humphrey JD. Normal basilar artery structure and biaxial mechanical behavior. Comp Meth Biomech Biomed Engr. 2008 doi: 10.1080/10255840801949793. in press. [DOI] [PubMed] [Google Scholar]
- Zeller PJ, Skalak TC. Contribution of individual structural components in determining the zero-stress state in small arteries. J Vasc Res. 1998;35:8–17. doi: 10.1159/000025560. [DOI] [PubMed] [Google Scholar]
- Zhou X, Lu J. Estimation of vascular open configuration using finite element inverse elastostatic method. Engr Comp. 2008 ePub ahead of press. [Google Scholar]