Inference for Nonregular Parameters in Optimal Dynamic Treatment Regimes

Abstract

A dynamic treatment regime is a set of decision rules, one per stage, each taking a patient’s treatment and covariate history as input, and outputting a recommended treatment. In the estimation of the optimal dynamic treatment regime from longitudinal data, the treatment effect parameters at any stage prior to the last can be nonregular under certain distributions of the data. This results in biased estimates and invalid confidence intervals for the treatment effect parameters. In this paper, we discuss both the problem of nonregularity, and available estimation methods. We provide an extensive simulation study to compare the estimators in terms of their ability to lead to valid confidence intervals under a variety of nonregular scenarios. Analysis of a data set from a smoking cessation trial is provided as an illustration.

1 Introduction

Many diseases such as mental illness, HIV infection, and substance abuse are clinically treated in multiple stages, adapting the treatment type and dosage to the ongoing measures of an individual patient’s response, adherence, burden, side effects, and preference. Dynamic treatment regimes represent one way to operationalize this sequential decision making. A dynamic treatment regime (DTR) is a sequence of decision rules, one per stage. Each decision rule takes a patient’s treatment and covariate history as input, and outputs a recommended treatment. The main motivations for considering sequences of treatments are high variability across patients in response to any one type of treatment, likely relapse, presence or emergence of co-morbidities, time-varying side effect severity, and reduction of costs and burden when intensive treatment is unnecessary¹.

A DTR is said to be optimal if it optimizes the mean outcome at the end of the final stage of treatment. Data for estimating the optimal DTR can come from either an observational longitudinal study or a sequential multiple assignment randomized trial (SMART)^2–5. In these designs, each patient is followed through stages of treatment and at each stage the patient is randomized to one of the possible treatment options. Experimental designs similar to SMART have been implemented in the treatments of schizophrenia⁶, depression⁷, and cancer^8,9.

Estimating the optimal DTR is a problem of sequential, multi-stage decision making. Murphy¹⁰ developed a semiparametric method for estimating the optimal DTR, an efficient version of which was provided by Robins¹¹. A nice discussion about the relationship between these two methods can be found in Moodie et al.¹². Other methods for estimating optimal DTRs in the literature include likelihood-based methods, both frequentist and Bayesian, developed by Thall and colleagues^8,13,14, and the semiparametric methods of Lunceford et al.¹⁵, and Wahed and Tsiatis^9,16.

Robins¹¹ considered the problem of inference for the parameters of the optimal DTR. As discussed by Robins, the treatment effect parameters at any stage prior to the last can be nonregular under certain longitudinal distributions of the data which he called exceptional laws. By nonregularity, we mean that the asymptotic distribution of the estimator of the treatment effect parameter does not converge uniformly over the parameter space (see section 2.4 for further details). This technical phenomenon of nonregularity has considerable practical consequences; it often causes bias in estimation, and leads to poor frequentist properties of the confidence intervals. Recently Moodie and Richardson¹⁷ provided a method called Zeroing Instead of Plugging In (ZIPI) for correcting the bias in the estimation of the optimal DTRs resulting under exceptional laws.

The main goals of this paper are to illustrate the problem of nonregularity, and to compare available estimation methods that attempt to address this problem. In section 2, we discuss the problem of nonregularity in detail. Section 3 provides a description of different methods that address the problem. We provide an extensive simulation study in section 4 to compare the estimators in terms of their ability to lead to valid confidence intervals using bootstrap. This is followed by an analysis of a data set from a longitudinal smoking cessation trial in section 5; the purpose is to demonstrate the applicability of the estimation methods in a real-life nonregular scenario. Finally an overall discussion is provided in section 6. Throughout this article, we assume that the data come from SMART designs. The main reason for this is to separate the issue of nonregularity from causal inference issues. However the problem of nonregularity also arises when observational data^11,17 are used; and the estimators proposed in section 3 should be applicable to observational data as well.

2 Estimation and Inference via Q-learning

2.1 Notation and Data Structure

For simplicity, we focus on studies with two stages. Longitudinal data on a single patient are given by the trajectory (O₁, A₁, O₂, A₂, O₃), where O_j (j = 1, 2) denotes the covariates measured prior to treatment at the beginning of the j-th stage, O₃ is the observation at the end of stage 2, and A_j (j = 1, 2) is the treatment assigned at the j-th stage subsequent to observing O_j. The data set consists of a random sample of n patients. Define the history at each stage as: H₁ = O₁, H₂ = (O₁, A₁, O₂). We consider a SMART design in which there are two possible treatments at each stage, A_j ∈ {−1, 1}; here we assume $P[A_j=-1\mid H_j]=P[A_j=1\mid H_j]=\frac{1}{2}$. The study can have either a single primary outcome Y observed at the end of stage 2, or two outcomes Y₁, Y₂ observed at the two stages. Note that the case of a single outcome Y observed at the end can be viewed as a case with Y₁ ≡ 0 and Y₂ = Y. We assume Y₁ = f₁(O₁, A₁, O₂) and Y₂ = f₂(O₁, A₁, O₂, A₂, O₃), with known functions f₁, f₂. A two-stage DTR consists of two decision rules, say (d₁, d₂), with d_j(H_j) ∈ _j, where _j is the set of possible treatments at the j-th stage.

One simple method to construct (d₁, d₂) is Q-learning^18–20. Q-learning, like Robins’ g-estimation of optimal structural nested mean models (hereafter simply referred to as Robins’ method), suffers from nonregularity – the common reason being an underlying non-smooth maximization operation. Here we will illustrate the problem due to nonregularity using Q-learning, since it can be viewed as a generalization of the least squares regression to multistage decision problems, and hence simpler to explain than Robins’ semiparametric efficient method. In Lemma 1 below, we provide conditions under which Q-learning is equivalent to an inefficient version of Robins’ method.

2.2 Q-learning with Linear Models

First let us define the Q-functions^19,20 for the two stages as follows:

$$\begin{array}{l}{Q}_2(H_2,A_2)=E\left[Y_2\mid H_2,A_2\right],\\ Q_1(H_1,A_1)=E[Y_1+\underset{a_2}{max}{Q}_2(H_2,a_2)\mid H_1,A_1].\end{array}$$

If the two Q-functions were known, the optimal DTR (d₁, d₂), using backwards induction (as in dynamic programming) argument, would be

$$d_j(h_j)=arg\underset{a_j}{max}{Q}_j(h_j,a_j),j=1,2.$$ (1)

In practice, the true Q-functions are not known and hence must be estimated from the data. Consider a linear model for the Q-functions. Let the stage-j (j = 1, 2) Q-function be modeled as

$$Q_j(H_j,A_j;{\beta }_j,{\psi }_j)={\beta }_j^T{H}_{j0}+({\psi }_j^T{H}_{j1})A_j,$$ (2)

where H_j0 and H_j1 are two (possibly different) summaries of the history H_j, with H_j0 denoting the “main effect of history” and H_j1 denoting the part of history that interacts with treatment (H_j0 and H_j1 include the intercept term). The Q-learning algorithm is:

1. Stage-2 regression: $({\widehat{\beta }}_2,{\widehat{\psi }}_2)=arg{min}_{{\beta }_2,{\psi }_2}\frac{1}{n}{\sum }_{i=1}^n{\left(Y_{2i}-Q_2(H_{2i},A_{2i};{\beta }_2,{\psi }_2)\right)}^2$.

2. Stage-2 optimal rule: d̂₂(h₂) = arg max_a2 Q₂(h₂, a₂; β̂₂,ψ̂₂).

3. Stage-1 pseudo-outcome: Ŷ_1i = Y_1i + max_a2 Q₂(H_2i, a₂; β̂₂,ψ̂₂), i = 1,…,n.

4. Stage-1 regression: $({\widehat{\beta }}_1,{\widehat{\psi }}_1)=arg{min}_{{\beta }_1,{\psi }_1}\frac{1}{n}{\sum }_{i=1}^n{\left({\widehat{Y}}_{1i}-Q_1(H_{1i},A_{1i};{\beta }_1,{\psi }_1)\right)}^2$.

5. Stage-1 optimal rule: d̂₁(h₁) = arg max_a1 Q₁(h₁, a₁; β̂₁,ψ̂₁).

The estimated optimal DTR using Q-learning is given by (d̂₁, d̂₂).

The following lemma gives a set of sufficient conditions under which Q-learning is equivalent to an inefficient version of Robins’ method.

Lemma 1

Consider linear models for the Q-functions as in (2). Assume that:

1. the parameters in Q₁ and Q₂ are distinct;

2. A_j has zero conditional mean given the history H_j, j = 1, 2; and

3. the covariates used in the model for Q₁ are nested within the covariates used in the model for Q₂, i.e., $(H_{10}^T,H_{11}^T{A}_1)\subset H_{20}^T$.

Then Q-learning is algebraically equivalent to an inefficient version of Robins’ method.

The proof is given in Appendix A.

2.3 The Inference Problem

With (2) as the model for Q-functions, the optimal DTR is given by

$$d_j(H_j)=arg\underset{a_j}{max}({\psi }_j^T{H}_{j1})a_j=\mathit{sign}({\psi }_j^T{H}_{j1}),j=1,2,$$ (3)

where sign(x) = 1 if x > 0, and −1 otherwise. Note that the term ${\beta }_j^T{H}_{j0}$ on the right side of (2) does not feature in the optimal DTR. Thus for estimating optimal DTRs, the ψ_j’s are the parameters of interest, while β_j’s are nuisance parameters. We want to perform inference (e.g., construct confidence intervals) on ψ_j’s.

Conducting inference on ψ_j’s is important due to the following reasons. First, if the confidence intervals (or hypothesis tests) for ψ_j reveal that there is no evidence that some components of the vector ψ_j are different from zero, then the corresponding components of the history vector H_j1 need not be collected to make decisions using the optimal DTR. This reduces the cost of data collection in a future implementation of the optimal DTR. Thus in the present context, confidence intervals (or hypothesis tests) can be viewed as a tool for doing variable selection. Second, it is important to know when there is insufficient support in the data to recommend one treatment over another, since in such cases treatment can be chosen according to other considerations like cost, familiarity, burden, preference etc. Third, as discussed by Robins¹¹, confidence intervals for ψ_j can lead to confidence intervals for d_j. In the following, we discuss the problem of nonregularity in inference.

2.4 Nonregularity in Inference

Note that the stage-1 pseudo-outcome (in the Q-learning algorithm) is

$${\widehat{Y}}_{1i}=Y_{1i}+\underset{a_2}{max}{Q}_2(H_{2i},a_2;{\widehat{\beta }}_2,{\widehat{\psi }}_2)=Y_{1i}+{\widehat{\beta }}_2^T{H}_{20,i}+\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid ,i=1,\dots ,n,$$ (4)

which is a non-smooth (e.g., non-differentiable at ${\widehat{\psi }}_2^T{H}_{21,i}=0$) function of ψ̂₂, because of the maximization operation. Since ψ̂₁ is a function of Ŷ_1i, i = 1,…,n, it is in turn a non-smooth function of ψ̂₂. As a consequence, the asymptotic distribution of $\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$ does not converge uniformly¹¹ over the parameter space of ψ = (ψ₁, ψ₂). More specifically, the asymptotic distribution of $\sqrt{n}({\widehat{\psi }}_1-{\psi }_1)$ is normal if ψ₂ is such that $P[H_2:{\psi }_2^T{H}_{21}=0]=0$, but is non-normal if $P[H_2:{\psi }_2^T{H}_{21}=0]>0$. This change in the asymptotic distribution happens abruptly. The (vector) parameter ψ₁ is called a nonregular parameter and the estimator ψ̂₁ is called a nonregular estimator; see Bickel et al.²¹ for the precise definition of nonregularity. Because of this nonregularity, given the noise level present in small samples, the estimator ψ̂₁ oscillates between the two asymptotic distributions across samples. As a result, usual Wald type confidence intervals perform poorly^11,17.

The issue of nonregularity can be better understood with a toy example discussed by Robins¹¹ (here is a slightly modified version). Consider the problem of estimating |μ| based on n i.i.d. observations X₁,…,X_n from N(μ, 1). Note that |X̄_n|is the maximum likelihood estimator of |μ|, where X̄_n is the sample average. It can be shown that the asymptotic distribution of $\sqrt{n}(\mid {\overline{X}}_n\mid -\mid \mu \mid )$ for μ = 0 is different from that for μ ≠ 0. Thus |X̄_n|is a nonregular estimator of |μ|. Also, for μ = 0, ${lim}_{n\to \infty }E[\sqrt{n}(\mid {\overline{X}}_n\mid -\mid \mu \mid )]=\sqrt{\frac{2}{\pi }}$. Robins referred to this quantity as the asymptotic bias of the estimator |X̄_n|. This asymptotic bias is one symptom of the underlying nonregularity, as discussed by Moodie and Richardson¹⁷.

In many situations where the asymptotic distribution of an estimator is unavailable, bootstrap is used as an alternative approach to conduct inference. But the success of bootstrap also hinges on the underlying smoothness of the estimator. When an estimator is nonsmooth, the ordinary (n out of n) bootstrap procedure produces an inconsistent bootstrap estimator²². Inconsistency of bootstrap in the above simple normal theory example has been discussed by Andrews²³. As shown by Shao²², an alternative resampling procedure called “m out of n bootstrap” is consistent in such nonsmooth scenarios. One concern regarding the use of this procedure is the slower rate of convergence than $\sqrt{n}$ even in a regular setting (e.g., when $P[H_2:{\psi }_2^T{H}_{21}=0]=0$). Moreover, a data-adaptive choice of the tuning parameter m in the present context of DTRs is not obvious; see however Bickel and Sakov²⁴ and Hall et al.²⁵ for data-adaptive choice of m in other contexts.

The above concerns regarding nonregularity led us to investigate possible regularizations of the estimation procedure, and then use bootstrap for inference. In the simulation study to follow, we will investigate the behavior of different types of bootstrap confidence intervals for the parameters ψ_j of the optimal DTR in both regular and nonregular settings.

3 Different Regularized Estimators

In this section, we will present two competing estimators to address the non-regularity problem described above. Limited theoretical results are available at this point, and consequently it is not clear which estimator is better. In this paper, we will study their relative merits and demerits in simulations.

From the discussion on nonregularity above, it is clear that ψ̂₁ is a non-regular estimator because the stage-1 pseudo-outcome Ŷ₁ is a non-smooth function (e.g., absolute value) of ψ̂₂. The estimators presented in this section “regularize” the nonregular estimator (sometimes called the “hard-max” estimator because of the maximum operation used in the definition) by shrinking or thresholding the effect of the term involving the maximum, e.g., $\mid {\widehat{\psi }}_2^T{H}_{21}\mid$, towards zero.

3.1 Hard-threshold Estimator

Recall that the pseudo-outcome ${\widehat{Y}}_1=Y_1+{\widehat{\beta }}_2^T{H}_{20}+\mid {\widehat{\psi }}_2^T{H}_{21}\mid$ is non-differentiable in ψ̂₂ only when ${\widehat{\psi }}_2^T{H}_{21}=0$, and so the corresponding estimator ψ̂₁ is problematic only when the true ${\psi }_2^T{H}_{21}$ is close to zero. The general form of the hard-threshold pseudo-outcome is

$${\widehat{Y}}_{1i}^{HT}=Y_{1i}+{\widehat{\beta }}_2^T{H}_{20,i}+\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid ·\mathbf{1}\{\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid >{\lambda }_i\},i=1,\dots ,n,$$ (5)

where λ_i (> 0) is the threshold for the i-th subject in the sample (possibly depending on the variability of the linear combination ${\widehat{\psi }}_2^T{H}_{21,i}$ for that subject). One way to operationalize this is to perform a preliminary test (for each subject in the sample) of the hypothesis $H_{0i}:{\psi }_2^T{H}_{21,i}=0$ (H_{21, i} is considered fixed in this test), set ${\widehat{Y}}_{1i}^{HT}={\widehat{Y}}_{1i}$ if H_0i is rejected, and replace $\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid$ with the “better guess” 0 in case H_0i is accepted. Thus the hard-threshold pseudo-outcome can be written as

$${\widehat{Y}}_{1i}^{HT}=Y_{1i}+{\widehat{\beta }}_2^T{H}_{20,i}+\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid ·\mathbf{1}\left\{\frac{\sqrt{n}\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid }{\sqrt{H_{21,i}^T{\widehat{\mathrm{\sum }}}_2{H}_{21,i}}}>z_{\alpha /2}\right\},i=1,\dots ,n,$$ (6)

where Σ̂₂ is the estimated covariance matrix of ψ̂₂. The corresponding estimator of ψ₁, denoted by ${\widehat{\psi }}_1^{HT}$, will be referred to as the hard-threshold estimator. The hard-threshold estimator is common in many areas like variable selection in linear regression and wavelet shrinkage²⁶. Moodie and Richardson¹⁷ proposed this estimator for bias correction in the context of Robins’ method, and called it Zeroing Instead of Plugging In (ZIPI) estimator.

Note that ${\widehat{Y}}_1^{HT}$ is still a non-smooth function of ψ̂₂ and hence ${\widehat{\psi }}_1^{HT}$ is a nonregular estimator of ψ₁. However, the problematic term $\mid {\widehat{\psi }}_2^T{H}_{21}\mid$ is shrunk (thresholded) towards zero, and hence one might expect that the degree of nonregularity is somewhat reduced. Moodie and Richardson¹⁷ showed that this estimator reduces the bias occurring in Robins’ method (efficient version of Q-learning). In the simulation study to follow, we will explore if this estimator can be used to construct valid confidence intervals for ψ₁. An important issue regarding the use of this estimator is the choice of significance level α of the preliminary test, which is an unknown tuning parameter. As discussed by Moodie and Richardson¹⁷, this is a difficult problem even in better-understood settings where preliminary test based estimators are used; and no widely applicable data-driven method for choosing α in this setting is currently available.

3.2 Soft-threshold or Shrinkage Estimator

The general form of the soft-threshold pseudo-outcome considered here is

$${\widehat{Y}}_{1i}^{ST}=Y_{1i}+{\widehat{\beta }}_2^T{H}_{20,i}+\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid ·{\left(1-\frac{{\lambda }_i}{\mid {\widehat{\psi }}_2^T{H}_{21,i}{\mid }^2}\right)}^{+},i=1,\dots ,n,$$ (7)

where x⁺ = x1{x > 0} stands for the positive part of a function, and λ_i (> 0) is a tuning parameter associated with the i-th subject in the sample (again possibly depending on the variability of the linear combination ${\widehat{\psi }}_2^T{H}_{21,i}$ for that subject). In the contexts of regression shrinkage ²⁷ and wavelet shrinkage²⁸, the third term in (7) is generally known as the nonnegative garrote estimator. As discussed by Zou²⁹, the nonnegative garrote estimator is a special case of the adaptive lasso estimator. As in the case of hard-threshold estimator, a crucial issue here is to choose a data-driven tuning parameter λ_i. Below we provide a choice following a Bayesian approach.

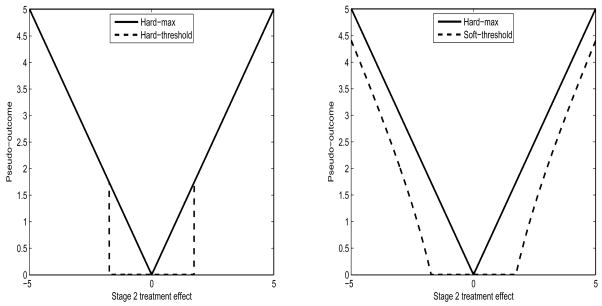
Like the hard-threshold pseudo-outcome, ${\widehat{Y}}_1^{ST}$ is also a non-smooth function of ψ̂₂ and hence ${\widehat{\psi }}_1^{ST}$ remains a nonregular estimator of ψ₁. However, the problematic term $\mid {\widehat{\psi }}_2^T{H}_{21}\mid$ is shrunk (or thresholded) towards zero, and hence one might expect that the degree of nonregularity is somewhat reduced. In the simulation study to follow, we will investigate how much improvement this estimator offers over the “hard-max” estimator, when it comes to constructing confidence intervals. Figure 1 presents the hard-max, the hard-threshold, and the soft-threshold pseudo-outcomes.

Figure 1.

Hard-threshold and Soft-threshold pseudo-outcomes compared with the Hard-max pseudo-outcome.

3.2.1 Choice of Tuning Parameter

A hierarchical Bayesian formulation of the problem, inspired by the work of Figueiredo and Nowak³⁰ in the area of wavelet-based image processing, can be used in the context of the soft-threshold estimator to choose λ_i’s in a data-driven way. It turns out that the estimator (7) with ${\lambda }_i=3H_{21,i}^T{\widehat{\mathrm{\sum }}}_2{H}_{21,i}/n,i=1,\dots ,n$, where Σ̂₂/n is the estimated covariance matrix of ψ̂₂, is an approximate empirical Bayes estimator. The following lemma will be used to derive the choice of λ_i.

Lemma 2

Let X be a random variable such that X|μ ~ N(μ, σ²) with known variance σ². Let the prior distribution on μ be given by μ|ϕ² ~ N(0, ϕ²),with Jeffrey’s noninformative hyper-prior on ϕ², e.g., p(ϕ²) ∝ 1/ϕ². Then an empirical Bayes estimator of |μ| is given by

$$\begin{array}{l}{\widehat{\mid \mu \mid }}^{EB}=X{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}\left(2\mathrm{\Phi }\left(\frac{X}{\sigma }\sqrt{{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}}\right)-1\right)\\ +\sqrt{\frac{2}{\pi }}\sigma \sqrt{{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}}exp\left\{-\frac{X^2}{2{\sigma }^2}{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}\right\},\end{array}$$ (8)

where Φ(·) is the standard normal distribution function.

The proof is given in Appendix B.

Clearly, ${\widehat{\mid \mu \mid }}^{EB}$ is a thresholding rule, since ${\widehat{\mid \mu \mid }}^{EB}=0$ for $\mid X\mid <\sqrt{3}\sigma$. Moreover, when $\mid \frac{X}{\sigma }\mid$ is large, the second term of (8) goes to zero exponentially fast, and

$$\left(2\mathrm{\Phi }\left(\frac{X}{\sigma }\sqrt{{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}}\right)-1\right)\approx (2I_{\{X>0\}}-1)=\mathit{sign}(X).$$

Consequently, the empirical Bayes estimator is approximated by

$${\widehat{\mid \mu \mid }}^{EB}\approx X{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}\mathit{sign}(X)=\mid X\mid {\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}.$$ (9)

Now for i = 1,…,n separately, put $X={\widehat{\psi }}_2^T{H}_{21,i}$, and $\mu ={\widehat{\psi }}_2^T{H}_{21,i}$ (for fixed H_21;i); and plug in ${\widehat{\sigma }}^2=H_{21,i}^T{\widehat{\mathrm{\sum }}}_2{H}_{21,i}/n$ for σ². This leads to a choice of λ_i in the soft-threshold pseudo-outcome (7):

$${\widehat{Y}}_{1i}^{ST}=Y_{1i}+{\widehat{\beta }}_2^T{H}_{20,i}+\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid ·{\left(1-\frac{3H_{21,i}^T{\widehat{\mathrm{\sum }}}_2{H}_{21,i}}{n\mid {\widehat{\psi }}_2^T{H}_{21,i}{\mid }^2}\right)}^{+},$$ (10)

$$\begin{array}{c}=Y_{1i}+{\widehat{\beta }}_2^T{H}_{20,i}+\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid ·\left(1-\frac{3H_{21,i}^T{\widehat{\mathrm{\sum }}}_2{H}_{21,i}}{n\mid {\widehat{\psi }}_2^T{H}_{21,i}{\mid }^2}\right)·\mathbf{1}\left\{\frac{\sqrt{n}\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid }{\sqrt{H_{21,i}^T{\widehat{\mathrm{\sum }}}_2{H}_{21,i}}}>\sqrt{3}\right\},\\ i=1,\dots ,n.\end{array}$$ (11)

The presence of the indicator function in (11) indicates that ${\widehat{Y}}_{1i}^{ST}$ is a thresholding rule for small values of $\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid$, while the term just preceding the indicator function makes ${\widehat{Y}}_{1i}^{ST}$ a shrinkage rule for moderate to large values of $\mid {\widehat{\psi }}_2^T{H}_{21,i}\mid$ (for which the indicator function takes the value one). Thus the current Bayesian formulation gives us a data-driven choice of the tuning parameters.

4 Simulation Study

In this section, we consider a simulation study to compare the performances of the hard-max, the hard-threshold, and the soft-threshold estimators under different nonregular scenarios. In this study, we vary the parameters of the generative model, the degree of nonregularity, and the type of bootstrap confidence interval.

Generative Model

Recall that the data consist of n patient trajectories, each of the form (O₁, A₁, O₂, A₂, O₃). Without loss of generality, we assume Y₁ ≡ 0 and Y₂ ≡ Y = O₃. Let μ_Y = E[Y|O₁, A₁, O₂, A₂], and ε be the associated error term. Then Y = μ_Y + ε, where

$${\mu }_Y={\gamma }_1+{\gamma }_2{O}_1+{\gamma }_3{A}_1+{\gamma }_4{O}_1{A}_1+{\gamma }_5{A}_2+{\gamma }_6{O}_2{A}_2+{\gamma }_7{A}_1{A}_2,$$

and ε ~ N(0, 1). Next, we consider binary treatments randomized with probability 1/2, e.g., P[A_j = 1] = P [A_j = −1] = 1/2, j = 1, 2. Also, the binary covariates O_j’s are generated as

$$\begin{array}{l}P[O_1=1]=P[O_1=-1]=1/2,\\ P[O_2=1\mid O_1,A_1]=1-P[O_2=-1\mid O_1,A_1]=\mathit{expit}({\delta }_1{O}_1+{\delta }_2{A}_1),\end{array}$$

where expit(x) = exp(x)/(1 + exp(x)). Note that γ₁,…,γ₇ and δ₁, δ₂ are the parameters that specify the generative model. These parameters will be varied in the examples to follow.

Analysis Model

$$\begin{array}{l}{Q}_2(H_2,A_2)={\beta }_{20}+{\beta }_{21}{O}_1+{\beta }_{22}{A}_1+{\beta }_{23}{O}_1{A}_1+\left({\psi }_{20}+{\psi }_{21}{O}_2+{\psi }_{22}{A}_1\right)A_2,\\ Q_1(H_1,A_1)={\beta }_{10}+{\beta }_{11}{O}_1+\left({\psi }_{10}+{\psi }_{11}{O}_1\right)A_1.\end{array}$$

Two dimensions of nonregularity: p and ϕ

Nonregularity in stage 1 parameters arises when the optimal stage 2 treatment is non-unique for at least some subjects in the population. With reference to the present generative model, a setting is nonregular if the linear combination γ₅ + γ₆O₂ + γ₇A₁ = 0 with positive probability. Also one might expect some nonregular behavior as γ₅ + γ₆O₂ + γ₇A₁ falls in a small neighborhood of zero (even though not exactly zero). In the following, we consider specific examples varying the “degree of nonregularity”, e.g., p = P[γ₅ + γ₆O₂ + γ₇A₁ = 0] and the “standardized effect size” defined as $\varphi =\mid E[{\gamma }_5+{\gamma }_6{O}_2+{\gamma }_7{A}_1]/\sqrt{\mathit{Var}[{\gamma }_5+{\gamma }_6{O}_2+{\gamma }_7{A}_1]}\mid$. The quantities p and ϕ, which depend on the distribution of the above linear combination, represent two dimensions of the nonregularity phenomenon. Note that the linear combination (γ₅ + γ₆O₂ + γ₇A₁) can take only four possible values corresponding to the four possible (O₂, A₁) cells. The cell probabilities can be easily calculated; the formulae are provided in Table 1.

Table 1.

Distribution of the linear combination (γ₅ + γ₆O₂ + γ₇A₁)

(O2, A1) cell	cell probability (averaged over O1)	value of the linear combination
(1, 1)	$q_1\equiv \frac{1}{4}\left(\mathit{expit}({\delta }_1+{\delta }_2)+\mathit{expit}(-{\delta }_1+{\delta }_2)\right)$	f1 ≡γ5 + γ6 + γ7
(1, −1)	$q_2\equiv \frac{1}{4}\left(\mathit{expit}({\delta }_1-{\delta }_2)+\mathit{expit}(-{\delta }_1-{\delta }_2)\right)$	f2 ≡γ5 + γ6 − γ7
(−1, 1)	$q_3\equiv \frac{1}{4}\left(\mathit{expit}({\delta }_1-{\delta }_2)+\mathit{expit}(-{\delta }_1-{\delta }_2)\right)$	f3 ≡γ5 − γ6 + γ7
(−1, −1)	$q_4\equiv \frac{1}{4}\left(\mathit{expit}({\delta }_1+{\delta }_2)+\mathit{expit}(-{\delta }_1+{\delta }_2)\right)$	f4 ≡ γ5 −γ6 − γ7

It follows that E[γ₅ + γ₆O₂ + γ₇A₁] = q₁f₁ + q₂f₂ + q₃f₃ + q₄f₄, and $E[{({\gamma }_5+{\gamma }_6{O}_2+{\gamma }_7{A}_1)}^2]=q_1{f}_1^2+q_2{f}_2^2+q_3{f}_3^2+q_4{f}_4^2$, where q₁,…,q₄ are the cell probabilities given in Table 1. From these two, one can calculate V ar[γ₅ + γ₆O₂ + γ₇A₁], and subsequently the effect size ϕ.

We want to conduct inference on ψ₁₀ and ψ ₁₁, the analysis model parameters associated with stage 1 treatment A₁. They can be expressed in terms of γ’s and δ’s, the parameters of the generative model, as follows. It turns out that

$$\begin{array}{r}{\psi }_{10}={\gamma }_3+q_1\mid f_1\mid -q_2\mid f_2\mid +q_3\mid f_3\mid -q_4\mid f_4\mid ,\\ \text{and}{\psi }_{11}={\gamma }_4+q_1^{\prime }\mid f_1\mid -q_2^{\prime }\mid f_2\mid -q_3^{\prime }\mid f_3\mid +q_4^{\prime }\mid f_4\mid ,\end{array}$$

where $q_1^{\prime }=q_3^{\prime }=\frac{1}{4}(\mathit{expit}({\delta }_1+{\delta }_2)-\mathit{expit}(-{\delta }_1+{\delta }_2))$, and $q_2^{\prime }=q_4^{\prime }=\frac{1}{4}(\mathit{expit}({\delta }_1-{\delta }_2)-\mathit{expit}(-{\delta }_1-{\delta }_2))$. In the following, we consider specific examples for varying p and ϕ. In Examples 1 − 4 below, we use δ₁ = δ₂ = 0.5. For this choice, we get the following values of the cell probabilities: q₁ = q₄ = 0.3078 and q₂ = q₃ = 0.1922. This choice of the δ’s also makes $q_1^{\prime }=q_2^{\prime }=q_3^{\prime }=q_4^{\prime }=.0578$.

Example 1 (p = 1, ϕ undefined)

Consider a setting where there is no treatment effect for any subject (any history) in either stage. This is achieved by setting γ₁ = … = γ₇ = 0, and δ₁ = δ₂ = 0.5. Then f₁ = f₂ = f₃ = f₄ = 0, and hence ψ ₁₀ = ψ ₁₁ = 0, p = 1, and ϕ is undefined (0/0). This is a fully nonregular scenario.

Example 2 (p = 0, ϕ infinite)

Consider a setting similar to Example 1, where there is a very weak stage 2 treatment effect for every subject (all possible history). This is achieved by setting γ₅ = 0.01 and γ_j = 0, ∀j ≠ 5, and δ₁ = δ₂ = 0.5. Then f₁ = f₂ = f₃ = f₄ = 0.01; ψ ₁₀ = ψ ₁₁ = 0, p = 0, and ϕ is infinite (0.01/0). This is a regular scenario, but close to nonregularity (it is hard to detect the very weak effect given the noise level in the data).

Example 3 ( $p=\frac{1}{2}$, ϕ = 1)

Consider a setting where there is no stage 2 treatment effect for half the subjects in the population, but a reasonably large effect for the other half of subjects. This is achieved by setting γ₁ = γ₂ = γ₄ = γ₆ = 0, γ₃ = −0.5, γ₅ = γ₇ = 0.5, and δ₁ = δ₂ = 0.5. Then f₁ = f₃ = 1, f₂ = f₄ = 0, ψ ₁₀ = ψ ₁₁ = 0, $p=\frac{1}{2}$ and ϕ = 1. This is a nonregular setting.

Example 4 (p = 0, ϕ = 1.0204)

Consider a setting where there is a very weak stage 2 treatment effect for half the subjects in the population, but a reasonably large effect for the other half of subjects. This is achieved by setting γ₁ = γ₂ = γ₄ = γ₆ = 0, γ₃ = −0.5, γ₅ = 0.5, γ₇ = 0.49, and δ₁ = δ₂ = 0.5. It follows that f₁ = f₃ = 0.99, f₂ = f₄ = 0.01, ψ ₁₀ = −0.0100, ψ ₁₁ = 0, p = 0, and ϕ = 1.0204. This regular example is close to the nonregular Example 3.

Example 5 ( $p=\frac{1}{4}$, ϕ = 1.4142)

Consider a setting where there is no stage 2 treatment effect for one-fourth of the subjects in the population, but others have a reasonably large effect. To achieve this, set γ₁ = γ₂ = γ₄ = 0, γ₃ = −0.5, γ₅ = 1, γ₆ = γ₇ = 0.5, δ₁ = 1, and δ₂ = 0. Then f₁ = 2, f₂ = f₃ = 1, f₄ = 0; the cell probabilities are equal, i.e., $q_1=q_2=q_3=q_4=\frac{1}{4}$; and $q_1^{\prime }=q_2^{\prime }=q_3^{\prime }=q_4^{\prime }=0.1155$. Consequently, ψ₁₀ = ψ₁₁ = 0, $p=\frac{1}{4}$, and ϕ = 1.4142. This is a nonregular setting.

Example 6 (p = 0, ϕ = 0.3451)

Consider a completely regular setting where there is a reasonably large stage 2 treatment effect for every subject in the population. This can be achieved by setting γ₁ = γ₂ = γ₄ = 0, γ₃ = −0.5, γ₅ = 0.25, γ₆ = γ₇ = 0.5, and δ₁ = δ₂ = 0.1. Then f₁ = 1.25, f₂ = f₃ = 0.25, and f₄ = −0.75; the cell probabilities are q₁ = q₄ = 0.2625, q₂ = q₃ = 0.2375; and $q_1^{\prime }=q_2^{\prime }=q_3^{\prime }=q_4^{\prime }=0.0125$. It follows that ψ₁₀ = −0.3688, ψ₁₁ = 0.0187, p = 0 and ϕ = 0.3451.

Note that in Example 5, the effect size ϕ is greater than Cohen’s³¹ benchmark large effect size (=0.8). Such a high effect size can be criticized as being unrealistic, based on the principle of clinical equipoise ³², which provides the ethical basis for medical research involving randomization. This principle says that there must be a honest, professional disagreement (high variability) among expert clinicians about the preferred treatment (and thus the standardized effect size of treatment is likely small). Hence this example might be somewhat down-weighted for overall comparison of performance. Furthermore, Example 6 violates the Hierarchical Ordering Principle ³³ in that the coefficient of the interaction term A₁A₂ (γ₇) is larger than the co-efficient of the main effect A₂ (γ₅). So this example might be given lower weight as well.

Competing Estimators

In the simulation, we will consider four estimators: the hard-max estimator (original Q-learning), the soft-threshold estimator, and the hard-threshold estimator with two values of the tuning parameter α, e.g., 0.2, which was empirically found to be a good choice by Moodie and Richardson¹⁷, and 0.08 which corresponds to the threshold used by the soft-threshold estimator proposed in this paper (from (11), the threshold used by the soft-threshold estimator is $\sqrt{3}=1.7321$; equating this point to z_α/2 and solving for α, we get α = 0.0833).

Different Bootstrap CIs

We consider three types of bootstrap CIs, e.g., percentile, hybrid, and double (percentile) bootstrap CIs. Let θ̂ be an estimator of θ and θ̂* be its bootstrap version. Then the 100(1 − α)% percentile bootstrap (PB) CI is given by $\left({\widehat{\theta }}_{(\frac{\alpha }{2})}^{\ast },{\widehat{\theta }}_{(1-\frac{\alpha }{2})}^{\ast }\right)$, and the 100(1 − α)% hybrid bootstrap (HB) CI is given by $\left(2\widehat{\theta }-{\widehat{\theta }}_{(1-\frac{\alpha }{2})}^{\ast },2\widehat{\theta }-{\widehat{\theta }}_{(\frac{\alpha }{2})}^{\ast }\right)$, where ${\widehat{\theta }}_{\gamma }^{\ast }$ is the 100γ-th percentile of the bootstrap distribution. The double bootstrap (DB) CI is calculated as follows:

1. Draw B₁ first-stage bootstrap samples from the original data. For each first-stage bootstrap sample, calculate the bootstrap version of the estimator θ̂*^b, b = 1,…,B₁.

2. Conditional on each first-stage bootstrap sample, draw B₂ second-stage (nested) bootstrap samples and calculate the double bootstrap versions of the estimator, e.g., θ̂**^bm, b = 1,…,B₁, m = 1,…,B₂.

3. For b = 1,…,B₁, calculate $u^{\ast b}=\frac{1}{B_2}{\sum }_{m=1}^{B_2}\mathbf{1}\{{\widehat{\theta }}^{\ast \ast bm}\le \widehat{\theta }\}$, where θ̂ is the estimator based on the original data.

4. The double bootstrap CI is given by $\left({\widehat{\theta }}_{\widehat{q}(\frac{\alpha }{2})}^{\ast },{\widehat{\theta }}_{\widehat{q}(1-\frac{\alpha }{2})}^{\ast }\right)$, where $\widehat{q}(\gamma )=u_{(\gamma )}^{\ast }$, the 100γ-th percentile of the distribution of u*^b, b = 1,…,B₁.

See Davison and Hinkley³⁴ and Nankervis³⁵ for details about double bootstrap CIs. One disadvantage of these CIs is that they are computationally very intensive.

We use B = 1000 bootstrap iterations to calculate the percentile and the hybrid bootstrap CIs. However, the double bootstrap CIs are based on B₁ = 500 first-stage and B₂ = 100 second-stage bootstrap iterations (due to the increased computational burden). The results in Tables 2 – 3 are based on N = 1000 Monte Carlo iterations.

Table 2.

Summary statistics and coverage rates of 95% and 90% nominal percentile (PB), hybrid (HB), and double (DB) bootstrap CIs for ψ₁₀ using the hard-max (HM), the hard-threshold with α = 0.08 (HT_0.08) and α = 0.2 (HT_0.20), and the soft-threshold (ST) estimators. A “*” indicates significantly different coverage rate than the nominal rate, using a test of proportion (Type I error rate = 0.05).

	Summary Statistics			Coverage of 95% CI			Coverage of 90% CI
Estimator	Bias	Var	MSE	PB	HB	DB	PB	HB	DB
Example 1: p = 1 and ϕ undefined (ψ10= ψ11 = 0)
HM	0.0003	0.0045	0.0045	96.8*	93.5*	93.6	92.9*	88.2	88.8
HT0.08	0.0017	0.0044	0.0044	97.0*	95.0	–	93.7*	90.3	–
HT0.20	0.0002	0.0050	0.0050	97.4*	92.8*	–	94.2*	86.9*	–
ST	0.0009	0.0036	0.0036	95.3	96.1	–	91.1	91.4	–
Example 2: p = 0 and ϕ infinite (ψ10 = ψ11 = 0)
HM	0.0003	0.0045	0.0045	96.7*	93.4*	93.6	92.4*	88.2	89.0
HT0.08	0.0010	0.0044	0.0044	97.1*	95.3	–	94.0*	90.5	–
HT0.20	0.0003	0.0050	0.0050	97.3*	93.5*	–	94.3*	87.1*	–
ST	0.0008	0.0036	0.0036	95.4	95.9	–	90.8	91.5	–
Example 3: $p=\frac{1}{2}$ and ϕ = 1 (ψ10 = ψ11 = 0)
HM	−0.0401	0.0059	0.0075	88.4*	92.7*	94.8	81.2*	86.1*	89.0
HT0.08	−0.0083	0.0058	0.0059	94.3	94.3	–	88.5	89.0	–
HT0.20	−0.0179	0.0062	0.0065	93.5*	93.5*	–	87.0*	88.1*	–
ST	−0.0185	0.0055	0.0058	93.4*	94.9	–	87.1*	89.4	–

Table 3.

Summary statistics and coverage rates of 95% and 90% nominal percentile (PB), hybrid (HB), and double (DB) bootstrap CIs for ψ₁₀ using hard-max (HM), hard-threshold with α = 0.08 (HT_0.08) and α = 0.2 (HT_0.20), and soft-threshold (ST) estimators. A “*” indicates significantly different coverage rate than the nominal rate, using a test of proportion (Type I error rate = 0.05).

	Summary Statistics			Coverage of 95% CI			Coverage of 90% CI
Estimator	Bias	Var	MSE	PB	HB	DB	PB	HB	DB
Example 4: p = 0 and ϕ = 1.0204 (ψ10 = −0.01, ψ11 = 0)
HM	−0.0353	0.0059	0.0072	89.6*	93.1*	94.4	82.9*	86.6*	90.2
HT0.08	−0.0037	0.0058	0.0058	94.6	94.1	–	88.9	89.0	–
HT0.20	−0.0130	0.0062	0.0064	93.9	92.8*	–	87.9*	87.9*	–
ST	−0.0138	0.0055	0.0057	94.1	95.0	–	87.4*	89.7	–
Example 5: $p=\frac{1}{4}$ and ϕ = 1.4142 (ψ10= ψ11 = 0)
HM	−0.0209	0.0069	0.0074	92.7*	93.1*	94.2	87.8*	89.0	88.4
HT0.08	−0.0059	0.0070	0.0071	93.9	93.2*	–	89.5	88.2	–
HT0.20	−0.0101	0.0072	0.0073	93.3*	93.0*	–	89.3	88.0*	–
ST	−0.0065	0.0069	0.0069	93.8	94.6	–	89.7	89.0	–
Example 6: p = 0 and ϕ = 0.3451 (ψ10 = −0.3688, ψ11 = 0.0187)
HM	0.0009	0.0067	0.0067	95.0	93.8	95.0	89.2	87.4*	88.2
HT0.08	0.0003	0.0081	0.0081	95.1	88.5*	–	90.1	82.9*	–
HT0.20	0.0011	0.0074	0.0074	94.8	91.2*	–	89.7	86.4*	–
ST	0.0052	0.0074	0.0074	94.8	91.7*	–	89.4	85.3*	–

4.1 Results

The simulation study compares the competing estimators on a variety of settings represented by Examples 1 – 6. We considered estimation and inference for both ψ₁₀ and ψ₁₁. However in the present examples, the effect of nonregularity turned out to be more pronounced for the parameter ψ₁₀ (main effect of A₁) than ψ₁₁ (interaction of A₁ with O₁). Hence we included results on ψ₁₀ only in Tables 2 and 3. Also in the following discussion, we will focus on ψ₁₀.

In Example 1 (top part of Table 2), where stage 2 effects for all possible histories are zero (i.e., the stage 2 optimal treatment is non-unique for every subject in the population), we see that there is no bias associated with the hard-max estimator; and the mean squared error (MSE) is essentially the same as the variance. However the percentile bootstrap CI (both 95% and 90%) has over-coverage (note that over-coverage translates to lower power of the corresponding hypothesis test), and the hybrid bootstrap CI (95%) has under-coverage compared to the nominal level. We have also studied the Wald type CIs for this setting (not included in this paper) and observed over-coverage (the problem with Wald type CIs in such nonregular settings is well-known^11,17). This suggests that the asymptotic distribution of the hard-max estimator has a lighter tail than a comparable normal distribution. However, the double bootstrap CIs have correct coverage. Note that both versions of the hard-threshold estimator fail to rectify the coverage rate, even though neither suffer from bias. However, the soft-threshold estimator offers correct coverage for both types of bootstrap CIs. Moreover, it gives the lowest MSE among the four estimators. Note that the soft-threshold estimator is also non-smooth (nonregular), and consequently the bootstrap distribution is inconsistent for the true asymptotic distribution of this estimator. But in this setting, it reduces the degree of nonregularity just enough so that the bootstrap CIs do not show the problem with coverage.

Even though Example 2 (middle part of Table 2) is a regular setting (p = 0), it is very close to Example 1 and hence affected by nonregularity. Results are similar to those in Example 1. Thus the presence of very small effects causes problems with coverage even in regular settings.

Example 3 (bottom part of Table 2) is a setting where the stage 2 optimal treatment is non-unique for half the subjects in the population ( $p=\frac{1}{2}$) and is unique for the remaining half, but the overall standardized stage 2 effect size ϕ (= 1) is quite large. Here the hard-max estimator is biased, and hence both the percentile and the hybrid bootstrap CIs under-cover the true value. However the double bootstrap CI gives correct coverage rate. Both versions of the hard-threshold estimator reduce bias and one of them (corresponding to α = 0.08) gives correct coverage, while the other also offers substantial improvement of the coverage rate. This is consistent with the findings of Moodie and Richardson¹⁷. The soft-threshold estimator also reduces bias, gives the lowest MSE among the four estimators, and provides correct coverage with the hybrid bootstrap method but not with the percentile method (even though it offers substantial improvement). Thus in this example, the hard-threshold estimator with α = 0.08 emerges as the winner, with the soft-threshold estimator at the second place. However, note that the value 0.08 of the tuning parameter α is not arbitrary – it corresponds to the threshold used by the soft-threshold estimator. If constructing confidence intervals is the main goal (so biased estimation is less of an issue), double bootstrap CI along with the hard-max estimator can also be used in this setting, although it is computationally more expensive.

Example 4 (top part of Table 3) is a regular setting, very similar to the nonregular setting in Example 3. Results are quite similar to those in Example 3. This is consistent with our previous observation (Example 2) that the presence of very small effects causes problems with coverage even in regular settings.

In example 5 (middle part of Table 3), the stage 2 optimal treatment is non-unique for one-fourth of the subjects in the population ( $p=\frac{1}{4}$) and the standardized effect size ϕ is very large (=1.4142). Again, the hard-max estimator is biased, and has low coverage of the CIs (except for double bootstrap). The hard-threshold and the soft-threshold estimators offer improvement in terms of bias as well as coverage. The soft-threshold estimator emerges as the best (lowest MSE and correct coverage rate) in this example.

Example 6 (bottom part of Table 3) is a regular setting (p = 0, with no extremely tiny stage 2 effect as in Examples 2 and 4), with the standardized effect size 0.3451. The reason for investigating this setting is to check if the regularized estimators (hard and soft threshold) perform poorly in settings where there is no need to regularize. As expected, the hard-max estimator performs well here. The soft-threshold estimator introduces some bias when there is none in the hard-max estimator and increases MSE; but still manages to provide correct coverage for the percentile bootstrap method. The hard-threshold estimators also give correct coverage for percentile CIs.

To summarize, the hard-max estimator is problematic in nonregular scenarios, except when used with the computationally intensive double bootstrap method for constructing confidence intervals. The hard-threshold estimator, if properly tuned, addresses the problem of bias but not the problem of light tail. The soft-threshold estimator seems to address both problems to a large extent. In the simulation, the soft-threshold estimator consistently produced the lowest MSE among the competing methods across all the nonregular scenarios. Also in all the nonregular settings, either the soft-threshold estimator or the hard-threshold estimator with α = 0.08 (this α corresponds to the threshold used by the soft-threshold estimator) emerged as the winner in terms of providing correct coverage rate of the bootstrap CIs. Even though the soft-threshold estimator incurs some bias in regular settings, it manages to provide reasonable coverage rate for small to moderate standardized effect sizes (we have studied up to around 0.35). Across all the scenarios considered here (Examples 1–6), the soft-threshold estimator emerged as more robust than the hard-threshold estimator to the degree of regularity of the underlying data distribution, probably because of its “soft” nature (the soft-threshold estimator is continuous everywhere even though it has two points of non-differentiability, whereas the hard-threshold estimator has two points of discontinuity – see Figure 1). Furthermore, note that overall the hybrid bootstrap CIs performed slightly better than the percentile bootstrap CIs in this simulation study. Hence the hybrid bootstrap CIs will be used in the data analysis to follow.

5 Analysis of Smoking Cessation Data

To demonstrate the occurrence of nonregularity and the use of the soft-threshold method in a real application, here we present the analysis of a data set from a randomized, two-stage, longitudinal, internet-based smoking cessation study conducted by the Center for Health Communications Research at the University of Michigan. The stage 1 of this study (Project Quit) was conducted to find an optimal multi-factor behavioral intervention to help adult smokers quit smoking; and the stage 2 (Forever Free) was a follow-on study to help those (among the participants of Project Quit) who already quit stay quit, and help those who failed at the previous stage with a second chance. Details of the study design and primary analysis of the stage 1 data can be found in Strecher et al.³⁶

At stage 1, although there were five two-level treatment factors, only two, e.g., source (of online behavioral counseling message) and story (of a hypothetical character who succeeded in quitting smoking) were significant in the analysis reported in Strecher et al.³⁶ For simplicity, we considered only these two treatment factors at stage 1 of our present analysis, which gave a total of 4 treatment combinations at stage 1 corresponding to the 2×2 design. The treatment factor source was varied at two levels, e.g., high vs. low personalized, coded 1 and −1; also the factor story was varied at two levels, e.g., high vs. low tailoring depth (degree to which the character in the story was tailored to the individual subject’s baseline characteristics), coded 1 and −1. Baseline variables at this stage included subjects’ motivation to quit (on a 1–10 scale), selfefficacy (on a 1–10 scale) and education (binary, ≤ high school vs. > high school, coded −1/1). At stage 2, originally there were 4 different treatment groups and a control group; however the 4 treatment groups were combined together for the present analysis because of very little difference between them. This resulted in only two choices of treatment at stage 2; this treatment variable was called FFarm, coded −1/1 (1=treatment, −1 = control).

There were two outcomes at the two stages of this study. The stage 1 outcome was binary quit status called PQ6Quitstatus (1=quit, 0=not quit) at 6 month from the date of randomization. The stage 2 outcome was binary quit status FF6Quitstatus at 6 months from the date of stage 2 randomization (i.e., 12 months from the date of stage 1 randomization).

An example DTR can have the following form: “At stage 1, if a subject’s baseline selfefficacy is greater than a threshold value (say 7, on a 1–10 scale), then provide the highly-personalized level of the treatment component source, and if the subject is willing to continue treatment, then at stage 2 provide treatment if he/she continues to be a smoker at the end of stage 1”. Of course characteristics other than selfefficacy or a combination of more than one subject characteristics can be used to specify a DTR. To find the optimal DTR, we applied both the hard-max and the soft-threshold estimators within the Q-learning framework. This involved:

1. a stage 2 regression (n = 281) of FF6Quitstatus using the model:

   $$\begin{array}{l}FF6\mathit{Quitstatus}={\beta }_{20}+{\beta }_{21}\mathit{motivation}+{\beta }_{22}\mathit{source}+{\beta }_{23}\mathit{selfefficacy}\\ +{\beta }_{24}\mathit{story}+{\beta }_{25}\mathit{education}+{\beta }_{26}PQ6\mathit{Quitstatus}\\ +{\beta }_{27}\mathit{source}\ast \mathit{selfefficacy}+{\beta }_{28}\mathit{story}\ast \mathit{education}\\ +\left({\psi }_{20}+{\psi }_{21}PQ6\mathit{Quitstatus}\right)\ast \mathit{FFarm}+{\epsilon }_2;\end{array}$$

2. finding both the hard-max pseudo-outcome (Ŷ₁) and the soft-threshold pseudo-outcome ( ${\widehat{Y}}_1^{ST}$) for the stage 1 regression:

   $$\begin{array}{l}{\widehat{Y}}_1=PQ6\mathit{Quitstatus}+{\widehat{\beta }}_{20}+{\widehat{\beta }}_{21}\mathit{motivation}+{\widehat{\beta }}_{22}\mathit{source}+{\widehat{\beta }}_{23}\mathit{selfefficacy}\\ +{\widehat{\beta }}_{24}\mathit{story}+{\widehat{\beta }}_{25}\mathit{education}+{\widehat{\beta }}_{26}PQ6\mathit{Quitstatus}\\ +{\widehat{\beta }}_{27}\mathit{source}\ast \mathit{selfefficacy}+{\widehat{\beta }}_{28}\mathit{story}\ast \mathit{education}\\ +\mid {\widehat{\psi }}_{20}+{\widehat{\psi }}_{21}PQ6\mathit{Quitstatus}\mid ;\end{array}$$

   $$\begin{array}{l}{\widehat{Y}}_1^{ST}=PQ6\mathit{Quitstatus}+{\widehat{\beta }}_{20}+{\widehat{\beta }}_{21}\mathit{motivation}+{\widehat{\beta }}_{22}\mathit{source}+{\widehat{\beta }}_{23}\mathit{selfefficacy}\\ +{\widehat{\beta }}_{24}\mathit{story}+{\widehat{\beta }}_{25}\mathit{education}+{\widehat{\beta }}_{26}PQ6\mathit{Quitstatus}\\ +{\widehat{\beta }}_{27}\mathit{source}\ast \mathit{selfefficacy}+{\widehat{\beta }}_{28}\mathit{story}\ast \mathit{education}\\ +\mid {\widehat{\psi }}_{20}+{\widehat{\psi }}_{21}PQ6\mathit{Quitstatus}\mid ·{\left(1-\frac{3\text{Var}({\widehat{\psi }}_{20}+{\widehat{\psi }}_{21}PQ6\mathit{Quitstatus})}{\mid {\widehat{\psi }}_{20}+{\widehat{\psi }}_{21}PQ6\mathit{Quitstatus}{\mid }^2}\right)}^{+};\end{array}$$

   and (3) for each of the two pseudo-outcomes, a stage 1 regression (n = 1401) of the pseudo-outcome using a model of the form:

   $$\begin{array}{l}{\widehat{Y}}_1\text{or}{\widehat{Y}}_1^{ST}={\beta }_{10}+{\beta }_{11}\mathit{motivation}+{\beta }_{12}\mathit{selfefficacy}+{\beta }_{13}\mathit{education}\\ +\left({\psi }_{10}^{(1)}+{\psi }_{11}^{(1)}\mathit{selfefficacy}\right)\ast \mathit{source}\\ +\left({\psi }_{10}^{(2)}+{\psi }_{11}^{(2)}\mathit{education}\right)\ast \mathit{story}+{\epsilon }_1.\end{array}$$

Note that the sample sizes at the two stages differ because only 281 subjects were willing to continue treatment into stage 2 (as allowed by the study protocol). Our stage 2 analysis was a usual regression analysis. No significant treatment effect was found at this stage, indicating the likely existence of nonregularity. At stage 1, for either estimator, 95% confidence intervals were constructed by hybrid bootstrap using 1000 bootstrap replications. The stage 1 analysis summary is presented in Table 4. In this case, the hard-max and the soft-threshold estimators produced similar results.

Table 4.

Regression coefficients and 95% hybrid bootstrap confidence intervals at stage 1, using both the hard-max and the soft-threshold estimators.

	Hard-max		Soft-threshold
Variable	Coefficient	95% CI	Coefficient	95% CI
motivation	0.04	(−0.00, 0.08)	0.04	(0.00, 0.08)
selfefficacy	0.03	(0.00, 0.06)	0.03	(0.00, 0.06)
education	−0.01	(−0.07, 0.06)	−0.01	(−0.07, 0.06)
source	−0.15	(−0.35, 0.06)	−0.15	(−0.35, 0.06)
source*selfefficacy	0.03	(0.00, 0.06)	0.03	(0.00, 0.06)
story	0.05	(−0.01, 0.11)	0.05	(−0.01, 0.11)
story*education	−0.07	(−0.13, −0.01)	−0.07	(−0.13, −0.01)

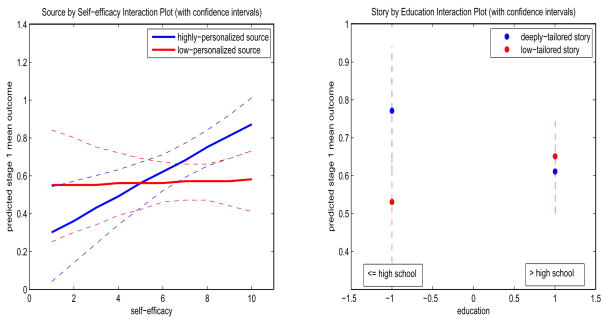
The conclusions from the present data analysis can be summarized as follows. We did not find any significant stage 2 treatment effect. So this analysis suggests that the stage 2 behavioral intervention need not be adapted to the smoker’s individual characteristics, interventions previously received, or stage 1 outcome. More interesting results are found at stage 1. It is found that subjects with higher level of motivation or selfefficacy are more likely to quit. The highly personalized level of source is more effective for subjects with a higher selfefficacy (≥ 7), and deeply tailored level of story is more effective for subjects with lower education (≤ high school); these two conclusions can be drawn from the interaction plots (with confidence intervals) presented in figure 2. Thus this secondary data analysis suggests that to maximize each individual’s chance of quitting over the two stages, the web-based smoking cessation intervention should be designed in future such that: (1) smokers with high self-efficacy (≥ 7) are assigned to highly personalized level of source, and (2) smokers with lower education are assigned to deeply tailored level of story.

Figure 2.

Interaction plots: (a) source by self-efficacy (left panel), (b) story by education (right panel), along with confidence intervals for predicted stage 1 pseudo-outcome.

6 Discussion

In this paper, we have illustrated the problem of nonregularity that arises in the context of DTRs in the estimation of the optimal current treatment rule, when the optimal treatments at subsequent stages are non-unique for at least some proportion of subjects in the population. We have illustrated the phenomenon using Q-learning as the estimation procedure, which is a simpler yet inefficient version of Robins’ method; however the problem of nonregularity arises in Robins’ method as well^11,17.

For some underlying data-generating models (e.g., Examples 3, 4, 5 in the simulation study), this nonregularity induces bias in the point estimates of the parameters of the optimal DTRs, which in turn causes under-coverage of the bootstrap confidence intervals. In contrast, in case of Examples 1 and 2, this nonregularity causes lightness of tail of the asymptotic distribution but no bias, as seen from the over-coverage of the percentile bootstrap CIs (equivalently conservative tests leading to lower power). The coexistence of these two not-so-well-related issues (they work in opposite directions, e.g., bias tends to make the CIs under-cover, whereas lightness of tail tends to make the CIs over-cover) makes this problem a unique and challenging one.

As mentioned in section 2.4, the phenomenon of nonregularity can be understood more clearly with a simpler problem, e.g., estimating |μ| (note that ψ₁₀ is a linear combination of terms like |μ|; see section 4) by |X̄_n| (similar to the hard-max estimator), where X̄_n is the sample average of n i.i.d. observations X₁,…,X_n from N (μ, 1). From section 2.4, we know that when μ = 0, |X̄_n| is a biased estimator of |μ| = 0, with $\mathit{bias}=E(\mid {\overline{X}}_n\mid )=\sqrt{\frac{2}{n\pi }}$. Because of this bias (wrong centering), bootstrap CIs exhibited gross under-coverage in a toy example. But once we used a bias-corrected estimate (corrected by the analytically calculated bias), the percentile bootstrap CI exhibited over-coverage. This suggests that the distribution of |X̄_n| is peaked around its mean, or to put it in another way, has light tails.

In the simulation study to compare the competing estimators of the optimal DTR, we considered estimation of ψ₁₀, which involve linear combinations of |f₁|, |f₂|, |f₃|, and |f₄| (terms like |μ|). Under the non-regular scenarios, some or all (depending on the degree of nonregularity p) of the f_i’s are zero; and hence a phenomenon similar to the one described above in the toy example happens for each |f_i| for which f_i = 0. Each such term has its associated bias, and each has its own lightness of tail, with bias being the dominant property. In some nonregular scenarios (Example 1), the bias associated with the individual |f_i|’s (in the expression for ψ₁₀) cancel each other out (note the opposite signs in front of |f_i|’s), and hence the lightness of tail is revealed, resulting in a percentile bootstrap CI that over-covers. In other nonregular examples, however, bias is not canceled out, and hence dominates the property of the hard-max estimator. Hence under-coverage of the bootstrap CIs is observed.

Nonregularity is an issue in the estimation of the optimal DTRs because it arises when there is no treatment effect at subsequent stages (equivalently, there is no unique optimal treatment at subsequent stages). Unfortunately often there is no or very weak treatment effect in the settings we are interested in (e.g., randomized trials on mental illness or substance abuse). Thus we want our estimator to enjoy good statistical properties (e.g., less bias, lower risk or MSE, correct coverage rate of CIs, good power to detect “local” alternatives, etc.) when the optimal treatment at subsequent stages is non-unique. In case of the hard-max estimator, unfortunately the point of non-differentiability coincides with the parameter value such that ${\psi }_2^T{H}_{21}=0$ (non-unique optimal treatment at the subsequent stage), which causes nonregularity (bias, higher MSE, low power). But the soft-threshold estimator (also, hard-threshold estimator), in some sense, redistributes the nonregularity from this “null point” to two different points symmetrically placed on either side of the “null point” (see Figure 1). This is one reason why the soft-threshold (also, hard-threshold) estimator works well in nonregular settings.

We have shown that using bootstrap confidence intervals along with the soft-threshold (also, hard-threshold in some cases) estimator reduces the degree of nonregularity, and gives correct coverage rate. Also, the double bootstrap method can be used along with the original hard-max estimator to address the nonregularity. But this method is highly computationally intensive and may be difficult to use in practice. An alternative method to construct CIs for ψ’s in nonregular settings is the score method due to Robins¹¹. We have not investigated this in our simulation study.

One can consider an alternative Bayesian approach to formulate an estimator similar to the soft-threshold estimator as follows. Let the data distribution ${\widehat{\psi }}_2^T{H}_{21}\mid {\psi }_2^T{H}_{21}\sim N({\psi }_2^T{H}_{21},{\sigma }^2)$ with known σ², and the prior distribution of ${\psi }_2^T{H}_{21}$ be a mixture of a point mass at 0 and N (0, 1), with mixing parameter p (0 < p < 1). Then the posterior distribution of ${\psi }_2^T{H}_{21}$ is a mixture distribution given by

$$\begin{array}{c}{f}_{\mathit{post}}({\psi }_2^T{H}_{21})=\widehat{w}·\mathbf{1}\{{\psi }_2^T{H}_{21}=0\}+(1-\widehat{w})·N\left(\frac{{\widehat{\psi }}_2^T{H}_{21}}{1+{\sigma }^2},\frac{{\sigma }^2}{1+{\sigma }^2}\right),\\ \text{where}\widehat{w}={\left\{1+\frac{1-p}{p}\sqrt{\frac{{\sigma }^2}{1+{\sigma }^2}}exp\left\{\frac{{({\widehat{\psi }}_2^T{H}_{21})}^2}{2{\sigma }^2(1+{\sigma }^2)}\right\}\right\}}^{-1}.\end{array}$$

One can use the median of this posterior distribution in place of ${\widehat{\psi }}_2^T{H}_{21}$ in the expression for Ŷ₁. Thus the Bayes estimator becomes

$${\widehat{Y}}_1^{\mathit{Bayes}}={\widehat{\beta }}_2^T{H}_{20}+\text{median}\text{of}{f}_{\mathit{post}}({\psi }_2^T{H}_{21}).$$

For using this, one has to replace σ² by ${\widehat{\sigma }}^2=H_{21}^T{\widehat{\mathrm{\sum }}}_2{H}_{21}/n$, and p by either some empirical estimate or a fixed value (e.g., $\frac{1}{2}$). In place of the above mixture prior, Johnstone and Silverman³⁷ suggest using the mixture of a point mass and a heavy-tailed distribution (e.g., double-exponential). This is a promising formulation that we want to investigate in future.

In this paper, we have focused on randomized trials only to separate the issue of nonregularity from causal inference issues. However the problem of nonregularity also arises when observational data^11,17 are used; and the hard-threshold and the soft-threshold estimators should be applicable in those settings as well. Also, here we have focussed on only two stages for clarity. However, it should be understood that Q-learning can be used for studies with more than two stages as well. In case of many stages, one can think of a scenario where some parameters are shared across stages, in which case a simultaneous version of Q-learning (as opposed to the recursive version discussed in this paper) would be more appropriate. Unfortunately nonregularity does not go away if a simultaneous estimation procedure is used; see Moodie and Richardson¹⁷ for a discussion on this with reference to Robins’ method. However, unlike the case of recursive estimation, it is not well understood at this point whether the threshold estimators (hard or soft) can reduce the nonregularity in simultaneous estimation. Moodie and Richardson¹⁷ gave a simulated nonregular example showing that hard-threshold or ZIPI estimator is not always better than simultaneous estimator of Robins. We did not investigate this issue in the current paper, but we recognize this as an important avenue of future research.

To conclude, we think in the estimation of optimal DTRs, appropriately tuned hard-threshold estimator and the soft-threshold estimator should be seriously considered as improved versions of Q-learning (and Robins’ method of estimation).

Appendix A: Proof of Lemma 1

Proof

Define the advantage at stage j as

$${\mu }_j(H_j,A_j)=Q_j(H_j,A_j)-\underset{a_j}{max}{Q}_j(H_j,a_j),j=1,2.$$

Note that μ_j(H_j, A_j) represents the expected difference in outcome when using A_j instead of the optimal treatment at stage j, for subjects with treatment and covariate history H_j who receive the optimal DTR at stages subsequent to j. According to Robins¹¹ (p. 201), this is simply the blip function with arg max_aj Q_j(H_j, a_j) as the reference treatment. Below we will establish the connection between Q-learning and Robins’ method using the advantage function; one can derive the connection using other blip functions (other choices of reference treatment) following similar steps. When Q-functions are modeled as in (2), the advantages become

$${\mu }_j(H_j,A_j;{\psi }_j)={\psi }_j^T{H}_{j1}{A}_j-\mid {\psi }_j^T{H}_{j1}\mid ,j=1,2.$$ (12)

Since by condition (i), no parameters are shared across stages, we will proceed stage by stage, starting with stage 2, doing recursive (rather than simultaneous) estimation. The notation ℙ_n will be used below to denote the empirical average over a sample of size n. Also, define m₁(H₁) = E[Q₁(H₁, A₁)|H₁] and m₂(H₂) = E[Q₂(H₂, A₂)|H₂].

Stage 2

At stage 2, Q-learning is a usual least squares regression problem. Thus the estimating equations are given by

$${\mathbb{P}}_n\left[\left(\begin{array}{c}{H}_{20}\\ H_{21}{A}_2\end{array}\right)(Y_2-H_{20}^T{\beta }_2-H_{21}^T{A}_2{\psi }_2)\right]=0.$$ (13)

From (13), it follows that

$${\widehat{\beta }}_2={({\mathbb{P}}_n(H_{20}{H}_{20}^T))}^{-1}\left[{\mathbb{P}}_n(H_{20}{Y}_2)-{\mathbb{P}}_n(H_{20}{H}_{21}^T{A}_2){\widehat{\psi }}_2\right]$$ (14)

where ψ̂₂ is the estimate of ψ₂ satisfying (13). Thus ψ̂₂ satisfies the estimating equation

$${\mathbb{P}}_n\left[(H_{21}{A}_2)(Y_2-H_{20}^T{\widehat{\beta }}_2-H_{21}^T{A}_2{\widehat{\psi }}_2)\right]=0.$$

On the other hand, the stage 2 estimating equation for Robins’ method (Robins¹¹, p. 211) is given by

$${\mathbb{P}}_n\left[\left(H_{21}{A}_2-E[H_{21}{A}_2\mid H_2]\right)\left(Y_2-{\mu }_2(H_2,A_2;{\psi }_2)-E[Y_2-{\mu }_2(H_2,A_2;{\psi }_2)\mid H_2]\right)\right]=0,$$ (15)

where V ar(Y₂−μ₂(H₂, A₂; ψ₂) − E[Y₂ − μ₂(H₂, A₂; ψ₂)|H₂]|H₂, A₂) is omitted (This is one of the reasons why Q-learning is an inefficient version). Note that E[H₂₁A₂|H₂] = 0, by condition (ii) of the lemma. From (12), ${\mu }_2(H_2,A_2;{\psi }_2)={\psi }_2^T{H}_{21}{A}_2-\mid {\psi }_2^T{H}_{21}\mid$. Then $E[{\mu }_2(H_2,A_2;{\psi }_2)\mid H_2]=-\mid {\psi }_2^T{H}_{21}\mid$, again by condition (ii). Also,

$$E[Y_2\mid H_2]=E\left[E[Y_2\mid H_2,A_2]\mid H_2\right]=E[Q_2(H_2,A_2)\mid H_2]=m_2(H_2).$$

Therefore, $Y_2-{\mu }_2(H_2,A_2;{\psi }_2)-E[Y_2-{\mu }_2(H_2,A_2;{\psi }_2)\mid H_2]=Y_2-m_2(H_2)-H_{21}^T{A}_2{\psi }_2$. Thus, ψ̂₂ in Robins’ method solves the following reduced version of (15):

$${\mathbb{P}}_n\left[\left(H_{21}{A}_2\right)\left(Y_2-m_2(H_2)-H_{21}^T{A}_2{\widehat{\psi }}_2\right)\right]=0,$$

for any choice of m₂(H₂) (with the conditional variance omitted). In particular, for $m_2(H_2)=H_{20}^T{\widehat{\beta }}_2$, where β̂₂ is given by (14), this estimating equation exactly matches with that of Q-learning.

Stage 1

For Q-learning, the stage 1 pseudo-outcome is

$${\widehat{Y}}_1=Y_1+\underset{a_2}{max}{Q}_2(H_2,A_2)=Y_1+H_{20}^T{\widehat{\beta }}_2+\mid {\widehat{\psi }}_2^T{H}_{21}\mid ,$$

and so the estimating equations are given by

$${\mathbb{P}}_n\left[\left(\begin{array}{c}{H}_{10}\\ H_{11}{A}_1\end{array}\right)\left(Y_1+H_{20}^T{\widehat{\beta }}_2+\mid {\widehat{\psi }}_2^T{H}_{21}\mid -H_{10}^T{\beta }_1-H_{11}^T{A}_1{\psi }_1\right)\right]=0.$$ (16)

Now from (13)

$${\mathbb{P}}_n\left[H_{20}\left(Y_2-H_{20}^T{\widehat{\beta }}_2-H_{21}^T{A}_2{\widehat{\psi }}_2\right)\right]=0.$$ (17)

Since by condition (iii) of the lemma, $(H_{10}^T,H_{11}^T{A}_1)\subset H_{20}^T$, it follows that

$$\begin{array}{r}{\mathbb{P}}_n\left[\left(\begin{array}{c}{H}_{10}\\ H_{11}{A}_1\end{array}\right)\left(Y_2-H_{20}^T{\widehat{\beta }}_2-H_{21}^T{A}_2{\widehat{\psi }}_2\right)\right]=0,\\ \text{or},{\mathbb{P}}_n\left[\left(\begin{array}{c}{H}_{10}\\ H_{11}{A}_1\end{array}\right)(H_{20}^T{\widehat{\beta }}_2)\right]={\mathbb{P}}_n\left[\left(\begin{array}{c}{H}_{10}\\ H_{11}{A}_1\end{array}\right)(Y_2-H_{21}^T{A}_2{\widehat{\psi }}_2)\right].\end{array}$$ (18)

Using (18) in (16), we get

$${\mathbb{P}}_n\left[\left(\begin{array}{c}{H}_{10}\\ H_{11}{A}_1\end{array}\right)\left(Y_1+Y_2-H_{21}^T{A}_2{\widehat{\psi }}_2+\mid {\widehat{\psi }}_2^T{H}_{21}\mid -H_{10}^T{\beta }_1-H_{11}^T{A}_1{\psi }_1\right)\right]=0.$$ (19)

Solving for β₁ gives,

$${\widehat{\beta }}_1={({\mathbb{P}}_n(H_{10}{H}_{10}^T))}^{-1}\left[{\mathbb{P}}_n\left(H_{10}(Y_1+Y_2-H_{21}^T{A}_2{\widehat{\psi }}_2+\mid {\widehat{\psi }}_2^T{H}_{21}\mid )\right)-{\mathbb{P}}_n(H_{10}{H}_{11}^T{A}_1){\widehat{\psi }}_1\right].$$ (20)

Thus ψ̂₁ satisfies

$${\mathbb{P}}_n\left[(H_{11}{A}_1)\left(Y_1+Y_2-H_{21}^T{A}_2{\widehat{\psi }}_2+\mid {\widehat{\psi }}_2^T{H}_{21}\mid -H_{10}^T{\widehat{\beta }}_1-H_{11}^T{A}_1{\widehat{\psi }}_1\right)\right]=0.$$

On the other hand for Robins’ method, the stage 1 pseudo-outcome (Robins¹¹, p. 208; see also Moodie and Richardson¹⁷) is Ỹ₁ = Y₁ + Y₂ − μ₂(H₂, A₂), and so the stage 1 estimating equation (Robins¹¹, p. 211) is given by

$${\mathbb{P}}_n\left[\left(H_{11}{A}_1-E[H_{11}{A}_1\mid H_1]\right)\left({\stackrel{\sim }{Y}}_1-{\mu }_1(H_1,A_1;{\psi }_1)-E[{\stackrel{\sim }{Y}}_1-{\mu }_1(H_1,A_1;{\psi }_1)\mid H_1]\right)\right]=0,$$ (21)

where again the conditional variance V ar(Ỹ₁−μ₁(H_1, A₁; ψ₁) −E[Ỹ₁ − μ₁(H₁, A₁; ψ₁)|H₁]|H₁, A₁ is omitted. Note that E[H₁₁A₁|H₁] = 0, by condition (ii) of the lemma. From (12), ${\mu }_1(H_1,A_1;{\psi }_1)={\psi }_1^T{H}_{11}{A}_1-\mid {\psi }_1^T{H}_{11}\mid$. Then $E[{\mu }_1(H_1,A_1;{\psi }_1)\mid H_1]=-\mid {\psi }_1^T{H}_{11}\mid$, again by condition (ii). Also,

$$\begin{array}{l}E[{\stackrel{\sim }{Y}}_1\mid H_1]=E[Y_1+Y_2-{\mu }_2(H_2,A_2)\mid H_1]\\ =E[Y_2-Q_2(H_2,A_2)+Y_1+\underset{a_2}{max}{Q}_2(H_2,a_2)\mid H_1]\\ =E\left[E[Y-Q_2(H_2,A_2)\mid H_2,A_2]\mid H_1\right]+E[Y_1+\underset{a_2}{max}{Q}_2(H_2,a_2)\mid H_1]\\ =0+E\left[E[Y_1+\underset{a_2}{max}{Q}_2(H_2,a_2)\mid H_1,A_1]\mid H_1\right]\\ =E[Q_1(H_1,A_1)\mid H_1]\\ =m_1(H_1).\end{array}$$

Finally, plug in Y₁ + Y₂ − μ₂(H₂, A₂; ψ̂₂) for Ỹ₁. Thus, ψ̂₁ in Robins’ method solves the following reduced version of (21):

$${\mathbb{P}}_n\left[\left(H_{11}{A}_1\right)\left(Y_1+Y_2-H_{21}^T{A}_2{\widehat{\psi }}_2+\mid {\widehat{\psi }}_2^T{H}_{21}\mid -m_1(H_1)-H_{11}^T{A}_1{\widehat{\psi }}_1\right)\right]=0.$$

for any choice of m₁(H₁) (again omitting the conditional variance). In particular, for $m_1(H_1)=H_{10}^T{\widehat{\beta }}_1$, where β̂₁ is given by (20), this estimating equation exactly matches with that of Q-learning.

In summary, the Q-learning algorithm as presented here is inefficient because: (a) it sets the conditional variances to be constant over (H_j, A_j), and (b) uses H_j1A_j instead of the “efficient choice” of the term S_eff;j (that attains semiparametric variance bound) in Robins’ estimating equation (see Robins¹¹, p. 212; more details in Robins³⁸).

Appendix B: Proof of Lemma 2

Proof

To estimate the hyper-parameter ϕ², first integrate out μ to get the marginal likelihood X|ϕ² ~ N(0, ϕ²+σ²). The corresponding Jeffrey’s prior on the variance parameter is p(ϕ²) ∝1=(ϕ²+σ²). Based on this formulation, the posterior distribution of ϕ² is given by

$$p({\varphi }^2\mid X)\propto {({\varphi }^2+{\sigma }^2)}^{-3/2}exp\left\{-\frac{X^2}{2({\varphi }^2+{\sigma }^2)}\right\}.$$

Hence the posterior mode of ϕ² is

$$\widehat{{\varphi }^2}=\text{arg}\underset{{\varphi }^2\ge 0}{max}p({\varphi }^2\mid X)={\left(\frac{X^2}{3}-{\sigma }^2\right)}^{+}.$$ (22)

Given ${\varphi }^2=\widehat{{\varphi }^2}$, now we will consider the data likelihood X|μ ~ N(μ, σ²) along with the prior μ| ϕ² ~ N(0, ϕ²) to derive an empirical Bayes estimator for |μ|. It is easy to show that the posterior distribution of μ is given by

$$\mu \mid X\sim N\left(\frac{X\widehat{{\varphi }^2}}{\widehat{{\varphi }^2}+{\sigma }^2},\frac{{\sigma }^2\widehat{{\varphi }^2}}{\widehat{{\varphi }^2}+{\sigma }^2}\right).$$ (23)

Now under the squared error loss, the Bayes estimator of |μ| is E_μ|X(|μ|) which can be calculated using (23). If Y ~ N(θ, τ²), then E|Y| is given by:

$$E\mid Y\mid =\theta \left(2\mathrm{\Phi }(\theta /\tau )-1\right)+\sqrt{\frac{2}{\pi }}\tau e^{-{\theta }^2/2{\tau }^2}.$$ (24)

In the present problem,

$$\begin{array}{r}Y=\mu \mid X,\theta =\frac{X\widehat{{\varphi }^2}}{\widehat{{\varphi }^2}+{\sigma }^2},{\tau }^2=\frac{{\sigma }^2\widehat{{\varphi }^2}}{\widehat{{\varphi }^2}+{\sigma }^2}.\\ \text{Hence},\frac{\theta }{\tau }=\frac{X}{\sigma }\sqrt{\frac{\widehat{{\varphi }^2}}{\widehat{{\varphi }^2}+{\sigma }^2}},\frac{{\theta }^2}{2{\tau }^2}=\frac{X^2}{2{\sigma }^2}\left(\frac{\widehat{{\varphi }^2}}{\widehat{{\varphi }^2}+{\sigma }^2}\right).\end{array}$$

From (22), we get

$$\begin{array}{l}\frac{\widehat{{\varphi }^2}}{\widehat{{\varphi }^2}+{\sigma }^2}=\frac{{(X^2-3{\sigma }^2)}^{+}}{X^2}={\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+},\\ \theta =X{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+},{\tau }^2={\sigma }^2{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+},\\ \frac{\theta }{\tau }=\frac{X}{\sigma }\sqrt{{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}},\frac{{\theta }^2}{2{\tau }^2}=\frac{X^2}{2{\sigma }^2}{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}.\end{array}$$

Thus an empirical Bayes estimator of |μ| is given by

$$\begin{array}{l}{\widehat{\mid \mu \mid }}^{EB}=X{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}\left(2\mathrm{\Phi }\left(\frac{X}{\sigma }\sqrt{{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}}\right)-1\right)\\ +\sqrt{\frac{2}{\pi }}\sigma \sqrt{{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}}exp\left\{-\frac{X^2}{2{\sigma }^2}{\left(1-\frac{3{\sigma }^2}{X^2}\right)}^{+}\right\}.\end{array}$$ (25)