A fast and efficient method to compensate for brain shift for tumor resection therapies measured between pre-operative and post-operative tomograms

Abstract

In this paper, an efficient paradigm is presented to correct for brain shift during tumor resection therapies. For this study, high resolution pre-operative (pre-op) and post-operative (post-op) magnetic resonance images were acquired for 8 in vivo patients, and surface/subsurface shift was identified by manual identification of homologous points between the pre-op and immediate post-op tomograms. Cortical surface deformation data was then used to drive an inverse problem framework. The manually identified subsurface deformations served as a comparison towards validation. The proposed framework recaptured 85% of the mean sub-surface shift. This translated to a sub-surface shift error of 0.4mm±0.4mm for a measured shift of 3.1mm±0.6mm. The patient's pre-op tomograms were also deformed volumetrically using displacements predicted by the model. Results presented allow a preliminary evaluation of correction both quantitatively, and visually. While intra-op MR imaging data would be optimal, the extent of shift measured from pre- to post-operative MR was comparable to clinical conditions. This study demonstrates the accuracy of the proposed framework in predicting full volume displacements from sparse shift measurements. It also shows that the proposed framework can be extended and used to update pre-op images on a time scale that is compatible with surgery.

I. Introduction

Image-guided surgical systems rely on establishing a relationship between the physical space in the operating room (OR) and the patient's pre-operative (pre-op) image tomograms. Tissue deformation and shift occurring during tumor resection therapies often can compromise this spatial relation thereby degrading the accuracy of neuronavigation-based procedures. In the literature, it has been reported that the brain can deform a centimeter or more in a non-uniform fashion throughout the brain [1] and that brain shift occurs due to a variety of reasons including gravity, edema, hyperosmotic drugs and pathology [2, 3, 4]. In an effort to compensate for intra-operative (intra-op) brain shift, the two main candidates are active intra-op imaging [5, 2, 6], and computational model-based techniques to correct guidance systems during surgery (which we call model-updated image-guided surgery - MUIGS) [7]. Intra-op imaging systems have been predominantly limited to intra-op magnetic resonance (iMR) imaging and intra-op ultrasonography (iUS). While iMR techniques offer a powerful solution to the problem, they have been questioned for their cost-effectiveness, and as a routine technique, are overly cumbersome. While iUS approaches are realizable now, the images often lack the clarity of their iMR counterparts. In their current state, intra-op imaging systems do not present a complete solution for brain shift. As a cost-effective and efficient method, computational models have been used successfully in MUIGS to correct for intra-op brain shift.

The most common MUIGS approach is to develop a patient-specific computer model of the patient's brain that can predict intra-op deformations based on prescribed forcing conditions. Once the model is selected, a systems integration design is constructed which links together tissue deformation measurements taken intra-operatively to model-driving inputs. Once the model is calculated, full volumetric displacements are available for correcting pre-op images to the intra-op state of the tissue. Invariably, the computational model is a critical component of any MUIGS system and a spectrum of computational models ranging from less physically plausible but very fast models through to very accurate biomechanical models requiring hours of compute time to solve have been presented in the literature [8, 9, 10, 11, 12, 13]. Warfield et al [14] were among the first to demonstrate that computational models can be used in a time frame that is consistent with the demands of neurosurgery. The results reported in [14, 15] are encouraging and suggest that more complex models can be used in MUIGS. Others have performed similar work in retrospective analysis and have shown impressive results [11, 16].

Another critical component of MUIGS is the integration of sparse intra-op data which serves to control the computational model. Sparse, in this context, means data with limited information and/or spatial extent. The integration of sparse intra-op data should not only increase the accuracy of the system but it should also meet the real time constraints of neurosurgery. Towards this end, we reported a framework [15] that combined a computational model with a linear inverse model and was used to predict intra-op brain shift. In this framework, a series of model deformations based on complex loading conditions such as brain shift due to gravity, volume changes due to drug reactions, tissue swelling due to edema was computed pre-operatively and these model solutions were used to construct an `atlas' of deformations. Sparse intra-op surface measurements were then used to constrain the model and volumetric brain shift was predicted using a linear inverse model. The computational model and the inverse model have been discussed in brief in the following section. This framework was investigated within a series of phantom experiments, two in-vivo cases and a simulation study. Dumpuri et al. [15] reported that the framework recaptured on an average 93% of surface shift for all the experiments and 85% of the subsurface shift for the phantom and simulation experiments. Sub-surface shift measurements were not available for the two in-vivo cases that were reported by Dumpuri et al [15].

In the work presented here, we use the aforementioned framework to validate sub-surface shift measurements in 8 in-vivo cases. More specifically, surface and sub-surface shift measurements were obtained by registering post-operative (post-op) magnetic resonance (MR) tomograms to the patient's pre-op MR tomograms. Patient-specific models and deformation atlases were generated for each of the 8 cases and sub-surface shifts predicted by the combined linear inverse and computational model were validated against the measured shift. Shift error and angular error between the measured and predicted positions of the sub-surface points have been presented in Section IV. Also, the patient's pre-op MR image volumes were deformed using volumetric shift prediction as generated by the combined computational and linear inverse model. Qualitative comparisons with the post-op MR image volumes have also been presented in Section IV. It should be noted that the analyses reported in this paper was performed retrospectively and it did not affect the outcome of the tumor resection therapy.

II. METHODS

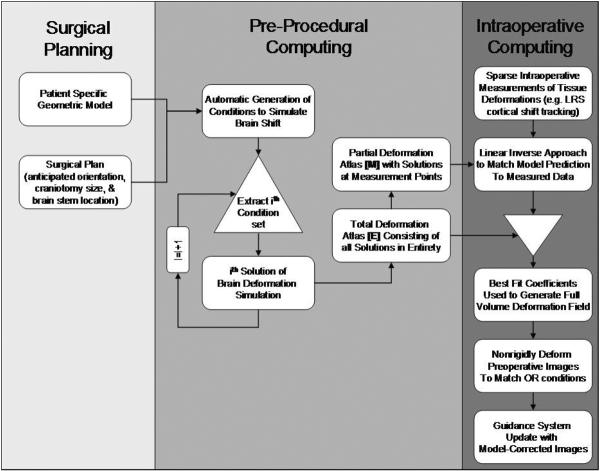
A general schematic of model-updated image-guided neurosurgery (MUIGNS) is shown in Figure 1. As seen in the figure, the computational model and the integration of intra-op data with the model are two important features of a MUIGNS system and these have been discussed in brief below.

Figure 1.

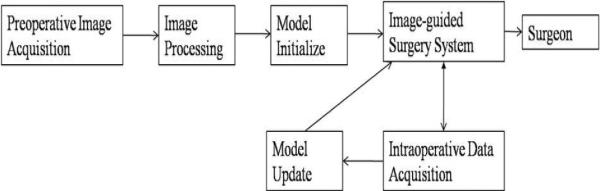
Schematic for Model-Updated Image-guided Neurosurgery (MUIGNS).

A. Computational Model

With respect to simulating brain deformation models, Hakim et al [17] showed that the transmission of intraventricular pressure throughout the brain parenchyma created a stress distribution that varied in magnitude and direction and made the observation that the “brain acts like a sponge”. In light of this fact, Paulsen et al. [19, 20] developed a 3D computational model based on Biot's theory of soil consolidation. In short, Biot's consolidation theory [21] gives a general description of the mechanical behavior of a poroelastic medium based on equations of linear elasticity for the solid matrix and Darcy's law for the flow of fluid through the porous matrix. According to this model, the brain is biphasic in nature and the volumetric strain rate depends on the changes in interstitial pressure and hydration. These equations have been described below and were used to model the deformation behavior of brain tissue.

$$\nabla •G\nabla \overrightarrow{u}+\nabla \frac{G}{1-2\gamma }(\nabla •\overrightarrow{u})-\alpha \nabla p=({\rho }_t-{\rho }_f)g$$ (1)

$$\alpha \frac{\partial }{\partial t}(\nabla •\overrightarrow{u})-\nabla •k\nabla p=-k_c(p-p_c)$$ (2)

where u is the displacement vector, p the interstitial pressure, G the shear modulus, γ the poisson's ratio, α the ratio of fluid volume extracted to volume change of the tissue under compression, ρ_t the tissue density, ρ_f the fluid density, g the gravitational unit vector, t the time, k_c the capillary permeability, p_c the intracapillary pressure, k the hydraulic conductivity. Intra-op CSF drainage reduces the buoyancy forces, which serve to counteract gravity forces thus causing gravitational forces to deform the brain. This effect of gravitational forces on the brain is modeled as a difference in density between tissue and surrounding fluid as given by the term on the right-hand side of Equation 1. Hyperosmotic drugs such as mannitol have the effect of reversing the blood–brain osmotic barrier, drawing water from the extracellular brain space, thereby decreasing brain volume. This decreased capillary pressure pulls interstitial fluid from the extracellular brain space causing a decrease in tissue volume and is modeled using the term on the right-hand side of Equation 2. Extensive validation studies have been conducted in porcine systems using this model [22, 20, 23, 24]. Miga et al. presented work concerned with gravity-induced shift and strategies to simulate retraction and resection [20, 7]. Roberts et al. assembled this work into a general approach to model-based corrections for guidance systems. Since these early results, continued developments towards the use of stereo pair measurements of brain shift [25], and ultrasound [16] has continued. In all, the results suggest that the computational model can capture 70% to 80% of the subsurface deformation in animal and limited human experiments. Building on this work, and the work by Davatzikos et al. [26], we have developed a three stage approach that uses the pre-op plan, an a priori understanding of brain shift, and pre-procedural computing to generate a fast, efficient, and accurate method to account for shift intra-operatively.

B. Pre-Op surgical Planning

One important aspect to our approach is to maximize the utilization of pre-surgical plans realized by the surgeon. While a full simulation of the procedure is considerably cumbersome, determining some a basic understanding of the surgeon's plan for brain presentation can be enormously useful in generating our shift compensation approach. In the framework being developed, four key pieces of pre-procedural information are determined: (1) the anticipated orientation of the head in the operating room (OR) for surgical exposure, (2) the anticipated area of the craniotomy and an approximation to its size, (3) the location of the brain stem in the patient's pre-op images, and (4) the location of the tumor and edema in the patient's pre-op images. With our surgical planning software tools, this information can be determined in a few minutes by the surgeon. This information is then utilized in generating a series of condition sets that can be used to represent different intraprocedural simulations of brain deformation, i.e. an `atlas' of deformations.

In order to perform simulations based on the surgical plan, a computer model must be constructed. To accomplish this, the patient's pre-op MR image volume is used to construct a geometric computer model. This process involves: (1) the utilization of automatic segmentation techniques [27] to extract the brain and interesting structures from the volumetric images, (2) generating a surface that includes the outer brain and internal structures of interest (e.g. tumor volume) and providing it as input to a volumetric mesh generator that breaks this domain into approximately a hundred thousand tetrahedral volume elements, and lastly, (3) incorporating the white/gray matter boundary using an image-to-grid thresholding technique. The mathematical model used to simulate brain deformations has been reported previously [8, 28]. Once this geometric model is built, the physics associated with soft-tissue deformation must be chosen and any number of numerical methods to solve partial differential equations can be employed to simulate intra-op brain shift (in this work, the physics is based on Biot's bi-phasic consolidation theory and the numerical solution method is the finite element method). In previous work, the computational model has been extensively reported and is capable of simulating deformations due to surgical manipulation, retraction, resection, the influence of hyperosmotic drugs, edema, gravity-induced shift, and swelling [24, 20, 15].

C. Pre-Procedural Computing

Once the pre-op plan and model are in place, a series of condition sets can be generated that will simulate a variety of intra-op deformations. Currently, we are employing three principle modes of deformation: (1) gravity-induced brain shift, (2) volumetric contraction due to hyperosmotic drug interactions, and (3) swelling due to the presence of edema around a tumor. An example of a condition set that allows the model to predict gravity-induced brain shift in the head-neutral supine condition is shown in Figure 2. Surface 1 is assumed to be stress-free. i.e., free to deform. Surfaces 3 and 4 (the brain stem region) are fixed for displacements, i.e., minimal deformation in the brain stem region is assumed, and Surfaces 2 and 5 are permitted to move along the cranial wall. Each condition set will have an estimated intra-op cerebrospinal fluid (CSF) drainage which also determines what surfaces are open to atmosphere and which are submerged. Parts of the brain surface above the CSF drainage level are assumed to reside at atmospheric pressure and parts below are non-draining surfaces.

Figure 2.

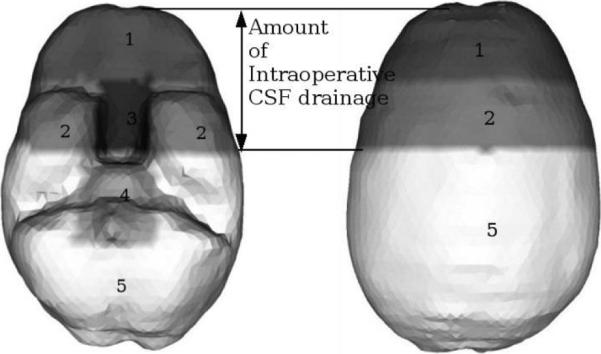
Boundary condition (BC) template set for a supine patient with neutral head orientation in the OR. Displacement BCs: Surface 1: Stress-free, i.e., free to deform, Surface 2 and 5: slide along the cranial wall but are not permitted to move along the normal direction, Surfaces 3,4: Fixed, i.e., cannot move. Pressure BCs: Surfaces 1, 2 and 3 reside at atmospheric pressure, Surfaces 4 and 5 are still submerged in CSF and therefore do not allow fluid drainage.

Figure 2 is a representative condition set. The reality of our framework is that the condition sets are perturbed systematically, and automatically to reflect changes to the OR presentation of the brain. For example, amount of intra-op CSF drainage and patient's head orientation in the OR are two factors that determine the amount of gravity-induced shift in our computational model. Varying amounts of CSF drainage translates to the delineation between Surface 2 and 5 in Figure 2 moving upwards in the case of less drainage, and downwards in the case of more. Similarly, different head orientations would translate to the delineation between surfaces 2 and 5 being at increasingly oblique angles to the horizontal shown in Figure 2.

Accounting for these varying amounts of gravity-induced shift has been reported previously by Dumpuri et al. [15]. In addition to these more mechanical-like events, physiological variability has also been incorporated. For example, when simulating tumor-growth induced edema, aberrant angiogenic activity can be simulated by changing capillary permeability in regions surrounding the tumor such that more fluid moves into the interstitial spaces. The framework developed in [15] allows us to vary the strength of that infusion as separate condition sets. And with each condition set, a new deformation is simulated using the computer model. Taking all these solutions in their entirety is what we have termed a total deformation atlas, (the variable [E] in the equation sets in the Appendix). If we take only parts of those solutions such as the areas of the brain surface where we obtain intra-op shift measurements, this subset of solution values is what we have termed a partial deformation atlas, (the variable [M] in the equation sets in the Appendix). Given that we only know deformations at the cortical surface, it is the partial deformation atlas that becomes of critical import for our compensation approach. It should be noted however that the incorporation of sparse subsurface measurements such as provided by iUS could readily be incorporated into this framework.

D. Intra-op Computing and Inverse Model

There is a degree of uncertainty associated with using the computational model in a purely predictive sense in the OR. For example, when predicting gravity-induced brain deformations, the patient head orientation and the amount of intra-op CSF drainage must be ascertained. The surgeon's pre-op plan can be used to approximate the patient's orientation in the OR, but it is difficult to measure the amount of fluid drainage. Also, in cases where mannitol is administered or other complex vascular events occur, it is difficult to differentiate the shift due to these and that from gravity. In addition, the surgeon can dynamically change the relationship of gravity to the patient by lowering or raising the head of the bed. Equations (1) and (2) are therefore solved for a range of possible sources of brain shift and the individual deformation solutions are assembled in the total deformation atlas [E]. For example, the patient head orientation and the amount of CSF drainage are two factors that cause the gravity-induced brain shift in our computational model. A rough estimate of the intra-op patient head orientation is obtained from the surgeon and this orientation is varied to account for possible changes in head position during the tumor resection therapy. Similarly for a given head orientation, the amount of CSF drainage level is varied and, equations (1) and (2) are solved for every possible combination of head orientation and CSF drainage level. All these displacement solutions are then assembled in the total deformation atlas [E]. The advantage of a deformation atlas is that this variability can be built-in to our condition sets, i.e. varying orientation configurations as well as other shift factors can be incorporated in our atlas of solutions. Therefore [E] is of size (n × 3) × m, where n is the number of nodes in the finite element mesh, 3 is the number of Cartesian displacement components at each node, and m the number of times the model is run in a forward manner or the number of model solutions. As noted above, we then construct a partial deformation atlas [M] for the areas of the brain surface where we obtain shift measurements. Therefore [M] is of size (n_s × 3) × m, where ns is the number of points for which sparse measurements were obtained. The different deformation solutions are combined using the following equation:

$$\mathrm{G}\left(\alpha \right)={\Vert \mathrm{M}\alpha -\mathrm{U}\Vert }^2+{\beta }^2{\Vert \alpha \Vert }^2+\varphi {\left[\mathrm{W}\right]}^{\mathrm{T}}\left[\mathrm{Y}\right]\left\{\alpha \right\}$$ (3)

where ∥ .∥ is the Eucledian norm, [M] the partial deformation atlas, U the measured shift on the cortical surface (i.e. sparse intra-op data), W the weighting vector, Y is the strain energy matrix, α the regression coefficients and, β the Tikhonov factor. The first term in the equation serves to minimize the error between the predicted model solutions and measured shift, the second term is a regularization factor and the third term minimizes the elastic energy across the deformation atlas and produces a spatially smooth displacement field. The vector of regression coefficients is determined from Equation 3. The measured sparse data act as control points and is used to constrain the inverse approach. In this study, sub-surface points served as unbiased error estimates to validate the accuracy of volumetric brain shift predicted by Equation (3). In our proposed framework Equation (3) is the only equation solved in the OR and therefore can be solved on a time scale that is compatible with surgical proceedings. Also, one of the advantages of Equation (3) is that it is a linear system which should meet the real time constraints of neurosurgery. In addition, as alluded to earlier, Equation (3) represents a relatively simple approach to incorporate measurement data and could easily be modified to accommodate sub-surface data. A more detailed description of the inverse approach can be found in [15]. Once the regression coefficients are determined by Equation (3) a full volumetric deformation field is calculated using total deformation atlas [E] multiplied by the regression coefficients, {α}.

In the past, we have used very sparse data sets of points to guide [15], e.g. 12–18 points distributed over the cortical surface. It would be desirable to generate more dense constraints to our approach but the results using this very sparse set of measurements has been considerable. This paper also utilizes a very sparse set of points but has the added benefit of subsurface validation targets, which was not previously possible in [15]. In addition, previous work in [15] only reflected two cases whereas this work involves the more considerable population of 8 patients. It should be noted though surface and subsurface shift measurements in this paper were obtained between pre-op and post-op MR brain images, the proposed framework can be easily translated to intra-op surface and sub-surface shift measurements.

E. Updating pre-op images based on Model Deformations

The last and an equally important step in a MUIGNS framework is the updating of pre-op images based on the full volume displacements predicted by the combined computational and linear inverse model. Since the finite element mesh for each patient is built using the patient's preop images and the displacements predicted by the constrained least squares approach are defined in a continuum manner over the finite element mesh, these displacements can be used to deform the pre-op images. An image-updating algorithm was initially presented in [20]. In [20], Miga et al. used a backcasting technique to deform the patient's pre-op images using displacements predicted by the model. We parallelized this image-deformation algorithm in order to meet the real time constraints of neurosurgery. This algorithm eliminates the problem of holes/tears in the updated image, produces a contiguously deformed image that is based on the governing equations for the forward model and translates the volumetric brain shift predicted by the model into images that can be used for guidance by the neurosurgeon. The predictions can also be used to simultaneously align any other pre-op data that may be of use to the surgeon (e.g. functional MR, positron emission tomography, diffusion tensor MR, etc).

F. Summary of Brain Shift compensation strategy

Figure 3 is a flow chart which demonstrates how the three stages (Sections 2.2, 2.3, and 2.4) interact with respect to our shift compensation strategy. The two components central to the Surgical Planning stage are: (1) the anticipated surgical information regarding the patient's presentation as estimated by the surgeon, and (2) the manipulation of the pre-op magnetic resonance image volumes to generate patient-specific models. Given that we have developed a strategy to automatically generate a variety of simulation condition sets, the Pre-Procedural Computing amounts to a computer cluster executing each simulation and storing the solution in what we have termed a deformation atlas. Given that we have sparse measurement data, the Intra-operative Computing stage will use a partial deformation atlas to construct a deformation reconstruction approach which best fits the measurement data. From there, new image volumes can be generated and the guidance can be updated.

Figure 3.

General shift compensation approach from surgical planning to procedural execution

III. PATIENT POPULATION

Eight patients (mean age of 51.4yrs, with 2 men) with brain tumors (primary or metastatic) were included in this study (shown in Table 1). All patients were enrolled after obtaining written informed consent for participation in this study, which was approved by the Institutional Review Board of the Vanderbilt University School of Medicine. After anesthetic induction, the patients were positioned on the operating room table and were secured to the table using a three-pin Mayfield skull clamp. This clamp attaches to the operative table and holds the head absolutely still during delicate brain surgery. All patients received diuretics (mannitol, 0.5–1.0 g/kg) and steroids (dexamethasone) immediately before incision. All patients underwent craniotomy for tumor resection and no side effects related to participating in this study were noted. Pre-op and post-op MR tomograms were acquired as 1.5T, T1-weighted, 3D-SPGR, 1×1×1.2mm voxel, gadolinium-enhanced and non-enhanced image volumes. It should be noted that the pre-op image volumes were acquired a day before or on the morning of the surgery and the post-op images were acquired a day after surgery. The pre-op and post-op MR volumes were registered using mutual information. The brain region is then segmented from these registered volumes using an atlas based segmentation method [29]. Textured brain surfaces are generated from these segmented MR tomograms and corresponding cortical features (vessel bifurcations, sulcal and gyri patterns) identified manually on these surfaces are used as measures of brain shift. Tumor and edema regions were identified and segmented manually from the gadolinium-enhanced pre-op image volumes. A patient-specific model was generated for each patient in a manner similar to the one reported in [15]. For each patient, brain shift was simulated with four different deformation atlases that reflected different assumptions about the surgical presentations of the patient: (I) Tumor was resected from the brain. Mannitol was not administered and gravity was the solitary factor causing shift, (II) Tumor was resected from the brain. Mannitol was administered and was the solitary factor causing shift, (III) Tumor was present and shift was induced by tissue swelling in the tumor and edematous region and with mannitol being administered to the patient, and (IV) all three aforementioned atlases were concatenated into one large deformation atlas. Atlas I employed 60 different patient orientations with 4 levels of intra-op CSF drainage for each orientation, resulting in 240 displacement solutions. Atlas II used three different capillary permeability values for each of the 60 patient orientations, thus resulting in a total of 180 different displacement solutions. In order to simulate displacement solutions for Atlas III, three different craniotomy sizes were assumed and for each craniotomy size, three different edematous tissue regions were assumed. For each edematous region, three different capillary permeability values and three different intracranial pressures were assumed. This resulted in a total of 81 different scenarios. Atlas IV thus consisted of 501 deformation data sets. With respect to the driving sparse data, 15–20 corresponding points were identified manually for each patient between the registered textured brain surfaces.

Table 1.

Patient Information. Tumor Types: Gr - Grade, Olig. - Oligodendroglioma, Mening. - Meningioma, Asto. - Astrocytoma, GBM -Glioblastoma Multiforme, Met. - Metastatic Tumor. Orientation: IS - refers to rotation about inferior-superior axis (e.g., IS 90d rot reflects patient's head parallel to the OR floor). Location: L: left, R: right, F:frontal, T: temporal, P:parietal.

Pt. #	Age,Sex	Tumor Type	Craniotomy (diameter,cm)	Orientation (deg.)	Location	Lesion size (cm.)
1	22,F	Gr (II) Olig.	7.7	IS 90d rot	L,F	5.2×6.2×6.0
2	52,M	Astro.	8.3	IS 90d rot	L,F	4.9×5.6×5.0
3	60,M	Mening.	5.5	IS 90d rot	R,F/T	4.5×6.4×4.3
4	77,M	Gr (IV) GBM	5.0	IS 90d rot	L,T	3.4×6.3×2.0
5	56,F	Met.	4.5	-	L,F	4.7×3.2×4.0
6	75,F	Gr (II) GBM	6.1	IS 15d rot	L,T	5.0×5.0×5.0
7	23,F	Gr (II) Astro.	6.4	Neutral	R,F	4.0×3.0×3.0
8	46,F	Gr (IV) GBM	4.3	IS 90d rot	R,T	3.0×3.0×3.0

Differences in position between the post-op and pre-op corresponding points were used as measures of brain shift and these displacements were used to constrain the inverse model. Nodes on the finite element mesh corresponding to these points are identified using a closest point algorithm and these nodes were used to compute the intra-op deformation atlas. Also, six to eight corresponding sub-surface points were identified on the registered MR tomograms and these points were used to validate sub-surface shifts predicted by the inverse model. Given the uncertainties in measurements due to segmentation and registration errors, surface shifts lesser than 3mm and sub-surface shifts less than 2mm were not included in this study and the sub-surface points were spatially distributed over the entire brain volume. As stated earlier, it should be noted that the shift measurements, model simulation and analyses were performed in a retrospective manner in order to simulate a potential application of the proposed framework within the OR and it did not affect the outcome of the reported tumor resection therapies. Also, the patient's pre-op MR image volumes were deformed using the volumetric shift predicted using the inverse model and qualitative comparisons with the post-op MR image volumes have been presented in the following section.

IV. RESULTS

Anatomical fiducials (such as ear lobes, eye sockets, and corresponding points in the brain stem region) were chosen between the pre-op and post-op MR tomograms to assess the accuracy of the mutual information algorithms that were used to register these image volumes. The mean difference in position between these points was found to be 1.0±0.3mm. It should be noted that this does not represent a registration error and detailed error analyses of the registration algorithms can be found in [30].

Table 2 summarizes the measured shift values for all the patients reported in this study. Surface landmarks were identified between the textured MR pre-op and post-op brain surfaces and sub-surface landmarks were identified manually between the pre-op and post-op MR brain image volumes. The positional difference between the points have been reported in the table as measured shift values and displacement values have been reported as absolute numbers in the table without depicting a direction using positive or negative signs. Figure 4 is a representative example that shows the surface and sub-surface points for Patient 1 used in this study.

Table 2.

Measured surface and sub-surface shift in mm for all eight patients. Mean ± standard deviation, and (maximum) measured values is reported.

Patient #	Measured Surface shift in mm	Measured Sub-surface shift in mm
1	8.2±2.2 (12.2)	2.6±1.6 (5.8)
2	9.2±1.3 (11.6)	4.0±1.2 (6.3)
3	8.8±1.9 (12.6)	3.7±0.9 (5.5)
4	5.4±0.9 (7.0)	2.6±1.6 (5.7)
5	10.6±2.4 (15.1)	3.1±1.6 (6.2)
6	5.3±0.8 (6.8)	2.4±1.3 (4.8)
7	9.4±1.1 (11.5)	3.2±1.4 (5.9)
8	5.3±0.9 (7.1)	2.6±1.6 (5.6)

Figure 4.

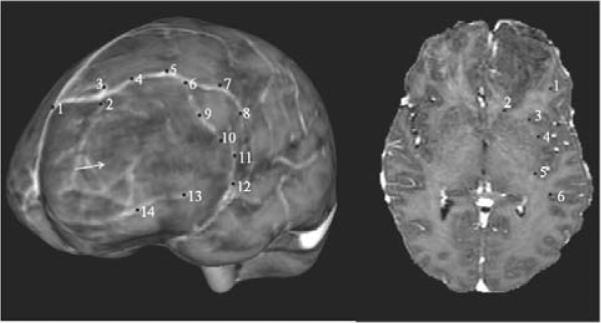
Surface (left) and sub-surface (right) points for Patient 1 that were used in the model. The arrow in the surface point distribution figure (left) points to the location of the tumor. Sub-surface points 1 and 2 are located superior (at a higher elevation) to the tumor, points 3,4 and 5 were located in plane with the tumor and point 6 is located inferior to the tumor. Surface points were used to constrain the linear inverse model and sub-surface points were used to validate the accuracy of the model. Though the same numbering scheme has been used in both halves of the figure, it should be noted that the points in the left-hand side do not correspond to the points in the right-hand side.

It should be noted that the surface points were used to constrain the inverse model and the sub-surface points served as unbiased error estimates. Also, the sub-surface points shown in the figure are not co-planar, but are distributed over the entire brain volume. Error between measured and predicted shift values has been reported in Table 3. Shift error in the table refers to the magnitude error between the measured and predicted shifted positions of the sub-surface points and angular error refers to the directional accuracy between the measured and predicted shifted positions of the sub-surface points. Averaging over all eight patients, Atlas IV the constrained linear inverse model produced a mean shift error of 0.4±0.4mm and a mean angular error of 9.5±1.1° with respect to a mean sub-surface shift of 3.1±0.6mm. As stated earlier, Atlas IV the concatenated deformation atlas contains deformation solutions simulating gravity-induced shift, brain shift due to hyperosmotic drugs such as mannitol and brain shift due to tissue swelling in the edematous region. The percent shift recaptured with the constrained linear inverse model using Atlas IV has been reported in Table 3. Averaging over all eight patients, the constrained linear inverse model recaptured 85% of the mean measured sub-surface shift.

Table 3.

Shift error (in mm) and Angular Error (in degrees) for all eight patients. Mean + Standard deviation (maximum) of the error and the measured values have been reported.

Patient #	Measured Surface Shift in mm	Measured Sub-Surface Shift in mm	Shift Error in mm				Angular Error in deg.
			Atlas I	Atlas II	Atlas III	Atlas IV	Atlas I	Atlas II	Atlas III	Atlas IV
1	8.2±2.2 (12.2)	2.6±1.6 (5.8)	0.6±0.5 (1.5)	0.7±0.4 (1.5)	0.7±0.4 (1.5)	0.4±0.4 (1.2)	8.4±1.3 (10.9)	8.4±1.3 (10.9)	9.4±1.6 (12.6)	8.4±1.3 (10.9)
2	9.2±1.3 (11.6)	4.0±1.2 (6.3)	0.8±0.4 (1.6)	0.6±0.5 (1.6)	0.6±0.4 (1.3)	0.6±0.4 (1.3)	9.6±1.2 (12.0)	9.4±2.2 (13.8)	9.6±1.2 (11.9)	9.6±1.2 (12.0)
3	8.8±1.9 (12.6)	3.7±0.9 (5.5)	0.7±0.5 (1.6)	0.8±0.4 (1.5)	0.8±0.3 (1.3)	0.4±0.4 (1.1)	10.4±2.0 (13.9)	10.1±2.2 (14.5)	10.1±2.2 (14.5)	10.4±2.0 (13.9)
4	5.4±0.9 (7.0)	2.6±1.6 (5.7)	0.6±0.5 (1.5)	0.7±0.5 (1.8)	0.7±0.5 (1.9)	0.4±0.4 (1.2)	9.6±1.2 (12.0)	8.4±1.3 (10.9)	8.4±1.3 (10.9)	8.1±1.3 (10.7)
5	10.6±2.4 (15.1)	3.1±1.6 (6.2)	0.8±0.3 (1.4)	0.9±0.3 (1.5)	0.6±0.3 (1.1)	0.4±0.4 (1.3)	11.4±1.3 (14.0)	11.2±1.8 (14.8)	11.2±1.8 (14.8)	11.4±1.3 (14.0)
6	5.3±0.8 (6.8)	2.4±1.3 (4.8)	0.8±0.4 (1.6)	0.6±0.5 (1.5)	0.6±0.5 (1.5)	0.4±0.3 (1.1)	9.4±2.2 (13.6)	10.1±2.2 (14.6)	9.6±1.2 (12.0)	9.4±2.2 (13.6)
7	9.4±1.1 (11.5)	3.2±1.4 (5.9)	0.5±0.3 (1.1)	0.6±0.4 (1.4)	0.6±0.3 (1.1)	0.5±0.3 (1.1)	9.5±2.3 (14.1)	8.9±2.5 (13.9)	8.9±2.5 (13.9)	9.5±2.3 (14.1)
8	5.3±0.9 (7.1)	2.6±1.6 (5.6)	0.6±0.5 (1.6)	0.7±0.5 (1.8)	0.6±0.4 (1.4)	0.4±0.4 (1.2)	9.5±2.3 (14.1)	10.1±2.2 (14.6)	9.6±1.2 (12.0)	9.4±2.2 (13.6)

A. Illustrative Results

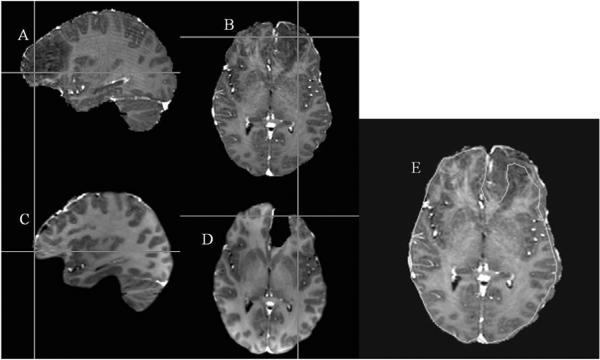
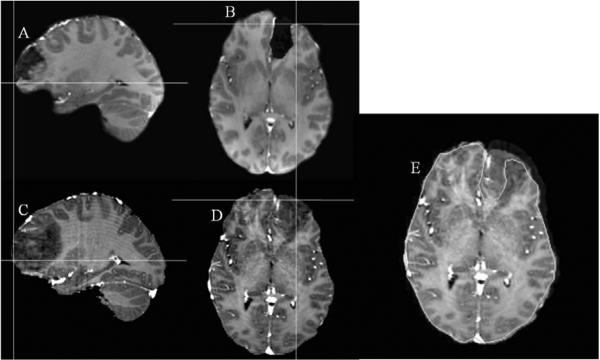
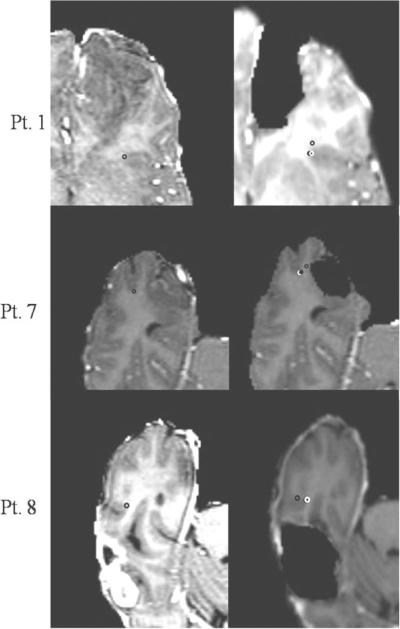
Figure 5 qualitatively illustrates the cortical surface shift for Patient 1 reported in this study. Figure 5A and 5B represent a sagittal and an axial slice from the patient's pre-op images. Figures 5C and 5D show the corresponding slices from the patient's post-op images. The cross-hairs show that a point picked on the cortical surface of the post-op MR surface (bottom row) actually lies beneath the surface in the pre-op MR images (top row). Figure 5E shows the outer edge of an axial slice of the post-op images (shown in green) overlaid on the corresponding axial slice of the pre-op MR images. Figure 6 demonstrates intra-op updating of pre-op images based on model predictions. For sake of continuity, post-op slices shown in Figures 5C and 5D have been used to qualitatively illustrate the shift correction. Figures 6A and 6B represent a sagittal and an axial slice from the patient's post-op images. Figures 6C and 6D show the corresponding slices from the image volume obtained using model predictions. It can be seen that the shift depicted by the cross-hairs in Figure 5 has been accounted for in Figure 6. Figure 6E shows the outer edge of an axial slice of the post-op images (shown in green) overlaid on the model-predicted images and demonstrates the matching accuracy of the proposed framework. It should be noted that though the tumor was removed from the brain tissue when building the deformation atlases, tumor was not removed from the brain volume when the pre-op images were deformed using the predicted displacements. In cases where the atlas contained a resected tumor solution within the basis, the displacements in the tumor region were interpolated from surrounding values. Figure 7 shows sample image updating results for a sub-surface point for Patients 1, 7 and 8. The first column shows a sub-surface point (represented as a black hollow circle) in the patient's pre-op image. The hollow black circle in the second column shows the position of the same point before brain shift and the solid black circle shows the true shifted position of the point. The white hollow circle in the second column shows the predicted shifted position of the point. For the sub-surface point shown in the figure, the model correction approach accounted for 81%, 80%, and 83% of the measured shift for each of the respective patients 1, 7, and 8.

Figure 5.

Qualitative representation of shift between pre-op and post-op MR images. 5A: Sagittal slice of the patient's pre-op image. 5B: Axial Slice of the patient's pre-op image. 5C: Corresponding sagittal slice of the patient's post-op image. 5D: Corresponding axial slice of the patient's post-op image. Cross-hairs in the bottom row represent a point picked on the cortical surface of the patient's post-op image actually lie beneath the parenchyma in the patient's pre-op image due to the presence of brain shift. 5E: Outer edge contour of an axial slice (shown in green) of the patient's post-op image overlaid on the patient's pre-op image.

Figure 6.

Demonstration of intra-op updating for the post-op slice show in Figure 5. 6A: Sagittal slice of the patient's post-op image. 5D: Corresponding axial slice of the patient's post-op image. 6C and 6D: Image updates using displacements predicted by the proposed framework. 6E: Outer edge contour of an axial slice (shown in green) of the patient's post-op image overlaid on the image obtained using model predictions.

Figure 7.

Image updating results for a sub-surface point chosen in Patients 1,7 and 8. Column 1: Sub-surface point (shown as a hollow black circle) in the patient's pre-op image. Column 2: Hollow black circle shows the same point in the patient's post-op image before brain shift. Solid black circle shows the “true” shifted position of the point and the white hollow circle shows the predicted shifted position of the point. True shift here refers to the shift measured using the registered pre-op and post-op point. Measured/True shift for patient 1: 5.5mm, Predicted shift: 4.5mm. Measured shift and Predicted shift for Patient 7: 4mm and 3.2 mm respectively. Measured shift and predicted shift for patient 8: 5.1mm and 4.2mm respectively.

V. DISCUSSION

The results presented in this study demonstrate that the combined computational and linear inverse model is capable of predicting full volume displacements and can be used in a MUIGNS system. The framework reported here relies on predicting brain shift using a patient-specific atlas of model solutions that are consistent with the forces causing brain shift. This series of model solutions are then combined in a linear fashion using the sparse measured data. Since the pre-op image volumes are acquired a day prior to surgery, the atlas of deformations can be computed a day prior to surgery using the parallelized computational model and the automatic boundary condition algorithm reported in [15]. This allows the shift correction strategy relayed by equation (1) to be executed almost instantly within the intra-op environment. As a result from this approach, the issue of intra-op compute time is diminished, and questions regarding integration become more prominent. Figures 6 and 7 qualitatively demonstrate the shift correction using displacements predicted by the combined computational and linear inverse model. In all eight cases presented, sub-surface points were chosen near the lateral ventricles and the tumor resection cavity to validate the sub-surface shift predicted by the model. Averaging over all the eight patient cases, the model recaptured 85% of the mean measured shift. Also, a shift of 4–6mm of the tumor boundary and a shift of 3–6mm at the lateral ventricles was observed in the registration studies and the model predictions. This is in agreement with the shift measurements reported in the literature [31, 32, 20]. As stated earlier, the proposed framework addresses the uncertainties associated with running the computational model in a purely predictive sense in the OR by trying to account for all possible sources of intra-op brain shift. As a result, the computational model is run in a forward manner multiple times to account for deformations due to gravitational forces, hypersomotic drugs, tissue swelling. These deformation solutions are then combined in a least-squares sense using the combined computational and linear inverse model. Figure 8 shows the distribution of regression coefficients that optimally combine the different deformation solutions for Patients 1, 7 and 8. Regression coefficients computed using the concatenated deformation atlas (Atlas IV reported in Section III) were used to generate the charts shown below. Atlas IV consisted of a total of 501 model solutions (240 of the displacement solutions were modeled to simulate gravity-induced shift, 180 to model shift due to mannitol and 81 due to tissue swelling and mannitol combined). Averaging over all eight patients, 45% of the nonzero regression coefficients belonged to gravity-induced shift, 46% to mannitol-induced shift and 9% to displacements modeled to simulate tissue swelling. These findings suggest that gravity and mannitol-induced shift may have an equal contribution in predicting the observed brain shift. We realize that these findings need to be validated in a bigger patient population before ascertaining the correlation between simulated boundary conditions and the observed brain shift. Nevertheless, these findings are intriguing and to our knowledge represent the first report to suggest a more prominent role for hyperosmotic drugs effects within brain shift compensation strategies. In addition, these results do suggest that the atlas-based framework can be used to account for the complex loading conditions that occur during tumor resection therapies.

Figure 8.

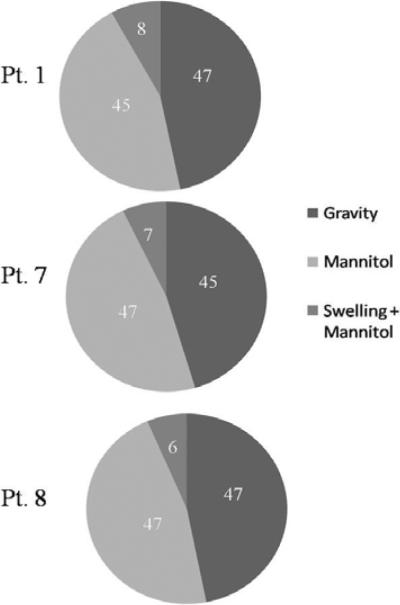
Distribution of regression coefficients for Patients 1, 7 and 8. Atlas IV (concatenated deformation atlas) was used to generate these charts. Though only three patients have been shown here, a similar distribution was observed for all eight patients reported in this study.

A few limitations of this study must be noted. First, we used the brain shift between pre-op and post-op image volumes in this study. Since the post-op MR image volumes were acquired a day after surgery, we understand that the shift used in this study is not representative of the intra-op brain shift. Differences between intra-op patient positioning (head orientation in the OR) and positioning of the head during post-op image acquisition, viscoelastic nature of the brain and the regeneration of CSF within the brain are factors that might have caused the brain to recover some of its intra-op brain shift. We acknowledge that the limitations of using post-op MR images as measures of brain shift, but unfortunately, sub-surface intra-op measurements were not available. To address this shortcoming, in each of the cases reported herein, intra-op cortical deformation measurements before and after resection were taken using a laser range scanner and the magnitude of surface shift was compared to that measured by the pre-post MR analysis conducted here. While direct correspondence could not be established between shifting structures, regionally it appears that approximately 25% of the brain shift occurring intra-operatively is recovered at the time of a postoperative MR. From this, it is evident that considerable brain shift is still present at the time of a post-operative MR. While the exact shift directions may differ due to the orientation of the patient in operating room versus the scanner, the atlases generated in this work can be easily extended to capture these configurations. A second limitation is that the model did not account for more direct interactions such as retractions and the brain tissue collapsing into the tumor resection cavity. It should be noted that retractors were not used in the cases reported in this work. However we hypothesize that surface loadings resulting from tissue retraction can be modeled in a forward manner as demonstrated in our previous work [24, 33]. Our vision of shift compensation would involve an atlas-based method to compensate for the more volumetric deformation events with a more straight predictive calculation for the more direct interactions such as that performed by retraction. We observed normal brain tissue collapsing into the tumor resection cavity during surgery for Patient 2 reported in this study. Though this phenomenon was not observed in the other patient cases, we do realize its importance especially in terms of intra-op brain shift and predicting tumor margins in the presence of intra-op brain shift. We are working on enhancing the existing computational model to account for this surface collapse. Also, corresponding points could not be identified near the tumor resection margins and in the regions where the brain tissue collapsed and we do realize that shift predictions for this patient are incomplete. Despite these model limitations, the computational time associated with running the inverse model and updating the pre-op images and the shift error analyses are encouraging and indicate that the linear inverse model reported herein combined with this parallel image updating technique is capable of predicting intra-op brain shift in a real time fashion.

VI. CONCLUSIONS

A framework to predict sub-surface shifts using a combined computational and linear inverse model has been utilized in a preliminary validation of our approach to brain shift correction. The framework reported relies on relatively inexpensive small scale computer clusters and can compute image updates on a time scale that is compatible with the surgical removal of tumor. The sub-surface error measurements and the qualitative image comparisons presented in this work are encouraging. Shift measurements used in this study were based on post-op images and we do have preliminary data that suggests this does not represent the extent of intra-op shift. However, all indications based on these results as well as past performance would indicate that model-based approaches to compensate for shift would be able to correct for 70–80% of shift. While the intra-op error would likely be larger than that reported here (0.4 ± 0.4 mm), we would suggest that the percent of capture would remain the same, i.e. 70–80%. In addition we are working on enhancing the computational model to account for brain shift due to the tissue collapsing into the tumor resection cavity. Lastly, while preliminary in nature, these results are the first to suggest the import of modeling hyperosmotic drugs whereby regression coefficients representing vascular effects were virtually weighted equally with the gravity-induced shift regression coefficients.

Table 4.

% shift recaptured for all eight patients using Atlas IV.

Patient #	% Shift Recapture
	Mean	Minimum
1	85	79
2	85	79
3	89	80
4	85	79
5	87	79
6	83	77
7	84	81
8	85	79