Abstract
Purpose
A new method is presented for synthesizing dose-response data for biochemical control of prostate cancer according to study design (randomized vs. non-randomized) and risk group (low vs. intermediate-high)
Methods and materials
Nine published prostate cancer dose escalation studies including 6539 patients were identified in the MEDLINE and CINAHL databases and reviewed to assess the relationship between dose and biochemical control. A novel method of analysis is presented in which the normalized dose-response gradient, γ50, is estimated for each study and subsequently synthesized across studies. Our method does not assume that biochemical control rates are directly comparable between studies.
Results
Non-randomized studies produced a statistically significantly higher γ50 than randomized studies for intermediate-high risk patients (γ50= 1.63 vs γ50= 0.93, p=0.03) and a borderline significantly higher (γ50= 1.78 vs γ50= 0.56, p=0.08) for low risk patients. No statistically significant difference in γ50 was found between low and intermediate-high risk patients (p=0.31). From the pooled data of low and intermediate-high risk patients in randomized trials, we obtain the overall best estimate of γ50=0.84 with 95% confidence interval 0.54–1.15.
Conclusions
Non-randomized studies over-estimate the steepness of the dose-response curve as compared to randomized trials. This is probably the result of stage migration, improved treatment techniques and a shorter follow-up in higher-dose patients that were typically entered more recently. This over-estimation leads to inflated expectations regarding the benefit from dose-escalation and could lead to under-powered clinical trials. There is no evidence of a steeper dose-response for intermediate-high risk compared to low risk patients.
Keywords: Prostate cancer, dose response, radiotherapy, systematic review
INTRODUCTION
Recent advances in radiation delivery techniques, such as conformal (1) and intensity modulated radiotherapy (IMRT), proton therapy and image guided therapy (2, 3), have allowed delivery of external beam radiotherapy doses exceeding 80 Gy in prostate cancer therapy with acceptable toxicity. A key quantity in rational consideration of the clinical gain from target dose escalation - and thereby the cost-effectiveness of advanced radiation therapy technologies - is the steepness of the radiation dose-control curve. Several studies, many of them non-randomized, have shown a benefit from dose escalation in this disease. Some authors have simply plotted outcome data from multiple studies on the same graph to obtain a dose response curve from the available data (4). As the analyzed studies are performed over a period of more than a decade of rapid technological and medical development, it is questionable whether this procedure is valid. On one hand, study-to-study variability in patient selection and treatment details will introduce variability in study outcomes which in turn will lead to more shallow dose response relationships. On the other hand, the fact that higher doses have been introduced more recently, could bias the outcome of these due to stage migration, improved therapy and shorter follow-up, which could create an artificially steep dose-response relationship. This has led us to propose an alternative analytical strategy presented here. A convenient measure of the steepness of the dose-response curve is the normalized dose-response gradient (5, 6), the γ50, and the method pools these intra-study steepness estimates across studies using a mathematical method similar to a meta-analysis. This paper presents a review of 9 published studies and a pooled analysis of γ50 in order to gain understanding of the shape of the underlying dose response curve for low and intermediate-high risk patients. Additionally, we perform a comparative analysis between randomized and non-randomized studies inspired by previous concerns that the latter may be upward biased.
METHODS AND MATERIALS
Study Identification
A MEDLINE and CINAHL search was conducted to identify published studies correlating radiation dose with biochemical control in the treatment of localized prostate cancer from 1966 to May 2008. Keywords used were: “prostate”, “radiotherapy”, “biochemical control” and “dose”. A study was eligible if it: (1) was published in a peer-reviewed journal; (2) specified the radiotherapy technique and total radiation dose prescribed to the target volume; (3) presented long-term biochemical control rates for two or more different radiation dose levels. Studies involving brachytherapy were excluded due to concerns over possible geographical misses as opposed to dose-limited failures and uncertainties in radiobiological parameters adjusting for dose-fractionation and dose-rate effects. Similarly, two hypofractionation studies (7, 8) were excluded to eliminate the effect of uncertainty in the α/β ratio for prostate cancer. If a study was published more than once, the most recently published data were used unless the required data could only be extracted from earlier publications. Studies with less than 200 patients were excluded from the analysis.
The exclusion of hypofractionation and brachytherapy studies obviously results in a smaller total cohort of patients reducing the statistical power of the analysis. This is, however, preferable compared to the possible systematic error that would be introduced by imprecise parameter estimates when correcting for fraction size, repair effects and inhomogeneous dose distributions.
Data extracted from each study included number of patients treated, risk groups, length of follow-up, type and technique of radiation delivery, dose prescription, and biochemical control (biochemical no evidence of disease, bNED) data.
Statistical Analysis
The idea of the present data analytical strategy is to estimate the value of γ50 for each study and then calculate a “best” overall γ50 value from the mean of these estimates weighted by their inverse variance. This way the steepness of the dose-response curve for a particular study is based on within-study comparison of otcome only, ideally a comparison between groups of patients randomly assigned to one of two dose levels. Thus, we can replace the commonly applied, strong assumption of homogeneity in response among studies with the much weaker assumption that the steepness of the underlying dose response function does not vary among studies. The analysis was performed separately for low risk patients and intermediate-high-risk patients.
A logistic dose response function, , is assumed, where u = a0 + bD for constant fraction size. Since , where D50 is the dose required to produce 50% biochemical control at a given follow-up time, we can derive γ50 from published tumour control probabilities p1 and p2 at two different dose levels, D1 and D2 (6).
| Equation 1 |
The standard error of the γ50 estimate, sγ50, may be calculated using one of three methods presented in the Appendix, depending on the published data available for each study. If biochemical control rates for more than two dose levels are reported, γ50 and its standard error are estimated from a logistic fit.
With values of γ50 and sγ50 established, a pooled analysis was performed by entering the data in the RevMan software (9) for statistical analysis and estimation of a pooled mean weighted by inverse variance.
RESULTS
Four randomized studies comprising a total of 2201 patients were identified (10-13) along with five non-randomized studies including a total of 4338 patients (14-18). Table 1 lists the included studies together with information on doses applied, follow up, the method of analysis we used to derive γ50 and sγ50 (HR, KM, KM point or regression), definition of biochemical control, and published control rates. One study (19) was excluded from our analysis because the patient cohort overlapped with a more than three times larger study (17).
Table 1.
Summary of the data extracted from 9 included studies
| STUDY | Randomized | No of patients |
Dose (Gy) | Follow- up |
Failure rate reported (y) |
Method of analysis* |
bNED (%) | bNED definition† |
|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Low (median) |
Int (median) |
High (median) |
Median (y) |
Risk group |
Low dose |
Int dose |
High dose |
||||||
| Zelefsky 1998 | − | 530 | 70.2 | 75.6 | 3 | 5 | KM | Low | 84 | 95 | ASTRO | ||
| KM | Int | 55 | 79 | ||||||||||
| KM | High | 19 | 53 | ||||||||||
| Hanks 2000 †† | − | 618 | 70 (<10f) | 73 (<10f) | 4.4 | 5 | KM | <10 f | 77 | 89 | ASTRO | ||
| <10 unf | 70 | 92 | |||||||||||
| 10–19.9 f | 72 | 86 | |||||||||||
| 73 (rest) | 78 (rest) | 10–19.9 | 51 | 82 | |||||||||
| >=20 f | 23 | 63 | |||||||||||
| >=20 unf | 29 | 26 | |||||||||||
| Pollack 2000 | − | 1127 | 66 | 70 | 78 | 4.3 | 4 | KM | Low | 73 | 85 | 84 | ASTRO |
| Int-high | 31 | 51 | 68 | ||||||||||
| Lyons 2000 | − | 738 | 68.4 | 74 | 3.4 | 5 | HR | Low | 81 | 98 | ASTRO | ||
| KM | Int-high | 41 | 75 | ||||||||||
| Zietman 2005 | + | 393 | 70.2 | 79.2 | 5 | 5 | KM | Low | 60 | 81 | ASTRO | ||
| Int-high | 63 | 80 | |||||||||||
| Kupelian 2005 | − | 1325 | 68.4 | 75.6 | 5.8 | 5 | KM point | Low | 75 | 79 | ASTRO | ||
| KM | Int | 63 | 72 | ||||||||||
| KM point | High | 38 | 46 | ||||||||||
| Peeters 2006 | + | 664 | 68 | 78 | 4.2 | 5 | HR | Low | 88 | 84 | ASTRO | ||
| Int | 64 | 79 | |||||||||||
| High | 48 | 66 | |||||||||||
| Dearnaley 2007 | + | 843 | 64 | 74 | 5 | 5 | HR | Low | 79 | 85 | PSA >2 And PSA >nadir + 50% |
||
| Int | 70 | 79 | |||||||||||
| High | 43 | 57 | |||||||||||
| Kuban 2008 | + | 301 | 70 | 78 | 8.7 | 8 | KM | Low | 63 | 88 | Phoenix | ||
| Int | 76 | 86 | |||||||||||
| High | 26 | 63 | |||||||||||
The method of analysis used to derive sγ50 as detailed in the text.
Biological No-Evidence of Disease definition used
Hanks divide in six risk subgroups according to PSA level and f (favourable) and u (unfavourable) parameters. We combine in two groups by inverse variance with groups defined by PSA only in this study.
Unfortunately, risk-group definitions vary between the studies; they do, however, generally involve initial PSA level, usually in combination with criteria on Gleason score and tumour stage. Some studies use low (PSA<10), intermediate (PSA 10–20), and high (PSA>20) risk as stratification whereas others combine the latter two into one intermediate-high risk group. We have chosen to follow the two-risk-group stratification in order to avoid excluding the two-stratum studies. If three risk groups are used in the original publications, γ-estimates from the intermediate and high risk data are combined using inverse variance weighting.
The study by Kuban et al (11) is one such case, where the intermediate risk group and the high risk group from the original study should be combined to the intermediate-high risk group used in this analysis. Unfortunately, the two observed control levels of the intermediate risk group are very close and the logistic dose model fails to give a biologically reasonable sigmoid curve, estimating negative values of both γ50 and D50. This is a result of our approach forcing the model to fit two data points precisely when the data are inherently noisy. The questionable fit of the sigmoid curve results in an unreasonably low estimate of the variance of γ50 for the intermediate risk group. As a result the intermediate risk group would dominate the estimate of γ50 from the intermediate-high risk group of the Kuban study after weighting by inverse variance, and the Kuban study would dominate the overall estimate of γ50 for the intermediate-high risk group derived in this study. We have therefore chosen to disregard the intermediate risk dataset from Kubans study. The intermediate-high risk group estimate from the Kuban study used in the remainder of this paper is therefore based on data from the high risk group only. This is an upper limit γ50 for the intermediate-high risk group since we disregarded the low estimate of γ50 from the intermediate risk group.
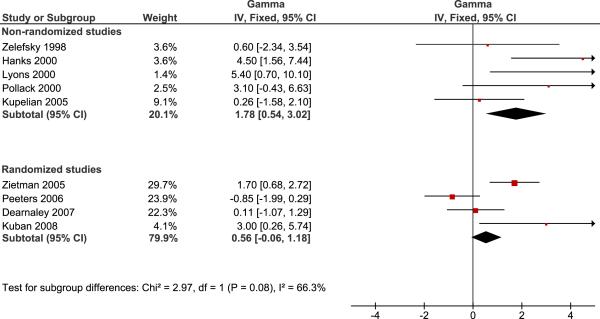
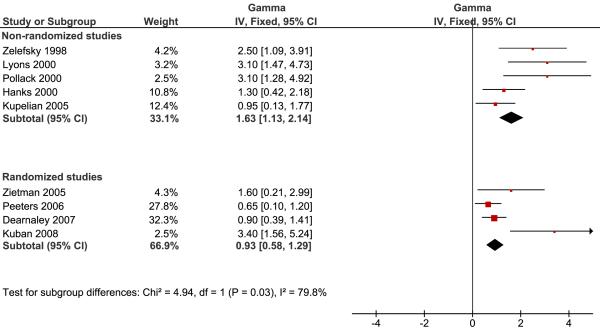
The results of the pooled analysis are given in figure 1 and 2 for the low risk group and the intermediate-high risk groups respectively. We note a borderline significant difference in γ50 between the randomized and non-randomized studies for low risk patients (p=0.08) and a significant difference for intermediate to high-risk patients (p=0.03).
Figure 1.
Pooled analysis of studies reporting the steepness of the dose response curve for low risk patients. Non-randomized and randomized studies are analyzed separately using inverse variance weighting. Horizontal lines in the forest plot indicate the range of the 95% CI of individual studies, while the left and right corner of the diamond shapes depict the 95% CI of the combined estimate.
Figure 2.
Pooled analysis of studies reporting the steepness of the dose response curve for intermediate to high risk patients. Non-randomized and randomized studies are analyzed separately and a significant difference between the pooled estimates is seen (p=0.03). The meaning of the symbols is explained in Figure 1
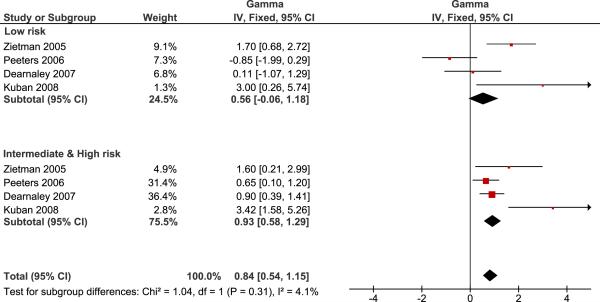
A pooled analysis by risk group with randomized studies (Figure 3) shows no evidence of a significant difference between γ50 estimates for low risk patients and intermediate-high risk patients (p=0.31). Since there is a significant difference between randomized and non-randomized studies, but no evidence of difference between risk groups, the best overall estimate of γ50 is obtained by pooling the risk groups of the randomized studies as in Figure 3. Overall, we estimate that the γ50 of the radiation dose response curve for prostate cancer is 0.84 with 95% confidence interval 0.54–1.15.
Figure 3.
Pooled analysis of the steepness of the radiation dose response curve in randomized trials compared between the low risk group and the intermediate-high risk group. No evidence of difference is seen (p=0.31).
DISCUSSION
Non-randomized studies overestimate the steepness of the dose response curve when patients are stratified by risk group. This is probably because the non-randomized studies are susceptible to bias due to a gradual improvement of multiple aspects of diagnosis and patient care as well as different length of follow-up in the dose groups. All of these factors tend to produce an apparent improvement in outcome which may be erroneously attributed in the data analysis to the higher doses being used in more recent cohorts. The length of follow up has previously been shown to be critical when using the ASTRO definition of biochemical failure (20). The non-randomized study by Kupelian et al (15) included only patients treated in 1995 and 1996 to reduce this problem. Some support for this approach - and the bias issues discussed here - comes from the fact that Kupelian’s γ50-estimate for the low and intermediate-high risk groups is lower than those derived from the other non-randomized studies. This also means the tests for differences between γ-estimates from randomized studies and non-randomized studies become more significant if the study by Kupelian is excluded (p=0.007 and p=0.003 for low and intermediate-high risk patients, respectively).
The over-estimation of γ50 from the non-randomized studies relative to the randomized trials may lead to overly optimistic expectations from, say, a 10% dose-escalation(21). Assume that the 5-year bNED is 80% after a dose of 70 Gy in 35 fractions. We want to design a randomized controlled trial with standard design parameters, significance level α=0.05 and statistical power, 1-β=0.9. If we assume γ50=1.63, the estimate from the non-randomized studies, a target sample size of 548 patients will be required. If γ50=0.93, the best estimate from the randomized trials, this same trial would need to accrue 1,208 patients. This has implications not only for simple dose escalation studies but also studies of, say, hypofractionated radiotherapy(22) .
Another consequence of the randomized trials being conducted more recently is that two of the four studies (10, 11) apply the newer Phoenix (or very similar) definition of biochemical failure (23), whereas all of the non-randomized studies use the 1996 ASTRO definition (24). Cheung et al studied the effect of changing the biochemical failure criteria on γ50 and concluded that γ50 varies with time for both a threshold definition and the ASTRO definition, but did not see a significant difference between the two measures after five years (19). Also, our results do not indicate that the randomized studies with the Phoenix definition give lower γ50 than the other two randomized studies. Thus, the difference in biochemical control definition is unlikely to explain the higher estimates of γ50 for non-randomized studies.
It has been argued that the dose-response curve of intermediate-high-risk prostate patients may be intrinsically higher than for low risk patients mainly based on the impression that more studies show differences between dose levels or treatment arms for this group of patients. We tested the null hypothesis that the γ50 is independent of risk subgroup for the entire cohort of patients. The result is presented in Figure 3. Our analysis does not support the hypothesis that the dose response curve is steeper in higher risk populations. However, the local steepness of the curve at a high tumor control probability will be lower (6). As a result, studies involving intermediate-high-risk patients have a higher power than studies involving the same number of low risk patients.
CONCLUSIONS
Estimates of the steepness of the dose response curve for biochemical control of prostate cancer differ between randomized controlled trials and non-randomized studies when risk group stratification is used. This provides yet another illustration of the role of randomization as a safeguard against systematic bias, even in studies where careful dosimetry and case stratification is performed. The literature data reviewed here provides no support for the hypothesized lack of a dose-response relationship for low risk disease. Our data indicate that, irrespective of risk group, the radiation dose response relationship for biochemical control in prostate cancer is fairly shallow, with a γ50=0.84 (95%CI: 0.54–1.15). In patient strata with higher control rates, the local value of γ will be lower.
Appendix: Estimation of the standard error of the γ50 estimate
Case I: Estimation from the hazard ratio and its confidence interval or reported p-value
If the hazard ratio is available with a confidence interval, the tumour control probability after a dose D2 is estimated from p̂2 = p1 θ, where θ is the hazard ratio and the notation p̂2 is used to distinguish this estimate from the observed Kaplan-Meier [KM] value p2. The standard error of θ, sθ, is estimated as the range of the 95% confidence interval divided by four. It is then possible to derive the relation between sθ and the desired standard error of γ50, sγ50, by propagation of error:
| Equation 2 |
If a 2-tailed p-value is given with the hazard ratio, but no confidence interval is available, we first find a value of the z parameter of the normal distribution, z0, corresponding to the published p-value. It can then be seen that by noting that ln(θ) is normally distributed under the null hypothesis.
Case II: Estimation from Kaplan-Meier estimates of p1 and p2
If the hazard ratio and confidence interval could not be extracted from the published data as described above, the KM survival curves was used to estimate sγ50 as follows:
The hazard ratio at a given time was found as . The hazard ratio should be constant in the proportional hazards model, but this is never fulfilled perfectly. We derived θ for a series of time points ranging form one year to the end of reporting, usually five years, and the values of θ were then averaged. The standard error of the estimate of θ can be approximated by using as previously, but with the p-value from a test of differences between the survival curves. Given sθ ,the standard error of γ50 can be found from Equation 2.
The derived sγ50 is an approximation, but the estimate ensures that more of the available observations are used and hence avoids the inherent underweighting of data from studies where only a point estimate from survival curves can be derived.
In one study (15), the KM survival curves of two patient subgroups did not include p-values from a test of differences between survival curves. In these cases we used an estimate of the standard error of the KM survival probability and propagation of error to derive the following expression for the standard error of the normalized slope
| Equation 3 |
where Ni is the number of patients at risk in arm i at time of evaluation.
Case III: Estimation from logistic regression of three dose-response levels
In one case (17), three levels of dose-response were reported. In this case we used a generalized linear regression algorithm to derive the dose response curve from the dose and response levels weighted by their inverse variance.
In general, the estimation by hazard ratio and its confidence interval is preferred since the method uses the entire dataset in the study and allows multivariate statistical analysis if used by the authors. The KM methods and the logistic regression on three dose levels are univariate and use only parts of the dataset as read from figures in the published data.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest: none
REFERENCES
- 1.Cahlon O, Hunt M, Zelefsky MJ. Intensity-modulated radiation therapy: supportive data for prostate cancer. Semin Radiat Oncol. 2008;18:48–57. doi: 10.1016/j.semradonc.2007.09.007. [DOI] [PubMed] [Google Scholar]
- 2.Ghilezan M, Yan D, Liang J, et al. Online image-guided intensity-modulated radiotherapy for prostate cancer: How much improvement can we expect? A theoretical assessment of clinical benefits and potential dose escalation by improving precision and accuracy of radiation delivery. Int J Radiat Oncol Biol Phys. 2004;60:1602–1610. doi: 10.1016/j.ijrobp.2004.07.709. [DOI] [PubMed] [Google Scholar]
- 3.Kupelian PA, Langen KM, Willoughby TR, et al. Image-guided radiotherapy for localized prostate cancer: treating a moving target. Semin Radiat Oncol. 2008;18:58–66. doi: 10.1016/j.semradonc.2007.09.008. [DOI] [PubMed] [Google Scholar]
- 4.Fowler JF, Ritter MA, Chappell RJ, et al. What hypofractionated protocols should be tested for prostate cancer? Int J Radiat Oncol Biol Phys. 2003;56:1093–1104. doi: 10.1016/s0360-3016(03)00132-9. [DOI] [PubMed] [Google Scholar]
- 5.Brahme A. Dosimetric precision requirements in radiation therapy. Acta Radiol Oncol. 1984;23:379–391. doi: 10.3109/02841868409136037. [DOI] [PubMed] [Google Scholar]
- 6.Bentzen SM, Tucker SL. Quantifying the position and steepness of radiation dose-response curves. Int J Radiat Biol. 1997;71:531–542. doi: 10.1080/095530097143860. [DOI] [PubMed] [Google Scholar]
- 7.Lukka H, Hayter C, Julian JA, et al. Randomized trial comparing two fractionation schedules for patients with localized prostate cancer. J Clin Oncol. 2005;23:6132–6138. doi: 10.1200/JCO.2005.06.153. [DOI] [PubMed] [Google Scholar]
- 8.Valdagni R, Italia C, Montanaro P, et al. Is the alpha-beta ratio of prostate cancer really low? A prospective, non-randomized trial comparing standard and hyperfractionated conformal radiation therapy. Radiother Oncol. 2005;75:74–82. doi: 10.1016/j.radonc.2004.12.019. [DOI] [PubMed] [Google Scholar]
- 9.Review Manager (RevMan) 5.0 ed. The Nordic Cochrane Centre, The Cochrane Collaboration; Copenhagen: 2008. [Google Scholar]
- 10.Dearnaley DP, Sydes MR, Graham JD, et al. Escalated-dose versus standard-dose conformal radiotherapy in prostate cancer: first results from the MRC RT01 randomised controlled trial. Lancet Oncol. 2007;8:475–487. doi: 10.1016/S1470-2045(07)70143-2. [DOI] [PubMed] [Google Scholar]
- 11.Kuban DA, Tucker SL, Dong L, et al. Long-term results of the M. D. Anderson randomized dose-escalation trial for prostate cancer. Int J Radiat Oncol Biol Phys. 2008;70:67–74. doi: 10.1016/j.ijrobp.2007.06.054. [DOI] [PubMed] [Google Scholar]
- 12.Peeters ST, Heemsbergen WD, Koper PC, et al. Dose-response in radiotherapy for localized prostate cancer: results of the Dutch multicenter randomized phase III trial comparing 68 Gy of radiotherapy with 78 Gy. J Clin Oncol. 2006;24:1990–1996. doi: 10.1200/JCO.2005.05.2530. [DOI] [PubMed] [Google Scholar]
- 13.Zietman AL, DeSilvio ML, Slater JD, et al. Comparison of conventional-dose vs high-dose conformal radiation therapy in clinically localized adenocarcinoma of the prostate: a randomized controlled trial. JAMA. 2005;294:1233–1239. doi: 10.1001/jama.294.10.1233. [DOI] [PubMed] [Google Scholar]
- 14.Hanks GE, Hanlon AL, Pinover WH, et al. Dose selection for prostate cancer patients based on dose comparison and dose response studies. Int J Radiat Oncol Biol Phys. 2000;46:823–832. doi: 10.1016/s0360-3016(99)00498-8. [DOI] [PubMed] [Google Scholar]
- 15.Kupelian P, Kuban D, Thames H, et al. Improved biochemical relapse-free survival with increased external radiation doses in patients with localized prostate cancer: the combined experience of nine institutions in patients treated in 1994 and 1995. Int J Radiat Oncol Biol Phys. 2005;61:415–419. doi: 10.1016/j.ijrobp.2004.05.018. [DOI] [PubMed] [Google Scholar]
- 16.Lyons JA, Kupelian PA, Mohan DS, et al. Importance of high radiation doses (72 Gy or greater) in the treatment of stage T1-T3 adenocarcinoma of the prostate. Urology. 2000;55:85–90. doi: 10.1016/s0090-4295(99)00380-5. [DOI] [PubMed] [Google Scholar]
- 17.Pollack A, Smith LG, von Eschenbach AC. External beam radiotherapy dose response characteristics of 1127 men with prostate cancer treated in the PSA era. Int J Radiat Oncol Biol Phys. 2000;48:507–512. doi: 10.1016/s0360-3016(00)00620-9. [DOI] [PubMed] [Google Scholar]
- 18.Zelefsky MJ, Leibel SA, Gaudin PB, et al. Dose escalation with three-dimensional conformal radiation therapy affects the outcome in prostate cancer. Int J Radiat Oncol Biol Phys. 1998;41:491–500. doi: 10.1016/s0360-3016(98)00091-1. [DOI] [PubMed] [Google Scholar]
- 19.Cheung R, Tucker SL, Lee AL, et al. Assessing the impact of an alternative biochemical failure definition on radiation dose response for high-risk prostate cancer treated with external beam radiotherapy. Int J Radiat Oncol Biol Phys. 2005;61:14–19. doi: 10.1016/j.ijrobp.2004.04.064. [DOI] [PubMed] [Google Scholar]
- 20.Vicini FA, Kestin LL, Martinez AA. The importance of adequate follow-up in defining treatment success after external beam irradiation for prostate cancer. Int J Radiat Oncol Biol Phys. 1999;45:553–561. doi: 10.1016/s0360-3016(99)00235-7. [DOI] [PubMed] [Google Scholar]
- 21.Bentzen SM. Radiobiological considerations in the design of clinical trials. Radiother Oncol. 1994;32:1–11. doi: 10.1016/0167-8140(94)90443-x. [DOI] [PubMed] [Google Scholar]
- 22.Bentzen SM, Ritter MA. The alpha/beta ratio for prostate cancer: what is it, really? Radiother Oncol. 2005;76:1–3. doi: 10.1016/j.radonc.2005.06.009. [DOI] [PubMed] [Google Scholar]
- 23.Roach M, 3rd, Hanks G, Thames H, Jr., et al. Defining biochemical failure following radiotherapy with or without hormonal therapy in men with clinically localized prostate cancer: recommendations of the RTOG-ASTRO Phoenix Consensus Conference. Int J Radiat Oncol Biol Phys. 2006;65:965–974. doi: 10.1016/j.ijrobp.2006.04.029. [DOI] [PubMed] [Google Scholar]
- 24.American Society for Therapeutic Radiology and Oncology Consensus Panel Consensus statement: guidelines for PSA following radiation therapy. Int J Radiat Oncol Biol Phys. 1997;37:1035–1041. [PubMed] [Google Scholar]