A NEW METHOD FOR SYNTHESIZING RADIATION DOSE RESPONSE DATA FROM MULTIPLE TRIALS APPLIED TO PROSTATE CANCER

Abstract

Purpose

A new method is presented for synthesizing dose-response data for biochemical control of prostate cancer according to study design (randomized vs. non-randomized) and risk group (low vs. intermediate-high)

Methods and materials

Nine published prostate cancer dose escalation studies including 6539 patients were identified in the MEDLINE and CINAHL databases and reviewed to assess the relationship between dose and biochemical control. A novel method of analysis is presented in which the normalized dose-response gradient, γ₅₀, is estimated for each study and subsequently synthesized across studies. Our method does not assume that biochemical control rates are directly comparable between studies.

Results

Non-randomized studies produced a statistically significantly higher γ₅₀ than randomized studies for intermediate-high risk patients (γ₅₀= 1.63 vs γ₅₀= 0.93, p=0.03) and a borderline significantly higher (γ₅₀= 1.78 vs γ₅₀= 0.56, p=0.08) for low risk patients. No statistically significant difference in γ₅₀ was found between low and intermediate-high risk patients (p=0.31). From the pooled data of low and intermediate-high risk patients in randomized trials, we obtain the overall best estimate of γ₅₀=0.84 with 95% confidence interval 0.54–1.15.

Conclusions

Non-randomized studies over-estimate the steepness of the dose-response curve as compared to randomized trials. This is probably the result of stage migration, improved treatment techniques and a shorter follow-up in higher-dose patients that were typically entered more recently. This over-estimation leads to inflated expectations regarding the benefit from dose-escalation and could lead to under-powered clinical trials. There is no evidence of a steeper dose-response for intermediate-high risk compared to low risk patients.

INTRODUCTION

Recent advances in radiation delivery techniques, such as conformal (1) and intensity modulated radiotherapy (IMRT), proton therapy and image guided therapy (2, 3), have allowed delivery of external beam radiotherapy doses exceeding 80 Gy in prostate cancer therapy with acceptable toxicity. A key quantity in rational consideration of the clinical gain from target dose escalation - and thereby the cost-effectiveness of advanced radiation therapy technologies - is the steepness of the radiation dose-control curve. Several studies, many of them non-randomized, have shown a benefit from dose escalation in this disease. Some authors have simply plotted outcome data from multiple studies on the same graph to obtain a dose response curve from the available data (4). As the analyzed studies are performed over a period of more than a decade of rapid technological and medical development, it is questionable whether this procedure is valid. On one hand, study-to-study variability in patient selection and treatment details will introduce variability in study outcomes which in turn will lead to more shallow dose response relationships. On the other hand, the fact that higher doses have been introduced more recently, could bias the outcome of these due to stage migration, improved therapy and shorter follow-up, which could create an artificially steep dose-response relationship. This has led us to propose an alternative analytical strategy presented here. A convenient measure of the steepness of the dose-response curve is the normalized dose-response gradient (5, 6), the γ_50, and the method pools these intra-study steepness estimates across studies using a mathematical method similar to a meta-analysis. This paper presents a review of 9 published studies and a pooled analysis of γ₅₀ in order to gain understanding of the shape of the underlying dose response curve for low and intermediate-high risk patients. Additionally, we perform a comparative analysis between randomized and non-randomized studies inspired by previous concerns that the latter may be upward biased.

METHODS AND MATERIALS

Study Identification

A MEDLINE and CINAHL search was conducted to identify published studies correlating radiation dose with biochemical control in the treatment of localized prostate cancer from 1966 to May 2008. Keywords used were: “prostate”, “radiotherapy”, “biochemical control” and “dose”. A study was eligible if it: (1) was published in a peer-reviewed journal; (2) specified the radiotherapy technique and total radiation dose prescribed to the target volume; (3) presented long-term biochemical control rates for two or more different radiation dose levels. Studies involving brachytherapy were excluded due to concerns over possible geographical misses as opposed to dose-limited failures and uncertainties in radiobiological parameters adjusting for dose-fractionation and dose-rate effects. Similarly, two hypofractionation studies (7, 8) were excluded to eliminate the effect of uncertainty in the α/β ratio for prostate cancer. If a study was published more than once, the most recently published data were used unless the required data could only be extracted from earlier publications. Studies with less than 200 patients were excluded from the analysis.

The exclusion of hypofractionation and brachytherapy studies obviously results in a smaller total cohort of patients reducing the statistical power of the analysis. This is, however, preferable compared to the possible systematic error that would be introduced by imprecise parameter estimates when correcting for fraction size, repair effects and inhomogeneous dose distributions.

Data extracted from each study included number of patients treated, risk groups, length of follow-up, type and technique of radiation delivery, dose prescription, and biochemical control (biochemical no evidence of disease, bNED) data.

Statistical Analysis

The idea of the present data analytical strategy is to estimate the value of γ₅₀ for each study and then calculate a “best” overall γ₅₀ value from the mean of these estimates weighted by their inverse variance. This way the steepness of the dose-response curve for a particular study is based on within-study comparison of otcome only, ideally a comparison between groups of patients randomly assigned to one of two dose levels. Thus, we can replace the commonly applied, strong assumption of homogeneity in response among studies with the much weaker assumption that the steepness of the underlying dose response function does not vary among studies. The analysis was performed separately for low risk patients and intermediate-high-risk patients.

A logistic dose response function, $P_{\text{Survival}}=\frac{\exp \left(u\right)}{1+\exp \left(u\right)}$, is assumed, where u = a₀ + bD for constant fraction size. Since ${\gamma }_{50}=D_{50}{\phantom{\mid }\frac{d{P}_{\text{Survival}}}{dD}\mid }_{D_{50}}$, where D₅₀ is the dose required to produce 50% biochemical control at a given follow-up time, we can derive γ₅₀ from published tumour control probabilities p₁ and p₂ at two different dose levels, D₁ and D₂ (6).

$${\gamma }_{50}=\frac{1}{4}\cdot \frac{1}{1-\frac{D_1}{D_2}}\cdot \left[\frac{D_1}{D_2}\cdot \ln \frac{p_2}{1-p_2}-\ln \frac{p_1}{1-p_1}\right]$$ Equation 1

The standard error of the γ₅₀ estimate, s_γ50, may be calculated using one of three methods presented in the Appendix, depending on the published data available for each study. If biochemical control rates for more than two dose levels are reported, γ₅₀ and its standard error are estimated from a logistic fit.

With values of γ₅₀ and s_γ50 established, a pooled analysis was performed by entering the data in the RevMan software (9) for statistical analysis and estimation of a pooled mean weighted by inverse variance.

RESULTS

Four randomized studies comprising a total of 2201 patients were identified (10-13) along with five non-randomized studies including a total of 4338 patients (14-18). Table 1 lists the included studies together with information on doses applied, follow up, the method of analysis we used to derive γ₅₀ and s_γ50 (HR, KM, KM point or regression), definition of biochemical control, and published control rates. One study (19) was excluded from our analysis because the patient cohort overlapped with a more than three times larger study (17).

Table 1.

Summary of the data extracted from 9 included studies

STUDY	Randomized	No of patients	Dose (Gy)			Follow- up	Failure rate reported (y)	Method of analysis*	bNED (%)				bNED definition†
			Low (median)	Int (median)	High (median)	Median (y)			Risk group	Low dose	Int dose	High dose
Zelefsky 1998	−	530	70.2		75.6	3	5	KM	Low	84		95	ASTRO
								KM	Int	55		79
								KM	High	19		53
Hanks 2000 ††	−	618	70 (<10f)		73 (<10f)	4.4	5	KM	<10 f	77		89	ASTRO
									<10 unf	70		92
									10–19.9 f	72		86
			73 (rest)		78 (rest)				10–19.9	51		82
									>=20 f	23		63
									>=20 unf	29		26
Pollack 2000	−	1127	66	70	78	4.3	4	KM	Low	73	85	84	ASTRO
									Int-high	31	51	68
Lyons 2000	−	738	68.4		74	3.4	5	HR	Low	81		98	ASTRO
								KM	Int-high	41		75
Zietman 2005	+	393	70.2		79.2	5	5	KM	Low	60		81	ASTRO
									Int-high	63		80
Kupelian 2005	−	1325	68.4		75.6	5.8	5	KM point	Low	75		79	ASTRO
								KM	Int	63		72
								KM point	High	38		46
Peeters 2006	+	664	68		78	4.2	5	HR	Low	88		84	ASTRO
									Int	64		79
									High	48		66
Dearnaley 2007	+	843	64		74	5	5	HR	Low	79		85	PSA >2 And PSA >nadir + 50%
									Int	70		79
									High	43		57
Kuban 2008	+	301	70		78	8.7	8	KM	Low	63		88	Phoenix
									Int	76		86
									High	26		63

^*The method of analysis used to derive s_γ50 as detailed in the text.

^†Biological No-Evidence of Disease definition used

^††Hanks divide in six risk subgroups according to PSA level and f (favourable) and u (unfavourable) parameters. We combine in two groups by inverse variance with groups defined by PSA only in this study.

Unfortunately, risk-group definitions vary between the studies; they do, however, generally involve initial PSA level, usually in combination with criteria on Gleason score and tumour stage. Some studies use low (PSA<10), intermediate (PSA 10–20), and high (PSA>20) risk as stratification whereas others combine the latter two into one intermediate-high risk group. We have chosen to follow the two-risk-group stratification in order to avoid excluding the two-stratum studies. If three risk groups are used in the original publications, γ-estimates from the intermediate and high risk data are combined using inverse variance weighting.

The study by Kuban et al (11) is one such case, where the intermediate risk group and the high risk group from the original study should be combined to the intermediate-high risk group used in this analysis. Unfortunately, the two observed control levels of the intermediate risk group are very close and the logistic dose model fails to give a biologically reasonable sigmoid curve, estimating negative values of both γ₅₀ and D₅₀. This is a result of our approach forcing the model to fit two data points precisely when the data are inherently noisy. The questionable fit of the sigmoid curve results in an unreasonably low estimate of the variance of γ₅₀ for the intermediate risk group. As a result the intermediate risk group would dominate the estimate of γ₅₀ from the intermediate-high risk group of the Kuban study after weighting by inverse variance, and the Kuban study would dominate the overall estimate of γ₅₀ for the intermediate-high risk group derived in this study. We have therefore chosen to disregard the intermediate risk dataset from Kubans study. The intermediate-high risk group estimate from the Kuban study used in the remainder of this paper is therefore based on data from the high risk group only. This is an upper limit γ₅₀ for the intermediate-high risk group since we disregarded the low estimate of γ₅₀ from the intermediate risk group.

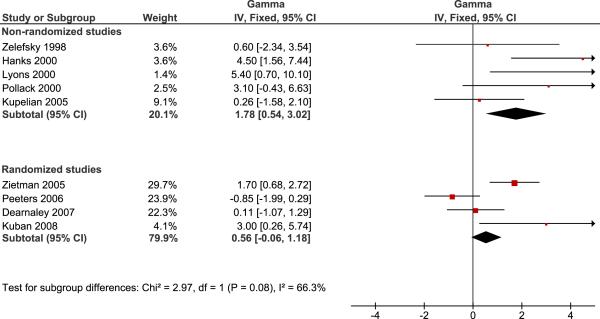
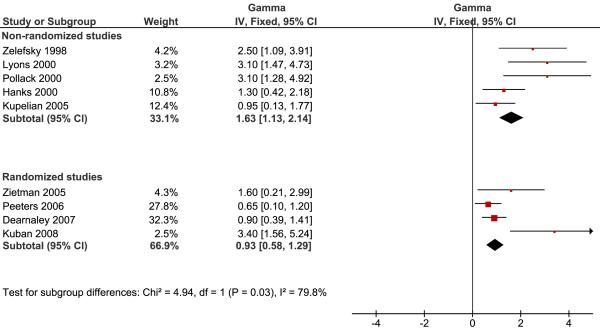
The results of the pooled analysis are given in figure 1 and 2 for the low risk group and the intermediate-high risk groups respectively. We note a borderline significant difference in γ₅₀ between the randomized and non-randomized studies for low risk patients (p=0.08) and a significant difference for intermediate to high-risk patients (p=0.03).

Figure 1.

Pooled analysis of studies reporting the steepness of the dose response curve for low risk patients. Non-randomized and randomized studies are analyzed separately using inverse variance weighting. Horizontal lines in the forest plot indicate the range of the 95% CI of individual studies, while the left and right corner of the diamond shapes depict the 95% CI of the combined estimate.

Figure 2.

Pooled analysis of studies reporting the steepness of the dose response curve for intermediate to high risk patients. Non-randomized and randomized studies are analyzed separately and a significant difference between the pooled estimates is seen (p=0.03). The meaning of the symbols is explained in Figure 1

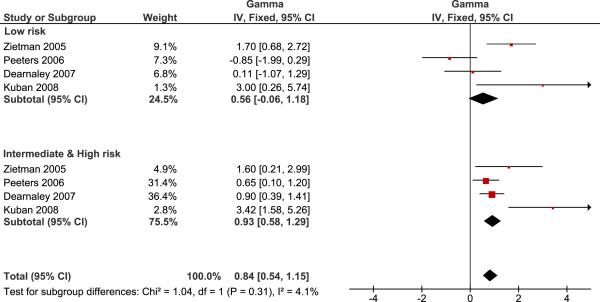
A pooled analysis by risk group with randomized studies (Figure 3) shows no evidence of a significant difference between γ₅₀ estimates for low risk patients and intermediate-high risk patients (p=0.31). Since there is a significant difference between randomized and non-randomized studies, but no evidence of difference between risk groups, the best overall estimate of γ₅₀ is obtained by pooling the risk groups of the randomized studies as in Figure 3. Overall, we estimate that the γ₅₀ of the radiation dose response curve for prostate cancer is 0.84 with 95% confidence interval 0.54–1.15.

Figure 3.

Pooled analysis of the steepness of the radiation dose response curve in randomized trials compared between the low risk group and the intermediate-high risk group. No evidence of difference is seen (p=0.31).

DISCUSSION

Non-randomized studies overestimate the steepness of the dose response curve when patients are stratified by risk group. This is probably because the non-randomized studies are susceptible to bias due to a gradual improvement of multiple aspects of diagnosis and patient care as well as different length of follow-up in the dose groups. All of these factors tend to produce an apparent improvement in outcome which may be erroneously attributed in the data analysis to the higher doses being used in more recent cohorts. The length of follow up has previously been shown to be critical when using the ASTRO definition of biochemical failure (20). The non-randomized study by Kupelian et al (15) included only patients treated in 1995 and 1996 to reduce this problem. Some support for this approach - and the bias issues discussed here - comes from the fact that Kupelian’s γ₅₀-estimate for the low and intermediate-high risk groups is lower than those derived from the other non-randomized studies. This also means the tests for differences between γ-estimates from randomized studies and non-randomized studies become more significant if the study by Kupelian is excluded (p=0.007 and p=0.003 for low and intermediate-high risk patients, respectively).

The over-estimation of γ₅₀ from the non-randomized studies relative to the randomized trials may lead to overly optimistic expectations from, say, a 10% dose-escalation(21). Assume that the 5-year bNED is 80% after a dose of 70 Gy in 35 fractions. We want to design a randomized controlled trial with standard design parameters, significance level α=0.05 and statistical power, 1-β=0.9. If we assume γ₅₀=1.63, the estimate from the non-randomized studies, a target sample size of 548 patients will be required. If γ₅₀=0.93, the best estimate from the randomized trials, this same trial would need to accrue 1,208 patients. This has implications not only for simple dose escalation studies but also studies of, say, hypofractionated radiotherapy(22) .

Another consequence of the randomized trials being conducted more recently is that two of the four studies (10, 11) apply the newer Phoenix (or very similar) definition of biochemical failure (23), whereas all of the non-randomized studies use the 1996 ASTRO definition (24). Cheung et al studied the effect of changing the biochemical failure criteria on γ₅₀ and concluded that γ₅₀ varies with time for both a threshold definition and the ASTRO definition, but did not see a significant difference between the two measures after five years (19). Also, our results do not indicate that the randomized studies with the Phoenix definition give lower γ₅₀ than the other two randomized studies. Thus, the difference in biochemical control definition is unlikely to explain the higher estimates of γ₅₀ for non-randomized studies.

It has been argued that the dose-response curve of intermediate-high-risk prostate patients may be intrinsically higher than for low risk patients mainly based on the impression that more studies show differences between dose levels or treatment arms for this group of patients. We tested the null hypothesis that the γ₅₀ is independent of risk subgroup for the entire cohort of patients. The result is presented in Figure 3. Our analysis does not support the hypothesis that the dose response curve is steeper in higher risk populations. However, the local steepness of the curve at a high tumor control probability will be lower (6). As a result, studies involving intermediate-high-risk patients have a higher power than studies involving the same number of low risk patients.

CONCLUSIONS

Estimates of the steepness of the dose response curve for biochemical control of prostate cancer differ between randomized controlled trials and non-randomized studies when risk group stratification is used. This provides yet another illustration of the role of randomization as a safeguard against systematic bias, even in studies where careful dosimetry and case stratification is performed. The literature data reviewed here provides no support for the hypothesized lack of a dose-response relationship for low risk disease. Our data indicate that, irrespective of risk group, the radiation dose response relationship for biochemical control in prostate cancer is fairly shallow, with a γ₅₀=0.84 (95%CI: 0.54–1.15). In patient strata with higher control rates, the local value of γ will be lower.

Appendix: Estimation of the standard error of the γ₅₀ estimate

Case I: Estimation from the hazard ratio and its confidence interval or reported p-value

If the hazard ratio is available with a confidence interval, the tumour control probability after a dose D₂ is estimated from p̂₂ = p₁ ^θ, where θ is the hazard ratio and the notation p̂₂ is used to distinguish this estimate from the observed Kaplan-Meier [KM] value p₂. The standard error of θ, s_θ, is estimated as the range of the 95% confidence interval divided by four. It is then possible to derive the relation between s_θ and the desired standard error of γ₅₀, s_γ50, by propagation of error:

$$S_{{\gamma }_{50}}=\frac{1}{4}\cdot \frac{1}{\frac{D_2}{D_1}-1}\cdot \frac{-\ln \left(p_1\right)}{(1-{\widehat{p}}_2)}\cdot S_{\theta }$$ Equation 2

If a 2-tailed p-value is given with the hazard ratio, but no confidence interval is available, we first find a value of the z parameter of the normal distribution, z₀, corresponding to the published p-value. It can then be seen that $S_{\theta }=\frac{\theta \ln \theta }{z_0}$ by noting that ln(θ) is normally distributed under the null hypothesis.

Case II: Estimation from Kaplan-Meier estimates of p₁ and p₂

If the hazard ratio and confidence interval could not be extracted from the published data as described above, the KM survival curves was used to estimate s_γ50 as follows:

The hazard ratio at a given time was found as $\theta \left(t\right)=\frac{\ln \left(p_2\left(t\right)\right)}{\ln \left(p_1\left(t\right)\right)}$. The hazard ratio should be constant in the proportional hazards model, but this is never fulfilled perfectly. We derived θ for a series of time points ranging form one year to the end of reporting, usually five years, and the values of θ were then averaged. The standard error of the estimate of θ can be approximated by using $S_{\theta }=\frac{\theta \ln \theta }{z_0}$ as previously, but with the p-value from a test of differences between the survival curves. Given s_θ ,the standard error of γ₅₀ can be found from Equation 2.

The derived s_γ50 is an approximation, but the estimate ensures that more of the available observations are used and hence avoids the inherent underweighting of data from studies where only a point estimate from survival curves can be derived.

In one study (15), the KM survival curves of two patient subgroups did not include p-values from a test of differences between survival curves. In these cases we used an estimate of the standard error of the KM survival probability and propagation of error to derive the following expression for the standard error of the normalized slope

$$S_{P_i}=K{M}_i\left(t\right)\cdot \sqrt{\frac{1-K{M}_i\left(t\right)}{N_i\left(t\right)}}\Rightarrow S_{{\gamma }_{50}}=\frac{1}{4}\cdot \frac{1}{1-\frac{D_1}{D_2}}\cdot \sqrt{{\left(\frac{D_1}{D_2}\right)}^2\cdot \frac{1}{N_2\cdot p_2\cdot (1-p_2)}+\frac{1}{N_1\cdot p_1\cdot (1-p_1)}}$$ Equation 3

where N_i is the number of patients at risk in arm i at time of evaluation.

Case III: Estimation from logistic regression of three dose-response levels

In one case (17), three levels of dose-response were reported. In this case we used a generalized linear regression algorithm to derive the dose response curve from the dose and response levels weighted by their inverse variance.

In general, the estimation by hazard ratio and its confidence interval is preferred since the method uses the entire dataset in the study and allows multivariate statistical analysis if used by the authors. The KM methods and the logistic regression on three dose levels are univariate and use only parts of the dataset as read from figures in the published data.