Abstract
The recent and rapid development of open source software tools for the analysis of neurophysiological datasets consisting of simultaneous multiple recordings of spikes, field potentials and other neural signals holds the promise for a significant advance in the standardization, transparency, quality, reproducibility and variety of techniques used to analyze neurophysiological data and for the integration of information obtained at different spatial and temporal scales. In this review we focus on recent advances in open source toolboxes for the information theoretic analysis of neural responses. We also present examples of their use to investigate the role of spike timing precision, correlations across neurons, and field potential fluctuations in the encoding of sensory information. These information toolboxes, available both in MATLAB and Python programming environments, hold the potential to enlarge the domain of application of information theory to neuroscience and to lead to new discoveries about how neurons encode and transmit information.
Keywords: information theory, mutual information, entropy, bias, open source
Introduction
Recent years have witnessed a sharp increase in the amount and complexity of data collected in neurophysiological experiments. Neurophysiologists can now record simultaneous neural activity, at temporal resolutions of tens of kHz, from tens to hundreds of intracranial electrodes (Csicsvari et al., 2003). From each electrode, both action potentials of individual neurons (reflecting the output of a cortical site) and local field potentials (LFPs; reflecting both population synaptic potentials and other types of slow activity such as spike afterpotentials) can be extracted. Moreover, electrophysiological recordings can now be accompanied by joint measurements of other brain signals, such as those recorded with optical imaging, electroencephalography (EEG) or functional magnetic resonance imaging (fMRI) (for a review, see Logothetis, 2008). In addition, increasingly detailed large-scale modeling produces sizable quantities of synthetic data that must be carefully analyzed to provide meaningful comparisons to experiments. While this richness provides unprecedented opportunities to understand brain organization at multiple levels, it poses to computational neuroscientists the enormous challenge of developing analytical tools to extract meaningful information from such complex data.
There is a strong argument that the development of the analytical tools for analyzing complex, multi-scale neurophysiological signals would be greatly helped by standardization, and public and transparent availability of the software implementing these analysis tools, together with sharing of experimental data (Ascoli, 2006; Teeters et al., 2008), as well as by the standardization of experimental and modeling neuroscience procedures (Nordlie et al., 2009). In recent months, several laboratories have taken on board this philosophy and have put a considerable effort into development, open source sharing and standardisation of the analysis tools they work with.
In this focused review we discuss the rapid growth of advanced open source analysis toolboxes for neuroscience data. After briefly outlining the advantages of this framework, we discuss in more detail publically available open source toolboxes of one particular type of neuroscientific analysis tools: those based on information theory. Then, focusing particularly on our own contributions, we use recent examples to illustrate the benefits that can be gained from using these information theoretic tools for the analysis of real and simulated data and for their detailed comparison.
The Role of Advanced Toolboxes for the Analysis of Neuropysiological Data in the Development of Neuroinformatics
Neuroinformatics is a discipline which deals with the development of information science infrastructures that support the progress of neuroscience (Ascoli, 2006; Gardner et al., 2008). There are at least two key elements of such infrastructures. The first element is the construction of publicly accessible databases collecting neuroscientific data from different levels of investigation. This offers theoreticians access to real data, which is essential to build, constrain and test meaningful models of brain function, as well as providing benchmark data for developing new analysis methods (Teeters et al., 2008). The second element consists of publicly available analysis tools to mine these databases and integrate data at different scales. This offers experimental laboratories access to advanced routines and algorithms, which go beyond the skills and expertise of an individual group. Importantly, the combination of expertise, algorithms and data at different levels could lead to scientific discoveries which would be impossible within a single laboratory or collaborative group (Insel et al., 2004).
While the full integration between repositories of large amounts of data and advanced routines is still a few years away, the public availability of analysis software for neurophysiological data has grown in recent years to a level which can be of immediate and substantial benefit to individual experimental laboratories and to collaborative networks of experimentalists and theoreticians. In the following, we briefly review the development of open source tools for the analysis of neurophysiological signals, with a particular focus on our own contribution.
Open Source Computational Toolboxes for the Analysis of Neurophysiological Data
A crucial element for computational analysis toolboxes is that they should be publicly released. For the group that developed the tool, this provides an opportunity to gain a broader user base, with wider recognition for and application of their techniques as well as greater feedback and testing. For the users of the tools, it allows exploration of a greater range of analysis techniques, reducing duplication of effort and improving reproducibility of results.
These benefits have long been recognized in other communities, such as bioinformatics and systems biology (De Schutter, 2008). In neuroscience, it has been recognized earlier in the modeling community, with the release of stand-alone applications for detailed compartmental single cell and network modeling (Bower and Beeman, 1998; Carnevale and Hines, 2006), and large scale network simulators (Gewaltig and Diesmann, 2007; Goodman and Brette, 2008). These developments allow modelers to concentrate more on the issue of biological relevance without having to worry about implementation details, as well as allowing easier reproducibility of results. Publically released codes have also had a clear benefit in the analysis of fMRI data (Cox, 1996; Duann et al., 2002; Friston et al., 2007) and EEG data (Delorme and Makeig, 2004) and were a key factor in boosting the development of neuroimaging and in the standardization of the resulting data and methods.
It is only more recently that code sharing is beginning to happen for tools related to the analysis of electrophysiological data. In part, this might be because analysis tools were being developed and adapted along with the experimental techniques, so it was hard to develop standard tools that could be meaningfully applied in different experimental circumstances. However, standard techniques are now starting to emerge and this is resulting in more groups releasing tools for electrophysiological data analysis. Examples of this include tools for spike sorting (Quiroga et al., 2004), tools for analysis of spike trains (Spacek et al., 2008; Goldberg et al., 2009) and for processing various types of neurophysiological data (Meier et al., 2008; Zito et al., 2008; Garcia and Fourcaud-Trocme, 2009).
The effectiveness and impact of open source analysis toolboxes depends in part on the programming language for which they are developed. In experimental neuroscience, the most common computing environment is MATLAB, a matrix-based interactive programming language with a wide base of scientific libraries and powerful functionality for plotting and data visualisation. It is well supported by industry and frequently interfaces directly with experimental hardware as a key component in the data acquisition chain. However, there are several open source alternatives that are growing in functionality and popularity. One such example is Python, a fully object-oriented programming language which is endowed with a range of scientific libraries for numerical computation, such as NumPy and SciPy. Python has rapidly gained momentum in the computational modeling and methods development community, as can be seen from the recent Python in Neuroscience special topic of Frontiers in Neuroinformatics (Koetter et al., 2008), which showcases some of the wide range of software already available. Python's flexibility as a scripting language is particularly valuable for taking outputs from one tool (for example a network simulator) and analyzing them with other tools (for example spike train analysis tools) programmatically.
Ideally, open source toolboxes should be available with interfaces allowing use from several programming languages in order to maximize the potential user base and allow greater interaction between different communities. For example, an analysis toolbox with both Python and MATLAB interfaces would ease comparison between simulations and experiment, as modelers could enjoy the performance and flexibility of Python, whereas experimenters could use it from within the MATLAB environment often used to acquire, pre-process and plot their data. While there are a number of community developed utilities to allow integration between computing environments, for example mlabwrap1 (MATLAB from Python) and pythoncall2 (Python from MATLAB) these can be difficult to install and must work around inherent differences in the data types and facilities of the different systems. A native interface following the idioms of the platform is generally easier for users familiar with a specific software environment. Having a single implementation of the algorithms with interfaces available for each language also has technical advantages, reducing code duplication and simplifying the maintenance of the software since changes and enhancements to the core routines only need to be made in a single location. However, this can be challenging for highly dynamic environments, such as MATLAB and Python, since it requires re-implementing many of the features built in to the environment, such as dynamic memory allocation and advanced data types, in a robust cross platform way. For example, the different dynamic memory models of MATLAB and Python mean it would be difficult to implement codes, such as those discussed below, in a common backend without requiring expensive memory copies which would affect performance. For these reasons we chose to implement separate native extensions for our software (discussed below), which can each take full advantage of the benefits of the respective systems without catering to the lowest common denominator of the feature sets.
Information Theory
Among the many mathematical tools to analyze neural data, one that has attracted substantial interest in sensory neuroscience over the last 20 years is information theory. Information theory is the mathematical theory that deals with measures of transmission of information in the presence of noise, and with their applications to the study of communication systems (Shannon, 1948). The most fundamental information theoretic quantity for studying neural codes is the mutual information I(S; R) between stimuli and neural responses, defined as follows:
| (1) |
where P(s) is the probability of presenting stimulus s, P(r) is the probability of observing a neural response r across all presentations (trials) of all stimuli and P(r|s) is the probability of observing r when a specific stimulus s is presented. I(S; R) quantifies the reduction of uncertainty about the stimulus that can be gained from observation of a single trial of the neural response. Its usefulness in neuroscience arises from the fact that it can be used to better understand how neurons transmit information, for example by quantifying and comparing the information about external correlates (such as different types of sensory stimuli) available in different candidate neural codes, each candidate code corresponding to a choice of how to represent the neural response.
The fact that information theoretic techniques quantify information gains in single trials (rather than on average across trials) makes them biologically relevant, because brains recognize sensory stimuli and take decisions on single trials. With respect to other single trial analysis techniques (such as decoding or reconstruction of the most likely stimulus that elicited the neural response) information theory has the advantage that it naturally takes into account all possible ways in which neurons can convey information (for example, by predicting the most likely stimulus, by reporting the uncertainty of the prediction, or by ruling out very unlikely stimuli) (Quiroga and Panzeri, 2009). Some ways in which mutual information can be used to gain insights into neural computations will be illustrated by examples in the following section.
The limited sampling bias problem
The major technical difficulty in computing mutual information from neural responses is that it requires knowledge of the full stimulus–response probability distributions (Eq. 1), and these probabilities must be measured from a limited number of stimulus–response trials. This leads to a systematic error (called limited sampling bias) in estimates of information, which can be prominent (Figure 1) and is difficult to correct for. Fortunately, there are several bias correction techniques which allow accurate estimates of information theoretic quantities from realistically collectable amounts of data (recently reviewed in Victor, 2006; Panzeri et al., 2007). However, these methods are complex and computationally demanding, and their performance depends on the statistics of neural data, which necessitates testing several methods with simulated neural responses with statistical properties close to that of real data. Therefore, the availability of high-performance toolboxes implementing many of the available bias correction techniques is crucial for widening the use of information theoretic tools among neuroscience laboratories.
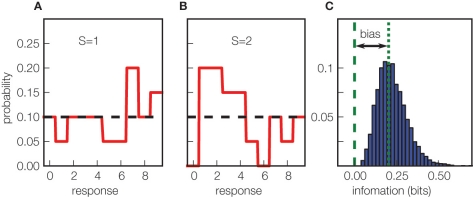
Figure 1.
The origin of the limited sampling bias in information measures. (A, B) Simulation of a toy uninformative neuron, responding on each trial with a uniform distribution of spike counts ranging from 0 to 9, regardless of which of two stimuli (S = 1 in (A) and S = 2 in (B)) are presented. The black dotted horizontal line is the true response distribution, solid red lines are estimates sampled from 40 trials. The limited sampling causes the appearance of spurious differences in the two estimated conditional response distributions, leading to an artificial positive value of mutual information. (C) The distribution (over 5000 simulations) of the mutual information values obtained (without using any bias correction) estimating Eq. 1 from the stimulus–response probabilities computed with 40 trials. The dashed green vertical line indicates the true value of the mutual information carried by the simulated system (which equals 0 bits); the difference between this and the mean observed value (dotted green line) is the bias.
Information theoretic toolboxes
Here we briefly describe three recently released open source toolkits that include implementations of information theoretic quantities and that were specifically designed and tested for analyzing recordings of neural activity.
The Spike Train Analysis Toolkit3 (Goldberg et al., 2009) is a MATLAB toolbox which implements several information-theoretic spike train analysis techniques. It is a comprehensive piece of software, covering a range of entropy and information bias correction methods. Particularly notable is the inclusion of the so-called metric space (Victor and Purpura, 1996) and binless (Victor, 2002) methods for estimating information theoretic quantities from spike trains, which to our knowledge are not available in any other package.
PyEntropy4 (Ince et al., 2009) is a Python module computing information quantities from discretized neural responses with a range of bias corrections, including the highly efficient shuffled information estimator (Panzeri et al., 2007). It also includes calculation of all required terms for the information breakdown (Pola et al., 2003), which can quantify the effect of different types of correlations on the information carried by population codes. One of its unique features is that it includes a novel algorithm for obtaining maximum entropy probability distributions over finite alphabet spaces under marginal constraints, which is useful for investigating correlations (see Cross-Neural Interactions and the Information Carried by Population Codes).
The Information Breakdown Toolbox5 (ibTB) (Magri et al., 2009) is a MATLAB toolbox implementing several of the information estimates and bias corrections mentioned above. Importantly, it does this via a novel algorithm to minimize the number of operations required during the direct entropy estimation, which results in extremely high speed of computation. It contains a number of algorithms which have been thoroughly tested and exemplified not only on spike train data (as for the above toolboxes), but also on data from analogue brain signals such as LFPs and EEGs.
Besides information theoretic toolboxes designed primarily for neuroscientific data, there are also other open-source information theoretic packages not designed specifically for neural data. One prominent example is the R package “entropy”6, which implements plug-in estimates of the entropy and mutual information, as well as a number of bias corrections.
It should be noted that our own two toolboxes (PyEntropy and ibTB) contain many information estimation algorithms implemented both in Python and MATLAB. As noted above, the availability of the same algorithm in multiple programming environments facilitates interactions between computational and experimental laboratories.
Recent Applications
Using information theory to compare models and experiments and to set the amount of noise in simulated models
Information theory is useful to compare models and experiments and elucidate the neural mechanisms underlying the generation of neural representations of sensory events. To illustrate this, we report a recent study combining experiment and theory and aimed at understanding the rules of translation between complex sensory stimuli and LFP oscillations at different frequencies, and illustrate how information theory helped us in this investigation.
Analysis of cortical LFPs reveals that cortical activity contains oscillations and fluctuations ranging over a wide range of frequencies, from a fraction of Hz to well over 100 Hz (Buzsaki and Draguhn, 2004). However, it is not known whether all parts of the spectrum of cortical fluctuations participate in encoding sensory stimuli, or whether there are frequency ranges which do not participate in encoding stimuli and instead reflect stimulus unrelated or ongoing activity. To address the issue of which frequency range of cortical fluctuations are involved in sensory function, we carried out an experimental study (Belitski et al., 2008) in which we recorded LFPs in the primary visual cortex of anesthetized macaques during binocular visual stimulations with naturalistic color movies. To understand which parts of the LFP spectrum were involved in encoding visual stimulus features, we computed the amount of information carried by LFP power in various bands about which part of a naturalistic color movie was being shown. We found that not all the frequency range was involved in stimulus coding: the power of LFPs carried information only in the low (<12 Hz) and gamma (60–100 Hz) frequency range (Figure 2C), and each of these two ranges carried independent visual information. To understand the origin of these two informative and independent frequency bands, we simulated the responses of a cortical recurrent network of excitatory and inhibitory neurons to time-dependent thalamic inputs (Mazzoni et al., 2008). When the dynamics of the simulated thalamic input matched those of real visual thalamic neurons responding to movies, the simulated network produced stimulus-related LFP changes that were in close agreement with those observed in primary visual cortex (see Figure 2A for individual simulated traces and Figure 2C for the results of information analysis of real and simulated data). Moreover, by systematically manipulating the dynamics of inputs to the network, we could shed light on the differential origin of the information at low and at gamma LFP frequencies. Gamma-range oscillations were generated by inhibitory–excitatory neural interactions and encoded static input spike rates, whereas slow LFP fluctuations were mediated by stimulus–neural interactions and encoded slow dynamic features of the input (Mazzoni et al., 2008).
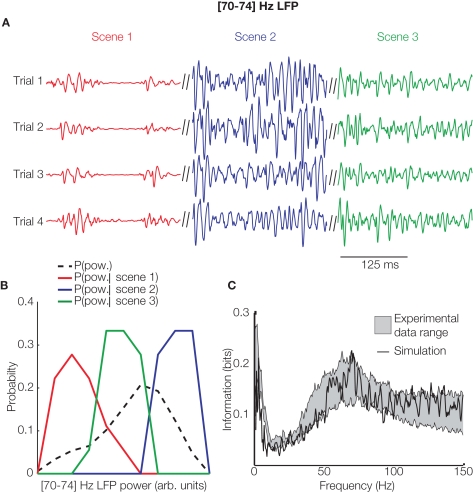
Figure 2.
Computing the information content of LFP spectrum in models and cortical data. (A) The time course of the 70–74 Hz component of simulated LFP's generated from the recurrent inhibitory–excitatory neural network model of Mazzoni et al. (2008) for four repetitions of the same thalamic input signal during three 2-s nonoverlapping movie intervals (“scenes”), each coded with a different color. The power of the 70–74 Hz band varies reliably from scene to scene. (B) The distribution across 30 trials of the time-averaged instantaneous power within each scene (red, green, and blue lines coded as in (A)) is different across different scenes and from the distribution of power across all available scenes (black dashed line). This shows that the power in this frequency band carries some single-trial information about movie scenes. (C) The mutual information (about which scene of the movie was being presented) carried by the power of the LFP recorded from primary visual cortex (grey area represents the mean ± SEM over recoding locations) and by the power of the LFP simulated by the recurrent network model of Mazzoni et al. (2008) (black line), from which this panel is reprinted. The model accurately reproduced the spectral information of recorded LFP's y = Wx
Information theory was helpful to this study in two ways. First, the computation of information about which scene of the movie was shown (exemplified in Figure 2B) takes into account all possible features in the movie, without any assumption of what specific feature was encoded. This afforded some generality in our conclusions. Moreover, this feature-independent information calculation could be easily replicated with the simulated model (Figure 2C), thereby allowing a simple computation from the model-output without having first to extract individual visual features from the movies, e.g., by a complicated array of model thalamic filters. Second, information theory was useful in setting the trial-to-trial variability of neural responses. This variability is partly due to ongoing cortical activity which can influence the neural responses as much as the stimulus does (Arieli et al., 1996). Since local network models do not naturally generate such ongoing activity, they are usually less variable than real responses, and it is, therefore, often necessary to add such noise to models in an ad-hoc way. A principled way to set noise parameters is to match the information carried about neural responses, because information reflects both the variability in neural responses due to stimulus input and that due to internal variability (de Ruyter van Steveninck et al., 1997). In our model (Mazzoni et al., 2008), we could replicate all experimentally measured information over all LFP frequencies and under several stimulation conditions with a simple “internal noise” process; thus, information theory provided a simple and principled metric to set this otherwise arbitrary model parameter.
Cross-neural interactions and the information carried by population codes
Nearby neurons in the central nervous system usually do not fire independently of the activity of other neurons, but rather interact: for example, the probability of near-simultaneous firing from two neurons is often significantly higher than the product of the probabilities of each neuron firing independently. Because of their ubiquitous presence, it has been suggested that interactions among neurons play an important role in shaping neural population codes (Averbeck et al., 2006). However, it has proven difficult to develop tools that can address the role of interactions in information processing quantitatively, and so it has remained difficult to ultimately understand whether neural interactions are epiphenomena or rather important ingredients of neural population codes.
In recent years, several groups have developed information theoretic tools to specifically address the impact of correlated firing on population codes, either by comparing the information encoded in the population to that of a hypothetical population with no correlations but the same single neuron properties (Pola et al., 2003; Schneidman et al., 2003), or by considering the information loss if a downstream system ignores correlations when decoding the response (Latham and Nirenberg, 2005; Oizumi et al., 2009). Our toolboxes include these quantities and thereby allow detailed investigations of the role of correlations in encoding and transmitting information. The advantage of using information theory to study the role of interactions is that mutual information automatically takes into account contributions of all interactions among neurons at all orders. This property is central because it allows an evaluation of the role of all possible types of interactions among neurons, for example by removing them from the response probabilities, and by quantifying how information changes with respect to the case in which the response probability was not manipulated.
A question which has recently attracted considerable interest regarding the role of interactions in information processing is whether it is possible to describe the interaction structure in neural networks only in terms of pair-wise interactions (Schneidman et al., 2006; Shlens et al., 2006; Tang et al., 2008). To investigate this question (Montani et al., 2009), we used a maximum-entropy approach (from the PyEntropy toolbox) to study the impact of interactions of any given order k on the encoding of information about whisker vibrations by a population of neurons in rat somatosensory cortex. The maximum entropy approach imposes on the neural population activity all known interactions up to any considered order k but no further structure. The result (Figure 3) was that to understand information coding and response distributions in this system, it is necessary to consider not only first order statistics (mean firing rate), but also second order (pair-wise correlations) and third order interactions. The fact that the information carried by the population can be understood with pair-wise and triple-wise correlations only, provides a tremendous simplification in terms of the number of parameters that must be estimated from the data to characterize the full response distribution, making analysis of sensory coding by relatively large populations more tractable from the experimental point of view.
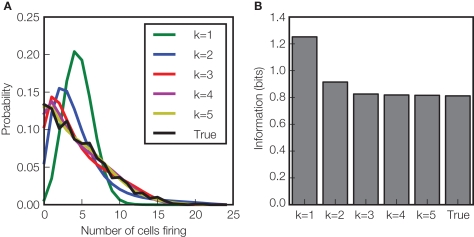
Figure 3.
Effect of higher order correlations on response distributions and information transmission. This figure illustrates the potential role of high order interactions in shaping the response distributions and the amount of information about the velocity of whisker deflection carried by population of neurons in rat somatosensory cortex (Montani et al., 2009). (A) The probability of the number of cells firing in a population of neurons (recorded simultaneously from 24 locations) in response to stimulus velocity 2.66 mm s−1 during the [5–25] ms post-stimulus time window. The experimentally observed “true” probability distribution (black line) is compared to that of a maximum entropy probability model, preserving all interactions up to order k (k = 1,…5), but imposing no other interactions of order higher than k. Clearly, the model discarding all interactions (k = 1) gives a distribution very far from the real one. Including interactions across neurons (k > 1) improves the fit dramatically, and including interactions of order 3 is enough to get a statistically acceptable fit (χ2, p < 0.05). (B) To investigate the effect of the interactions on information, we simulated a system with these maximum entropy stimulus conditional distributions, generating the same number of trials as were available in the experimental data set. The information in this hierarchical family of model systems (averaged over 1000 simulations) is plotted and compared to the information carried by the “true” distribution observed experimentally. Correlations of order three are required to match the information carried by the true neural population responses, but fourth order and above had no effect on the information transmitted. Data from Montani et al. (2009) were redrawn and reanalyzed to create this figure.
The information carried by the temporal structure of neural responses
Another problem which has received considerable attention over the last few years concerns the role of spike times in encoding information. The most established hypothesis on how sensory information is represented in the brain is the spike count coding hypothesis (Adrian, 1928), which suggests that neurons represent information by the number of spikes discharged over some relevant time window. Another hypothesis is the spike timing encoding hypothesis, which suggests that the timing of spikes may add important information to that already carried by spike counts (MacKay and McCulloch, 1952; Optican and Richmond, 1987; Hopfield, 1995; Victor and Purpura, 1996).
Information theory can also be used to characterize the temporal resolution needed to read out the information carried by spike trains. This can be performed by sampling the spike train at different temporal precisions, Δt, (Figure 4A) and computing the information parametrically as a function of Δt (de Ruyter van Steveninck et al., 1997). The temporal precision required to read the temporal code can then be defined as the largest Δt that still provides the full information obtained at higher resolutions. If this precision is equal to the overall length of the window over which neurons carry information, information is carried only by the number of spikes. As an example, we carried out this type of analysis on the responses of neurons from the VPm thalamic nucleus of rats whose whiskers were stimulated by fast white noise deflections (Montemurro et al., 2007). We found that the temporal precision Δt at which neurons transmitted information about whisker deflections was finer than 1 ms (Figure 4B), suggesting that these neurons use high precision spike timing, rather than spike counts over long windows, to carry information.
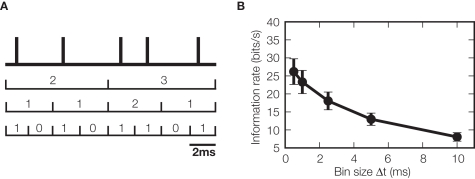
Figure 4.
Effect of temporal resolution of spike times on information. (A) The response of a neuron is initially recorded as a series of spike times. To investigate the temporal resolution at which spike times carry information, the spike train is binned at a variety of different time resolutions, by labeling the response at each time with the number of spikes occurring within that bin, thereby transforming the response into a discrete integer sequence. (B) The information rate (information per unit time) about whisker deflections carried by VPm thalamic neurons as a function of bin width, Δt, used to bin neural responses (data from Montemurro et al. (2007) were redrawn and reanalyzed to create this panel). Information rate increased when decreasing the bin width even down to a resolution as fine as 0.5 ms, the limit of the experimental setup. This shows that a very fine temporal resolution is needed to read out the sensory messages carried by these thalamic spike trains.
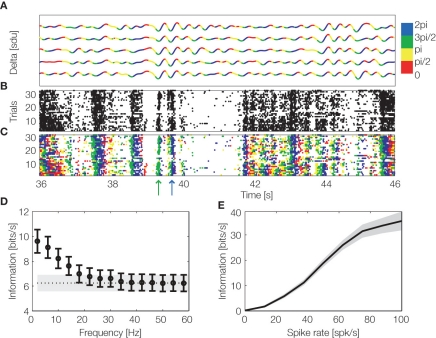
Information theory can also be used to investigate whether spike times carry information when measured relative to the time shifts in the excitability of the local network, which are revealed by changes in phase of LFPs. Recent studies (Montemurro et al., 2008; Kayser et al., 2009) revealed that in visual and auditory cortices, spike times with respect to the phase of low-frequency (<12 Hz) LFPs carry large amounts of information about naturalistic sensory stimuli which cannot possibly be obtained from spike count codes (Figure 5).
Figure 5.
Encoding of information by spike count and phase of firing. LFPs and spiking activity were recorded from primary visual cortex of anesthetized macaques during binocular presentation of a naturalistic color movie. (A) Delta band (1–4 Hz) LFP traces from an example recording site during five repetitions of the same visual stimulus. The line is colored according to the phase quadrant of the instantaneous LFP phase. (B) Multiunit spiking activity from the same site over thirty repetitions of the same movie stimulus. (C) The same multiunit activity as in (B), but with spikes colored according to the concurrent instantaneous LFP phase quadrant at which they were emitted (phase of firing). The movie scenes indicated by green and blue arrows can be better discriminated by considering phase of firing (colored spikes) than by using the spike counts alone (black spikes). (D) Black circles show information carried by the LFP phase of firing as a function of the LFP frequency (mean ± SEM over the entire dataset). The black dashed line shows the spike count information (averaged over the dataset, with grey area showing SEM). For LFP frequencies below 20 Hz the phase of firing carries more information than the spike count. (E) Information carried by delta band phase of firing was calculated for movie scenes eliciting exactly the same spike rate and was plotted as a function of the elicited spike rate. This shows that the information carried by phase of firing is not redundant with spike rate, since it is able to disambiguate stimuli eliciting exactly the same spike rate. Figure reproduced (with permission) from Montemurro et al. (2008).
Conclusions
Given the steady increase in the volume and complexity of neurophysiological data, it is likely that open-source analysis toolboxes will play an increasingly important role in systems level neuroscience. This will provide theoretical and experimental neurophysiology laboratories with clear benefits in terms of transparency and reproducibility, costs, time management, quality and standardization of algorithms. Over the next few years, the combination of publicly available neurophysiological databases, and of software tools able to draw together empirical information collected at different scales, will provide the opportunity to tackle questions about brain function which cannot be addressed with a more traditional single laboratory approach.
The information theoretic toolboxes specifically highlighted and exemplified in this focused review offer a number of advanced techniques to study neural population codes. These tools can facilitate the comparison between computational and experimental insights into neural information processing, and can contribute to increasing our knowledge about neural codes. In particular, the open availability of analysis techniques, which would otherwise be demanding to implement, will ensure that they are now also accessible to many neurophysiological laboratories without previous information theoretic expertise. Given that neurophysiological data, collected in such laboratories with a different question in mind, could be very valuable to address other questions on neural coding, it is likely that the availability of such new software may lead to new results on how neurons process information, even through reanalyzing already collected datasets; thereby, potentially reducing the use of animals.
Conflict of Interest Statement
The authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are indebted to C. Magri, M. Montemurro, N. Brunel, C. Kayser, N.K. Logothetis, M. Maravall, and D. Swan for valuable collaboration. This research was supported by the BMI project at the Department of Robotics, Brain and Cognitive Sciences of IIT, by the EPSRC (EP/E002331/1) CARMEN e-science project, by the BBSRC, and by the San Paolo Foundation.
Key Concepts
- Local field potential
Local field potential (LFP) is a neurophysiological signal obtained by low-pass filtering extracellular recordings, typically using a frequency cutoff in the range of 100–300 Hz. It captures the fluctuations generated by the slow components of synaptic and neural events in the vicinity of the recording electrode.
- Open source
Open source (http://www.opensource.org) is a software development method in which the source code is made available under a license which allows free redistribution and the creation of derived works. In an academic context it offers obvious advantages in terms of reproducibility of results, open access, easier collaboration, increased flexibility, and lower cost.
- Mutual information
It is a measure of how well an observation of one stochastic variable reduces the uncertainty about another. When it is defined using base-2 logarithms (as in Eq. 1) the reduction of uncertainty it expresses is measured in units of bits. One bit corresponds to a reduction of uncertainty by a factor of two (for example, a correct answer to a yes/no question).
Biographies
Stefano Panzeri is a Senior Research Fellow at the Italian Institute of Technology, Genoa, Italy. His current research focuses on understanding how neuronal populations encode and transmit sensory information.
Robin A. A. Ince is currently studying for a Ph.D. at the University of Manchester, working on information theoretic analysis of neural data and numerical optimisation of information theoretic quantities.
Footnotes
References
- Adrian E. D. (1928). The Basis of Sensation. New York, Norton [Google Scholar]
- Arieli A., Sterkin A., Grinvald A., Aertsen A. (1996). Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science 273, 1868–1871 10.1126/science.273.5283.1868 [DOI] [PubMed] [Google Scholar]
- Ascoli G. A. (2006). The ups and downs of neuroscience shares. Neuroinformatics 4, 213–216 10.1385/NI:4:3:213 [DOI] [PubMed] [Google Scholar]
- Averbeck B. B., Latham P. E., Pouget A. (2006). Neural correlations, population coding and computation. Nat. Rev. Neurosci. 7, 358–366 10.1038/nrn1888 [DOI] [PubMed] [Google Scholar]
- Belitski A., Gretton A., Magri C., Murayama Y., Montemurro M. A., Logothetis N. K., Panzeri S. (2008). Low-frequency local field potentials and spikes in primary visual cortex convey independent visual information. J. Neurosci. 28, 5696–5709 10.1523/JNEUROSCI.0009-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bower J. M., Beeman D. (1998). The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System, 2nd edn. New York, Springer-Verlag [Google Scholar]
- Buzsaki G., Draguhn A. (2004). Neuronal oscillations in cortical networks. Science 304, 1926–1929 10.1126/science.1099745 [DOI] [PubMed] [Google Scholar]
- Carnevale N. T., Hines M. L. (2006). The NEURON Book. Cambridge, Cambridge University Press [Google Scholar]
- Cox R. W. (1996). AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput. Biomed. Res. 29, 162–173 10.1006/cbmr.1996.0014 [DOI] [PubMed] [Google Scholar]
- Csicsvari J., Henze D. A., Jamieson B., Harris K. D., Sirota A., Bartho P., Wise K. D., Buzsaki G. (2003). Massively parallel recording of unit and local field potentials with silicon-based electrodes. J. Neurophysiol. 90, 1314–1323 10.1152/jn.00116.2003 [DOI] [PubMed] [Google Scholar]
- de Ruyter van Steveninck R. R., Lewen G. D., Strong S. P., Koberle R., Bialek W. (1997). Reproducibility and variability in neural spike trains. Science 275, 1805–1808 10.1126/science.275.5307.1805 [DOI] [PubMed] [Google Scholar]
- De Schutter E. (2008). Why are computational neuroscience and systems biology so separate? PLoS Comput. Biol. 4, e1000078. 10.1371/journal.pcbi.1000078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A., Makeig S. (2004). EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 134, 9–21 10.1016/j.jneumeth.2003.10.009 [DOI] [PubMed] [Google Scholar]
- Duann J.-R., Jung T.-P., Kuo W.-J., Yeh T.-C., Makeig S., Hsieh J.-C., Sejnowski T. J. (2002). Single-trial variability in event-related BOLD signals. NeuroImage 15, 823–835 10.1006/nimg.2001.1049 [DOI] [PubMed] [Google Scholar]
- Friston K. J., Ashburned J., Kiebel S. J., Nichols T. E., Penny W. D. eds. (2007). Statistical Parametric Mapping: The Analysis of Functional Brain Images. London, UK, Academic Press [Google Scholar]
- Garcia S., Fourcaud-Trocme N. (2009). OpenElectrophy: an electrophysiological data- and analysis-sharing framework. Front. Neuroinformatics 3:14. 10.3389/neuro.11.014.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner D., Akil H., Ascoli G. A., Bowden D. M., Bug W., Donohue D. E., Goldberg D. H., Grafstein B., Grethe J. S., Gupta A., Halavi M., Kennedy D. N., Marenco L., Martone M.E., Miller P. L., Müller H.-M., Robert A., Shepherd G. M., Sternberg P. W., Van Essen D. C., Williams R.W. (2008). The neuroscience information framework: a data and knowledge environment for neuroscience. Neuroinformatics 6, 149–160 10.1007/s12021-008-9024-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gewaltig M.-O., Diesmann M. (2007). NEST (Neural Simulation Tool). Scholarpedia 2, 1430. 10.4249/scholarpedia.1430 [DOI] [Google Scholar]
- Goldberg D. H., Victor J. D., Gardner E. P., Gardner D. (2009). Spike train analysis toolkit: enabling wider application of information-theoretic techniques to neurophysiology. Neuroinformatics 7, 165–178 10.1007/s12021-009-9049-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman D., Brette R. (2008). Brian: a simulator for spiking neural networks in python. Front. Neuroinformatics 2:5. 10.3389/neuro.11.005.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopfield J. J. (1995). Pattern recognition computation using action potential timing for stimulus representation. Nature 376, 33–36 10.1038/376033a0 [DOI] [PubMed] [Google Scholar]
- Ince R. A., Petersen R. S., Swan D. C., Panzeri S. (2009). Python for information theoretic analysis of neural data. Front. Neuroinformatics 3:4. 10.3389/neuro.11.004.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Insel T. R., Volkow N. D., Landis S. C., Li T. K., Battey J. F., Sieving P. (2004). Limits to growth: why neuroscience needs large-scale science. Nat. Neurosci. 7, 426–427 10.1038/nn0504-426 [DOI] [PubMed] [Google Scholar]
- Kayser C., Montemurro M. A., Logothetis N. K., Panzeri S. (2009). Spike-phase coding boosts and stabilizes information carried by spatial and temporal spike patterns. Neuron 61, 597–608 10.1016/j.neuron.2009.01.008 [DOI] [PubMed] [Google Scholar]
- Koetter R., Bednar J., Davison A., Diesmann M., Gewaltig M.-O., Hines M., Muller E. (eds) (2008). Python in neuroscience. Front. Neuroinformatics http://www.frontiersin.org/neuroinformatics/specialtopics/8/ [DOI] [PMC free article] [PubMed]
- Latham P. E., Nirenberg S. (2005). Synergy, redundancy, and independence in population codes, revisited. J. Neurosci. 25, 5195–5206 10.1523/JNEUROSCI.5319-04.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis N. K. (2008). What we can do and what we cannot do with fMRI. Nature 453, 869–878 10.1038/nature06976 [DOI] [PubMed] [Google Scholar]
- MacKay D. M., McCulloch W. S. (1952). The limiting information capacity of a neuronal link. Bull. Math. Biol. 14, 127–135 [Google Scholar]
- Magri C., Whittingstall K., Singh V., Logothetis N. K., Panzeri S. (2009). A toolbox for the fast information analysis of multiple-site LFP, EEG and spike train recordings. BMC Neurosci. 10, 81. 10.1186/1471-2202-10-81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzoni A., Panzeri S., Logothetis N. K., Brunel N. (2008). Encoding of naturalistic stimuli by local field potential spectra in networks of excitatory and inhibitory neurons. PLoS Comput. Biol. 4, e1000239. 10.1371/journal.pcbi.1000239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meier R., Egert U., Aertsen A., Nawrot M. P. (2008). FIND – a unified framework for neural data analysis. Neural. Netw. 21, 1085–1093 10.1016/j.neunet.2008.06.019 [DOI] [PubMed] [Google Scholar]
- Montani F., Ince R. A., Senatore R., Arabzadeh E., Diamond M. E., Panzeri S. (2009). The impact of high-order interactions on the rate of synchronous discharge and information transmission in somatosensory cortex. Philos. Transact. A Math. Phys. Eng. Sci. 367, 3297–3310 [DOI] [PubMed] [Google Scholar]
- Montemurro M. A., Panzeri S., Maravall M., Alenda A., Bale M. R., Brambilla M., Petersen R. S. (2007). Role of precise spike timing in coding of dynamic vibrissa stimuli in somatosensory thalamus. J. Neurophysiol. 98, 1871–1882 10.1152/jn.00593.2007 [DOI] [PubMed] [Google Scholar]
- Montemurro M. A., Rasch M. J., Murayama Y., Logothetis N. K., Panzeri S. (2008). Phase-of-firing coding of natural visual stimuli in primary visual cortex. Curr. Biol. 18, 375–380 10.1016/j.cub.2008.02.023 [DOI] [PubMed] [Google Scholar]
- Nordlie E., Gewaltig M. O., Plesser H. E. (2009). Towards reproducible descriptions of neuronal network models. PLoS Comput. Biol. 5, e1000456. 10.1371/journal.pcbi.1000456 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oizumi M., Ishii T., Ishibashi K., Hosoya T., Okada M. (2009). A general framework for investigating how far the decoding process in the brain can be simplified. Adv. Neural. Inf. Process. Syst. 21, 1225–1232 [Google Scholar]
- Optican L. M., Richmond B. J. (1987). Temporal encoding of two-dimensional patterns by single units in primate inferior temporal cortex. III. Information theoretic analysis. J. Neurophysiol. 57, 162–178 [DOI] [PubMed] [Google Scholar]
- Panzeri S., Senatore R., Montemurro M. A., Petersen R. S. (2007). Correcting for the sampling bias problem in spike train information measures. J. Neurophysiol. 98, 1064–1072 10.1152/jn.00559.2007 [DOI] [PubMed] [Google Scholar]
- Pola G., Thiele A., Hoffmann K. P., Panzeri S. (2003). An exact method to quantify the information transmitted by different mechanisms of correlational coding. Network 14, 35–60 10.1088/0954-898X/14/1/303 [DOI] [PubMed] [Google Scholar]
- Quiroga R. Q., Nadasdy Z., Ben-Shaul Y. (2004). Unsupervised spike detection and sorting with wavelets and superparamagnetic clustering. Neural. Comput. 16, 1661–1687 10.1162/089976604774201631 [DOI] [PubMed] [Google Scholar]
- Quiroga R. Q., Panzeri S. (2009). Extracting information from neuronal populations: information theory and decoding approaches. Nat. Rev. Neurosci. 10, 173–185 10.1038/nrn2578 [DOI] [PubMed] [Google Scholar]
- Schneidman E., Berry M. J., II, Segev R., Bialek W. (2006). Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 440, 1007–1012 10.1038/nature04701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneidman E., Bialek W., Berry M. J., II. (2003). Synergy, redundancy, and independence in population codes. J. Neurosci. 23, 11539–11553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 [Google Scholar]
- Shlens J., Field G. D., Gauthier J. L., Grivich M. I., Petrusca D., Sher A., Litke A. M., Chichilnisky E. J. (2006). The structure of multi-neuron firing patterns in primate retina. J. Neurosci. 26, 8254–8266 10.1523/JNEUROSCI.1282-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spacek M., Blanche T., Swindale N. (2008). Python for large-scale electrophysiology. Front. Neuroinformatics 2:9. 10.3389/neuro.11.009.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang A., Jackson D., Hobbs J., Chen W., Smith J. L., Patel H., Prieto A., Petrusca D., Grivich M. I., Sher A., Hottowy P., Dabrowski W., Litke A. M., Beggs J. M. (2008). A maximum entropy model applied to spatial and temporal correlations from cortical networks in vitro. J. Neurosci. 28, 505–518 10.1523/JNEUROSCI.3359-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teeters J. L., Harris K. D., Millman K. J., Olshausen B. A., Sommer F. T. (2008). Data sharing for computational neuroscience. Neuroinformatics 6, 47–55 10.1007/s12021-008-9009-y [DOI] [PubMed] [Google Scholar]
- Victor J. D. (2002). Binless strategies for estimation of information from neural data. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 66, 051903. 10.1103/PhysRevE.66.051903 [DOI] [PubMed] [Google Scholar]
- Victor J. D. (2006). Approaches to information-theoretic analysis of neural activity. Biol. Theory 1, 302–316 10.1162/biot.2006.1.3.302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victor J. D., Purpura K. P. (1996). Nature and precision of temporal coding in visual cortex: a metric-space analysis. J. Neurophysiol. 76, 1310–1326 [DOI] [PubMed] [Google Scholar]
- Zito T., Wilbert N., Wiskott L., Berkes P. (2008). Modular toolkit for data processing (MDP): a Python data processing framework. Front. Neuroinformatics 2:8 10.3389/neuro.11.008.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]