Investigation of Sparse Data Mouse Imaging Using Micro-CT with a Carbon-Nanotube-Based X-ray Source

Abstract

There has been a renewed interest in algorithm development for image reconstruction from highly incomplete data in computed tomography (CT). Such algorithms may lead to reduced imaging dose and time, and to the design of innovative configurations tailored to specific imaging tasks. In recent years, a carbon-nanotube (CNT)-based field-emission x-ray source has been developed, which offers easy electronic control of radiation and thus can be an ideal candidate for gated imaging. We have recently proposed algorithms for image reconstruction from fan- and cone-beam data collected at highly sparse angular views through minimization of the total-variation (TV) of the image subject to the condition that the estimated data are consistent with the measured data. In this work, we investigate and demonstrate the application of the TV-minimization algorithm to reconstructing images from mouse data acquired with a CNT-based CT scanner at a number of views much lower than what is used in conventional CT imaging. The results demonstrate that the TV-minimization algorithm can yield images with quality comparable to those obtained from a large number of views by use of the conventional algorithms. The significance of the work may lie in that the substantial reduction of projection views promised by the TV-minimization algorithm can be exploited for reducing imaging dose and time or for improving temporal resolution in tasks such as dynamic imaging.

Introduction

Image reconstruction from incomplete projection data has been actively investigated over the past several decades, for such techniques may potentially lead to increased imaging speed and improved radiation-dose efficiency[1-5].

In recent years, inspired by the work on compressed sensing in statistics and signal processing[6,7], extensive research has been carried out to develop algorithms for accurate reconstruction of medical CT images from sparsely sampled data, including data acquired at a small number of views or over a limited angular range. We have recently proposed algorithms for reconstructing images from fan- and cone-beam projection data collected at highly sparse angular views, through minimizing the image TV subject to the condition that the estimated data are consistent with the measured data[8,9]. This optimization-based image-reconstruction algorithm, which we refer to as the TV-minimization algorithm, can also incorporate additional prior knowledge about the imaged subject and accommodate non-conventional scanning configurations, such as in cone-beam CT for radiotherapy[10]. These algorithms may provide opportunities for innovative design of tomographic imaging systems and hardware components

In the past decade, a CNT-based X-ray source has been developed, in which the X-rays are generated by field emission electrons from the CNT, instead of the conventional thermionic cathode[11,12]. This CNT-based X-ray source has been demonstrated to possess a number of intrinsic advantages over conventional X-ray tubes. In addition to its high temporal resolution and capabilities for spatial and temporal modulation, the CNT-based X-ray source offers easy electronic control of the radiation and thus can potentially be an ideal candidate for gated imaging. Furthermore, stationary-source CT scanners without gantry rotation may be developed by use of CNT-based multi-pixel X-ray sources[13], which may find applications in security scan and other non-conventional CT imaging situations.

In this work, we investigate and demonstrate the application of the TV-minimization algorithm to reconstructing images from real mouse data acquired with a CNT-based micro-CT system, at a number of views much lower than what is required in conventional CT imaging. The results of this study demonstrate that from sparse projection data, the TV-minimization algorithm can yield images with quality comparable to those obtained from a large number of views by use of conventional algorithms. The significance of the work lies in that the substantial reduction of projection views promised by the TV-minimization algorithm can be exploited for reducing imaging dose and time, and for designing innovative imaging configurations.

1 Materials and Methods

1.1 Micro-CT system with a CNT-based X-ray source

A custom-made micro-CT system equipped with a CNT-based X-ray source was used to collect projection data of a mouse subject[12]. The main components, besides the X-ray source, included a rotation stage and a flat-panel detector. The system employed a circular cone-beam geometry by keeping the X-ray source and the detector stationary and by spinning the subject on a rotation stage.

The CNT-based X-ray source can be switched on electronically by changing the gate voltage applied on the CNT cathode through a high voltage pulse generator. The X-ray waveform is readily adjustable by generating a corresponding voltage waveform from the pulse generator. The detector is a high-speed CMOS flat-panel sensor with a CsI scintillator plate coupled to a photo diode array, and it has a 5.0 cm×5.0 cm active area with 1032×1032 detector units and a spatial resolution of 5.0 μm×5.0 μm. For the scanning configuration of the micro-CT system used in this study, the distance between the source and the center of rotation is 160.9 mm , whereas the distance between the the source and the detector is 240.5 mm .

1.2 Image reconstruction from sparse data

We model the cone-beam X-ray projection by a discrete linear system,

$$\mathit{g}=M\mathit{f}$$ (1)

where vector g is the measured projection data, vector f denotes the discrete image, and M is the system matrix representing the discrete line integral along projection rays. The reconstruction problem considered here is tantamount to finding the solution to Eq. (1). When applied to highly sparse data, conventional analytic reconstruction algorithms will yield images with obscuring aliasing artifacts. Instead, we reconstruct images using the TV-minimization algorithm, which has been extensively investigated with simulation as well as real-data experiments, and has demonstrated the potential to yield accurate reconstruction from sparse fan- and cone-beam projection data[8,9,14-19].

The TV-minimization algorithm reconstructs the image by seeking a solution to the following con-strained optimization problem:

$$\begin{array}{c}\hfill f^{\ast }=\mathrm{argmin}{\Vert \mathit{f}\Vert }_{\mathrm{TV}}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.\mid M\mathit{f}-\mathit{g}\mid \le \epsilon \text{and}\mathit{f}\ge 0\hfill \end{array}$$ (2)

where the image TV, ${\Vert f\Vert }_{\mathrm{TV}}={\sum }_{i=1}^n\mid \nabla f_i\mid$, is the ℓ–1 norm of the discrete gradient magnitude of the image, and the relaxation parameter ε is introduced to account for the inconsistency in measured data. The TV-minimization algorithm alternates between a projection-onto-convex-sets (POCS) operation for constraint enforcement (non-negative voxel values and relaxed agreement between reconstructed image and measured data) and a steepest-descent operation for cost function minimization[8,9].

2 Results

In the experimental study, cone-beam projection data was collected at 600, uniformly distributed angular views using the CNT-based micro-CT system, and we used this 600-view data set as the full data set. Because the truth of the image is not available, and because the FDK algorithm is the standard choice for small animal micro-CT systems of such kind, we reconstructed a volume image using the FDK algorithm from the full data set and used it as the gold standard. We show a transverse slice and a sagittal slice of this full data FDK- reconstructed image in Fig. 1, in which the gray level display window is chosen to show both the bone structures and soft tissues. A volume-rendered image of this full-data FDK reconstruction is displayed in Fig. 2, where the display window has been chosen to focus on the skeleton of the imaged mouse. The same display windows of the cross-sectional image and the volume-rendered image will be used for the sparse data reconstructions below.

Fig. 1.

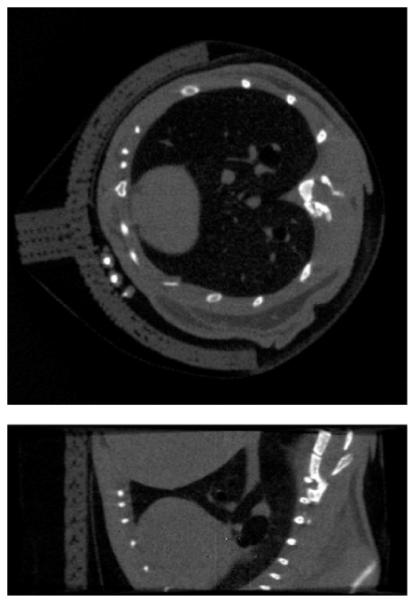
A transverse slice (top) and a sagittal slice (bottom) of the image reconstructed by use of the FDK algorithm from the full data set of 600 projections

Fig. 2.

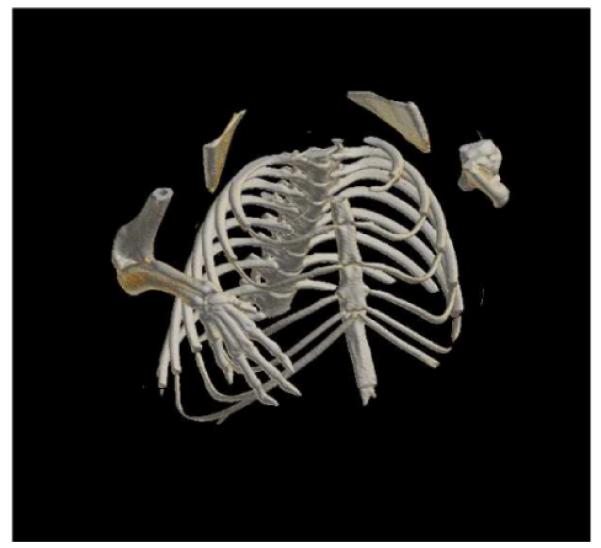
Volume-rendered image of the 600-view FDK reconstruction

We obtained sparse data sets by extracting from the full data projections at 30, 60, and 100 angular views, which contain 5%, 10%, and 17%, respectively, of the amount of the full data. We considered in this study only the sparse data where the extracted projections are distributed uniformly over the 2π scanning range, while in general the angular distribution could be arbitrary and the TV-minimization algorithm can be readily applied to sparse data sets at non-uniformly distributed angular views. From the sparse data sets, we reconstructed volume images using the TV-minimization algorithm and the FDK algorithm, and compared them with the full-data FDK-reconstructed image. All image arrays contain 512 × 512 × 200 voxels, where each voxel has a physical size of 66 μm×66 μm×66 μm.

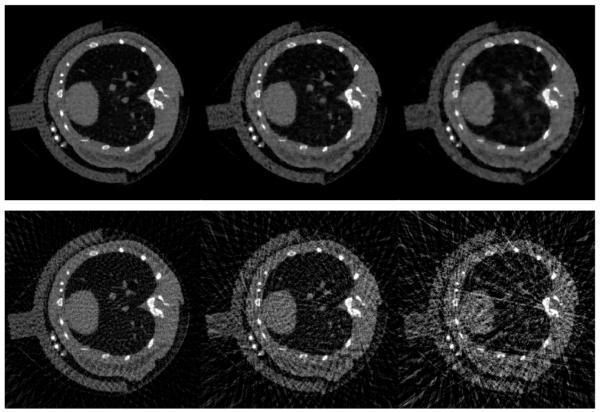
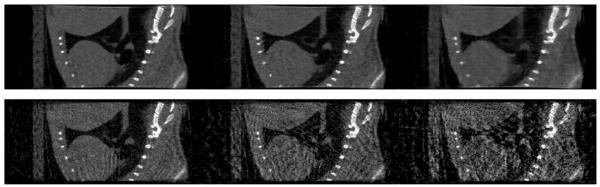
We display in Figs. 3 and 4 the transverse and sagittal slices of the images reconstructed by use of the TV-minimization algorithm and the FDK algorithm from the sparse data sets containing 100, 60, and 30 projection views. Also shown are the same slices of the 600-view FDK-reconstructed image, which serve as the gold standard. One can observe from the results that when the projection data for reconstruction is reduced, the TV-minimization algorithm appears to yield images of quality comparable to the gold standard. In contrast, the FDK-reconstructed images are degraded by streaking artifacts and noise.

Fig. 3.

A transverse slice of the images reconstructed by use of the TV-minimization (top row) and FDK (bottom row) algorithms, from projection data of 100 (left column), 60 (middle column), and 30 (right column) angular views

Fig. 4.

A sagittal slice of the images reconstructed by use of the TV-minimization (top row) and FDK (bottom row) algorithms, from projection data of 100 (left column), 60 (middle column), and 30 (right column) angular views

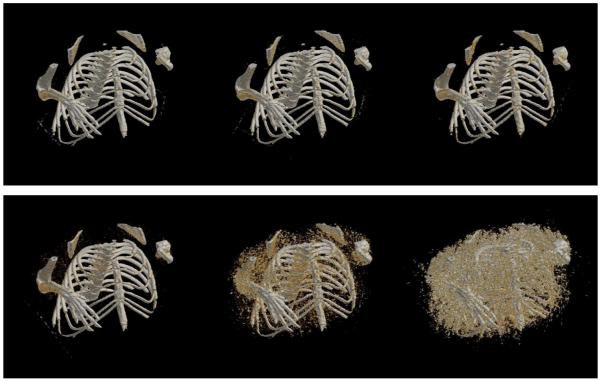
In Fig. 5, we display the volume-rendered images of the sparse data reconstructions by use of the TV-minimization and FDK algorithms. Compared with the gold standard in Fig. 2, one can observe that from the 100-view data, both TV-minimization and FDK algorithms are able to recover most of the bone structures, with the TV result slightly less noisy. When projection data used for reconstruction is reduced to 60 and 30 views, the TV-reconstructed images appear quite similar to the gold standard image, with slight loss of details. In contrast, the FDK reconstructions are severely obscured by artifacts and, for the 30-view case, yield little useful information.

Fig. 5.

Volume-rendered images reconstructed by use of the TV-minimization (top row) and FDK (bottom row) algorithms, from projection data of 100 (left column), 60 (middle column), and 30 (right column) angular views

3 Discussion

In this work we investigated the application of the TV-minimization algorithm for sparse data mouse imaging from real cone-beam projection data acquired by a micro-CT system equipped with a CNT-based X-ray source. The results indicate that the TV-minimization algorithm has the potential to yield mouse images of practical utility from data acquired at a substantially reduced number of angular views than what is required by the current standard algorithms for micro-CT mouse imaging. The results suggest that the TV-minimization algorithm may be suited for a stationary-source CT or tomosynthesis system, in which multiple compact CNT X-ray source is distributively constructed for lifting the limitation imposed by the gantry rotation. In addition, the versatility of the TV-minimization algorithm may enable innovative design of cost-effective CT and to-mosynthesis imaging systems with CNT-based X-ray sources non-uniformly distributed over non-circular or general trajectories, which could potentially yield substantial scanning speed-up and enhanced dose efficiency, at the cost of minimum sacrifice of image quality.