Cortical Thickness or Grey Matter Volume? The Importance of Selecting the Phenotype for Imaging Genetics Studies

Abstract

Choosing the appropriate neuroimaging phenotype is critical to successfully identify genes that influence brain structure or function. While neuroimaging methods provide numerous potential phenotypes, their role for imaging genetics studies are unclear. Here we examine the relationship between brain volume, grey matter volume, cortical thickness and surface area, from a genetic standpoint. Four hundred and eighty-six individuals from randomly ascertained extended pedigrees with high-quality T1-weighted neuroanatomic MRI images participated in the study. Surface-based and voxel-based representations of brain structure were derived, using automated methods, and these measurements were analysed using a variance-components method to identify the heritability of these traits and their genetic correlations. All neuroanatomic traits were significantly influenced by genetic factors. Cortical thickness and surface area measurements were found to be genetically and phenotypically independent. While both thickness and area influenced volume measurements of cortical grey matter, volume was more closely related to surface area than cortical thickness. This trend was observed for both the volume-based and surface-based techniques. The results suggest that surface area and cortical thickness measurements should be considered separately and preferred over gray matter volumes for imaging genetic studies.

1. Introduction

Despite evidence that most neurological and psychiatric illnesses are genetically mediated, the identification of genes that predispose brain-related disorders has been difficult. One strategy for unraveling the genetic determinants of these complex illnesses is the use of endophenotypes, also called intermediate phenotypes (Gottesman and Shields, 1967; Gottesman and Gould, 2003), which are quantitative traits that are genetically correlated with illness. Neuroimaging methods provide an array of potential endophenotypes for these disorders (Glahn et al., 2007). Although there is mounting evidence that quantitative indices derived from brain structure and function are heritable (Baaré et al., 2001; Thompson et al., 2001; Geschwind et al., 2002; Peper et al., 2007; Glahn et al., 2007), and associated with neuropsychiatric disorders (McDonald et al., 2006; Honea et al., 2008; Goldman et al., 2008, 2009; van der Schot et al., 2009), it is unclear which genes influence these traits or the biological mechanisms that govern these measurements. The search for genes that influence brain-related traits could be improved by choosing imaging phenotypes that are closest to a single gene action (Wojczynski and Tiwari, 2008). However, given the complexity and multi-dimensional nature of imaging data, it is critical to determine the appropriate measurements to be employed. In this report, we examine issues surrounding the use of imaging-derived grey matter measurements in imaging genetics studies.

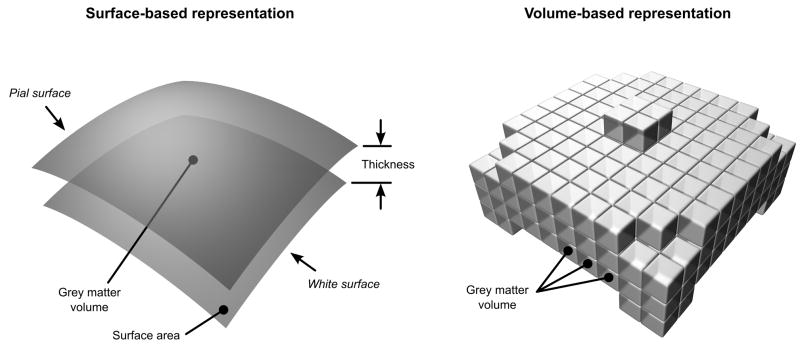
Although the human brain is gyrencephalic, with no absolute linear relationship between brain volume and surface area (Hofman, 1985; Armstrong et al., 1995), simple geometric laws still hold within the cortical mantle, where the grey matter volume is defined as the amount of grey matter that lies between the grey-white interface and the pia mater (Figure 1, left). Previous findings suggest that cortical surface area and cortical thickness are independent, both globally and regionally, that grey matter volume is a function of these two indices and each of these three measurements are heritable (Winkler et al., 2009; Panizzon et al., 2009). Furthermore, Panizzon et al. (2009) reported that surface area and cortical thickness are genetically uncorrelated. Thus, volume measurements, which combine aspects of both traits, are likely influenced by some combination of these genetic factors. Since different definitions of a phenotype potentially lead to different genetic findings (Rao, 2008), it would seem that surface or thickness measures would have advantages over volume measures for gene discovery.

Figure 1.

Geometrical relationship between cortical thickness, surface area and grey matter volume. In the surface-based representation, the grey matter volume is a quadratic function of distances in the surfaces and a linear function of the thickness. In the volume-based representation, only the volumes can be measured directly and require partial volume-effects (not depicted) to be considered.

Cortical anatomy, which is structured as a corrugated two-dimensional sheet of tissue, can be well represented by surface models, which facilitate the analysis of relationships between cortical regions and provide superior visualisation (van Essen et al., 1998). Intersubject and even interspecies registration can be accomplished using surface-based representations (van Essen et al., 2001), allowing matching of homologies without relying directly on spatial smoothing as in volume-based methods (Ashburner and Friston, 2000). Computational advances in surface reconstruction (Mangin et al., 1995; Dale et al., 1999; Fischl et al., 1999a) and the availability of software packages also facilitates its use. Despite these advantages, quantitative methods based on purely volumetric representations of the brain are still common. Amongst these, voxel-based morphometry (VBM) (Wright et al., 1995; Bullmore et al., 1999; Ashburner and Friston, 2000; Good et al., 2001) is a relatively fast, straightforward method, that quantifies the amount of grey matter existing in a voxel and permits a comparison across subjects (Figure 1, right). VBM requires that voxels are classied according to different tissue types, usually grey matter, white matter and cerebrospinal fluid (GM/WM/CSF). To allow comparison across subjects, images are non-linearly aligned to standard brain, where a common coordinate system can be defined, and volumes are corrected for local shrinkages and expansions using the Jacobian determinants of the warps at each voxel (Good et al., 2001). In this way, VBM allows for the quantification of the grey matter volumes, globally and regionally, using either the voxels directly or regions of interest.

In this study, we compare measurements obtained with VBM methods, with measurements from surface-based representations of the brain in genetically informative samples. We focus our attention to determining the genetic control over (1) the volume of the grey matter computed using surface-based and volume-based representations of the brain, (2) the cortical surface area and (3) the cortical thickness.

2. Method

2.1. Participants

Subjects participated in the Genetics of Brain Structure and Function Study, GOBS, a collaborative effort involving the Southwest Foundation for Biomedical Research, the University of Texas Health Science Center at San Antonio (UTHSCSA) and the Yale University School of Medicine. To date, more than 1000 individuals from randomly selected families of Mexican-American ascent, who live in San Antonio, Texas, USA, have been recruited. The data presented here is based on the analysis of the T₁-weighted MRI images from the 486 subjects scanned before December 31st, 2008. A summary of the pedigree structure is presented on Table 1. The mean age of this group was 48.6±13.2 years (min = 26.1, max = 85.1) and 302 were females. All participants provided written informed consent on forms approved by the institutional review board at the UTHSCSA.

Table 1.

Structure of the pedigree.

Familial relationship	Number of pairs
Self	486
Parent-offspring	164
Siblings	192
Grandparent-grandchild	14
Avuncular	298
Half-siblings	50
Double 1st cousins	1
3rd degree	530
4th degree	478
5th degree	193
6th degree	47

2.2. Acquisition of Images

The images were acquired at the Research Imaging Center, UTHSCSA, using a Siemens MAGNETOM Trio 3 T system (Siemens, Erlangen, Germany), with a high-resolution, T₁-weighted, 3D Turbo-FLASH sequence with an adiabatic inversion contrast pulse with the following scan parameters: TR/TI/TE = 2100/785/3.04 ms, flip angle = 13°, voxel size (isotropic) = 0.8 mm. Each subject was scanned 7 (seven) times, consecutively, using the same protocol, and a single image was obtained by linearly coregistering these images and computing the average, allowing improvement over the signal-to-noise ratio and reducing motion artifacts (Kochunov et al., 2006).

2.3. Processing of Images

Image analysis followed two separate pathways: the generation of surface representations of the cortex and the segmentation of the brain into GM, WM and CSF, in their voxel-based representation. The first part was conducted using the FreeSurfer software package (Athinoula A. Martinos Center for Biomedical Imaging, Harvard University, Cambridge, MA, USA), while the second was performed using the FMRIB Software Library – FSL (Oxford Centre for Functional MRI of the Brain, University of Oxford, UK).

2.3.1. Surface-based Analysis

The surface-based analysis followed the procedures described by Dale et al. (1999) and Fischl et al. (1999a). Images are corrected for magnetic field inhomogeneities, affine-registered to the Talairach-Tournoux atlas (Talairach and Tournoux, 1988) and skull-stripped. The voxels belonging to the WM are identified based on their locations, on their intensities and on the intensities of the neighbouring voxels. The two hemispheres are separated and the WM voxels are grouped into a mass of connected voxels using a six-neighbours connectivity scheme. A mesh of triangular faces is tightly built around the WM, using two triangles per exposed voxel face. The mesh is smoothed using an algorithm that takes into account the local intensity in the original images (Dale and Sereno, 1993), at a subvoxel resolution, using trilinear interpolation. Topological defects are corrected (Fischl et al., 2001) ensuring that the surface has the same topological properties of a sphere. A second iteration of smoothing is applied, resulting in a realistic representation of the interface between grey and white matter. This surface is referred to simply as white surface. The external cortical surface, which corresponds to the pia mater, is produced by nudging outwards the white surface towards a point where the tissue contrast is maximal, maintaining constraints on its smoothness and on the possibility of self-intersection (Fischl and Dale, 2000). This surface is referred to simply as the pial surface.

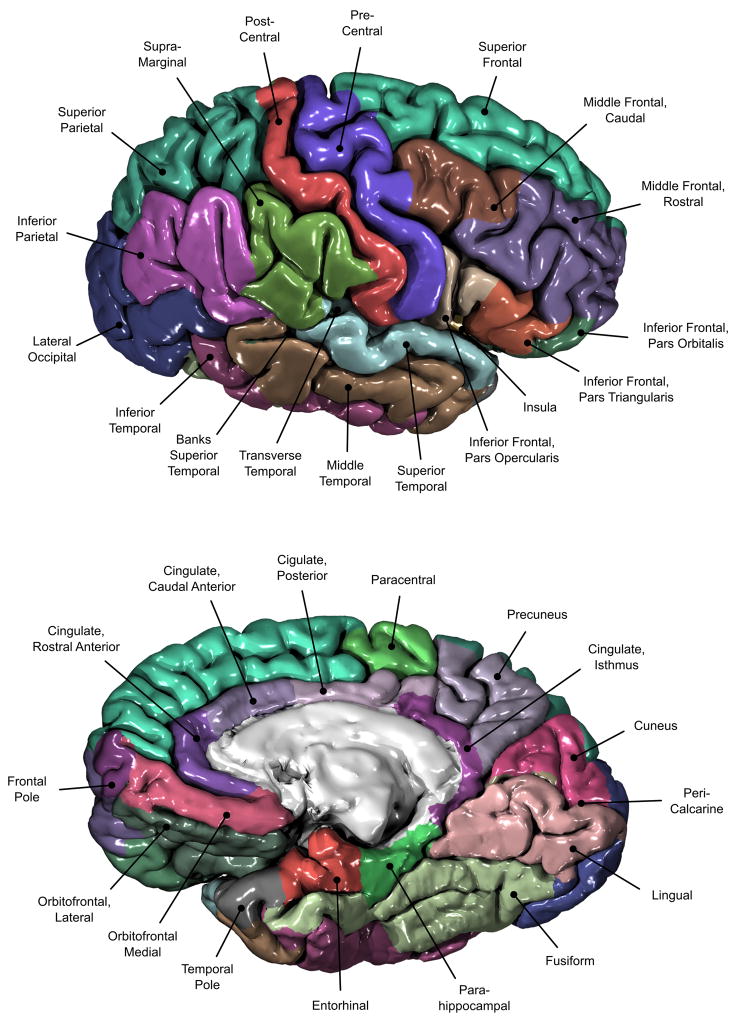
These surfaces are parcellated into smaller regions using an automated process (Fischl et al., 2004). For each subject, this is done by first homeomorphically mapping the pial surface to a spherical coordinate system (Fischl et al., 1999b), where the folding patterns are matched to an average map. An a priori atlas of probabilities for regions of interest is used in a Bayesian approach to establish probabilities that a given vertex belongs to a certain label. In a second, iterative step, the surface is treated as an anisotropic, non-stationary Markov random field, where for each vertex, the labels assigned to its neighbours are also considered. The labelling is iterated until no vertices change their assignments (Fischl et al., 2002, 2004). We used the regions of the atlas developed by Desikan et al. (2006), recently modified to include the insula as an independent region of interest (Figure 2).

Figure 2.

The 34 cortical regions of the Desikan et al. (2006) atlas. Some regions are buried inside sulci and cannot be fully observed.

2.3.2. Volume-based Analysis

The volume-based pipeline started with skull-stripped images produced in an intermediate step of the surface-based pipeline, allowing a direct comparison between the methods. Images were segmented in GM, WM and CSF using the FAST module of FSL, which models the problem of classification into different classes as a hidden Markov random field (HMRF), an extension of hidden Markov models that assumes that the observations come from an underlying Markov random field (Kunsch et al., 1995). Thus, the assignment of a voxel to a class depends on its immediate spatial neighbours in the three-dimensional space, and the problem is treated by obtaining the maximum likelihood estimate of the parameters using an expectation-maximization (EM) algorithm (Zhang et al., 2001). The output of this HMRF-EM framework is an image where the value at each voxel corresponds to the proportion of the volume of the voxel that is occupied by a tissue class.

Estimation of these partial volume effects for each voxel is of paramount importance here, as it allows one to compute the amount of a certain class of tissue present in a region by summing the partial volume effects at each voxel of that region. The segmentation as described above operated in the images in the subject space, not transformed to a standard coordinate space. The subsequent analyses were conducted in the subject space as well, obviating the need to correct the intensities of voxels for local stretchings or shrinkages.

2.3.3. Combining Surface-based and Volume-based Analyses

Voxels identified inside the space delimited by the pial and white surfaces were classified as belonging to the cortex, producing a representation of the cortical mantle in terms of voxels, tractable in a VBM-like approach. The cortex was further parcellated in the same scheme as the surface representation by assigning to each cortical voxel the same label as the closest vertex in the surfaces.

For each region defined in the voxel-based representation, the volume of grey matter was computed by integrating the partial volume effects from the images segmented using the HMRF-EM algorithm. From the surface-based representations, regional measurements for average cortical thickness, surface area and grey matter volume were obtained. Area was measured at the white suface. Global measurements for area and the grey matter volume were computed by summing the values of the parcellations, whereas a global measure of the average thickness was obtained by weighting the regional thicknesses by their corresponding surface areas. The global brain volume was produced in an intermediate step of the surface based pipeline, and includes the volumes for brain stem and cerebellum.

The cortical parcellations were projected from the surfaces into the volumetric space in a binary, not fuzzy fashion, so partial volume effects were not allowed. While this is a clearly desirable feature for the cortex as a whole, since partial volume effects were already considered within the HMRF-EM framework, this has potential to produce minor inaccuracies when computing how the grey matter volume differ across regions within the ribbon. However, these borderline voxels have the same chance of being assigned to either of two bordering regions and there is no net effect that would produce bias for any particular region.

2.4. Quantitative Genetic Analyses

2.4.1. Estimation of Heritabilities

For genetic analyses we used the Sequential Oligogenic Linkage Analysis Routines (SOLAR; Department of Genetics, Southwest Foundation for Biomedical Research, San Antonio, Texas, USA). The estimates produced by SOLAR are based in a variance components method (Lange et al., 1976; Hopper and Mathews, 1982; Amos, 1994; Almasy and Blangero, 1998), in which the phenotypic variance, ${\sigma }_{px}^2$, for a quantitative trait x, can be considered as a sum of a genetic component ${\sigma }_{gx}^2$ and a residual component ${\sigma }_{ex}^2$,

$${\sigma }_{px}^2={\sigma }_{gx}^2+{\sigma }_{ex}^2$$ (1)

The residual component includes all effects not accounted for by the genetic component, and is attributed to environmental effects and experimental error. The genetic component, ${\sigma }_{gx}^2$, can further be decomposed into an additive, ${\sigma }_{ax}^2$, and a dominance component, ${\sigma }_{dx}^2$:

$${\sigma }_{px}^2={\sigma }_{ax}^2+{\sigma }_{dx}^2+{\sigma }_{ex}^2$$ (2)

For a given pedigree, x is assumed to follow a multivariate normal distribution, and in a more generic formulation, the covariance between two non-inbred individuals i and j, drawn from a population in Hardy-Weinberg equilibrium, with random mating, is given by:

$${\mathrm{\Omega }}_{ij}=2{\mathrm{\Phi }}_{ij}{\sigma }_{ax}^2+{\mathrm{\Delta }}_{ij}{\sigma }_{dx}^2+{\delta }_{ij}{\sigma }_{ex}^2$$ (3)

in which Ω_ij = Cov_p{x_i, x_j}, Φ_ij is the coefficient of relationship between the individuals i and j, Δ_ij is the probability that i and j share both alleles identically by descent and δ_ij is the Kronecker function. For any pair of subjects, the values for Φ_ij and Δ_ij can be calculated, being for siblings, for instance 1/2 and 1/4, respectively, and 1/2^k and 0 for most other relationships, where k is the degree of relationship (Amos, 1994). The residual term ${\delta }_{ij}{\sigma }_{ex}^2$ account for individual effects not explicitly modeled. This generic model can be extended to accommodate known environmental and other genetic effects (Hopper, 1993; Blangero et al., 2001). In this model, the broad sense heritability for the trait x is defined as the ratio ${\sigma }_{gx}^2/{\sigma }_{px}^2$ and the narrow sense heritability is defined as ${\sigma }_{ax}^2/{\sigma }_{px}^2$. The term heritability is often associated with the narrow sense (Falconer and Mackay, 1996) and is represented by h². To have realistic estimates, it is useful to include in the model the effects of potential confounding variables, such as age and sex. This is done by regressing the phenotype against different combinations of covariates of interest and those found to be significant remain in the model and the residuals are used to obtain maximum likelihood estimates of the variance components, instead of the actually measured raw phenotypes (Eaves et al., 1978; Barrett, 2008). For this study, we used as covariates age, sex, the product of age and sex, the square of age, as well as the product of sex with the square of age.

A statistic for hypothesis testing was computed as Γ = 2(L₁ − L₀), in which L₀ is the maximum log-likelihood under the null hypothesis of no genetic additive effect and L₁ is the maximum log-likelihood of the alternative hypothesis (Elston and Stewart, 1971; Lange et al., 1976). Under certain conditions, Γ is distributed as a 50:50 mixture of a ${\chi }_0^2$ (point mass) distribution and a ${\chi }_1^2$ distribution (Self and Liang, 1987). Despite relying on a multivariate normal assumption, the variance components method is robust to departures from normality, such as skewness, although it can lead to an excess of false positives under leptokurtic conditions (Almasy and Blangero, 2008). To eschew this possibility, different transforms can be applied and, for this study, we used an inverse normal transformation based on ranks, applied directly to the phenotype measurements (Allison et al., 1999; Servin and Stephens, 2007).

2.4.2. Genetic and Phenotypic Correlations

A simple phenotypic correlation between any two traits x and y can be computed as ρ = Cov_p{x, y}/(σ_pxσ_py). The Cov_p{x, y} = ρ_pσ_pxσ_py can be decomposed into genetic and residual effects, Cov_p{x, y} = Cov_g{x, y} + Cov_e{x, y}, which can be rewritten as ρ_pσ_pxσ_py = ρ_gσ_gxσ_gy + ρ_eσ_exσ_ey, in which ρ_g and ρ_e are the genetic and environmental correlations, respectively. These figures represent the extent of shared residual additive genetic and environmental influences on the traits (Almasy et al., 1997). The products σ_gxσ_gy, as well as σ_exσ_ey are obtained by replacing, in a model similar to the Equation 3, the elements Ω_ij = Cov_p{x_i, x_j} for the covariance between the traits, Cov_p{x_i, y_j} (Falconer and Mackay, 1996; Williams et al., 1999). From the same model, partial phenotypic correlations (ρ_p), that include the effect of covariates, are obtained as:

$${\rho }_p={\rho }_g\sqrt{h_i^2{h}_j^2}+{\rho }_e\sqrt{1-h_i^2}\sqrt{1-h_j^2}$$ (4)

For this study, we computed the simple Galton-Pearson correlation coefficient between measurements and partial phenotypic correlations derived from the estimation of the heritabilities, which considers the effect of significant nuisance variables.

3. Results

3.1. Global Measurements and Their Relationship

The average brain volume, including cerebellum and brain stem, was 1.136 ± 0.121 × 10⁶ mm³. The grey matter volume, measured in the surface-based representation was 4.744 ± 0.450 × 10⁵ mm³, which was higher than the same volume measured using the volume-based representation, for which we obtained 3.336 ± 0.409 × 10⁵ mm³. We observed a higher variability on the measurements of global surface area than on average thickness. The average surface area for the whole cortex, was 1.547±0.146×10⁵ mm², while the average cortical thickness in the same areas was 2.589±0.107 mm. Cortical grey matter volumes measured by the two different methods were highly correlated (see Table 2 and Figure 3). The correlation between the surface area and grey matter volume was also high. In contrast, thickness correlated poorly with grey matter volume and with surface area. This trend was observed globally and regionally.

Table 2.

Relationship between measurements.

	Global		Regional
Structure pairs	R2	p	R̄2	SD	min	max
Grey Volume* vs. Grey Volume**	0.8034	2.9e-112	0.8450	0.0722	0.6523	0.9623
Grey Volume* vs. Surface Area	0.7881	3.3e-105	0.7844	0.0839	0.4893	0.9042
Grey Volume* vs. Average Thickness	0.1815	2.7e-005	0.1668	0.0919	0.0461	0.4585
Surface Area vs. Average Thickness	0.0003	5.0e-001	0.0108	0.0132	<0.0001	0.0477
Grey Volume** vs. Surface Area	0.5701	7.1e-044	0.6319	0.0904	0.4372	0.7913
Grey Volume** vs. Average Thickness	0.2850	6.6e-011	0.2035	0.0995	0.0438	0.4872

R² is the goodness of a linear fit; SD is the standard deviation.

^*Measurement in the surface-based representation.

^**Measurement in the volume-based representation.

Figure 3.

Correlations between global measurements. Each point represents a pair of measurements for each subject. R² is the variance explained by a linear regression model. The significances are shown on Table 2.

* Measurement in the surface-based representation.

** Measurement in the volume-based representation.

The brain volume was more strongly correlated with the overall amount of grey matter measured using the surface-based method (R² = 0.865, p = 2.5 × 10⁻¹⁴⁸) than using the volume-based method (R² = 0.687, p = 7.9 × 10⁻⁷⁰). The brain volume was also highly correlated with the surface area of the cortex (R² = 0.856, p = 1.8 × 10⁻¹⁴²), but was not correlated with cortical average thickness (R² = 0.046, p = 0.153).

3.2. Heritabilities

All global measurements were heritable. For brain volume, h² = 0.696, standard error (SE) = 0.097, p = 6.6 × 10⁻¹⁴. The heritability for the surface area was h² = 0.705, SE = 0.109, p = 1.1 × 10⁻¹¹ and for average cortical thickness, h² = 0.691, SE = 0.119, p = 1.7 × 10⁻¹⁰. For the grey matter volume in the surface representation, we found h² = 0.723, SE = 0.099, p = 1.6 × 10⁻¹⁴ and for the voxel-based representation, h² = 0.667, SE = 0.103, p = 2.1 × 10⁻¹². Table 3 shows regional heritabilities, computed using data from both hemispheres. Results for each hemisphere, separately, can be found in the Supplemental Material.

Table 3.

Heritabilities (h²) for regional traits, both hemispheres considered.

	Average Thickness			Surface Area			Grey Volume*			Grey Volume**
Structure name	h2	SE	p	h2	SE	p	h2	SE	p	h2	SE	p
Frontal lobe
Superior frontal gyrus	0.46	0.13	1.1e-05	0.62	0.12	5.8e-09	0.64	0.11	5.1e-11	0.55	0.11	1.2e-08
Middle frontal gyrus; rostral division	0.48	0.12	3.1e-06	0.45	0.12	1.6e-05	0.49	0.11	4.0e-07	0.42	0.12	1.7e-05
Middle frontal gyrus; caudal division	0.53	0.12	3.0e-07	0.56	0.12	1.0e-07	0.58	0.11	3.5e-09	0.58	0.11	1.0e-09
Inferior frontal gyrus; pars opercularis	0.45	0.10	3.3e-08	0.66	0.11	3.7e-10	0.70	0.10	1.6e-12	0.69	0.10	5.6e-13
Inferior frontal gyrus; pars triangularis	0.32	0.11	6.4e-04	0.39	0.13	2.3e-04	0.43	0.13	7.9e-05	0.43	0.12	2.8e-05
Inferior frontal gyrus; pars orbitalis	0.24	0.11	6.1e-03	0.29	0.12	2.5e-03	0.19	0.10	1.9e-02	0.26	0.11	2.3e-03
Orbitofrontal cortex; lateral division	0.41	0.11	3.0e-05	0.60	0.11	8.6e-09	0.57	0.11	4.5e-09	0.58	0.11	2.3e-09
Orbitofrontal cortex; medial division	0.48	0.12	5.8e-06	0.57	0.11	1.5e-08	0.57	0.11	3.5e-09	0.53	0.11	3.5e-08
Frontal pole	0.47	0.12	5.9e-06	0.28	0.10	9.9e-04	0.34	0.11	1.0e-04	0.38	0.13	4.8e-04
Precentral gyrus	0.59	0.11	6.0e-09	0.75	0.11	4.2e-11	0.77	0.10	1.2e-13	0.66	0.10	1.1e-10
Paracentral lobule	0.59	0.13	3.0e-07	0.47	0.14	8.0e-05	0.48	0.13	7.1e-06	0.49	0.12	4.7e-06
Temporal lobe – Medial aspect
Entorhinal cortex	0.43	0.12	2.2e-05	0.44	0.12	9.9e-06	0.33	0.11	4.6e-04	0.33	0.11	5.1e-04
Parahippocampal gyrus	0.41	0.11	4.1e-05	0.64	0.11	3.3e-10	0.64	0.12	1.7e-08	0.61	0.12	1.6e-08
Temporal pole	0.26	0.10	1.7e-03	0.25	0.12	1.7e-02	0.24	0.11	1.2e-02	0.19	0.11	3.2e-02
Fusiform gyrus	0.40	0.12	2.3e-05	0.58	0.10	5.9e-10	0.61	0.10	1.3e-11	0.65	0.10	4.6e-13
Temporal lobe – Lateral aspect
Superior temporal gyrus	0.79	0.11	5.1e-13	0.64	0.11	5.8e-10	0.79	0.09	5.9e-16	0.68	0.10	3.9e-12
Middle temporal gyrus	0.42	0.12	1.5e-05	0.48	0.11	1.0e-07	0.58	0.10	1.2e-11	0.48	0.10	9.5e-09
Inferior temporal gyrus	0.57	0.11	1.0e-07	0.54	0.12	1.0e-06	0.63	0.11	1.2e-08	0.65	0.12	2.2e-09
Transverse temporal cortex	0.71	0.11	4.5e-11	0.73	0.11	3.0e-12	0.65	0.10	5.9e-12	0.70	0.10	2.1e-13
Banks of the superior temporal sulcus	0.47	0.12	7.6e-06	0.41	0.11	3.5e-06	0.49	0.11	1.4e-08	0.51	0.11	5.3e-09
Parietal lobe
Postcentral gyrus	0.83	0.11	2.3e-13	0.58	0.11	2.8e-08	0.64	0.11	1.1e-10	0.64	0.10	3.5e-11
Supramarginal gyrus	0.55	0.12	1.0e-07	0.58	0.10	9.6e-11	0.53	0.10	3.4e-10	0.57	0.10	5.1e-12
Superior parietal cortex	0.50	0.13	3.4e-06	0.61	0.11	1.4e-08	0.56	0.12	5.0e-07	0.53	0.11	2.0e-07
Inferior parietal cortex	0.51	0.12	5.0e-07	0.59	0.11	2.7e-10	0.59	0.10	5.0e-12	0.61	0.11	2.6e-12
Precuneus cortex	0.50	0.12	1.1e-06	0.76	0.11	5.6e-14	0.75	0.10	7.0e-15	0.76	0.10	8.3e-15
Occipital lobe
Lingual gyrus	0.56	0.13	6.0e-07	0.61	0.12	1.0e-07	0.63	0.13	1.7e-08	0.66	0.12	7.7e-10
Pericalcarine cortex	0.35	0.12	2.5e-04	0.64	0.10	1.4e-11	0.66	0.10	1.9e-11	0.64	0.10	5.3e-12
Cuneus cortex	0.50	0.13	1.8e-05	0.42	0.11	7.7e-06	0.49	0.12	9.0e-07	0.61	0.12	3.4e-09
Lateral occipital cortex	0.69	0.11	6.4e-12	0.54	0.12	2.0e-06	0.52	0.12	1.6e-06	0.49	0.12	5.0e-06
Cingulate cortex
Rostral anterior division	0.21	0.11	1.4e-02	0.49	0.12	2.2e-06	0.59	0.12	3.8e-08	0.63	0.12	9.7e-09
Caudal anterior division	0.51	0.13	5.7e-06	0.36	0.12	1.8e-04	0.23	0.10	4.4e-03	0.27	0.11	1.7e-03
Posterior division	0.50	0.12	6.0e-07	0.61	0.11	2.2e-09	0.52	0.12	1.0e-07	0.54	0.12	1.0e-07
Isthmus division	0.70	0.11	2.1e-09	0.82	0.10	1.9e-15	0.74	0.10	9.3e-15	0.78	0.09	1.1e-15
Insular cortex	0.60	0.12	1.0e-07	0.79	0.11	3.8e-13	0.71	0.11	1.9e-12	0.78	0.10	3.1e-15

^*Measurement in the surface-based representation.

^**Measurement in the volume-based representation.

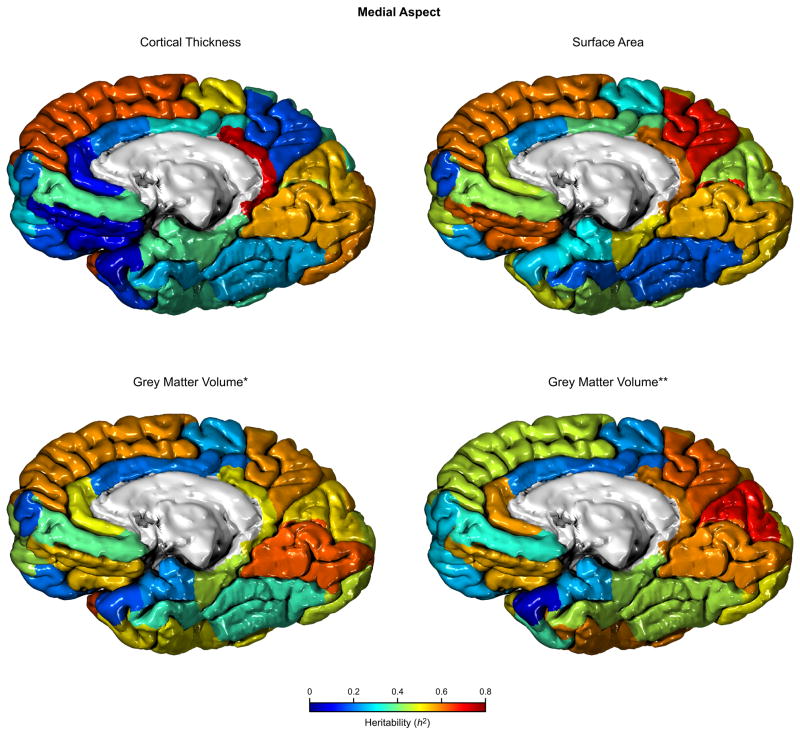
Global brain volume was a significant covariate for all heritability estimates, except for cortical thickness. When brain volume was included together with surface area as covariate, the significance of both covariates was substantially reduced. As a general trend, even for the regional grey volume measurements, global surface area was a more significant nuisance variable. The impact on the final estimates for h² of including brain volume when surface area was also included was negligible. Provided that surface area, grey matter and brain volumes were found to be highly correlated (see below), our model for the regional heritabilities did not include all these potential covariates, but global surface area and average cortical thickness instead. The regional heritabilities with these covariates included is shown on Table 4 and Figures 4 and 5.

Table 4.

Heritabilities (h²) for regional traits, both hemispheres considered, including global surface area and cortical average thickness as covariates.

	Average Thickness			Surface Area			Grey Volume*			Grey Volume**
Structure name	h2	SE	p	h2	SE	p	h2	SE	p	h2	SE	p
Frontal lobe
Superior frontal gyrus	0.63	0.12	3.3e-10	0.61	0.11	1.0e-09	0.59	0.11	7.6e-09	0.47	0.12	1.6e-05
Middle frontal gyrus; rostral division	0.29	0.13	4.2e-03	0.47	0.13	6.2e-06	0.44	0.13	5.9e-05	0.28	0.14	1.2e-02
Middle frontal gyrus; caudal division	0.46	0.12	1.8e-05	0.40	0.11	2.3e-05	0.42	0.12	1.4e-05	0.43	0.12	1.1e-05
Inferior frontal gyrus; pars opercularis	0.31	0.09	8.0e-05	0.42	0.11	4.3e-05	0.51	0.11	5.0e-07	0.54	0.11	1.0e-07
Inferior frontal gyrus; pars triangularis	0.33	0.13	2.8e-03	0.36	0.12	1.6e-04	0.37	0.13	4.3e-04	0.36	0.13	3.4e-04
Inferior frontal gyrus; pars orbitalis	0.17	0.11	5.4e-02	0.24	0.12	1.3e-02	0.20	0.12	2.9e-02	0.26	0.12	6.7e-03
Orbitofrontal cortex; lateral division	0.10	0.11	1.6e-01	0.62	0.11	1.1e-08	0.55	0.11	1.0e-07	0.57	0.12	5.0e-07
Orbitofrontal cortex; medial division	0.38	0.11	9.0e-05	0.44	0.11	5.1e-06	0.39	0.12	1.3e-04	0.34	0.12	9.4e-04
Frontal pole	0.21	0.12	3.8e-02	0.17	0.10	3.0e-02	0.18	0.11	3.0e-02	0.28	0.14	1.1e-02
Precentral gyrus	0.56	0.11	4.3e-09	0.57	0.12	1.0e-06	0.64	0.12	1.2e-08	0.46	0.14	3.3e-04
Paracentral lobule	0.53	0.12	2.4e-06	0.32	0.13	3.3e-03	0.25	0.12	1.2e-02	0.24	0.13	2.8e-02
Temporal lobe – Medial aspect
Entorhinal cortex	0.38	0.12	9.6e-05	0.31	0.12	1.0e-03	0.23	0.12	1.3e-02	0.25	0.12	8.8e-03
Parahippocampal gyrus	0.39	0.12	9.9e-05	0.51	0.12	1.0e-06	0.46	0.14	3.0e-04	0.45	0.14	3.0e-04
Temporal pole	0.06	0.10	2.7e-01	0.27	0.12	7.7e-03	0.17	0.11	5.8e-02	0.07	0.11	2.5e-01
Fusiform gyrus	0.26	0.12	5.2e-03	0.19	0.10	1.2e-02	0.35	0.11	3.8e-05	0.45	0.10	4.0e-07
Temporal lobe – Lateral aspect
Superior temporal gyrus	0.65	0.12	6.0e-09	0.50	0.12	7.4e-06	0.65	0.11	4.5e-10	0.52	0.12	5.0e-06
Middle temporal gyrus	0.15	0.11	7.1e-02	0.49	0.11	4.0e-07	0.52	0.11	1.0e-07	0.36	0.11	7.5e-05
Inferior temporal gyrus	0.36	0.11	1.3e-04	0.44	0.12	3.3e-05	0.51	0.12	3.7e-06	0.60	0.12	1.0e-07
Transverse temporal cortex	0.44	0.12	6.4e-05	0.67	0.11	1.5e-11	0.52	0.11	2.9e-08	0.61	0.11	3.1e-10
Banks of the superior temporal sulcus	0.28	0.12	6.3e-03	0.38	0.12	1.8e-04	0.40	0.12	4.1e-05	0.49	0.12	1.9e-06
Parietal lobe
Postcentral gyrus	0.73	0.11	3.6e-12	0.43	0.11	3.2e-06	0.49	0.10	1.0e-07	0.54	0.10	4.3e-09
Supramarginal gyrus	0.35	0.11	4.5e-04	0.34	0.11	1.7e-04	0.33	0.11	2.8e-04	0.51	0.11	9.5e-09
Superior parietal cortex	0.36	0.12	4.8e-04	0.51	0.11	6.0e-07	0.58	0.11	1.1e-08	0.58	0.12	1.0e-07
Inferior parietal cortex	0.41	0.13	2.2e-04	0.43	0.12	3.5e-06	0.51	0.11	2.8e-08	0.64	0.12	3.7e-10
Precuneus cortex	0.17	0.12	7.0e-02	0.69	0.11	6.2e-11	0.59	0.11	3.9e-09	0.63	0.13	1.0e-07
Occipital lobe
Lingual gyrus	0.57	0.11	5.9e-09	0.57	0.12	3.0e-07	0.64	0.12	5.6e-10	0.59	0.12	1.8e-08
Pericalcarine cortex	0.46	0.11	2.2e-06	0.68	0.10	1.9e-11	0.64	0.10	6.7e-11	0.63	0.10	2.1e-11
Cuneus cortex	0.56	0.12	1.0e-07	0.45	0.12	9.6e-06	0.53	0.11	1.0e-07	0.70	0.12	4.2e-11
Lateral occipital cortex	0.60	0.11	2.5e-08	0.54	0.11	1.7e-06	0.48	0.12	1.6e-05	0.51	0.13	2.7e-05
Cingulate cortex
Rostral anterior division	0.12	0.10	9.8e-02	0.47	0.12	1.2e-05	0.50	0.12	1.9e-06	0.58	0.12	1.0e-07
Caudal anterior division	0.22	0.12	2.3e-02	0.23	0.10	4.5e-03	0.20	0.10	7.5e-03	0.22	0.10	5.8e-03
Posterior division	0.32	0.12	6.1e-04	0.39	0.14	1.2e-03	0.21	0.12	2.2e-02	0.20	0.13	4.1e-02
Isthmus division	0.72	0.11	7.2e-10	0.60	0.12	2.0e-07	0.51	0.11	8.0e-07	0.59	0.12	1.0e-07
Insular cortex	0.50	0.13	7.2e-06	0.76	0.13	1.7e-09	0.65	0.12	9.7e-09	0.79	0.11	6.4e-12

^*Measurement in the surface-based representation.

^**Measurement in the volume-based representation.

Figure 4.

Heritability (h²) for the cortical regions using different traits, lateral aspect.

* Measurement in the surface-based representation.

** Measurement in the volume-based representation.

Figure 5.

Heritability (h²) for the cortical regions using different traits, medial aspect.

* Measurement in the surface-based representation.

** Measurement in the volume-based representation.

With respect to regional variability, a simple average of the heritabilities from Table 4 shows an h̄² = 0.458 ± 0.149 for the regional surface area and h̄² = 0.501 ± 0.142 for thickness. For the grey matter volume in surface-based representation, h̄² = 0.489 ± 0.1615. For the grey matter volume in the voxel-based representation, h̄² = 0.482 ± 0.146. While none of these figures approach the global measurements, they provide a rough estimate of how the heritability varies across the brain.

3.3. Genetic and Phenotypic Correlations Between Measurements

Both surface-based and volume-based measurements of global grey matter volume were strongly correlated with the global surface area, genetically, environmentally and phenotypically (see Table 5). In contrast, cortical thickness correlated poorly and slightly negatively with surface area. Cortical thickness also correlated poorly with grey matter volume. The estimated genetic correlation was higher than the environmental (non-genetic) when the volume was computed in the surface-based representation, while the volume-based followed the opposite trend. The correlations were high between both measurements of grey matter volume.

Table 5.

Genetic (ρ_g), environmental (ρ_e) and phenotypic (ρ_p) correlations between global measurements.

Structure pairs	ρg	ρe	ρp
Grey Volume* vs. Grey Volume**	+0.904 [9.2e-12]	+0.866 [1.7e-03]	+0.891†
Grey Volume* vs. Surface Area	+0.848 [3.1e-10]	+0.853 [3.9e-03]	+0.849†
Grey Volume* vs. Average Thickness	+0.387 [4.0e-03]	+0.235 [3.6e-01]	+0.343 [2.1e-12]
Surface Area vs. Average Thickness	−0.154 [2.9e-01]	−0.215 [4.0e-01]	−0.172 [5.0e-04]
Grey Volume** vs. Surface Area	+0.857 [4.8e-10]	+0.661 [1.3e-02]	+0.795†
Grey Volume** vs. Average Thickness	+0.235 [9.5e-02]	+0.428 [6.9e-02]	+0.297 [2.4e-10]

^*Measurement in the surface-based representation.

^**Measurement in the volume-based representation.

^†The algorithm did not converge within the precision limit.

The correlations of the brain volume with grey matter volume measured in the surface-based representation were high genetically (ρ_g = 0.886, p = 5.0 × 10⁻¹²), environmentally (ρ_e = 0.903, p = 1.4 × 10⁻³) and phenotypically (ρ_p = 0.890, p-value did not converge). Similarly, correlations with the grey matter measured in the volume-based representation were strong (ρ_g = 0.896, p = 1.5×10⁻¹¹; ρ_e = 0.770, p = 2.0×10⁻³; ρ_p = 0.855, p-value did not converge). The correlations were also high between brain volume and cortical surface area (ρ_g = 0.878, p = 1.3 × 10⁻¹⁰; ρ_e = 0.895, p = 1.9×10⁻³; ρ_p = 0.883, p-value did not converge), although low and not significant between brain volume and average cortical thickness (ρ_g = 0.161, p = 2.4 × 10⁻¹; ρ_e = 0.006, p = 9.8 × 10⁻¹; ρ_p = 0.113, p = 2.1 × 10⁻²). The lack of convergence for some p-values often means extremely low significance levels, lower than the computing precision level, with an actual p < 10⁻³⁰⁷.

While we found differences in genetic, environmental and phenotypic correlations across the cortex, generally the same trend observed for global measurements held. Remarkably, the correlations between cortical thickness and surface area were erratic and clearly non-significant for the majority of the regions. On the other hand, grey matter volume and surface area were highly and more significantly correlated and, as for the global measurements, the correlation between thickness and grey volume lied in intermediate levels between these extremes. The regional correlations are shown in Table 6.

Table 6.

Genetic (ρ_g), environmental (ρ_e) and phenotypic (ρ_p) correlations between regional measurements for cortical thickness, surface area and grey matter volume, all measured using the surface-based representation. Global cortical average thickness and surface were included as covariates. The significance is between brackets.

	Cortical Thickness vs. Surface Area			Cortical Thickness vs. Grey Volume			Grey Volume vs. Surface Area
Structure name	ρg	ρe	ρp	ρg	ρe	ρp	ρg	ρe	ρp
Frontal lobe
Sup. frontal g.	−0.48 [1.9e-03]	−0.13 [5.4e-01]	−0.35 [6.3e-13]	−0.14 [3.8e-01]	+0.11 [5.8e-01]	−0.04 [3.9e-01]	+0.92 [4.4e-08]	+0.90 [1.5e-04]	+0.91†
Mid. frontal g., rostral div.	−0.45 [1.3e-01]	+0.16 [2.5e-01]	−0.05 [3.2e-01]	−0.33 [3.2e-01]	+0.41 [3.4e-03]	+0.17 [2.1e-04]	+0.96†	+0.94†	+0.95†
Mid. frontal g., caudal div.	+0.17 [4.1e-01]	−0.20 [1.6e-01]	−0.04 [4.4e-01]	+0.38 [6.4e-02]	+0.01 [9.6e-01]	+0.18 [1.9e-04]	+0.89†	+0.91†	+0.91†
Inf. frontal g., opercularis	+0.30 [1.6e-01]	−0.34 [2.5e-03]	−0.11 [2.3e-02]	+0.50 [1.1e-02]	−0.07 [5.5e-01]	+0.16 [7.3e-04]	+0.97 [8.0e-06]	+0.94 [1.1e-08]	+0.95 [7.9e-224]
Inf. frontal g., triangularis	+0.22 [4.0e-01]	−0.12 [3.8e-01]	+0.00 [9.4e-01]	+0.45 [9.8e-02]	+0.11 [4.7e-01]	+0.23 [3.9e-07]	+0.96 [8.6e-04]	+0.95 [1.2e-07]	+0.95 [1.9e-228]
Inf. frontal g., orbitalis	+0.41 [3.4e-01]	−0.14 [1.9e-01]	−0.03 [5.0e-01]	+0.71 [1.2e-01]	+0.25 [1.8e-02]	+0.33 [9.0e-14]	+0.94 [4.0e-02]	+0.87 [1.7e-10]	+0.88 [1.4e-140]
Orbitofrontal g., lat. div.	+0.06 [8.7e-01]	−0.42 [1.8e-03]	−0.23 [4.5e-07]	+0.37 [3.2e-01]	+0.18 [1.4e-01]	+0.20 [1.2e-05]	+0.92 [9.3e-08]	+0.73 [8.4e-04]	+0.84 [2.0e-114]
Orbitofrontal g., med. div.	−0.27 [1.9e-01]	−0.06 [6.6e-01]	−0.14 [2.2e-03]	+0.46 [4.3e-02]	+0.34 [6.4e-03]	+0.38 [4.4e-17]	+0.91 [2.6e-03]	+0.86 [1.0e-07]	+0.80 [4.4e-97]
Frontal pole	+0.17 [6.8e-01]	−0.19 [6.0e-02]	−0.12 [7.9e-03]	+0.41 [3.5e-01]	+0.25 [2.0e-02]	+0.28 [5.1e-10]	+0.98 [5.2e-02]	+0.86 [4.5e-12]	+0.88 [1.2e-139]
Precentral g.	+0.10 [5.4e-01]	−0.27 [1.2e-01]	−0.06 [2.0e-01]	+0.46 [2.9e-03]	+0.24 [2.1e-01]	+0.37 [4.9e-15]	+0.91 [1.1e-06]	+0.80 [1.3e-03]	+0.87 [5.9e-150]
Paracentral lobule	−0.17 [4.5e-01]	+0.23 [1.3e-01]	+0.05 [2.5e-01]	+0.39 [1.4e-01]	+0.47 [1.6e-03]	+0.42 [9.5e-19]	+0.82 [3.1e-02]	+0.94 [2.4e-09]	+0.90 [6.0e-156]
Temporal lobe - Medial aspect
Entorhinal cortex	−0.37 [1.5e-01]	−0.12 [3.4e-01]	−0.21 [5.8e-06]	+0.19 [5.3e-01]	+0.45 [2.5e-04]	+0.36 [6.0e-15]	+0.76 [3.1e-02]	+0.75 [3.3e-08]	+0.75 [1.2e-73]
Parahippocampal g.	−0.32 [1.2e-01]	−0.29 [4.9e-02]	−0.30 [1.8e-10]	+0.54 [3.2e-02]	+0.57 [3.6e-04]	+0.56 [7.0e-36]	+0.63 [4.7e-03]	+0.53 [2.5e-03]	+0.57 [8.6e-38]
Temporal pole	+0.32 [6.1e-01]	+0.11 [2.8e-01]	+0.13 [3.5e-03]	+0.25 [7.8e-01]	+0.65 [3.2e-10]	+0.60 [4.0e-49]	+1.00 [2.2e-02]	+0.76 [1.2e-09]	+0.81 [1.1e-96]
Fusiform g.	+1.00 [5.9e-03]	−0.15 [1.3e-01]	+0.09 [4.4e-02]	+0.96 [4.6e-04]	+0.22 [5.8e-02]	+0.43 [3.8e-23]	+0.97 [4.8e-04]	+0.90 [1.1e-13]	+0.90†
Temporal lobe - Lateral aspect
Sup. temporal g.	+0.36 [4.8e-02]	−0.38 [3.4e-02]	+0.02 [6.1e-01]	+0.71 [2.8e-06]	+0.17 [4.3e-01]	+0.51 [8.5e-28]	+0.88 [1.9e-06]	+0.79 [9.0e-05]	+0.83 [1.3e-106]
Mid. temporal g.	+0.28 [3.7e-01]	−0.17 [1.7e-01]	−0.03 [4.8e-01]	+0.44 [1.5e-01]	+0.22 [9.6e-02]	+0.27 [5.6e-09]	+0.97 [4.2e-07]	+0.88 [5.1e-06]	+0.92 [6.5e-178]
Inf. temporal g.	+0.11 [6.3e-01]	−0.09 [5.0e-01]	−0.01 [8.3e-01]	+0.47 [2.3e-02]	+0.25 [8.7e-02]	+0.35 [5.9e-14]	+0.92 [4.6e-05]	+0.90 [6.5e-07]	+0.91†
Trans. temporal cortex	−0.40 [1.8e-02]	+0.05 [7.7e-01]	−0.20 [2.4e-05]	+0.04 [8.2e-01]	+0.51 [8.1e-04]	+0.28 [4.5e-09]	+0.89 [8.8e-09]	+0.83 [9.3e-05]	+0.86†
Banks sup. temporal s.	+0.21 [4.7e-01]	+0.07 [5.6e-01]	+0.12 [1.3e-02]	+0.40 [1.4e-01]	+0.31 [1.4e-02]	+0.34 [2.1e-13]	+0.96 [6.7e-10]	+0.94 [8.6e-08]	+0.95†
Parietal lobe
Postcentral g.	+0.36 [2.5e-02]	+0.03 [8.6e-01]	+0.21 [6.8e-06]	+0.81 [2.0e-08]	+0.31 [1.9e-01]	+0.61 [1.4e-45]	+0.83 [2.2e-05]	+0.91 [7.1e-09]	+0.87†
Supramarginal g.	−0.26 [2.9e-01]	+0.00 [9.8e-01]	−0.09 [4.6e-02]	−0.03 [9.1e-01]	+0.20 [8.8e-02]	+0.12 [7.6e-03]	+0.96 [6.0e-04]	+0.95 [1.2e-09]	+0.95†
Sup. parietal cortex	+0.59 [7.5e-03]	−0.19 [1.7e-01]	+0.13 [5.4e-03]	+0.71 [6.2e-04]	+0.25 [1.0e-01]	+0.44 [6.6e-22]	+0.98 [8.1e-46]	+0.86 [5.8e-06]	+0.92 [4.2e-178]
Inf. parietal cortex	+0.45 [6.4e-02]	−0.43 [2.1e-03]	−0.08 [8.6e-02]	+0.50 [1.7e-02]	−0.12 [4.1e-01]	+0.15 [1.2e-03]	+0.99 [2.3e-07]	+0.90 [1.2e-06]	+0.94 [4.7e-207]
Precuneus cortex	−0.05 [8.7e-01]	−0.31 [5.6e-02]	−0.18 [9.4e-05]	+0.03 [9.1e-01]	+0.16 [2.6e-01]	+0.10 [3.0e-02]	+0.99 [2.3e-11]	+0.78 [5.1e-03]	+0.92†
Occipital lobe
Lingual gyrus	+0.16 [3.5e-01]	+0.01 [9.7e-01]	+0.09 [5.7e-02]	+0.54 [6.4e-04]	+0.38 [6.4e-02]	+0.47 [8.8e-23]	+0.91 [1.9e-11]	+0.89 [7.5e-04]	+0.90 [1.3e-155]
Pericalcarine cortex	+0.16 [3.3e-01]	+0.04 [8.2e-01]	+0.11 [2.7e-02]	+0.52 [1.7e-03]	+0.60 [6.9e-04]	+0.55 [5.9e-33]	+0.93 [1.8e-10]	+0.76 [1.6e-03]	+0.87†
Cuneus cortex	+0.35 [6.1e-02]	+0.09 [5.8e-01]	+0.22 [3.5e-06]	+0.70 [4.7e-05]	+0.46 [1.2e-02]	+0.59 [2.3e-39]	+0.92 [8.7e-06]	+0.89 [1.8e-06]	+0.90 [1.1e-155]
Lat. occipital cortex	−0.05 [7.7e-01]	+0.13 [4.7e-01]	+0.03 [5.8e-01]	+0.35 [4.8e-02]	+0.35 [4.7e-02]	+0.35 [1.2e-12]	+0.92 [3.1e-05]	+0.93 [1.3e-12]	+0.92 [4.0e-180]
Rostral ant. div.	+0.17 [6.3e-01]	−0.36 [2.1e-03]	−0.20 [1.3e-05]	+0.59 [8.8e-02]	+0.20 [9.4e-02]	+0.27 [1.6e-09]	+0.91 [2.1e-05]	+0.78 [1.1e-04]	+0.84 [2.7e-112]
Caudal ant. div.	+0.18 [6.1e-01]	+0.09 [3.8e-01]	+0.11 [1.5e-02]	+0.60 [1.1e-01]	+0.48 [8.1e-06]	+0.50 [5.4e-30]	+0.88 [1.8e-02]	+0.87 [1.5e-12]	+0.87 [3.5e-132]
Post. div.	−0.58 [1.5e-02]	+0.27 [6.6e-02]	−0.07 [1.2e-01]	−0.17 [5.6e-01]	+0.57 [5.4e-06]	+0.34 [5.8e-12]	+0.87 [1.1e-02]	+0.91 [9.0e-08]	+0.88 [2.2e-164]
Isthmus div.	−0.21 [1.8e-01]	−0.13 [5.9e-01]	−0.18 [2.3e-04]	+0.32 [4.5e-02]	+0.22 [2.8e-01]	+0.27 [1.5e-08]	+0.86 [5.0e-06]	+0.87 [1.3e-04]	+0.86 [2.0e-124]
Insular cortex	−0.30 [7.9e-02]	+0.10 [7.0e-01]	−0.16 [1.5e-03]	+0.21 [2.4e-01]	+0.54 [7.5e-03]	+0.35 [1.2e-12]	+0.84 [1.9e-07]	+0.73 [4.9e-02]	+0.80†

^†The algorithm did not converge within the precision limit.

4. Discussion

4.1. Relationship Between Surface-based and Volume-based Representations

Despite absolute differences between grey matter volume estimates based on each representation of the brain, the high correlation between these measurements validates each technique, and suggests that either method can be used to quantify how the global amount of grey matter varies across subjects. Strong agreement at regional level suggests that these measurements are likewise valid. However, it should be noted that regions were defined in the surface-based representation and then projected to the volumetric space, rather than directly defining regions of interest from volumetric atlases or coordinate systems as would be done in VBM-like analyses. It is possible that the agreement between surface-based and volume-based cortical parcellations might have been reduced, had these measurements been obtained separately. Indeed, in VBM methods, the definition of regions relies heavily on the accuracy and precision of registration methods (Klein et al., 2009) and of the atlas itself.

4.2. Choice of Traits for Genetic Studies

Since all brain traits studied were heritable to some extent, globally or regionally, it might appear that any of such traits could be of interest for genetic studies. A closer inspection, however, reveals that grey matter volume, which is a composite of two other traits (surface area and thickness), might not be the best choice. The variability for surface area measurements was higher than for the cortical thickness, implying that the variability found on grey matter volume is more closely linked to surface area than to thickness. The regional area is measured on the surface between adjacent landmarks, giving a higher, quadratic weight to tangential (horizontal) than to vertical (radial) distances, explaining why volume is more correlated with area. Furthermore, grey matter volume was genetically and environmentally correlated with surface area and, to a much lesser extent, with thickness.

While the geometric relationship between surface area and cortical thickness (Figure 1) alone is sufficient to demonstrate their spatial orthogonality, it does not suffice to suggest their biological independence. However, the results indicate that surface area has a poor genetic, environmental and phenotypic correlation with cortical thickness, regionally and globally, which is evidence for the hypothesis that area and thickness are from distinct genetic origins. Based on these results, and consistent with findings from Panizzon et al. (2009), we advocate that, for imaging genetic studies, cortical thickness and surface area as separate traits of interest should be preferred over grey matter volumes.

The findings presented here also suggest that imaging methods that only provide measurements of gray matter volume may be less sensitive for gene identification than those that disentangle cortical thickness and surface area. Although VBM and similar methods have shown to be useful for a variety of non-genetic studies, their benefit for imaging genetics may be limited by not discriminating genetically independent traits as thickness and area. Moreover, studies performed in a voxel-per-voxel basis generally require that the images are aligned to a common space, which, together with the segmentation method, has the potential for introducing additional confoundings, such as misalignment, misclassification, as well as false detection of normal variants of folding patterns as focal changes on grey matter volume (Ashburner and Friston, 2007).

Yet, despite these disadvantages, volume-based techniques might have their place for the analysis of gray matter in subcortical structures and for multivariate analysis that include voxel-based functional imaging, such as functional MRI or positron emission tomography (PET). Novel algorithms to measure cortical thickness in a volumetric fashion have been recently developed (Hutton et al., 2008; Scott et al., 2009; Aganj et al., 2009; Acosta et al., 2009), which might eschew some or all of the limitations discussed above. Advantages of these approaches include faster computing time, which might be a feature of interest for large studies or when processing capacity is scarce. These novel methods deserve a careful investigation about their potential in the context of genetic studies.

We note that the idea that cortical surface area and cortical thickness represent processes with independent genetic control is sound phylogenetically and ontogenetically. There is increasing evidence that evolution has operated more on the surface area of the brain, which variation between species is more pronounced, than on cortical thickness, which remained roughly constant in comparison (Mountcastle, 1998; Roth and Dicke, 2005; Fish et al., 2008). Although some correlation between cortical thickness and area across species has been found (Herculano-Houzel et al., 2008), the genetic factors that control cortical thickness appear to differ from those that influence surface area. Were cortical thickness and surface area mostly determined by the same set of genes or pathways, it would be expected to find strong correlations between both, which is not the case.

From an ontogenetic standpoint, the neurons that populate the cortex migrate to their final locations (Berry and Rogers, 1965; Rakic, 1972) by following the path (scaffolding) determined the basal processes of neuroepithelial and radial cells (Kosodo and Huttner, 2009), and their final destinations, the cortical layers II–VI, are formed in an inside-out pattern (Pierani and Wassef, 2009). On the other hand, it has been hypothesised that each functional cortical column of the brain corresponds to several of what has been called “ontogenetic columns” of precursor, proliferative cells from the ventricular zone in the embryo (Rakic, 1988; Rakic et al., 2009). Experiments by Chenn and Walsh (2003) demonstrated that the brain surface area is influenced by the proliferation of these precursor cells, providing additional evidence for separate pathways that control cortical area and thickness. These hypotheses do not preclude other possible mechanisms that might underlie independent genetic control thickness and area. The ingrowth of the thalamo-cortical and cortico-cortical fibres on the late fetal and perinatal development, and their myelination, which form an intricate network within and across cortical layers, has the potential of resulting in more pronounced horizontal than vertical growth (Kostović and Jovanov-Miloševí, 2006). The migration of interneurons within the cortex (tangential) (Polleux et al., 2002) also has the potential to influence both thickness and area, though not necessarily on the same proportion. Moreover, the development of the neuropil of pyramidal cells (Zhang, 2004) may not be uniform over all directions, possibly growing at different rates and reaching different lengths vertically and horizontally. Therefore, the exact biological underpinnings of the genetic independence between area and thickness have a number of putative mechanisms and is a question that remains open.

4.3. Genetic Influences on Structural Measurements

Heritability estimates for global measurements from this study are consistent with other published, twin studies (Peper et al., 2007; Schmitt et al., 2008). The estimate for brain volume included the cerebellum, which might be a source of difference if compared to reports by other groups.

Regionally, there are remarkable similarities in the distribution of genetic influences across the cortex in terms of surface area and grey matter volume, measured in the surface-based representation. For the grey matter volume in the volume-based representation, the pattern resembles the volume measured in the surface-based, although some regions follow the pattern of heritability of the thickness, suggesting that the weight of which thickness and surface area determine the volume in the voxel-based representation may be variable across the cortex.

The heritabilities for thickness followed a distinctive pattern if compared with other traits, which corroborates to the finding that thickness is under different genetic control. While the definitions of the regions of the Desikan et al. (2006) atlas follow macroanatomic landmarks, not cytoarchitectonic, there is evidence suggesting that there is a substantial overlap between them (Fischl et al., 2008), and the higher regional variability suggests that regional differences on thickness might reflect underlying, regional cytoarchitectonic differences. The spatial distribution of heritabilities for surface area follows a more homogeneous pattern, particularly for the lateral aspect of the brain, suggesting a smaller degree of regional variation on genetic infuences.

Results for the cortical thickness measurements are generally in agreement with the report of Lenroot et al. (2009), who parcellated the brain using a different scheme. Remarkable similarities include, for instance, high genetic effect on the thickness of the postcentral and superior temporal gyri and the very low heritability estimates for the precuneus region. There are, however, several important differences, which might be due to differences in the delimitations of the regions. For the 10 regions reported by Panizzon et al. (2009), who used a similar parcellation scheme in a sample of twins, the measurements reported here are roughly in the same range for surface area and for cortical thickness, although there are differences, possibly attributable, at least partially, to different imaging protocols and genetic analysis. The present study included subjects from both sexes and in a wider age range, which makes it more generalisable. Finally, the findings shown here are derived from extended pedigrees, which is a more powerful and efficient study design than sibling-pairs, of which twin studies are a particular case (Blangero et al., 2003).

Since grey matter volume is a function of surface area and cortical thickness, there are no clear reasons to try to interpret regional grey matter volume differences in terms of genetic influences, particularly for the results obtained from voxel-based representations, where, as discussed, the mixture of thickness and area might follow an unknown and variable proportions across the cortical mantle.

In this report we avoided determining specific, numeric thresholds for p-values to accept or reject any hypotheses, although the numbers that support the conclusions survive a relatively assumption-free, false discovery rate (FDR) method (Benjamini and Hochberg, 1995) at q = 0.05. Attempts to rigorously define a threshold for family-wise error rate would have to consider the non-independence of the tests with an unknown covariance structure. We opted, instead, to clearly disclose all the p-values. Nevertheless, we underscore that, as important as the p-values themselves, are the trend that both the heritabilities and their associated significances follow, which support the conclusions hereby presented.