Abstract
Although in vitro transport/inhibition studies are commonly performed on impure drug candidates to screen for pharmacokinetic properties in early development, quantitative guidelines concerning acceptable impurity levels are lacking. The broad goal was to derive models for the effect of impurity on transport and inhibition studies and identify the maximum allowable impurity level that does not bias assay results. Models were derived and simulations performed to assess the impact of impurity on substrate properties Kt and Jmax and inhibition Ki. Simulation results were experimentally challenged with known amount of impurity, using the intestinal bile acid transporter as a model system. For substrate uptake studies, glycocholate served as substrate and was contaminated with either a very strong, strong, or moderate impurity (i.e. taurolithocholate, chenodeoxycholate, or ursodeoxycholate, respectively). For inhibition studies, taurocholate and glycocholate was the substrate/inhibitor pair, where glycocholate was contaminated with taurolithocholate. There was high agreement between simulation results and experimental observations. Not surprisingly, in the inhibition assay, potent impurity caused test compound to appear more potent than the test compound’s true potency (i.e. reduced inhibitory Ki). However, results in the transport scenario surprisingly indicated that potent impurity did not diminish test compound potency, but rather increased substrate potency (i.e. reduced Michaelis-Menten substrate Kt). In general, less than 2.5% impurity is a reasonable target, provided the impurity is less than 10-fold more potent than test compound. Study results indicate that careful consideration of possible impurity effect is needed when QSAR analysis cannot explain high compound potency from transport or inhibition studies.
INTRODUCTION
Transport and inhibition studies are routinely performed in early development to screen for absorption, distribution, metabolism and excretion (ADME). For example, a current project in our laboratory concerns the targeting of an intestinal transporter for drug delivery purposes (Balakrishnan and Polli, 2006). The transporter is the human Apical Sodium-dependent Bile Acid Transporter (hASBT). ADME considerations in this project motivate the screening for substrates and inhibitors of hASBT, in order to construct a quantitative structure-activity relationship (QSAR) model for inhibitors and substrates of this transporter. Test compounds are currently being synthesized to evaluate the chemical structural features that allows for hASBT inhibition, as well as translocation by hASBT (Balakrishnan et al., 2006a).
However, test compounds in early development often contain chemical impurities, including intermediates that bear structural similarity to the target test compound. The presence of such impurities has potential to affect the results of pharmacologic assays, including ADME screening results. The Journal of Pharmacology and Experimental Therapeutics does not provide guidelines about compound purity. Since January 2007, the Journal of Medicinal Chemistry now requires that key target compounds possess purity of 98% or more. However, well developed guidelines and their rationale about acceptable level of impurity, based upon possible impurity impact on assay results during early development, are surprisingly lacking. Guidance on impurity effects on ADME screening studies would be helpful.
The present study concerns two types of ADME transport studies: inhibition studies and transport/uptake studies. Presumably, in a competitive binding study (e.g. inhibition study), impurity with a potency greater than test compound potency may cause test compound to appear more potent than actually is. This expectation was found to be correct here and quantitative guidelines are provided. Surprisingly, an expectation that a potent impurity would diminish the apparent potency of a test compound in the uptake assay (i.e. increase Michaelis-Menten Kt) was found here to be incorrect. Rather, potent impurity, which reduces test compound flux, resulted in test compound to appear to possess higher substrate affinity (i.e. exhibit a lower Kt). This study provides quantitative guidelines, which are currently lacking, about maximum impurity levels to avoid bias on transporter parameter estimates (i.e. Kt, Jmax, and Ki) in early drug discovery. Results have implications for other types of early discover assays, such as pharmacologic binding studies.
METHODS
Overall Study Design
Both simulation studies and experimental studies were performed, for both transport/uptake studies, as well as inhibition studies. Table 1 summarizes the four types of studies. In transport/uptake studies, the impurity is a contaminant of the substrate. Simulation studies were conducted over a wide range of conditions. The experimental uptake studies employed taurolithocholic acid (TLCA), chenodeoxycholic acid (CDCA), and ursodeoxycholic acid (UDCA) as very strong, strong, and moderate potent impurities, respectively. In inhibition studies, the impurity is a contaminant of the inhibitor.
Table 1.
Experimental design.
| Simulation/Experiment | Type of study | Substrate | Inhibitor | Impurity |
|---|---|---|---|---|
| Kt (μM) | Ki (μM) | Ki (μM) | ||
| Simulation | Transport/uptake | 5, 50, 500 | none | Ki = 0.05–500 |
| Experiment | Uptake | GCA (Kt ≈ 11) | none | TLCA (Ki = 0.11) CDCA (Ki = 1.39) UDCA (Ki = 24.2) |
| Simulation | Inhibition | 5 | 0.05–50 | Kj = 0.5–50 |
| Experiment | Inhibition | TCA (Kt = 5.03) | GCA (Ki = 5.05) | TLCA (Kj = 0.40) |
Materials
[3H]-Taurocholic acid (10 μCi/mmol) and [14C]-glycocholic acid (55 mCi/mmol) were purchased from American Radiolabeled Chemicals, Inc, (St. Louis, MO). Taurocholic acid (TCA), glycocholic acid (GCA), taurolithocholic acid TLCA, and ursodeoxycholic acid UDCA were from Sigma Aldrich (St. Louis, MO). CDCA was obtained from TCI America (Portland, OR). Geneticin, fetal bovine serum (FBS), trypsin, and DMEM were purchased from Invitrogen (Rockville, MD). All other reagents and chemicals were of the highest purity commercially available.
Cell Culture
Stably-transfected hASBT-MDCK cells were cultured as previously described (Balakrishnan et al., 2005). Briefly, cells were grown at 37 °C, 90% relative humidity, 5% CO2 atmosphere and fed every 2 days. Culture media consisted on DMEM supplemented with 10% FBS, 50 units/mL penicillin, and 50 μg/mL streptomycin. Geneticin was added at 1 mg/mL to maintain selection pressure. Cells were passaged after 4 days or after reaching 90% confluency.
Uptake Studies
Uptake studies were performed to obtain kinetic parameters that relate to compound binding and subsequent translocation into the cell monolayer. Stably-transfected hASBT-MDCK cells were grown on 12-well plates (3.8 cm2, Corning, Corning, NY) and grown under conditions described above. Briefly, cells were seeded at a density of 1.5 million/well and induced with 10 mM sodium butyrate 12–15 h at 37 °C prior to study on day 4. Cells were washed thrice with Hank’s balanced salt solution (HBSS) or modified HBSS prior to uptake assay. Studies were conducted at 37 °C, 50 rpm for 10 min in an orbital shaker. Uptake buffer consisted of either HBSS, which contains 137 mM NaCl, or a sodium-free, modified HBSS where NaCl was replaced by 137 mM tetraethylammonium chloride (pH 6.8). Since ASBT is sodium dependent, studies using sodium-free buffer allowed for the measurement of passive uptake. Kinetics of hASBT-mediated GCA uptake (n=3) was assessed at different donor concentrations (1–200 μM spiked with 0.2 μCi/mL of [14C]-GCA), in presence and absence of impurity. When impurity was present, each GCA donor solution was contaminated with TLCA, CDCA, or UDCA (i.e. impurity) to yield a mole fraction of impurity, Xi, of 2, 4, 6, 8, and 10%, respectively. Ki of these impurities was obtained from GCA-uptake inhibition studies (see below).
At the end of the assay, active uptake was stopped by washing the cells thrice with chilled sodium-free buffer. Cells were then lysed with 0.25 mL of 1 N NaOH overnight, allowing for complete evaporation, and reconstituted with 0.50 mL of 0.5 N HCl. Cell lysate was counted for associated radioactivity using an LS6500 liquid scintillation counter (Beckmann Instruments, Inc., Fullerton, CA).
Inhibition Assay
To characterize hASBT binding affinities, cis-inhibition studies of TCA or GCA uptake were conducted as described. Cells were exposed to donor solutions containing relevant substrate (2.5 μM TCA + 0.5 μCi/ml [3H]-TCA or 5 μM GCA + 0.2 μCi/mL [14C]-GCA) and inhibitor (1–200 μM) for 10 min. GCA inhibition of TCA was measured in absence and presence of impurity. When impurity was present, each GCA donor solution was contaminated with TLCA (i.e. impurity) to yield a mole fraction of impurity, Xj, of 2, 4, 6, 8, and 10 %, respectively. TLCA inhibition of TCA uptake was also measured to obtain Kj (see below). After 10 min, donor solution was removed, cells washed three times with chilled sodium-free buffer, lysed, and counted for associated radioactivity (i.e TCA). Inhibition data were analyzed in terms of inhibition constant Ki as described below.
Simulation of Substrate Transport: Impurity Effect on Substrate Flux
To assess the impact of impurity on substrate flux, simulations were performed using eqn 1 and 2 (appendix A) for scenarios with and without impurity, respectively. Equations 1 and 2 are denoted the impurity-present model and the impurity-absent model, respectively, for transport/uptake studies.
| (1) |
| (2) |
Flux in the presence of impurity (JXi) was calculated using eqn 1 over a range of Kt, Xi and Ki values. Substrate Kt was 5, 50, and 500 μM; substrate concentration (S) was 1/10 of Kt. Impurity level (Xi) was varied from 0 to 10% mole fraction, with greater sampling for larger Kt scenarios. Ki was 0.05, 0.5, 5, 50, and 500 μM, respectively. Jmax, PABL and Pp were fixed to 0.5 pmol/cm2/s, 70 × 10−6 cm/s, and 0.5 × 10−6 cm/s, respectively, in all cases (Balakrishnan et al., 2007). Eqn 2 (i.e. flux without impurity, J) is eqn 1 when Xi = 0. The ratio JXi/J was calculated as a metric for impurity effect on flux and plotted against Xi. It is important to note that S was the actual assigned substrate concentration in donor; the concentration of substrate and impurity (when Xi > 0) was greater than S.
Simulation of Substrate Transport: Impurity Effect on Kt and Jmax Estimates
To assess impurity effect on Kt and Jmax estimates from transport studies, simulated flux data was generated from impurity-present model (eqn 1). Across the simulations, Kt was 5, 50, or 500 μM, while Jmax was 0.5 pmol/cm2/s. Since the aim of these simulation studies is to measure impurity effect on bias on estimated Kt and Jmax parameter fits, these Kt values (i.e. 5, 50, and 500 μM) and Jmax value (i.e. 0.5 pmol/cm2/s) are denoted as “true Kt” and “true Jmax”, respectively. In simulations, S was 1/20, 1/10, 1/5, ½, 1, 2, 5, 10 and 20 times Kt to assure saturation of active transport. PABL and Pp were 70 × 10−6 cm/s and 0.5 × 10−6 cm/s, respectively. Simulated flux data was subsequently fitted to impurity-absent model (eqn 2), for each unique condition (i.e. unique Kt, Ki, and Xi scenario). Nonlinear regression was used to simultaneously estimate Kt and Jmax using SigmaPlot 8.0 (SPSS®Inc; Chicago, IL). In all cases, r2 = 1.000. Results are discussed in terms of resulting bias in Kt and Jmax, due to impurity, relative to “true Kt” and “true Jmax” values that were employed in simulating flux data. Kt estimates were plotted against impurity level for each “true Ki” level. Similar plots were graphed for Jmax estimates. Estimation error in Kt (or Jmax) that exceeded 20% was considered unacceptably biased.
Simulation of Inhibition Studies: Impurity Effect on Ki Estimate
To simulate impurity influence on Ki estimate, eqn 3 (appendix B) was used to simulate inhibition profiles, where inhibitor was contaminated with impurity. Equation 3 is the impurity-present inhibition model.
| (3) |
It should be noted that, in contrast to transport simulations above where Ki is the inhibition constant of the impurity that contaminates the substrate, here Ki is the unbiased inhibition constant of the inhibitor (i.e. the value to be measured in the inhibition study). Kj is the unbiased inhibition constant of the impurity that contaminates the inhibitor. Impurity is present in inhibitor at level Xj. Across simulations, Kt, Jmax, PABL and Pp were fixed to be 5 μM, 0.5 pmol/cm2/s, 70 × 10−6 cm/s and 0.5 × 10− 6 cm/s, respectively, which reflects active TCA transport across hASBT-MDCK monolayers (Balakrishnan et al., 2007) Ki was 0.05, 0.5, 5, 50, and 500 μM. Inhibitor concentration was 1/20, 1/10, 1/5, ½,1, 2, 5, 10, and 20 times Ki. Impurity Kj was 0.5, 5, and 50 μM. An entire inhibition profile was generated for each level of impurity (Xj), which ranged from 0 to 10% mole fraction. Each inhibition profile (i.e. unique Ki, Kj, and Xj scenario) was fitted to impurity-absent inhibition model (eqn 4, appendix B) using nonlinear regression. Only Ki was estimated, while all other parameters assumed their true values. In all cases, r2 = 1.000, except for one extreme inhibition study simulation (Ki = 500 μM) where r2 < 0.6.
| (4) |
Results are discussed in terms of resulting bias in Ki, due to impurity, relative to “true Ki” values that were employed in simulating inhibition profile. Ki estimates were plotted against impurity level for each “true Kj” level. Estimation error in Ki that exceeded 20% was considered unacceptable bias.
Impurity Effect on Active Uptake Kinetic Estimates: Experimental Evidence
A series of uptake experiments where model substrate GCA was contaminated with model impurities TLCA, CDCA or UDCA were conducted in order to confirm simulation predictions. These bile acids were selected for several reasons. Previous data from our laboratory have shown GCA Kt to be 11.0 ± 1.9 μM. Ki for TLCA, CDCA, and UDCA were 0.50 ± 0.05 μM, 1.94 ± 0.17 μM, and 22.6 ± 3.0 μM, respectively (Balakrishnan et al., 2006b). TLCA, CDCA, and UDCA were chosen as impurities due to their high structural similarity to the substrate probe (i.e. GCA) and since they represent cases were Kt/Ki ≈ 100, 10, and 1, respectively.
The uptake format was chosen to keep Pp at a minimum since high passive permeability (i.e. low monolayer integrity on transport format) was found to hinder proper evaluation of impurity impact on active transport parameter estimates. For uptake studies, PABL was set to 1.5 × 10−4 cm2/s in analyzing experimental data (Balakrishnan et al., 2007). Since the impurity-present uptake and inhibition models are based on the assumption of competitive inhibition between the compound of interest and the impurity, a Dixon’s analysis was performed to investigate the inhibition mechanism of TLCA on GCA uptake.
Analysis of Experimental Data from Uptake Studies
Experimental data from GCA uptake studies (Xi = 0–10%, with and without sodium), and from impurity-mediated inhibition of GCA uptake were combined and fitted simultaneously to eqn 1, 2, 4, and 5 in WinNonlin 5.2 (Pharsight, Mountain View, CA) using nonlinear regression to obtain “unbiased” estimates of GCA Kt, Jmax, Ki, and Pp. Subsequently, values of these “unbiased” estimates were applied to eqn 1 (i.e. impurity-present uptake model) to simulate GCA uptake profiles when Xi was 2, 4, 6, 8, and 10 %, respectively. Predicted “biased” Kt and Jmax were obtained by nonlinear fitting of these subsequent curves to eqn 2.
| (5) |
In order to challenge the predictive accuracy of the impurity-present model, GCA uptake in presence of impurity was fitted to eqn 2 (i.e. impurity-absent uptake model) to obtain observed “biased” GCA kinetic estimates Kt and Jmax for each level of impurity mole fraction, Xi. Predicted bias and observed bias were compared.
Analysis of Experimental Data from Inhibition Studies
Compared to data analysis of uptake studies, the same approach was taken to challenge the impurity-present inhibition model and analyze impurity effect on GCA Ki. GCA inhibition of TCA uptake (with and without TLCA as impurity) and TLCA inhibition profile were fitted simultaneously to eqns 3 and 4, respectively, using nonlinear regression to obtain “unbiased” estimates of Ki, Kj, Jmax, and Pp. TCA Kt was obtained from parallel uptake studies. Subsequently, values of these “unbiased” estimates were applied to eqn 3 (i.e. impurity-present inhibition model) to simulate GCA inhibition profiles when Xj was 2, 4, 6, 8, and 10 %, respectively. Predicted “biased” Ki was obtained by nonlinear fitting of these curves to eqn 4.
In order to challenge the predictive accuracy of the impurity-present inhibition model, GCA inhibition studies in presence of impurity were fitted to eqn 4 (impurity-absent inhibition model) to obtain observed “biased” GCA Ki for each level of impurity mole fraction, Xj. Predicted bias and observed bias were compared.
RESULTS
Simulation results are presented first, followed by supporting experimental observations (Table 1).
Simulation of Substrate Transport: Impurity Effect on Substrate Flux
Simulations indicate that impurity generally decreased substrate flux across cell monolayers. For example, Fig. 1 illustrates the decrease in flux of a moderate substrate (i.e. Kt = 50 μM) in the presence of increasing amount of impurity, particularly for the more potent impurities. A 20% decrease in flux was observed when the impurity was a strong inhibitor (i.e. Ki = 0.5 μM; open circles) and present at about 3.5% molar fraction level. Meanwhile, only a 0.5% mole fraction of a most strong inhibitor (i.e. Ki = 0.05 μM; closed circles) was needed to cause a 20% decrease in flux. Simulations covering a broader range of Kt values showed similar trends, including the susceptibility of weaker substrates to more pronounced impurity effects (see supplemental data Fig. a).
Figure 1. Decrease in total flux of substrate across a monolayer due to presence of impurity.
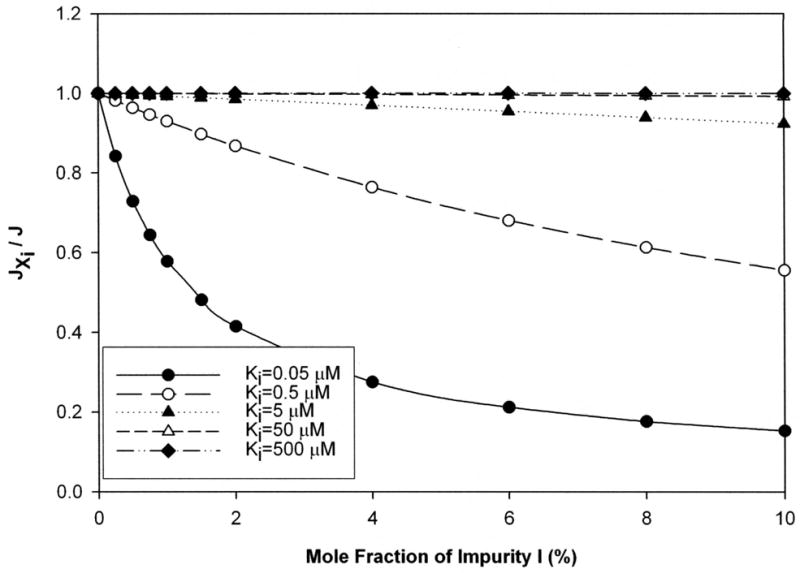
Total flux of a substrate (J) was simulated using eqn 2 (i.e. impurity-absent model) for Kt level of 50 μM. Equation 1 (i.e. impurity-present model) modeled the influence of impurity on substrate total flux (JXi). When impurity present, Xi varied from 0 to 10 %, over five different levels of Ki (0.05, 0.5, 5, 50, and 500 μM respectively). impurity effect was assessed by the ratio of fluxes in the presence and absence of impurity (i.e. ratio of JXi versus J). The ratio JXi/J is 1 when no impurity is present and then decreases consistently as impurity level increased. The drop in total flux was more dramatic as the potency of the inhibitor increased.
Figure 2 illustrates the effect of impurity potency on flux profile of a strong substrate (Kt = 5 μM). Impurity level was Xi = 2%. In general, greater inhibition potency of impurity resulted in reduced substrate flux. For example, a most strong impurity (Ki = 0.05 μM) reduced substrate flux about three-fold at 50 μM substrate concentration. Of note, an impurity whose Ki is equal to the substrate’s Kt (i.e. Ki = 5 μM), had no marked effect. Meanwhile, the impurities with 10-fold (i.e. Ki = 0.5 μM) and 100-fold (i.e. 0.05 μM) greater potency provided notable flux reduction. Qualitatively similar results were observed for the effect of impurity potency on moderate (Kt = 50 μM) and weak (Kt = 500 μM) substrate (data not shown), although the effects are more dramatic.
Figure 2. Flux profile of a substrate with Kt of 5 μM in presence of 2% mole fraction impurity.
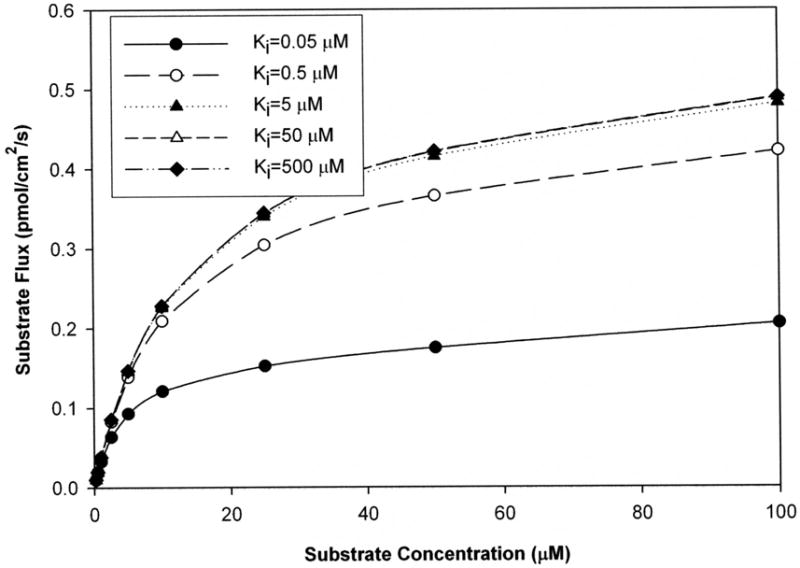
Simulations were performed where Ki values of impurity varied from 0.05 to 500 μM. The total flux of substrate decreased with impurity potency. Apparent Jmax and apparent Kt both also decreased with impurity potency. For example, when the impurity Ki was 5 μM, apparent Jmax and apparent Kt were 0.48 pmol/cm2/s and 12 μM respectively. However, when Ki was 0.05 μM, apparent Jmax and apparent Kt were both 2.5-fold lower than these values.
Simulation of Substrate Transport: Impurity Effect on Kt and Jmax Estimates
The impact of impurity on Kt and Jmax was assessed by fitting simulated data from eqn 1 (i.e. impurity-present model) onto eqn 2 (i.e. impurity-absent model). This approach mimics the perhaps common scenario in early discovery where impurity is present but data analysis assumes no impurity. Bias in kinetic estimates was negative, to reduce the estimated values of Kt and Jmax. While this effect in Jmax is intuitive, this effect on Kt would appear to be unexpected. As described above, impurity reduced substrate flux, but resulted in the substrate to appear as a substrate with greater affinity than it truly possesses (i.e. estimated Kt < “true” Kt).
Figure 3 illustrates estimated Kt as a function of impurity level for a strong substrate (5 μM). Bias was deemed to occur when impurity caused more than a 20% error in estimate. From Fig. 3, the impurity potency needed to be at least 10-fold higher than that of the substrate to cause bias. When Kt/Ki = 10, the impurity level needed to cause bias was always about 2.5% mole fraction. For example, Xi = 2.5% lead the estimated Kt to be 4 μM when Kt/Ki = 10. Simulations covering a broader range of Kt values showed similar trends, including the susceptibility of weaker substrates to impurity effects (see supplemental data Fig. b)
Figure 3. Impact of impurity on Kt estimates from transport studies when impurity not considered.
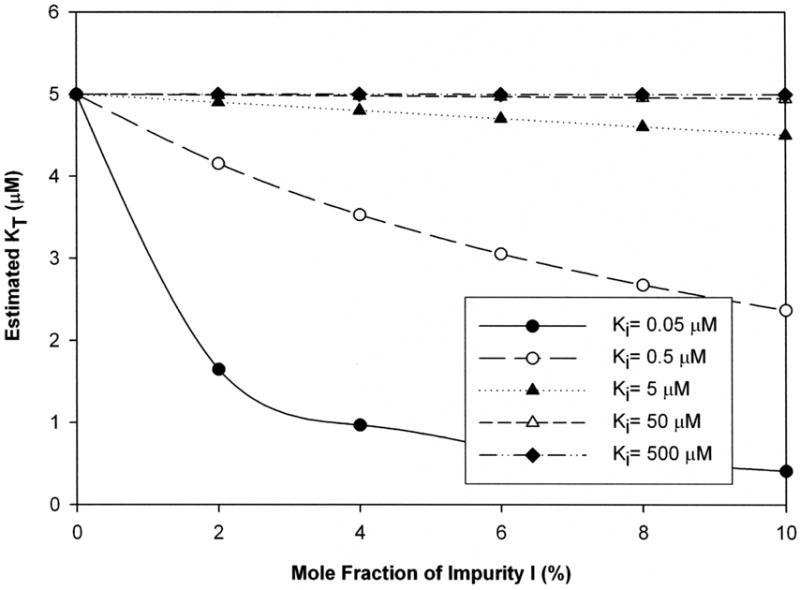
Kt value was 5 μM. The mole fraction of impurity Xi varied from 0 to 10 %. Ki values were 0.05 (filled circle), 0.5 (open circle), 5 (filled triangle), 50 (open triangle), or 500 μM (filled diamond). Impurity generally reduced estimated Kt. An estimated Kt of 80% or less than the “true Kt” value was considered unacceptably biased. Impurity level and inhibitory potency each promoted bias. Bias in Kt estimates was increasingly sensitive to impurity level when “true Kt” was at least 10-fold larger than Ki, and was very large when Kt while Ki was strong. Interestingly, analogous plots for bias in Jmax followed identical trends (supplemental data).
Table 2 summarizes the relationship between Kt/Ki ratio and the necessary Xi to cause bias. In Table 2, regardless whether the potency of the substrate was 5 μM, 50 μM, or 500 μM, Kt/Ki ratio of 10 always resulted in Kt bias, although bias required the impurity level to be at least 2.5 % mole fraction. When Kt/Ki = 100, about 0.25% impurity caused 20% bias, depending on Kt value. However, when Kt/Ki = 1 or less, bias did not manifest for even Xi = 10%.
Table 2.
Necessary impurity level to cause 20% bias on Kt estimates from transport studies.
| Potency of substrate | Kt/Kia | Necessary Xi level to cause bias in Kt |
|---|---|---|
| Strong (Kt = 5 μM) | ≤ 1 | Never a concern when Xi ≤ 10% |
| 10 | ≥ 2.5% | |
| 100 | ≥ 0.5% | |
| Moderate (Kt = 50 μM) | ≤ 1 | Never a concern when Xi ≤ 10% |
| 10 | ≥ 2.5% | |
| 100 | ≥ 0.25% | |
| 1000 | ≥ 0.1% | |
| Weak (Kt = 500 μM) | ≤ 1 | Never a concern when Xi ≤ 10% |
| 10 | > 2.5% | |
| 100 | ≥ 0.25% | |
| 1000 | Trace | |
| 10000 | Trace |
Kt/Ki reflects the ratio of the “true” affinity constant of the substrate of interest versus the inhibition constant of its impurity.
Regarding effect of impurity on Jmax, plots of estimated Jmax versus Xi were identical to those in Fig 3. Interestingly, Xi levels had the same relative effect on Jmax as on Kt (Supplemental data Fig. c). Although presented for impurity effect on Kt bias, Table 2 equally applies for Jmax bias. For example, when Kt/Ki = 1 or less, bias in Jmax did not manifest.
While the effect on Jmax is intuitive, this effect of impurity to reduce Kt would appear to be unexpected. Kt is often interpreted as an affinity parameter, such that impurity effects would result in the substrate to appear as a substrate with greater affinity than it truly possesses (i.e. estimated Kt < “true” Kt). Figure 2 illustrates the basis for this effect. Figure 2 was generated for Xi = 2% for a strong substrate (Kt = 5 μM). For the scenario Ki = 0.5 μM (open circles), estimated Jmax and Kt were 0.415 pmol/cm2/s and 4.15 μM, respectively, which are each 17% less than “true” values of 0.5 pmol/cm2/s and 5 μM, respectively. In this scenario, it can be interpreted than impurity effect to reduce Jmax estimate causes a proportional effect on Kt estimate, vis-à-vis the Jmax effect. Since Kt is the concentration at half Jmax, and since impurity reduces apparent Jmax, impurity reduces apparent Kt.
Simulation of Inhibition Studies: Impurity Effect on Ki Estimates
In addition to transport studies, inhibition studies are frequently performed in development and design to evaluate the ability of a compound to inhibit the transport of a known substrate. Data are often interpreted as an inhibition constant (Ki). Here, impurity Jimp contaminates inhibitor I and competes against I (and substrate) for the same transporter in a non-cooperative fashion (see Supplemental Data Fig. d). By virtue of impurity contributing additional inhibition, impurity can produce negative bias in Ki estimates from inhibition studies.
The extent of this bias is illustrated in Fig. 4 (substrate Kt = 5 μM) for a strong inhibitor (Ki = 5 μM) and shows bias depended on the affinity of the impurity (i.e. Kj) and its mole fraction, Xj. For example, a very strong impurity (Ki = 5 μM) at Xi = 2.5% caused 20% bias in estimated Ki, resulting in apparent Ki to be 4 μM. Simulations covering a broader range of Ki values showed similar trends, including the susceptibility of weaker inhibitors to more pronounced impurity effects (see supplemental data Fig. e). The impact of impurities on inhibition results mimics the above effect on transport studies.
Figure 4. Impact of impurity on Ki estimate from inhibition studies when inhibitor contaminated with impurity.
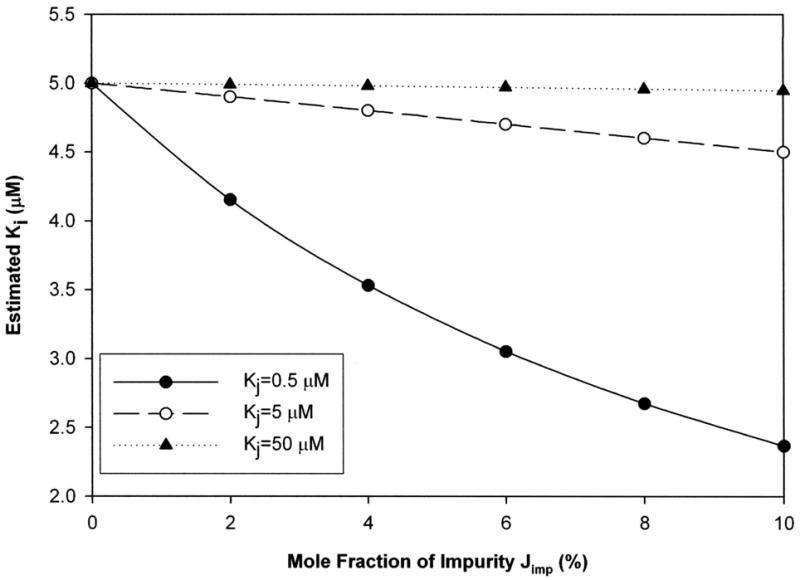
Ki is inhibition constant of inhibitor. Kj is inhibition constant of impurity. Impurity contaminated the inhibitor. “True Ki” value was 5 μM. Impurity level was varied from 0 to 10% mole fraction. Kj was 0.5 (filled circle), 5 (open circle) and 50 μM (filled triangle), respectively. Impurity generally resulted in either no effect or decreased apparent Ki. An estimated Ki of 80% or less than the “true Ki” was considered unacceptably biased. When present, bias was always negative (i.e. estimated Ki less than “true Ki”). No bias in Ki estimate was observed when the ratio Ki/Kj is 1 or less. However, Ki/Kj ratios of 10 or higher caused Ki bias when impurity level exceeded 2.5%. No fit was obtained for Ki 500 μM (data not shown).
Table 3 summarizes the relationship between Ki/Kj ratio and the impurity level required to produce bias on Ki estimates. Results in Table 3 from inhibition studies mimic results in Table 2 from transport studies, although Table 3 concerns Ki/Kj ratio while Table 2 concerns Kt/Ki ratio. In Table 3, no bias manifested when Ki/Kj ≤ 1, similar to an observation in Table 2. Also, for either a strong or moderate inhibitor, Ki/Kj = 10 resulted in bias when Xj was at least 2.5%, similar to an observation in Table 2. For a moderate inhibitor, Xj = 0.6% caused bias in Ki when Ki/Kj = 100.
Table 3.
Necessary impurity level to cause 20% bias on Ki estimates from inhibition studies.
| Potency of Inhibitor | Ki/Kja | Necessary Xj level to cause bias in Ki |
|---|---|---|
| Most strong (Ki = 0.05 μM) | ≤ 0.1 | Never a concern when Xj ≤ 10% |
| Very strong (Ki = 0.5 μM) | ≤ 1 | Never a concern when Xj ≤ 10% |
| Strong (Ki = 5 μM) | ≤ 1 | Never a concern when Xj ≤ 10% |
| 10 | 2.5% | |
| Moderate (Ki = 50 μM) | ≤ 1 | Never a concern When Xj < 10% |
| 10 | ≥ 2.5% | |
| 100 | ≥ 0.6% | |
| Weak (Ki = 500 μM) | Eqn 4 (appendix B) did not adequately fit data. | |
Ki/Kj reflects the ratio of the “true” inhibition constant of the inhibitor of interest versus the inhibition constant of its impurity.
Impurity Effect on Active Uptake Kinetic Estimates: Experimental Evidence
A series of uptake experiments where model substrate glycocholic acid (GCA) was contaminated with model impurities taurolithocholic acid (TLCA), chenodeoxycholic acid (CDCA) or ursodeoxycholic acid (UDCA). GCA Kt is about 10 μM, such that Kt/Ki for TLCA, CDCA, and UDCA were about 100, 10, and 1, respectively (Balakrishnan et al., 2006b). TLCA was found to be a competitive inhibitor of GCA uptake (Supplemental Data Fig. f).
Figure 5 shows bias on GCA Kt and Jmax estimates from uptake when TLCA was present as impurity. These estimates were always negatively biased by presence of TLCA at the entire range of Xi studied. Unbiased Kt and Jmax of substrate were 12.6 (±1.1) uM and 0.424 (±0.041) pmol/cm2/s, while TLCA Ki was 0.11 (±0.01) uM. When Xi = 2% observed Kt and Jmax estimates of GCA were 3.76 (±0.87) μM and 0.113 (±0.004) pmol/cm2/s, representing an estimation error of 70 and 73% respectively. From Fig. 5A, interpolation predicts that a 0.24% mole fraction of TLCA would produced a 20% bias on GCA Kt estimate (experimental Kt GCA/Ki TLCA = 114) reflecting the high level of agreement between model predictions and observed results (r2 = 0.979 for Kt and 0.995 for Jmax).
Figure 5. Impact of taurolithocholate on glycocholate kinetic estimates from uptake studies.
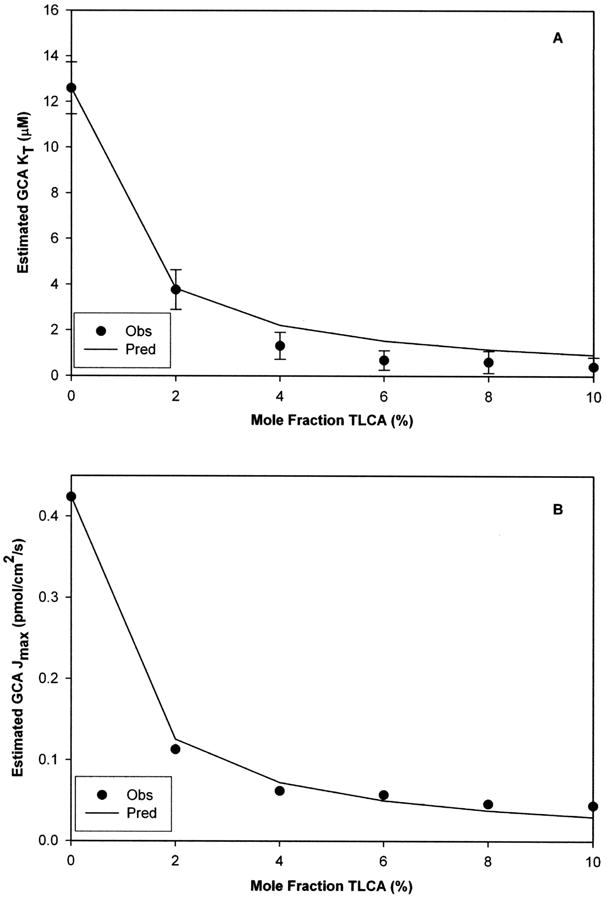
Mole fraction of TLCA was varied from 0 to 10%. TLCA contamination produced negative bias on GCA kinetic estimates (i.e. increased “apparent” affinity and decreased “apparent” capacity in panels A and B, respectively). A 2% mole fraction of TLCA generated approximately 70% error on the estimation of both GCA Kt and Jmax. These experimental observations followed the model predicted trends. Unbiased Kt and Jmax of substrate were 12.6 (±1.1) μM and 0.424 (±0.041) pmol/cm2/s, while TLCA Ki was 0.11 (±0.01) μM. Data are presented as mean (±S.E.M.). (S.E.M. bars smaller than symbol in panel B).
Identical experiments were performed with GCA contaminated with CDCA as impurity. Unbiased GCA Kt and Jmax were 11.0 (±1.8) μM and 0.153 (±0.013) pmol/cm2/s respectively, while unbiased CDCA Ki = 1.39 (±0.39) μM (Kt/Ki = 7.92). While CDCA caused negative bias on GCA Jmax regardless of impurity load, Kt estimates were biased only when Xi > 2%. Figure 6 show the bias effect of CDCA on GCA Kt and Jmax. Experimentally, a 6% mole fraction of CDCA caused a 20% drop on estimated GCA Kt relative to the unbiased value, while 4% caused similar estimation error on Jmax. The ability of the model to predict biased Kt estimates was modest (r2 = 0.806) and good to predict Jmax (r2 = 0.908).
Figure 6. Impact of chenodeoxycholate on glycocholate kinetic estimates from uptake studies.
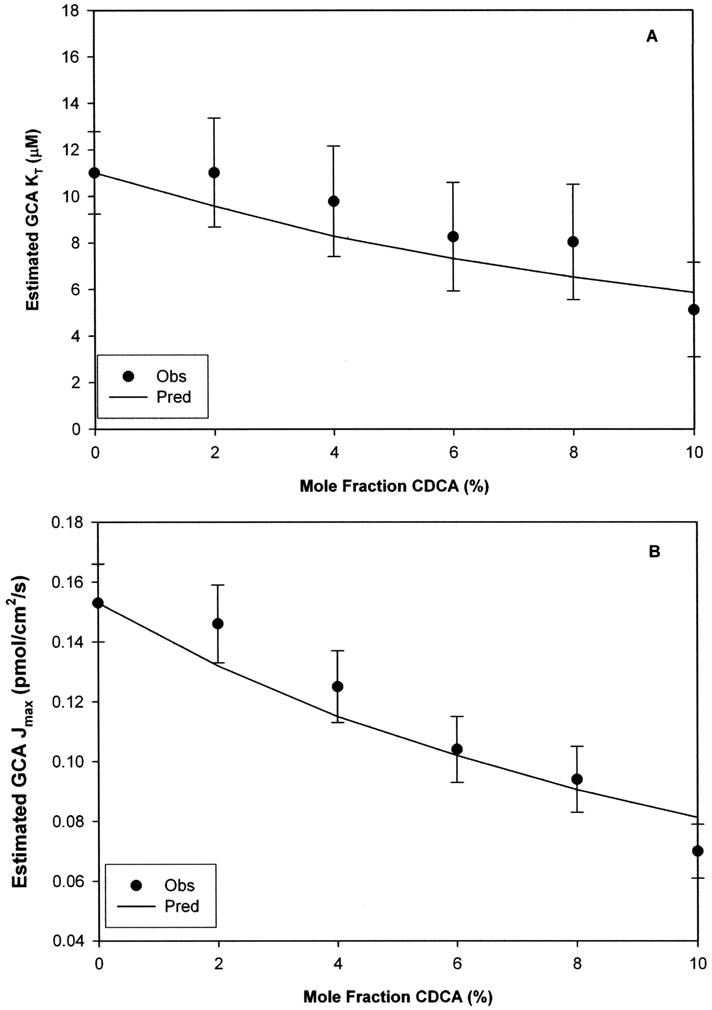
Experimentally CDCA contamination produced modest negative bias on GCA Kt (panel A) and GCA Jmax (panel B), particularly compared to the larger bias shown in Fig 7. This more modest level of bias reflects CDCA impurity is less potent than TLCA impurity in Fig 7. However, even a 10% mole fraction of CDCA impurity caused 50% bias in estimated GCA Kt and Jmax (Fig 8 panels A and B, respectively). Unbiased Kt and Jmax of GCA substrate were 11.0 (±1.8) μM and 0.153 (±0.013) pmol/cm2/s, while CDCA Ki was 1.39 (±0.39) μM. Data are presented as mean (±S.E.M.).
Identical studies were also performed with GCA-UDCA as substrate-impurity pair. Unbiased GCA Kt was 9.82 (±0.79) μM. Unbiased UDCA Ki was 24.2 (±2.8) μM, such that Kt/Ki = 0.40 for this GCA-UDCA pair. Unlike the above GCA-TLCA and GCA-CDCA pairs, it was not possible to obtain biased estimates for the GCA-UDCA pair due to poor inhibitory potency of the UDCA impurity.
Impurity Effect on Inhibition Constant Estimates: Experimental Evidence
To evaluate the impact of impurity on Ki estimates from inhibition assays, GCA-mediated inhibition of taurocholic acid (TCA) uptake was measured in absence and presence of TLCA as impurity (Xj = 0–10%). Xj here represents the mole fraction of impurity Jimp (i.e. TLCA) contaminating inhibitor I (i.e. GCA) (Supplemental Data Fig. d). This inhibitor-impurity pair was chosen to represent a Ki/Kj ≈ 10 based on previous data (Balakrishnan et al., 2006b). Figure 7 shows bias on GCA Ki estimates as a function of TLCA mole fraction. Unbiased GCA Ki was 5.05 (±0.48) μM, while unbiased TLCA Kj was 0.40 (±0.04) μM (Ki/Kj = 12.6). TLCA contamination caused negative bias on GCA inhibition constant estimation over the entire range of Xj. For example, when TLCA was present at a 2% mole fraction, observed GCA Ki estimate was 4.39 (±0.32) μM. Interpolation of predicted data identified a critical Xj level of 1.95% to obtain a 20% bias on GCA Ki estimation. The impurity-present model predicted observed bias on Ki (r2= 0.919).
Figure 7. Impact of taurolithocholate on glycocholate Ki when taurolithocholate was present as impurity.
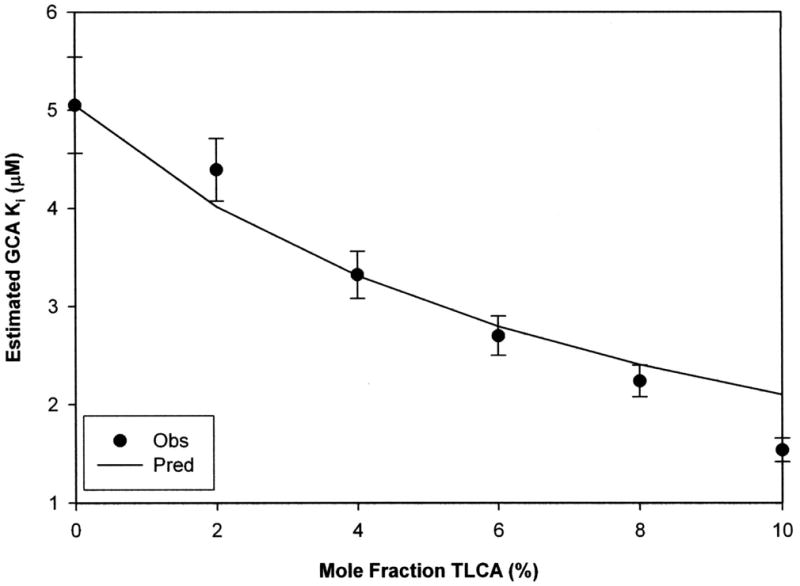
TLCA contamination produced negative bias on GCA “apparent” affinity. The 4% mole fraction of TLCA caused 34% error in GCA Ki estimation. Predicted bias anticipated these experimental observations. Unbiased Ki of GCA was 5.05 (±0.48) μM, while TLCA Kj was 0.40 (±0.04) μM. Data are presented as mean (±S.E.M.).
DISCUSSION
Implications for ADME Screening and hASBT Studies
Transport and inhibition studies are routinely performed in early development to screen for ADME. A current project in our laboratory concerns the targeting of hASBT for drug delivery purposes (Balakrishnan and Polli, 2006). ADME considerations motivate the screening for substrates and inhibitors of hASBT, in order to construct a QSAR model for inhibitors and substrates of this transporter.
hASBT (SLC10A2) is a 348 aminoacid transmembrane protein that mediates the active uptake of bile acids in the small intestine playing a critical role in the bile acid enterohepatic recirculation (Hagenbuch and Dawson, 2004). The total bile acid pool in humans (3–5 g) recirculates several times a day giving a turnover of 12–18 g/day (Hofmann, 1999). However, no more than 0.5 g are lost in the feces daily, reflecting the high capacity and efficiency of this transporter (Hofmann and Mysels, 1992). This suggests that some drugs with poor oral absorption may benefit from conjugation to bile acids by utilizing hASBT as carrier to enter the enterocyte. Despite the enormous potential of hASBT as target for bile acid containing prodrugs, only a few examples of its use can be found in the literature (Sievanen, 2007). Employing this approach, the oral bioavailability of acyclovir was enhanced in rats via a bile acid conjugate prodrug of acyclovir (Tolle-Sander et al., 2004). Also, hASBT is a promising pharmacological target, where hASBT inhibitors could lower blood cholesterol (Buchwald et al., 2002). Hence, hASBT is a target for novel substrates and inhibitors. An understanding of impurity effects on transport and inhibition assays is needed and the subject of this report.
Since January 2007, the Journal of Medicinal Chemistry now requires that key target compounds possess purity of 98% or more. Results here support this requirement and indicate that, in transport and uptake studies, impurity can cause an underestimation in Jmax, as well as an underestimation in Kt. This impact on apparent Kt appears to be surprising, since impurity would cause the apparent affinity of a substrate to be more potent than its true potency. Results of these simulation studies imply that transport studies results that conclude a drug candidate to be a potent substrate merit inspection, to assure that impurity is not causing over-favorable results, particularly if a chemical reactant, precursor, or side product is known to be a potent inhibitor.
For example, in employing hASBT as a carrier for drug delivery and a bile acid prodrug where TCA (Ki = 5 μM) is the targeting moiety, a result of Kt = 50 μM could reflect several scenarios, such as: 1) the target compound to possess Kt = 50 μM; 2) the target to possess Kt = 500 μM but also be contaminated with a most strong impurity (Ki = 0.05 μM) at a level of Xi = 0.075%; 3) the target to possess Kt = 500 μM but also be contaminated with a very strong impurity (Ki = 0.5 μM) at a level of Xi = 0.8%; or 4) the target to possess Kt = 500 μM but also be contaminated with a impurity (Ki = 5 μM) at a level of Xi = 8%.
Experience to date suggests scenario “1” as most likely, which is favorable as the intent is to measure unbiased parameters, but emphasizes purification methods should be designed to remove critical impurities from target compound. Scenario “2” does not appear likely, as the lowest Ki to date is 0.5μM or about 10-fold less potent that this scenario requires. Scenario “4” is not practically possible, since this scenario would require at least 8% impurity by TCA, which will not occur with purification effort. Scenario “3” represents a potentially real and challenging situation, where a relatively small amount (i.e. Xi = 0.8%) of most potent impurity (e.g. TLCA with Ki = 0.5 μM) contaminates the target. However, formation of TLCA from unreacted taurocholate is not expected. Consideration of these scenarios supports a 97.5% to 98% purity level, as long as very potent impurities are not present. For target compounds of high interest, inhibition data that show a drug candidate to be potent inhibitor merit inspection that impurity is not causing over-favorable results, particularly if a chemical reactant, precursor, or side product is known to be a potent inhibitor.
Results from this study motivates purification methods to eliminate, if not minimize, unreacted bile acid in target bile acid prodrug compounds. Additionally, in the case of conjugates of highly potent bile acids, enough hydrolytic stability must be assured in the transport/inhibition buffer so that regeneration of the parent targeting moiety does not occur during the course of the assay. Unfortunately, target compounds that show moderate or weak affinity cannot be completely excluded from potential bias, as small amounts of very strong impurity can bias results and evade conventional detection. Hence, the ultimate benefit of these findings may be the need for careful consideration of impurity effect on transport and inhibition results, particularly when QSAR analysis cannot explain high compound potency.
In conclusion, the present study concerns two types of ADME transport studies: inhibition studies and transport/uptake studies. Presumably, in a competitive binding study (e.g. inhibition study), impurity with a potency greater than test compound potency may cause test compound to appear more potent than actually is. This expectation was found to be correct here and offers quantitative guidelines. Surprisingly, an expectation that a potent impurity would diminish the apparent potency of a test compound in the uptake assay (i.e. increase Michaelis-Menten Kt) was found here to be incorrect. Rather, potent impurity, which reduces test compound flux, resulted in test compound to appear to possess higher substrate affinity (i.e. exhibit a lower Kt). This study provides quantitative guidelines, which are currently lacking, about maximum impurity levels to avoid bias on transporter parameter estimates (i.e. Kt, Jmax, and Ki) in early drug develpment. Results have implications for other types of early discover assays, such as pharmacologic binding studies.
Supplementary Material
Acknowledgments
This work was support in part by National Institutes of Health grants DK67530 (to JEP).
List of Abbreviations
- hASBT
human apical sodium-dependent bile acid transporter
- SLC
Solute carrier family
- MDCK
Madin-Darby canine kidney
- HBSS
Hanks balanced salt solution
- ABL
aqueous boundary layer
- QSAR
quantitative-structure activity relationship
- GCA
glycocholic acid
- TCA
taurocholic acid
- TLCA
taurolithocholic acid
- UDCA
ursodeoxycholic acid
APPENDIX A
Derivation of Influence of Impurity on Solute Flux
The objective of this appendix is to derive eqn 1, which models the impact of impurity on solute flux in transport studies. For the flux of a solute across a monolayer, where solute is translocated both passively and actively, but where inhibitor is present to inhibit active solute flux,
| (A1) |
where Jmono is total flux across cell monolayer, S is concentration of solute, I is the concentration of inhibitor, Pp is the passive permeability of solute, Kt and Jmax are the Michaelis-Menten constants for active transport, and Ki is the inhibitor affinity of I. Inhibitor I is an impurity present in the solute S. Only a single impurity is present. For example, in the design of bile acid conjugates to serve as prodrugs to target hASBT, the bile acid conjugate is the solute, but can be contaminated with unreacted bile acid, which was a starting material in conjugate synthesis.
The mole fraction impurity in the sample is
| (A2) |
where Xi is mole fraction of impurity in the sample.
| (A3) |
Substituting eqn A3 into eqn A1,
| (A4) |
The flux in eqn A4 is the flux across a monolayer where solute is both actively and passively translocated, but where an impurity inhibits active solute transport. It should be emphasized that S is actual solute concentration.
From eqn A4, the monolayer permeability can be considered to be
| (A5) |
Since flux across a monolayer is in series with the aqueous boundary layer (ABL),
| (A6) |
where Papp is apparent permeability and PABL is the permeability of S across the ABL.
Substituting eqn A5 into eqn A6,
| (A7) |
| (A8) |
With impurity present in solute, the apparent flux is JXi= Papp ·S, such that
| (A9) |
Eqn A9 describes the flux of a solute across a monolayer, in the presence of an ABL, where solute is translocated actively and passively, and where impurity inhibits solute active transport.
If no impurity is present or if impurity does not inhibit solute active transport, eqn A9 simplifies to
| (A10) |
Eqn A9 and A10 are eqn 1 and 2 in the Methods section and represent the impurity-present transport model and impurity-absent transport model, respectively.
APPENDIX B
Derivation of Influence of Impurity on Apparent Inhibitor Performance
The objective of this appendix is to derive eqn 4, which models the impact of impurity on apparent inhibitor performance in inhibition studies. This derivation employs a Michalis-Menten approach to the scenario where impurity inhibits transporter function (Copeland, 2000).
Figure 4 represents the inhibition of a transporter E by two mutually exclusive inhibitors I and Jimp, where S is a substrate, I is an inhibitor and Jimp is an impurity of I which also inhibits E.
where Kt, Ki, and Kj are denoted affinity constants of S, I, and Jimp for the transporter.
If (i.e. rapid equilibrium),
| (B1) |
If ,
| (B2) |
The rate of translocation of substrate S is
| (B3) |
and the total concentration of transporter at any time is
| (B4) |
| (B5) |
| (B6) |
Where Jmax = k2·Et is the maximum flux when transporter is saturated.
At steady state,
| (B7) |
| (B8) |
Substituting Kt into eqn B8,
| (B9) |
Substituting eqn B1, B2, and B9 into eqn B6,
| (B10) |
which expresses the rate of translocation of substrate S by a transporter in presence of two mutually exclusive inhibitors.
Allowing passive flux of solute across a monolayer, eqn B10 yields
| (B11) |
where Pp is the passive permeability of solute across the monolayer.
Let be the mole fraction of inhibitor Jimp contaminating inhibitor I. For example, I is a prodrug synthesized by conjugation of a bile acid and a drug, Jimp is an impurity (e.g. unreacted bile acid) that is also an inhibitor of hASBT.
| (B12) |
Substituting eqn B12 into eqn B11 and considering the presence of an ABL (Appendix A),
| (B13) |
where is JXj is the total flux of a solute S (both active and passive) in presence of two inhibitors when an ABL is considered.
If impurity Jimp is not present or if does not inhibit the transporter, eqn B13 simplifies to
| (B14) |
Eqn B13 and B14 are eqn 3 and 4 in the Experimenal Section and represent the impurity-present inhibition model and impurity-absent inhibition model, respectively.
References
- Balakrishnan A, Hussainzada N, Gonzalez P, Bermejo M, Swaan PW, Polli JE. Bias in estimation of transporter kinetic parameters from overexpression systems: Interplay of transporter expression level and substrate affinity. J Pharmacol Exp Ther. 2007;320:133–144. doi: 10.1124/jpet.106.107433. [DOI] [PubMed] [Google Scholar]
- Balakrishnan A, Polli JE. Apical sodium dependent bile acid transporter (ASBT, SLC10A2): a potential prodrug target. Mol Pharm. 2006;3:223–230. doi: 10.1021/mp060022d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balakrishnan A, Sussman DJ, Polli JE. Development of stably transfected monolayer overexpressing the human apical sodium-dependent bile acid transporter (hASBT) Pharm Res. 2005;22:1269–1280. doi: 10.1007/s11095-005-5274-8. [DOI] [PubMed] [Google Scholar]
- Balakrishnan A, Wring SA, Coop A, Polli JE. Influence of charge and steric bulk in the C-24 region on the interaction of bile acids with human apical sodium-dependent bile acid transporter. Mol Pharm. 2006a;3:282–292. doi: 10.1021/mp0600135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balakrishnan A, Wring SA, Polli JE. Interaction of native bile acids with human apical sodium-dependent bile acid transporter (hASBT): influence of steroidal hydroxylation pattern and C-24 conjugation. Pharm Res. 2006b;23:1451–1459. doi: 10.1007/s11095-006-0219-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchwald H, Williams SE, Matts JP, Boen JR. Lipid modulation and liver function tests. A report of the Program on the Surgical Control of the Hyperlipidemias (POSCH) J Cardiovasc Risk. 2002;9:83–87. doi: 10.1177/174182670200900203. [DOI] [PubMed] [Google Scholar]
- Copeland RA. Enzymes: a practical introduction to structure, mechanism, and data analysis. J. Wiley; New York: 2000. [Google Scholar]
- Hagenbuch B, Dawson P. The sodium bile salt cotransport family SLC10. Pflugers Arch. 2004;447:566–570. doi: 10.1007/s00424-003-1130-z. [DOI] [PubMed] [Google Scholar]
- Hofmann AF. The continuing importance of bile acids in liver and intestinal disease. Arch Intern Med. 1999;159:2647–2658. doi: 10.1001/archinte.159.22.2647. [DOI] [PubMed] [Google Scholar]
- Hofmann AF, Mysels KJ. Bile acid solubility and precipitation in vitro and in vivo: the role of conjugation, pH, and Ca2+ ions. J Lipid Res. 1992;33:617–626. [PubMed] [Google Scholar]
- Sievanen E. Exploitation of bile acid transport systems in prodrug design. Molecules. 2007;12:1859–1889. doi: 10.3390/12081859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolle-Sander S, Lentz KA, Maeda DY, Coop A, Polli JE. Increased acyclovir oral bioavailability via a bile acid conjugate. Mol Pharm. 2004;1:40–48. doi: 10.1021/mp034010t. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


