Abstract
This review describes a novel view on stages in motor learning based on recent developments of the notion of synergies, the uncontrolled manifold hypothesis, and the equilibrium-point hypothesis (referent configuration) that allow to merge these notions into a single scheme of motor control. The principle of abundance and the principle of minimal final action form the foundation for analyses of natural motor actions performed by redundant sets of elements. Two main stages of motor learning are introduced corresponding to (1) discovery and strengthening of motor synergies stabilizing salient performance variable(s), and (2) their weakening when other aspects of motor performance are optimized. The first stage may be viewed as consisting of two steps, the elaboration of an adequate referent configuration trajectory and the elaboration of multi-joint (multi-muscle) synergies stabilizing the referent configuration trajectory. Both steps are expected to lead to more variance in the space of elemental variables that is compatible with a desired time profile of the salient performance variable (“good variability”). Adjusting control to other aspects of performance during the second stage (for example, esthetics, energy expenditure, time, fatigue, etc.) may lead to a drop in the “good variability”. Experimental support for the suggested scheme is reviewed.
Keywords: Synergy, equilibrium-point hypothesis, referent configuration, motor learning, prehension
1. Two views on stages in motor learning
The process of motor learning has been traditionally viewed as a staged process. The most influential scheme of Bernstein (1996) views it as a sequence of three stages. First, there is a stage of freezing redundant degrees-of-freedom ( DOF’s); note that motor redundancy is typical of virtually any voluntary movement. Then there is a step of releasing the previously frozen DOF’s. Finally, the controller learns to use the external forces rather than to fight them. Several studies provided experimental support for the mentioned scheme (Newell, 1991; Newell , Broderick, Deutsch, & Slifkin, 2003; Vereijken, van Emmerik, Whiting, & Newell, 1992).
Note, however, that some of the basic premises of the suggested scheme look questionable. Consider, for example, the idea that controlling a multi-joint limb with a few kinematic DOF’s “frozen” is easier than an object with all the DOF’s free to move. During quick actions of a multi-joint limb, strong motion-related torques act at each individual joint. This means that avoiding motion of a joint means not “easier control” but requires sophisticated adjustments of commands to the joint to make sure that it does not move (cf. Koshland, Gerilovsky, & Hasan, 1991; Latash, Aruin, & Zatsiorsky, 1999). Muscle co-contraction is another strategy that is commonly viewed as a means of “freezing” joints (e.g., McIntyre, Mussa-Ivaldi, & Bizzi 1996; Woollacott, Inglin, & Manchester, 1988). Note, however, that muscle co-contraction can only modulate joint excursion in response to perturbations, but it cannot eliminate joint motion (e.g., Zatsiorsky, 2002). The commonly accepted idea that the number of DOF’s can be estimated based on experimentally recorded excursions of performance variables (for example, joint excursions over the course of a movement) is far from being obvious. Indeed, the number of kinematic DOF’s cannot be changed without a major orthopedic surgery. Larger or smaller joint excursions mean exactly that, not that the number of DOF’s is changing.
However, the original idea of Bernstein was built on deep introspection and detailed observations of skilled and not very skilled movements. In this review, I do not want to question the presence of stages in motor learning but instead offer a different interpretation for such stages, an interpretation that implies changes not in the number of DOF’s but in how the DOF’s are coordinated. This view is based on recent advances in the field of motor synergies (reviewed in Latash, 2008; Latash, Scholz, & Schöner, 2002, 2007) based on the principle of motor abundance (Gelfand & Latash,1998). This principle views the typical multi-DOF design of biological motor systems not as redundant (a source of computational problems) but as abundant (luxurious). The problem becomes not to eliminate apparently redundant DOF’s but to organize all the DOF’s in such a way that adequate performance is combined with a possibility of performing other tasks and reacting quickly to unexpected perturbations that are common during everyday movements.
2. Synergies and the uncontrolled manifold (UCM) hypothesis
The principle of abundance assumes that, when the central nervous system faces a problem of motor redundancy, it does not search for a unique, optimal solution (as, for example, in optimization approaches, reviewed in Seif-Naraghi and Winters (1990)) but rather facilitates families of solutions that are equally able to solve the task. This concept allows introduction of a definition for the commonly used notion of motor synergy, a definition that allows to identify synergies (and non-synergies!) and to quantify them. The definition is based on a few axiomatic notions. Assume that any motor system may be described, at a selected level of analysis, with a set of elemental variables. Examples may be joint rotations (for kinematic multi-joint movement analysis), muscle forces (for joint torque analysis), motor units (for muscle activation pattern analysis), etc. The elemental variables are not expected to show built-in patterns of interdependence; in other words, they can be manipulated by the controller one at a time, at least hypothetically. I also assume that the system, as a whole, is supposed to produce a value or a time profile of a performance variable (it may be multi-dimensional), which gets contribution from all elemental variables. A synergy is going to be defined as a neural organization that ensures co-variation among elemental variables (along time or across repetitive attempts at a task) that stabilizes the value or time profile of the performance variable.
A computational method to assess synergies has been developed within the uncontrolled manifold (UCM) hypothesis (Scholz & Schöner 1999; reviewed in Latash, Kang, & Patterson, 2002; Latash, Scholz, & Schöner, 2007). The UCM hypothesis assumes that the controller acts in a space of elemental variables, organizes in that space a sub-space (a UCM) corresponding to a desired value of a performance variable and then limits most variance of elemental variables to that sub-space. In other words, elemental variables co-vary in such a way that variance of the performance variable is minimal.
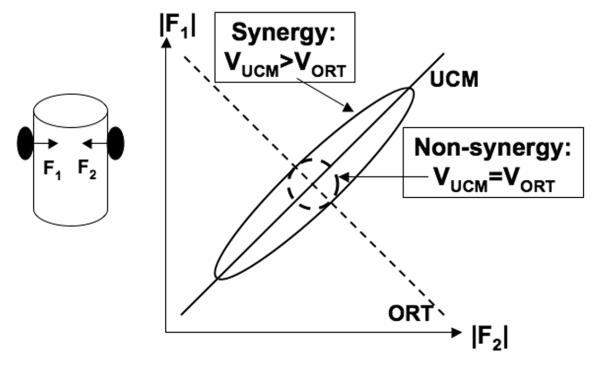
Imagine, for example, that a two-element system faces the task of producing the difference between the outputs of the two elements of exactly 0. One can imagine, for example, the task of using precision grip (with two opposing digits) to hold an object in the air (see the left drawing in Fig. 1). The constraint of avoiding the object motion along the line of normal force action means that the sum of the two forces should be zero. This constraint, however, does not prescribe the magnitudes of each of the two forces. It can be represented with a straight line on the force-force plane corresponding to the equation |F1|-|F2| = 0 (Fig. 1). This line represents a UCM for the redundant two-dimensional system of elemental variables (digit forces) corresponding to the one-dimensional performance variable (resultant force, FRES = 0). The line orthogonal to the first one (ORT, the dashed line in Fig. 1) corresponds to changing FRES.
Fig. 1.
An illustration of force variability in a two-digit precision grip (see the left panel). The ellipses represent data distributions across a large number of trials. The solid slanted line (the uncontrolled manifold, UCM) corresponds to F1 + F2 = 0, while the dashed line (ORT) corresponds to a change in the resultant force (FRES). If most digit force variance is within the UCM (an ellipse elongated along the solid slanted line, VUCM > VORT), this by definition corresponds to a two-digit synergy stabilizing FRES. A circular data distribution corresponds to a non-synergy with respect to FRES.
Because of the unavoidable physiological tremor (and possibly other reasons), the object will never be held perfectly steadily; so, FRES is expected to show small deviations from zero. If a person is asked to perform several trials of keeping the object steadily in space, the data points are expected to show deviations from the UCM corresponding to a small variance in the ORT direction. However, how much variance will such an experiment show parallel to the UCM? This is a non-trivial question. Indeed, if achieving zero FRES is the only important task component, all combinations of digit forces within the UCM are equally capable of solving the task. The subject of this mental experiment may select a comfortable force magnitudes for each digit and reproduce it across trials or allow the two forces to vary broadly as long as they do not deviate too much from the UCM.
One can introduce a quantitative index reflecting the relative amount of variance compatible with a required constant value of the FRES (along the UCM, VUCM) and leading to changes in FRES (along the ORT direction, VORT). In general, both UCM and ORT sub-spaces may have different dimensionalities. To make VORT and VUCM comparable, they have to be normalized by the number of DOF’s within each sub-space. Then, one can use an index, for example ΔV = (VUCM - VORT)/VTOT, where VTOT stands for total variance, and each variance index is computed per DOF within the corresponding spaces. This index is computed in such a way that ΔV > 0 means that most variance in the space of elemental variables is compatible with a fixed value of the performance variable. In other words, elemental variables co-vary to minimize deviations of the performance variable from its desired value. Therefore, according to the introduced definition, ΔV > 0 means a synergy stabilizing that performance variable. If ΔV = 0, a conclusion can be made that elemental variables do not stabilize the performance variable (a non-synergy). In some cases, ΔV < 0 may be observed. This may be interpreted as co-variation of elemental variables destabilizing the performance variable. A number of recent studies have suggested that this may happen in tasks that require a quick change in the performance variable (Olafsdottir, Yoshida, Zatsiorsky, & Latash, 2005; Shim, Olafsdottir, Zatsiorsky, & Latash, 2005; Wang, Asaka, Zatsiorsky, & Latash, 2006).
Fig. 1 illustrates the most simple case with a linear UCM. Typically, the UCM is non-linear, for example in the task of reaching with a multi-joint limb when the endpoint coordinate (performance variable) in a non-linear function of joint angles (elemental variables). In such cases, the UCM may be approximated using the null-space of a Jacobian matrix (J) that links small changes in elemental variables to changes in the selected performance variable (the elemental and performance variables can include variables in different units).
Typically, analysis within the UCM hypothesis is performed across trials, using snap-shots of the action at comparable phases (for an exception see Scholz, Kang, Patterson, & Latash, 2003). This method does not explicitly consider time derivatives of elemental variables. The issue of timing in motor synergies is a complex one, and it is beyond the scope of this paper; interested readers are invited to read the following papers on this topic (Friedman, Skm, Zatsiorsky, & Latash, 2009; Goodman, Shim, Zatsiorsky, & Latash, 2005; Latash, Shim, & Zatsiorsky, 2004; Schöner, 2002).
Another limitation of the currently used versions of the UCM method is that they rely on linear approximations of the UCM and its orthogonal sub-space even though the UCM itself may be nonlinear. An alternative method involves the creation of uncorrelated, surrogate data sets from the original data (Kudo, Tsutsui, Ishikura, Ito, & Yamamoto, 2000; Martin, Greger, Norris, & Thach, 2002; Müller & Sternad 2004; Latash et al., 2004) and further comparison of data distributions in the original and in the surrogate sets. Unlike the UCM approach, this method does not perform analysis in the space of elemental variables but in the space of task-relevant performance variables. Müller and Sternad (2004) developed this method to estimate three contributing factors to performance variability, which they address as noise, tolerance, and co-variation. Another related approach (Cusumano & Cesari, 2006) links manifold geometry analysis and analysis of variance by introducing a notion of goal-equivalent manifold (GEM). This approach considers, in particular, such factors as sensitivity of solutions within the UCM to deviations of elemental variables (also addressed by Scholz and Schöner (1999)).
3. The equilibrium-point hypothesis and the notion of referent configuration
The equilibrium-point (EP) hypothesis is over 40 years old (Feldman, 1966). Despite the severe criticisms and numerous experimental studies, it has been neither disproved nor broadly accepted (for reviews see Feldman and Levin (1995, 2009); Ostry and Feldman (2004)). A few recent publications have presented updated critical reviews on the EP-hypothesis (Feldman & Latash, 2005; Feldman & Levin, 2009). Here, I will only emphasize a few main points.
The EP-hypothesis is based on three major principles, two from physics and one from physiology.
The first physical principle states that, if one wants to control a complex dynamic system (and there is little argument that the system for movement production is a complex dynamic system), the controller has to manipulate parameters of the system, while its performance emerges given these parameters and the laws of physics that govern all the complex interactions within the system and between the system and the external world. A controller cannot, in principle, directly prescribe performance variables of the system such as, for example, trajectories, forces, torques, muscle activation levels, and any variables that can be computed based on the mentioned ones.
The second physical principle states that any physical system tries to reach a state of minimal potential energy. In the context of the control of voluntary movements, this principle implies that any system tries to reach a level of minimal muscle activation given its centrally specified parameters, and the anatomical and external contstraints. This has been addressed as the principle of minimal final action, related to the famous principle of minimal interaction (Feldman, Goussev, Sangole, & Levin, 2007; Gelfand & Tsetlin, 1967; Latash, 2008).
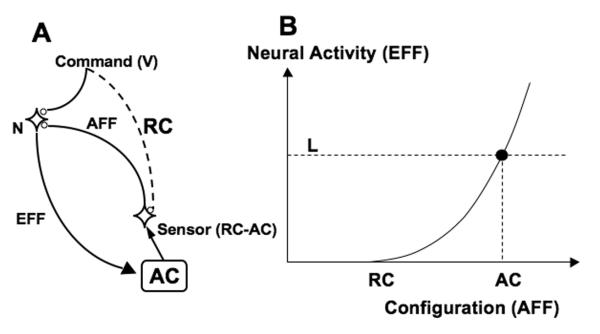
The physiological principle is based on the threshold nature of activation of the neural cells. Setting a threshold value of a neuron (for example, by a change in the level of subthreshold membrane depolarization) defines a range of external input signals that would lead to generation of action potentials. Now imagine that neuronal activity affects the source of the input signals. This scheme turns into a feedback loop, which can (but does not have to) lead to an equilibrium state of the system involving all its elements and the source of the external input signals (see Fig. 2A).
Fig. 2.
An illustration of control with referent configurations. Sending a command expressed in membrane potential units (V) to a target group of neurons (N) results in an efferent (EFF) signal that ultimately leads to a change in actual configuration (AC) of the system. The same signal leads (after processing, shown by the dashed line) to a referent configuration (RC). A sensor measures the difference between RC and AC and projects back to N. In other words, setting a referent configuration (RC) defines a range of actual configurations (AC) that lead to activation of N; larger (AC-RC) values lead to higher activation levels. The activation of N produces a mechanical effect that moves AC towards RC. When the two coincide, the neuron becomes silent, and the system stays at RC. If an external load (L) prevents AC from moving towards RC, an equilibrium state is reached (EP) corresponding to non-zero neuronal (and muscle) activation.
In case of single-muscle control, the combination of the three pricniples leads to a scheme within which the controller specifies a parameter (the first principle) representing the threshold of the tonic stretch reflex (the third principle). Given the value of the threshold, in a steady-state, the interaction between the muscle (including its reflex loops) and the external load leads to an equilibrium point (a combination of muscle length and force). If the external force is removed, the muscle will shorten until its length corresponds to the threshold of the tonic stretch reflex, and then it will be silent (the second principle).
This scheme can be generalized for multi-muscle, multi-joint, multi-effector, and whole-body systems (and beyond, see Feldman (2008); Feldman and Levin (2009)). For each level of description, the controller is assumed to specify parameters that define a referent configuration (set of values) for important performance variables. Then, a neuronal mechanism is organized, similar to the tonic stretch reflex, that tries to move the actual configuration towards the referent one. This mechanism leads to an equilibrium state that may differ from the referent configuration because of the anatomical and external constraints.
Fig. 2A illustrates this general scheme. It is somewhat similar to figures illustrating the EP-hypothesis for a single muscle (see, for example, Feldman (1986)). The controller sends a command to a neuron (N); this command depolarizes the target membrane and modulates threshold for action potential generation by N. Output of N (efferent command, EFF) results in changes of muscle activations that lead to shifts in the actual configuration of the body (AC). Given external conditions, the signal from the controller may also be viewed as specifying a referent configuration (RC), defined as a configuration, at which all the muscles would be at thresholds for their activation. A sensor neuron provides feedback (afferent signal, AFF) to neuron N reflecting the difference between RC and AC (Fig. 2B).
If AC differs from RC (to the right of RC in Fig. 2B), the neuron N is activated and its activation is higher for larger deviations of AC from RC. The activation of the neuron produces a mechanical effect that moves AC towards RC. When the two coincide, the neuron becomes silent, and the system stays at RC. If something (for example, an external load, L) prevents AC from moving, an equilibrium state is reached corresponding to non-zero neuronal (and muscular) activation and a combination of positional and force variables.
4. Synergies organized by equilibrium-point control
There are two types of relations between the introduced notion of synergies and the EP-hypothesis. The first one is that the principle of control with referent configurations may by itself lead to synergic relations among elemental variables.
Consider the earlier example of holding an object statically in the air with two digits (the thumb and a finger, TH and FG) opposing each other. For simplicity, consider this task in a planar case (Fig. 3). The task may be associated with four constraints Zatsiorsky & Latash, 2008). First the resultant normal force should be zero. Second, the resultant tangential force should be equal in magnitude and directed against the force of gravity (load, L). Third, the resultant moment of force should be equal in magnitude and directed against the external moment of force (M). Fourth, the normal forces should be suffient to prevent slippage given the friction coefficient, k. Formally, the four constraints are:
| (1) |
| (2) |
| (3) |
| (4) |
where the superscripts refer to normal (n) and tangential (t) forces, d and r are lever arms of the normal and tangential forces respectively, and k is friction coefficient.
Fig. 3.
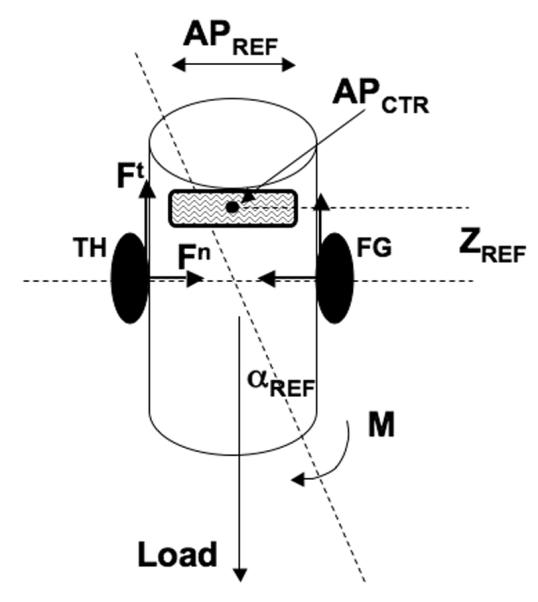
An illustration of a two-digit precision grip in a planar case. An external load and moment of force (L and M) act on the hand-held object. The controller sets four parameters forming referent configuration: The size and location of the referent aperture (APREF and APCTR), referent vertical position (ZREF), and referent orientation (αREF).
According to the referent configuration hypothesis, the control of this action may be described with a set of salient referent coordinates (referent configuration). Such a set may include referent aperture (APREF; see Pilon, De Serres, & Feldman, 2007), location of its central point (APCTR), referent position in the vertical direction (ZREF), and referent orientation of the object with respect to the vertical (αREF). Fig. 3 illustrates the four control parameters. Note that setting any APREF that is smaller than the actual aperture ensures that constraint (1) is satisfied without any additional control. Even if APCTR does not coincide with the center of the object, the object will move until the two opposing digit forces are in balance. So, a synergy illustrated in an earlier example (Fig. 1) may be a direct result of the type of control with APREF. APCTR defines where in external space the two opposing normal forces are balanced as illustrated in Fig. 1.
Setting a referent vertical coordinate ZREF will similarly lead to satisfying constraint (2). The object will continue to move until this equation is satisfied. And along similar lines, setting αREF allows to balance the external moment of force for the required orientation of the object (vertical in Fig. 3).
The first three constraints may be satisfied by any APREF (smaller than actual aperture!). The fourth constraint, however, requires that the difference between APREF and the actual aperture is large enough to produce normal forces that are sufficient to allow the system to produce required tangential forces given the friction conditions. Note that the discrepancy between APREF and the actual aperture is due to the rigid walls of the object that prevent the digits from moving towards each other and lead to the generation of normal forces.
This simple illustrations shows that synergies among elemental performance variables may be by-products of the EP mode of control without any additional computational steps or special feedback loops. In the illustration, the co-variation of elemental variables was due to explicit mechanical task constraints. Several studies have suggested that synergies may be seen in the absence of such explicit constraints, i.e. reflecting a preference of the controller that may not have a simple mechanical initerpretation (Latash, Scholz, Danion, & Schöner, 2001; Niu, Latash, & Zatsiorsky, 2008). Moreover, sometimes synergies are seen in some subjects but not in others. These observations suggest that some of the synergies may be related to setting a referent coordinate of a variable that is not easy to guess and that does not have a straightforward mechanical interpretation. Finding such variables in one of the current challenges.
5. Synergies within the equilibrium-point hypothesis
Another link between the idea of control with referent configurations and the idea of synergies is in trying to define relations among variables describing referent configurations at different levels of the neuromotor hierarchy.
Consider the task of pointing with a multi-joint limb. If the only important constraint is to place the endpoint into the target, to achieve a final steady-state the controller has to specify referent coordinates of the endpoint (that may not coincide with the target coordinates, depending on the external force field) and stability properties of the endpoint at the final steady-state (cf. control of endpoint impedance, Hogan 1985). Let me refer to these two multi-dimensional parameters as a {R,C} pair.
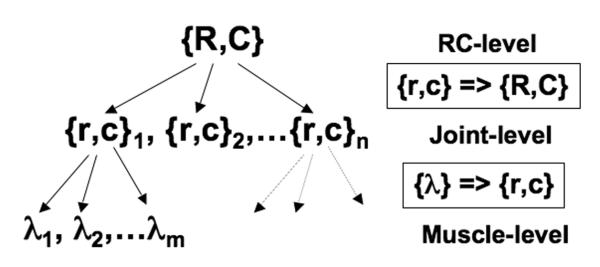
To implement this, the central nervous system has to act through the only controllable elements, to which it has direct access, that is muscles. One can consider this process as involving two steps (Fig. 4). At each step, a seeming problem of motor redundancy occurs. First, given a desired {R,C} pair, the controller has to select a set of {r,c} pairs for individual joints. The {r,c} pairs refer to the reciprocal and co-activation commands, as introduced within the EP-hypothesis (Feldman, 1980). They define the midpoint of the range within which both agonist and antagonist muscles controlling this particular rotation are activated and the size of the range, respectively. Then, since each joint is typically crossed by more than two muscles, for each {r,c} pair the control variables (threshold of the tonic stretch reflex, λ) for all the muscles crossing the joint has to be defined. However, the principle of abundance suggests that such problems may not be solved by “eliminating redundant DOF’s”, but all the {r,c} pairs at the joint level may be organized into a synergy stabilizing {R,C}, while all the λs at the muscle level may be organized to stabilize {r,c}.
Fig. 4.
A hypothetical control hierarchy within the equilibrium-point hypothesis. The three levels, {R,C}, {r,c} and {λ} involve few-to-many mappings and may be expected to be linked by synergies: multi-λ => {r,c} and multi-{r,c} => {R,C}.
Indeed, even EP control of a single muscle may be viewed as a synergy among the hugely redundant set of its motor units that stabilizes the equilibrium point. This synergy is based on the action of the tonic stretch reflex. Mechanisms for λ-synergies stabilizing {r,c} ({λ}=>{r,c}) and for {r,c}-synergies stabilizing {R,C} ({r,c}=>{R,C}) are currently unknown. Both feedback-based and feedforward control hypotheses have been suggested that might bring about such synergies (Latash, Shim, Smilga, & Zatsiorsky, 2005; Goodman & Latash, 2006).
The idea of a {R,C} <=> {r,c} <=> {λ} hierarchy of synergies is still beyond the current means of experimental exploration and verification. The biggest problem seems to be the lack of reliable “lambdameters”, a major challenge for the development of the field.
6. What may be the purpose of motor synergies?
Before moving to the issue of changes in synergies with practice, it is useful to touch upon a very basic question formulated as the title of this subsection. At first glance, the answer is nearly obvious: Synergies reduce variability of performance given the natural (and possibly irreducible) variability of elements, for example as in schemes that consider level-dependent motor noise (Harris & Wolpert, 1998; Jones, Hamilton, & Wolpert, 1988). Indeed, many studies of single-element actions have shown a nearly proportional increase in standard deviation with the action magnitude (Newell & Carlton, 1993; Slifkin & Newell, 1999; Christou, Grossman, & Carlton, 2002). Organizing a specific co-variation among elemental variables may be a means of reducing variability of performance. Indeed, several publications have suggested that multi-digit synergies do avoid an expected increase in force variability with force magnitude increase in certain tasks (Latash, Scholz, Danion, & Schöner, 2002; Scholz, Danion, Latash, & Schöner, 2002; Shinohara, Li, Kang, Zatsiorsky, & Latash, 2003; Shinohara, Scholz, Zatsiorsky, & Latash, 2004).
However, several more detailed recent studies have suggested that synergies have only a small effect on the variability of performance (Gorniak, Duarte, & Latash, 2008; Shapkova, Shapkova, Goodman, Zatsiorsky, & Latash, 2008). Indeed, when a redundant set of elements is involved in a task, variance of each element increases substantially. This is expected to lead to an increase in performance variance. At the same time, co-variation among elemental variables is ensured by synergies. This co-variation brings variance of the performance variable down, very close to values expected in a single-element task.
So, why would the controller increase variance of elements and at the same time organize a synergy stabilizing their combined effect? Would it not be easier to keep the elemental variance unchanged and not worry about synergies?
Indeed, since performance variance by definition depends on variance orthogonal to the UCM (VORT in Fig. 1), why should the controller worry about VUCM (to ensure the essential VUCM > VORT inequality), which by definition has no effect on that particular performance variable? A few studies (Gera et al., 2009; Scholz, Schöner, & Latash, 2000; Zhang, Scholz, Zatsiorsky, & Latash, 2008) have suggested an answer: The controller facilitates large VUCM to achieve two goals: (1) To be able to perform secondary tasks that use the same set of elemental variables with no detrimental effects on performance of the first task; and (2) To be able to handle unexpected external or internal perturbations.
To illustrate the first function consider a task of carrying a mug of hot coffee in the right hand. You come to a closed door with a handle that has to be pressed down to open the door. Your other arm is busy. What do you do? One solution is to open the door by pressing on the handle with the elbow of the arm that carries the mug. This action involves several proximal arm joints that are also involved in keeping the mug oriented vertically. Having large VUCM with respect to the task of not spilling coffee allows to use some of the elements for such a secondary task without changing the control rule, as long as that secondary task can be performed without leaving the original UCM.
In one of the first studies of multi-joint reaching using the UCM approach, quick-draw shooting at a target was used (Scholz et al., 2000). Arm joint rotations were united into a synergy stabilizing the orientation of the gun barrel wit respect to the direction from the back-sight to the target over the whole movement duration. In one of the series, a rubber band was attached to the arm crossing the elbow joint such that it produced minimal force at the initial position but developed considerable forces during elbow extension in the course of the quick-draw shooting action. Seven out of nine participants hit the target at the first trial (movement time about 250 ms). This result suggests that effects of the perturbation on joint motion were channeled into the corresponding UCM such that the gun barrel was aligned with the target at the moment of shooting. To summarize, the available data suggest that the purpose of multi-element synergies is to allow the controller (the central nervous system) to perform several tasks simultaneously without a detrimental interference and to deal with unexpected perturbations.
7. Experimental studies of stages in learning motor synergies
Only a handful of studies explored changes in indices of synergies with practice. Theoretically, if one assumes that with practice performance becomes less variable, three main scenarios may be expected relevant to the operational definition of synergies within the UCM framework (Fig. 5). Less variable performance means that VORT computed with respect to the salient performance variable is expected to decrease. The different scenarios differ in changes in VUCM, which by definition has no effect on the performance variable. 1). VUCM can stay unchanged, decrease less than VORT, or even increase such that the relative difference between VUCM and VORT increases (the synergy becomes stronger); 2). VUCM can decrease in proportion to the change in VORT such that the relative difference between VUCM and VORT does not change (the synergy stays unchanged); and 3). VUCM can decrease more than VORT leading to drop in the synergy index (synergy weakens).
Fig. 5.
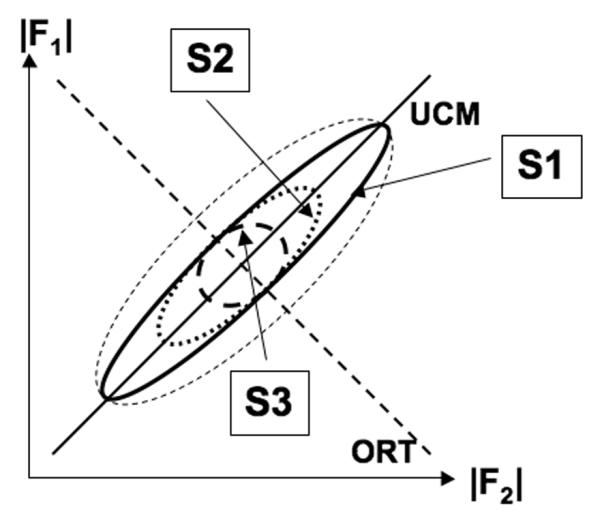
Three scenarios of changes in the “good” and “bad” components of variance (VUCM and VORT) with practice. In all three cases, VORT is expected to drop. VUCM may drop less (or be unchanged or even increase) as compared to VORT (the synergy becomes stronger – scenario #1, S1), VUCM may drop proportionally to VORT (no change in the synergy strength – scenario #2, S2), or it may drop more than VORT (the synergy weakens – scenario #3, S3).
Experimental evidence for all three scenarios has been published. Studies of changes in joint coordination indices in two-arm pointing tasks have shown both a drop in the index of synergies (a larger drop in VUCM as compared to the drop in VORT, scenario #3) and a proportional drop in VUCM and VORT (scenario #2) (Domkin, Laczko, Jaric, Johansson, & Latash, 2002; Domkin, Laczko, Djupsjöbacka, Jaric, & Latash, 2005). A study of the effects of practice of a very unusual multi-finger force production task showed an increase in the synergy strength (a large drop in VORT without a comparable drop in VUCM, Kang, Shinohara, Zatsiorsky, & Latash, 2004). Similar results were found in a much more simple task but performed by persons with Down syndrome (Latash, Kang, & Patterson, 2002; Scholz et al., 2003). An increase in synergy strength was also documented in a study of the effects of practice on multi-muscle synergies in a postural task performed in challenging conditions (Asaka, Wang, Fukushima, & Latash, 2008).
One study demonstrated a sequence of two stages in a multi-finger force production task performed under unstable conditions and with unexpected transcranial magnetic stimuli (TMS) applied over the contralateral primary cortical motor area (Latash, Yarrow, & Rothwell, 2003), an increase in the synergy index with practice followed by its weakening. More specifically, the first stage was characterized by a significant drop in VORT with minimal changes in VUCM, while during the second phase VUCM decreased with little change in VORT (similar to results of the aforementioned study by Domkin et al. (2002)). The two stages could be interpreted as developing a synergy with respect to the explicit task requirement and then tuning performance with respect to other factors such as coping with the perturbing effects of the TMS stimuli. This tuning of the performance involves selecting particular combinations of elemental variables within the UCM. As a result, it leads to smaller areas within the UCM that are used by the subject resulting in a drop in the synergy index. Note that the two stages have little to do with the number of DOF’s, as in the mentioned classical three-stage scheme (cf. Vereijken et al., 1992): The number of DOF never changes, but their coordination is adjusted.
The earlier mentioned studies could also be interpreted within this scheme. The two-arm pointing task was probably too easy, and the subjects were close to a plateau of performance (a low value of VORT) after a relatively small number of trials. Further, they adjusted their performance not to perform the task more accurately (since there was little room left for improvement) but to select a subset of solutions within the UCM that satisfied other constraints (see a recent study of the effects of additional constraints on data distributions within the UCM, Zhang et al., 2008). These constraints could, for example, include minimizing fatigue, avoiding clumsy configurations, or dealing with some other aspects of performance. A drop in VUCM with a smaller change in VORT led to a seeming drop in the synergy index. In other mentioned studies, the task was probably novel and challenging enough such that the subjects cared most about reducing the variability of the most salient variable, which primarily led to a drop in VORT.
8. Stages in learning synergies within the equilibrium-point hypothesis
The process of learning synergies allows an interpretation based on the framework offered by the EP-hypothesis. Consider, first, possible reasons for emergence and strengthening of synergies. If a task requires accurate performance of a mechanical variable, given an external force field, an adequate control trajectory may be viewed as a time function {R(t),C(t)}. This first stage of practice may be viewed as finding and refining the control trajectory. By itself, as demonstrated earlier, this mode of control may be expected to lead to synergies within the space of elemental mechanical (and possibly also EMG) variables stabilizing the required performance variable. A synergy may be expected to emerge and strengthen with practice as more and more adequate time profile of the control trajectory is found.
The next step is elaboration of a synergy, {r(t),c(t)}=>{R(t),C(t)}, stabilizing the control trajectory against possible internally and externally generated perturbations. This process is expected to lead to a further drop in VORT without necessarily being accompanied by a drop in VUCM. The two mentioned steps correspond to the first of the two hypothesized stages of learning motor synergies. At those stages, having a broad range of “good variability” (quantified as VUCM) may be viewed as beneficial because larger VUCM reflects a neural organization that allows to channel effects of spontaneous internal perturbations (for example, those associated with signal-dependent noise, Jones et al., 2002) as well as unexpected changes in the external force field into the UCM subspace (e.g., Gorniak, Feldman, & Latash, 2009).
There is a possibility of another process going in parallel to the first one, that is the elaboration of {λ(t)}=>{r(t),c(t)} synergies. On the one hand, an assumption on multi-λ synergies stabilizing {r(t),c(t)} control functions at the joint level sounds only natural. However, a number of recent studies have cast doubt on the possibility of simultaneous synergy elaboration at two levels of the control hierarchy (Gorniak, Zatsiorsky, & Latash, 2007a, 2007b, 2009). These studies explored multi-digit actions in accurate two-hand force production tasks involving two pairs of fingers (two per hand) and in prehensile tasks involving one or two hands. Both tasks can be viewed as controlled in a hierarchical fashion. At the upper level of the hierarchy, the task is shared between the two hands or between the thumb and the virtual finger (an imagined digit with the mechanical action equal to that of the actual digits opposing the thumb; Arbib, Iberall, and Lyons (1985); MacKenzie and Iberall (1994)). At the lower level, hand action is shared between fingers and virtual finger action is shared between actual fingers. The mentioned studies showed that strong synergies stabilizing total force produced by sets of effectors at the upper level of the hierarchy were commonly (but not always!) associated with weak or lacking synergies at the lower level.
Indeed, large VUCM, which is a pre-requisite for a strong synergy at a higher level of a hierarchy, for example at the {R(t),C(t)} level implies large variance of the {r(t),c(t)} functions that get contribution from both VORT and VUCM. However, at the lower level of the hierarchy, large {r(t),c(t)} variance is, by definition, VORT and, as such, may require unreasonably high magnitudes of VUCM to create synergies at that level.
After both an adequate control trajectory and synergies stabilizing it are elaborated, VORT may be expected to have a value that is very close to its practically attainable minimum. What could be reasons for further practice? They can indeed be many and varied. Practice may be seen as a task of discovering relevant constraints that may not be obvious when the task is met for the first time. For example, practice may serve to satisfy self-imposed constraints related to esthetics, avoiding fatigue, energy expenditure, and maybe other factors. Since VORT is already very small, search for solutions that satisfy such constraints can only be performed within the UCM leading to a drop in VUCM. According to the introduced definition, this leads to weakening synergies stabilizing the primary performance variable.
In the language of the EP-hypothesis, the second stage is associated with a decrease in the range of {r,c} variation compatible with the required {R,C}. Somewhat counter-intuitively, it may be associated with elaboration of particular co-variation patterns of muscle control variables, that is, stronger {λ}=>{r,c} synergies. Such synergies are expected to lead to a drop in the variance at the {r,c} level. Since VORT is already at its minimal value, this drop can only lead to a decrease in VUCM, that is to weakening the {r,c}=>{R,C} synergies.
9. Final comments
To summarize, I would like to revisit the main points made in this review:
The recent developments of the notion of synergies, the computational method of the UCM hypothesis, and the main ideas of the EP-hypothesis are not only compatible but beg to be merged into a common scheme of control of multi-element systems;
Effects of practice of motor tasks can be discussed within this scheme as consisting of two stages: The elaboration of strong synergies stabilizing salient performance variables and optimizing other aspects of performance (leading to a drop in the index of such synergies);
The hierarchical principle of control may lead to non-trivial and unexpected changes in indices of synergies related to changes in “good variability” (VUCM) at the different levels.
Overall, I believe that researchers in the field of motor control (and motor learning) currently face an exciting phase of scientific inquiry offered by the mentioned recent developments. There are new computational tools and new theoretical insights into the most central and notoriously hard problems such as the nature of neural control variables and the coordination of redundant systems. These tools and insights are waiting to be applied to both basic and applied studies of human movements, including motor learning.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errorsmaybe discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Arbib MA, Iberall T, Lyons D. Coordinated control programs for movements of the hand. In: Goodwin AW, Darian-Smith I, editors. Hand function and the neocortex. Springer Verlag; Berlin: 1985. pp. 111–129. [Google Scholar]
- Asaka T, Wang Y, Fukushima J, Latash ML. Learning effects on muscle modes and multi-mode synergies. Experimental Brain Research. 2008;184:323–338. doi: 10.1007/s00221-007-1101-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein NA. On dexterity and its development. In: Latash ML, Turvey MT, editors. Dexterity and its development. Lawrence Erlbaum Associates; Mahwah, NJ: 1996. pp. 1–244. [Google Scholar]
- Christou EA, Grossman M, Carlton LG. Modeling variability of force during isometric contractions of the quadriceps femoris. Journal of Motor Behavior. 2002;34:67–81. doi: 10.1080/00222890209601932. [DOI] [PubMed] [Google Scholar]
- Cusumano JP, Cesari P. Body-goal variability mapping in an aiming task. Biological Cybernetics. 2006;94:367–379. doi: 10.1007/s00422-006-0052-1. [DOI] [PubMed] [Google Scholar]
- Domkin D, Laczko J, Jaric S, Johansson H, Latash ML. Structure of joint variability in bimanual pointing tasks. Experimental Brain Research. 2002;143:11–23. doi: 10.1007/s00221-001-0944-1. [DOI] [PubMed] [Google Scholar]
- Domkin D, Laczko J, Djupsjöbacka M, Jaric S, Latash ML. Joint angle variability in 3D bimanual pointing: Uncontrolled manifold analysis. Experimental Brain Research. 2005;163:44–57. doi: 10.1007/s00221-004-2137-1. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics. 1966;11:565–578. [Google Scholar]
- Feldman AG. Superposition of motor programs. I. Rhythmic forearm movements in man. Neuroscience. 1980;5:81–90. doi: 10.1016/0306-4522(80)90073-1. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (λ-model) for motor control. Journal of Motor Behavior. 1986;18:17–54. doi: 10.1080/00222895.1986.10735369. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Goussev V, Sangole A, Levin MF. Threshold position control and the principle of minimal interaction in motor actions. Progress in Brain Research. 2007;165:267–281. doi: 10.1016/S0079-6123(06)65017-6. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Latash ML. Testing hypotheses and the advancement of science: Recent attempts to falsify the equilibrium-point hypothesis. Experimental Brain Research. 2005;161:91–103. doi: 10.1007/s00221-004-2049-0. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. Positional frames of reference in motor control: Their origin and use. Behavioral and Brain Sciences. 1995;18:723–806. [Google Scholar]
- Feldman AG, Levin MF. The equilibrium-point hypothesis--past, present and future. Advances in Experimental Medicine and Biology. 2009;629:699–726. doi: 10.1007/978-0-387-77064-2_38. [DOI] [PubMed] [Google Scholar]
- Friedman J, Skm V, Zatsiorsky VM, Latash ML. The sources of two components of variance: An example of multifinger cyclic force production tasks at different frequencies. Experimental Brain Research. 2009;196:263–277. doi: 10.1007/s00221-009-1846-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelfand IM, Latash ML. On the problem of adequate language in movement science. Motor Control. 1998;2:306–313. doi: 10.1123/mcj.2.4.306. [DOI] [PubMed] [Google Scholar]
- Gelfand IM, Tsetlin ML. On mathematical modeling of the mechanisms of the central nervous system. In: Gelfand IM, Gurfinkel VS, Fomin SV, Tsetlin ML, editors. Models of the structural-functional organization of certain biological systems. Nauka; Moscow: 1966. pp. 9–26. (1966) (in Russian, a translation is available in 1971 edition by MIT Press: Cambridge MA) [Google Scholar]
- Gera G, deFreitas S, Latash ML, Monahan K, Schöner G, Scholz JP. Motor abundance contributes to solving multiple kinematic task constraints. Motor Control. 2009 doi: 10.1123/mcj.14.1.83. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman SR, Latash ML. Feedforward control of a redundant motor system. Biological Cybernetics. 2006;95:271–280. doi: 10.1007/s00422-006-0086-4. [DOI] [PubMed] [Google Scholar]
- Goodman SR, Shim JK, Zatsiorsky VM, Latash ML. Motor variability within a multi-effector system: Experimental and analytical studies of multi-finger production of quick force pulses. Experimental Brain Research. 2005;163:75–85. doi: 10.1007/s00221-004-2147-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorniak SL, Duarte M, Latash ML. Do synergies improve accuracy? A study of speed-accuracy trade-offs during finger force production. Motor Control. 2008;12:151–172. doi: 10.1123/mcj.12.2.151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorniak SL, Feldman AG, Latash ML. Joint coordination during bimanual transport of real and imaginary objects. Neuroscience Letters. 2009;456:80–84. doi: 10.1016/j.neulet.2009.03.084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorniak SL, Zatsiorsky VM, Latash ML. Hierarchies of synergies: An example of the two-hand, multi-finger tasks. Experimental Brain Research. 2007a;179:167–180. doi: 10.1007/s00221-006-0777-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorniak SL, Zatsiorsky VM, Latash ML. Emerging and disappearing synergies in a hierarchically controlled system. Experimental Brain Research. 2007b;183:259–270. doi: 10.1007/s00221-007-1042-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorniak SL, Zatsiorsky VM, Latash ML. Hierarchical control of static prehension: II. Multi-digit synergies. Experimental Brain Research. 2009;194:1–15. doi: 10.1007/s00221-008-1663-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogan N. The mechanics of multi-joint posture and movement control. Biological Cybernetics. 1985;52:315–331. doi: 10.1007/BF00355754. [DOI] [PubMed] [Google Scholar]
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394:780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- Jones KE, Hamilton AF, Wolpert DM. Sources of signal-dependent noise during isometric force production. Journal of Neurophysiology. 2002;88:1533–1544. doi: 10.1152/jn.2002.88.3.1533. [DOI] [PubMed] [Google Scholar]
- Kang N, Shinohara M, Zatsiorsky VM, Latash ML. Learning multi-finger synergies: An uncontrolled manifold analysis. Experimental Brain Research. 2004;157:336–350. doi: 10.1007/s00221-004-1850-0. [DOI] [PubMed] [Google Scholar]
- Koshland GF, Gerilovsky L, Hasan Z. Activity of wrist muscles elicited during imposed or voluntary movements about the elbow joint. Journal of Motor Behavior. 1991;23:91–100. doi: 10.1080/00222895.1991.9942026. [DOI] [PubMed] [Google Scholar]
- Kudo K, Tsutsui S, Ishikura T, Ito T, Yamamoto Y. Compensatory coordination of release parameters in a throwing task. Journal of Motor Behavior. 2000;32:337–345. doi: 10.1080/00222890009601384. [DOI] [PubMed] [Google Scholar]
- Latash ML. Synergy. Oxford University Press; New York: 2008. [Google Scholar]
- Latash ML, Aruin AS, Zatsiorsky VM. The basis of a simple synergy: Reconstruction of joint equilibrium trajectories during unrestrained arm movements. Human Movement Science. 1999;18:3–30. [Google Scholar]
- Latash ML, Kang N, Patterson D. Finger coordination in persons with Down syndrome: Atypical patterns of coordination and the effects of practice. Experimental Brain Research. 2002;146:345–355. doi: 10.1007/s00221-002-1189-3. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G. Structure of motor variability in marginally redundant multi-finger force production tasks. Experimental Brain Research. 2001;141:153–165. doi: 10.1007/s002210100861. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JF, Danion F, Schöner G. Finger coordination during discrete and oscillatory force production tasks. Experimental Brain Research. 2002;146:412–432. doi: 10.1007/s00221-002-1196-4. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Motor control strategies revealed in the structure of motor variability. Exercise and Sport Science Reviews. 2002;30:26–31. doi: 10.1097/00003677-200201000-00006. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Toward a new theory of motor synergies. Motor Control. 2007;11:275–307. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Zatsiorsky VM. Is there a timing synergy during multi-finger production of quick force pulses? Experimental Brain Research. 2004;159:65–71. doi: 10.1007/s00221-004-1933-y. [DOI] [PubMed] [Google Scholar]
- Latash ML, Shim JK, Smilga AV, Zatsiorsky V. A central back-coupling hypothesis on the organization of motor synergies: A physical metaphor and a neural model. Biological Cybernetics. 2005;92:186–191. doi: 10.1007/s00422-005-0548-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Yarrow K, Rothwell JC. Changes in finger coordination and responses to single pulse TMS of motor cortex during practice of a multi-finger force production task. Experimental Brain Research. 2003;151:60–71. doi: 10.1007/s00221-003-1480-y. [DOI] [PubMed] [Google Scholar]
- MacKenzie CL, Iberall T. The grasping hand. North-Holland; Amsterdam: 1994. [Google Scholar]
- McIntyre J, Mussa-Ivaldi FA, Bizzi E. The control of stable postures in the multijoint arm. Experimental Brain Research. 1996;110:248–264. doi: 10.1007/BF00228556. [DOI] [PubMed] [Google Scholar]
- Martin TA, Greger BE, Norris SA, Thach WT. Throwing accuracy in the vertical direction during prism adaptation: Not simply timing of ball release. Journal of Neurophysiology. 2001;85:2298–2302. doi: 10.1152/jn.2001.85.5.2298. [DOI] [PubMed] [Google Scholar]
- Müller H, Sternad D. Decomposition of variability in the execution of goal-oriented tasks: Three components of skill improvement. Journal of Experimental Psychology: Human Perception and Performance. 2004;30:212–233. doi: 10.1037/0096-1523.30.1.212. [DOI] [PubMed] [Google Scholar]
- Newell KM. Motor skill acquisition. Annual Reviews in Psychology. 1991;42:213–237. doi: 10.1146/annurev.ps.42.020191.001241. [DOI] [PubMed] [Google Scholar]
- Newell KM, Broderick MP, Deutsch KM, Slifkin AB. Task goals and change in dynamical degrees of freedom with motor learning. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:379–387. doi: 10.1037/0096-1523.29.2.379. [DOI] [PubMed] [Google Scholar]
- Newell KM, Carlton LG. Force variability in isometric responses. Journal of Experimental Psychology: Human Perception and Performance. 1993;14:37–44. [PubMed] [Google Scholar]
- Niu X, Latash ML, Zatsiorsky VM. Prehension synergies in the grasps with complex friction patterns: Local vs. synergic effects and the template control. Journal of Neurophysiology. 2007;98:16–28. doi: 10.1152/jn.00058.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olafsdottir H, Yoshida N, Zatsiorsky VM, Latash ML. Anticipatory covariation of finger forces during self-paced and reaction time force production. Neuroscience Letters. 2005;381:92–96. doi: 10.1016/j.neulet.2005.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostry DJ, Feldman AG. A critical evaluation of the force control hypothesis in motor control. Experimental Brain Research. 2003;153:275–288. doi: 10.1007/s00221-003-1624-0. [DOI] [PubMed] [Google Scholar]
- Pilon J-F, De Serres SJ, Feldman AG. Threshold position control of arm movement with anticipatory increase in grip force. Experimental Brain Research. 2007;181:49–67. doi: 10.1007/s00221-007-0901-8. [DOI] [PubMed] [Google Scholar]
- Shim JK, Olafsdottir H, Zatsiorsky VM, Latash ML. The emergence and disappearance of multi-digit synergies during force production tasks. Experimental Brain Research. 2005;164:260–270. doi: 10.1007/s00221-005-2248-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slifkin AB, Newell KM. Noise, information transmission, and force variability. Journal of Experimental Psychology: Human Perception and Performance. 1999;25:837–851. doi: 10.1037//0096-1523.25.3.837. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Danion F, Latash ML, Schöner G. Understanding finger coordination through analysis of the structure of force variability. Biological Cybernetics. 2002;86:29–39. doi: 10.1007/s004220100279. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Kang N, Patterson D, Latash ML. Uncontrolled manifold analysis of single trials during multi-finger force production by persons with and without Down syndrome. Experimental Brain Research. 2003;153:45–58. doi: 10.1007/s00221-003-1580-8. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G. The uncontrolled manifold concept: Identifying control variables for a functional task. Experimental Brain Research. 1999;126:289–306. doi: 10.1007/s002210050738. [DOI] [PubMed] [Google Scholar]
- Scholz JP, Schöner G, Latash ML. Identifying the control structure of multijoint coordination during pistol shooting. Experimental Brain Research. 2000;135:382–404. doi: 10.1007/s002210000540. [DOI] [PubMed] [Google Scholar]
- Schöner G. Timing, clocks, and dynamical systems. Brain and Cognition. 2002;48:31–51. doi: 10.1006/brcg.2001.1302. [DOI] [PubMed] [Google Scholar]
- Seif-Naraghi AH, Winters JM. Optimized strategies for scaling goal-directed dynamic limb movements. In: Winters JM, Woo SL-Y, editors. Multiple muscle systems. Biomechanics and movement organization. Springer-Verlag; New York: 1990. pp. 312–334. [Google Scholar]
- Shapkova E. Yu., Shapkova AL, Goodman SR, Zatsiorsky VM, Latash ML. Do synergies decrease force variability? A study of single-finger and multi-finger force production. Experimental Brain Research. 2008;188:411–425. doi: 10.1007/s00221-008-1371-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinohara M, Scholz JP, Zatsiorsky VM, Latash ML. Finger interaction during accurate multi-finger force production tasks in young and elderly persons. Experimental Brain Research. 2004;156:282–292. doi: 10.1007/s00221-003-1786-9. [DOI] [PubMed] [Google Scholar]
- Shinohara M, Li S, Kang N, Zatsiorsky VM, Latash ML. Effects of age and gender on finger coordination in maximal contractions and submaximal force matching tasks. Journal of Applied Physiology. 2003;94:259–270. doi: 10.1152/japplphysiol.00643.2002. [DOI] [PubMed] [Google Scholar]
- Vereijken B, van Emmerik REA, Whiting HTA, Newell KM. Free(z)ing degrees of freedom in skill acquisition. Journal of Motor Behavior. 1992;24:133–142. [Google Scholar]
- Wang Y, Asaka T, Zatsiorsky VM, Latash ML. Muscle synergies during voluntary body sway: Combining across-trials and within-a-trial analyses. Experimental Brain Research. 2006;174:679–693. doi: 10.1007/s00221-006-0513-8. [DOI] [PubMed] [Google Scholar]
- Woollacott M, Inglin B, Manchester D. Response preparation and posture control. Neuromuscular changes in the older adult. Annals of the New York Academy of Sciences. 1988;515:42–53. doi: 10.1111/j.1749-6632.1988.tb32964.x. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM. Kinetics of human motion. Champaign, IL; Human Kinetics: 2002. [Google Scholar]
- Zatsiorsky VM, Latash ML. Multi-finger prehension: An overview. Journal of Motor Behavior. 2008;40:446–476. doi: 10.3200/JMBR.40.5.446-476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Scholz JP, Zatsiorsky VM, Latash ML. What do synergies do? Effects of secondary constraints on multi-digit synergies in accurate force-production tasks. Journal of Neurophysiology. 2008;99:500–513. doi: 10.1152/jn.01029.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]