Abstract
Purpose
The purpose of this study was to refine the 2006 Crouter 2-regression model to eliminate the misclassification of walking/running when starting an activity in the middle of a minute on the ActiGraph clock.
Methods
Forty-eight participants [mean (sd) age 35 yrs (11.4)] performed 10-min bouts of various activities ranging from sedentary behaviors to vigorous physical activity. Eighteen activities were divided into three routines and 20 participants performed each routine. Participants wore an ActiGraph accelerometer on the hip and a portable indirect calorimeter was used to measure energy expenditure. Forty-five routines were used to develop the refined 2-regression model and 15 routines were used to cross-validate the model. Coefficient of variation (CV) was used to classify each activity as continuous walking/running (CV≤10) or intermittent lifestyle activity (CV>10).
Results
An exponential regression equation and a cubic equation using the natural log of the 10-sec counts were developed to predict METs every 10-sec for walking/running and intermittent lifestyle activities, respectively. The refined method examines each 10-sec epoch and all combinations of the surrounding five 10-sec epochs to find the lowest CV. In the cross-validation group, the refined method was not significantly different from measured METs for any activity (P>0.05) except cycling (P<0.05). In addition, the 2006 and refined 2-regressin models had similar accuracy and precision for estimating energy expenditure during structured activities.
Conclusion
The refined 2-regression model should eliminate the misclassification of transitional minutes when changing activities that start and stop in the middle of a minute on the ActiGraph clock, thus improving the estimate of free-living energy expenditure.
Keywords: Motion Sensor, Physical Activity, Oxygen Consumption, Activity Counts Variability
Introduction
Accelerometers are objective measurement tools that allow researchers to track the frequency, intensity, and duration of physical activity bouts that individuals perform. The ActiGraph [formerly Manufacturing Technology Incorporated (MTI) ActiGraph, and Computer Science Applications Inc. (CSA)] accelerometer is a commonly used device for assessing physical activity. Since the first version of the ActiGraph was created, over 15 different regression equations have been developed relating ActiGraph counts to energy expenditure (EE). The original ActiGraph equations used a single linear regression line to predict EE from the ActiGraph counts˙min−1. These single regression equations were developed using either walking and running (3, 9, 10, 12, 14, 16) or moderate-intensity lifestyle activities (10, 15). In general, regression equations developed on walking and jogging slightly overestimate the energy cost of walking and light activities, while they greatly underestimate the energy cost of moderate-intensity lifestyle activities. In contrast, regression equations developed using moderate intensity lifestyle activities provide a closer estimate of EE for moderate-intensity activities, but greatly overestimate the energy cost of sedentary and light activities and underestimate the energy cost of vigorous activities (1, 5).
To overcome the limitations of single regression equations, Crouter and colleagues developed a 2-regression model for the ActiGraph that distinguishes between continuous walking/running and intermittent lifestyle activity based on the variability in the accelerometer counts (7). Specifically, the 2006 Crouter 2-regression model for the ActiGraph incorporated three parts: 1) an inactivity threshold so that when the ActiGraph recorded ≤ 50 counts˙min−1 the individual was credited with 1 MET; 2) when the counts˙min−1 were > 50 and the coefficient of variation (CV) of six consecutive 10 second epochs was ≤ 10% (indicating that the individual was performing continuous walking or running) an exponential regression equation was used; and 3) when the counts˙min−1 were > 50 and the CV was > 10% (indicating that the individual was performing an intermittent lifestyle activity) a cubic regression equation was used. By differentiating continuous walking/running from intermittent lifestyle activities, the 2006 Crouter 2-regression model provided a substantial improvement compared to single regression equations for estimating EE and time spent in light (< 3 METs), moderate (3–6 METs), and vigorous (≥ 6 METs) physical activity during structured activity bouts (7).
Recently, Kuffel et al. (11) demonstrated that the 2006 Crouter 2-regression model has a problem in detecting continuous walking and running bouts when the activity bout starts in the middle of a minute on the ActiGraph clock. The 2006 Crouter 2-regression model was developed using structured activity bouts and assumes that each bout of activity starts exactly at the start of a minute on the ActiGraph clock. Thus, when an activity bout starts in the middle of a minute on the ActiGraph clock, the CV will be greater than 10% due to greater variability in the counts. Thus that minute will be misclassified as a lifestyle activity, resulting in an overestimation of EE and activity level.
The purpose of this study was to refine the 2006 Crouter 2-regression model to eliminate the misclassification of walking/running when starting the activity in the middle of a minute on the ActiGraph clock. We hypothesized that by examining each 10-sec epoch and all combinations of the surrounding five 10-sec epochs, it could be determined if each 10-sec epoch was part of a continuous walking/running bout lasting at least one minute. Using this method, it should eliminate the misclassification of walking/running bouts that begin part way through a minute on the ActiGraph clock.
Methods
Subjects
Twenty four males [Mean (Standard deviation) Age: 36 yrs (12.8); Height: 177.8 cm (7.1); Body mass: 83.9 kg (20.2); BMI: 25.9 kg˙m−2 (5.2); Resting VO2: 3.6 ml˙kg−1˙min−1 (0.8)] and 24 females [Mean (Standard deviation) Age: 35 yrs (10.3); Height: 165.4 cm (5.8); Body mass: 62.3 kg (12.3); BMI: 22.7 kg˙m−2 (4.0); Resting VO2: 3.4 ml˙kg−1˙min−1 (0.8)] from the University of Tennessee, Knoxville and surrounding community volunteered to participate in the study. The procedures were reviewed and approved by the University of Tennessee Institutional Review Board before the start of the study. Each participant signed a written informed consent and completed a Physical Activity Readiness Questionnaire (PAR-Q) before participating in the study. Participants were excluded from the study if they had any contraindications to exercise, or were physically unable to complete the activities.
Procedures
This study was part of a larger study using the same participants and the methods are published in more detail elsewhere (4–7). In addition, the data used in this study were used for the development and cross-validation of the 2006 Crouter 2-regression model (7). Prior to testing, participants had their height and weight measured (in light clothing, without shoes) using a stadiometer (Seca Corp., Columbia, MD) and a physician’s scale (Health-o-meter, Inc., Bridgeview, IL), respectively. Participants performed various lifestyle and sporting activities that were divided into three routines (Table 1). Twenty participants performed each routine, with two participants completing all three routines and eight participants completing two routines. Participants performed each activity in a routine for 10 minutes, with a 1 to 2 minute break between each activity which were performed in order from the lowest energy cost to the highest energy cost. Oxygen consumption (VO2) was measured continuously throughout the routine by indirect calorimetry (Cosmed K4b2, Rome Italy). Participants wore an ActiGraph accelerometer on the right hip for the duration of the routine. For the Cosmed K4b2 and ActiGraph, 2 kg was added to account for the added weight of the devices. Routine 1 was performed in the Applied Physiology Laboratory, routine 2 was performed at University facilities, and routine 3 was performed at either the participant’s home or the investigator’s home. The participants who did not perform routine 1 were asked to sit quietly for 5 minutes before the start of the routine so that a resting VO2 could be measured.
Table 1.
Activities performed in each routine.
| Routine 1 | Routine 2 | Routine 3 |
|---|---|---|
| Lying | Slow Track Walk (~ 3 mph) | Vacuuming |
| Standing | Fast Track Walk (~ 4 mph) | Sweeping/Mopping |
| Computer Work | Basketball | Washing Windows |
| Filing Papers | Racquetball | Washing Dishes |
| Ascending/Decending Stairs | Slow Track Run (~ 5 mph) | Lawn Mowing |
| Stationary Cycling (~100 Watts) | Fast Track Run (~ 7 mph) | Raking Grass/Leaves |
Indirect calorimetry
The Cosmed K4b2 weighs 1.5 kg, including the battery, and a specially designed harness. The Cosmed K4b2 has been shown to be a valid device when compared to the Douglas Bag method during cycle ergometry (13). Prior to each test, the oxygen and carbon dioxide analyzers were calibrated according to the manufacturer’s instructions. During each test a gel-seal was used to help prevent air leaks from the face mask. For more detail see Crouter et al. (7).
ActiGraph accelerometer
The ActiGraph accelerometer (model 7164) is a small (2.0 × 1.6 × 0.6 in) and lightweight (42.5 grams) uniaxial accelerometer, and can measure accelerations in the range of 0.05 to 2 G’s and a band limited frequency of 0.25 to 2.5 Hz. These values correspond to the range in which most human activities are performed. An 8-bit analog-to-digital converter samples at a rate of 10 Hz and these values are then summed for the specified time period (epoch). The ActiGraph was worn at waist level at the right anterior axillary line in a nylon pouch that was attached to a belt. The ActiGraph was initialized using 1-second epochs and the time was synchronized with a digital clock so the start time could be synchronized with the Cosmed K4b2. At the conclusion of the test, the ActiGraph data were downloaded to a laptop computer for subsequent analysis. A total of three ActiGraph accelerometers were used during the study. For each subject, one of the three accelerometers was chosen at random to be used. The ActiGraph accelerometers were calibrated at the start and end of the study. On both occasions, the calibration fell within ± 3.5% of the reference value, which is within the manufacturer’s standards.
Data analysis
Breath-by-breath data were collected by the Cosmed K4b2, which was averaged over a 1 min period. For each activity, the VO2 (ml˙min−1) was converted to VO2 (ml˙kg−1˙min−1) and then to METs by dividing by 3.5. For each activity, the MET value for minutes 4 to 9 were averaged and used for the subsequent analysis.
The ActiGraph accelerometer data were collected in 1-second epochs and were converted to counts per 10 seconds using a Visual Basic program. We chose to use 1-second epochs to allow greater flexibility during our data analysis, but to apply the newly developed method, data can be collected in 10-second epochs.
Statistical treatment
Statistical analyses were carried out using SPSS version 16.0 for windows (SPSS Inc., Chicago, IL). For all analyses, an alpha level of 0.05 was used to indicate statistical significance. All values are reported as mean (standard deviation). Independent t-tests were used to examine the difference between genders for anthropometric variables.
For the development of the refined 2-regression model, the same 45 tests that were used to develop the 2006 Crouter 2-regression model were chosen to develop the refined 2-regression model and the same 15 tests used for the cross-validation of the 2006 Crouter 2-regression model were also used to cross-validate the refined 2-regression model. This was done for the purpose of allowing direct comparisons to be made between the 2006 and refined 2-regression models. Due to waist mounted accelerometers not being able to detect cycling activity, cycling was not used in the development of the refined 2-regression model.
The same general principles were used to develop the refined 2-regression model as were used in the development of the 2006 2-regression model. Each activity performed by an individual was classified into groups based on the CV value of the 10 second counts; CV from 0.1% to 10 % (CV ≤ 10), and CV of >10%, or not able to calculate (CV > 10). During the walking and running, the CV was almost always less than 10%, while for the other activities the CV was almost always greater than 10%. One exception was during activities such as lying, sitting, and standing where the counts per minute could be zero for a full minute; thus the CV is not able to be calculated and it was defined as a CV of zero. In these cases they were placed in the CV > 10% group for the purpose of developing the regression equation.
To overcome the problem of misclassifying walking activity when starting and stopping in the middle of a minute, each 10-sec epoch and all combinations of the five surrounding 10-sec epochs were examined to determine if each 10-sec epoch was part of a continuous walking/running bout or an intermittent lifestyle activity bout. Specifically, each 10-second epoch and the surrounding five 10-sec epochs were examined in the following manner: 10-sec epoch of interest and 1) the five 10-sec epochs before, 2) the four 10-sec epochs before and one 10-sec epoch after, 3) the three 10-sec epochs before and two 10-sec epochs after, 4) the two 10-sec epochs before and three 10-sec epochs after, 5) the one 10-sec epoch before and four 10-sec epochs after, and 6) the five 10-sec epochs that followed (Appendix Tables 1–3). After the CV was calculated for each possible condition, the lowest CV from the six possible strings of 10-sec epochs was used. If this CV was less than or equal to 10%, it was determined that the CV was part of a rhythmic locomotor activity (i.e., walking or running) and the walk/run regression equation was applied to the 10-sec epoch. If the lowest CV was greater than 10%, it was determined that it was part of an intermittent lifestyle activity and the lifestyle equation was applied to the 10-sec epoch. By examining each 10-sec epoch in this manner it could be determined if each 10-sec epoch was part of a continuous walking or running bout lasting 1 minute or longer and the start and finish of that walking/running bout could be determined to the nearest 10 seconds, regardless of where the bout of activity started on the ActiGraph clock. Regression analyses were then used to predict METs from the counts per 10 seconds for the CV ≤ 10 and CV > 10 groups.
Appendix Table 1.
Depiction of how the coefficient of variation (CV) is calculated for six consecutive 10 second epochs within in a minute on the ActiGraph clock for the 2006 Crouter 2-regression model.
| Time | Counts per 10-s | CV (%) |
|---|---|---|
| 13:02:10 | 918 | 1.670 |
| 13:02:20 | 907 | |
| 13:02:30 | 936 | |
| 13:02:40 | 923 | |
| 13:02:50 | 927 | |
| 13:03:00 | 893 | |
| 13:03:10 | 858 | 60.204 |
| 13:03:20 | 877 | |
| 13:03:30 | 421 | |
| 13:03:40 | 0 | |
| 13:03:50 | 556 | |
| 13:04:00 | 996 | |
CV = standard deviation ÷ mean * 100
Appendix Table 3.
Depiction of how the coefficient of variation (CV) is calculated for six 10 second epochs for the 2006 Crouter 2-regression model and refined 2-regression model.
| Time | Counts per 10-s |
CV for 2006 Crouter 2- regression model |
CV Forward 5 |
CV Backward 5 |
CV back 1 forward 4 |
CV back 2 forward 3 |
CV back 3 forward 2 |
CV back 4 forward 1 |
Lowest CV |
|---|---|---|---|---|---|---|---|---|---|
| 13:02:10 | 918 | 1.670 | 1.67 | 1.67 | |||||
| 13:02:20 | 907 | 3.15 | 1.67 | 1.67 | |||||
| 13:02:30 | 936 | 3.46 | 3.15 | 1.67 | 1.67 | ||||
| 13:02:40 | 923 | 23.95 | 3.46 | 3.15 | 1.67 | 1.67 | |||
| 13:02:50 | 927 | 56.65 | 23.95 | 3.46 | 3.15 | 1.67 | 1.67 | ||
| 13:03:00 | 893 | 58.76 | 1.67 | 56.65 | 23.95 | 3.46 | 3.15 | 1.67 | |
| 13:03:10 | 858 | 60.204 | 60.2 | 3.15 | 58.76 | 56.65 | 23.95 | 3.46 | 3.15 |
| 13:03:20 | 877 | 69.24 | 3.46 | 60.2 | 58.76 | 56.65 | 23.95 | 3.46 | |
| 13:03:30 | 421 | 23.95 | 60.2 | 58.76 | 56.65 | 23.95 | |||
| 13:03:40 | 0 | 56.65 | 60.2 | 58.76 | 56.65 | ||||
| 13:03:50 | 556 | 58.76 | 60.2 | 58.76 | |||||
| 13:04:00 | 996 | 60.2 | 60.2 |
CV = standard deviation ÷ mean * 100; Use of the 2006 Crouter 2-regression model results in a 60 second walking bout (13:02:10 to 13:03:00), however using the refined 2-regression model shows that the walking bout was 80 seconds long (13:02:10 to 13:03:20).
A one-way repeated measures ANOVA was used to compare actual and predicted METs (2006 Crouter 2-regression model and refined 2-regression model) for each activity using the cross-validation group. In addition, a one-way repeated measures ANOVA was used to compare actual and predicted METs for all 18 activities combined. Pairwise comparisons with Bonferroni adjustments were performed to locate significant differences when necessary.
Modified Bland-Altman Plots were used to graphically show the variability in individual error scores (actual METs minus estimated METs) (2). This allowed for the mean error score and the 95% prediction interval to be shown. Devices that display a tight prediction interval around zero are deemed accurate. Data points below zero signify an overestimation, while points above zero signify an underestimation.
Results
Data for one participant in the developmental group (routine 3) were missing due to an error that occurred during the downloading process.
Similar to the 2006 Crouter 2-regression model, for activities with a CV ≤ 10% (walking and running) an exponential curve was used for the refined 2-regression model. For activities where the CV was > 10%, however, a cubic curve was used for the natural log (Ln) of the counts˙10 sec−1. For the inactivity threshold we propose using a threshold of 8 counts˙10 sec−1, which approximates the threshold of 50 counts˙min−1 used with the 2006 2-regression model (7), to distinguish inactivity (e.g., sitting and lying) from light activity. Thus, when the value is ≤ 8 counts˙10 sec−1, an individual will be credited with 1.0 MET, since this more accurately predicts these sedentary activities.
The refined 2-regression model to predict gross energy expenditure (METs) from the ActiGraph counts would consist of three parts (2-regression model with an inactivity threshold);
If the counts˙10 sec−1 are ≤ 8, energy expenditure = 1.0 MET,
-
If the counts˙10 sec−1 are > 8
and the CV of the counts per 10 sec are ≤ 10, then energy expenditure (METs) = 2.294275 * (exp(0.00084679 * ActiGraph counts˙10 sec−1)) (R2 = 0.739; SEE = 0.250),
or the CV of the counts per 10 sec are > 10, then energy expenditure (METs) = 0.749395 + (0.716431 * (Ln(ActiGraph counts˙10 sec−1))) – (0.179874 * (Ln(ActiGraph counts˙10 sec−1))2) + (0.033173 * (Ln(ActiGraph counts˙10 sec−1))3) (R2 = 0.840; SEE = 0.863)
Finally, once a MET value has been calculated for each 10 sec epoch within a minute on the ActiGraph clock, the average MET value of 6 consecutive 10-sec epochs within each minute is calculated to obtain the average MET value for that minute (see Appendix Table 4).
Appendix Table 4.
Depiction of how METs are calculated using the 2006 Crouter 2-regressin model and the refined 2-regression model.
| Time | Counts per 10-s |
2006 CV |
CV Forward 5 |
CV Back 5 |
CV back 1 forward 4 |
CV back 2 forward 3 |
CV back 3 forward 2 |
CV back 4 forward 1 |
Lowest CV |
2006 Crouter 2- regression model METs |
Refined 10 second MET Value |
Refined Average MET value for minute |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 13:02:10 | 918 | 1.670 | 1.67 | 1.67 | 5.01 | 4.99 | 4.99 | |||||
| 13:02:20 | 907 | 3.15 | 1.67 | 1.67 | 4.95 | |||||||
| 13:02:30 | 936 | 3.46 | 3.15 | 1.67 | 1.67 | 5.07 | ||||||
| 13:02:40 | 923 | 23.95 | 3.46 | 3.15 | 1.67 | 1.67 | 5.01 | |||||
| 13:02:50 | 927 | 56.65 | 1.17 | 23.95 | 3.46 | 3.15 | 1.67 | 1.17 | 5.03 | |||
| 13:03:00 | 893 | 58.76 | 1.67 | 56.65 | 23.95 | 3.46 | 3.15 | 1.67 | 4.89 | |||
| 13:03:10 | 858 | 60.204 | 60.2 | 3.15 | 58.76 | 56.65 | 23.95 | 3.46 | 3.15 | 6.95 | 4.74 | 5.15 |
| 13:03:20 | 877 | 3.46 | 60.2 | 58.76 | 56.65 | 23.95 | 3.46 | 4.82 | ||||
| 13:03:30 | 421 | 23.95 | 60.2 | 58.76 | 56.65 | 23.95 | 5.83 | |||||
| 13:03:40 | 0 | 56.65 | 60.2 | 58.76 | 56.65 | 1.00 | ||||||
| 13:03:50 | 556 | 58.76 | 60.2 | 58.76 | 6.47 | |||||||
| 13:04:00 | 996 | 60.2 | 60.2 | 8.04 |
For the 2006 Crouter 2-regression model a MET value is calculated for each minute on the ActiGraph clock, based on the coefficient of variation (CV) of the six consecutive 10-sec epochs for that minute. For the refined 2-regression model the MET value is calculated for each 10-sec epoch, based on the lowest CV for that 10-sec epoch and all combinations of the surrounding five 10-sec epochs, and then an average MET value is calculated for each minute.
Table 2 shows the measured METs and estimated METs for the cross-validation group using the 2006 Crouter 2-regression model and the refined 2-regression model. The 2006 Crouter 2-regression model and refined 2-regression model were within 0.75 and 0.89 METs, respectively of mean measured METs for all activities (P > 0.05), except cycling (P < 0.05). For the slow walk, racquetball, and slow run, there were small but significant differences between the 2006 Crouter 2-regression model and the refined 2-regression model. In addition, the correlation between the predicted METs from the refined 2-regression model and measured METs was high (r = 0.97; P < 0.001), which was similar to the correlation between the 2006 2-regression model and measured METs (r = 0.96; P < 0.001).
Table 2.
Energy expenditure (METS) of the cross-validation group for the Cosmed K4b2, the 2006 Crouter 2-regression model and the refined 2-regression model, during various activities.
| Cosmed K4b2 measured values |
2006 Crouter 2-regression model |
Refined 2-regression model | |||
|---|---|---|---|---|---|
| Mean (SD) | Mean (SD) | RMSE | Mean (SD) | RMSE | |
| Lying | 0.91 (0.20) | 1.00 (0.00) | 0.20 | 1.00 (0.00) | 0.20 |
| Standing | 1.19 (0.18) | 1.00 (0.00) | 0.25 | 1.00 (0.00) | 0.25 |
| Computer Work | 1.03 (0.13) | 1.00 (0.00) | 0.12 | 1.00 (0.00) | 0.12 |
| Filing papers | 1.56 (0.16) | 1.30 (0.67) | 0.60 | 1.51 (0.70) | 0.70 |
| Ascending/ Descending Stairs | 6.83 (0.65) | 6.08 (1.29) | 1.18 | 5.94 (1.18) | 1.21 |
| Cycling (avg. 79 watts)a | 5.70 (1.25) | 1.93 (1.28)* | 4.17 | 2.01 (1.40)* | 4.13 |
| Slow walk (avg. 85 m˙min−1) | 3.33 (0.32) | 3.73 (0.42) | 0.51 | 3.66 (0.43)# | 0.47 |
| Fast walk (avg. 100 m˙min−1) | 4.41 (0.82) | 4.71 (0.58) | 0.57 | 4.68 (0.60) | 0.55 |
| Basketball | 7.33 (0.52) | 7.89 (0.99) | 0.76 | 7.51 (0.76) | 0.38 |
| Racquetball | 6.63 (0.46) | 7.29 (0.64) | 0.97 | 6.99 (0.49)# | 0.70 |
| Slow run (avg. 159 m˙min−1) | 8.06 (0.63) | 7.76 (0.96) | 1.04 | 7.87 (1.02)# | 1.05 |
| Fast run (avg. 179 m˙min−1) | 9.41 (1.63) | 8.34 (1.13) | 1.29 | 8.29 (1.43) | 1.31 |
| Vacuum | 3.37 (0.51) | 3.58 (0.76) | 1.39 | 3.75 (0.86) | 1.30 |
| Sweep/mop | 3.32 (0.56) | 3.26 (0.61) | 0.35 | 3.33 (0.91) | 0.52 |
| Washing windows | 2.86 (0.93) | 2.86 (0.40) | 0.52 | 2.79 (0.62) | 0.36 |
| Washing Dishes | 1.98 (0.33) | 1.61 (0.83) | 0.86 | 1.45 (0.64) | 0.80 |
| Lawn Mowing | 6.06 (0.59) | 5.50 (0.73) | 0.83 | 5.60 (0.58) | 0.70 |
| Raking grass/leaves | 3.69 (0.89) | 3.73 (0.66) | 0.27 | 3.90 (0.91) | 0.30 |
| Average for all activities without cycling | 4.23 (2.68) | 4.15 (2.62) | 0.69 | 4.13 (2.57) | 0.64 |
| Average for all activities with cycling | 4.31 (2.63) | 4.03 (2.61) | 0.88 | 4.02 (2.56) | 0.84 |
RMSE, root mean square error.
Significantly different from Cosmed K4b2 (P < 0.05),
Significantly different from 2006 Crouter 2-regression model (P < 0.05),
Cycling was not included for the development of the 2006 or refined 2-regression models.
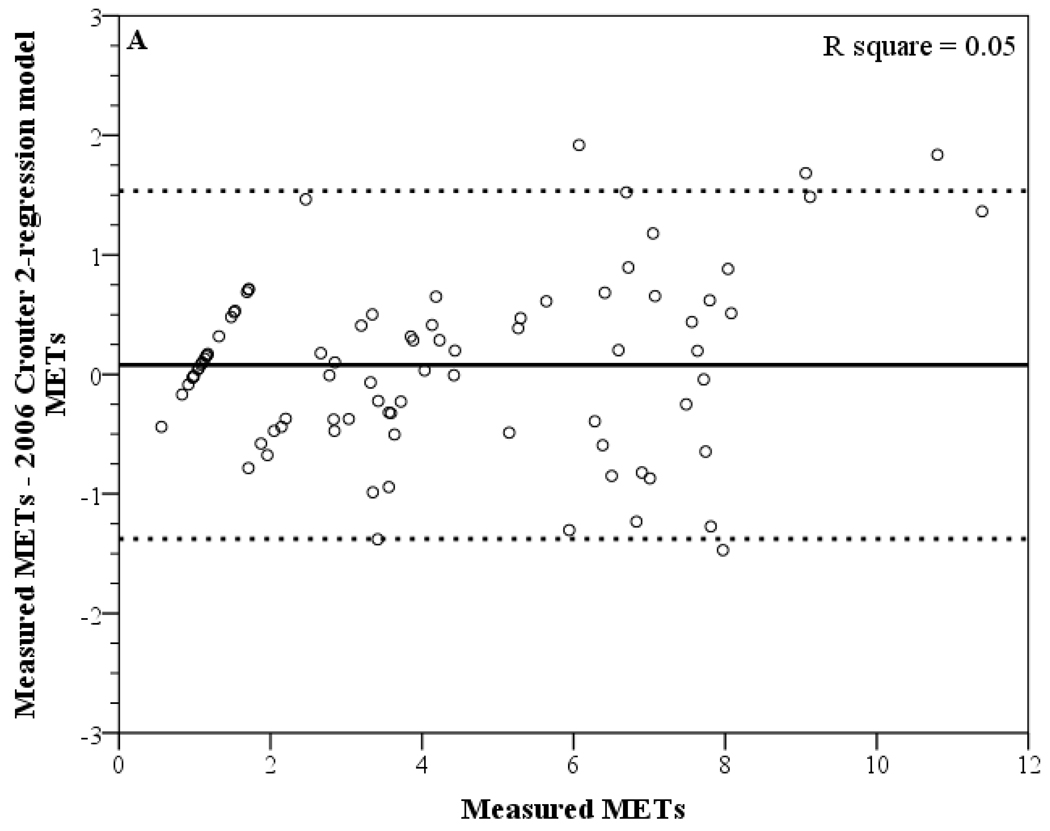
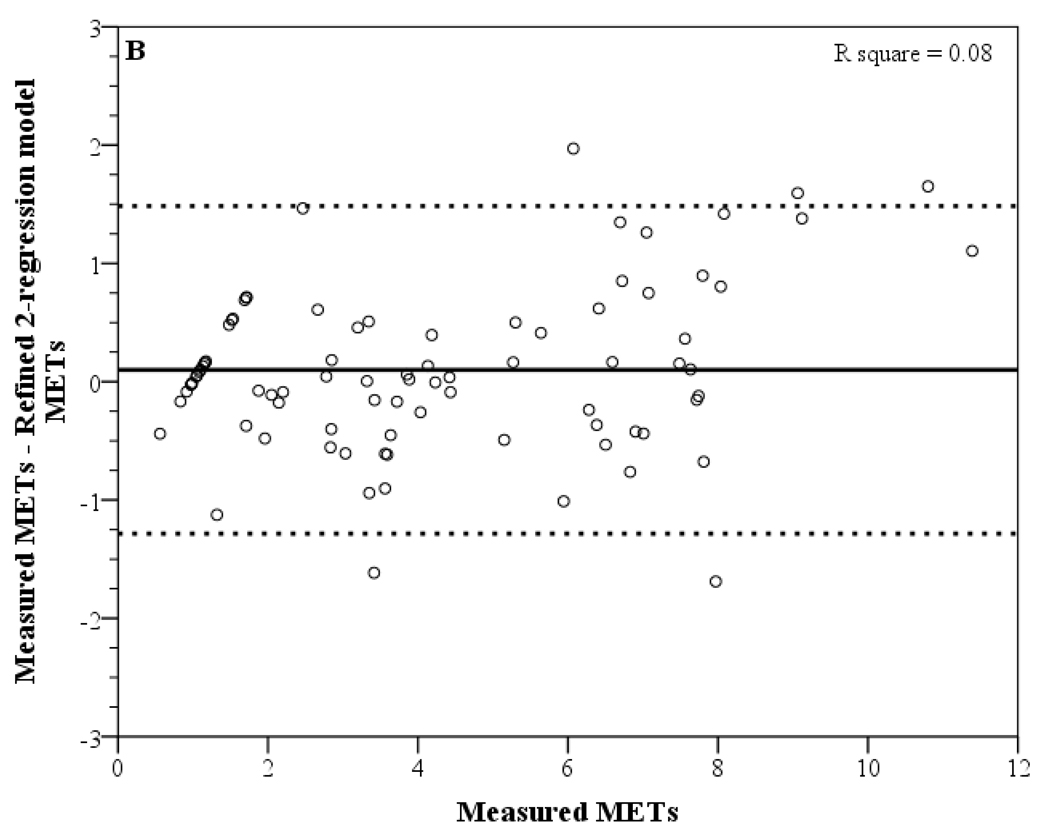
The Bland-Altman plots show that the 2006 Crouter 2-regression model and the refined 2-regression model had similar accuracy during structured 10-minute bouts (Figure 1). The refined 2-regression model had a mean bias of 0.10 METs [95% prediction interval (% PI); −1.28, 1.48], while the 2006 Crouter 2-regression model had a mean bias of 0.08 METs (95% PI; −1.38, 1.54). Similar accuracy between the 2006 Crouter 2-regression model and the refined 2-regression model was also confirmed by the differences in the root mean square error (RMSE) values. The RMSE values between the 2006 and refined 2-regression models were not significantly different (P > 0.1).
Figure 1.
Bland-Altman plots depicting error scores (actual minus estimation) for (A) the 2006 Crouter 2-regression model and (B) the refined 2-regression model. Solid line represents the mean and dashed lines represent the 95% prediction interval of the observations. Cycling is not included in these graphs.
Discussion
This study describes a refinement to the 2006 2-regression model to predict EE using the ActiGraph accelerometer. The refined 2-regression model examines each 10-sec epoch and the surrounding five 10-sec epochs to determine if the 10-sec epoch is part of a continuous walking/running bout lasting 1 minute or longer. In addition, the refined 2-regresison model estimates EE every 10-seconds. These changes were needed to eliminate the misclassification of walking/running activity and overestimation of EE when walking/running bouts started and stopped in the middle of a minute on the ActiGraph clock, which was a limitation of the 2006 Crouter 2-regression model. Lastly, the refined 2-regression model has similar accuracy and precision as the 2006 Crouter 2-regression model during structured activities.
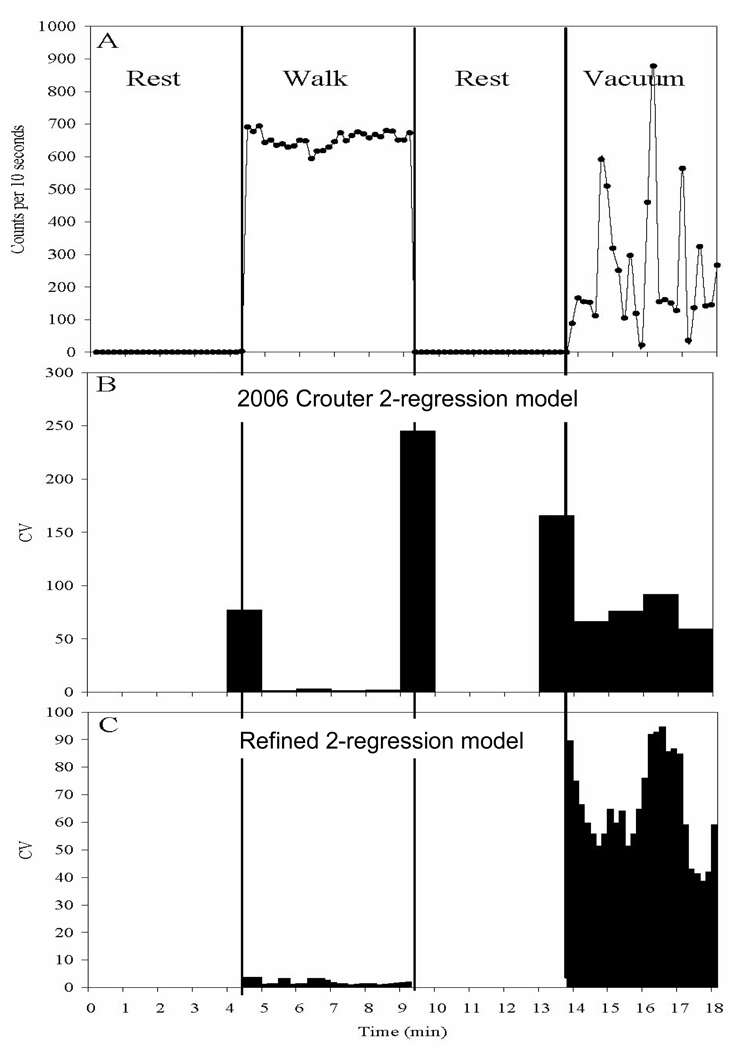
The 2006 Crouter 2-regression model provided a significant improvement for estimating EE compared to single linear regression models (7), but the 2006 method was developed on 10-min structured bouts of physical activity that always started exactly in synchronization with the ActiGraph clock. We later found that when a walking bout started in the middle of a minute, it was incorrectly classified as intermittent lifestyle activity for that minute due to the high CV (11). Thus, the refined 2-regression model was developed to overcome this issue by examining each 10-sec epoch, and the surrounding five 10-sec epochs. Figure 2 shows an example of 3 different activities, with the transitions from one activity to the next occurring in the middle of a minute on the ActiGraph clock. It can be seen that with the 2006 Crouter 2-regression model, the transitional minutes from rest to walk, walk to rest, and rest to vacuuming have much higher CVs than the other minutes for each respective activity (Figure 2b). This is due to there being a mixture of rest and the activity of interest, and is not a true reflection of the type of activity performed. With the refined 2-regression model, the CV is calculated for each 10-sec epoch, thus when the transition from one activity to the next occurs, the new activity can be detected within 10-seconds resulting in an improved ability to recognize the general type of activity performed (Figure 2c).
Figure 2.
A) Counts per 10 seconds for three activities, which start and stop in the middle of a minute, resembling how free-living data would appear. B) The coefficient of variation (CV) of six 10-sec epochs over a minute period using the 2006 Crouter 2-regression model. (Note that the first and final minutes of the walking bout would be misclassified as lifestyle physical activity since CV>10.) C) CV of six 10-sec epochs over a minute period using the refined 2-regression method.
The refined 2-regression model has some distinct differences from the original 2006 Crouter 2-regression model that should be discussed. The major change is that the CV and METs are calculated for each 10-sec epoch, which has several implications. First, the inactivity threshold is now examined for each 10 second epoch; therefore when the counts per 10 seconds are ≤ 8 the individual is credited with 1.0 MET, whereas when using the 2006 2-regression model an inactivity threshold of ≤ 50 counts˙min−1 was used. Second, with the 2006 2-regression model, the CV was examined for six consecutive 10-sec epochs within each minute on the ActiGraph clock, which did not take into consideration changing of activities that may occur within the minute on the ActiGraph clock. The refined 2-regression model now examines each 10-sec epoch and all combinations of the surrounding five 10-sec epochs. By examining all combinations of the surrounding five 10-sec epochs it can be determined if each 10-sec epoch is part of a continuous walking/running bout regardless of where it starts on the ActiGraph clock. Third, the refined 2-regression model uses the natural log of the counts per 10-seconds for the cubic equation used to predict METs for the lifestyle equation.
The refined 2-regression model has important improvements over the 2006 Crouter 2-regression model. First, the refined method provides a closer estimate of EE to measured EE during free-living activities. Recently we have shown that the refined 2-regression model significantly improved upon the 2006 Crouter 2-regression model for estimating METs and time spent in light, moderate, and vigorous physical activity during 6-hrs of free-living activity (8). Specifically, the refined 2-regression model predicted on average a mean (SD) of 2.09 (1.5) METs for the 6-hr period compared to a mean of 2.33 (1.6) METs for the 2006 Crouter 2-regression model and 1.91 (1.2) METs for indirect calorimetry. In addition, the 2006 Crouter 2-regression model and the Freedson, Hendelman, and Swartz equations were all significantly different from indirect calorimetry for time spent in light, moderate, and vigorous physical activity while the refined 2-regression equation was not significantly different. Specifically, the measured time in MVPA was 51.6 (56.3) minutes during the 6-hr period, while the refined 2-regression model predicted 74.4 (62.8) minutes and the 2006 Crouter 2-regression model predicted 94.9 (70.5) minutes. Since individuals start and stop activities at will in a free-living environment most of these transitions would occur part-way through a minute on the ActiGraph clock. Thus, the 2006 Crouter 2-regression model would frequently misclassify the first and last minutes of walking/running bouts as intermittent lifestyle activity, resulting in an overestimation of EE. The refined method should correct this overestimation and provide a closer estimate of actual EE during free-living activity.
A second improvement is that the refined equation allows for walking/running bouts as brief as 1 minute in duration to be detected, whereas with the 2006 Crouter 2-regression model, if a walking bout started in the middle of a minute it would need to be at least 2 minutes long to be detected. It should be noted, however, that METs are predicted every 10-seconds and walking/running bouts could be estimated to the nearest 10-seconds with the refined 2-regression model, which becomes important considering that the majority of activities performed in a free-living setting will not start and stop exactly in synchronization with the beginning and end of a minute on the ActiGraph clock. Thus, while the bout duration needed to detect a walking bout for the refined and 2006 2-regression models is not drastically different, the ability to detect when the walking/running bout started to the nearest 10-sec using the refined 2-regression model is an important improvement.
For reporting purposes, we have chosen to average the MET values each minute on the ActiGraph clock for a single summary MET value for each minute of activity, but researchers should not feel this is the only way to present energy expenditure using this equation. For each 10-sec epoch a CV and MET value are calculated, thus depending on the outcomes of interest the METs could be reported in different ways. For example, if one was interested in only walking behavior, an individual could choose to average the MET values during the walking bouts, rather than each minute, to get an average MET value for the walking bouts. Based on preliminary results from a separate study in which 57 females wore an ActiGraph accelerometer for five days, the refined 2-regression model predicted 26.1 (17.1) minutes per day of continuous moderate and vigorous walking/running compared to 18.1 (13.9) minutes per day for the 2006 Crouter 2-regression model (unpublished data). This translates into 8.0 minutes of continuous walking/running time being misclassified as lifestyle activity with the 2006 Crouter 2-regression model. Assuming an average count per minute value of 4000, this would mean that the 2006 Crouter 2-regression model would overestimate the misclassified minutes by approximately 3.5 METs per minute. Future research should investigate these issues to better understand how the data should be reported.
In conclusion, the refined 2-regression model, which examines each 10-second epoch and all combinations of the surrounding five 10-secound epochs, improves upon the 2006 Crouter 2-regression model. The refined 2-regression model examines each 10-second interval and determines whether it is part of a string of six consecutive 10-s epochs with consistent accelerometer counts. It then predicts the energy expenditure (METs) of the 10-second bout based upon a regression equation representing either intermittent, lifestyle activity or rhythmic locomotion and eliminates the misclassification of transitional minutes when activities change, with the greatest effect seen on the transition between rest and walking/running bouts that start and stop part way through a minute. In addition, the refined 2-regression model has similar accuracy to the 2006 Crouter 2-regression model for predicting MET values of structured bouts of activity. Further research is needed to validate the refined 2-regression model in free-living environments.
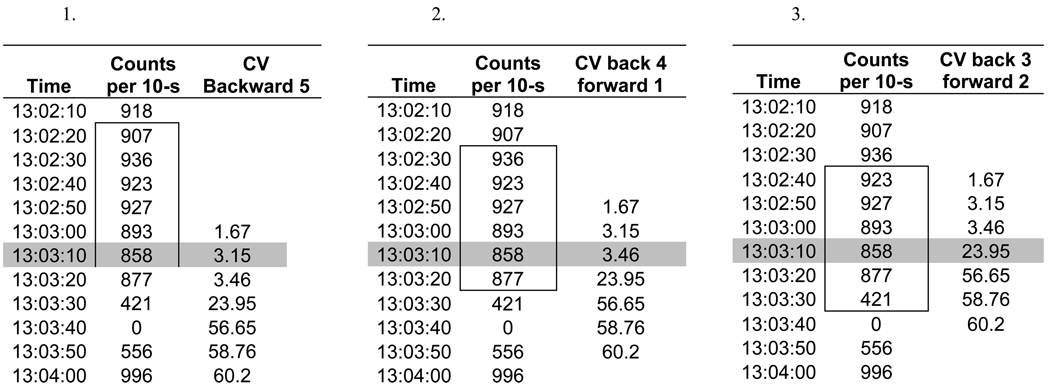
Appendix Table 2.
Depiction of how the coefficient of variation (CV) is calculated for six 10 second epochs for the refined 2-regression model. Each 10-second epoch and the surrounding five 10-sec epochs were examined in the following manner: 10-sec epoch of interest and 1) the five 10-sec epochs before, 2) the four 10-sec epochs before and one 10-sec epoch after, 3) the three 10-sec epochs before and two 10-sec epochs after, 4) the two 10-sec epochs before and three 10-sec epochs after, 5) the one 10-sec epoch before and four 10-sec epochs after, and 6) the five 10-sec epochs that followed.
 |
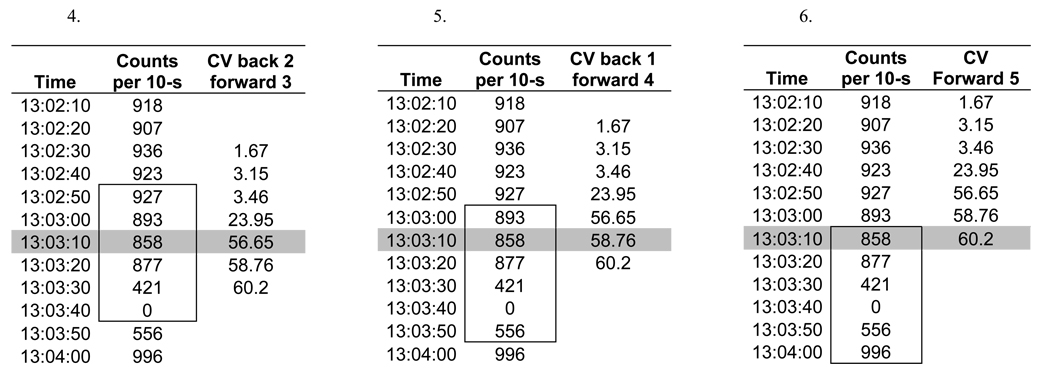 |
CV = standard deviation ÷ mean * 100; For demonstration, the same data is used as is presented in appendix table 1 and the 10 second epoch at 13:03:10 is used as a common reference point in all tables and the data used to calculate the CV for the epoch is boxed in. The CV is calculated for each 10 second epoch and the surrounding five 10 second epochs and the lowest CV from each calculation is used for that 10 second epoch.
Acknowledgements
This research was supported by the Charlie and Mai Coffey Endowment in Exercise Science and NIH Grant 01R21 CA122430-01. No financial support was received from any of the activity monitor manufacturers, importers, or retailers. The results of the present study do not constitute endorsement by ACSM.
References
- 1.Bassett DR, Jr, Ainsworth BE, Swartz AM, Strath SJ, O'Brien WL, King GA. Validity of four motion sensors in measuring moderate intensity physical activity. Med Sci Sports Exerc. 2000;32(9 Suppl):S471–S480. doi: 10.1097/00005768-200009001-00006. [DOI] [PubMed] [Google Scholar]
- 2.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet North Am Ed. 1986;1:307–310. [PubMed] [Google Scholar]
- 3.Brage S, Wedderkopp N, Franks PW, Andersen LB, Froberg K. Reexamination of validity and reliability of the CSA monitor in walking and running. Med Sci Sports Exerc. 2003;35(8):1447–1454. doi: 10.1249/01.MSS.0000079078.62035.EC. [DOI] [PubMed] [Google Scholar]
- 4.Crouter SE, Bassett DR., Jr A New 2-regression Model for the Actical Accelerometer. Br J Sports Med. 2008;42(3):217–224. doi: 10.1136/bjsm.2006.033399. [DOI] [PubMed] [Google Scholar]
- 5.Crouter SE, Churilla JR, Bassett DR., Jr Estimating energy expenditure using accelerometers. Eur J Appl Physiol. 2006;98(6):601–612. doi: 10.1007/s00421-006-0307-5. [DOI] [PubMed] [Google Scholar]
- 6.Crouter SE, Churilla JR, Bassett DR., Jr Accuracy of the Actiheart for the assessment of energy expenditure in adults. Eur J Clin Nutr. 2008;62:704–711. doi: 10.1038/sj.ejcn.1602766. [DOI] [PubMed] [Google Scholar]
- 7.Crouter SE, Clowers KG, Bassett DR., Jr A novel method for using accelerometer data to predict energy expenditure. J Appl Physiol. 2006;100(4):1324–1331. doi: 10.1152/japplphysiol.00818.2005. [DOI] [PubMed] [Google Scholar]
- 8.Crouter SE, DellaValle DM, Kuffel E, Frongillo EA, Haas JD, Bassett DR., JR Validity of Accelerometry During Free-Living Activity [Abstract] Med Sci Sports Exerc. 2009;41:S129. [Google Scholar]
- 9.Freedson PS, Melanson E, Sirard J. Calibration of the Computer Science and Applications, Inc. accelerometer. Med Sci Sports Exerc. 1998;30(5):777–781. doi: 10.1097/00005768-199805000-00021. [DOI] [PubMed] [Google Scholar]
- 10.Hendelman D, Miller K, Baggett C, Debold E, Freedson P. Validity of accelerometry for the assessment of moderate intensity physical activity in the field. Med Sci Sports Exerc. 2000;32(9 Suppl):S442–S449. doi: 10.1097/00005768-200009001-00002. [DOI] [PubMed] [Google Scholar]
- 11.Kuffel EE, Crouter SE, Haas JD, Frongillo EA, Bassett DR., JR Validity of estimating minute-by-minute energy expenditure with accelerometry (abstract) Med Sci Sports Exerc. 2008;40:S415. [Google Scholar]
- 12.Leenders NY, Nelson TE, Sherman WM. Ability of different physical activity monitors to detect movement during treadmill walking. Int J Sports Med. 2003;24(1):43–50. doi: 10.1055/s-2003-37196. [DOI] [PubMed] [Google Scholar]
- 13.McLaughlin JE, King GA, Howley ET, Bassett DR, Jr, Ainsworth BE. Validation of the COSMED K4b2 portable metabolic system. Int J Sports Med. 2001;22(4):280–284. doi: 10.1055/s-2001-13816. [DOI] [PubMed] [Google Scholar]
- 14.Nichols JF, Morgan CG, Chabot LE, Sallis JF, Calfas KJ. Assessment of physical activity with the Computer Science and Applications, Inc., accelerometer: laboratory versus field validation. Res Q Exerc Sport. 2000;71(1):36–43. doi: 10.1080/02701367.2000.10608878. [DOI] [PubMed] [Google Scholar]
- 15.Swartz AM, Strath SJ, Bassett DR, Jr, O'Brien WL, King GA, Ainsworth BE. Estimation of energy expenditure using CSA accelerometers at hip and wrist sites. Med Sci Sports Exerc. 2000;32(9 Suppl):S450–S456. doi: 10.1097/00005768-200009001-00003. [DOI] [PubMed] [Google Scholar]
- 16.Yngve A, Nilsson A, Sjostrom M, Ekelund U. Effect of monitor placement and of activity setting on the MTI accelerometer output. Med Sci Sports Exerc. 2003;35(2):320–326. doi: 10.1249/01.MSS.0000048829.75758.A0. [DOI] [PubMed] [Google Scholar]