Bayesian Variable Selection for Multivariate Spatially-Varying Coefficient Regression

Summary

Physical activity has many well-documented health benefits for cardiovascular fitness and weight control. For pregnant women, the American College of Obstetricians and Gynecologists currently recommends 30 minutes of moderate exercise on most, if not all, days; however, very few pregnant women achieve this level of activity. Traditionally, studies have focused on examining individual or interpersonal factors to identify predictors of physical activity. There is a renewed interest in whether characteristics of the physical environment in which we live and work may also influence physical activity levels. We consider one of the first studies of pregnant women that examines the impact of characteristics of the built environment on physical activity levels. Using a socioecologic framework, we study the associations between physical activity and several factors including personal characteristics, meteorological/air quality variables, and neighborhood characteristics for pregnant women in four counties of North Carolina. We simultaneously analyze six types of physical activity and investigate cross-dependencies between these activity types. Exploratory analysis suggests that the associations are different in different regions. Therefore we use a multivariate regression model with spatially-varying regression coefficients. This model includes a regression parameter for each covariate at each spatial location. For our data with many predictors, some form of dimension reduction is clearly needed. We introduce a Bayesian variable selection procedure to identify subsets of important variables. Our stochastic search algorithm determines the probabilities that each covariate’s effect is null, non-null but constant across space, and spatially-varying. We found that individual level covariates had a greater influence on women’s activity levels than neighborhood environmental characteristics, and some individual level covariates had spatially-varying associations with the activity levels of pregnant women.

1. Introduction

A recent population-based study found that while approximately two-thirds of pregnant women reported some leisure activity during pregnancy, less than one-sixth reported meeting the recommendations for activity (Evenson et al., 2004). Physical activity during pregnancy has well-established benefits, including prevention of excess weight gain (Clapp and Little, 1995) and reduced risk of certain complications such as gestational diabetes (Dempsey et al., 2004) and preeclampsia (Saftlas et al.). During pregnancy, women change their activity patterns and tend to adopt more health promoting behaviors (e.g., avoidance of cigarettes or binge drinking). If healthy behavioral patterns established during pregnancy could be maintained afterwards, a woman’s weight status and general health could be improved. There is renewed interest in whether characteristics of the physical environment in which women live and work influence physical activity levels during pregnancy. In this paper we study the associations between six types of moderate to vigorous physical activity and several factors including personal characteristics, meteorological/air quality variables, and neighborhood characteristics for pregnant women in four counties of North Carolina.

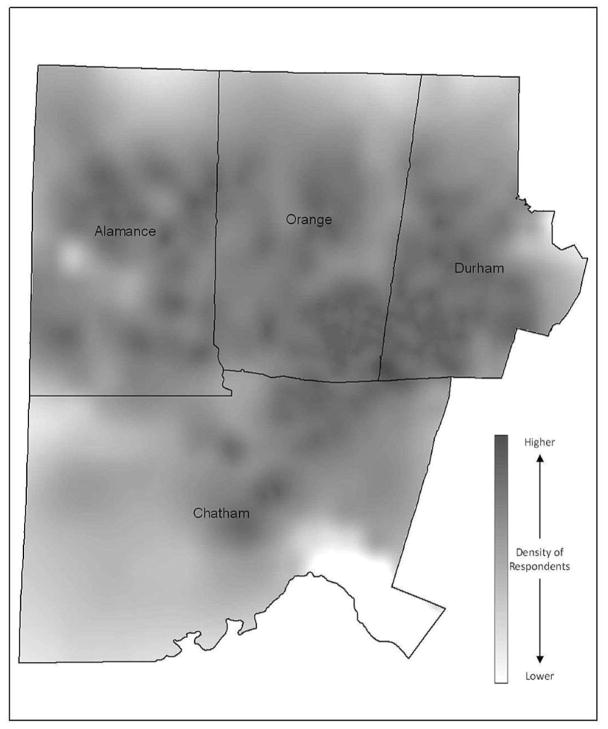
Physical activity patterns are highly dependent on geographic location. Our data includes women from Orange, Durham, Alamance, and Chatham counties in central North Carolina (Figure 1). These counties are quite heterogeneous, with communities ranging from the more urban area of downtown Durham, to the college town of Chapel Hill, to rural areas of Alamance, Chatham, and northern Orange counties. Properly accounting for spatial clustering of the responses is needed to study the effects of our predictors on physical activity (Reich et al., 2006, Hoeting et al., 2006).

Figure 1.

Population density of the PIN3 study participants.

These sources of spatial heterogeneity made investigators suspect that some exposures may have different associations with physical activity in different areas. For example, sidewalks may be more important on busy streets than on quieter ones. Porches on homes in rural areas may be associated with both larger lots and residents more likely to spend considerable time in outdoor household physical activity related to gardening or farm upkeep; however, in Chapel Hill, a porch may be a marker of living in a new urbanist neighborhood development distinguished by homes on smaller lots in an area designed specifically to encourage walking. Identifying spatially-varying effects can both improve the predictive model and also reveal confounders or missing interactions that, when accounted for, can improve our understanding of the effect of these exposures on physical activity. To capture these spatially-varying effects, we extend the spatially-varying coefficient model of Gelfand et al. (2003) to the multivariate setting.

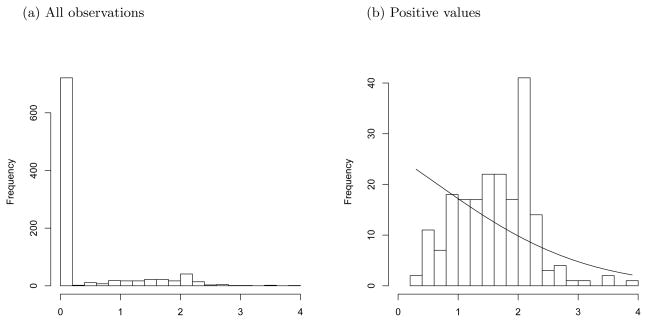
Implementing the multivariate spatially-varying coefficients model for these data is challenging for two reasons: (1) the data are clearly non-Gaussian, with a large proportion of zeros corresponding to women with no moderate to vigorous activity of a given type, and (2) there are 29 predictors, so allowing all of the predictors to have spatially-varying effects leads to an over-parameterized model. Figure 2 plots the transformed (log[activity+1]) transportation activity levels. Nearly 80% of the women in the study reported no transportation-related (e.g., walking or bicycling to destinations) moderate to vigorous physical activity. One approach would be to dichotomize the data and apply spatial logistic or probit regression to the binary responses (e.g., Kelsall and Diggle, 1998; Paciorek, 2007). While this approach would simplify the analysis, it ignores the large differences in the non-zero responses, e.g., the difference between a woman who rides her bike to work compared to a woman who walks uphill to the bus stop. We elect to retain all the information in the data and simultaneously analyze the zero and continuous non-zero responses.

Figure 2.

Plot of log(transportation-related activity +1). The solid line in Panel (b) is the N(−1.82, 2.44) density fit using MLE.

Stein (1992) introduces a truncated normal distribution for spatial data. Exploratory analysis shows that this model is not flexible enough to fit the positive observations and have sufficient mass at zero to accommodate the large proportion of zeros. For example, Figure 2b plots the truncated normal density with parameters estimated using MLE. The estimated truncated normal has nearly 80% of its mass at zero, matching the sample proportion, but the fit above zero is unsatisfactory. Therefore, we develop a zero-inflated spatially-referenced truncated Gaussian model. Zero-inflated models are common for spatial count data (e.g., Agarwal, 2002) and non-spatial semicontinuous data (Olsen and Schafer, 2001; Berk and Lachenbruch, 2002; Albert and Shen, 2005; Zhang et al., 2006) but have not been applied to semicontinuous spatial data. There is an important distinction between our approach and previous non-spatial models for semicontinuous data. These models include two regression coefficients for each predictor: the first is used to model the probability at zero and the second is used to predict the magnitude of the non-zero responses. Our model includes only a single regression coefficient for each predictor, and thus allows both the zero and non-zero observations to inform about the regression coefficients.

To reduce the dimension of the model we develop a stochastic search variable selection (e.g., George and McCulloch, 1993; Chipman, 1996; George and McCulloch, 1997; Mitchell and Beauchamp; 1998) procedure for spatially-varying coefficients. The literature on variable selection for spatial data is limited. Hoeting et al. (2006) and Huang and Chen (2007) propose classical variable selection methods for univariate Gaussian spatial data without spatially-varying coefficients. Smith and Fahrmeir (2007) develop a Bayesian variable selection method for univariate data on a lattice with spatially-varying coefficients. Their approach is to perform local variable selection, that is, to allow for a different subset of the covariates to be included at different lattice points. They use an Ising prior to encourage neighboring lattice points to include similar variables. Our approach differs from Smith and Fahrmeir in several ways. Their model is tailored to univariate Gaussian data on a lattice; our data are multivariate, zero-inflated, and not on a lattice. Also, we take a more global view to variable selection in that we select the same variables throughout the spatial domain but allow some of their effects to vary. Smith and Fahrmeir’s model does not explicitly place prior probability on variables being completely removed from the model or included throughout the spatial domain with the same effect across space. This is appropriate for their analysis of fMRI data in which the objective is to uncover “hot spots” with a small number of covariates. However, in our setting with many variables, encouraging these models is desirable. Our prior gives non-zero mass to three models for each covariate and for each outcome: (1) no association, (2) spatially non-varying association, and (3) spatially-varying association. This allows us to include efficiently a large number of predictors in the model, without forcing each to have a spatially-varying effect. Our hierarchical model encourages variables to be included/excluded consistently across activity types, producing a more interpretable multivariate model.

The paper proceeds as follows. Section 2 describes the PIN3 physical activity data. Section 3 develops the statistical model, the zero-inflated model and variable selection algorithm. Computational details are given in Section 4. The methods are applied in Section 5 to PIN3 data. Section 6 concludes.

2. Description of the data

The third phase of the Pregnancy, Infection, and Nutrition (PIN3) Study recruited pregnant women seeking prenatal care at the University of North Carolina Hospitals. Because of the cachement area of UNC Hospitals, most study women resided in Orange, Durham, Alamance, or Chatham counties in central North Carolina. One aim of the study was to investigate patterns of physical activity during pregnancy. We examine factors related to physical activity during the second trimester of pregnancy in six domains, including recreational activity, work activity, transportation activity, child or adult care activity, and both indoor and outdoor household activities.

Women enrolled in the study were interviewed about their moderate and vigorous activity in the past week. Moderate to vigorous activity was defined in the questionnaire as activity that raised the woman’s heart rate. The questionnaire assessed both frequency and duration of activity in each of the six domains. Intensity of activity was assessed using published metabolic (MET) tables (Ainsworth, 2000). The MET, 1 kilocalorie per kilogram per hour, is defined as the amount of energy the body uses when sitting quietly. Reported activities were converted to MET equivalents based on the published tables. Examples of MET equivalents for activities reported in the PIN3 study include indoor household activities like vacuuming (3.5 METs), outdoor household activities like raking the lawn (4.3 METs), transportation activities like biking less than 10 mph (4.0 METs), or recreational activities such as a swimming slow freestyle laps (7 METs) or running at a 8.5 minute mile pace (11.5 METs). The number of MET minutes per week in each activity domain was then calculated by summing over the activities within each domain, weighted by the duration of each activity reported. For example, a woman who swam slow laps for one hour twice per week (and reported no other recreational activities) would be assigned 7 × 2 × 60 MET minutes of recreational moderate to vigorous activity; a woman who reported biking <10mph to work for 10 minutes each direction 5 days per week would be assigned 4 × (10 + 10) × 5 MET minutes of moderate to vigorous transportation-related activity.

Potential predictors of physical activity during pregnancy include sociodemographic, meteorological, and neighborhood environmental factors. Because women with fewer socioeconomic resources are less likely to meet recommendations for physical activity (Evenson et al., 2004), we include as predictors household income (measured as percent of the poverty line, which adjusts income for the number of household members supported on that income), years of maternal education, marital status (married or unmarried), employment status (working outside the home or not), and an indicator of black race, all of which have been associated with socioeconomic status in the PIN data. Other maternal-level predictors of interest include biologic factors (age in years and body mass index), an indicator of whether the mother is pregnant with her first child (women with previous children may be less likely to have time for recreational activities and more likely to spend time in child care activities), an indicator of diagnosis of gestational diabetes in pregnancy, and an indicator of whether the mother reported smoking cigarettes during pregnancy. Meteorological variables of interest include weekly average ozone (obtained from the US EPA, http://www.epa.gov/ttn/airs/airsaqs/) and weekly average temperature and precipitation (obtained from the National Climate Data Center, http://cdo.ncdc.noaa.gov/CDO/cdo). Meteorological data was taken from the nearest of the six stations in the study area. We use ozone data from ten monitoring locations from the four counties in the study and adjacent counties. Since ozone is fairly homogeneous over space and only one of the ten stations measures ozone year-round, we use the average of the reported ozone values over the ten stations as the daily ozone value. Because women reported activity levels as a weekly summary, it is unclear whether meteorological variables will be as closely related to activity as they would be if daily information on activity were available.

Finally, investigators are also interested in whether activity levels were associated with physical characteristics of the neighborhood built environment, measured at the level of each woman’s street segment (defined as the minimal length of street not intersected by another road; e. g. the length of her block). The neighborhood environment may influence physical activity behavior, though results in the literature have been mixed (Laraia et al. 2007; Yen et al. 1998; Ross, 2000). Although neighborhood quality scales have been developed for urban neighborhoods (Caughy et al. 2001), our exploratory work suggests that these measures, developed in inner-city environments, may be inappropriate for our primarily small-town and rural study area, so that we examine the neighborhood environment through multiple individual-level indicators. These included whether the segment was urban or rural, the speed limit, whether or not the residential units were in good condition, whether or not the grounds were in good condition, whether or not abandoned residential units were present, and whether public spaces on the segment (such as parks) were in poor condition. In addition, raters of each street segment noted whether litter or graffiti were present, whether houses on the street had decorations (e. g. a wreath on the front door), whether borders (like fences or hedges) separated yards from the street, presence of signs (including neighborhood entrance signs and crime watch signs), whether most homes had porches, whether people were visible in their yards or along the street, whether there were playgrounds on the street segment, and whether a sidewalk was present along the segment. Descriptive statistics for these predictors for the n = 921 participants are presented in Table 1.

Table 1.

Summary statistics for the predictor variables in PIN3 data. Only the sample mean (proportion) is given for binary variables.

Variable	Mean	SD	Variable	Mean	SD
Percent of poverty line	440.02	218.38	Bad residential units	0.04	–
Maternal education	16.18	2.75	Bad residential kept grounds	0.10	–
Black	0.15	–	Abandoned residential units	0.02	–
Married	0.82	–	Bad public spaces	0.07	–
Age (years)	29.72	4.58	Litter	0.44	–
First birth	0.49	–	Graffiti	0.02	–
Body mass index (BMI)	25.12	6.38	Decoration	0.78	–
Gestational diabetes	0.04	–	Border	0.26	–
Smoker	0.08	–	Entrance sign	0.12	–
Working	0.71	–	Crime watch	0.08	–
Ozone (ppb)	27.8	10.4	Porches	0.78	–
Temperature (F)	59.46	15.25	People	0.39	–
Precipitation (In)	0.13	0.14	Playground	0.05	–
Urban	0.70	–	Sidewalk	0.35	–
Speed limit (MPH)	28.67	8.39

3. Variable selection for the multivariate spatially-varying coefficient model

Because the observed physical activity has a high proportion of zeros (Figure 2), we use a truncated normal model. However, exploratory analysis suggests that there is more mass at zero than can be accounted for by the truncated normal model. Section 3.1 introduces a zero-inflated truncated normal model for these data. Section 3.2 describes the spatially-varying coefficients model relating the predictors to physical activity, and Section 3.3 proposes a Bayesian variable selection algorithm to search for the subset of the predictors best fitting the data.

3.1 Zero-inflated truncated normal spatial model

Let y_li be the observed activity level of type l for subject i with spatial location (lat/long of residence) s_i, l = 1, …, k and i = 1, …, n. We assume

$$y_{li}=\{\begin{array}{ll}0\hfill & \text{with}\text{probability}{p}_l\hfill \\ z_{li}^{+}\hfill & \text{with}\text{probability}1-p_l,\hfill \end{array}$$ (1)

where z_li ∈ ℛ is a latent variable, $z_{li}^{+}=max(0,z_{li})$, and p_l ~ Unif(0,1) is the additional mass at zero for activity type l that can not be explained by the truncated normal model. An extension of this model would allow the probability p_l to vary with individual; however, the probability of no activity under the proposed model is

$$\text{Prob}(y_{li}=0)=p_l+(1-p_l)\ast \text{Prob}(z_{li}\le 0),$$ (2)

so although p_l is constant across individuals, Prob(y_li = 0) is not. We assume p_l is constant across individuals to avoid identifiability problems.

To account for potential correlation between activity types, we model the latent process as multivariate normal

$$z_{li}={\mu }_{li}+{\epsilon }_{li},$$ (3)

where μ_li is the spatially-varying mean, the errors are (ε_1i, …, ε_ki)′ ~ N(0,Σ^e), and Σ^e ~ InvWishart(k + 0.1, 0.1I) is the k × k cross-covariance matrix. Since the mass at zero in (2) depends on z_li’s density, both non-zero and zero observations provide information about the mean μ_li and covariance Σ^e.

3.2 Spatially-varying coefficients model

Spatial correlation and covariate effects are modelled in the mean using the spatially-varying coefficient model of Gelfand et al. (2003),

$${\mu }_{li}=\sum _{j=0}^p{x}_{ji}{\beta }_{lj}({\text{s}}_i)$$ (4)

where x_0i = 1 for all i, x_ji is the value of the j^th covariate for subject i, and β_lj(s_i) is the corresponding regression parameter for activity type l. The spatially-varying coefficient model allows the regression parameters for the j^th covariate and l^th activity type, β_lj = β_lj(s₁), …, β_lj (s_n))′, to be different in different locations. The regression coefficients are taken to be independent across covariates, but correlated across activity type because it is likely that covariates have a similar effect on multiple activity types. We assume ${\mathit{\beta }}_j=({\mathit{\beta }}_{1j}^{\prime },\dots ,{\mathit{\beta }}_{kj}^{\prime }{)}^{\prime }$ is a Gaussian process with mean θ_j ⊗ 1_n and separable covariance

$$\mathit{Cov}({\mathit{\beta }}_j)=K_j\otimes {\mathrm{\sum }}_j^s,$$

where θ_j = (θ_1j, …, θ_kj)′, the scalar θ_lj is the spatial average of β_lj, 1_n is the n-vector of ones, K_j is the n × n spatial correlation matrix, and ${\mathrm{\sum }}_j^s$ is the k × k covariance matrix that controls the cross-covariance between activity types. We select a separable prior for computational convenience. Also, since most covariates are included as spatially-varying with high probability for a small subject of the activity types, identifying more complicated spatial structures would be difficult.

We assume the Matern spatial correlation (Handcock and Wallis, 1994), that is, the (i, i′)^th element of K_j is

$$\frac{{(2{\nu }_j^{1/2}||s_i-s_{i^{\prime }}||/{\rho }_j)}^{{\nu }_j}}{2^{{\nu }_j-1}\mathrm{\Gamma }({\nu }_j)}{B}_{{\nu }_j}(2{\nu }_j^{1/2}||s_i-s_{i^{\prime }}||/{\rho }_j),$$

where B_νj is the modified Bessel function. The Matern correlation has two parameters: ν_j controls the smoothness (i.e., the degree of differentiability) of the process and ρ_j controls the range of spatial correlation. If ν_j = 0.5 we have the exponential correlation exp(||s_i − s_i′||/ρ_j), and if ν_j = ∞ we have the squared-exponential correlation $exp({\left|\right|s_i-s_{i^{\prime }}\left|\right|}^2/{\rho }_j^2)$. We choose priors ν_j ~ Uniform(0.5,2.5) and ρ_j ~ Uniform(0.2,2.5). Under these priors, the prior 95% interval for the spatial correlation for any pair of locations separated by 10% of the spatial domain’s maximum diameter in Figure 1 is (0.01, 0.99).

3.3 Bayesian variable selection

Including all of the covariates described in Section 2 in the spatially-varying coefficient model gives an over-parameterized model. Therefore, we propose a Bayesian variable selection model that reflects the prior belief that many of the variables should be included in the model, but only a small number have spatially-varying effects. We consider three possible relationships between activity type l and the j^th covariate, x_j:

1. x_j is removed from the model and β_lj(s_i) = 0 for all s_i,

2. x_j’s effect is constant across space and β_lj(s_i) = θ_lj for all s_i, or

3. x_j’s effect varies spatially and β_lj(s_i) varies from location-to-location.

Our Bayesian variable selection routine uses stochastic search variable selection to compute the posterior probability of each of these three relationships.

The overall average effect θ_lj is given the spike and slab prior, popularized for variable selection in the usual linear regression setting by George and McCulloch (1993). That is,

$${\theta }_{lj}={\gamma }_{1lj}{\alpha }_{lj},$$ (5)

where γ_1lj ∈ {0, 1} and α_lj ~ N(0,σ_j). If γ_1lj = 0 then θ_lj = 0 and x_j’s average (over space) effect on activity type l is zero.

To determine which regression parameters should be allowed to vary spatially, the prior for the columns and rows of the covariance matrix ${\mathrm{\sum }}_j^s$ also have positive mass at zero. Let

$${\mathrm{\sum }}_j^s=\text{diag}({\gamma }_{21j},\dots ,{\gamma }_{2kj}){\mathrm{\Omega }}_j\text{diag}({\gamma }_{21j},\dots ,{\gamma }_{2kj}),$$ (6)

where γ_2lj ∈ {0, 1} and Ω_lj ~ InvWishart(k + 0.1, 0.1I_k). If γ_2lj = 0 then β_lj(s_i) = θ_lj for all s_i and the effect is x_j is constant across space for activity type l.

Since we believe there is always some spatial correlation in the residual activity due to missing covariates, we fix γ_1l0 and γ_2l0 to be one for all l. The prior for remaining binary variable inclusion indicators ensures that the effects are not allowed to vary spatially unless the overall average is non-zero. We choose the prior

$$p({\gamma }_{1lj},{\gamma }_{2lj})=\{\begin{array}{ll}1-{\pi }_{1j},\hfill & {\gamma }_{1lj}=0\text{and}{\gamma }_{2lj}=0\hfill \\ {\pi }_{1j}(1-{\pi }_{2j}),\hfill & {\gamma }_{1lj}=1\text{and}{\gamma }_{2lj}=0\hfill \\ {\pi }_{1j}{\pi }_{2j},\hfill & {\gamma }_{1lj}=1\text{and}{\gamma }_{2lj}=1\hfill \end{array}$$ (7)

In this prior, π_1j is the prior probability that x_j is included in the model (either constant or spatially-varying) for activity type l and π_2j is the conditional probability that the effect of x_j varies spatially given that it is included in the model for activity type l.

Note that the prior probabilities π_1j and π_2j and variance ${\sigma }_j^2$ are shared across activity types. The hyperpriors areπ_1j ~ Beta(a₁,b₁), π_2j ~ Beta(a₂,b₂), and ${\sigma }_j^2\sim \text{InvGamma}(0.5,0.5)$; this hierarchical model facilitates pooling information regarding the importance of x_j across activity types. Integrating over π_1j gives mean inclusion probability E(γ_1lj) = a₁=(a₁ + b₁) and correlation Cor(γ_1lj, γ_1l′j) = 1/(1 + a₁ + b₁). Therefore, the prior favors sparse models if a₁ < b₁ and favors models with the same predictors for all response types with small a₁ and b₁. We use a₁ = a₂ = b₁ = b₂ = 1 for the PIN3 data analysis in Section 5 to give uniform priors for each inclusion probability.

Collinearity can be problematic for variable selection. Often when a group of important predictors are highly correlated variable selection methods will select only a single member of the group or miss the group altogether. We assume that the inclusion indicators γ_1lj and γ_2lj and regression coefficients α_lj and β_lj(s_i) are independent across covariates. Inspecting the posteriors of the inclusion indicators suggests that collinearly is not a large problem for our data. An alternative to the independent prior in the presence of collinearity is powered correlation prior of Krishna et al. (2009), which uses non-independent priors for the inclusion indicators and regression coefficients to combat collinearity.

4. Computing methods

To facilitate MCMC sampling, we introduce auxiliary variables g_li which indicate whether the y_li is drawn from the point mass of zero or the truncated normal model in (1), that is, g_li ~ Bern(p_l) and

$$y_{li}\mid g_{li}=\{\begin{array}{ll}0\hfill & \text{if}{g}_{li}=1\hfill \\ z_{li}^{+}\hfill & \text{if}{g}_{li}=0.\hfill \end{array}$$ (8)

g_li is updated via Gibbs sampling; for observations with y_li > 0 g_li is fixed at zero, for observations with y_li = 0 the full conditional probability that g_li = 1 is p_l/(p_l + (1 − p_l) * Prob(z_li < 0)). The proportion p_l is updated from its full conditional p_l ~ Beta(1 + Σg_ji, 1 + n − Σg_ji).

The latent variables z_li for observations with y_li = g_li = 0 are drawn using Gibbs sampling from their truncated normal full-conditionals; if g_li = 1 z_li no longer appears in the likelihood and it is updated from its normal prior. The covariance matrices Σ^e and Ω_lj are drawn using Gibbs sampling from their inverse Wishart full-conditionals and ρ_j and ν_j are drawn using Metropolis-Hastings sampling with Gaussian candidate distributions. Candidates with no prior mass are simply rejected.

For computational convenience, we rewrite the spatially-varying mean as

$${\mu }_{li}=\sum _{j=0}^p{x}_{ji}[{\gamma }_{1lj}{\alpha }_{lj}+{\gamma }_{2lj}{\beta }_{lj}({\text{s}}_i)],$$ (9)

where ${\alpha }_{lj}\sim \text{N}(0,{\sigma }_{\alpha }^2)$, β_j ~ N(0,K_j ⊗ Ω_j). The parameters in μ_li are updated using blocked-Gibbs sampling with blocks Θ_lj = {γ_1lj, γ_2lj, α_lj, β_lj}. To derive the full-conditionals, let Θ_(lj) be the set of all parameters not included in Θ_lj. We draw from p(Θ_lj|z, Θ_(lj)) by first integrating over (α_lj, β_lj) and drawing (γ_1lj, γ_2lj) from p(γ_1lj, γ_2lj|z, Θ_(lj)) and then drawing (α_lj, β_lj) from p(α_lj, β_lj|γ_1lj, γ_2lj, z, Θ_(lj)).

Define the residuals (not removing the x_j’s effect on the l^th activity type) as r_li = z_li − μ_li + x_ji [γ_1ljα_lj + γ_2ljβ_lj(s_i)] and simply r_l′i = z_l′i − μ_l′i for l′ ≠ l. Also, let U⁻¹ = Σ^e and V⁻¹ = Ω_j. Routine algebra shows that

$$p({\gamma }_{1lj},{\gamma }_{2lj}\mid \text{z},{\mathrm{\Theta }}_{(lj)})\propto \mid {\mathrm{\sum }}_r{\mid }^{1/2}exp\left(\frac{1}{2}{\widehat{\mathit{\beta }}}^{\prime }{\mathrm{\sum }}_r\widehat{\mathit{\beta }}\right)p({\mathit{\gamma }}_{1j},{\mathit{\gamma }}_{2j}),$$ (10)

where Σ_r = (U_llΓX′XΓ + Δ⁻¹)⁻¹,

$$\begin{array}{c}\mathrm{\Delta }=\left(\begin{array}{cc}{\sigma }_{\alpha }^2& 0\\ 0& V_{ll}{K}_j\end{array}\right),X=\left(\begin{array}{cccc}{x}_{j1}& x_{j1}& & 0\\ ⋮& & \ddots & \\ x_{jn}& 0& & x_{jn})\end{array}\right),\\ \widehat{\mathit{\beta }}=\left(\begin{array}{c}0\\ \mathrm{\Gamma }{X}^{\prime }{\sum }_{l^{\prime }=1}^k{U}_{l{l}^{\prime }}{\text{r}}_{l^{\prime }}^{\prime }+\mathrm{\Omega }{\sum }_{l^{\prime }\ne l}^k{V}_{l{l}^{\prime }}{\mathit{\beta }}_{l^{\prime }j}^{\prime }\end{array}\right)\end{array}$$

and Γ is the (n + 1) × (n + 1) diagonal matrix with diagonal elements γ_1lj, γ_2lj, …, γ_2lj. The posterior probability of each (δ_1lj, δ_2lj) combination is computed and (δ_1lj, δ_2lj) is drawn accordingly. Given (δ_1lj, δ_2lj), $({\alpha }_{lj},{\mathit{\beta }}_{lj}^{\prime }{)}^{\prime }$ is drawn from a multivariate normal distribution with mean Σ_rβ̂ and covariance Σ_r.

5. Analysis of the PIN3 data

In this section we analyze the PIN3 data described in Section 3. This is a multivariate model for activity in the six domains (work, recreational, outdoor household, indoor household, adult and child care, and transportation) as a function of demographic and other person-level variables as well as meteorological and neighborhood-level variables.

Figure 3a shows the inclusion probabilities for each covariate and activity type. To illustrate the effect of jointly modeling the inclusion probabilities across response type, Figure 3b shows the inclusion probabilities using a fixed prior across activity types (i.e., with π_1j = π_2j = 0.5 and σ_l = 1). The inclusion probabilities are more consistent across activity types under the joint model. For example, employment status is included for only 4 of the 6 activity types with fixed priors for the inclusion probabilities. All six inclusion probabilities are higher under the joint model and employment status is included for all 6 activity types. Also, borrowing strength across activity types removes some variables with inclusion probabilities just over 0.5 for one activity type (speed limit, bad residential units), which are likely to be spurious associations.

Figure 3.

Posterior inclusion probabilities (mean of γ_1jl) for the full model (Panel (a)) and the model with fixed prior inclusion probabilities (i.e., with π_1j = π_2j = 0.5 and σ_j = 1, Panel (b)). Panels (c) and (d) plot the posterior probabilities of being selected as a spatially-varying coefficient (mean of γ_2jl) and the conditional probability of being included with a spatially-varying coefficient given the variable is included in the model (mean of γ_2jl/mean of γ_1jl). Gray and black boxes represent probabilities greater than 0.5 and 0.9, respectively. The “+” and “−” for the inclusion probabilities indicate the sign of the posterior mean of overall average effect θ_jl.

Table 2 gives the 95% intervals for the zero-inflation parameters and the residual correlations. Outdoor household and transportation-related activity have the largest proportions of zero in the data set, and these activities generally have the largest zero-inflation parameters p_l (95% intervals (0.26, 0.40) for outdoor household and (0.16, 0.30) for transportation) which represent the excess mass at zero not explained by the truncated normal model. These parameters are clearly separated from zero, motivating the zero-inflated model even after accounting for covariate effects and spatial correlation. For the other four types of activity, a truncated Gaussian distribution fits fairly well, and the zero-inflation parameters are near zero. The residual correlation between indoor household activity and all other activities except transportation and recreational activity are significantly positive, and the only other significantly non-zero correlation is between care and recreation. Indoor household activity may serve as an indicator of women’s overall activity level in this group of women in mid to late pregnancy. Due to this correlation the posterior probability at zero in Table 2a (“posterior”) is larger than the observed proportion at zero for indoor activity.

Table 2.

Summary of the zero-inflation parameters and residual correlation. Table (a) gives the sample proportion of zeros and the posterior 95% intervals for the average (over subjects) zero probability $p_l+(1-p_l){\sum }_{i=1}^n\mathit{Prob}(z_{li}<0)/n$ (“posterior”) and the zero-inflation parameters p_l. Table (b) gives the 95% intervals for the elements of D^−1/2Σ^eD^−1/2, where D is k × k diagonal matrix with elements ${\mathrm{\sum }}_{ll}^e$.

(a) Zero-inflation parameters pl
	Working	Rec	Outdoor	Indoor	Care	Trans
Sample	0.70	0.37	0.82	0.35	0.60	0.78
Posterior	(0.70, 0.77)	(0.40, 0.51)	(0.75, 0.83)	(0.42, 0.54)	(0.61, 0.70)	(0.72, 0.80)
pl	(0.01, 0.13)	(0.00, 0.01)	(0.26, 0.40)	(0.00, 0.01)	(0.01, 0.13)	(0.16, 0.30)

(b) Residual correlation parameters in Σe
	Rec	Outdoor	Indoor	Care	Trans
Work	(−0.14, 0.06)	(−0.09, 0.18)	(0.07, 0.27)	(−0.12, 0.14)	(−0.07, 0.18)
Recreational		(−0.04, 0.18)	(−0.03, 0.12)	(0.01, 0.19)	(−0.06, 0.15)
Outdoor			(0.04, 0.25)	(−0.07, 0.18)	(−0.18, 0.10)
Indoor				(0.07, 0.25)	(−0.15, 0.05)
Care					(−0.04, 0.20)

Individual-level factors tended to be more strongly associated with physical activity levels than neighborhood environmental factors, with several factors having posterior inclusion probabilities > 0.90. Education, age, number of previous births, and employment status are important predictors of at least five of the six activity types (Figure 3a). In particular, more highly educated women tend to have higher levels of recreational, outdoor household, care, and transportation activity and lower levels of work-related and indoor household activity. These women may be more likely to have sedentary jobs and to hire domestic workers to help with household chores, freeing more time for leisure activity and playing with children. The data show that activity patterns differ by race; black women generally exert more energy on work and transportation-related activities and less energy on recreational, outdoor household, and child and adult care activities. Also, women with high BMI are less likely to participate in recreational or outdoor household activities. Gestational diabetes and smoking were associated with increased work activity, which is perhaps a reflection of the demographics of these conditions.

Ozone is a predictor of outdoor household and child and adult care activities. The posterior mean of the ozone coefficient is positive for outdoor household activity, that is, women are more likely to be active outdoors when the ozone is high. This is somewhat surprising given the well-documented health effects of ozone exposure (National Research Council, 2008), especially for susceptible groups. To investigate this issue further, we refit the model with separate ozone effects for women with (n=643) and without (n=278) at least 16 years of education. For the high education group ozone is included with probability 0.47 for child and adult care and no more than 0.38 for the other activities. The posterior mean for the overall average effect α for child and adult care is −0.04, which corresponds to roughly a 4% decrease in MET minutes per week (exp(−.04)=.96) for a standard deviation (10.4 ppb) unit increase in ozone. In contrast, for the low education group ozone is an important predictor for only outdoor household activity (probability 0.67) and the posterior mean for the overall average effect is 0.09, which corresponds to roughly a 9% increase in MET minutes per week for a standard deviation unit increase in ozone. Therefore, the association between physical activity and ozone is dependent on education level.

Ozone is highly related to temperature. The posterior correlation of the inclusion indictors γ_1lj for temperature and ozone was −0.45 for recreational activity (the absolute correlation was less than 0.4 for all other covariate pairs and activity types), so there is some uncertainty whether ozone, temperature, or both should be included in the model for recreational activity. To test whether temperature was properly accounted for we added a quadratic temperature term and the association between ozone and outdoor activity persisted. Ozone levels tend to be higher in summer when recreational and outdoor household activity is more frequent, and given that reporting is only on a weekly basis, presence of high ozone for the week could very well be a marker of a week with nice weather and only one red or orange ozone day. Along these lines, higher temperatures were associated with more recreational and outdoor household activity, and lower child and adult care activity (perhaps because children participated in recreational activity).

Several neighborhood characteristics are also identified as important predictors of activity. Women in neighborhoods with abandoned residential units engage in more child care and transportation activity, perhaps a sign of lower socioeconomic status. Also, outdoor household activity increases in neighborhoods with porches and no sidewalks. This may be because such lots are more common in rural areas in which yards are larger and opportunities for outdoor household activities, such as gardening, are more plentiful. However, the presence of a sidewalk increases the average amount of transportation activity, perhaps because mothers are more likely to walk or bike to work or other places.

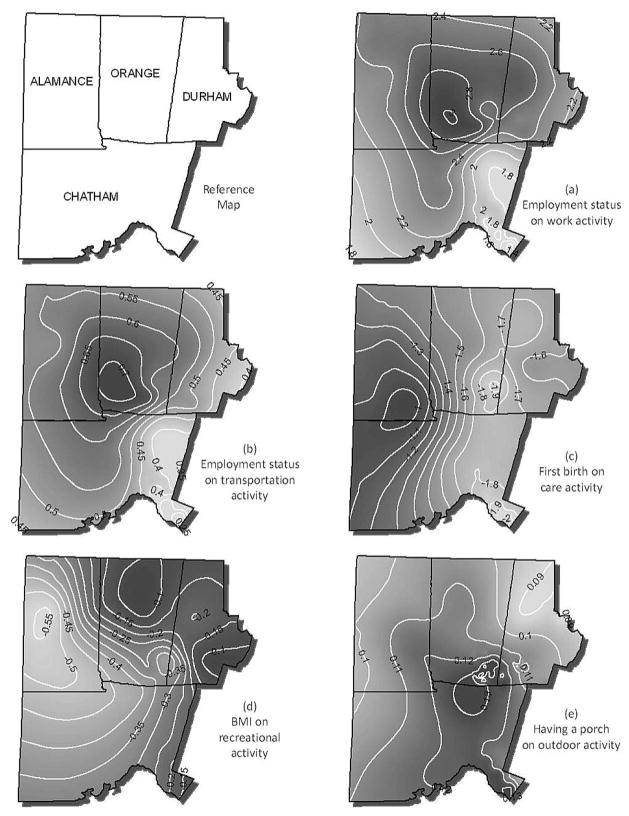
Figure 3c plots the posterior probability that each covariate is a spatially-varying effect. As expected, only a small number of the covariates have spatially-varying effects. Four associations, employment status with working and transportation activity, BMI with recreational activity, and the first birth indicator with adult and child care activity, have inclusion probability greater than 0.9. This indicates a strong signal from the data because the prior probability of a spatially-varying effect is only 0.25. Figure 4 shows that employed women are generally more active in working and transportation throughout the spatial domain. The association between employment status and work-related activity (Figure 4a) is strongest in urban areas and weakest in rural areas, perhaps because women in rural areas may consider some outdoor household activities on farms to be work-related activities. Employment status is also identified as having a spatially-varying effect on transportation activity, with a stronger effect (Figure 4b) in the rural parts of Alamance and western Orange counties.

Figure 4.

Posterior mean of the spatially-varying effects, β

While not having given birth previously was associated with lower levels of child and adult care activity, this effect (Figure 4c) was weaker in rural areas of northern Chatham and southern Alamance counties. The negative association between BMI and recreational activity is the strongest in the Chapel Hill area (southeast Orange County) and in southwest Alamance county.

None of the neighborhood variables are included as spatially-varying effects with probability greater than 0.5. The variable most likely to be included is the effect of porch on work activity. This variable is included in the model with probability 0.56 and is included as a spatially-varying effect with probability 0.39. Therefore the conditional probability of being spatially-varying given inclusion in the model is higher than 0.5 (Figure 3d). Figure 4e shows that the positive effect of having a porch is the largest in rural Chatham County in which a porch may indicate a house with greater acreage requiring upkeep.

One possible explanation for spatially-varying effects is missing interactions, either with variables already in the model or with variables not included in the study. Although it is not computationally feasible to include all possible interactions between the p = 31 covariates, we can search for important interactions using the results of the spatially-varying coefficients model. For example, regressing the posterior mean of spatially-varying BMI effect for recreational activity on the other predictors reveals several interactions. Six variables are significant at the α = 0.05 level: household income, black race, urban residence, and presence of abandoned residential units are positively associated with the BMI effect, while age and bad residential units are negatively associated with the BMI effect. The association between BMI and recreational activity is generally negative, so these results indicate that the association between BMI and recreational activity is the strongest for older, less affluent, non-black women in rural areas. Regressing the posterior mean of spatially-varying first-birth effect for care activity on the other predictors also reveals several interactions. Education, age, urban residence, and presence of a sidewalk are negatively associated with the spatially varying effect, thus pregnant women with that have previously given birth with these characteristics spend more effort on care activity. Marital status, BMI, speed limit of nearest road segment, and presence of bad residential units, litter, and a crime watch sign are negatively associated with the spatially-varying effect.

Finally we conduct a sensitivity analysis to determine the effect of the prior for the covariance matrix for the spatially-varying effects. We used Ω_j ~ InvWishart(k + ε, εI_k) with ε = 0.1 in the analysis above. We also tried ε = 0.01 and ε = 1. The average (sd) over covariate and activity type inclusion probability for the spatially-varying effects was 0.084 (0.209) for ε = 0.01, 0.194 (0.239) for ε = 0.1, and 0.181 (0.171) for ε = 1. Therefore, there is some sensitivity to this hyperprior, with ε = 0.1 giving the largest range of posterior inclusion probabilities, and thus the most separation between important and unimportant predictors. For all three hyperpriors, the four predictors with inclusion probability greater than 0.9 (shaded black in Figure 3c) were included as spatially-varying with probability greater than 0.5.

6. Discussion

In this paper we developed a Bayesian hierarchical model to analyze data from an epidemiologic study designed to assess whether neighborhood environmental characteristics had a noticeable effect on physical activity levels of pregnant women. To adequately model these complex data, we develop a spatial model for semicontinuous data which allows the effect of a subset of the predictors to vary over the spatial domain. We found that while some neighborhood characteristics were associated with physical activity levels, these associations were not particularly strong, especially in relation to individual characteristics of the women under study, such as age or level of education. We also found a positive relationship between weekly average ozone exposure and outdoor activity; this association held only for mothers with less than 16 years of education, suggesting a need for further education about the effects of ozone exposure for the pregnant population.

Another important direction of research in this area is to identify factors that lead to a change in activity from pre-pregnancy to postpartum. We cannot fully address this question with these data because we do not have pre-pregnancy activity data collected in a similar manner as in pregnancy. However, the survey does include a self-reported binary indicator of whether the mother regularly exercised three months before pregnancy. When we included this variable as a predictor in our hierarchical model it was an important predictor of recreational activity only, and the associations between the other predictors and the outcome remained largely the same.

Other future work involves examining determinants of change in physical activity levels from pregnancy to the postpartum. In this study, a subset of subjects provided physical activity data when their children were 3 and 12 months of age. While neighborhood environmental characteristics were not strongly associated with activity levels during pregnancy, we anticipate some different trends in the postpartum period. For example, a woman might be unlikely to walk or jog with her infant in a stroller without having a sidewalk. We are interested in extending the methods to account for longitudinal, multivariate responses in order to determine whether neighborhood environmental characteristics may be related to change (or retention) of activity levels during the postpartum period.