Effects of environmental instabilities on endpoint stiffness during the maintenance of human arm posture

Abstract

Using the upper limb to manipulate objects or tools requires maintenance of stable arm posture. The ability to maintain stable postures is dependent on the mechanical properties of the arm, which can be characterized by estimates of endpoint stiffness. In this study we quantified the endpoint stiffness of the human arm during postural interactions with mechanically imposed unstable loads. The purpose was to determine the extent to which arm stiffness is adapted according to the mechanical properties of the environment during postural tasks. We estimated the endpoint stiffness of the right arms of eight subjects as they interacted with four haptic environments: rigid, unstable along the direction of maximal endpoint stiffness and orthogonal to this direction, and a high-strength unstable environment also aligned to the orientation of maximal endpoint stiffness. The size and orientation of endpoint stiffness were quantified for each haptic condition. Stiffness size was increased along the directions of the destabilizing environments (p<0.003). However, the environments had no significant effect on stiffness orientation (p>0.26). These findings suggest that at a fixed posture interactions with unstable environments can induce moderate, task-appropriate changes in limb mechanics that are tuned to the environment. However, these changes are small relative to those that can be obtained by changing limb posture.

I. INTRODUCTION

Using the upper limb to manipulate objects in our physical world requires the ability to maintain a stable arm posture. The ability to maintain stable postures is dependent on the mechanical properties of the arm, which can be characterized by estimates of endpoint stiffness. Many functional tasks, such as the use of hand tools, compromise the stability of the arm along specific directions [1], and direction-specific adaptations in endpoint stiffness may be needed to perform these tasks effectively. Such preferential changes in endpoint stiffness have been reported during movements through unstable environments [2], but this has yet to be observed during the maintenance of posture [3]. These contrasting results may reflect a fundamental difference in the ability to adapt stiffness during movement and posture [4]. Alternatively, the adaptation observed during reaching may reflect an involuntary response due to interactions with unstable loads used in those experiments, which have not yet been evaluated during postural tasks assessing endpoint stiffness regulation.

The goal of this study was to quantify the 3D endpoint stiffness of the human arm during postural interactions with mechanically unstable loads. All measurements were made in the 3 degrees of freedom (DOF) relevant to positioning the limb in space. Subjects interacted with four haptic environments, oriented relative to the direction of maximal endpoint stiffness for each subject. We hypothesized that interactions with destabilizing environments would result in preferential increases in arm stiffness, oriented along the direction of the environmental instability. The nature of such adaptation should provide insight into the degree with which arm mechanics can be tuned to the mechanical properties of the environment, at a fixed posture.

II. Methods

A. Subjects

Eight right-handed subjects, 26 to 29 years of age (6 males and 2 females), participated in this study. Subjects had no history of neurological or orthopedic impairments of the upper arms. Subjects gave written, informed consent and were free to withdraw at any time. This protocol was approved by the Institutional Review Board of Northwestern University’s Office for the Protection of Research Subjects.

B. Equipment

A robotic manipulator [HapticMaster; Moog FCS, The Netherlands] was programmed to simulate haptic environments with which subjects interacted and to provide the 3D displacement and force measurements necessary for estimating endpoint stiffness. To account for compliance in the robot’s drive mechanism, we redundantly recorded endpoint displacement with a motion analysis system [Optotrak 3020; Northern Digital, Waterloo, Ontario] at 250 frames/second. Linear interpolation was performed to resample these data at 1.25 kHz to match the sampling rate of the collected force data before further processing. A common clock was used to synchronize data from the robot and motion analysis systems.

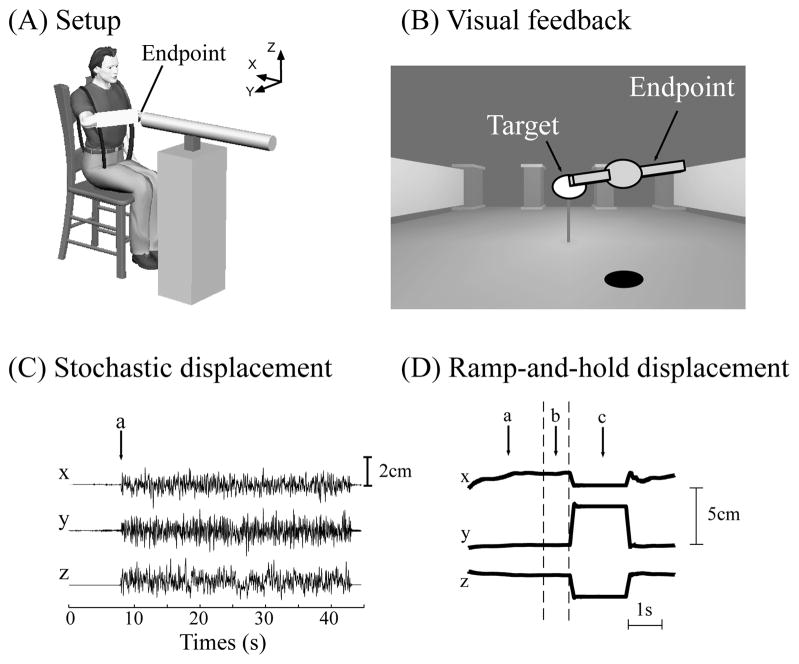
Subjects used their right arm to interact with the robot while maintaining a common posture. Subjects were seated with the trunk securely strapped to a rigid chair (Fig. 1A). They supported the arm against gravity while holding the shoulder at ~ 70º abduction and ~ 45º flexion in the horizontal plane. The elbow was flexed to ~ 90º. The wrist was immobilized using a custom-fitted fiberglass cast, which was attached to the robot. Endpoint displacement and force data were used to provide subjects with real-time visual feedback while interacting with the robot (Fig. 1B).

Fig 1.

(A) Experiment setup with (B) visual feedback of position and force, and (C, D) displacement perturbation characteristics used for estimating 3D endpoint stiffness.

C. Experimental Protocol

A preliminary experiment was used to produce a baseline estimate of arm impedance while subjects interacted with an isotropically rigid (50 kN/m) environment (R). The robot applied a 35 s stochastic displacement perturbation to the arm (Fig. 1C, ‘a’) [6] while subjects maintained a target force of 10 N in each of the ±X, ±Y, or ±Z directions.

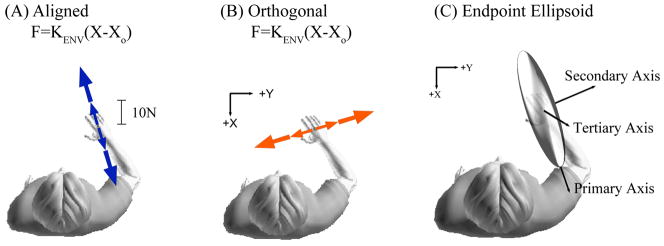
In a second experimental session we quantified the mechanical properties of the arm as subjects interacted with four haptic environments. The sequential order of exposure to the environments was randomized. The strength and orientation of these environments was based on the initial endpoint stiffness estimate; these environments were isotropically rigid (R), destabilizing in the direction aligned to maximal stiffness (A; Fig. 2A), destabilizing in the direction aligned to maximal stiffness but of higher strength (HA; Fig. 2A), and orthogonal to maximal stiffness (O; Fig. 2B). All movements along the destabilizing environments were constrained to a 3D line along the direction of the destabilizing load.

Fig 2.

Orientation of destabilizing haptic environments (A) aligned and (B) orthogonal to maximum endpoint stiffness ellipsoid; (C) 3D stiffness ellipsoid having primary, secondary, and tertiary axes.

As displayed in Fig. 2A and 2B, the destabilizing environments were programmed so that as subjects moved their hand (x) away from the neutral position (x_o) of the environment, the robot pushed the hand further with a force (F) proportional to the distance between the hand and the neutral point, according to: F = K_ENV (x-x_o). The strength of the destabilizing environments was relative to the baseline estimates of endpoint stiffness size. The size of K_ENV was either within the range of arm stiffness magnitudes corresponding to the primary and secondary axes or exceeding the magnitude of the primary axis of the endpoint stiffness ellipsoid.

In each trial, subjects moved to the neutral position of the environment and applied the target force (Fig. 1D, ‘a’) for a uniformly distributed random period of time between 0.5–1.5 s (Fig. 1D, ‘b’), after which a single ramp-and-hold perturbation was triggered (Fig. 1D, ‘c’). Perturbations had a velocity of 400 mm/s and duration of 100 ms. Target hold times and perturbation directions were randomized.

Perturbations were applied along the direction of the primary, secondary, and tertiary principal axes of endpoint stiffness (Fig 2C) so that the recorded displacements and endpoint forces spanned 3DOF. Approximately 10 perturbations were repeated for each perturbation direction for a total of ~60 perturbations for each environment. During all experiments subjects were instructed to maintain the prescribed posture and not to react to the applied perturbations.

III. Data Analysis

A. Quantifying endpoint impedance

Because this study was concerned with postural control, we focused our analyses on endpoint stiffness. We used continuous stochastic and discrete ramp-and-hold displacement perturbations of posture and recorded the 3D forces generated in response.

In the preliminary experiment we applied stochastic perturbations and used nonparametric system identification techniques to estimate the size, shape, and orientation of endpoint stiffness. The dynamics equations describing impedance were estimated non-parametrically [7], then parameterized by fitting a second order model with inertial, viscous, and elastic parameters over the frequency range of 0–10 Hz using least squares optimization [8]. This resulted in 3×3 matrices characterizing endpoint inertia, viscosity, and stiffness.

In the second experimental session we applied ramp-and-hold perturbations. A least squares linear regression model was used to estimate endpoint impedance from the response forces as well as the recorded displacements and computed velocities and accelerations. Before the regression force and displacement data were low-pass filtered at 13 Hz using a fourth order, two-sided Butterworth filter after removing the pre-perturbation mean; displacement data were then numerically differentiated to calculate velocity and acceleration. Data were segmented from 50 ms before perturbation onset to 110 ms following the beginning of the hold period, to include 210 ms following perturbation onset. This method also provided 3×3 matrices characterizing the inertial, viscous, and elastic properties of the arm.

The three principal axes of the estimated 3D inertia, viscosity, and stiffness were used to characterize the directional characteristics of arm impedance. The primary principal axis of each defined the orientation of maximal stiffness, viscosity, and inertia. The orientations of the axes were quantified using spherical coordinates; the azimuth described counter-clockwise rotation from the X-axis within the horizontal plane, and the elevation described rotation from the azimuth above the horizontal plane. The overall size was quantified by squaring the magnitude of each of the three principal axes, summing the three, then taking the square root.

For the initial experiment, the quality of both the nonparametric and parametric fits was evaluated for each trial using the multiple correlation coefficient, R², to characterize the relationship between the predicted and measured endpoint forces. For the nonparametric and parametric fits the average R² value over the frequency range of 0–10 Hz was 0.92±0.01 (mean ± standard deviation) and 0.82±0.04, respectively, and were similar to those reported before [6].

In the second set of experiments it was necessary to use ramp-and-hold perturbations to assess impedance during interactions with the unstable loads. This is because the use of stochastic perturbations to estimate endpoint stiffness during interactions with unstable loads can lead to biased estimates [9]. We did, however, compare estimates of limb mechanics using both methods in subjects interacting with the rigid haptic environment. We found that the shape of stiffness ellipsoids estimated using both methods was not statistically different (p=0.46). The shape of the stiffness ellipsoid was defined as the ratio between the primary and secondary axes [3].

B. Quantifying the effects of mechanical environments on arm impedance

Since this study was concerned with postural control, we chose to focus on the static component of endpoint impedance, endpoint stiffness. We evaluated endpoint stiffness adaptation by comparing differences in the size and orientation of the principal axes of the stiffness ellipsoid between environments. All statistical analyses were performed using a 1-way ANOVA to test for the effect of the environment. Post-hoc comparisons were made using paired t-tests with a Bonferroni correction for multiple comparisons. Significance was defined at the p<0.05 level.

IV. Results

The least squares linear regression model was appropriate for characterizing 3D endpoint impedance. Across all subjects and environments, the average R² was 83.9 ± 1.4 % (mean ± standard deviation). Also, R² values were uniform across environments. The effect of the environment on R² was not significant (p=0.70), suggesting that the least squares approach characterized limb mechanics equally well across the four environments.

We also evaluated the cross-validation accuracy of the regression model. For each subject, we randomly selected half of the collected trials to estimate endpoint inertia, viscosity, and elasticity. These parameters were used to predict the force response for the remaining collected trials. The average R² for cross-validated data was 83.0 ± 1.9%, which was statistically indistinguishable (paired t-test; p > 0.05) from the overall R² across trials. Collectively, these results suggested that the inertial, viscous, and elastic parameters obtained using ramp-and-hold perturbations provided an accurate characterization of the arm’s dynamic response to the ramp-and-hold perturbations.

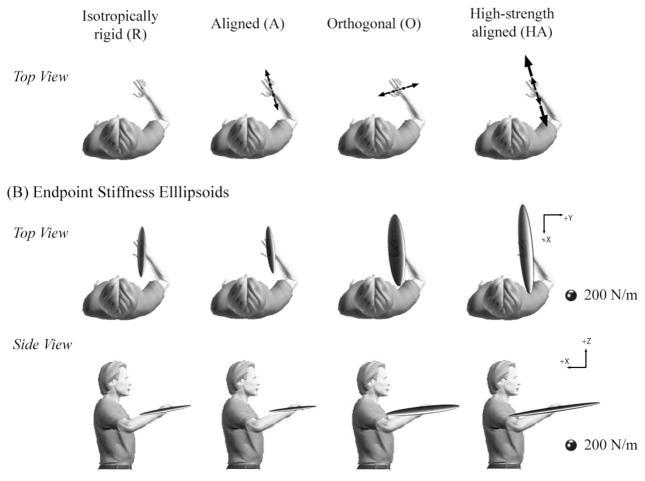
The size and orientation of the estimated inertia and viscosity ellipsoids were consistent across environments (Fig 3). The haptic environments did not have a significant influence on the size or orientation of the primary, secondary, or tertiary axes of endpoint inertia (Fig 3B; all p>0.42). Likewise, the orientation of maximal endpoint viscosity, corresponding to the primary axis of viscosity, was highly consistent across environments (Fig 3C); the orientation of this axes’ azimuth (p=0.18) and elevation (p=0.60) was not significantly affected by the tested environments.

Fig 3.

Representative ellipsoids of 3D endpoint stiffness during interaction with each of the haptic environments.

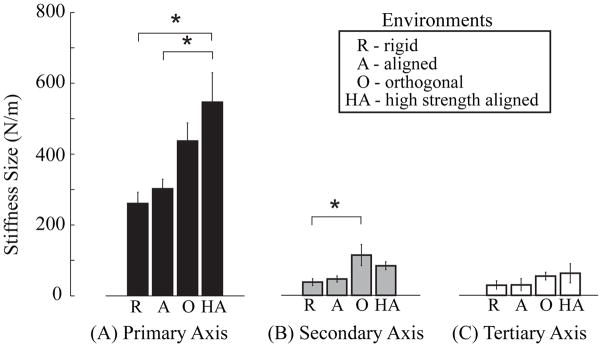
Endpoint stiffness was adapted according to the environment with which subjects interacted. Specifically, the magnitude of endpoint stiffness increased along the direction of the destabilizing environment (Fig. 4A; p=0.003), although the orientation of endpoint stiffness was not influenced by the environments (all p>0.26).

Fig 4.

Average stiffness size across eight subjects for the (A) primary, (B) secondary, and (C) tertiary ellipsoid axes during interaction with each of the haptic environments.

The magnitude of the primary axis of endpoint stiffness was greatest during interactions with the higher-strength destabilizing environment in the same direction (‘HA’; Fig. 4A). Post-hoc tests showed that for interactions with the HA environment, the magnitude of endpoint stiffness in this direction was greater than that for interactions with the lower-strength A environment in the same direction (p=0.007), as well as for the R environment (p=0.01).

The environments with which subjects interacted also had a significant effect on the magnitude of the secondary principal axis of endpoint stiffness (p=0.01). The magnitude of the secondary axis was largest during interactions with the environment that was destabilizing in the same direction (‘O’; Fig. 4B; orthogonal to maximal stiffness). Post-hoc tests revealed that the secondary principal axis of stiffness was significantly larger during interactions with the O environment, relative to its magnitude during interactions with the R (p=0.03) environment.

The magnitude of endpoint stiffness along the tertiary axis of endpoint stiffness was not influenced by the environment with which subjects interacted (Fig. 4C; p=0.45).

V. Conclusion

This study examined whether 3D limb mechanics are adapted, at a fixed posture, to the mechanical properties of destabilizing haptic environments with which a subject interacts. The present results demonstrate that 3D endpoint stiffness is modulated according to the orientation and strength of destabilizing haptic environments. The primary feature of the adaptation presented here was a modest, yet task-appropriate change in the size of endpoint stiffness. During interactions with directional, destabilizing environments with a negative stiffness magnitude that exceeded or approached the magnitude of maximal endpoint stiffness in the same direction, endpoint stiffness was increased in that direction. The orientation of maximal endpoint stiffness, however, was unchanged.

Our results suggest that at a fixed posture, the degree to which endpoint stiffness can be adapted to the functional requirements of a task is limited. Studies have shown, however, that changes in posture can have a profound effect on the orientation of maximal arm stiffness [6, 10]. We have also shown that during unconstrained tasks, posture selection may be the preferred mechanism to regulate endpoint stiffness, while changes in muscle activation may be subservient [6].

The present results demonstrate a consistent change in arm mechanics that was tuned to the environment but restricted by the fact that the arm was held at a fixed posture. No muscle activity was recorded in this study, so suggesting the specific type of muscle activation that could have contributed to the present results would be speculation. However, previous work from our group suggests that stretch sensitive reflex responses are adapted according to the mechanical properties of the environment [5]. Reflex adaptation could have, to some degree, contributed to the present results, but the functional link between the stiffness adaptation presented here and multjoint reflex adaptation observed in our previous work is still unknown. It is possible that such reflex adaptation may be the result of an involuntary mechanism that functions to stabilize the arm before more functionally appropriate actions, such as a change in posture, can be enacted.