Solid-tumor radionuclide therapy dosimetry: New paradigms in view of tumor microenvironment and angiogenesis

Abstract

Purpose: The objective of this study is to evaluate requirements for radionuclide-based solid tumor therapy by assessing the radial dose distribution of beta-particle-emitting and alpha-particle-emitting molecules localized either solely within endothelial cells of tumor vasculature or diffusing from the vasculature throughout the adjacent viable tumor cells.

Methods: Tumor blood vessels were modeled as a group of microcylindrical layers comprising endothelial cells (one-cell thick, 10 μm diameter), viable tumor cells (25-cell thick, 250 μm radius), and necrotic tumor region (>250 μm from any blood vessel). Sources of radioactivity were assumed to distribute uniformly in either endothelial cells or in concentric cylindrical 10 μm shells within the viable tumor-cell region. The EGSnrc Monte Carlo simulation code system was used for beta particle dosimetry and a dose-point kernel method for alpha particle dosimetry. The radioactive decays required to deposit cytocidal doses (≥100 Gy) in the vascular endothelial cells (endothelial cell mean dose) or, alternatively, at the tumor edge [tumor-edge mean dose (TEMD)] of adjacent viable tumor cells were then determined for six beta (³²P, ³³P, ⁶⁷Cu, ⁹⁰Y, ¹³¹I, and ¹⁸⁸Re) and two alpha (²¹¹At and ²¹³Bi) particle emitters.

Results: Contrary to previous modeling in targeted radionuclide therapy dosimetry of solid tumors, the present work restricts the region of tumor viability to 250 μm around tumor blood vessels for consistency with biological observations. For delivering ≥100 Gy at the viable tumor edge (TEMD) rather than throughout a solid tumor, energetic beta emitters ⁹⁰Y, ³²P, and ¹⁸⁸Re can be effective even when the radionuclide is confined to the blood vessel (i.e., no diffusion into the tumor). Furthermore, the increase in tumor-edge dose consequent to beta emitter diffusion is dependent on the energy of the emitted beta particles, being much greater for lower-energy emitters ¹³¹I, ⁶⁷Cu, and ³³P relative to higher-energy emitters ⁹⁰Y, ³²P, and ¹⁸⁸Re. Compared to alpha particle emitters, a ∼150–400 times higher number of beta-particle-emitting radioactive atoms is required to deposit the same dose in tumor neovasculature. However, for the alpha particle emitters ²¹¹At and ²¹³Bi to be effective in irradiating viable tumor-cell regions in addition to the vasculature, the carrier molecules must diffuse substantially from the vasculature into the viable tumor.

Conclusion: The presented data enable comparison of radionuclides used for antiangiogenic therapy on the basis of their radioactive decay properties, tumor neovasculature geometry, and tumor-cell viability. For alpha particle emitters or low-energy beta particle emitters, the targeting carrier molecule should be chosen to permit the radiopharmaceutical to diffuse from the endothelial wall of the blood vessel, while for long-range energetic beta particle emitters that target neovasculature, a radiopharmaceutical that binds to newly formed endothelial cells and does not diffuse is preferable. The work is a first approximation to modeling of tumor neovasculature that ignores factors such as pharmacokinetics and targeting capability of carrier molecules. The calculations quantify the interplay between irradiation of neovasculature, the surrounding viable tumor cells, and the physical properties of commonly used radionuclides and can be used to assist estimation of radioactivity to be administered for neovasculature-targeted tumor therapy.

INTRODUCTION

Targeted radionuclide therapy involves the use of cancer-cell-targeting radiopharmaceuticals that selectively concentrate in the vicinity of the tumor. Currently, this cancer treatment modality is mainly directed against hematopoietic and small, metastatic tumors, which are difficult to treat with surgery or external-beam radiation, whereas its employment in the therapy of solid tumors is problematic, one of the commonly postulated reasons being the unfavorable penetration and nonuniform radiotracer and dose distribution in this case. Since a high interstitial pressure is found within solid tumors,¹ the distribution of radiolabeled molecules is often limited to regions adjacent to tumor vasculature, especially when macromolecules, such as monoclonal antibodies, are used as carriers.^{2, 3, 4}

The dosimetry of internal radionuclide therapy has long been of interest.^{5, 6, 7, 8, 9} Most internal dose calculations employ the medical internal radiation dose guidelines, which are based on the assumption of uniform radionuclide distribution in homogeneous media of varying shapes and sizes. However, nonuniform intratumoral activity has been demonstrated for most intravenously administered radiotracers.^{10, 11} Since the spatial heterogeneity of dose and activity distribution is usually considered a limiting factor in the success of therapy, the use of higher-energy beta emitters with the ability to deliver radiation dose over a longer range^{11, 12} continues to be considered essential for treatment of larger sized tumors.

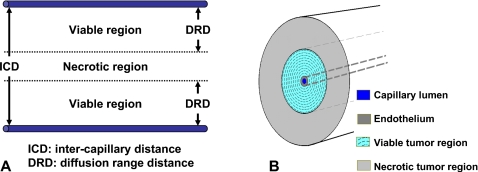
Folkman¹³ introduced the hypothesis that tumor growth is angiogenesis-dependent and this has been confirmed by a recent work (reviewed by Folkman¹⁴). Tumors begin as small clusters of abnormal cells growing in an organ∕tissue. In early tumor expansion, as in embryonic development, growing cells rapidly outstrip the supply of nutrients and oxygen. Since such tumor-cell clusters cannot grow larger than 1 or 2 mm in diameter without their own blood supply, they stimulate the proliferation of endothelial cells in nearby healthy vessels and thereby recruit new capillaries (neovasculature). Continued tumor growth depends on an expanding vascular network within the tumor to supply necessary oxygen and nutrients. Tumor cells form microcylinders around capillary blood vessels.¹⁵ As a tumor grows [Fig. 1], the distance from the nearest blood vessel may exceed the diffusion range distance (DRD) of oxygen and nutrients (∼150–250 μm),^{4, 16} resulting in anoxic conditions and cell death.^{4, 15, 16, 17, 18} Consequently, larger tumors usually have alternating viable and necrotic regions, as shown in Fig. 1A. In normal tissues, the microvascular density per intercapillary distance fairly accurately reflects the metabolic demands of the cells; in contrast, in tumor tissues, cells within oxygen diffusion range of the vasculature are viable, and beyond this radius of oxygen and nutrient support, an abrupt shift to necrosis is observed.^{15, 18} Actually, virtually all cells are obliged to reside within 100 μm of a capillary blood vessel.¹⁹ Assuming there are no viable cells in the avascular necrotic regions, any radiation dose deposited within these volumes is redundant. Therefore, (i) the use of radionuclides whose range is greater than that of the viable region is not essential for the success of targeted radionuclide therapy, and (ii) a less-than-uniform radionuclide distribution is acceptable as long as the dose deposited within the viable region is cytocidal.

Figure 1.

Schematics of (a) tumor vasculature and (b) cross-sectional view of capillary blood vessel model (drawing not to scale). The lumen of capillary in the center is 10 μm in radius, the thickness of endothelium is 10 μm, and the outermost radius of viable tumor region is 250 μm. The viable tumor region is divided into 10 μm concentric shells for evaluation of radial dose distributions. Beyond the viable tumor region, the necrotic tumor region extends to a radius of 1 cm or maximum particle range of radionuclide to be evaluated, whichever is larger. Vessel is 10 cm in length.

This work is a first-approximation modeling of radiation dosimetry in a neovascularized solid tumor without reference to pharmacokinetics, tumor targeting, or systemic toxicities. We use a tumor neovasculature model to compare the dose distribution in a solid tumor in which beta particle and alpha particle emitters of differing energies and particle ranges are present. To this end, we have evaluated the dosimetry of several radionuclides in a simplified blood-capillary vessel model [Fig. 1B]. Radial dose distribution (RDD) is therefore evaluated either for radioactivity present exclusively within microvessels, or for radiotracers diffusing into the tumor, beginning with capillary endothelial cells and expanding successively into more distant regions. Based on DRD of oxygen and nutrients, we defined the viable tumor region as within 250 μm of a capillary∕vessel. Dose distributions are calculated by Monte Carlo simulation for beta emitters and an integration method for alpha emitters. The radioactivity required to deposit a minimum cytocidal radiation dose of 100 Gy in the viable tumor region is determined accordingly. The purpose of this paper is to introduce considerations in radionuclide dosimetry that have traditionally stayed outside the modeling approaches reported thus far. The data aim to assist the development of guidelines for the effective use of therapeutic radionuclides that accounts for tumor vasculature and the estimation of radioactivity to be administered in targeted radionuclide therapy.

METHODS

A capillary blood vessel was modeled as a 10 cm long cylinder [cross-section of the cylinder is shown in Fig. 1B]. The capillary lumen in the center, 10 μm in radius, was surrounded by a 10 μm thick band of endothelial cells and a viable tumor-cell region with a ≤250 μm radius.^{4, 15, 16, 17, 18} Necrotic tissue, whose radius was assumed to either extend 750 micrometer beyond the viable region or equal the maximum particle range of the radionuclide to be evaluated, whichever was greater, was defined beyond the viable tumor region.

Since upon intravenous injection the penetration of a radiopharmaceutical is often limited to regions adjacent to the endothelium of the blood vessel, the source radioactivity was assumed to be distributed within a band surrounding the capillary lumen. For nondiffusing or minimally diffusing radiolabeled compounds (e.g., a radiolabeled antiangiogenic antibody), the radioactivity was specified to concentrate only within endothelial cells, i.e., the radial thickness of the radioactive source band was 10 μm. For diffusing radiotherapeutic agents (e.g., a low molecular weight, radiolabeled molecule with high affinity to a tumor-cell surface antigen), the thickness of the radioactive source band was increased successively from 10 to 400 μm (to approximate radioactivity diffusing outward), i.e., approaching and finally surpassing the viable tumor region (250 μm). In both cases, the radial radiation dose distributions around the vessel were evaluated for a series of varied source radioactivity band thicknesses. As a first approximation, radioactivity is assumed to be uniformly distributed within a source band for all the band thicknesses.

For radiation dosimetry, the viable tumor region was divided into concentric cylindrical shells, 10 μm in thickness. To approximate an infinitely long blood vessel, energy deposition in each shell was evaluated in the 1 cm central portion of the vessel cylinder to avoid edge effects. The average radiation dose in each shell was calculated accordingly. Doses in the endothelial cells and capillary lumen were also examined.

Radial radiation dose distribution in this blood vessel model was assessed for eight radionuclides of therapeutic potential. Six of them are beta emitters: Phosphorus-32 (³²P), phosphorus-33 (³³P), copper-67 (⁶⁷Cu), yttrium-90 (⁹⁰Y), iodine-131 (¹³¹I), and rhenium-188 (¹⁸⁸Re); and two are alpha emitters: Astatine-211 (²¹¹At) and bismuth-213 (²¹³Bi). The physical properties of the eight radionuclides²⁰ are listed in Tables 1, 2.

Table 1.

Physical properties of beta particle emitters.

Radionuclide	Half-life	Mean particle energy (MeV)	Maximum energy (MeV)	Maximum range (mm)
Y-90	64.1 h	0.933	2.284	11.3
Re-188	17.0 h	0.763	2.120	10.4
P-32	14.3 d	0.695	1.710	8.2
I-131	8.0 d	0.182	0.606	2.3
Cu-67	61.8 h	0.140	0.576	2.1
P-33	25.4 d	0.0764	0.249	0.63

Table 2.

Physical properties of alpha particle emitters.

Radionuclide	Half-life	Mean particle energy (MeV)	Maximum energy (MeV)	Maximum range (μm)
Bi-213	46 min	8.32	8.38	90
At-211	7.2 h	6.79	7.45	75

Radioactivity requirement

From dose distribution calculations, the radioactive concentration required for each radionuclide within endothelial cells lining the tumor vasculature and in nearby regions was determined. For an effective cytocidal effect, we assumed that it is essential to deposit a radiation dose of 100 Gy in every viable tumor cell. The 100 Gy target dose was used as a reference in this work, as this is the approximate dose frequently applied in low dose rate brachytherapy procedures. In practice, the cytocidal dose depends on many factors such as the dose rate, the specific type and stage of cancer being treated, and the type of radiation (therefore, the relative biological effect) to be used. Results from this study should be scaled accordingly for specific applications. Since the radiation dose at the edge of the viable tumor region is always less than that in a region closer to the endothelial cells, we calculated the initial radioactivity (IR) required to deliver a cumulative target dose of 100 Gy at viable tumor edge, 250 μm from the center of the blood vessel, and 230 μm from the endothelial cells, assuming complete on-site decay of the activity, i.e., a lasting target binding of the administered radiopharmaceutical.

Radiation dosimetry of beta emitters

The radial dose distribution of beta-emitting radionuclides was calculated using the EGSnrc code system.²¹ The electron gamma shower (EGS) system of computer code is a general-purpose package for Monte Carlo simulation of the coupled transport of electrons and photons in an arbitrary geometry. EGSnrc is a new, enhanced version of EGS developed at the National Research Council of Canada.²¹

For each beta-emitting radionuclide, a spectrum was first calculated following the method described in ICRU Report 56.²² The spectrum was weighted to account for multiple beta transition pathways and the transition end-point energies were obtained from ICRP Publication 38 (Ref. ²³) and the National Nuclear Data Center.²⁴ In EGS Monte Carlo simulations, the energy of each starting particle was first sampled from the beta spectrum. The position of the starting point was then determined so that the distribution of starting points was uniform within a cylindrical band with specified radioactive band thickness. The directional distribution of the starting particle was assumed to be isotropic. Energy deposition in each of the 10 μm shells in the 1 cm central portion of the blood vessel, as described above and illustrated in Fig. 1B, was scored. Atomic relaxations including the emission of characteristic x rays and∕or Auger or Coster–Kronig electrons were modeled explicitly in the simulations.²¹ Tissue composition from ICRU Report 44 (Ref. ²⁵) was used in the simulations. No variance reduction technique was employed. To estimate the uncertainty in the calculation, ten batches each of 1×10⁷ starting particles were initiated for each radionuclide and the average and standard deviations of the energy deposition in each shell were evaluated. The average dose in each shell was calculated by dividing the energy deposition by the tissue mass in the shell (a tissue density of 1 g∕cm³ was assumed).

For validation of EGS simulation results, radial dose distributions of yttrium-90 (⁹⁰Y) and phosphorus-33 (³³P) were calculated by integration of an empirical electron energy-loss equation. Cole²⁶ experimentally determined that for electrons of 20 eV to 20 MeV, there is an empirical relation between the electron energy E_e (keV) and range X (μm) in unit density materials

$$E_e=5.9{\left(X+0.007\right)}^{0.565}+0.00413X^{1.33}-\mathrm{0.367.}$$ (1)

Therefore, the energy-loss expression for electrons can be obtained by differentiation of Eq. 1

$$d{E}_e∕dX=3.333{\left(X+0.007\right)}^{-0.435}+0.0055X^{0.33}.$$ (2)

For an electron of energy Ei and range X(Ei), Eq. 2 evaluated at [X(Ei)−x] is the energy-loss expression of the particles after passing a distance x through the medium.²⁷ To determine the dose distributions, a dose-point kernel (DPK) method was used. First, the dose distribution around a point source was calculated using Eq. 2 and weighted by the beta spectrum. The depth-dose distribution thus obtained was used to numerically integrate dose contributions from the same radioactivity distribution as in the EGS simulations.

Some of the beta emitters also release gamma photons during decay. Since the dose delivered by gamma photons in the immediate vicinity of the decay is generally substantially smaller than that from beta particles, the dose contribution from gamma emissions was not considered in the calculations.

Radiation dosimetry of alpha emitters

The dosimetry for alpha emitters was evaluated using the DPK method as described above for beta emitters. The dose distribution around a point source was obtained with transport of ions in matter (TRIM) software,²⁸ a comprehensive program included in stopping and range of ions in matter, a group of programs for calculating the stopping and range of ions (10 eV∕amu–2 GeV∕amu) in matter using a full quantum mechanical treatment of ion-atom collisions. TRIM will compute both the final 3D distribution of the ions and also all kinetic phenomena associated with the energy loss of the ions in a layered target.²⁸

The decay schemes of the alpha emitters and their daughters were obtained from ICRP Report 38 (Ref. ²³) and National Nuclear Data Center.²⁴ Both alpha-emitting radionuclides have accompanying beta radiations. Since the energy-loss density of a beta particle is much lower than that of an alpha particle, the dose contribution from beta emissions is at least 50-fold less than that from alpha emissions.²⁹ This was also confirmed in our calculations. Therefore, the beta contribution was ignored in the dose evaluation of alpha emitters.

For the validation of the DPK-TRIM calculation, empirical equations were also used to calculate the dose distribution around a point source. The empirical equation for the range of alpha particles in 15 °C, 760 mm Hg air is³⁰

$$X_{\text{air}}=0.318E^{3∕2},$$ (3)

where X_air is in cm and E in MeV. In other media, the range is³¹

$$X=0.56\rho A^{1∕3}{X}_{\text{air}},$$ (4)

where A is the atomic mass number of the medium and ρ is the density in mg∕cm³. For tissues, the effective atomic mass number A_eff can be calculated by

$$\sqrt{A_{\text{eff}}}={\left(\sum _{i=1}^L\frac{w_i}{\sqrt{A_i}}\right)}^{-1},$$ (5)

where w_i is the weight fraction of element A_i. Combining Eqs. 3, 4, 5, the relation between alpha energy E_α (keV) and range X (μm) in a unit density, waterlike medium is

$$E_{\alpha }=417.7X^{2∕3}$$ (6)

and the energy-loss expression is

$$d{E}_{\alpha }∕d_X=278.5X^{-1∕3}.$$ (7)

Equation 7 was used to calculate the dosimetry of ²¹¹At and ²¹³Bi using the DPK method. Dose distributions thus calculated were compared to those of the DPK-TRIM method.

RESULTS

The radial dose distributions in the capillary blood vessel model were calculated for six beta-emitting and two alpha-emitting nuclides. The radioactive band thickness evaluated for each radionuclide was from 10 (no diffusion) to 400 μm (diffusion range 380 μm). The endothelial cell mean dose (ECMD), tumor-edge mean dose (TEMD), and initial radioactivity necessary to deposit a cumulative dose of 100 Gy at the edge of the viable tumor-cell region (IR) were determined for various radioactive band thicknesses.

Beta particle emitters

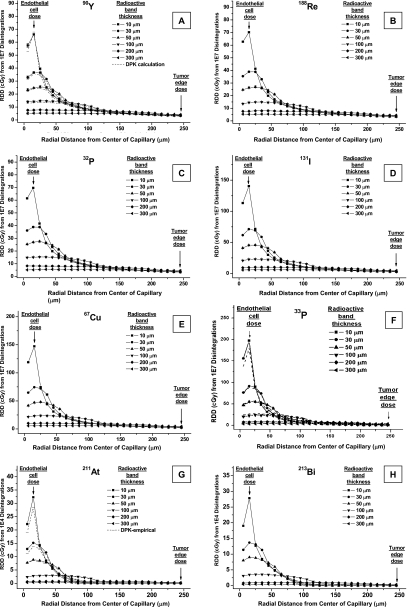
Figure 2A shows the radial dose distribution from 1×10⁷ disintegrations of ⁹⁰Y. The beta spectrum end-point energy is 2.28 MeV and its maximum range is ∼11.3 mm (Table 1). The solid lines are EGS simulation values and the dashed lines are DPK calculation values; the difference between the two is in no case greater than 12%. The worst-case uncertainty of EGS simulations is 10%.

Figure 2.

RDD of radionuclides in capillary blood vessel model of [(A)–(F)] beta emitters from 1×10⁷ disintegrations and [(g) and (h)] alpha emitters from 10 000 disintegrations. (A) ⁹⁰Y, (B) ¹⁸⁸Re, (C) ³²P, (D) ¹³¹I, (E) ⁶⁷Cu, (F) ³³P, (G) ²¹¹At, and (H) ²¹³Bi. [(A)–(F)] Solid lines are EGS simulations and in (A) and (F), dashed lines are DPK calculations. [(G) and (H)] Solid lines are DPK-TRIM calculations and in (G), dashed lines are DPK values obtained using empirical equations.

When the ⁹⁰Y radioactive band thickness is 10 μm, which is the model for radioactivity present only in the endothelium, radiation dose in the endothelial band is, as expected, significantly higher than in the viable tumor region (Fig. 2). As the distance from the center of the capillary lumen increases, the local dose in the tumor region decreases rapidly at first. Beyond a radius of 50 μm, the rate of decrease is much slower. Local dose at 250 μm (viable tumor edge) is approximately 5% of the peak dose.

As the radioactivity diffuses outward, the radioactive band thickness increases and the source density decreases. The peak local dose is lower, but TEMD changes only slightly, until the diffusion range exceeds 250 μm.

The EGSnrc simulated dose distributions for ¹⁸⁸Re, ³²P, ¹³¹I, ⁶⁷Cu, and ³³P are plotted in Fig. 2B, 2C, 2D, 2E, 2F, respectively. The dose distributions for ³³P were also validated with DPK calculations [dashed lines in Fig. 2F]. The radial dose distributions for all these other beta-emitting radionuclides follow the same pattern. However, for a radionuclide with less energetic electrons, i.e., shorter-range beta emissions, the decrease in the local dose beyond the source-containing region is somewhat steeper. For example, the end-point energy of ³³P is 0.249 MeV and its maximum range is ∼0.63 mm (Table 1). When the radioactive band thickness is 10 μm, local dose at 250 μm is only ∼0.24% of the peak dose.

Alpha particle emitters

Figure 2G shows the radial dose distribution of ²¹¹At from 10 000 disintegrations. The mean alpha energy of this radionuclide is 6.79 MeV and the average range is 60 μm.²⁰ Here, again, the solid lines are DPK-TRIM calculations and the dashed lines are DPK values obtained using empirical equations. For alpha emitters, the difference between these two methods is less than 20%. The dose distribution of ²¹³Bi [Fig. 2H] follows the same pattern.

Comparison of the dose deposited in the irradiated endothelial cells shows that the dose from the alpha-particle-emitting radionuclides [Fig. 2G, 2H] is ∼150–400 times higher than that of the beta particle emitters [Fig. 2A, 2B, 2C, 2D, 2E, 2F]. When an alpha emitter is carried by a nondiffusing molecule, depending on targeting molecular mechanism, the nuclide can be localized at the cell membrane or within the cell. In our evaluation, a complete internalization (therefore, a uniform distribution in the endothelium) was assumed. For molecules attached to the surface of cell membrane only, since cell diameter is 1∕7–1∕9 of the maximum alpha range, the penetration of dose deposition would be even shallower. In both cases, since the range of alpha particles is much shorter than the size of the tumor, the local dose beyond 100 μm is zero when radioactivity is present only within the endothelial cells. Consequently, the tumor edge receives radiation only if the radiotherapeutic agent diffuses sufficiently into the tumor, i.e., the distance between the radionuclide and the tumor edge is smaller than the range of the emitted alpha particles.

DISCUSSION

In the new treatment modality of tumor-neovasculature-targeting radionuclide therapy, a radiopharmaceutical is injected intravenously and selectively concentrates in newly recruited tumor capillary blood vessels. Radiation dose is thus deposited locally in the actively proliferating endothelial cells and the surrounding tumor cells. One branch of the modality, termed endoradiotherapy, aims to destroy the blood vessel, thus depriving the tumor cells of oxygen and nutrition supplies.³² However, viable tumor cells might still have the ability to recruit new blood vessels, be supplied by other nearby normal vessels, or migrate to generate metastases at other sites. In addition, there is clinical evidence that antiangiogenic therapy can normalize the tumor vasculature and microenvironment at least transiently. Therefore, for therapy of neovascularized tumors, a combination of cytotoxic therapy and antiangiogenic treatment is desirable.³³

In radionuclide therapy, uniformity in radioactivity distribution (and therefore radiation dose distribution) throughout the tumor is usually sought and heterogeneous activity distribution is generally considered a drawback.³⁴ Contrary to earlier calculations of dosimetry in targeted radionuclide therapy of solid tumors,^{11, 35} the present work restricts the region of tumor viability to 250 μm around tumor blood vessels. Aiming to deliver sufficient dose at the viable tumor edge rather than throughout a solid tumor, our calculations indicate that most frequently used beta emitters can be expected to be tumoricidal even when the radionuclide is confined to the blood vessel (i.e., no diffusion).

The radiation dose distribution resulting from an isotope distributed within microcylinders around a capillary blood vessel depends on its radiation characteristics and the source activity distribution. Since targeted radionuclide therapy is characterized by nonuniformities in radiation dose distribution, the mean absorbed dose in the tumor might not be the best predictor of radiotherapeutic efficacy; rather, local absorbed dose in the viable tumor region is more important for the evaluation of a radionuclide therapy modality.

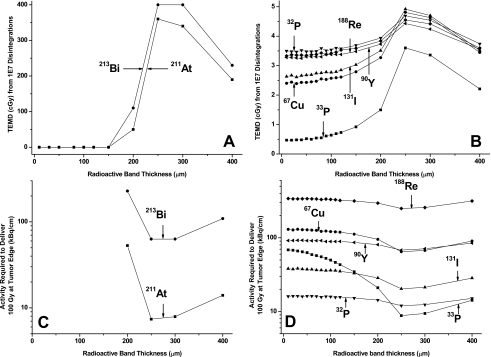
The TEMD from 1×10⁷ disintegrations as a function of the radioactive band thickness is shown in Fig. 3A (alpha emitters) and Fig. 3B (beta emitters). The IR required to deliver 100 Gy at tumor edge is plotted in Figs. 3C, 3D. For alpha emitters, since the particle maximum range (75–90 μm) is shorter than the viable tumor dimension (≤250 μm), the tumor-edge cells receive no radiation dose until the diffusion region is sufficiently large that the most energetic alpha particles reach the tumor edge [Fig. 3A]. For a given amount of total activity, the maximum tumor-edge dose is achieved (therefore, the IR required to deliver 100 Gy at tumor edge is smallest) when the source activity distribution overlaps with the viable tumor region. For energetic, long-range beta emitters, such as ⁹⁰Y, ³²P, and ¹⁸⁸Re, the TEMD curves are relatively flat when the radioactive band thickness is narrow (less than 120 μm), indicating the radiation dose at tumor edge is little affected by the outward diffusion of activity until the diffusion range exceeds 120 μm and approaches the viable tumor edge. For ⁹⁰Y, even when the radioactivity diffuses throughout the viable tumor region (with a radioactive band thickness of 250 μm), the increase in tumor-edge dose compared to that of the nondiffusion case is only 25%. The variation in IR is small for the energetic beta emitters. For less energetic beta emitters such as ¹³¹I, ⁶⁷Cu, and ³³P, the TEMD and IR [Figs. 3B, 3D] are between that of energetic beta emitters and alpha emitters.

Figure 3.

[(A) and (B)] TEMDs from 1×10⁷ disintegrations at various radioactive band thickness; (A) alpha emitters and (B) beta emitters. [(C) and (D)] Activities required to deliver 100 Gy at tumor edge for various radioactive band thickness; (C) alpha emitters and (D) beta emitters.

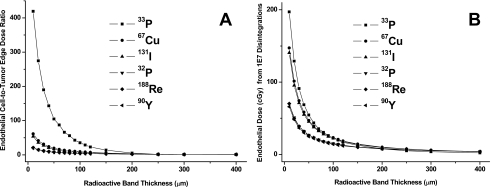
The endothelial-cell-to-tumor-edge dose ratios of beta emitters for various diffusion ranges are plotted in Fig. 4A. With no diffusion, the endothelial-cell-to-tumor-edge dose ratio is ∼420 for ³³P and ∼20 for ⁹⁰Y. When the radioactivity diffuses outward, this ratio becomes unity when the diffusion range approaches and surpasses the viable tumor edge. The endothelial doses of beta-emitting nuclides from 1×10⁷ disintegrations are plotted in Fig. 4B. Without diffusion, endothelial cells receive a higher dose with lower-energy beta emitters. The differences among various radionuclides become smaller as the diffusion range increases.

Figure 4.

(A) Endothelial-cell-to-tumor-edge dose ratios of beta particle emitters for various radiopharmaceutical diffusion ranges. (B) Doses to endothelial cells from 1×10⁷ disintegrations of beta particle emitters at various radioactive band thickness.

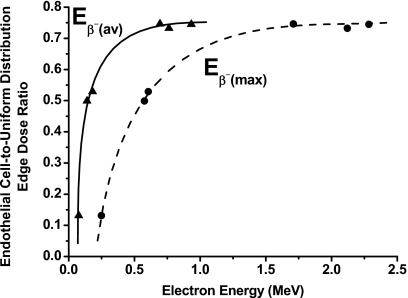
When the end point of treatment is to deposit a cytocidal dose in all the tumor cells, the ratio of tumor-edge doses at radioactive band thickness of 10 (no diffusion, radioactivity in endothelial cells only) and 250 μm (optimal radiopharmaceutical diffusion range) is an indication of the benefit achievable by radionuclide diffusion. Figure 5 plots this ratio as a function of mean [E_β⁻(av)] and maximum [E_β⁻(max)] beta energies. For beta-emitting radionuclides with E_β⁻(av)≥0.7 MeV [E_β⁻(max)≥1.7 MeV], the ratio changes slowly, indicating the tumor-edge dose increases only slightly with diffusion. For low-energy beta emitters, however, this ratio is much smaller and has a very steep slope, demonstrating that radionuclide diffusion is essential for the tumor edge to receive an adequate dose. As shown above, penetration into the tumor is also vital for alpha particle emitters.

Figure 5.

Ratio of endothelial-cell-to-tumor-edge doses at radioactive band thickness of 250 μm (uniform radioactivity distribution throughout viable tumor region) as function of mean [E_β⁻(av)] and maximum [E_β⁻(max)] beta particle energies.

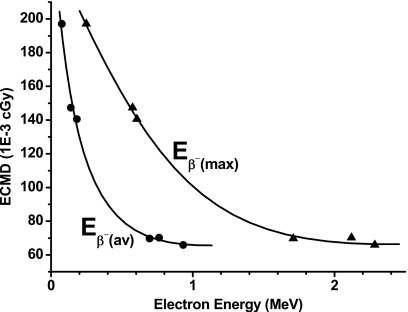
When the end point of treatment is to destroy the newly recruited capillary blood vessels, a radiopharmaceutical without diffusion would be preferred. Figure 6 plots the endothelial cell mean dose (from 10 000 disintegrations) as a function of E_β⁻(av) and E_β⁻(max) when the radioactivity is constrained within the endothelial cells. As expected, the dose is highest with decreased beta-particle energy, i.e., more energy is deposited locally. Consequently, ³³P is the most effective among beta emitters for antiangiogenesis radiation therapy, although not as effective as alpha emitters which have the additional advantage of their high LET.

Figure 6.

ECMD from 10 000 disintegrations when radioactivity is constrained within 10 μm as function of mean [E_β⁻(av)] and maximum [E_β⁻(max)] beta particle energies.

We estimated the radioactivity to be administered in neovasculature-targeting radioimmunotherapy based on our simulation data. For radionuclides confined to the endothelium, the radioactivity required for delivery of a 100 Gy target dose to the tumor edge and∕or endothelial cells is listed in Tables 3, 4. The number of radio atoms per endothelial cell is estimated by assuming that each endothelial cell is a compressible sphere, 10 μm in diameter. It is evident that the endothelial cells receive much more radiation dose than the tumor edge in all cases. However, once the endothelial cells acquire a radiation dose sufficiently high to functionally destroy the blood vessel, the tumor-edge cells will suffer from a combined effect of radiation damage and deprivation of oxygen and nutrients. Therefore, a smaller dose at the tumor edge might suffice.

Table 3.

EC-associated radioactivity (IR) needed to deposit 10 000 cGy for beta particle emitters confined to endothelium.

Nuclide	10 000 cGy at tumor edge			10 000 cGy per endothelial cell
	kBq∕cm	Radioactive atoms per cm	Radioactive atoms per ECa	kBq∕cm	Radioactive atoms per cm	Radioactive atoms per ECa	Tumor edge dose (cGy)
Y-90	91.6	3.05×1010	1.69×106	4.56	1.52×109	8.43×104	498
Re-188	340.2	3.00×1010	1.67×106	16.1	1.42×109	7.90×104	474
P-32	16.1	2.87×1010	1.59×106	0.81	1.44×109	8.02×104	502
I-131	38.0	3.79×1010b	2.11×106b	0.71	7.08×108b	3.93×104b	187
Cu-67	130.0	4.17×1010	2.32×106	2.12	6.81×108	3.78×104	163
P-33	68.4	2.17×1011	1.20×107	0.16	5.07×108	2.81×104	24

^aEstimated by assuming each endothelial cell is a compressible sphere, 10 μm in diameter.

^bMust be multiplied by ∼20 to correct for low specific activity of ¹³¹I.

Table 4.

EC-associated IR needed to deposit 10 000 cGy for alpha particle emitters confined to endothelium.

10 000 cGy per endothelial cell
Nuclide	kBq∕cm	Radioactive atoms per cm	Radioactive atoms per ECa	Tumor edge dose (cGy)
Bi-213	0.902	3.59×106	1.99×102	0
At-211	0.0826	3.10×106	1.72×102	0

^aEstimated by assuming each endothelial cell is a compressible sphere, 10 μm in diameter.

The radioactivity requirements in Tables 3, 4 are calculated assuming binding of any radionuclide administered to the target and an infinite radioactivity residence time (during which the radionuclide stays in the target) at that site. In practice, however, the biological half-life of the isotope (i.e., removal of the radioactive compound from the target area) must also be considered. As a first approximation to this effect, if the residence time of radioactivity in the tumor is T, then the percentage (P) of atoms decayed at the target can be estimated as

$$P={100}^{\star }\left(1-N_T∕N_0\right)={100}^{\star }\left(1-\text{exp}\left(-{0.693}^{\star }\left(T∕T_{1∕2}\right)\right)\right),$$ (8)

where N₀ is the total number of atoms initially binding to the target, N_T is the remaining undecayed atoms at time T, and T_1∕2 is the physical half-life of the radionuclide. Therefore, for a certain percentage of atoms to decay at the target, the expected residence time of radioactivity can be calculated as

$$T=T_{1∕2}^{\star }\text{\hspace{0.17em}ln}\left(1-P∕100\right)∕\left(-0.693\right).$$ (9)

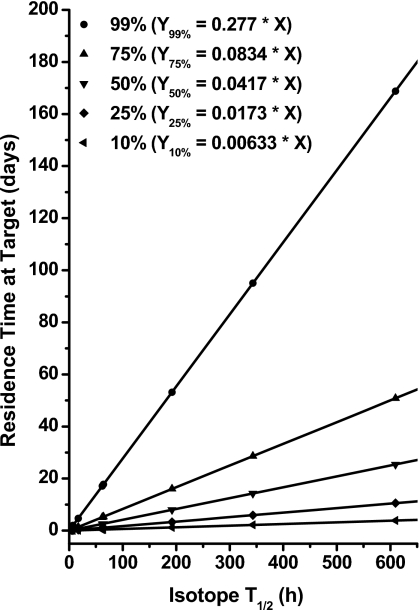
The required residence time for an isotope to have 99%, 75%, 50%, 25%, and 10% of atoms decayed at the target is plotted in Fig. 7 for radionuclides with varied half-lives. For radioisotopes with a short half-life, such as ²¹³Bi, a residence time of less than 10 h would be sufficient for most atoms to decay at the target. For isotopes with a long half-life, such as ³³P, a significant proportion of radioactive atoms might leave the target prior to their decay. These findings reiterate the importance of matching the physical half-life of an isotope with that of the carrier molecule.³⁶

Figure 7.

Required residence time for isotope to have 99%, 75%, 50%, 25%, and 10% of atoms decayed at target. In equations, X is the isotope half-life in hours and Y is the required residence time in target in days.

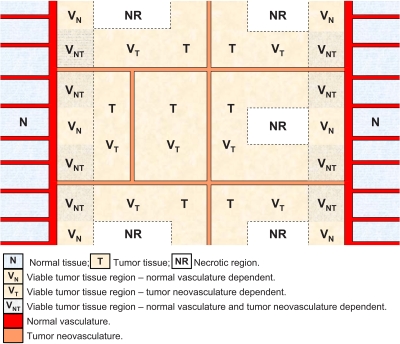
Tumor environment is yet another factor to be considered. A tumor is usually surrounded by or adjacent to normal tissue with normal vasculature. Therefore, a viable region in a tumor could depend on the normal vasculature or neovasculature or both for its supply of oxygen and nutrients. Figure 8 is a schematic showing the types of regions that are likely to be present within solid tumors. Assuming that only tumor neovasculature is targeted, tumor cells within the neovasculature-dependent viable region (V_T in Fig. 8) can be eliminated by either antiangiogenic agents or radionuclides. For regions that also depend on normal vasculature (V_NT), nonradioactive antiangiogenic agents would not be effective; but if the neovasculature is targeted with radionuclides, such tumor cells could be killed so long as the range of the particulate emission(s) equals or exceeds the V_NT cell region and the energy deposited is cytocidal. However, for viable tumor tissue regions that depend solely on normal vasculature for survival (V_N region), antiangiogenic agents (radioactive∕nonradioactive) will never be curative. Consequently, if the goal is the deposition of a tumoricidal dose in every tumor cell, tumor-cell targeting radiopharmaceuticals are the only option. In practice though, other factors must also be taken into account, such as the cross-irradiation dose contribution when long-range beta emitters are used, and the hypoxic conditions at tumor margins. Cross-irradiation occurs if two neovasculatures are sufficiently close such that radionuclides binding to one blood vessel deposit considerable energy within the viable tumor region of the other vessel, leading to underestimation of radiation dose deposited in the irradiated tumor cells. For the viable tumor edge, i.e., tumor cells that are at the end of the oxygen or nutrition diffusion range, the cells are likely to be within a hypoxic environment and relatively resistant to radiation, thereby requiring a higher radiation dose.³⁷

Figure 8.

Schematic of tumor blood supply.

In our first-order approximations, homogeneous radioactivity distributions were assumed for different diffusion ranges. In reality, the biodistribution is often complex and depends on the targeting mechanism of specific molecules. For tumor-targeting radiopharmaceuticals administered intravenously, the radial distribution around a vessel is more likely to be higher toward the lumen of the vessel, decreasing with the distance. While this will not affect our conclusion with long-range radionuclide (energetic beta emitters), for shorter-range beta and alpha emitters a larger administered dose of radiopharmaceutical would be necessary for effective tumor-edge control with a tumoricidal end point. Finally, since the viability of cells within neovascularized solid tumors is heterogeneous, a uniform dose distribution may not be a necessity in radionuclide therapy. Instead, local dose distribution at viable tumor regions, rather than a mean dose inthe tumor, should be evaluated for a treatment regimen.

CONCLUSIONS

For neovascularized tumors, the treatment with neovasculature-targeting radionuclide therapy should have a twofold end point: To functionally destroy the newly recruited capillary blood vessels (i.e., functional or necrotic death of endothelial cells) and to prohibit the reproduction of viable tumor cells (i.e., reproductive or mitotic death of tumor cells). When a short-range radionuclide (such as alpha emitters and low-energy beta emitters) is used, a nondiffusing radiopharmaceutical is preferred for an antiangiogenic end point, but the radiopharmaceutical must diffuse through the viable tumor region for a tumoricidal end point. When an energetic beta emitter is used, since the tumoricidal benefit achievable with diffusion is limited, a nondiffusing radiopharmaceutical should be chosen. Radioactive antiangiogenic agents would not be effective for viable tumor tissue regions that depend on normal vasculature for oxygen and nutrient supplies. In selecting the radiopharmaceutical for treatment, it is important to match the physical half-life of a radionuclide with the residence time of its carrier molecule in the target. The presented data quantify the interplay between irradiation of the new vasculature, the surrounding viable tumor cells, and the physical properties of commonly used radionuclides, and can be used to assist estimation of radioactivity to be administered for neovasculature-targeted tumor therapy.