Computational exploration of mobile ion distributions around RNA duplex

Abstract

Atomically detailed distributions of ions around an A-form RNA are computed. Different mixtures of monovalent and divalent ions are considered explicitly. Studies of tightly bound and of diffusive (but bound) ions around 25 base pairs RNA are conducted in explicit solvent. Replica exchange simulations provide detailed equilibrium distributions with moderate computing resources (20 nanoseconds of simulation using 64 replicas). The simulations show distinct behavior of single and doubly charged cations. Binding of Mg²⁺ ion includes tight binding to specific sites while Na⁺ binds only diffusively. The tight binding of Mg²⁺ is with a solvation shell while Na⁺ can bind directly to RNA. Negative mobile ions can be found near the RNA but must be assisted by proximate and mobile cations. At distances larger than 16Å from the RNA center, a model of RNA as charged rod in a continuum of ionic solution provides quantitative description of the ion density (the same as in atomically detailed simulation). At shorter distances, the structure of RNA (and ions) have significant impact on the pair correlation functions. Predicted binding sites of Mg²⁺ at the RNA surface are in accord with structures from crystallography. Electric field relaxation is investigated. The relaxation due to solution rearrangements is completed in tens of picoseconds, while the contribution of RNA tumbling continues to a few nanoseconds.

I. Introduction

RNA is an important biological molecule with a diverse set of biological functions ¹. It is also intriguing from a chemical physics viewpoint since it is a highly charged linear polymer with unusual interactions with its counter ions. Each monomer in RNA carries a single (negatively charged) phosphate group, leading to a large spatial charge density. The linear charge density of the A-form of RNA is about 0.31 eÅ⁻¹. Such high concentration of negative charges requires a significant number of counter ions to keep the solution neutral. The combination of the high charge density of the polyelectrolyte (the RNA) and high density of counter ions result in a number of intriguing phenomena not found in simple electrolytes. For example, we find (i) ions binding sites near the RNA molecule ² and (ii) a cloud of ions surrounding the polyelectrolyte ³. Ion mixtures of different charges (eg. Na⁺ and Mg⁺²) are frequently necessary to ensure biological function.

The excess electrostatic repulsion between elementary units of RNA in the absence of counter ions is extremely high. If the repulsion is left “as is” it will reduce the flexibility of the macromolecule and increase the persistence length of the polymer making the stretched conformation a more plausible state ⁴. Empirically we find that many sequences fold into complex reasonably compact conformations ^{5, 6}. The effective electrostatic repulsion of monomers in RNA must be reduced or balanced by other interactions. Indeed, shielding by counter ions reduces the “naked” RNA charges and plays a crucial role in the determination of RNA structure and dynamics. With shielding (and “ion condensation” ³) the electrostatic repulsions between phosphate groups are made comparable to the attractive short-range hydrogen bonding and hydrophobic stacking. These concrete short-range interactions provide stability to specific RNA folds. Overcoming (long-range) electrostatic repulsion is important kinetically as well. These interactions must be reduced to allow the relevant groups to approach each other and turn on the attractive short-range interactions.

With the above stated, it is no surprise that counter ions make a significant contribution to the energetic, stability, and dynamics of RNA, as was demonstrated in numerous experimental and theoretical studies (for reviews see 3, 7-12). Of particular simplicity and insight is Manning’s condensation theory ¹³. In this theory counter ions are found to accumulate (condense) near a wire with constant charge density. The number of condensed ions is only weakly dependent on the bulk concentration of the counter ions if the charge density of the polymer is above a critical value.

On the other hand RNA is not an infinitely long linear wire. Biological A-form RNA has a finite width and length and complex helical shape that is likely to impact ionic distributions at short distances. Short distances are where the Manning theory makes its most intriguing observations. Moreover, besides the condensation effect, concrete binding sites of individual ions (retaining or not retaining their primary solvation shells) are of considerable interest. These binding sites are illustrated experimentally by X-ray crystallography ^14-17, and play a significant role in determining three-dimensional structure and function of RNA. The finite size of the ions and their tightly bound solvation shells are necessary to accurately describe ion-RNA binding. Intriguing observations about the impact of the size of the ions in RNA folding were made in ¹⁸. A theoretical description of concrete binding sites and of finite sizes of ions can be done effectively with the Molecular Dynamics approach ^19-32. Other theoretical studies made significant contributions to our understanding of different forms of ionic binding ^{3, 33-35}.

Studies of the bound (but diffusive) ion clouds that neutralize a significant fraction of the charge of the polyelectrolyte are of considerable interest and are usually studied with distribution functions. The high mobility of the ions makes it possible to measure distributions but not locations of individual ions. Experimental techniques, such as SAXS spectroscopy ^36-39 and AES ⁴⁰, are averages over time and space and when joined with simulations can provide a comprehensive picture of polyelectrolyte solutions. Here we focus on unified computer simulations of disparate phenomena such as bulk solution of electrolytes, diffusive clouds around RNA and specific binding of ions at the RNA surface. We compare ion binding sites predicted by the simulation to those observed in X-ray diffraction experiments. Comparison to properties of diffusive cloud of ions in SAXS experiments and the simulation is in progress (Serdal Kirmizialtin, Suzette Pabit, Lois Pollack and Ron Elber, work in progress).

Theoretical and computational studies of ionic distribution around nucleotides span decades ^{3, 20-22, 24-27, 29, 30, 33-35} However, most of the investigations focused on DNA, which is similar but crucially different from RNA. The most obvious experimental evidence for the difference is the richer set of three-dimensional structures that RNA folds into ^41-44. Indeed RNA molecules perform a wide range of biophysical functions including coding, transport, catalysis, and more while DNA has a narrower function and is a storage device for genetic information. Even at the common double helix level RNA and DNA differ. RNA prefers the A-form under physiological conditions while DNA adopts the B-form.

The growing interest in RNA and its interactions with ions motivates the present study. However, another important (and necessary) incentive is the significant advancement in computer power and simulation methodology. The calculations presented here were difficult to pursue about ten years ago. We use Replica Exchange simulations ⁴⁵ on 64 cores to simulate thermal properties of the system over a period of twenty nanoseconds. These simulations make it possible to obtain quantitative distribution functions of ion atmospheres around the A form of RNA.

Besides questions about specific binding sites and a quantitative description of ionic atmospheres around A form of RNA we are also interested in mixtures of different counter ions, their possible correlations, and their interactions with RNA. For example, it is well known that a minimal amount of doubly charged cations such as Mg²⁺ is required for some RNA molecules to fold (see for instance ^{7, 8, 12, 39, 40, 46-48}). This observation suggests a profound difference in the interaction of singly and doubly charged cations. Can these differences be explained and reproduced in simulations?

The ion atmosphere clearly depends on the conformation of the RNA that we wish to study. We have chosen to use the A-form of RNA due to its simplicity, general theoretical understanding of related shapes (charged cylinders), and its abundance as a typical secondary structure element in more complex RNA shapes. Other groups have simulated RNA in an ionic environment ^{23, 24, 27, 29, 31, 49, 50} however, these studies were not focused on ionic mixtures and their interactions with RNA.

Concrete binding sites were illustrated experimentally by X-ray crystallography, providing excellent structural models that can be further analyzed to understand thermodynamic properties of ions that binds to specific sites near the RNA molecule ¹⁴. Ion that can be found between 0 and 10Å from the line of center of the RNA are called “near RNA”. The cutoff distance above was not chosen arbitrarily but is based on clearly separated phases of charge neutralization that we discuss later in the paper.

A significant challenge in studying binding of ions to a polyelectrolyte is the solvation shell. The first solvation shell is strongly bound to the cation and the removal of these water molecules upon binding to the RNA (if required) is associated with a significant free energy barrier. The large barrier makes the sampling of these transitions difficult with Molecular Dynamics. While water exchanges at the first solvation shell of Na⁺ are frequent, exchanges of water molecules at the first solvation shell of the magnesium ions are extremely rare. The last are observed only at the highest temperatures of the replica exchange simulations. As a result we do not observe binding of “bare” magnesium ions to RNA atoms (without a bridging water molecule). Interestingly as we discuss later in the manuscript the crystallographically observed binding sites of the magnesium ions, that are modeled from the scattering data without their first solvation shell, are well reproduced in the simulations with magnesium ions that retain their first solvation shell.

II. Methods

All the calculations were carried out with the Molecular Dynamics package MOIL ⁵¹. MOIL is a general-purpose suite of programs for simulations of macromolecules. The suite of programs is available for free download at https://wiki.ices.utexas.edu/clsb/wiki. A graphic user interface (written in tcl/tk) and a visualization program, ZMOIL, are tightly coupled to the simulation package and are also available from the same web site. All the images of the RNA and the ions of this manuscript were plotted with ZMOIL.

Originally MOIL included only a force field for protein simulations⁵². Recently nucleic acid force fields of AMBER f99 ⁵³ and OPLS ⁵⁴ were implemented in MOIL. We have extensive experience with OPLS (OPLS-UA and OPLS-AA) for protein simulations and the TIP3P water model and it therefore made sense for us to continue using the OPLS-AA force field also for RNA simulations. The OPLS-AA parameters for the nucleic acid bases of RNA are readily available⁵⁴. We choose to use AMBER f99 for the bonded terms while keeping the nonbonded term as OPLS-AA. The bonded term has negligible contributions anyway since in all the simulations (with the exclusion of one) the RNA was rigid. In the single simulation in which the RNA was allowed to tumble (see Discussions) its covalent structure was further rigidified by distance constraints between the phosphates (and therefore the impact of the covalent parameters was small). The parameters used are provided in Supplementary Material.

Ideally the simulations would allow the motions of solvent and RNA; however, in the present case there are a number of reasons why a rigid RNA for the study of ionic solvation is a better choice:

1. The RNA A-form is a rigid molecule. For example the persistence length of RNA is of order of 500Å⁵⁵ while the B-factors are especially small (about 8 per residue) ¹⁶.

2. Our study focuses on the properties of the ions, their thermodynamic properties and their mobility near the polyelectrolyte. There is a vast number of studies that model the RNA as rigid and describe the properties of the ions by continuum theories. These theories provide useful insight and reproduce numerous experiments (see for instance^{37, 39, 56}). It is desirable to bridge these studies with calculations that take into account the microscopic structure of solvent and ions. Keeping the RNA rigid makes the comparison with these studies more straightforward and natural.

3. The quality of force fields for simulations of RNA is still under debate (for a recent publication see Besseova et al⁵⁷). Focusing on ion dynamics while keeping the RNA rigid reduces the uncertainties in the calculations, and makes comparison to other theories and experiments more meaningful.

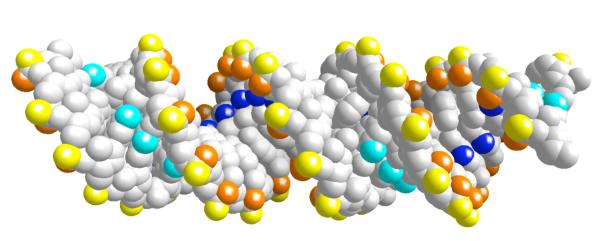
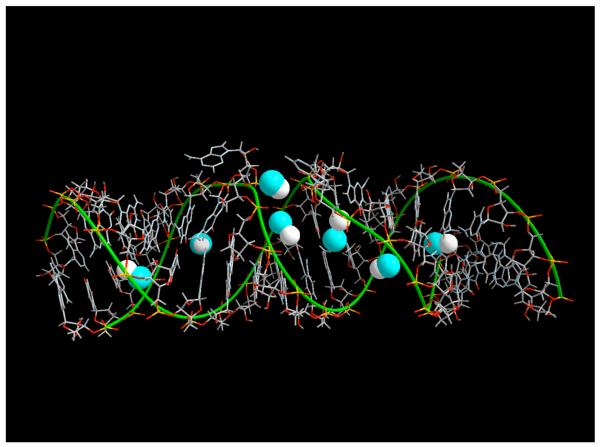
We considered the RNA strand (GCAUCUGGGCUAUAAAAGGGCGUCG) and its complementing sequence and constructed an ideal A-form of RNA for the simulation. This sequence was selected because of experimental preferences (Lois Pollack, private communication). The A-form was embedded in a periodic box (size 58.8×58.8×88.2ų) of aqueous solution of about 29,200 atoms (figure 1). We simulated five different excess concentrations of ions (0.4M Na⁺, 0.2M Mg⁺², 0.3M Na⁺ & 0.05M Mg⁺², 0.2M Na⁺ & 0.1M Mg⁺², and 0.1M Na⁺ & 0.15M Mg⁺²). The excess was with respect to neutralizing cations (total charge of 48|e|) that are added separately from the concentrations mentioned above. This neutralization technique makes the definition of the concentrations somewhat more complicated than usual. The excess ions influence the distributions of the rest of the charged particles (the neutralizing ions are not necessarily bound near the RNA). Therefore the simulated concentrations are at variance with the concentrations quoted above, which are added to the ions that neutralize the RNA charges.

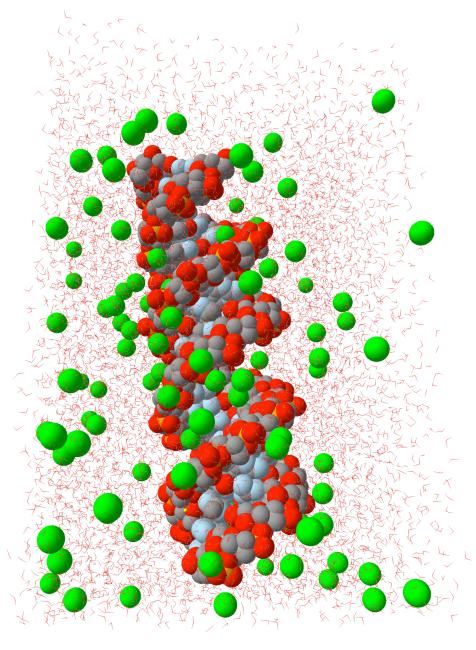
Figure 1.

A three-dimensional picture of the RNA molecule, the water box and the sodium ions around the RNA molecule. This is a snapshot in time taken after the equilibration period.

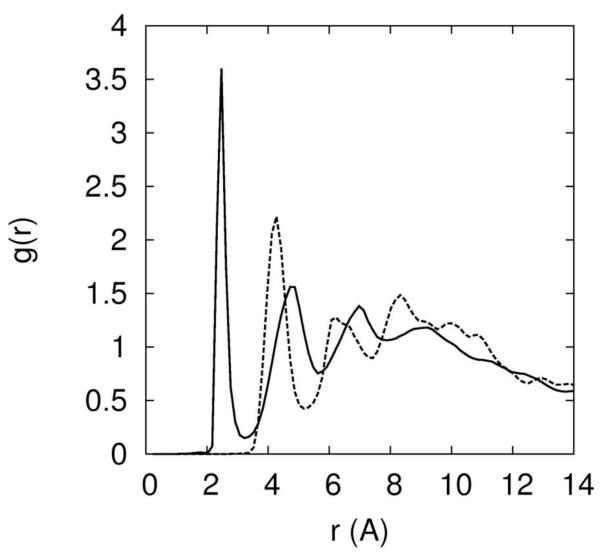
To determine the actual simulated concentrations we probe the distributions of the ions as a function of distance from the RNA (figure 2). At sufficiently large distances (that can be achieved in our finite system) the concentrations approach constant values. The convergence is evident for Mg⁺² distribution (figure 2b) but is not so obvious for Na⁺ (figure 2a). These constant values are identified as the asymptotic bulk concentrations. The asymptotic concentrations of the three ions in different mixed solutions are listed below in brackets (sodium, chloride, magnesium) following the corresponding excess concentration: 0.4 Na⁺ (0.53,0.53,0.0), 0.2Mg²⁺ (0.0,0.45,0.20), 0.3 Na⁺ 0.05Mg²⁺ (0.39,0.43,0.035), 0.2Na⁺ 0.1Mg²⁺ (0.28,0.43,0.076), 0.1Na⁺ 0.15 Mg²⁺ (0.19,0.43,0.11). In the rest of the article we always refer to the set-up concentrations. The translation from excess to asymptotic concentration is given by the data above. Clearly, the asymptotic concentration is influenced more by the excess sodium than by the excess magnesium. This is an indication (not surprisingly) that Mg²⁺ ions bind more tightly to the RNA.

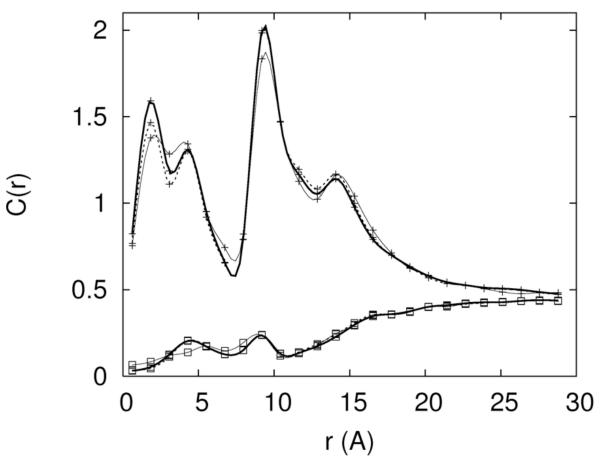
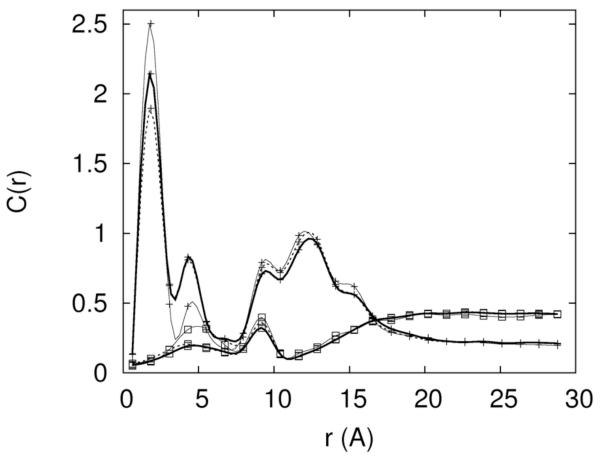
Figure 2.

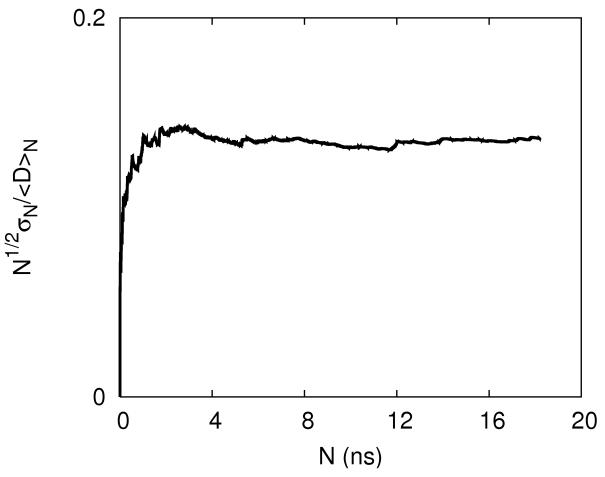
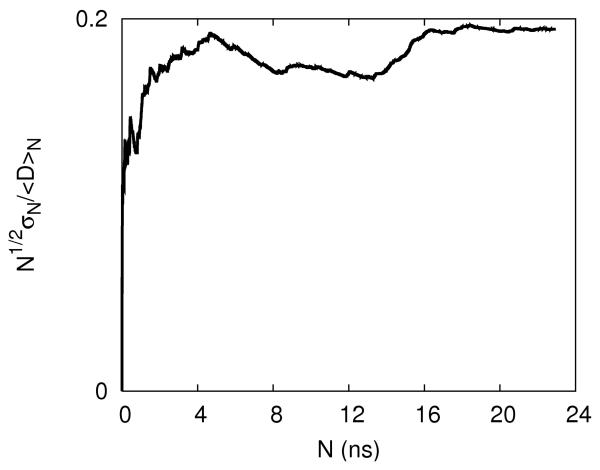
An illustration of the convergence of the equilibrium distributions during the replica exchange simulations. 2.a-The concentrations of Na⁺ (cross) and Cl⁻ (open square) are shown as a function of distance from the line of the center of the RNA molecule. The thin solid line, dashed line and thick solid line are the calculated distributions from 5-10, 5-15 and 5-20 nanoseconds respectively. 2.b-the same as 2a this time for magnesium. 2.c- An alternative convergence criteria is defined as the square root of the number of data points N times the ratio of variance to the mean of the observable D. Here D is defined as the total number of ions within 5Å distance from the RNA. The convergence criterion as a function of data points is shown for Na⁺ ions. 2.d Same as 2c this time the observable is the average number of Mg⁺² ions. It is the case of slowest convergence.

Ions were placed in the box by replacing oxygen atoms of water molecules in the pure water box by the ions. This procedure provides reasonable but suboptimal initial configurations for the equilibrium simulations. The initial configurations were therefore equilibrated extensively.

A sampled equilibrium configuration is shown in figure 1. In figure 1 we show a finite A-form of the RNA double helix. The water molecules are red sticks and the sodium ions are in green. Note the very deep grooves that are typical of the A form. The grooves are less pronounced in the B form of polynucleotide which is the common double helix of DNA. These deep grooves add considerable structure to the double helix and its interactions with ions and create a diverse map of ionic binding sites.

We simulated the thermal properties of the solution while keeping the RNA molecule frozen. Only the water molecules and the ions were free to move. Only in one simulation (described in the Discussion) that probes the relaxation of the electric field in RNA we allow the RNA to tumble. The water molecules were kept rigid using a symmetric matrix SHAKE algorithm⁵⁸. Particle Mesh Ewald⁵⁹ was used to compute long-range electrostatic interactions. The distance cutoff for the Lennard Jones and electrostatic interactions was 9Å and 12Å respectively. The total energy conservation was tested by running a single simulation in the NVE ensemble with a time step of 1.5 femtosecond. The drift was less than 0.3 percent over a period of one nanosecond suggesting that our integration protocol is sound. The NVE simulation was not used in further analyses. In the production runs the sampling was from the canonical ensemble using velocity scaling every 40 steps. No energy or temperature drifts were observed during the production runs.

Replica exchange simulations were carried out for each of the ion mixtures mentioned above. The 64 replicas were distributed between temperatures 296 and 450K and were run on 64 independent cores. The procedure to choose the temperatures and their actual values are summarized in Supplementary Materials. Attempts for an exchange between a pair of replicas at nearby temperatures were sampled at random. On the average, in every 5 picoseconds a flip for each of the replica pairs was attempted. To maintain output simplicity, each of the processors was assigned a fixed temperature and full coordinate and velocity vectors were transmitted between the cores. Sending only the temperatures reduces communication data considerably, however, the output is somewhat more difficult to interpret. The communication overhead was found to be negligible compared to the cost of integrating the equations of motion. Therefore no attempt to optimize communication times was made.

Acceptance or rejection of a replica flip is decided according to ⁴⁵

$$P_{\mathit{acc}}=\min \left[1,\exp \left(\left({\beta }_i-{\beta }_j\right)\left(U\left(r_i\right)-U\left(r_j\right)\right)\right)\right]$$

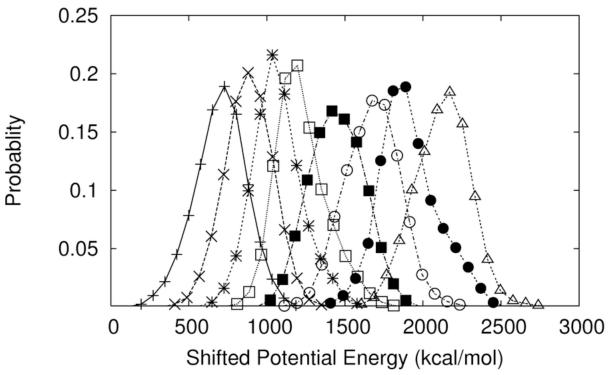
The configuration of a replica k is denoted by r_k, the potential energy is U (r_k), and the inverse temperature is β_k = 1/k_BT_k. The average acceptance probability of attempted temperature flips was about 0.2 to 0.3. Significant overlaps between the energy distributions of the runs at different temperatures were observed allowing for frequent exchanges between the alternative temperatures and more rapid approach to the equilibrium distribution at room temperature. In figure 3 we show a sample of potential energy distributions (at eight different temperatures) illustrating the substantial overlaps between the distributions that allow efficient exchange rates between the replicas.

Figure 3.

An illustration of the quality of overlaps between replicas in the simulations. The distribution of the potential energies sampled during the runs of replicas 13-20 with temperatures 319.5(+), 321.6(X), 323.6(*), 325.6(open squares), 327.7 (filled squares), 329.8 (open circles), 331.9 (filled circles), and 334.1 (open triangles). The origin of the potential energy was shifted to guide the eye; the bin size that was used to collect the statistics was 40 kcal/mol.

The total length of the simulation for each ionic concentration was about 20 nanoseconds. The first 5 nanoseconds were used for equilibration. To check the convergence of the simulation we divide the rest of the data into three sets and calculate the ion distributions as a function of distance from RNA between 5-10ns, 5-15ns and 5-20ns time intervals. We show in figure 2a the sodium and chloride ion distributions as a function of distance from the center of the RNA in pure NaCl aqueous solution (0.4M), figure 2b is for pure MgCl₂ aqueous solution (0.2M). The distributions at distances larger than 5Å of the time windows 5-15ns and 5-20ns deviate only slightly from each other in the last two sets, suggesting that the calculations converged. The deviations are most significant for the first time slice (5-10ns), but even there the locations of the peaks are quite accurate. Below 5Å the differences between the first time slice and the other two time windows are the largest. However, even the largest deviations do not impact significantly the peak positions. The shorter distances from the RNA center correspond to smaller volumes and lower statistics that explain the larger error bars. Interestingly the 5-15 and 5-20ns distributions appear converged even for the chloride ions. The distribution of the chloride ion is (of course) depleted significantly near the RNA. Together with the small volume close to the origin the statistics of chloride ions is significantly more sparse and the calculations are more difficult compared to cations.

The calculations of the statistical error bars assume that the data points D_i generated by the trajectories are sampled independently from the equilibrium distributions. It is assumed that there is no long-range correlation between the sample points that are used to compute observables. The long-range correlation causes a slow change in the observables that is sometimes called “drift”. This (non-trivial) assumption cannot be verified rigorously in typical simulations. However, we tested it as described below using an independent heuristic.

If there is no “drift” then the averages computed from these samples follow the law of large numbers from statistics ⁶⁰. The law of large numbers states that the mean, ⟨D⟩_N of N data points divided by its standard deviation σ_N should be proportional to N^1/2, i.e. the function c(N)= N^1/2σ_N/⟨D⟩_N is a constant for sufficiently large N. If the function c(N) is not a constant, then a drift is present and the sampling is incomplete. We use c(N), the convergence function, as a test. This test is heuristic since it is possible to find a c(N ) which appears to be constant as a function of N in unconverged simulations if the time scale of starting the drift is much longer than the simulation time. However, in practice and in conjunction with replica exchange, we found it to work quite well. The high temperature replica allow for more rapid mixing and observation of drift (if exists) at shorter time scales.

In figure 2.c-d we show two convergence-plots of a number of ions bound to RNA. The first plot is typical (converging after about 5 nanoseconds of simulation) and the second is more surprising, illustrating late convergence (around 16ns). It was illustrated that tens of nanoseconds of simulation times are required to converge binding of ions to DNA ⁶¹. However, these simulations were done at room temperature. Our replica exchange simulations equilibrate faster, as evident from the measures of convergence that were presented above.

III Results

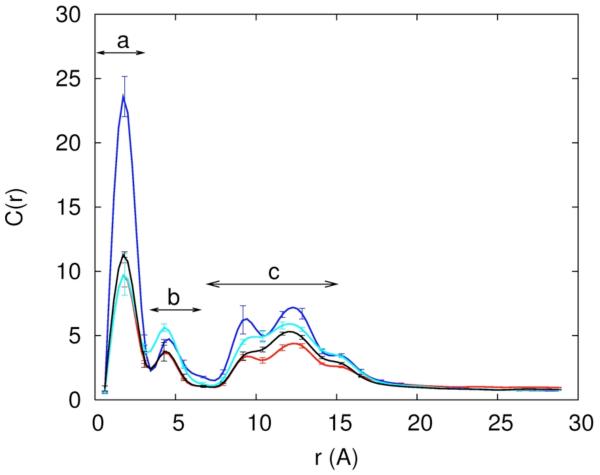
In figure 4 we show the ion concentration as a function of distance from the RNA line of center. Figure 4.a illustrates the distribution of Na⁺ in four different mixtures: pure NaCl 0.4M, 0.3M (and 0.05M Mg²⁺ concentration), 0.2M (0.1 Mg²⁺), 0.1M (0.15M Mg²⁺). The concentrations are normalized with respect to the bulk ion concentrations, at large distances from the RNA all normalized ions concentrations approach a constant value of 1. Figure 4.b includes the corresponding plot for Mg²⁺.

Figure 4.

The normalized concentration profile of ions as a function of distance from the line of center of the RNA. The normalization is to one at large distances. 4.a – Concentration profiles of Na⁺ ions ( 0.4M NaCl -- red 0.05M MgCl₂ and 0.3M NaCl -- blue; 0.1M MgCl₂ and 0.2 NaCl – cyan; 0.15M MgCl₂ and 0.1M NaCl – black) Letters on top correspond to site binding regions at the RNA 4.b Concentration profiles of Mg⁺² ions ( 0.05M MgCl₂ and 0.3M NaCl -- blue; 0.1M MgCl₂ and 0.2M NaCl – cyan; 0.15M MgCl₂ and 0.1M NaCl – black; 0.2M MgCl₂ – red) .Letters on top of the plots mark the different binding regions at the RNA.

The box size that we employed in the calculations is sufficiently large to reach flat equilibrium distribution far from RNA in most of the simulations. Aqueous solution of MgCl₂ reaches bulk properties as a function of distance from the line of center of the RNA at about 18Å. In contrast, the RNA charges extend their influence in NaCl solution to about 25Å. This is another illustration that the magnesium ions bind more closely to the RNA following the discussion about the effective bulk concentration of the pure salts and their mixtures.

At short distances the distributions we obtained for all mixtures (including the pure salt cases) are more complex than distributions from analytical models that simplify the detailed structure of the RNA and of the solvent molecules. Some of the short range effects are related to the detailed structure of the RNA. However, other ”anomalities” are related to the types of ionic binding (near RNA or loosely bound ions). This is (of course) not surprising. What is remarkable and illustrated in the Discussions is that analytical theories are quantitative at distances of about 16 angstrom from the RNA line of center (the most extended RNA atoms are within 12Å from the line of center).

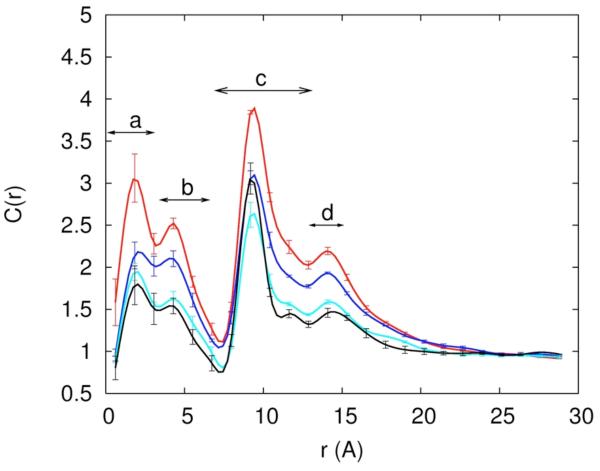
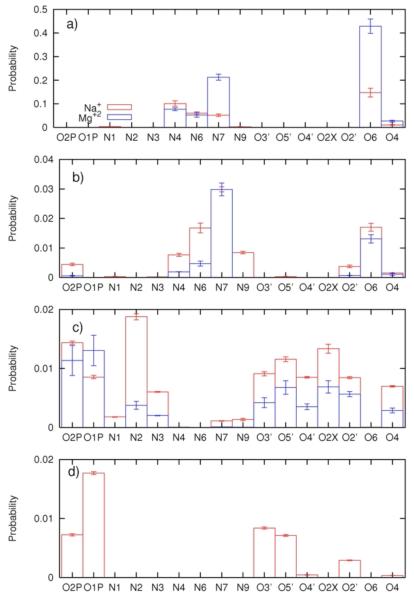
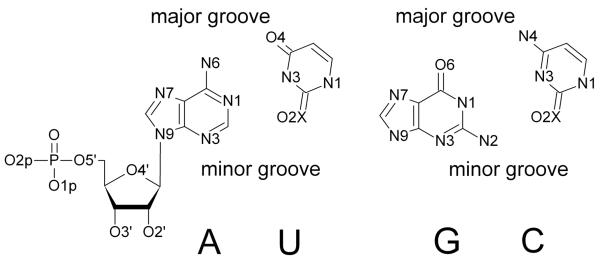
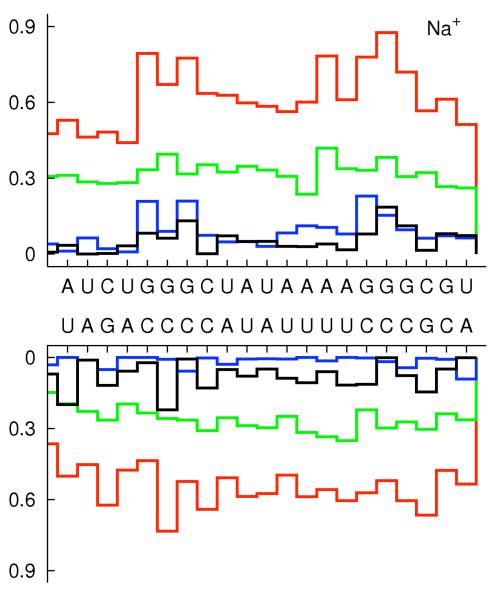
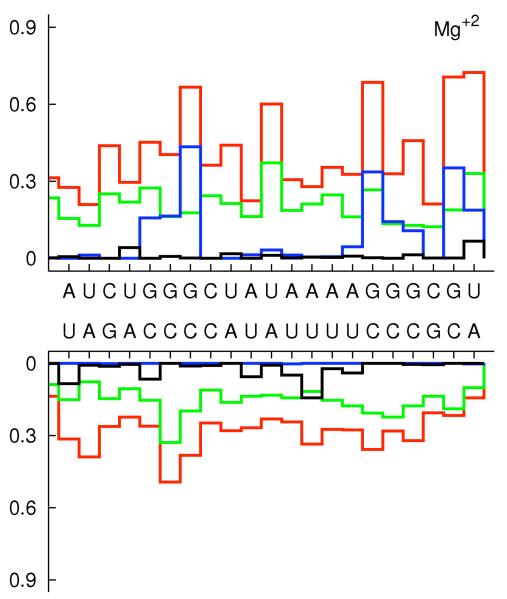
In figure 5 we associate the four peaks (a, b, c, and d) in the distance distributions with specific negatively charged atoms at the RNA surface. To make it easier to develop an intuitive understanding of the different sites we identify them on the chemical formulas of the RNA backbone and base pairs (figure 6.a), and by color coding a space filling model of the RNA molecule (figure 6.b-c). For example, binding sites at the deep grooves (for Mg²⁺) are highlighted with blue for N7 and red for O6 (figure 6.c).

Figure 5.

Probability density of finding Na⁺(red) and Mg⁺²(blue) within 5Å from the electronegative sites on RNA. Different plots correspond to different regions defined in Figure 4.

Figure 6.

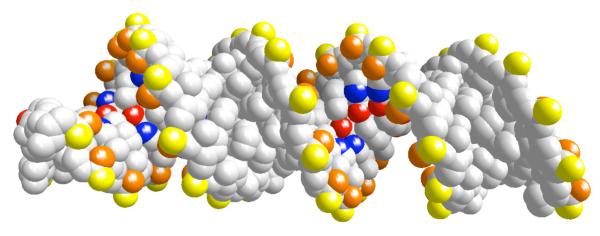
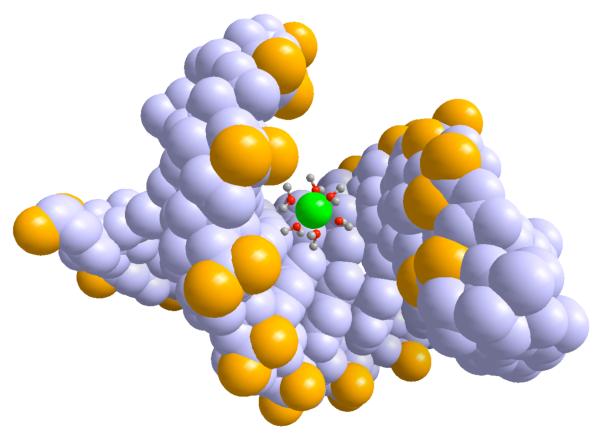
Ion binding sites displayed on the nucleotides 6.a The chemical formula and the names of the electronegative sites 6.b Sodium binding sites O1P(yellow), O2P(orange), N2 (cyan) and N7 (blue) and 6.c is magnesium binding sites with O1P(yellow), O2P(orange), O6 (red) and N7 (blue) Sequence dependence of number of ions within 5_Å from non-hydrogen atoms of nucleotide (red), from phosphate oxygens (green), major grooves (blue), and minor grooves (black). 6.d is for Na⁺ ions and 6.e is for Mg⁺² 6.f typical snapshot from the simulation where hydrated Mg⁺² (green) binds to the major groove. Oxygens of phosphates are shown with yellow.

To examine the impact of sequence variations we analyzed the ion distributions around the RNA taking into account base pair changes (figure 6.d-e). The first two base pairs from each end terminal of the strands are excluded to prevent end effects. It is interesting that the average number of ions changes dramatically with the nucleotide type and the type of the cation. The number of ions around a nucleotide (red lines) is a relatively smooth function for Na⁺ and is rather symmetric for the two strands. The spread of the monovalent ions makes it hard to identify sequence specific interactions of Na+ ions. For Mg²⁺ we observe ion localization on one strand of the RNA duplex. This asymmetry between the strands may be responsible for helix bending in high concentrations of divalent and trivalent ions. We found that ions bind primarily to oxygens of phosphates, and to the major and minor grooves. The number of ions, which are not magnesium, that are bound to oxygens of phosphates (green lines) is generally higher than the number of ions that are bound to the major (blue) and the minor (black) grooves. The exceptions are a few specific binding sites to magnesium. Mg²⁺ shows a strong coordination with guanine in the major groves. This is similar to the experimentally observed magnesium coordination with B-form DNA ⁶² and A-form RNA duplexes ^{14, 15, 17}. A typical Mg²⁺ ion in the major groove which is bound to G is shown in figure 6.f. The binding sites in the minor grooves are less tight. Nevertheless, even with a weaker signal it is clear that the magnesium preferred to bind to uridine bases. Our observation is in good agreement with the systematic analysis of binding sites of divalent cations in several high-resolution crystal structures of B-form DNA duplexes which illustrates that the binding in minor grooves is primarily to A-T rich regions ⁶³. The highly specific and strong binding of magnesium is reflected in enhanced fractional binding of magnesium to the RNA with decreased concentration (figure 4b and 6e). This non-linear binding may explain why a minute concentration of magnesium is sufficient to induce RNA folding.

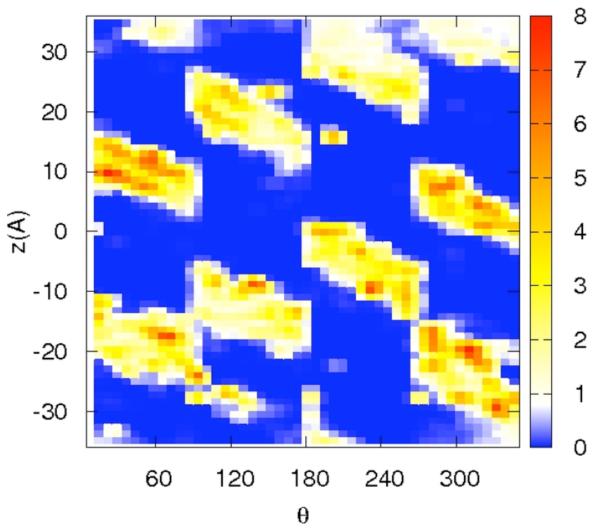
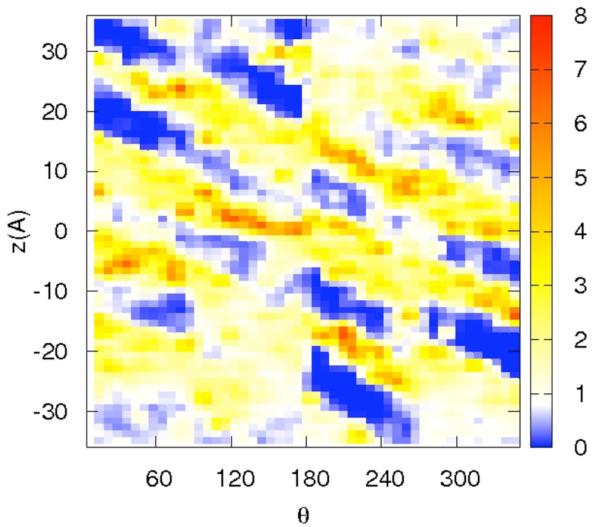
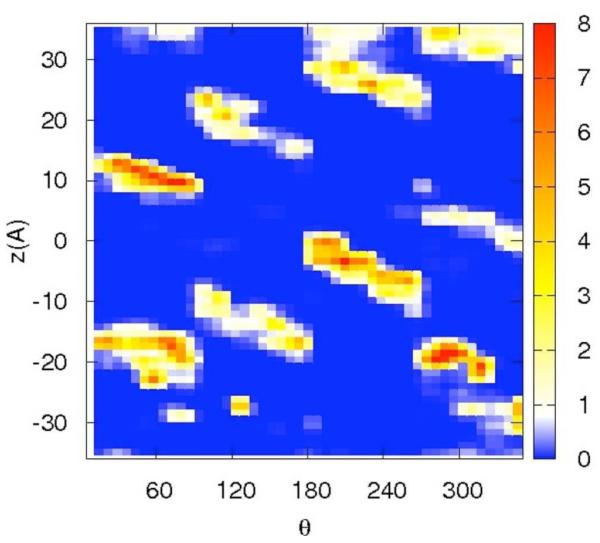
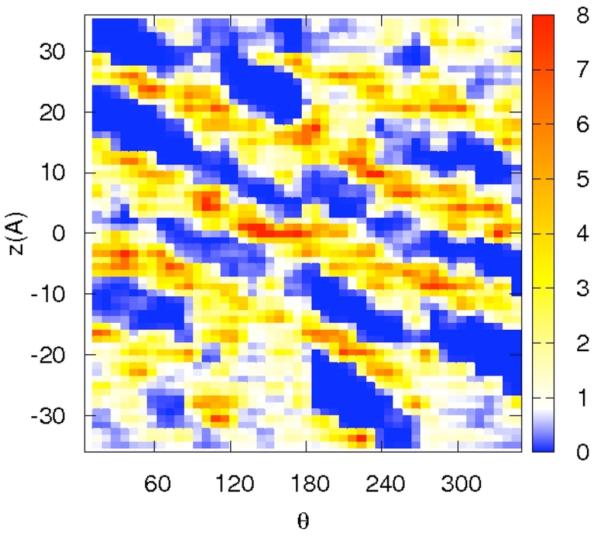
Correlation of distances from the RNA center and a binding site on the surface may be ambiguous since a distance is just one degree of freedom out of three per particle. For sodium that binds at some distance from the RNA surface, differentiating between diffusive and specific binding using only the distance is problematic. To ensure that specific binding indeed occurs we show in figure 7a-d the distributions of the ions along two spatial coordinates that are orthogonal to the distance from the RNA center. The z coordinate follows the RNA axis and θ is the rotational angle along the RNA axis. The panels 7a-b are for the sodium ion and the panel 7c-d are for the magnesium. Figures 7a and 7c are computed for short distances between the ions and the line of center of the RNA 2 < r < 8 Å while the panels 7b and 7d are for longer distances, 8 < r < 15 Å.

Figure 7.

The distribution of cations as a function of two variables: the position along the RNA long axis (z), and the rotational angle of the double helix θ. The two dimensional distributions are plotted using color-coded contours with the red denoting the highest density, white the bulk and blue the lowest. Note the clear diagonal lines that follow the maxima of the distributions and are the deep grooves of the RNA. The calculation was repeated twice, once for tightly bound ions (2<r<8Å) and second for loosely bound ions (8<r<15Å). 7a-b – the distribution of 0.4 Na⁺. 7c-d – the distribution of 0.2 Mg²⁺

The panels of figure 7 show non-uniform and highly variable binding of the ions on the RNA surface. Not surprisingly and consistent with the distance distribution, the two-dimensional plots are showing more structured distributions for magnesium compared to sodium ion. They also illustrate that at short distances the binding is localized and likely to be activated (i.e. there is no continuum of significant probability density that makes it possible for the magnesium ion to be mobile near the surface). The localization is not so clear for the sodium ion. Even at the short distances the probable position of the sodium ions are nearly connected.

At the shortest distances (peak (a) and peak b of figure 4.a and the first and second panels of figure 5) the sodium ions are distributed between N4, N6, N7 and O6 in roughly equal amounts. The peak (c) at about 12Å in the distance distribution of the sodium ion is the highest and is dominated with binding to N2 (panel c) of figure 5). The binding to the phosphate groups (O1P and O2P) and to the atoms O3′ O5′ O4′ O2X and O2′ is also significant. The binding to the phosphate groups is extended also to peak (d) in the distance distribution (about 10Å from the RNA center). By having the highest concentration at some distance from the RNA the sodium ion is bound to the RNA mostly “diffusively” (see also figure 7.b). The fourth sodium peak (panel (d) of figure 5) is associated (again) with the diffusive long-range attraction of the negatively charged phosphate groups.

The interactions of magnesium ions with RNA are more structured. The first peak of the magnesium ion in the distribution of distances from the RNA (figure 4.b) is significantly higher than that of the sodium ion. Examining potential candidates for specific binding in figure 5 panel (a and b), O6 is the best candidate. Interestingly the magnesium peak nearest to the RNA (figure 4.b) is affected significantly by the presence of the sodium ions in the ion mixtures that we considered. A magnesium ion binding to one dominating site is also evident in the (significantly lower) peak (b), in which the binding is to N7. The N7 is close to the O6 atom suggesting that the two peaks correspond to the same binding site. Further evidence to the specific binding of Mg²⁺ to the RNA surface is presented in figure 7c in which the red spot of high probability of finding the magnesium form isolated islands in the z,θ space (for distances between two and eight Å).

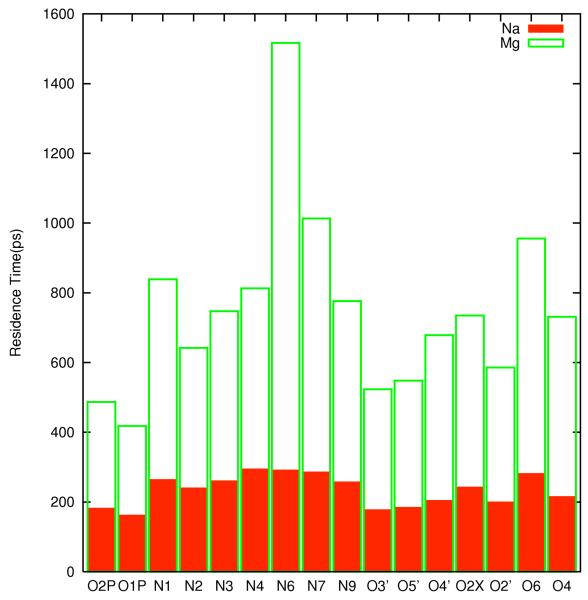
Another useful measure of “diffusive” versus “tight” behavior is kinetic. In figure 8.a we show the average residence time of sodium and magnesium ions near the RNA. The residence times were computed from two 36 nanoseconds straightforward molecular dynamics trajectories of pure NaCl [0.4M] or MgCl₂ [0.2M] by taking the initial coordinates from already converged replica exchange simulations mentioned previously. We consider an ion i that binds to one of the negative atoms of the RNA at time zero and at time τ_i is found for the first time within a distance of 6Å along the line connecting the RNA center and the negative atom towards the aqueous solution. For L events the average escape time is defined as $\frac{1}{L}{\sum }_i{\tau }_i$.

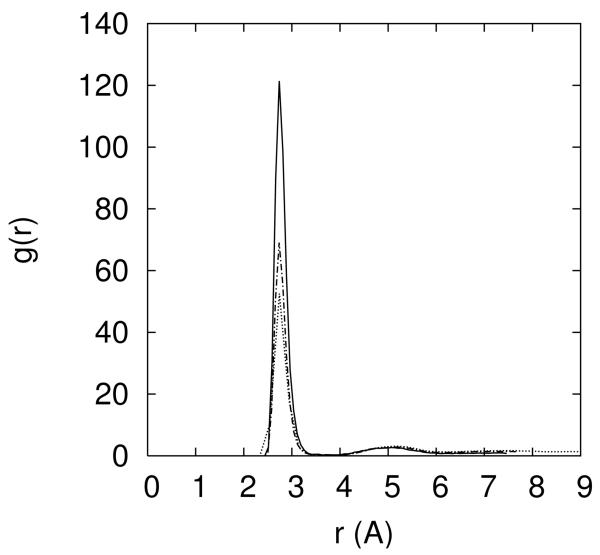
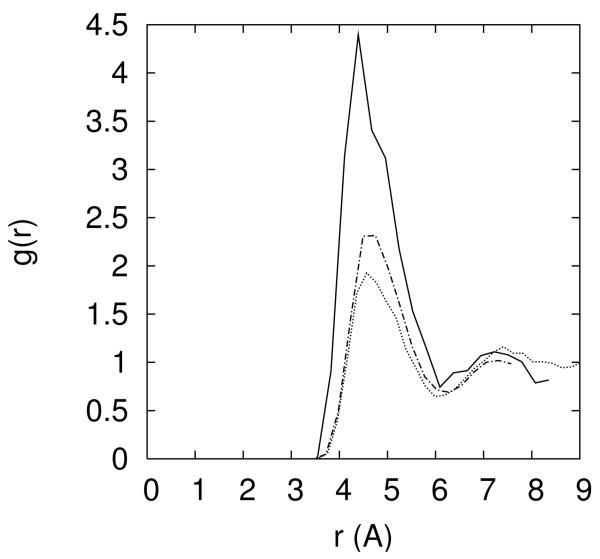
Figure 8.

8.a-Escape times of Na⁺ and Mg⁺² ions from the electronegative binding sites. 8.b Atom pair distance distribution function between O2P and sodium ion (solid line) and O2P and magnesium ion (dashed-dotted line). Note the sharp peak at 2.3Å for the sodium distribution that suggests a bare binding of the ion to the RNA atom (no intermediate water molecules). On the other hand the magnesium ion cannot remove its solvation shell in our simulation and the binding in 8b is with intermediate water between the ion and O2P.

For reference we also report the times for free diffusion. In our computational model the bulk diffusion constant D of the sodium ion is 0.24Ųps⁻¹. We use the diffusion formula 6Dt ≈ r², at r ≈ 6Å to estimate the time of free diffusion 6·0.24·t ≈ 6² (t≅25ps). The distance of 6Å was estimated based on the width of the second solvation shell peak (figure 8.b). The estimated time is about a factor of 10 shorter than the residence times near RNA for Na⁺ ions (figure 8a). The difference cannot be explained by changes limited to the diffusion constant, since the diffusion constant of sodium near RNA (0 ≤ r ≤ 12Å) is 0.17Ųps⁻¹ while far away from the RNA (22Å ≤ r ≤ 29Å), it is 0.23Ųps⁻¹ when estimated directly from the simulation. The factor of 10 in residence time at bulk and near RNA at 300K implies moderate activation free energy of 2.5 k_BT. The observation that the residence time of the sodium ion varies by less than a factor of two from site to site suggests rather uniform RNA surface from the perspective of Na⁺. Hence Na⁺ binding is diffusive.

The water solvation shell of the sodium ion is not strongly attached. Binding to RNA atoms (and escaping) includes dismantling and re-establishing a solvation shell without significant free energy barrier (figure 8.b). In contrast, magnesium binding to RNA is always with a solvation shell (and at least one water molecule separates the magnesium from the negatively charged RNA atom, figure 8.b). This is not to say that desolvated magnesium is necessarily unimportant. To explore bare Mg²⁺ binding to RNA, we prepared an initial configuration with magnesium ions directly bound to RNA. These magnesium ions remain bound in room temperature simulations for 5 nanoseconds. The barrier for the removal of water from magnesium ion and replacing the water molecule by an RNA atom is too large to be sampled efficiently even at the highest temperatures of the replica exchange simulation. At present we cannot assess the probability of bare magnesium binding and the calculations of the rate estimate are left for future studies.

The diffusion of the magnesium ion is significantly slower near the RNA compared to bulk diffusion. The bulk value of the diffusion constant is about 0.14Ųps⁻¹. To diffuse roughly 6Å will require about 43ps which is about 20 times faster than the average residence times computed from the simulations. At variance with the general behavior we observe long residence time of ions bound to N6. The residence time increases by another factor of two to about 1500 picoseconds which is consistent with a free energy barrier of 3.5 k_BT.

The proposed Mg²⁺ binding sites can be compared directly to crystallography (figure 9). We overlay the RNA structure we simulated with a structure from the Protein Data Bank PDB⁶⁴ (entry -- 1y99¹⁵). While the sequence of the PDB entry is different from the sequence we simulate, we examine binding only to CG pairs, which reduces the effect of sequence diversity. White spheres in figure 9 correspond to magnesium binding sites that are observed in experimental crystallographic studies. The cyan spheres are peaks of probability density of magnesium occupation as determined by the simulations. We binned the ion coordinates from the Molecular Dynamics trajectories in boxes of edges of 0.5Å to determine the frequency of appearance and the probability density, ρ_i, i.e. we compute the following average of the i – th box ${\rho }_i={\sum }_{j,n}\Delta \left(r_i-r_{jn}\right)/{\sum }_{j,n}1$ where the index j runs over the different (degenerate) ions and the index n runs over the time slices. The function Δ is 1 / 0.5³ if r_jn is in the box determined by r_i and zero otherwise. The probability density is normalized with respect to the bulk water density which is 0.334 particle/ ų. The probability densities, at the positions of the cyan spheres, are ~5 times higher than the water bulk density.

Figure 9.

An overlay of magnesium ions detected in crystallography and the peak of the ionic distribution observed in the simulations. The white spheres are magnesium-binding sites determined by crystallography. The cyan spheres are peaks of the probability density of magnesium ions determined from the simulations. Each cyan sphere was extracted from the simulations based on a peak in the probability density (~5 times larger than the bulk water density) and modeling the binding site to CG pairs according to the simulation data. The RNA molecules in the computations and in the experiment are different and therefore the modeling of the binding of the CG pair was necessary. Note an open base pair in the crystallographic structure, which causes the only significant deviation of the simulation data compared to the experiment. From the MD simulation of A-form RNA we observe that Mg⁺² is located between G-C base pairs with an average distance of 4.3±0.3Å to O6 of Guanine and 5.4±0.8Å to N4 of Cytosine. The G-C pair with Mg⁺² ion located on the average distance to these groups is used as a model. This model is overlaid onto the X-ray structure wherever a Mg⁺² binding site is present at the G-C pair. See text for more details.

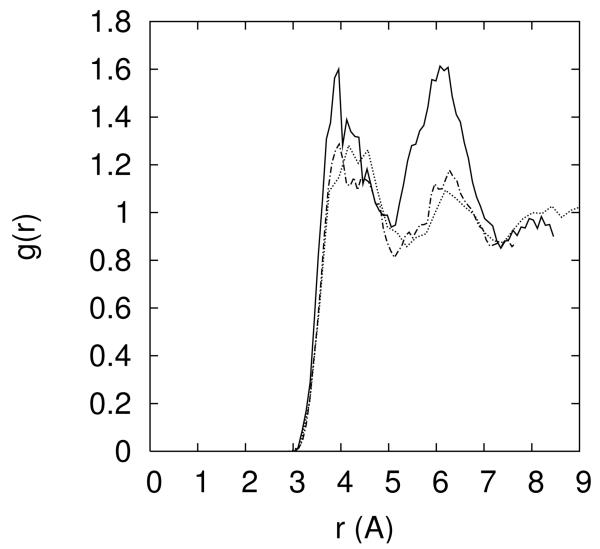
In figure 10.a we show the distribution function of the negative chloride ion as a function of distance from the RNA. While the statistics are poorer compared to the cations (it is of course less likely to find a negatively charged chloride ion near RNA) there are two surprises in this figure. The first is that chloride succeeds in getting very close to the RNA. The second is the significant structure of the curves. The position of the chloride distribution maxima roughly follow peaks (a) and (c) of the sodium and the magnesium ion distributions, illustrating the correlation between the position of the negative ion and the mobile cations. We define a binding site when the density of the ion is two times higher than the density of bulk water, with this definition and in contrast to another study⁶⁵, we were not able to identify specific chloride ion binding sites on the A form of RNA.

Figure 10.

10.a -The distribution of the Cl⁻ ion as a function of distance from the line of center of the RNA for different ionic solutions (0.4M NaCl – red; 0.05M MgCl₂ and 0.3M NaCl -- blue; 0.1M MgCl₂ and 0.2M NaCl – cyan; 0.15M MgCl₂ and 0.1M NaCl – black; 0.2M MgCl₂ – gray). 10.b Distance pair correlation function of Na⁺ and Cl⁻ plotted for three cases: (i) both ions are near the RNA and each of their distances is smaller than 15Å (solid line), (ii) both ions are reasonably far from the RNA (r>15Å), and (iii) pair correlation function extracted from a 0.4M solution of NaCl (dashed-dot). Note that the bulk distribution is very similar to distribution (ii) – ions that are at least 15Å away from the RNA. 10.c – the same as 10b but this time for the correlation between two chloride ions. 10.d – the same as 10b but this time for the correlation between two sodium ions. 10.e- two dimensional pair correlation function $g(r_1,r_2)=\frac{<N_i\left(r_1\right)N_j\left(r_2\right)>}{\left(4\pi r_1^2{\rho }_i\delta r_i\right)\left(4\pi r_2^2{\rho }_i\delta r_j\right)}$ is defined where < N_i(r₁)N_j(r₂) > is the time average of total number of ion i found between r₁ and r₁ + δr_i and at the same time the total number of ion j found between r₂ and $r_2+\delta r_j\cdot {\rho }_k=\frac{N_k}{V}$ is the bulk density of ion k. Pair correlation between Na-Cl–Cl-Cl and Na-Cl – Na-Na is plotted for ions far from the RNA (r>15Å) with a contour coloring showing the function gas blue 1, cyan 20, white 50, yellow 100, orange 150 and red 200. 10.f Same as 10.e this time ions are close (r<15Å).

The high correlation between chloride ion and a cation is illustrated also in figure 10.b in which the pair correlation function of sodium and chloride has a pronounced peak at distances from RNA that are closer than 15 angstrom. This intriguing observation suggests that the spatial peak positions of the chloride ions are influenced not only by the RNA macroion but also by interactions with counterions. In figure 10.c we show the correlation of Na⁺ - Na⁺, and in figure 10.d the correlation of two chloride ions. Figure 10.e-f shows two dimensional correlations. It is no surprise that the correlations of the ions of the same charge are much weaker than of ions of different charges. The more interesting observation is that the correlations of same charge ions are enhanced as we get closer to the RNA. The enhancement of the chloride-chloride correlation near the RNA is assisted by an intermediate gluing atom which is likely to be sodium ion.

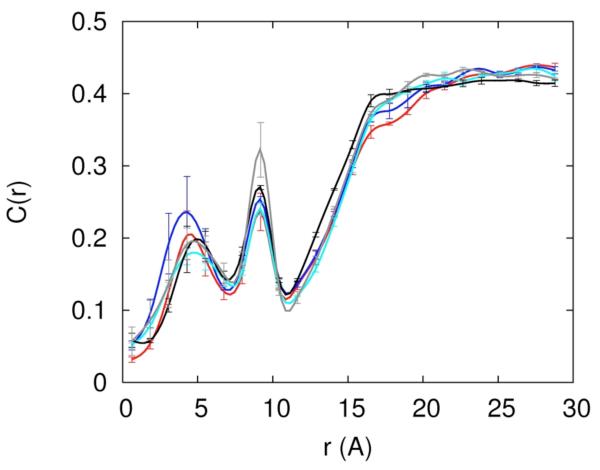
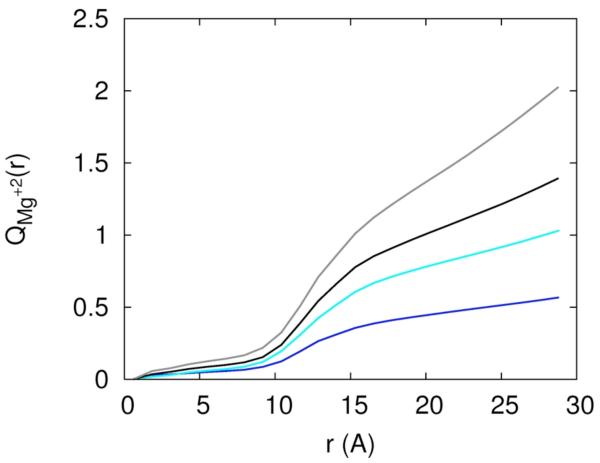
The existence of separate mechanisms or phases of ion binding was discussed extensively in the past². Figure 11a is a plot of the collective charge of the mobile ions as a function of distance, and it shows two phases in which the RNA charge is neutralized. The charge is normalized to one at large distances, i.e. at distances in which the RNA charge is completely neutralized. The first phase of neutralization is between 0 to 7Å and the second phase is between 7 and 15Å. We call ions that are found in the first phase “near RNA” and the second phase “diffusively bound”. In the first phase the accumulation of charge is slower and most of the neutralization occurs in the second phase. There are two competing effects that determine the rate of neutralization as a function of distance: volume and electrostatic attraction. Clearly, ions that are closer to the RNA line of center feel the strongest electrostatic attraction; however, the volume at short distances is smaller than at large distances and is particularly excluded from the ion by the volume of the RNA. This means that only relatively small number of neutralizing ions can be found at these distances without impacting other mobile ions. The second phase of neutralization corresponds to a significantly larger volume and therefore includes a much larger number of neutralizing ions.

Figure 11.

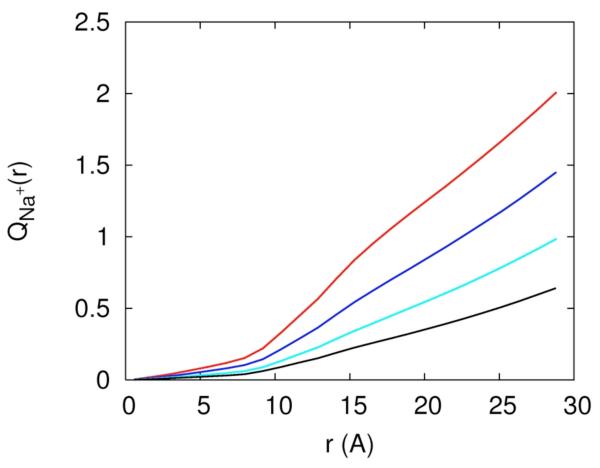
Accumulation of charge as a function of distance from the RNA line of center, 11.a – the total accumulated mobile charge normalized with respect to the net charge of the RNA (−48e). The color codes explained in figure 10a. 11.b – the same as figure 11a, this time for the charge of the sodium ion only. 11.c – the same as figure 11a, this time for the charge contributed by the magnesium ion.

In figure 11.b we examine the contribution of Na⁺ to RNA charge neutralization. The separation to three phases of neutralization strength defined by the derivative of the accumulated charge as a function of distance from the RNA is evident but is not as sharp as we have seen in figure 11a. The first phase from 0-7Å from the RNA line of center is of a slow growth with the number of ions. The next phase between 7-15Å corresponds to the loosely bound ions that make dominant contribution to neutralizing the RNA charge.

In figure 11.c we show the integrated charge as a function of distance of magnesium ions from the line of center of the RNA. In contrast to the sodium ion three different slopes of Q(r) as a function of r are clearly present. The number of tightly bound magnesium ions is affected only slightly by the presence of sodium atoms. Changing the concentration of the magnesium ion changes the slope of the different phases but not their presence.

IV Discussions

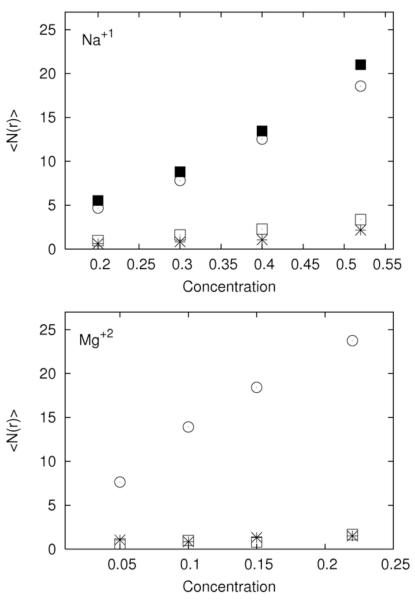
It is well known that small amount of divalent ions are necessary to fold some RNA molecules. The interplay between “near RNA” and diffusive binding in a mixture of cations is of considerable interest. In our simulations the mixtures were set in such a way that the total positive charge is fixed. In figure 12 we examined the number of ion bound at different sites at the RNA surface. The figure shows when the binding to a site is significant (region c for sodium and magnesium ions – figure 4). Note that since region c is further from the RNA the volume associated with that region is more significant than binding sites closer to the RNA. The two ions are competing for roughly the same sites. The double charge of the magnesium ion makes it a more effective binder and it binds to the site in excess to its concentration. Indeed as the concentration of magnesium decreases the sodium ions is having hard time replacing a position that the free magnesium ions bound to. The number of magnesium ion decays sub linearly as the magnesium concentration is reduced, while the number of sodium ions bound decreases super linearly. The strong binding of magnesium to specific sites may explain while only minute concentration of magnesium is sufficient to fold RNA.

Figure 12.

Average number of bound ions as a function of asymptotic concentration for the regions defined in figure 4. 12.a - is the number of Na⁺ ions for the regions a (star), b (open square), c (open circle), and d (solid square). 12.b - is the same quantity for Mg⁺² ions. Symbols have the same meaning as in 12a.

Another intriguing question about the present simulation is the applicability of continuum approximate theories and their consistency with the simulations. The challenge is to predict the distribution of the mobile ions around the polyelectrolyte. At short distances the analytical theory is bound to fail since the atomically detailed structure of the RNA, the mobile ions, and of the water molecules have significant impact. Indeed the pair correlation functions and ion distributions are showing significant structure (figure 4) that cannot be reproduced in simple analytical theories. At sufficiently large distances we expect the simple theory to be more quantitative. A sensible model of the RNA and ion distribution around it is of two concentric cylinder model. The inner cylinder at r = a has a constant (surface) charge density σ which is embedded in dielectric medium ε (dielectric constant of 80). On the outer cylinder r = R the electric field goes to zero. An analytical solution can be found for this model for the linear Poisson-Boltzmann equation⁶⁶

$$\varphi =-\frac{4\pi \mid \sigma \mid }{\epsilon {\kappa }_D}\frac{K_0\left({\kappa }_{D}r\right)I_1\left({\kappa }_{D}R\right)+I_0\left({\kappa }_{D}r\right)K_1\left({\kappa }_{0}R\right)}{K_1\left({\kappa }_{D}a\right)I_1\left({\kappa }_{D}R\right)-I_1\left({\kappa }_{D}a\right)K_1\left({\kappa }_{D}R\right)}$$

Where φ is the electrostatic potential k_B Boltzmann constant T temperature κ_D inverse Debye length and the functions I_n and K_n are the n^th order modified Bessel functions of the first and second kind respectively.

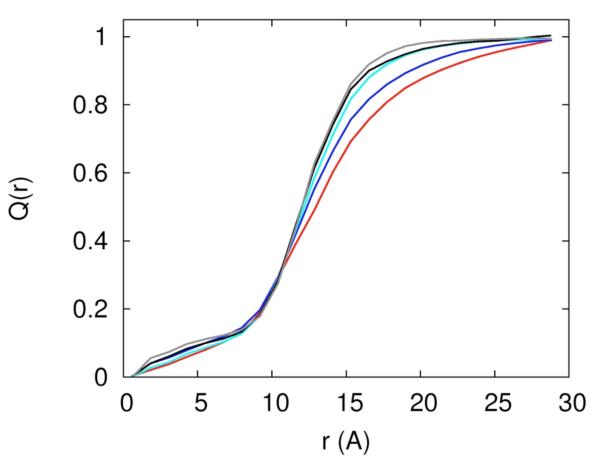
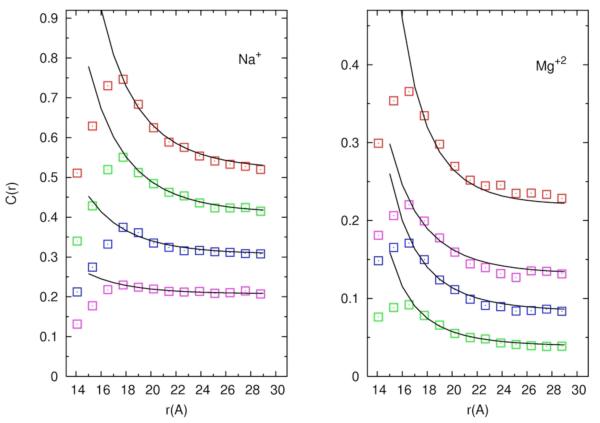
To apply the formula we need to know the effective charge density of the RNA. The charge density is influenced by the “near-RNA” ions that are not explicitly included in the continuum picture and is not the bare charge of the polyelectrolyte. We decided to make the charge density of the RNA a free parameter. The other parameters, the inner circle radius is a = 11.2Å and outer circle radius is R = 30Å (R = 30Å is practically R~ ∞) and the Debye’s inverse length,κ_D is determined from the simulation conditions. With a single free parameter of the ion charge density we successfully fit the analytical solution to the simulated curves at distances larger than 16Å for a wide range of sodium and magnesium concentration (figure 13). The fitted charged densities are provided in table I and are in good agreement with the net charge that remains on the RNA once the “near RNA” charges are taken into account

Figure 13.

Concentration profile of condensed but not nearly bound ions to RNA. Open squares are simulation results and solid lines are fit by Poisson Boltzmann Equation. 13.a - the distributions of Na⁺ ions for different ionic solutions (0.4M NaCl – red; 0.05M MgCl₂ and 0.3M NaCl – green; 0.1M MgCl₂ and 0.2M NaCl – blue; 0.15M MgCl₂ and 0.1M NaCl – magenta0.2M MgCl₂ ). 13.b the distribution of Mg⁺² ions for different ionic solutions. 0.2M MgCl₂ is red and the rest of the symbols follow the same order as in 13.a

Table 1.

A comparison between the net charge of RNA at r=11.2Å calculated from the simulation and from the fitted charge density using the Poisson Boltzmann equation.

	PB	Exact
0.4Na (pure)	32	32.7
0.3Na	28	31.8
0.2Na	28	31.9
0.1Na	29	31.2
0.2Mg(pure)	34	32.5
0.15Mg	29	31.2
0.10Mg	30	31.9
0.05Mg	32	31.8

The success of the simple theory beyond 16Å from the RNA line of center is reassuring, However it also points out to significant limitation of this type of theory. It is difficult to trust concrete predictions about the distribution and the energetics of the “near RNA” ions using this type of theory since the deviation between theory and simulations are simply very large. It would be of interest in the future to compare our results to non-linear Boltzmann solution with detailed RNA structures.

Another exploitation of the present investigation is the analysis of electric field relaxation data. In a recent Time-resolved Stokes-shift experiment⁶⁷ and a follow-up simulation study⁶⁸ it was proposed that electric field relaxation in DNA (or RNA) that proceeds for tens of nanoseconds has its origin in solvent dynamics. More precisely the relaxation was attributed to the response of the water molecules to the changes in the electric field. Arguments were given by others^{69, 70} that the relaxation of the electric field in solution should be much faster than the time scale observed experimentally⁶⁷ and therefore another mechanism should be investigated.

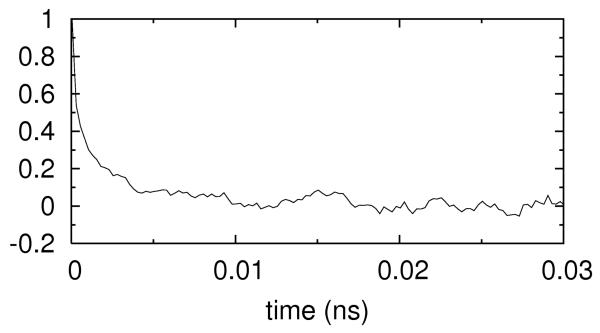
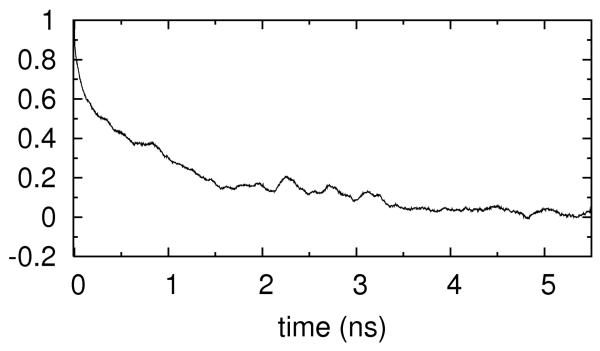
We considered the electric field relaxation in the context of our simulations. We placed a probe 0.5Å away from the N6 atom of the base number 38 and examine the changes in the electric field at the probe position as a function of time. The correlation function $C\left(t\right)=\frac{\langle \delta E\left(t\right)\delta E\left(0\right)\rangle }{\langle \delta E^2\left(0\right)\rangle }$, was computed where δE(t) = E(t)–⟨E⟩_∞ and < E >_∞ is ensemble average of the electric field. Linear response theory ⁷¹ connects equilibrium correlation function and the relaxation time. Using the fixed RNA simulations with concentrations of 0.4M Na⁺, we expect to capture the contribution of the ionic solution to the electrostatic correlation. The relaxation time was found to be picoseconds (figure 14a). In contrast, when the RNA is allowed to tumble, (and the relaxation is no longer pure solvent contribution), the relaxation time increases significantly and becomes a few nanoseconds (figure 14b). Hence RNA motions (and not solution dynamics) are the cause for the slow relaxation time.

Figure 14.

Autocorrelation function of the electrical field fluctuations at the center of RNA molecule. 14.a shows the autocorrelation function when RNA is kept rigid. 14.b is the same as 14.a but RNA is allowed to tumble.

The tumbling of the RNA was modeled as follows. We use the AMBER covalent energy terms for all the atoms in the RNA and added distance constraints between the phosphates atoms to enhance the RNA rigidity (all the parameters are included in the Supplementary Material). The RNA was allowed to tumble in the solvent box during the integration of the equations of motion while maintaining its overall rigidity.