Abstract
Artifacts caused by patient motion during scanning remain a serious problem in most MRI applications. The prospective motion correction technique attempts to address this problem at its source by keeping the measurement coordinate system fixed with respect to the patient throughout the entire scan process. In this study, a new image-based approach for prospective motion correction is described, which utilizes three orthogonal 2D spiral navigator acquisitions (SP-Navs) along with a flexible image-based tracking method based on the Extended Kalman Filter (EKF) algorithm for online motion measurement. The SP-Nav/EKF framework offers the advantages of image-domain tracking within patient-specific regions-of-interest and reduced sensitivity to off-resonance-induced corruption of rigid-body motion estimates. The performance of the method was tested using offline computer simulations and online in vivo head motion experiments. In vivo validation results covering a broad range of staged head motions indicate a steady-state error of the SP-Nav/EKF motion estimates of less than 10 % of the motion magnitude, even for large compound motions that included rotations over 15 degrees. A preliminary in vivo application in 3D inversion recovery spoiled gradient echo (IR-SPGR) and 3D fast spin echo (FSE) sequences demonstrates the effectiveness of the SP-Nav/EKF framework for correcting 3D rigid-body head motion artifacts prospectively in high-resolution 3D MRI scans.
Keywords: Motion artifact, Kalman filter, rigid-body, Navigator
Introduction
Artifacts caused by patient motion during scanning remain a serious problem in most clinical and research MRI applications. In fast single-shot sequences, such as dynamic 2D echo-planar imaging (EPI), between-scan motion can introduce significant motion-related variance to the voxel-time courses and disrupt the spin excitation history of the acquisition (1,2). In multi-shot 2D and 3D sequences, within-scan patient motion results in k-space data inconsistencies, causing artifacts such as ghosting, blurring and ringing in the images themselves. Offline image registration can mitigate most between-scan motion artifacts in time-series data (3–5), but cannot correct for changes in the spin excitation history caused by through-plane motion. In addition, while some within-scan motion artifacts can be corrected retrospectively using knowledge of the motion history derived from either navigator scans (6,7) or overlapping k-space data (8,9), most of these methods are limited by the inability to 1) fully correct for through-plane motion in 2D sequences and 2) avoid k-space data inconsistencies caused by interpolation errors.
An alternative approach to motion correction, which shares none of these drawbacks, is modify the pulse-sequence online, in real-time, during the acquisition itself. Some of the first real-time methods used straight-line navigators to prospectively correct for linear translations of organs in the chest (10–12). Since then, navigators with more sophisticated k-space trajectories have been developed for higher order motion correction. Ward et al. used orbital (circular) navigators (O-Navs) (13) acquired in three orthogonal 2D planes for prospective correction of full 3D rigid-body motion artifacts in 2D EPI (14). To account for motion outside the plane of each navigator (through-plane motion effects), multiple O-Navs are acquired in series where each O-Nav provides an adjustment to the subsequent O-Nav planes. Spherical navigators (S-Navs), which generalize the O-Nav trajectory to 3D shells in k-space, do not suffer from through-plane motion effects and can be used to estimate 3D rigid-body motion in a single navigator (15–17). However, the spherical technique works best for rotations along the navigator trajectory as apposed to rotations across them (15). In addition, a real-time application of the S-Nav remains missing due in part to the slow iterative procedure required to register S-Nav magnitude data (15). One of the most recent real-time navigator techniques, introduced by van der Kouwe (18), used an optimized "cloverleaf" k-space trajectory for prospective correction of 3D rigid-body motion in 3D spoiled gradient echo sequences. Compared to the orbital and spherical trajectories, the cloverleaf method offers the advantages of a more rapid k-space readout, together with improved translation estimation by including linear segments through the center of k-space (18).
In some applications, prospective motion correction can be achieved through self-navigation. Thesen et al. described a self-navigated approach for 2D EPI called “Prospective Acquisition CorrEction", or PACE, where each individual time-series volume is reconstructed online and registered to the first volume in the sequence (19). While the image-base tracking (registration) procedure in PACE provides accurate 3D rigid-body motion estimates, the correction itself is performed on a slow volume-by-volume basis, or approximately every four seconds (19). Zaitsev et al. (20) and Speck. et al. (21) developed an optical tracking device for improved real-time slice-by-slice correction in 2D EPI. In general, the advantage of optical tracking is that it does not require modification of the pulse-sequence. However, this comes at a price of requiring significant additional hardware to implement, including a MRI compatible camera system mounted inside the scanner room and repeated calibration for optimal tracking performance (22).
In this study, we present an alternative image-based framework for prospective motion correction called "PROMO" (PROspective MOtion correction). The PROMO approach utilizes three orthogonal 2D spiral navigator acquisitions (SP-Navs) along with a flexible image-based tracking method based on the Extended Kalman Filter (EKF) algorithm (23,24) for real-time motion measurement. The Kalman filter framework for image-based tracking in MRI was introduced by White et al. (25), and applied in 3D spiral-navigated image sequences by Shankaranarayanan et al. (26,27) and Roddey et al. (28) and in MR spectroscopy by Keating et al. (29). Spincemaille et al. also recently introduced a novel application of the Kalman filter for real-time separation of cardiac and respiratory components in navigator data (30). Here, we describe the PROMO motion correction method in detail and provide some preliminary results in 3D inversion recovery spoiled gradient echo (IR-SPGR) and fast spin echo (FSE) sequences.
Methods
Spiral navigator acquisition
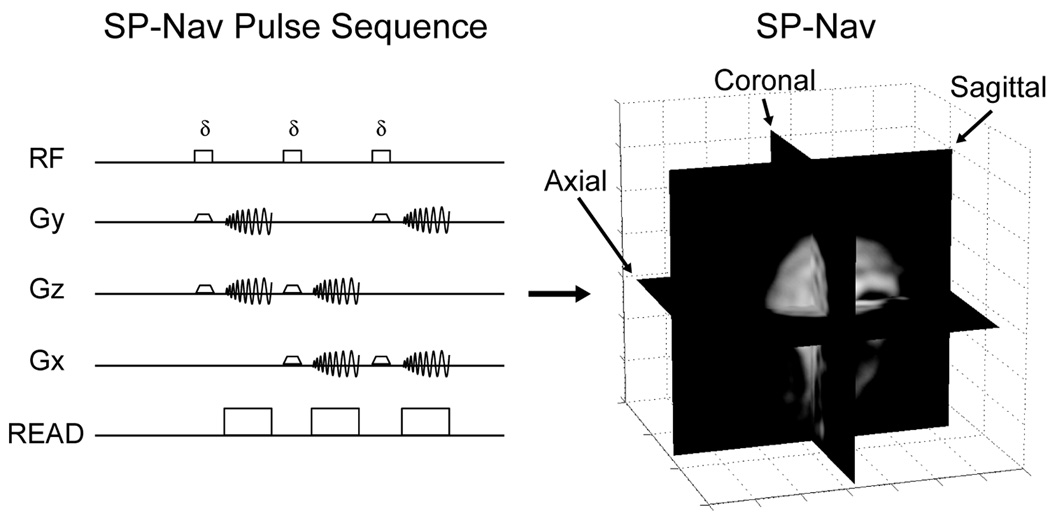
The navigator acquisition included three orthogonal low flip-angle, thick-slice, single-shot spiral acquisitions (SP-Navs) with the following pulse-sequence parameters: TE/TR = 3.4/14 ms, Flip (δ) = 8° (to minimize the impact of signal saturation on the acquired 3D volume), BW = ±125 kHz, field-of-view (FOV) = 32 cm, effective in-plane resolution = 10 × 10 mm, reconstruction matrix = 128 × 128, slice thickness = 10 mm. Spiral readouts were selected because they provide an efficient k-space coverage and allow for image-based tracking with reduced sensitivity to distortion. The off-resonance effect is somewhat mitigated by the optimization of spiral length since the requirement for the in-plane resolution of the navigators is not very high. Initial experiments were done without any trajectory measurement. However, it should be noted that in case of severe off-resonance (> ± 100 Hz) the measurement errors will increase significantly. To avoid this, we perform center frequency correction (prescan software on the scanner) before every scan. The orientation convention adopted in this work defined the x-axis as the left-right direction, the y-axis as the anterior-posterior direction, and the z-axis as the inferior-superior direction with respect to the patient. The axial, sagittal, and coronal planes of each SP-Nav spanned the x-y, y-z, and the x–z axes, respectively. The SP-Nav pulse-sequence and example reconstructed image is shown in Fig. 1.
FIG. 1.
SP-Nav pulse-sequence and reconstructed image used for motion tracking.
Integration in 3D IR-SPGR and 3D FSE
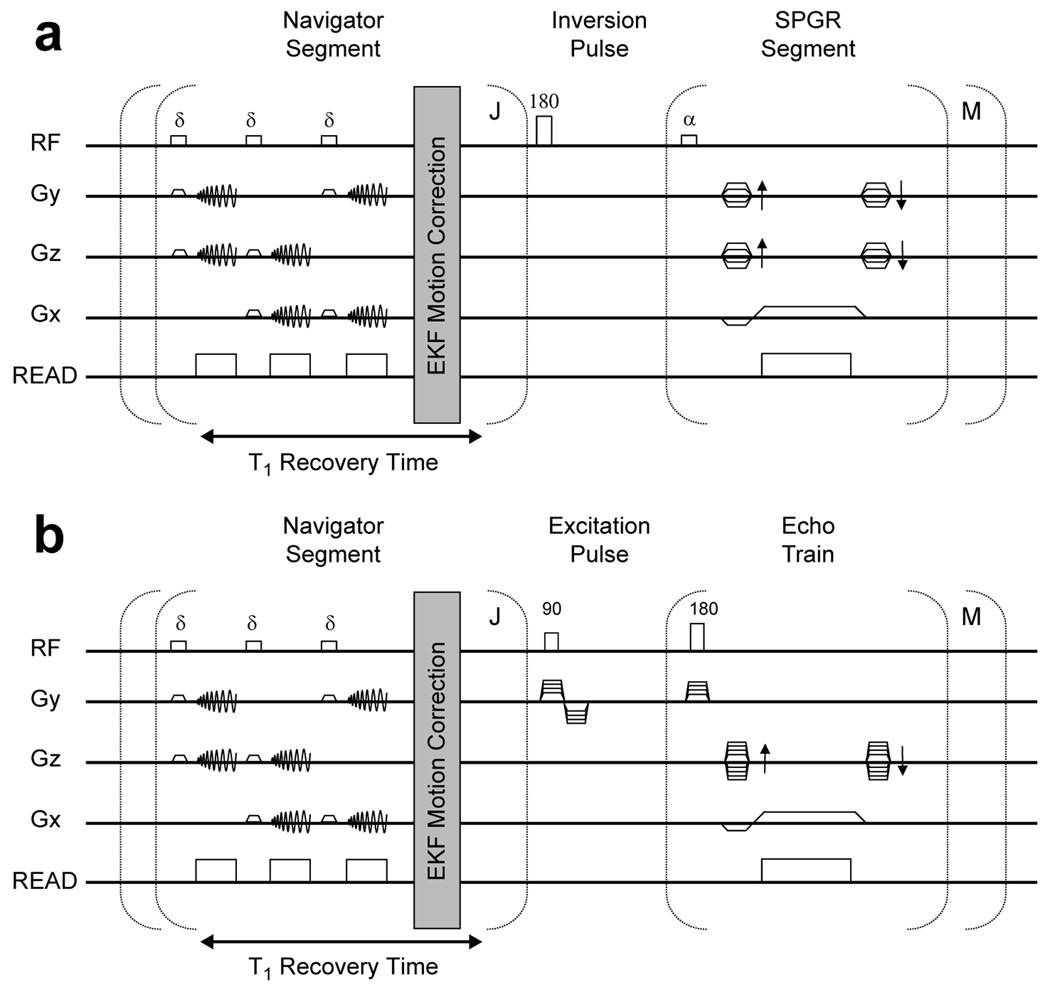
SP-Navs were integrated into a 3D IR-SPGR and 3D FSE sequence (Fig. 2). To enable prospective correction without impacting scan time, multiple SP-Navs were played out during the intrinsic longitudinal (T1) recovery time of the two sequences. Immediately after acquisition, each SP-Nav was reconstructed and used as input to the EKF motion tracking and correction algorithm (described next). The time required to collect a single SP-Nav was approximately 42 ms, followed by 6 ms for image reconstruction of all three planes. To allow ample time for estimation and feedback, the repetition time for each SP-Nav was programmed for 100 ms. A total of J = 5 SP-Navs (~500 ms) were acquired during the T1 recovery times of both sequences, which were programmed for approximately 700 ms and 1200 ms, respectively. For the IR-SPGR sequence, a recessed elliptical centric ky-kz ordering was used for the imaging segment (31), with an entire ky-kz plane acquired after each inversion pulse. The thickness of the IR pulse was twice that of the imaging slab. The IR-SPGR pulse-sequence parameters were: TE/TR = 3.9/8.7 ms, Inversion time (TI) = 270 ms, Flip (α) = 8°, BW = ± 15.63 kHz, FOV = 24 cm, voxel size = 1.25 × 1.25 × 1.2 mm, # k-space segments (M) = 192. For the 3D FSE sequence, an eXtended Echo Train Acquisition (XETA) (32) was used with the following parameters: TE/TR = 110/2500 ms, Flip = 90°, BW = ± 31.25 kHz, FOV = 24 cm, voxel size = 1.25 × 1.25 × 1.2 mm, echo train length (ETL) = 90, M = 90. The overall scan times of the IR-SPGR and FSE sequences were 8 min and 4.5 min, respectively. All scans were collected using a 1.5T GE Signa HDx system (Waukesha, WI) using an 8-channel head coil.
FIG. 2.
Spiral-navigated (a) 3D IR-SPGR and (b) 3D FSE pulse-sequence. A train of J = 5 SP-Navs are played out prior to each of the M inversion or excitation pulses of the two sequences, respectively. Prospective motion correction is performed after each individual SP-Nav using the EKF algorithm.
EKF motion tracking and correction
Dynamic state space model
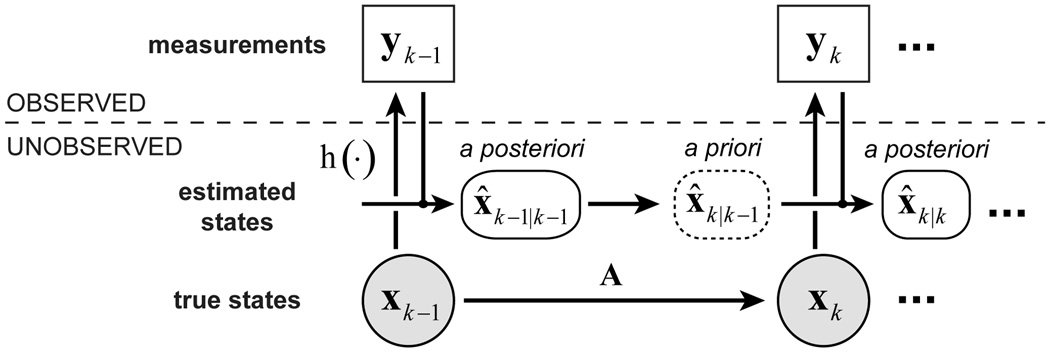
Real-time 3D rigid-body motion tracking and correction on the SP-Nav data was performed using the well-known EKF algorithm (23). The EKF itself provides recursive state estimates in nonlinear dynamic systems perturbed by Gaussian noise. The basic dynamic state-space model of the EKF, as implemented here, is shown in Fig. 3 and can be written as a set of system equations of the form
| [1] |
| [2] |
xk is the (unobserved) state of the dynamic system at time-step k and yk are the (observed) measurements. Also shown in Fig. 3 are the EKF state estimates, which are described in detail later.
FIG. 3.
Dynamic state space model of the EKF. The a priori state is used to update the pulse-sequence at each time step.
For image-based motion tracking, xk = [tx, ty, tz, θx, θy, θz]T is a 6-dimensional vector of rigid-body motion parameters, where the first three and last three elements are translations and rotations in x-y-z space, respectively and yk is an Nv-dimensional vector of voxel intensities of the k-th SP-Nav, where Nv is the total number of voxels in all three navigator planes. The time evolution of the state vector is given by the 6 × 6 state transition matrix A and the Gaussian process noise by w, with mean zero and covariance Q. Because of the relatively unpredictable nature of patient head motions over the sampling interval of the SP-Navs, the dynamics are modeled using a simple random walk, with A as the identity matrix. h(·);ℝ6 → ℝN, is a nonlinear vector-valued function of the current state called the measurement model, which describes how the states are observed through the noisy measurements. For image-based tracking, the measurement model h(·) describes a 2D interpolation into a fixed reference navigator yref (collected at the beginning of the scan) at the locations specified by xk. The exact mathematical form of h(·) is provided in the Appendix. To improve the robustness of the tracking to potential variations in the mean signal level of each SP-Nav, the measurements yk are forced to have unit norm at each time-step. The error in the measurement process is given by the Gaussian measurement noise v, with mean zero and covariance R. In the dynamic state-space model above, the noise processes are time-invariant and statistically independent (i.e. E(wvT) = 0).
From a Bayesian point of view, the a posteriori filtering density P(xk|y0:k) of the state given the complete history of observations y0:k = {y0,y1,…,yk} constitutes the complete solution to the motion tracking problem. The EKF algorithm provides recursive estimates of the conditional mean of the a posteriori filtering density x̂k|k = E[xk|y0:k] = ∫xkP(xk|y0:k)dxk using a two-stage recursion of prediction and correction at each time-step. Here, x̂k|k refers to the corrected, or a posteriori state estimate at time-step k, given all the measurements up to and including yk. For prospective motion correction in MRI, an additional scanner update step is included in the recursion.
Prediction
In the prediction step, the state transition matrix A and assumed process noise covariance Q are used to predict the state and error covariance at each time-step. With A as the identity matrix, the predicted state and error covariance become
| [3] |
| [4] |
where x̂k|k−1 is the predicted or a priori state estimate at time-step k, given the a posteriori state estimate x̂k−1|k−1 at the previous time-step k-1 (see Fig 3). P̂k|k−1 = E[(xk − x̂k|k−1)(xk − x̂k|k−1)T] is a priori state estimation error covariance at time-step k, given the a posteriori state estimation error covariance P̂k−1|k−1 at k-1.
Update
For prospective motion correction, the predicted state x̂k|k−1 of the EKF is used to update the scanner pulse-sequence prior to collecting the measurements yk. This includes updating the slice, phase, and frequency encoding of the imaging volume as well as the navigators, given the 3D translations and rotations in x̂k|k−1. A real-time communication system described in Ref (33) and implemented as in Ref (34), was used for efficient and near real-time communication of SP-Nav data, EKF state estimates, and associated meta data between the EKF module and the scanner pulse-sequence/receive chain.
Correction
Immediately following the scanner update, the measurements yk are acquired and used to correct the predicted state x̂k|k−1 and error covariance P̂k|k−1. The basic idea of EKF correction is to approximate the nonlinear function h(·) using a Taylor series expansion around x̂k|k−1 and apply the standard linear Kalman filter equations to the new linearized model. In this study, the first-order iterated EKF correction was implemented (23), which truncates the Taylor series to first-order and iterates the correction a total of N times. The first-order iterated EKF correction is analogous to performing an online Gauss-Newton optimization of the following nonlinear cost function (35)
| [5] |
for i = 0, 1, …, N. When N is set to zero, the first-order iterated EKF correction reduces to the standard EKF correction. Details of how the cost function Ci(xk) is minimized given the online updates to the scanner pulse-sequence are provided in the Appendix.
The first term on the left hand side of Eq. [5] is the “data prediction error” while the second term on the right hand side of Eq. [5] is the “model estimation error”. Note, most offline intensity-based image registration algorithms are based on iteratively minimizing the “data prediction error”, or some variant of this function. The EKF can therefore be viewed as a generalization of traditional intensity-based image registration that incorporates an additional model for the dynamics and is uniquely suited for online applications because 1) it is causal in nature and 2) does not require iterating the cost function (by setting N = 0), which is important in time-sensitive applications. Thus, in the limit of infinitely large process noise covariance Q, the “model estimation error” is effectively ignored when minimizing the cost, and the EKF is analogous to traditional image-based least-square registration with N iterations. The weighting of the “data prediction error” and “model estimation error” to the overall cost depends on both error terms Q and R. Selection of these priors is an important step in optimal EKF performance and is described next.
Filter tuning
Because the EKF is unchanged by scaling Q and R by the same factor, it is often convenient to define a single scalar that controls the relative weighting of the “data prediction” and “model estimation errors”. To do this, we factor Q and R into
| [6] |
| [7] |
where and are scalars, and Q̅ and R̅ are matrices of unit norm containing the structure of the respective noise processes. The ratio then controls the effective "bandwidth" of the filter, with increased tracking ability on the one hand (high weighting of data information with low values of S) and increased noise suppression on the other (high weighting of model information with high values of S). Throughout the remainder of this work, we refer to S as the “smoothness factor”.
The noise covariance structure, or entries of Q̅ and R̅, can be selected to utilize prior knowledge about the object’s dynamics and measurement errors, respectively. Given the physical constraints of the patient inside the MRI environment, some of the off-diagonal entries of Q̅ will likely be non-zero. However, for the sake of simplicity, we assume each motion parameter is independent, thus Q̅ is diagonal and can be written
| [8] |
where the first three and last three elements have units mm2/TN2 and rad2/TN2, respectively, with TN being the time between the onset of two consecutive SP-Navs. In addition, we assume the measurement errors are white, thus R̅ is diagonal, and the inverse can be written
| [9] |
The scalars along the diagonal of provide a means of weighting the contributions of each voxel to the motion estimate and thus setting the appropriate weights di to zero provides a principled approach for motion tracking within a priori regions-of-interest (ROIs). This procedure is described next.
ROI tracking
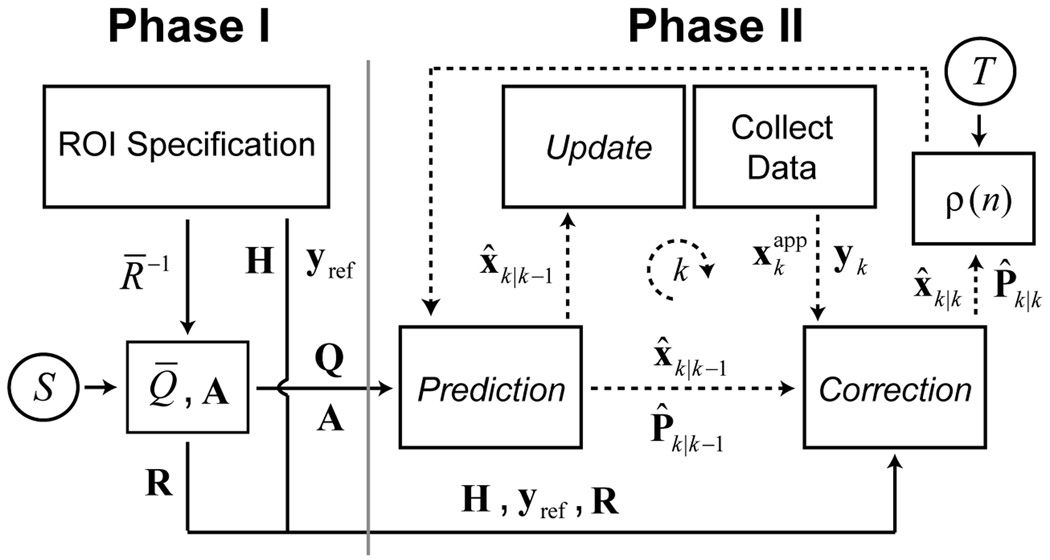
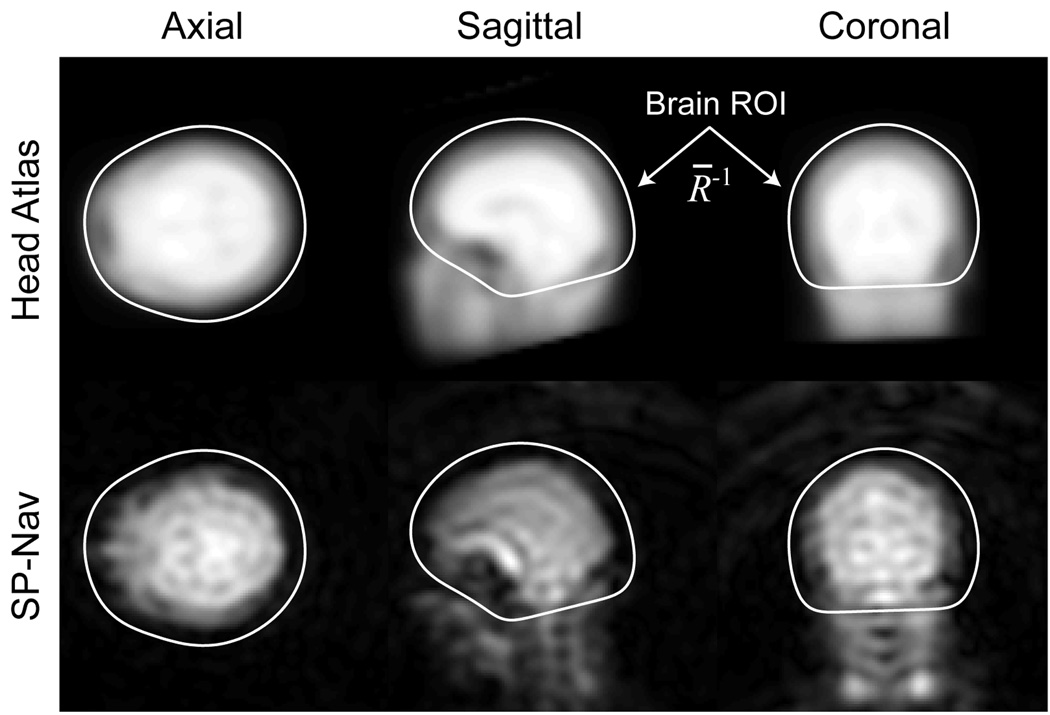
The advantage of image-based ROI tracking with the EKF is that the estimation can focus on a particular region (ROI) in object space while ignoring other regions that may corrupt the rigid-body motion estimates. In this study, a brain ROI is adapted to each patient to remove the effects of non-rigid motion of the neck and jaw. The general procedure is shown schematically in Fig. 4 and can be separated into two principal phases. During the first phase (Phase I), a train of 20 SP-Navs are played out in rapid succession immediately prior to the start of the “dummy” scans. During collection of this SP-Nav train, the EKF is used to register a fixed 3D proton density (PD) weighted head atlas to the patient. Once the registration is complete, the entries of R̅−1 (data weights) are set to the voxel values in a 3D binary brain mask, defined in atlas space. The construction of both the 3D head atlas and associated brain mask was performed offline and is described in detail in Ref (28). Immediately after the brain ROI is specified, a series of 4 dummy scans are acquired to allow equilibration of the longitudinal magnetization. Once the dummy scans are complete, the final EKF parameters, such as the Jacobian H (see the Appendix for a description of the Jacobian and how it is calculated), reference navigator yref (which is set to the last SP-Nav prior to scan start) and covariance matrices Q and R are calculated and stored in memory. The entire duration of Phase I takes approximately 10 s. An example reference navigator, registered head atlas and brain ROI are shown in Fig. 5.
FIG. 4.
Online EKF schematic for patient-specific ROI tracking. is the “applied” state used to collect the measurements yk and is described in the Appendix.
FIG. 5.
Results from Phase I of the EKF tracking procedure showing the SP-Nav reference image (bottom row), registered head atlas (top row), and brain ROI (white lines). All voxels outside of the brain ROI in the SP-Nav are ignored during tracking.
In the second phase (Phase II), the “tuned” EKF is run online for prospective motion correction during the scan. Because the SP-Navs are only acquired during the T1 recovery period of the pulse-sequences, no correction is performed during the imaging segment itself, which typically lasts about 2 s. To account for this, motion corrupted k-space segments were re-acquired at the end of the scan. To determine which segments needed to be re-acquired a simple “rescan metric” was defined
| [10] |
where x̂−(n) and x̂+(n) are used to denote the a posteriori motion estimates (in mm and deg) immediately prior and immediately after the collection of the n-th k-space segment, respectively. All k-space segments with ρ(n) greater than or equal to a user-specified threshold T are then marked for rescanning. In this study, the rescan threshold was selected based on in vivo experiments performed during no motion and is described in the section titled “In vivo validation experiment”.
Offline simulations
Offline Monte Carlo simulations were used to test the performance of the EKF for motion tracking in the SP-Nav sequence. For each Monte Carlo run, a time-series of 10 SP-Navs was synthesized by interpolating into a single isotropic 3D SP-Nav volume (collected with similar acquisition parameters to the online 2D SP-Navs). To simulate online motion correction, the orientation of each synthesized SP-Nav was determined by combining both the simulated motion with the predicted state of the EKF at each time-point. Two different simulation experiments were performed. The first tested simple 1D motions in each parameter separately and the second tested compound random amplitude motions in all parameters simultaneously. In all experiments, step functions were used to simulate motion (starting at the forth time-point) so that the convergence behavior of the EKF could easily be visualized using different filter parameters. Both “large” and “small” motions were tested using either a 10 mm/deg or 1 mm/deg step (for the 1D simulation experiment) or constraining the vector norm across all parameters (in mm and deg) to be either 10 or 1 (for the compound motion experiment), respectively. Prior to estimation, random Rician noise was added to each image with various signal-to-noise ratios (SNR). The measurement noise level of the EKF was determined empirically for each SNR level using the mean (within brain) signal magnitude estimated from the native 3D SP-Nav volume. Thus, when testing the effect of different “smoothness factors” S, only the process noise level of the EKF was varied. All simulations were performed on a Dell Precision workstation using Matlab (Mathworks, Inc.).
Online in vivo experiments
Three different types of in vivo experiments were performed to test the online performance of the SP-Nav/EKF tracking framework in the 3D IR-SPGR and 3D FSE sequences. Prior to scanning, all subjects provided informed consent in accordance with the University of California, San Diego institutional review board.
In vivo validation experiment
The first in vivo experiment was designed to assess the steady-state accuracy of the SP-Nav/EKF motion estimates. The basic procedure consisted of modifying the IR-SPGR sequence (Fig. 2a) to collect the same three volumes back-to-back (V1, V2, and V3). During the scan, a highly motivated volunteer was instructed to either remain motionless throughout ("no-motion" trial), or make a single brief motion during the middle of the second volume (V2) and remain in that position until the end of the scan ("motion" trial). No instruction was given as to what type of motion to perform, only to vary the magnitude and direction of motion from trial to trial. During each trial, prospective motion correction was performed with respect to the reference navigator of the first volume. After the scans were complete, three quantities were estimated for each trial: 1) the steady-state EKF motion estimate, calculated by averaging the online motion estimates during V3, 2) the steady-state error of the EKF motion estimates, calculated offline by registering V1 to V3 using an iterative 3D rigid-body registration algorithm, and 3) the “true” motion of the subject, calculated by combining the steady-state EKF estimate with the steady-state error. Prior to computing these quantities, all motion plots were inspected to verify the subject did not move during the collection of V1 or V3. Each trial of the validation experiment required approximately 24 minutes of scanning and a total of 15 trials were performed (2 “no motion” trials and 13 “motion trials”). The rescan threshold T was selected based on data obtained during the two “no motion” trials. The mean ρ(n) during all six volumes of both trials was 0.31, with a minimum of 0.07 and a maximum of 0.68. Thus, to be conservative, the rescan threshold T was set to 1 for all subsequent in vivo scans in this study.
Repeated staged motion experiment
The second in vivo experiment was designed to assess the performance of the SP-Nav/EKF framework for reducing 3D rigid-body head motion artifacts in the MRI scans themselves under relatively controlled conditions. Three types of scans were performed on a single subject: 1) a scan without motion correction where the subject was asked to perform repeated staged motions continuously during the scan (PROMO OFF condition), 2) a scan with motion correction where the subject was asked to repeat the same motions as in (1) (PROMO ON condition), and 3) a baseline scan without motion correction where the subject was asked to stay as still as possible (NO MOTION condition). Two types of staged head motions were performed: 1) "side-to-side" motion and 2) "nodding" motion.
Real life experiment
The final in vivo experiment was designed to assess the overall performance of the SP-Nav/EKF framework for reducing 3D rigid-body head motion artifacts in the MRI scans under realistic conditions. To do this, two healthy young males were scanned (ages 10 and 11) with the 3D IR-SPGR sequence with and without PROMO correction twice (total of 4 scans per subject). Young males were recruited because of their known tendency to move during the scan sequence despite being instructed not to. No specific instruction was given to either subject, only to remain “as still as possible”.
Results
Offline simulations
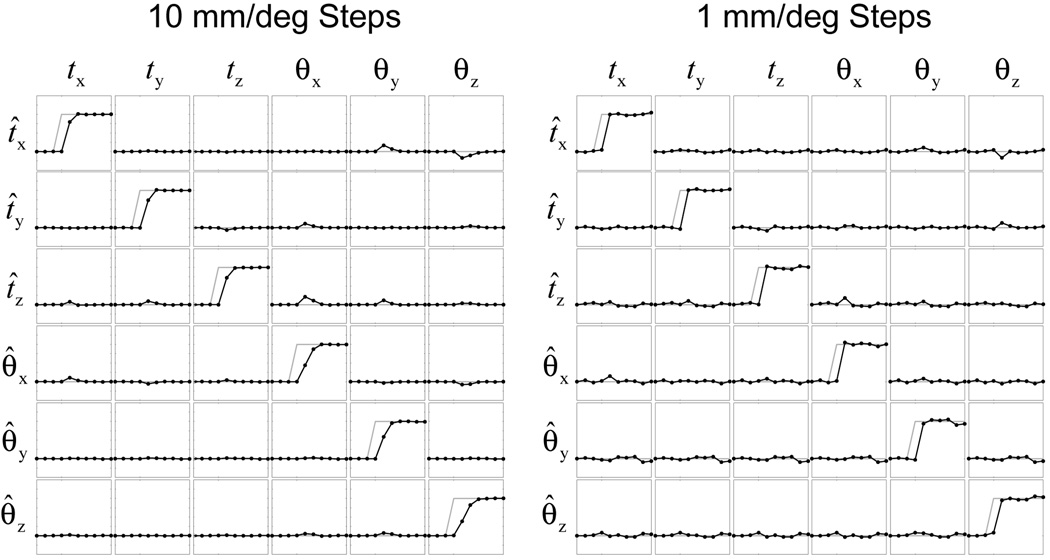
EKF tracking results for the 1D steps along each motion parameter are shown in Fig. 6 for both “large” (10 mm/deg) and “small” (1 mm/deg) motion magnitudes with an SP-Nav SNR of 10 (which approximates the actual SNR of the online SP-Navs). The results are shown in “matrix” format where the columns indicate the simulated parameter and the rows indicate the estimated parameter. Not surprisingly, the error variance in the estimates due to noise is more apparent for the “small” sub-voxel motions than the “large” motions.
FIG. 6.
EKF tracking results for 1D motion steps. The true motion is shown in gray and the estimated motion in black. A total of 6 trials (columns) where used to create each 6 × 6 matrix. Off-diagonal plots indicate the “cross-talk” error of the EKF.
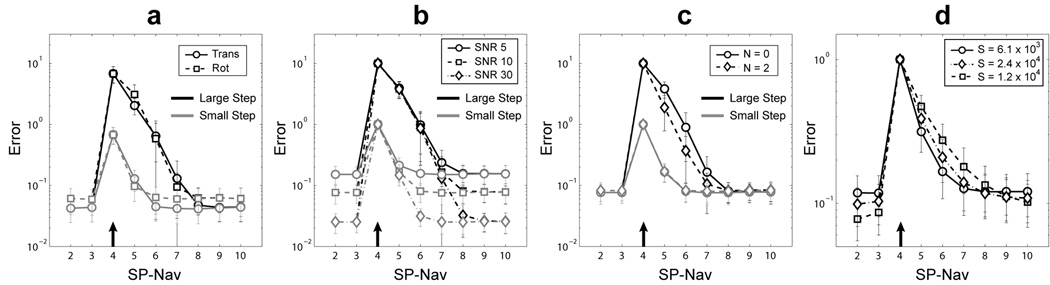
EKF tracking results for compound random amplitude motion steps are shown in Fig 7. For all plots, the average norm error ± std over 500 Monte Carlo runs are shown. Figure 7a shows the norm error for translations and rotations. Figure 7b shows the effect of SNR on the overall (norm across all six parameters) EKF tracking error. Figure 7c shows the effect of adding additional iterations (N) on the overall tracking error for a fixed SNR of 10. Only N = 2 iterations are shown because increasing the number of iterations beyond this point had little effect on the tracking results (algorithm had converge to a local minimum). In Figure 7a, b, and c, the “smoothness factor” is set arbitrarily low (S = 6.1 × 103) to remove the weight of the “model estimation error” on the Kalman cost function and reducing S any further had minimal effect on the tracking performance. Because only the “data prediction error” is used during estimation, one can interpret the iterated EKF in Fig. 7c as a standard image-based least-squares registration with N iterations. Figure 7d shows the effect of increasing the “smoothness factor” (i.e., increasing the weight on the “model estimation error”) on the overall tracking error for “small” motions only with a fixed SNR of 10.
FIG. 7.
Average EKF tracking errors (over 500 Monte Carlo runs) for compound random amplitude motion steps plotted on a log scale. (a) Translation and rotation error for “large” and “small” motion steps. (b) Overall error (norm across all six parameters) as a function of SNR for “large” and “small” motion steps. (c) Overall error as a function of EKF iteration (N) for “large” and “small” motion steps with an SNR of 10. (d) Overall error as a function of “smoothness factor” S for “small” motion steps with an SNR of 10. In all plots, the arrow indicates the onset of the motion. Time-point 1 is omitted as the predicted state (motion) of the EKF is zero.
In vivo validation experiment
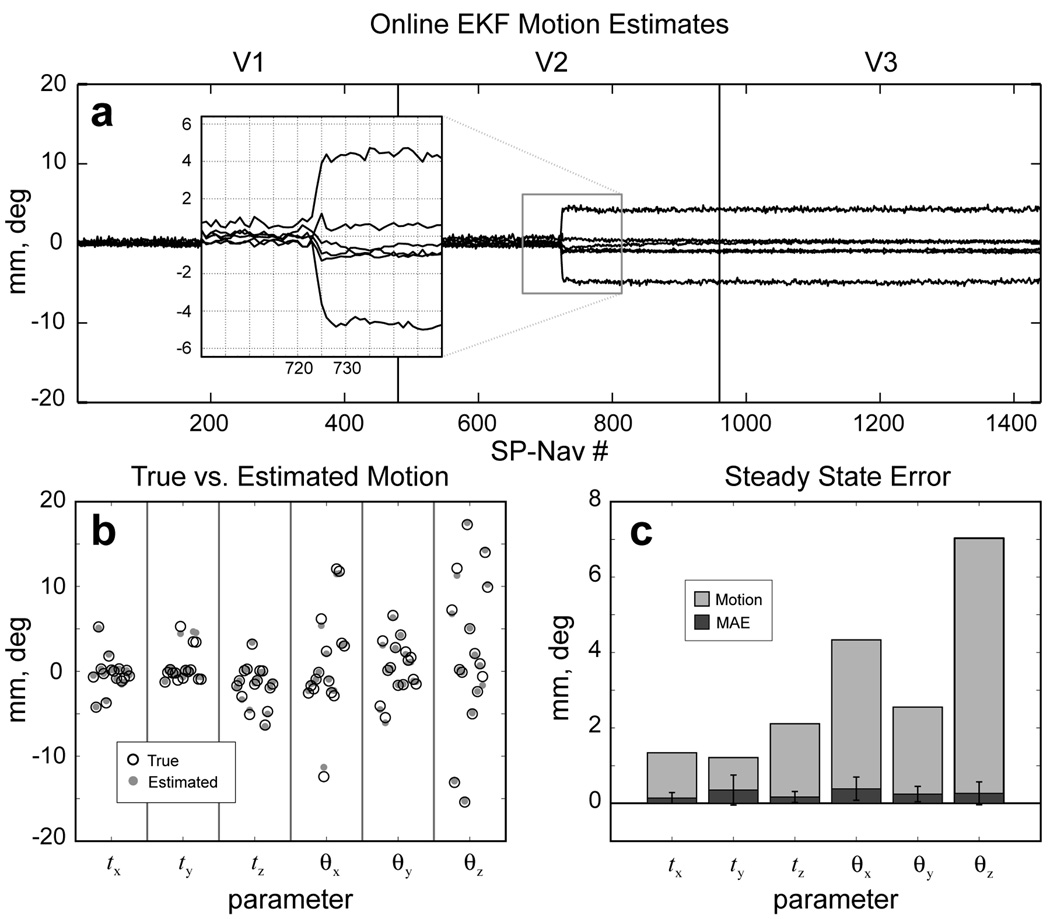
Results from the in vivo validation experiment are shown in Fig. 8. Online motion estimates for a single representative “motion-trial” are shown in Fig. 8a. Note how the subject made a single brief motion during the middle of V2 and remained fixed in this position throughout the remainder of the scan. The steady-state EKF motion estimates are plotted against the "true" motion of the subject for all 15 trials in Fig. 8b. The mean absolute steady-state error (MAE) ± std and mean magnitude of the “true” motion across all trials is shown in Fig. 8c. The MAE ± std was calculated to be: tx = 0.14 ± 0.15 mm, ty = 0.35 ± 0.39 mm, tz = 0.17 ± 0.15 mm, θx = 0.39 ± 0.31 deg, θy = 0.25 ± 0.20 deg, and θz = 0.27 ± 0.30 deg. The mean magnitude of the “true” motion was calculated to be: tx = 1.34 mm, ty = 1.22 mm, tz = 2.11 mm, θx = 4.33 deg, θy = 2.55 deg, and θz = 7.03 deg. The overall steady-state error (mean across all parameters and trials) was 0.26 and the overall magnitude of motion (mean across all parameters and trials) was 3.09, which yields an expected overall steady-state error of less then 10 % of the true motion.
FIG. 8.
Results from the in vivo validation experiment. (a) Online motion estimates for a single representative “motion” trial. Insert shows a close-up of the tracking estimates during the motion onset interval. (b) The “true” vs. steady-state EKF motion estimates over all 15 experimental trials. (c) The mean absolute steady-state EKF error (MAE, dark gray) compared with the mean magnitude of the “true” motion (light gray) for each parameter across all trials.
Repeated staged motion experiment
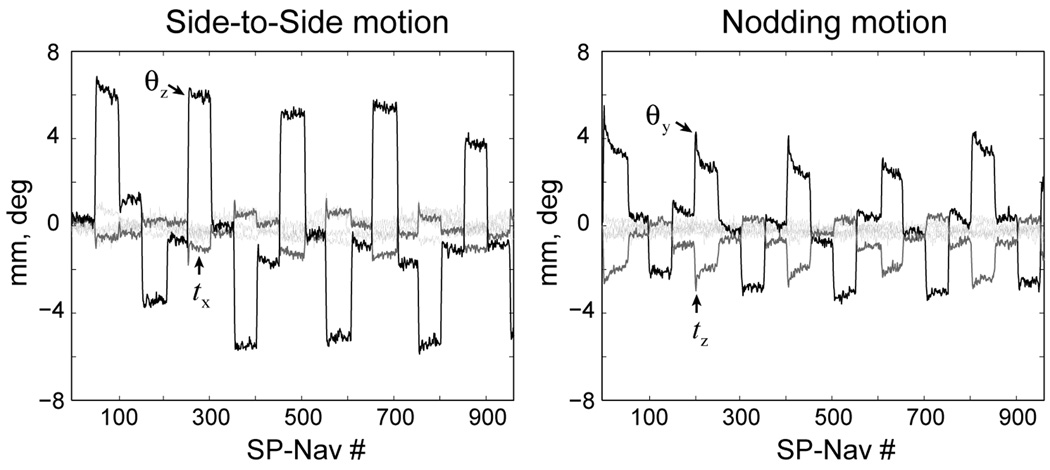
Online EKF motion estimates obtained during the repeated staged “side-to-side” and “nodding” motion experiments for the two PROMO ON 3D IR-SPGR scans are shown in Fig. 9. As shown in the figure, “side-to-side” motion is characterized by rotations around the z-axis and translations around the x-axis, while “nodding” motion were characterized by rotations around the y-axis and translations around the z-axis. Although not shown, similar motion estimates were evident during all other “side-to-side” and “nodding” motion experiments.
FIG. 9.
Example EKF motion estimates for the PROMO ON IR-SPGR scan during the “side-to-side” and “nodding” motion experiments.
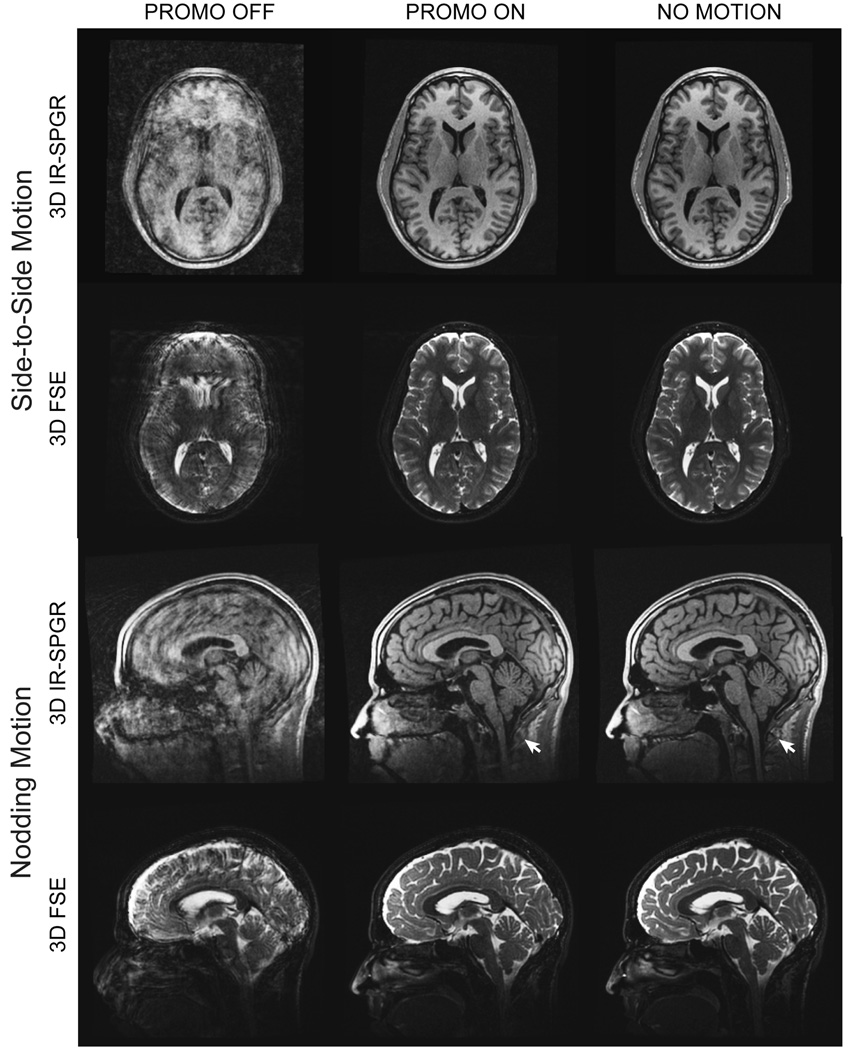
The images from the repeated staged motion experiment are shown in Fig. 10. In order to compare corresponding slices, all reconstructed volumes were registered and resampled (using high dimensional sinc interpolation) to the NO MOTION 3D FSE volume. As evident in the figure, the PROMO corrected images have significantly reduced motion artifacts for both types of staged motion to a level that is qualitatively similar to the NO MOTION scans.
FIG. 10.
Reconstructed images for the repeated staged motion experiment. Only a single axial and sagittal slice through the volumes are shown. The number of rescanned k-space segments for the PROMO ON scans using a threshold of T = 1 were (from top to bottom) 20, 10, 35 and 5, respectively. The two images highlighted with arrows are shown again in Fig. 11.
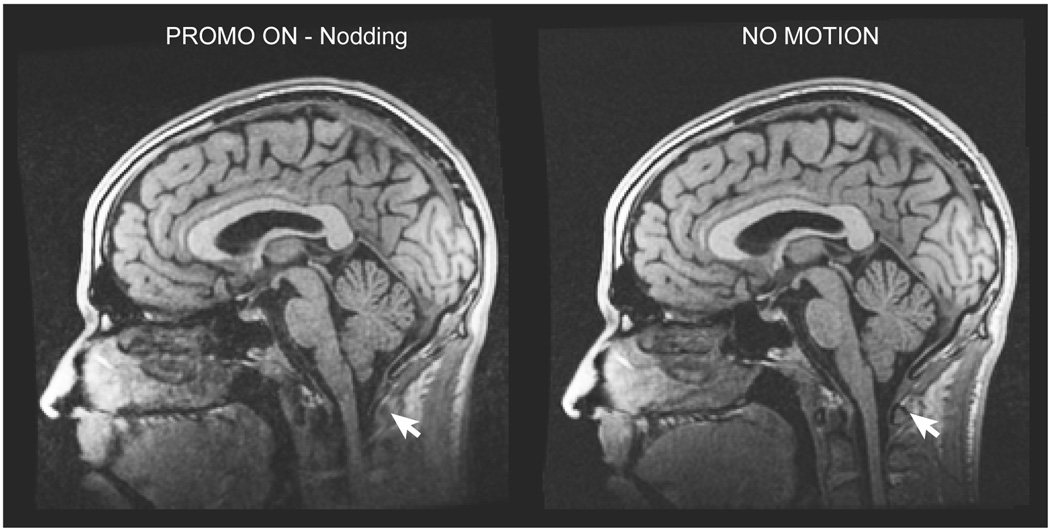
A close-up of the PROMO ON and NO MOTION IR-SPGR sagittal slices shown in Fig 10 for the “nodding” motion experiment are shown by themselves in Fig. 11. The white arrows in the figure highlight an area of the neck outside the EKF brain mask that underwent non-rigid motion during the scan and was subsequently uncorrected in the final image.
FIG. 11.
Comparison of the PROMO ON 3D IR-SPGR scan during “nodding” motion and the NO MOTION 3D IR-SPGR scan. White arrows highlight a region of the neck outside the brain ROI of the EKF, which moved non-rigidly during the scan and is subsequently uncorrected in the image.
Real life experiment
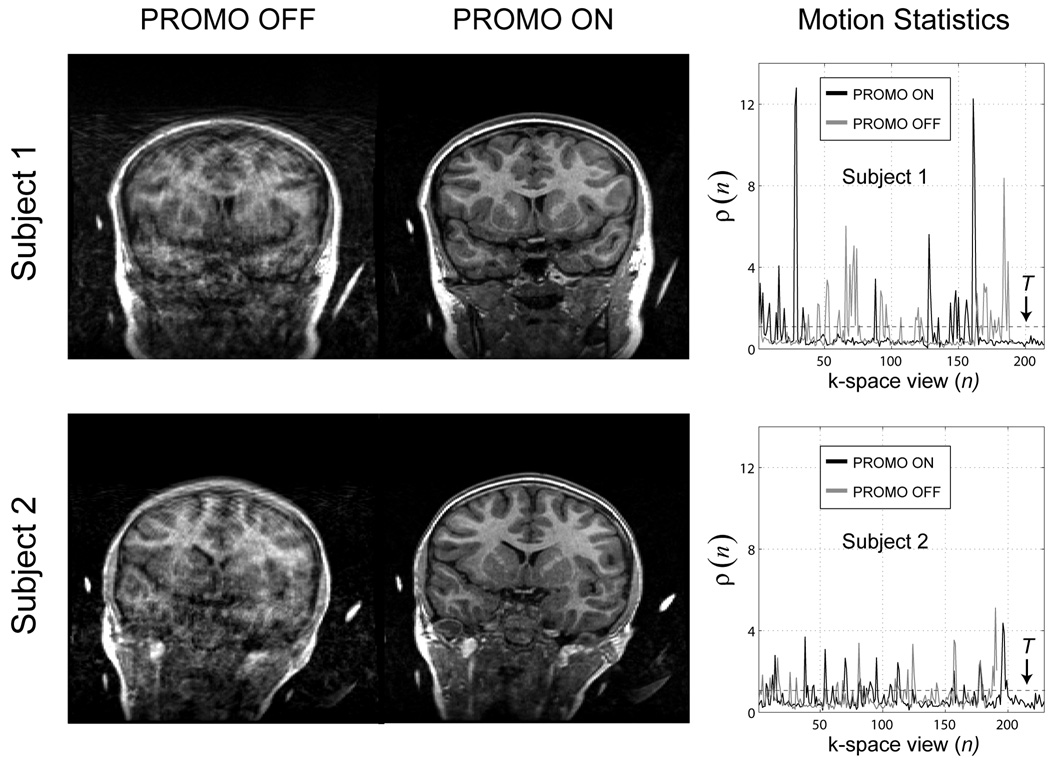
Corresponding coronal sections through the PROMO ON and PROMO OFF IR-SPGR scans for each of the two young male subjects are shown in Fig. 12. Both sets of PROMO ON and PROMO OFF scans were selected from the set of 4 to have qualitatively similar motion statistics as assessed with the “rescan metric” ρ(n), also included in the figure. Again, the images with PROMO correction have significantly reduced motion artifacts compared to the images without correction. The number of rescanned k-space segments for Subject 1 and Subject 2 using a threshold of T = 1 were 23 and 38, respectively.
FIG. 12.
Real life images taken from two healthy young males with and without PROMO correction along with the “rescan metric” ρ(n).
Discussion
This work describes a new technique for prospective motion correction that utilizes three orthogonal 2D spiral navigator acquisitions (SP-Navs) along with a flexible image-based tracking method based on the EKF algorithm for online motion measurement. A preliminary application of the SP-Nav/EKF tracking framework in 3D IR-SPGR and 3D FSE pulse-sequences demonstrates the effectiveness of the approach for significantly reducing 3D rigid-body motion artifacts prospectively in these sequences.
Offline simulations
Offline simulations revealed some important properties of the SP-Nav/EKF framework for rigid-body motion tracking. Figure 6 demonstrated how both “large” and “small” 1D translations and rotations in all three degrees of freedom could be estimated with minimal transient “cross-talk” error. The term “cross-talk” error is used here to describe the apparent motion in one parameter due to motion in another (i.e. the off-diagonal plots in Fig. 6). While there was a tendency for rotations to have slightly larger “cross-talk” errors than translations, this effect was minimal and in general, both rotations and translations could be estimated with similar accuracy and precision.
Figure 7 shows the performance of the SP-Nav/EKF framework for tracking compound random amplitude motion steps using various filter parameters and SNR levels. Consistent with the 1D motion simulation results, Figure 7a shows how translations and rotations could be estimated with similar accuracy and precision. Reducing the SP-Nav SNR increased the overall error due to noise (i.e. the baseline error when in the steady-state), but had little effect on the overall tracking error due to “large” and “small” compound motions, i.e. the filter response times (Fig. 7b). Thus, the number of SP-Navs (post motion onset) required to estimate “large” and “small” compound motions was relatively insensitive to SP-Nav SNR. Furthermore, increasing the number of EKF iterations (N) at each time-point (which increases the computation time significantly) was generally unnecessary, as it only marginally improved the overall tracking error for “large” compound motions but had no effect on the overall tracking error for “small” compound motions (Fig. 7c). An inspection of Fig 7a, b and c revealed that on average, 2–3 SP-Navs (post motion onset) were required to estimate “large” compound motions while only about 1–2 SP-Navs were required for “small” compound motions, regardless of the number of EKF iterations. This result suggests that the majority of the transient SP-Nav/EKF tracking error comes from through-plane motion of the SP-Navs, which is greater for “large” compound motions. Transient tracking errors caused by through-plane motion was also observed using orthogonal 2D orbital navigators (14) and is likely to have contributed substantially to the transient “cross-talk” errors in the 1D simulations. However, as demonstrated in Fig. 6 and 7, this effect is mitigated when collecting multiple navigators back-to-back such that the through-plane motion component is reduced iteratively in time. The set of 5 SP-Navs played out during the 3D IR-SPGR or 3D FSE sequences should therefore be sufficient even in extreme situations where the patient makes a “large” transient motion during this interval.
Finally, varying the “smoothness factor” S (i.e., changing the degree to which the motion model influences the tracking estimates) resulted in a trade-off between increased noise suppression on the one hand (low filter bandwidths with high values of S) and reduced tracking error due to transient motion on the other (high filter bandwidths with low values of S). This is evidenced in Fig. 7d. Because the level of noise suppression was relatively small compared with the increase in overall tracking error, low “smoothness factors” (and no EKF iterations) were used for all subsequent in vivo scans. It should be noted that this finding is not surprising given 1) the large number of measurement voxels in each SP-Nav (effectively about 16,000 after masking) compared to the small number of rigid-body motion parameters to be estimated at each time-point and 2) the image SNR is relatively high (SNR = 10). Both of these factors suggest that the “data prediction error” should contribute more information to the Kalman cost than the “model estimation error”. However, it should also be noted that although the model information played a relatively minor role in the current application of the Kalman filter for tracking in the SP-Nav sequence, in applications where 1) there is reduced information in the measurements through either reduced SNR or number of imaging voxels (e.g., self-navigated head motion tracking in 2D EPI slice data), 2) there are more rapid image-based measurements available online, 3) there are more than six parameters in the state vector (e.g. modeling non-rigid motion or including velocity terms), and 4) there are strong regularities over time in the state parameters (e.g. when tracking cardiac or respiratory motion), increasing the weight on the dynamic model will likely play a more important role during tracking.
In vivo validation experiment
The steady-state error in the online SP-Nav/EKF motion estimates was quantified in vivo using real biological staged head motions (Fig. 8). In general, the accuracy of the in vivo estimates scaled with the magnitude of motion, with larger head motions leading to larger estimation errors. However, these errors were consistently less than one tenth of the overall magnitude, even for trials that included large compound motions with rotations over 15 deg (Fig. 8b and c). While the accuracy of the estimates from a single SP-Nav could not be assessed in vivo, an inspection of the tracking results suggests that the steady-state level of accuracy was reached in about 2–3 SP-Navs, consistent with the offline simulation results (c.f. insert in Fig. 8a). It should be noted that the range of motion magnitudes tested in this study was more than double the range used to benchmark the orbital (14), spherical (15) and cloverleaf (18) methods and yet in all trials the error never exceed the 10% level for any parameter and was typically well below this mark. It should also be noted that our validation procedure focused on motions that are more “likely” to be experienced in practice, given the nature of the scanner environment. Thus, not all parameters were tested to an equal extent during the validation experiment because the head coil itself limited some types of motions from being performed. This is evidenced by the fact that the subject made larger rotations versus translations during the validation experiment (c.f. “true” motion in gray in Fig. 8c).
Repeated staged motion experiment
Results from the repeated staged motion experiment demonstrated the effectiveness of the SP-Nav/EKF framework for reducing periodic “nodding” and “side-to-side” head motion artifacts in both the 3D IR-SPGR and 3D FSE sequences (Fig. 10). Because the EKF was “tuned” to estimate rigid-body motion within the brain ROI, areas outside this region were ignored and subsequently uncorrected in the final images. This is illustrated in Fig. 11, which shows a close-up of the PROMO ON 3D IR-SPGR scan during “nodding” motion and the NO MOTION 3D IR-SPGR scan. The area highlighted with a white arrow in the figure corresponds to a region in the neck outside the brain ROI that is uncorrected in the image.
Real life experiment
The results from the real life experiments on the two healthy young males again demonstrated the overall effectiveness of the SP-Nav/EKF framework for significantly reducing 3D rigid-body head motion artifacts in 3D IR-SPGR scans under real life conditions (Fig. 12). Qualitatively similar motion statistics, as quantified using the “rescan metric” ρ(n), suggests that the improvement in image quality was not due to an overall difference in the level of motion between the two scans (Fig. 12).
Advantages/limitations
The image-based SP-Nav/EKF tracking framework implemented in this study offers several advantages over existing k-space-based orbital (14), spherical (15) and cloverleaf navigator techniques (18). All k-space-based navigator methods require precise and reproducible k-space sampling trajectories from shot-to-shot such that rotations and translations in image-space can be estimated from k-space magnitude and phase information, respectively. Consequently, any effect that violates the assumptions of this Fourier model, such as 1) off-resonance due to magnetic field inhomogeneities and susceptibility differences, 2) gradient instabilities and 3) non-rigid motion of the object, will degrade the accuracy and precision of k-space-based rigid-body motion estimates. The SP-Navs, on the other hand, provide reduced sensitivity to motion estimation inaccuracies due to off-resonance by blurring these effects equally in all directions in image-space. Moreover, tracking in image-space allows for masking areas of the object that may corrupt the rigid-body motion estimates. In this study, we show how the EKF can be “tuned” during the “dummy” acquisition period to prevent non-rigid motion of the neck and jaw from corrupting the rigid-body estimates of the brain and skull. This type of masking using a k-space-based approach is difficult and requires tuning the RF pulse to excite only the rigid-body tissue component (s). However, although the motion estimates from a single SP-Nav have reduced sensitivity to off-resonance, any slow change in SP-Nav image quality over time due to scanner instabilities or time-varying off-resonance effects will corrupt the SP-Nav rigid-body motion estimates and ultimately reduce the quality of the final reconstructed images.
In terms of time requirements, a single 3-plane SP-Nav can be collected and reconstructed in approximately the same time (48 ms) as a 3-plane orbital navigator (33 ms) (14) and spherical navigator (27 ms) (15), but requires substantially more time than a single cloverleaf (4.2 ms) (18). Therefore, the cloverleaf method may be advantageous in certain steady-state sequences where there is no intrinsic sequence “dead time” for navigator acquisition. However, in non-steady-state sequences such as 3D IR-SPGR and 3D FSE, a train of SP-Navs can be played out during the intrinsic T1 recovery period of the acquisition without adding to the overall scan time. However, no motion correction is performed during the imaging segment itself, which typically lasts about 2 s. To account for this, corrupted k-space segments were rescanned at the end of the sequence depending on whether an online “rescan metric” exceeded a user-specified threshold. In this study, all in vivo scans were performed using a rescan threshold of T = 1, derived empirically from repeated no motion scans. This type of rescan procedure should be generally acceptable in most clinical applications, given that the number of rescanned k-space segments for the two young (and fairly uncooperative) males who participated in this study only resulted in an additional scan time of 50 s (Subject 1) and 90 s (Subject 2), respectively.
One limitation of the EKF tracking algorithm, as implemented in this study, is the inability to correct (rather than just ignore) non-rigid motion. In principle, however, one can augment the EKF state vector to include higher order motion parameters for nonlinear motion tracking. Velocity and acceleration terms can also be incorporated in the dynamic model when more rapid measurement information is available. For example, Sprincemaille et al. recently applied the linear Kalman filter with first-order constant velocity (CV) dynamics for rapid (~15 ms) real-time separation of cardiac and respiratory waveforms from navigator least-squares motion estimates (30). In general, the flexibility afforded by the dynamic state-space model framework of the EKF should allow for online image-based tracking of many different body parts using various types of measurements including 2D slice information for self-navigated tracking in EPI time-series data (25).
Summary
In summary, the results presented in this paper demonstrate the effectiveness of the PROMO motion correction technique for significantly reducing 3D rigid-body motion artifacts prospectively in high-resolution 3D scans. While the current implementation focused on spiral-navigated 3D IR-SPGR and 3D FSE scans, the flexible image-based EKF tracking procedure in PROMO may be useful in other applications such as self-navigated prospective motion correction in 2D EPI time-series data.
Acknowledgements
Funding for this work was provided by GE Healthcare Inc. and the following NIH grants: 1R01AG031224, 1U01AG024904-02, 5 U24 RR021382-04, U54 NS056883-01
Appendix
To describe the online first order iterated EKF algorithm for prospective motion correction in the scanner sequence, let M(x) be a 4 × 4 affine transform matrix that is parameterized by the state variable x = [tx, ty, tz, θx, θy, θz]T
| [11] |
where
| [12] |
| [13] |
and cx, cy and cz are the cosines and sx, sy and sz are the sines of the parameters θx, θy and θz, respectively. Furthermore, let X;ℝ4×4 → ℝ6×1 be a function which describes the inverse mapping between the affine transform matrix M(x) and the state vector x
| [14] |
where mij is the ij-th entry of M(x) and atan2 is the four quadrant inverse tangent.
Now let x0 = [0 0 0 0 0 0]T be the initial state of the EKF at time k = 0 and yref = h(x0) be the initial fixed reference SP-Nav. In the ideal online correction scenario, the affine transform matrix M(x̂k|k−1 associated with the predicted state x̂k|k−1 is then used to update the scanner pulse-sequence at each time-step prior to collecting the measurements yk. However, to generalize the method in case this condition is not met (e.g., if real-time communication is interrupted or the previous corrected state x̂k−1|k−1 is not obtained in the time allowed), let be the actual “applied” state used to collect yk. Now, let be the “adjusted” state that takes into account the potential mismatch between the predicted and “applied” state at time-step k. When the predicted state is equal to the “applied” state at each time-step, the “adjusted” state is simply the initial state x0.
The goal of EKF correction is to use the measurements yk to refine the predicted state x̂k|k−1 and error covariance P̂k|k−1 at each time-step. Recall, this is accomplished by minimizing the cost
| [15] |
using i = 0, 1, …, N iterations. The first order iterated EKF (Gauss-Newton) solution to such an optimization problem is the following update function
| [16] |
where , Hi is the Jacobian of the measurement function h(·) evaluated at the “adjusted” state , and is the Kalman gain. Details of the derivation of Eq. [16] is provided in many texts including Ref. (23) and is omitted here due to space constraints. At the end of all iterations, the a posteriori state x̂k|k is set to and the a posteriori covariance P̂k|k is set to (I−KN+1HN+1)P̂k|k−1. Note, when no iterations are performed (i.e. N = 0) Eq. [16] reduces to the standard EKF. It should also be noted that when predicted state is equal to the “applied” state at each time-step and N = 0, the Jacobian Hi is always evaluated around the initial state x0 and thus can be calculated once and stored in memory.
To describe the details of the measurement function h(·), let yax, ysa and yco be the respective 2D axial, sagittal and coronal images of the concatenated reference navigator vector yref = [vec(yax)T vec(ysa)T vec(yco)T]T, where the operator vec(·);ℝm×m → ℝ2m×1 concatenates a 2D matrix into a 1D vector. Furthermore, let rax, rsa, and rco be 4 × M matrices of initial (homogenous) voxel coordinates for yax, ysa and yco, respectively. Then, the measurement function h(x) can be written
| [17] |
where Pax = diag([1 1 0 1]T), Psa = diag([0 1 1 1]T) and Pco = diag([1 0 1 1]T) are matrices which project the transformed 3D homogenous coordinates onto the respective planes of the reference prior to interpolation. In this study, 2D linear interpolation was used throughout.
References
- 1.Hajnal JV, Myers R, Oatridge A, Schwieso JE, Young IR, Bydder GM. Artifacts due to stimulus correlated motion in functional imaging of the brain. Magn Reson Med. 1994;31(3):283–291. doi: 10.1002/mrm.1910310307. [DOI] [PubMed] [Google Scholar]
- 2.Friston KJ, Williams S, Howard R, Frackowiak RS, Turner R. Movement-related effects in fMRI time-series. Magn Reson Med. 1996;35(3):346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- 3.Cox RW, Jesmanowicz A. Real-time 3D image registration for functional MRI. Magn Reson Med. 1999;42(6):1014–1018. doi: 10.1002/(sici)1522-2594(199912)42:6<1014::aid-mrm4>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 4.Friston KJ, Ashburner J, Frith C, Poline JB, Heather JD, Frackowiak RSJ. Spatial Registration and Normalization of Images. Human Brain Mapping. 1995;2:165–189. [Google Scholar]
- 5.Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5(2):143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- 6.Korin HW, Felmlee JP, Ehman RL, Riederer SJ. Adaptive technique for three-dimensional MR imaging of moving structures. Radiology. 1990;177(1):217–221. doi: 10.1148/radiology.177.1.2399320. [DOI] [PubMed] [Google Scholar]
- 7.Ehman RL, Felmlee JP. Adaptive technique for high-definition MR imaging of moving structures. Radiology. 1989;173(1):255–263. doi: 10.1148/radiology.173.1.2781017. [DOI] [PubMed] [Google Scholar]
- 8.Liu C, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52(6):1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
- 9.Pipe JG. Motion correction with PROPELLER MRI: application to head motion and free-breathing cardiac imaging. Magn Reson Med. 1999;42(5):963–969. doi: 10.1002/(sici)1522-2594(199911)42:5<963::aid-mrm17>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 10.Firmin D, Keegan J. Navigator echoes in cardiac magnetic resonance. J Cardiovasc Magn Reson. 2001;3(3):183–193. doi: 10.1081/jcmr-100107467. [DOI] [PubMed] [Google Scholar]
- 11.Norris DG, Driesel W. Online motion correction for diffusion-weighted imaging using navigator echoes: Application to RARE imaging without sensitivity loss. Magn Reson Med. 2001;45(5):729–733. doi: 10.1002/mrm.1099. [DOI] [PubMed] [Google Scholar]
- 12.Weih KS, Driesel W, von Mengershausen M, Norris DG. Online motion correction for diffusion-weighted segmented-EPI and FLASH imaging. Magma. 2004;16(6):277–283. doi: 10.1007/s10334-004-0036-x. [DOI] [PubMed] [Google Scholar]
- 13.Fu ZW, Wang Y, Grimm RC, Rossman PJ, Felmlee JP, Riederer SJ, Ehman RL. Orbital navigator echoes for motion measurements in magnetic resonance imaging. Magn Reson Med. 1995;34(5):746–753. doi: 10.1002/mrm.1910340514. [DOI] [PubMed] [Google Scholar]
- 14.Ward HA, Riederer SJ, Grimm RC, Ehman RL, Felmlee JP, Jack CR., Jr Prospective multiaxial motion correction for fMRI. Magn Reson Med. 2000;43(3):459–469. doi: 10.1002/(sici)1522-2594(200003)43:3<459::aid-mrm19>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- 15.Welch EB, Manduca A, Grimm RC, Ward HA, Jack CR., Jr Spherical navigator echoes for full 3D rigid body motion measurement in MRI. Magn Reson Med. 2002;47(1):32–41. doi: 10.1002/mrm.10012. [DOI] [PubMed] [Google Scholar]
- 16.Irarrazabal P, Nishimura DG. Fast three dimensional magnetic resonance imaging. Magn Reson Med. 1995;33(5):656–662. doi: 10.1002/mrm.1910330510. [DOI] [PubMed] [Google Scholar]
- 17.Wong ST, Roos MS. A strategy for sampling on a sphere applied to 3D selective RF pulse design. Magn Reson Med. 1994;32(6):778–784. doi: 10.1002/mrm.1910320614. [DOI] [PubMed] [Google Scholar]
- 18.van der Kouwe AJ, Benner T, Dale AM. Real-time rigid body motion correction and shimming using cloverleaf navigators. Magn Reson Med. 2006;56(5):1019–1032. doi: 10.1002/mrm.21038. [DOI] [PubMed] [Google Scholar]
- 19.Thesen S, Heid O, Mueller E, Schad LR. Prospective acquisition correction for head motion with image-based tracking for real-time fMRI. Magn Reson Med. 2000;44(3):457–465. doi: 10.1002/1522-2594(200009)44:3<457::aid-mrm17>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 20.Zaitsev M, Dold C, Sakas G, Hennig J, Speck O. Magnetic resonance imaging of freely moving objects: prospective real-time motion correction using an external optical motion tracking system. Neuroimage. 2006;31(3):1038–1050. doi: 10.1016/j.neuroimage.2006.01.039. [DOI] [PubMed] [Google Scholar]
- 21.Speck O, Hennig J, Zaitsev M. Prospective real-time slice-by-slice motion correction for fMRI in freely moving subjects. Magma. 2006;19(2):55–61. doi: 10.1007/s10334-006-0027-1. [DOI] [PubMed] [Google Scholar]
- 22.Dold C, Zaitsev M, Speck O, Firle EA, Hennig J, Sakas G. Prospective head motion compensation for MRI by updating the gradients and radio frequency during data acquisition. Med Image Comput Comput Assist Interv Int Conf Med Image Comput Comput Assist Interv. 2005;8(Pt 1):482–489. doi: 10.1007/11566465_60. [DOI] [PubMed] [Google Scholar]
- 23.Gelb A. Applied Optimal Estimation. MIT Press; 1974. [Google Scholar]
- 24.Kalman RE. A New Approach to Linear Filtering and Prediction Problems. Transactions of the ASME--Journal of Basic Engineering. 1960;82(Series D):35–45. [Google Scholar]
- 25.White NS, Shankaranarayanan A, Han ET, Gaddipati A, Roddey C, Dale A. Prospective motion correction using nonlinear predictive filtering; Proceedings of the 15th Annual Meeting of the ISMRM; Berlin, Germany. 2007. [Google Scholar]
- 26.Shankaranarayanan A, Han ET, Roddey C, White N, Kuperman J, Santos J, Rettmann D, Schmidt E, Dale A. Motion insensitive 3D T2 and T1-weighted imaging with a real-time, image-based PROspective MOtion correction technique (3D PROMO) and automated re-acquisition of motion-corrupted k-space segments; Proceedings of the 16th Annual Meeting of the ISMRM; Toronto, Canada. 2008. [Google Scholar]
- 27.Shankaranarayanan A, Roddey C, White N, Han ET, Rettmann D, Santos J, Schmidt E, Dale A. Motion insensitive 3D imaging using a novel real-time image-based 3D PROspective MOtion correction method (3D PROMO); Proceedings of the 15th Annual Meeting of the ISMRM; Berlin, Germany. 2007. [Google Scholar]
- 28.Roddey C, Shankaranarayanan A, Han ET, White N, Dale A. Motion insensitive imaging using 3D PROspective MOtion (PROMO) correction with region-of-interest tracking. Toronto, Canada. Berkeley, USA: ISMRM; 2008. [Google Scholar]
- 29.Keating B, Roddey J, Deng W, Dale A, White N, Stenger V, Ernst T. 3-D Prospective Motion Correction for MR Spectroscopy; 17th Annual Meeting of the ISMRM; Honolulu, HI. 2009. [Google Scholar]
- 30.Spincemaille P, Nguyen TD, Prince MR, Wang Y. Kalman filtering for real-time navigator processing. Magn Reson Med. 2008;60(1):158–168. doi: 10.1002/mrm.21649. [DOI] [PubMed] [Google Scholar]
- 31.Lin C, Bernstein MA. 3D magnetization prepared elliptical centric fast gradient echo imaging. Magn Reson Med. 2008;59(2):434–439. doi: 10.1002/mrm.21448. [DOI] [PubMed] [Google Scholar]
- 32.Busse RF, Hariharan H, Vu A, Brittain JH. Fast spin echo sequences with very long echo trains: design of variable refocusing flip angle schedules and generation of clinical T2 contrast. Magn Reson Med. 2006;55(5):1030–1037. doi: 10.1002/mrm.20863. [DOI] [PubMed] [Google Scholar]
- 33.Santos JM, Graham AW, Pauly JM. In: Flexible Real-Time Magnetic Resonance Imaging Framework. EMBS PottAICI, editor. San Fransicso, CA: 2004. [DOI] [PubMed] [Google Scholar]
- 34.Santos JM, Cunningham CH, Lustig M, Hargreaves BA, Hu BS, Nishimura DG, Pauly JM. Single breath-hold whole-heart MRA using variable-density spirals at 3T. Magn Reson Med. 2006;55(2):371–379. doi: 10.1002/mrm.20765. [DOI] [PubMed] [Google Scholar]
- 35.Bell BM, Cathey FW. The iterated Kalman filter update as a Gauss-Newton method. IEEE Trans Automatic Control. 1993;38(2):294–297. [Google Scholar]