Abstract
The mechanisms of enzymes are intimately connected with their overall structure and dynamics in solution. Experimentally it is considerably challenging to provide detailed atomic level information about the conformational events that occur at different stages along the chemical reaction path. Here, theoretical tools may offer new potential insights that complement those obtained from experiments that may not yield an unambiguous mechanistic interpretation. In this study we apply molecular dynamics simulations of bovine pancreatic ribonuclease A, an archetype ribonuclease, in order to study the conformational dynamics, structural relaxation, and differential solvation that occurs at discreet stages of the transesterification and cleavage reaction. Simulations were performed with explicit solvation with rigorous electrostatics, and utilize recently developed molecular mechanical force field parameters for transphosphorylation and hydrolysis transition state analogs. Herein, we present results for the enzyme complexed with the dinucleotide substrate cytidilyl-3′,5′-adenosine (CpA) in the reactant, and transphosphorylation and hydrolysis transition states. A detailed analysis of active site structures and hydrogen bond patterns are presented and compared. The integrity of the overall backbone structure is preserved in the simulations, and support a mechanism whereby His12 stabilizes accumulating negative charge at the transition states through hydrogen bond donation to the non-bridge oxygens. Lys41 is shown to be highly versatile along the reaction coordinate, and can aid in the stabilization of the dianionic transition state, while being poised to act as a general acid catalyst in the hydrolysis step.
I. Introduction
The pancreatic ribonuclease A (RNase A) family contains proteins, which decompose the RNA polymer chain [1, 2]. Many members of this family display pathological side effects. For example, human angiogenin [3] is implicated in cancer and in vascular and rheumatoid diseases [4]; eosinophil derived neurotoxin and eosinophil cationic protein are neurotoxic in vivo and are involved in hypereosinophilic syndromes and allergy [5]; and bovine pancreatic seminal RNase has antispermatogenic and immunosuppressive activity [6].
The process of RNA depolymerization involves the interaction of the enzyme with the polymeric substrate in the active site and its correct alignment on the surface of the enzyme through multiple binding subsites (Scheme 1). According to the established nomenclature [7], the active site is partitioned into subsites Bi and Pi, which interact, respectively, with the RNA bases and phosphate groups [8]. Subsite B1 has a strong specificity for pyrimidine bases, with a 30-fold kinetic preference for cytidine versus uridine. The specificity is conferred by residue Thr45, which is strictly conserved in all RNases [9]. The protein cleaves the P-O5′ (scissile) bond on the 3′ side of pyrimidine bases bound at B1. Residues His12, His119, and Lys41 (subsite P1) are strictly conserved among RNase homologs and play key roles in the reaction [2, 7, 10]. Subsite B2 is highly conserved and recognizes all bases, having a preference for adenine [11]. Other subsites (e.g., P2 and B3) are more variable among homologs.
Scheme 1.
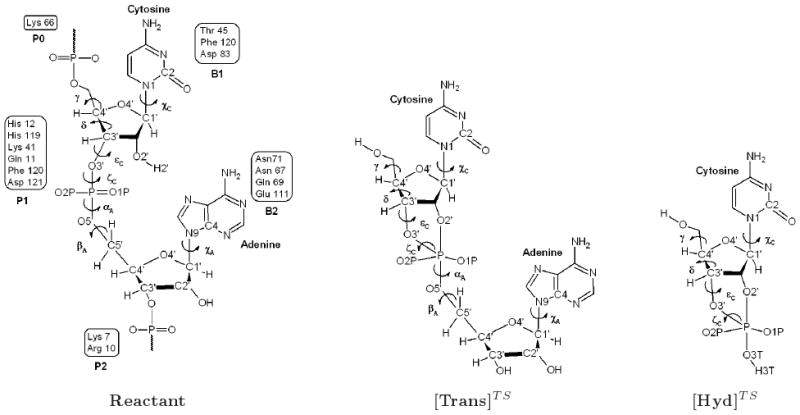
Schematic representation of the RNase A active site with a bound RNA ligand (CpA). The subsites interacting with RNA bases (Bi) and phosphate groups (Pi) are indicated for the reactant state (left). The transphosphorylation ([Trans]TS) and hydrolysis ([Hyd]TS) transition state mimics are shown in the middle and right, respectively. The atomic names and torsional angles discussed in the text are indicated.
Bovine pancreatic ribonuclease A is an ideal system for a theoretical study of the structural and dynamic basis of enzyme catalysis. This endoribonuclease is a single polypeptide of molecular mass 13.7 kDa and a sequence length of 124 amino acids, which catalyzes the breakdown of 3′,5′-phosphodiester linkage of single stranded RNA. A particularly wide range of biochemical, physical, and crystallographic data are available for this enzyme [2, 7, 12–14]. These have led to proposals for the catalysis of the hydrolysis of RNA by a two-step mechanism [15], in which a cyclic phosphate intermediate is formed and subsequently hydrolyzed. Both steps are thought to involve in-line displacement at the phosphorus and to be catalyzed by the concerted action of a general acid and a general base. In spite of the accumulated experimental information, a detailed understanding of the origin of the rate enhancement produced by RNase A has not been achieved, and there remains some debate regarding several aspects of the chemical mechanism [16–23].
Theoretical calculations are potentially powerful tools that, together with experiment, can provide deep insight into the details of catalytic mechanisms. In order to provide insight into mechanism, it is necessary to characterize and understand the changes in enzyme conformation and contacts that occur along the reaction coordinate, particularly at the transition state. It is difficult to obtain direct structural information about a transition state from experiment. In the case of phosphoryl transfer reactions, for example, vanadate transition state mimics have been commonly used and characterized with X-ray crystallography [25–28]. Borah et al. [27] studied the structure of RNase A with a uridine vanadate (U>v) transition state analog by 51V and proton NMR spectroscopy in solution, and by joint neutron and X-ray diffraction (2.0 Å resolution) in a crystalline environment. Some years later Ladner et al. [28] studied the same complex at 1.3 Å resolution. The overall enzyme structure and the relative position of the key active-site residues, His12, His119 an Lys41, are similar, while the V-O bond distances and angles present significant differences (see Tables S1 and S2). However, the results obtained solely based on analysis of a complex with a pentavalent organo-vanadate have to be taken with some skepticism, as vanadate transition state mimics might be only marginally relevant to the true oxyphosphorane transition state [29]. Very recently, X-ray crystallography was used to study the influence of four naturally occurring 5-pyrophosphate linked substituents on the binding of adenylic RNase A inhibitors, the analysis of which enabled kinetic data on the binding to be rationalized [30]. In solution, Loria et al. have performed extensive NMR spin-relaxation experiments on the μs-ms dynamics of RNase A [31], studies of the apo and substrate-mimicked states [32], and characterization of the dynamics at different stages along the reaction coordinate [33] including the transition state [34]. These and other experimental studies provide a wealth of information about RNase A that are linked, albeit sometimes indirectly, to its structure and binding at different stages of the reaction. Nonetheless, to date a detailed study of the structure and dynamics of RNase A at various critical points along the catalytic chemical pathway in solution has not been reported.
In this work we investigate the structure and dynamics of RNase A - 3′,5′-CpA in solution with molecular dynamics simulations of the reactant state, and transphosphorylation and hydrolysis transition state mimics (Scheme 1). Transition state mimics were modeled by the CHARMM force field parameters for reactive phosphoryl transfer intermediates [35]. Simulations of RNase A have been previously reported by other authors, [18, 36–41], however, the present work is, to our knowledge, the first time that simulations of oxyphosphorane transition states for RNase A have been studied. The simulations provide insight into the flexibility of the bound ligands and the interaction of the surrounding active site residues to stabilize the trigonal bipyramidal geometry of the transition state/intermediates of the transphosphorylation and hydrolysis reactions.
The paper is organized as follows. The Computational Details section describes the force field models and simulation set up. The Results section presents simulation results for the reactant model, transphosphorylation transition state mimic model and hydrolysis transition state mimic model. The Discussion section places the simulation results into a broader biological context, and makes detailed comparison with experiments. The Conclusion section summarizes the main points of the paper and outlines future research directions.
II. Computational details
The starting structure for all-atom molecular dynamic simulations of RNase A complexed with cytidilyl-3′,5′-adenosine (CpA) in solution was taken from Protein Data Bank with accession number 1RPG [42], where the structure was determined at a resolution of 1.4 Å. The CpA structure was built from the crystal results for the inhibitor complex, d(CpA), by introducing the 2′ oxygen into the deoxy sugar. The transphosphorylation and hydrolysis transition state mimics were built from the previous complex using a “patch” to introduce a dianionic pentavalent cyclic phosphorane transition state mimic with 2′ (nucleophile) and 5′ (leaving group) positions oriented axially [35]. The position of the hydrogen atoms were determined using HBUILD facility in the program CHARMM [43, 44], Ver. c32a1. Atomic charges, van der Waals, and force-field parameters corresponded to the all-atom CHARMM27 nucleic acid force field [45–47] with extension to transition state mimics [35] and TIP3P water model [48]. In the reactant state, His12 and His119 are neutral and protonated, respectively, in states appropriate for their proposed roles as general base and acid catalysts for the transphosphorylation reactions. In the transition state mimics, both of these residues are protonated since the general base has already accepted a proton from the nucleophile, and the general acid is loaded to donate a proton to the leaving group. All other residues were assumed to be in their standard ionization states in solution at neutral pH.
The aqueous solvation environment was created by retaining the 164 crystallographic water positions, and further solvating the system with bulk water molecules and ions. Additional water molecules were included by overlaying a pre-equilibrated rhombic dodecahedral cell of 8,346 TIP3P water molecules, centering it at the center of mass of the complex using statistics methodology, and deleting water molecules with oxygen atom lying in a radius of 2.8 Å from any non-hydrogen atom of the protein, enzyme or crystallographic waters. The ion atmosphere consisted of Na+ and Cl− ions that were added at random positions to neutralize the net +6 charge of the solute and reach the physiologic extracellular concentration of 0.15 M. The reactant simulation corresponded to the entire protein (1,859 atoms), the ligand (63 atoms), 7,548 water molecules, 6 Cl− ions to neutralize the net positive charge of the solute and 42 additional counter and coions (21 Cl−1 and 21 Na+1 ions). The transition state mimic simulations were prepared in an analogous fashion.
Periodic boundary conditions were used along with the isothermal-isobaric ensemble (NPT) at 1 atm and 298 K via an extended system pressure algorithm [49] and Nosé-Hoover thermostat [50, 51]. Electrostatic interactions were treated rigorously using the smooth particle mesh Ewald method (PME) [52–54] with a κ value of 0.35 Å−1 and direct-space cut-off of 12 Å, 72 FFT grid points for each of the lattice directions, and 4th-order B-spline interpolation for spreading the atomic charges to the FFT grid. Nonbonded interactions were performed using a cutoff of 12 Å with shifted van der Waals potential to smooth the Lennard-Jones term. Nonbond pair lists were maintained out to 13.0 Å and updated heuristically. Newton's equations of motion were integrated numerically using the leapfrog Verlet algorithm within a timestep of 1 fs [55], while atomic coordinates were saved for analysis every 0.5 ps. Covalent bond lengths involving hydrogen were constrained using the SHAKE algorithm [56].
Water molecules were initially relaxed for 5000 steps of steepest descents energy minimization keeping all solute atom and ion positions restrained to their initial coordinates using a harmonic potential constant of 10 kcal·mol−1· Å−2. The restraints on the ions were then released, and the solvent (water and ions) were relaxed with 5000 steps of conjugate gradient minimization, keeping the solute positions restrained. From this starting point, restrained molecular dynamics was performed starting at 0 K and heating to 298 K over 20 ps, and carried out to 220 ps, during the course of which the harmonic restraints on the solute atoms were slowly released. The production phase molecular dynamics then began, and covered 6.0 ns, the last 5 ns of which is used for analysis. All the simulations were performed with the CHARMM biomolecular program [43, 44], Ver. c32a1.
III. Results
This section presents molecular dynamics simulation results for RNase A in three different model states along the catalytic reaction: the reactant state complex (3′,5′-CpA), the transphosphorylation transition state mimic ([Trans]TS) and hydrolysis transition state mimic ([Hyd]TS) models (Scheme 1). Representative structures from the simulation are shown in Fig. 1. Results are compared with available crystallographic data in Tables S1 and S2. The results are divided into different subsections for each model structure.
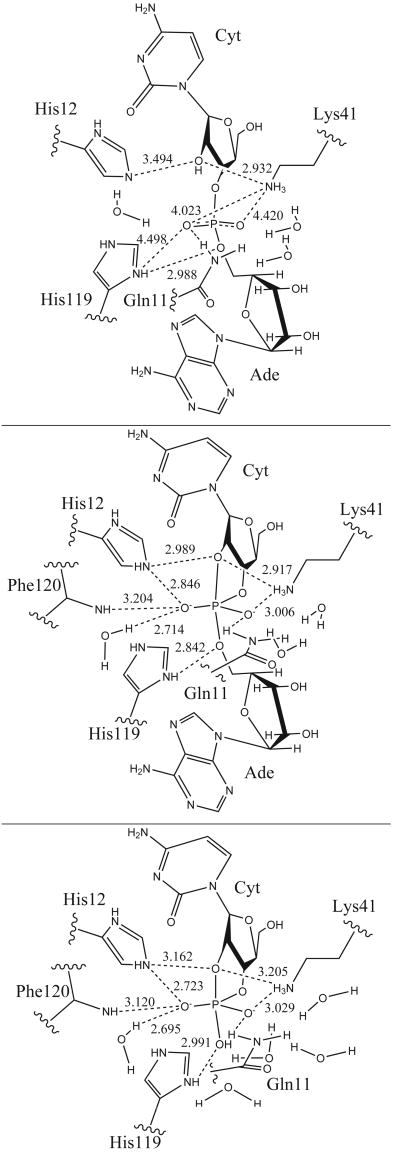
FIG. 1.
Structure of the Reactant model at top, [Trans]TS in the middle and [Hyd]TS at the bottom. Some MD average distances between heavy atoms are depicted.
First, the root-mean-square deviation (RMSD) and the ligand conformation are shown. The glycosyl dihedral angles χC(O4′−C1′−N1−C2) and χA(O4′−C1−N9−C4) describe, respectively, the orientation of the cytidine and adenine rings with respect to the sugar [57, 58], whereas the pseudorotation phase angle P [59] describes the sugars ring conformation, and the backbone torsion angles (α, β, γ, δ, ε and ζ) characterize the conformation of the sugar-phosphate backbone (Scheme 1). Then, we discuss the geometry of the active-site, focusing attention on the conformation of key residues and their interaction with the substrate and solvent molecules. The side chain of residue His119 can adopt two conformations denoted as A (χ1(N−Cα−Cβ−Cγ) ∼ 160°) and B (χ1 ∼ −80°) [60], which are related by a 142° rotation about Cα − Cβ bond and 38° rotation about the Cβ − Cγ bond. Conformation A is the “active” conformation that promotes catalysis, whereas conformation B is an “inactive” conformation [42]. In the crystallographic structure of the complex, conformation A is observed [42]. The criteria for the existence of hydrogen bonds of the form D − H ⋯ A, where D and A are the hydrogen bond donor and acceptor, respectively, are 1) a maximum H ⋯ A distance R of 2.4 Å, 2) a minimum angle of 120° and 3) a hydrogen bond lifetime τ ≥ 5.0 ps. Finally radial distribution functions (RDFs) of water molecules around phosphoryl and phosphorane oxygens are calculated. The RDF's are denoted gXY(r) where the subscript XY refers to the distribution of Y atoms around X atoms. Analysis for all trajectories was over the last 5 ns of production simulation, following pre-equilibration and 1 ns of unrestrained equilibration dynamics.
A. Reactant model
In this subsection, results are presented for the simulations of the RNase A - 3′,5′-CpA complex in the reactant state (Scheme 1 and Fig. 1). The RMSD with respect to the initial conformation as a function of the simulation time is shown in Fig. S1. The RMSD reaches equilibrium after 1 ns and fluctuates stably with an average value of 1.46 ± 0.11 Å.
Conformational dynamics
The time evolution of key dihedral angles that define the conformation of the substrate and the His119 residue are shown in Supporting Information (Fig. S2) and the average values are list in Table S3. The glycosyl dihedral angles, χC and χA, are in the anti conformation in the crystallographic structure [42]. The fluctuations of these dihedral angles are very small, signifying that the χC and χA anti conformations are stable throughout the simulation. The average values are -161.0° and -65.7° respectively. However, the conformation of the ribose shows some differences with respect to the crystallographic structure. In particular, the cytidine ribose essentially stays at North C3′-endo throughout the simulation in contrast with the South C2′-endo conformation encountered at the crystallographic structure [42]. On the other hand, the adenosine ribose is observed in the simulations to sample both the South C2′-endo conformation as in the crystal structure, and the North C3′-endo pucker. The average values are 23.2° and 140.8° respectively (Fig. S2 and Table S3). The tendency of the simulation to occupy a C3′-endo pucker is due to the fact that the sugar rings are the native ribose sugars of RNA, whereas in the crystal structure, the substrate is d(CpA), having the ribose replaced with deoxyribose in order to render the complex inactive (recall, it is the 2′OH group that acts as nucleophile in the transphosphorylation). Whereas classical B-form DNA tends to have C2′-endo sugar pucker, RNA typically has a C3′-endo sugar pucker similar to an A-form helix that reduces the steric repulsion between the 2′ and 3′ oxygens [61]. In addition, the dinucleotide phosphodiester backbone torsional angle undergoes a transition from gauche+ (γC), trans (γA) in the crystallographic structure to the more stable gauche+, gauche+ in the simulation, which was also observed by Brünger et al. [36]. Consequently, these differences in pucker between the simulation and crystal structure have relevance for the native reactive substrate. Finally, it is noteworthy that the side chain of His119 maintains its active A conformation of the crystallographic structure throughout the simulation, with a mean χ1 value of 166.9° and χ2 of -104.2° (see Fig. S2 in Supporting Information).
Hydrogen bond interactions
The average distances between atoms participating in protein-substrate hydrogen bonds, with the hydrogen-bond occupancies, average time and number of events are listed in Table I. Time evolution of selected distances between protein and ligand atoms is plotted in Fig. S3. In the crystal structure of RNase A - 3′,5′-d(CpA) complex [42] the ligand phosphate group interacts with His12, His119, Gln11, Phe120 and a water molecule (Table S1). In our reactant model simulation, this group makes a strong hydrogen bond with the imidazolium side chain of His119, and weaker hydrogen bond interactions with Gln11, Lys41, His12, Phe120 and solvent water (Table I).
TABLE I.
Statistics of protein-ligand and water-ligand hydrogen-bonds observed in the simulation of the reactant model. The criteria for the existence of hydrogen bonds are 1) a maximum H ⋯ A(acceptor) distance of 2.4 Å 2) a minimum of 120° and 3) a hydrogen bond lifetime τ ≥ 5.0 ps. The occupancy, Occ, is defined as the total lifetime of each hydrogen bond by the production time. The events are the number of times each hydrogen bond is formed.
All distances are in Å. HSP stands for a doubly protonated His, while HSD stands for a His protonated at Nδ position. O1P and O2P represent pro-R and pro-S oxygens, respectively.
| Atom pair | Distance | Hydrogen bond | ||||
|---|---|---|---|---|---|---|
| MD† | MD‡ | X-Ray* | Occupancy | Lifetime-Average(ps) | Events | |
| LYS 41 Hζ1 - ADE O1P | 4.294(0.937) | 4.420(0.693) | 4.7 | 0.03 | 33.02 | 5 |
| LYS 41 Hζ2 - ADE O1P | 4.260(0.877) | 0.01 | 25.00 | 2 | ||
| LYS 41 Hζ3 - ADE O1P | 4.311(0.827) | 0.01 | 15.00 | 4 | ||
| ADE 2 H3T - ADE O1P | 5.400(0.616) | 5.198(0.522) | 5.1 | 0.01 | 30.00 | 1 |
| WATER - ADE O1P | 3.1 | 1.72 | 25.70 | 335 | ||
| GLN 11 Hε21 - ADE O2P | 2.419(0.571) | 3.212(0.455) | 4.2 | 0.57 | 37.24 | 76 |
| LYS 41 Hζ1 - ADE O2P | 4.254(0.863) | 4.023(0.736) | 4.9 | 0.02 | 22.50 | 4 |
| LYS 41 Hζ2 - ADE O2P | 4.138(0.855) | 0.01 | 15.00 | 4 | ||
| LYS 41 Hζ3 - ADE O2P | 4.313(0.789) | 0.00 | 20.00 | 1 | ||
| HSP 119 Hδ1 - ADE O2P | 3.696(0.312) | 4.498(0.318) | 3.8 | 0.00 | 10.00 | 1 |
| CYT 1 H2′ - ADE O2P | 1.916(0.394) | 2.741(0.236) | 0.88 | 79.56 | 55 | |
| WATER - ADE O2P | 3.1 | 1.19 | 43.46 | 137 | ||
| LYS 41 Hζ1 - CYT O2′ | 2.900(0.754) | 2.932(0.253) | 0.32 | 56.96 | 28 | |
| LYS 41 Hζ2 - CYT O2′ | 2.867(0.819) | 0.36 | 152.06 | 12 | ||
| LYS 41 Hζ3 - CYT O2′ | 3.093(0.725) | 0.20 | 100.51 | 10 | ||
| WATER 11 - CYT O2′ | 3.836(0.344) | 0.00 | 10.00 | 2 | ||
| HSP 119 Hδ1 - CYT O3′ | 2.901(0.405) | 3.318(0.241) | 4.4 | 0.03 | 12.47 | 12 |
| WATER - CYT O3′ | 0.01 | 11.67 | 3 | |||
| HSP 119 Hδ1 - ADE O5′ | 2.141(0.394) | 2.988(0.242) | 2.7 | 0.81 | 59.87 | 68 |
| WATER 5892 - ADE O5′ | 0.00 | 10.00 | 1 | |||
| HSD 12 Nε2 - CYT H2′ | 3.250(0.202) | 3.494(0.279) | 0.03 | 14.98 | 9 | |
| WATER 11 - CYT H2′ | 3.836(0.344) | 0.24 | 12.82 | 92 | ||
Arithmetic average hydrogen bond distance over the last 5 ns of the production simulation, with standard deviation in parentheses.
Arithmetic average distance between the corresponding heavy atoms of the last 5 ns of the production trajectory, with standard deviation in parentheses.
X-Ray data from Zegers et al. [42]
The O2P phosphate oxyanion (pro-S oxygen) makes a strong hydrogen bond interaction with cytosine H2′ (the nucleophile) and side chain of residue Gln11 with average distances < R > of 1.916 Å and 2.419 Å, and hydrogen bond occupancies Occ of 0.88 and 0.57, respectively (Table I). For the last 2 ns of the production dynamics, the interaction between O2P and Gln11 becomes slightly weaker (Fig. S3). The O1P oxyanion (pro-R) does not interact directly with any residue of the enzyme. The O2P and O1P oxygens interact with water molecules throughout the simulation. The imidazole side chain of His12 forms a water bridge with O2P for most of the simulation. This same water molecule forms a hydrogen bond with the 2′OH of cytosine. Together, these interactions form a hydrogen bond network that stabilizes the orientation of the nucleophile. The O3′ phosphoryl oxygen is hydrogen bonded to the imidazolium side chain of protonated His119 in the last 1.5 ns (< R > = 2.901 Å and Occ = 0.03), while the interaction between O5′ phosphoryl oxygen and His119 remains strong throughout the simulation, < R > = 2.141 Å and Occ = 0.81 (Table I and Supporting Information Fig. S3). It is worth mentioning, that this last hydrogen bond interaction was not observed in previous reported simulations by Haydock et al. and Brünger et al. [18, 36].
Residue Lys41 is positioned at a distance of 3.7 Å from O3′ oxygen in the crystal structure [42], whereas in the reactant state simulation, the average distance is 5.00 Å (Table S1). The side chain of Lys41 forms weak hydrogen bond interactions with O1P and O2P phosphoryl oxygens, and a strong hydrogen bond interaction with the 2′-hydroxyl oxygen, O2′ (Table I and Fig. S3). The average heavy-atom distances and hydrogen bond group occupancies involving Lys41 are 4.420 Å and 0.05, respectively, for O1P, 4.023 Å and 0.03, respectively, for O2P, and 2.932 Å and 0.88, respectively, for O2′.
Solvation of the substrate
Determination of ligand-solvent interactions in the active site is of paramount importance to reveal the role of specific water molecules and bulk solvent effects in the enzymatic mechanism. We analyzed two aspects of ligand-solvent interactions: specific hydrogen bond interactions with active site water molecules, and radial distribution functions of water solvent around key atoms of the substrate.
The CpA ligand makes a variety of hydrogen bonds with various water molecules in the active site (Table I). Each atom of the ligand capable of hydrogen bonding was observed to form hydrogen bonds with several different water molecules in the course of the production simulation, with the exception of the 2′-hydroxyl group and O5′ oxygen that only interact transiently with a single water molecule in the course of the simulation. The longest average hydrogen bond lifetime τ is 43.46 ps and corresponds to the O2P phosphoryl oxygen, whereas the largest “occupancy”, 1.72, corresponds to water interactions with O1P phosphoryl oxygen. Note that in this case the hydrogen bond occupancy is > 1 because it accounts for the possibility of making simultaneous hydrogen bonds with multiple water molecules, and in this sense is more similar to an average coordination number.
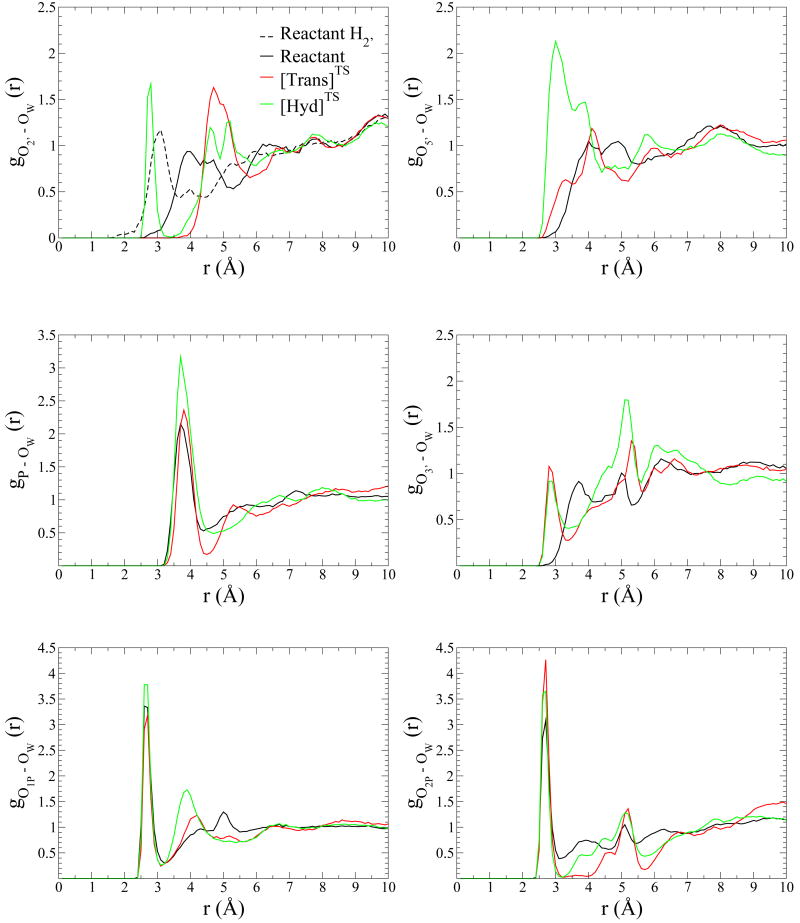
Radial distribution functions are shown in Fig. 2. Broadly speaking, the RDF's describe three kind of situations:
FIG. 2.
Distribution of water around phosphorus atom, phosphate and phosphorane oxygens's atoms is shown for reactant model in black, [Trans]TS model in red and [Hyd]TS model in green. O2′ is at top left corner, at top right corner O5′/O3T is depicted, phosphorus atom is in the middle left and on the right side is O3′ oxygen, finally O1P is at the botton left corner and at the right corner O2P are shown. Reactant H2′, which is at top left corner, represents the reactant's 2′-hydroxyl proton's RDF.
i) a very sharp peak at the first solvation layer followed by a deep minimum with a very low probability. This is indicative of tightly bound and highly ordered water molecules interacting directly with the atom, with slow or negligible water exchange. We will refer to this regime as a highly ordered water interaction. This is the case for O1P and O2P. The first one shows the largest peak among the RDF's for the reactant complex simulation, 3.4 at 2.6 Å and falls to 0.3 at 3.2 Å while O2P RDF is 3.1 at 2.7 Å and falls to 0.4 at 3.1 Å.
ii) a pronounced peak at the first solvation layer followed only by a modest decrease to a local minimum that still has significant probability. This is indicative of a reasonably ordered first solvation layer that is able to readily exchange with bulk solvent. We will denote this regime as a fully-exposed solvent interaction. This is the case for gP−OW in the reactant simulation.
iii) a weak first peak followed by a fairly disordered fluctuations in the RDF that gradually relax to bulk values. This behavior is indicative of poorly solvated areas, or limited solvent accessibility. We will classify these atoms as poorly solvated atoms. This is the regimen we found for gO2′−OW, gO5′−OW and gO3′−OW. Those RDF start to increase for distances > 3.0 Å (Fig. 2).
B. Transphosphorylation transition state mimic model, [Trans]TS
In this subsection we show the results obtained for the RNase A - 3′,5′-CpA transphosphorylation transition state mimic model (Scheme 1 and Fig. 1). The RMSD with respect to the initial conformation as a function of the simulation time is shown in Fig. S1. The RMSD reaches equilibrium after 1 ns and fluctuate stably with an average value of 1.24 ± 0.10 Å.
Conformational dynamics
The time evolution of χC and χA glycosyl dihedral angles are shown in Fig. S2 and the average values are listed in Table S4. The fluctuations of both dihedral angles are small, signifying that the χC and χA anti conformations remain stable throughout the simulation as in the reactant model. The average values are -158.9° and -63.1°, respectively. The cytidine ribose stays in the North C3′-endo throughout the simulation, while the adenosine ribose occupies mainly a South C2′-endo conformation with infrequent and short-lived transitions to a North C3′-endo pucker. The average values are 10.1° and 149.4° respectively. From ∼ 5300 ps to ∼ 5700 ps the α and γA phosphodiester dihedral angles undergo a conformational transition from trans to gauche+ and from gauche+ to trans, respectively (Fig. S4) known as a crankshaft motion, and is often observed in BI↔BII transitions [62]. Finally, the imidazolium side chain of residue His119 retains an active A-type conformation as in the reactant model, with a mean χ1 value of 165.9° and χ2 value of -108.6° (Fig. S2).
Hydrogen bond interactions
Hydrogen bond formation between the ligand and the protein residues in the active site is described in Table II, in which the average distances between atoms participating in protein-ligand hydrogen bonds, with the hydrogen-bond occupancies, average time and number of events are listed. The time evolution of selected distances between protein and ligand atoms is plotted in Supporting Information Fig. S4. In the [Trans]TS simulation, the phosphodiester group makes strong hydrogen bond interactions with the two catalytic histidines, His12 and His119, Gln11, Phe120 and a water molecule, and somewhat weaker interactions with Lys41 and some water molecules.
TABLE II.
Statistics of protein-ligand and water-ligand hydrogen-bonds observed in the simulation of the [Trans]TS mimic model. The criteria for the existence of hydrogen bonds are 1) a maximum H ⋯ A(acceptor) distance of 2.4 Å 2) a minimum of 120° and 3) a hydrogen bond lifetime τ ≥ 5.0 ps. The occupancy, Occ, is defined as the total lifetime of each hydrogen bond by the production time. The events are the number of times each hydrogen bond is formed.
All distances are in Å. HSP stands for a doubly protonated His.
| Atom pair | Distance | Hydrogen bond | |||
|---|---|---|---|---|---|
| MD† | MD‡ | Occupancy | Lifetime-Average(ps) | # Events | |
| GLN 11 Hε21 - CYT O1P | 1.984(0.246) | 2.917(0.183) | 0.94 | 85.81 | 56 |
| LYS 41 Hζ1 - CYT O1P | 2.956(0.640) | 3.006(0.235) | 0.09 | 14.49 | 30 |
| LYS 41 Hζ2 - CYT O1P | 2.938(0.579) | 0.10 | 13.73 | 39 | |
| LYS 41 Hζ3 - CYT O1P | 2.811(0.571) | 0.11 | 14.87 | 37 | |
| WATER - CYT O1P | 1.09 | 48.64 | 114 | ||
| HSP 12 Hε2 - CYT O2P | 1.877(0.192) | 2.846(0.157) | 0.99 | 218.90 | 23 |
| PHE 120 HN - CYT O2P | 2.246(0.246) | 3.204(0.224) | 0.73 | 28.35 | 131 |
| WATER 11 - CYT O2P | 2.714(0.117) | 1.00 | 391.92 | 13 | |
| HSP 12 Hε2 - CYT O2′ | 2.374(0.205) | 2.989(0.189) | 0.36 | 14.44 | 127 |
| LYS 41 Hζ1 - CYT O2′ | 3.040(0.717) | 2.917(0.183) | 0.23 | 23.21 | 50 |
| LYS 41 Hζ2 - CYT O2′ | 3.071(0.721) | 0.25 | 24.07 | 53 | |
| LYS 41 Hζ3 - CYT O2′ | 2.908(0.778) | 0.32 | 28.01 | 58 | |
| HSP 119 Hδ1 - CYT O3′ | 2.602(0.230) | 3.155(0.166) | 0.05 | 11.44 | 24 |
| WATER - CYT O3′ | 0.52 | 18.46 | 143 | ||
| HSP 119 Hδ1 - ADE O5′ | 1.851(0.117) | 2.842(0.104) | 1.00 | 638.75 | 8 |
| WATER - ADE O5′ | 0.14 | 15.12 | 46 | ||
Arithmetic average hydrogen bond distance for 5 ns of the production simulation, with standard deviation in parentheses.
Arithmetic average distance between the corresponding heavy atoms in 5 ns of the production trajectory, with standard deviation in parentheses.
The O1P equatorial non-bridge oxygen makes a strong hydrogen bond interaction with the side chain of Gln11, which was not seen in the reactant model, in addition to hydrogen bonding with water molecules. Also observed at this position was a weaker hydrogen bond interaction with the side chain of Lys41 (Table II). The average O1P hydrogen bond distance and occupancy with Gln11 are 1.984 Å and 0.94, respectively, while the average distance between O1P and Nζ of Lys41 is 3.006 Å with a hydrogen bond group occupancy of 0.30. Equatorial oxygen O2P makes strong hydrogen bond interactions with imidazolium side chain of His12 and a water molecule, and somewhat weaker interactions with the main chain of Phe120 (Table II and Fig. S4). The average O2P hydrogen bond distances and occupancies are 1.877 Å and 0.99 with His12, 2.246 Å and 0.73 with Phe120, and 2.714 Å and 1.00 with the water molecule. As in the reactant model, O1P and O2P interact with water molecules throughout the simulation. In the [Trans]TS simulation, His12 interacts directly with the O2P equatorial oxygen, instead of via a water bridge as in the reactant state simulation. The side chain of His12 also hydrogen bonds with the O2′ axial oxygen with an average distance of 2.374 Å and hydrogen bond occupancy of 0.36.
The imidazolium side chain of His119 forms a strong hydrogen bond interaction throughout the simulation with the O5′ axial oxygen and a weak interaction with O3′ equatorial oxygen, similar to the reactant model. However, the His119 residue, which is protonated in all of the simulations, is closer to the dianionic phosphorane in the [Trans]TS simulation than to the monoanionic phosphate in the reactant state simulation. The average hydrogen bond distances are 1.851 Å and 2.602 Å respectively. The hydrogen bond between His119 and O5′ is observed to exchange only eight times during the [Trans]TS simulation, and has an average lifetime of 638.7 ps. The cationic Lys41 side chain forms strong interactions with the O2′ axial oxygen (< R >=2.917 Å and Occ=0.80) and weaker interactions with O1P equatorial oxygen (< R >=3.006 Å and Occ=0.30).
Solvation of the substrate
The [Trans]TS simulation exhibits a variety of interactions between the ligand substrate and solvent (Table II). Each hydrogen-bonding atom of the CpA ligand interacts with several different water molecules in the course of the [Trans]TS simulation. However, it is noteworthy that the O2P equatorial oxygen only interacts with a single water molecule. The largest hydrogen bond group occupancy (1.09) corresponds to hydrogen bond interactions with O1P equatorial oxygen. On the other hand, O2′ axial oxygen does not form any hydrogen bond with water molecules, instead interacting almost exclusively with the side chain of Lys41.
Inspection of the RDF's (Fig. 2) indicate the O2P and O1P present signatures of highly ordered water interactions. The former exhibits the largest peak among the RDF's of the [Trans]TS complex, 4.3 at 2.7 Å that drops to 0.02 at 3.2 Å while O1P's RDF is 3.2 at 2.7 Å and falls to 0.2 at 3.1 Å. The observed peak value for O2P is significantly larger than the peak value in the reactant model (3.1), and suggest an important solvent stabilization of the negative charge accumulated at the non-bridge oxygens in the dianionic transition state. On the other hand, the fact that the peak falls to a near 0 value in the case of O2P indicates that exchange is very slow. With respect to the rest of the phosphorane oxygen atoms (axial O5′ and O2′ oxygens and equatorial O3′ ), the RDFs present signatures of a poorly solvated situation that indicate less ordered solvent and more rapid exchange relative to the RDFs for the equatorial O2P and O1P atoms. In the [Trans]TS simulation, the O3′ and O5′ RDFs begin to increase earlier than the corresponding reactant state simulation RDFs, while the opposite occurs for the O2′ RDFs. The latter begins to increase for distances > 4.0 Å and presents a maximum value of 1.6 at 4.7 Å which falls to 0.6 at 5.8 Å.
C. Hydrolysis transition state mimic, [Hyd]TS
In this section we present the results for the RNase A - 3′,5′-CpA hydrolysis transition state mimic model (Scheme 1 and Fig. 1). The RMSD with respect to the initial conformation as a function of the simulation time is shown in Fig. S1. The RMSD reaches equilibrium after 1 ns and fluctuate stably with an average value of 1.27 ± 0.11 Å, very similar to the [Trans]TS simulation.
Conformational dynamics
The time evolution of this dihedral angle is shown in Supporting Information Fig. S2 and the average value is list in Table S4. The fluctuation of the dihedral angle is very small signifying that the χC anti conformation is very stable throughout the simulation, like in the reactant model and [Trans]TS model simulations. The average value is -161.6°. The cytidine ribose stays in the North C3′-endo pucker throughout the simulation with an average value of 15.9°. Finally, the imidazolium side chain of His119 is retained in the active A conformation like in the reactant and [Trans]TS models, with a mean χ1 value of 154.5° and χ2 value of -105.8°. The torsional dihedral angles do not undergo any significant conformational transitions (Fig. S5).
Hydrogen bond interactions
Hydrogen bond formation between the ligand and the protein residues in the active site is described in Table III, in which the average distances between atoms participating in protein-ligand hydrogen bonds, with the hydrogen-bond occupancies, average time and number of events are listed. The time evolution of selected distances is plotted in Supporting Information Fig. S5. In the [Hyd]TS simulation, the phosphodiester group makes strong hydrogen bond interactions with both catalytic histidines, His12 and His119, the backbone of Phe120, the side chains of Gln11 and Lys41, and solvent molecules.
TABLE III.
Statistics of protein-ligand and water-ligand hydrogen-bonds observed in the simulation of the [Hyd]TS model. The criteria for the existence of hydrogen bonds are 1) a maximum H ⋯ A(acceptor) distance of 2.4 Å 2) a minimum of 120° and 3) a hydrogen bond lifetime τ ≥ 5.0 ps. The occupancy, Occ, is defined as the total lifetime of each hydrogen bond by the production time. The events are the number of times each hydrogen bond is formed.
All distances are in Å. HSP stands for a doubly protonated His.
| Atom pair | Distance | Hydrogen Bond | |||
|---|---|---|---|---|---|
| MD† | MD‡ | Occupancy | Lifetime-Average(ps) | # Events | |
| GLN 11 Hε21 - CYT O1P | 2.053(0.388) | 2.963(0.284) | 0.86 | 62.54 | 71 |
| LYS 41 Hζ1 - CYT O1P | 2.957(0.776) | 3.029(0.385) | 0.21 | 62.65 | 17 |
| LYS 41 Hζ2 - CYT O1P | 2.988(0.627) | 0.14 | 46.56 | 16 | |
| LYS 41 Hζ3 - CYT O1P | 2.814(0.668) | 0.22 | 59.48 | 19 | |
| WATER - CYT O1P | 1.47 | 39.38 | 193 | ||
| HSP 12 Hε2 - CYT O2P | 1.729(0.119) | 2.723(0.099) | 1.00 | 573.33 | 9 |
| HSP 119 Hδ1 - CYT O2P | 3.102(0.308) | 3.863(0.288) | 0.00 | 10.00 | 1 |
| PHE 120 HN - CYT O2P | 2.157(0.259) | 3.120(0.231) | 0.85 | 50.17 | 88 |
| WATER 397 - CYT O2P | 2.695(0.131) | 0.99 | 341.33 | 15 | |
| HSP 12 Hε2 - CYT O2′ | 2.488(0.197) | 3.162(0.171) | 0.13 | 11.67 | 57 |
| LYS 41 Hζ1 - CYT O2′ | 3.173(0.683) | 3.205(0.383) | 0.12 | 55.47 | 11 |
| LYS 41 Hζ2 - CYT O2′ | 3.274(0.821) | 0.15 | 83.88 | 9 | |
| LYS 41 Hζ3 - CYT O2′ | 3.135(0.839) | 0.19 | 64.65 | 15 | |
| WATER 6130 - CYT O2′ | 13.333(13.670) | 0.55 | 188.34 | 15 | |
| HSP 119 Hδ1 - CYT O3′ | 2.165(0.230) | 2.961(0.149) | 0.79 | 31.77 | 128 |
| WATER - CYT O3′ | 0.40 | 14.48 | 144 | ||
| HSP 119 Hδ1 - CYT O3T | 2.060(0.296) | 2.991(0.252) | 0.88 | 76.77 | 59 |
| WATER - CYT O3T | 0.19 | 12.47 | 79 | ||
Arithmetic average hydrogen bond distance for 5 ns of the production simulation, with standard deviation in parentheses.
Arithmetic average distance between the corresponding heavy atoms in the production trajectory, with standard deviation in parentheses.
The equatorial non-bridge O1P atom forms a strong hydrogen bond interaction with the side chain of residue Gln11. After 2 ns, the interaction weakens and is partially replaced with an interaction with the side chain of Lys41 that gets stronger (see Table III and Fig. S5). The hydrogen bond occupancies are 0.86 and 0.57 respectively. The reactant state, [Trans]TS and [Hyd]TS simulations all show strong interactions between O1P and the side chain of Gln11, but only the [Trans]TS and [Hyd]TS simulations predict a hydrogen bond interaction between O1P and Lys41, this interaction being most prominent in the hydrolysis transition state mimic. The [Trans]TS and [Hyd]TS simulations also both show strong interactions between O1P and side chain of Gln11, being stronger in the [Trans]TS model. The O2P equatorial oxygen makes 3 strong interactions with residues His12, Phe120 and a water molecule. One of them, His12 Hε2-O2P, is essentially locked for over the last 5 ns of simulation, with an average hydrogen bond distance of 1.729 Å and occupancy of 1.00 with only 9 observed exchange events and an average lifetime of 573.33 ps. On the other hand, the hydrogen bond between O2P and the backbone of Phe120 is weaker, with a hydrogen bond occupancy of 0.85 and an average distance average of 2.157 Å. The O1P and O2P equatorial oxygens interact with water molecules throughout the simulation as in the reactant and [Trans]TS models, but quite remarkably, the O2P interacts exclusively with a single water molecule as in the [Trans]TS simulation. On the other hand, the axial O2′ oxygen makes weak interactions with the side chain of His12, Lys41 and a water molecule. The average O2′-His12 distance is 2.488 Å hydrogen bond occupancy is 0.13, and average lifetime is 11.67 ps. The interaction between O2′ and Lys 41 is stronger, with hydrogen bond group occupancy of 0.46. Analysis of the interactions of Lys41 suggest this residue interacts with the O2′ axial oxygen over the first 2110 ps, while in last 2890 ps it interacts with the O1P equatorial oxygen. In turn, during the last 2890 ps of the simulation, O2′ hydrogen bonds with a water molecule (average heavy atom distance of 2.859 Å), while there was no interaction between O2′ and water molecules during the first 2110 ps. The entry of this water molecule into the active site is thus connected with the movement of Lys41 toward the O1P equatorial oxygen. Finally, the side chain of residue His119 makes 2 strong interactions with the O3′ equatorial oxygen and the terminal O3T axial oxygen, with hydrogen bond occupancies of 0.79 and 0.88, respectively, and average distances of 2.165 Å and 2.060 Å respectively.
Solvation of the substrate
Each of the phosphoryl oxygens of the CpA ligand form hydrogen bonds with residues of the enzyme during the course of the simulation (Table III), with the exception of the O2P equatorial oxygen and O2′ axial oxygen. The overall hydrogen bond pattern is similar to that of the [Trans]TS simulation, with a few notable exceptions. The hydrogen bonding interactions between O1P and Lys41 is strengthened in the [Hyd]TS simulation (group Occ 0.57) relative to the [Trans]TS simulation (group Occ 0.30), whereas the interaction of O1P with Gln11 is reduced. The O2P was observed to make transient hydrogen bonding interaction with the protonated His119 residue not present in the [Trans]TS simulation, whereas the interaction of O2′ with the protonated His12 and Lys41 residues are less pronounced. Moreover, in the [Hyd]TS simulation, the O3′ atom of cytidine acquires a more significant hydrogen bond with His119 with Occ 0.79, whereas this interaction is greatly reduced in the [Trans]TS simulation (Occ 0.05). In the [Hyd]TS simulation, the proposed general acid His119 is observed to make a strong hydrogen bond with the activated water nucleophile/terminal hydroxyl group of cytidine (O3T in Table III). The O1P, O2P, O2′ and O3′ atoms maintain additional strong hydrogen bond interactions with water molecules in the [Hyd]TS simulation. Unlike the [Trans]TS simulation, the [Hyd]TS simulation exhibits a significant solvent interaction with the O2′ axial oxygen. The solvent interaction with the largest lifetime average (341.33 ps) corresponds to a hydrogen bond between a water molecule and the O2P equatorial oxygen, while the largest hydrogen bond group occupancy (1.47) corresponds to the O1P equatorial oxygen.
Radial Distribution Function analysis reveal a highly ordered water interaction for the O1P, O2P and O2′ oxygens. The non-bridging equatorial oxygens O1P and O2P have the highest probability in their RDF with water oxygens, with maximum value of 3.8 and 3.7, respectively, both located at 2.7 Å. The minima for O2P is considerably lower than that for O1P, consistent with the larger number of solvent exchange events for the latter. The gO2′−OW RDF for the [Hyd]TS model has an ordered first solvation peak (1.7 at 2.8 Å), unlike that of the reactant and [Trans]TS models. Additionally, the axial oxygen in the [Hyd]TS model (shown in Fig. 2 as O5′) is solvent exposed, and exhibits a broad solvation peak with maximum of 2.1 at 3.0 Å which falls to 0.7 at 4.4 Å. Comparison of these peak values with the RDF's of the reactant and [Trans]TS simulations indicates the preferential solvent stabilization at this position in the hydrolysis transition state mimic. Together with the gP−OW RDF, the hydrolysis transition state is more highly solvated than the reactant state and [Trans]TS model.
IV. Discussion
The present work presents a series of molecular dynamics simulations of RNase A - 3′,5′-CpA complex and its transphosphorylation and hydrolysis transition state mimic models. These simulations employ a set of recently developed force field parameters for oxyphosphorane transition states or intermediates which are consistent with the CHARMM27 all-atom empirical force field for nucleic acids[35]. The parameters were developed based on density-functional calculations, with partial atomic charges derived from electrostatic potential fitting and Lennard-Jones parameters reproducing interaction energies with water molecules. Bonded energy terms (bond, angle and torsion parameters) were also derived from the density-functional calculations and renormalized to maintain compatibility with the existing CHARMM27 parameters for standard residues. Thus, the parameters used in this work reproduce the main geometrical and electronic characteristics of important oxyphosphorane intermediates based on density-functional theory, but within a molecular mechanical approximation. This has allowed us to provide key structural information on how these reactive intermediates are structurally recognized in the active site of RNase A, using classical MD simulations with reasonable time scales. One has to consider that this type of data can be difficult to be accessed from experiments, due to the difficulty of trapping reactive intermediates, and to the inherent limitations of using vanadate species as oxyphosphorane analogs [29]. The RNase A cleavage appears to be limited by the product release step [32, 63, 64], which is 1.7×103 for 3′-CMP [33] and 1400-2900 s−1 for UpA [11]. The main advantage of the use of a classical force field is the computational efficiency that allows for sufficiently long time scales as to get statistically relevant results. However, there are also important limitations of the present approach that should be remarked upon. For instance, a non-polarizable force field is used in a system significantly charged, which results in a lack of significant dispersion effects in the present model. In addition, due to the use of a classical force field, there is no possibility of providing with a reaction profile as a function of covalent bond formation and cleavage, and one is limited to the analysis of structural information. Still important insights on the reaction mechanism can be inferred from the structural data presented here. In the present section, we make a discussion on the relevance of our structural findings for the classical catalytic reaction mechanism. In this so-called classical mechanism, RNase A cleaves RNA substrates in a two-step process, by general acid-base catalysis. In the first step (transphosphorylation, [Trans]TS structure), the RNA chain is cleaved by a phosphate ester exchange, in which the 2′-hydroxyl group of ribose attacks the phosphate ester linkage (P–O2′ bond is formed) and the O5′ oxygen of the next nucleotide is ejected (P–O5′ bond is cleaved). In the second step (hydrolysis [Hyd]TS structure), the P–O2′ bond of the 2′,3′ cyclic phosphate is cleaved by an attacking activated water molecule to generate a 3′-terminal phosphate group and regenerate the 2′-hydroxyl group. The principal catalytic groups for these reactions are the side chains of His12 and His119 and the cationic amino group of Lys41. In the so-called classical mechanism, the most accepted one among experimentalists, His12 acts as a general base, while His119 acts as an acid in the transphosphorylation step, and in the hydrolysis step His12 acts as an acid, while His119 acts as a base. However, the exact role of each of these residues is still a matter of discussion, and different mechanisms have been proposed [16–23]. We analyze now the structural information relevant from our dynamics with respect to these three important residues and the role of solvent molecules in the stabilization of oxygen oxyphosphoranes.
Regarding Lys41, our MD simulations demonstrate that this residue is more flexible in the reactant model than in the transition state mimic models. The cationic side chain of Lys41 hydrogen bonds with O1P and O2P phosphate oxygens as well as cytosine O2′ oxygen in the reactant model, while in the [Trans]TS and [Hyd]TS models Lys41 only forms significant hydrogen bonds to the O2′ axial oxygen and O1P equatorial oxygen (Tables I, II and III). The interaction with the equatorial oxygen gets stronger proceeding from the reactant model to the transphosphorylation and hydrolysis transition state models (hydrogen bond group occupancy of 0.03-0.05, 0.30 and 0.57 respectively). This is consistent with the early supposition that Lys41 provides preferential electrostatic stabilization of the reactive intermediate/transition state [29, 65]. Whereas the interaction of Lys41 with the non-bridge equatorial oxygen becomes stronger in proceeding from the reactant to the transition states, the interaction with the O2′ oxygen becomes slightly weaker. The interaction between Lys41 and the O2′ position is of interest, as Lys41 is known to have a reduced pKa (8.6-9.1) [66], has been observed crystallographically to undergo structural change in the pH range 8.0-8.8 [67], and has even been suggested to act as general base/acid catalyst instead of His12 [19, 20, 22]. It is possible that Lys41 might have a depressed pKa due to interaction with nearby hydrophobic groups, as has been observed for a lysine residue in enolase. [68] However, to reconcile this question would require the calculation of the pKa value of Lys41 (and possibly other residues) using a combined quantum mechanical/molecular mechanical (QM/MM) simulation and free energy perturbation approach. This is beyond the scope of the current work that focuses on the structure and dynamics at different stages along the reaction coordinate. It is, nonetheless, of importance to note that the simulations predict a stable hydrogen bond interaction with the O2′ nucleophile in the reactant state that is preserved in proceeding to the transition state. In the ionized form, Lys41 could assist in catalysis by increasing the acidity of the nucleophile and facilitating proton transfer to His12. Alternately, the interaction of Lys41 with the nucleophile might implicate a more active role as a general base catalyst, although this would require further simulation and QM/MM calculations to fully test.
On the other hand, His12 has a very weak interaction with the CpA reactant model. Instead, in both transition state mimics, His12, in protonated form, makes strong hydrogen bond interactions with the O2P equatorial oxygen. The hydrogen bond occupancy is 0.99 for the [Trans]TS mimic and 1.0 for [Hyd]TS mimic (Tables II and III). Thus, the simulation results suggest that interaction with His12 may be important to stabilize the excess of negative charge at O2P as the reaction proceeds. In addition, the O2P equatorial oxygen makes two strong hydrogen bond interactions in the transition state mimic models that provide stabilization of its negative charge: one hydrogen bond interaction with the main chain of residue Phe120, and the other with a water molecule. On the other hand, the interaction between His12 and the O2′ axial oxygen is not strong in either of the transition state mimic simulations. The hydrogen bond occupancies are 0.36 for the [Trans]TS and 0.13 for the [Hyd]TS. This last occupancy is not what one would expect if His12 were to play the role of a general acid catalyst as in the classical mechanism[16]. Nonetheless, this small occupancy might be partially offset by an indirect interaction via a bridging water molecule between His12 and the O2′ axial oxygen that becomes evident in the last 3 ns of the simulation.
The results for Lys41 and His12 suggest that Lys41 may play a more versatile, and possibly more active role in RNase A catalysis, which could lead to its use as a base catalyst in the transphosphorylation step and an acid catalyst in the hydrolysis step [19–21] instead of His12. A recent QM/MM study on the hydrolysis step of the reaction by Elsässer et al. [22] lends further support to the interpretation of our results, pointing to Lys41 as the acid catalyst of the reaction and His12 as a hydrogen-bond stabilizer of the excess of negative charge at the equatorial phosphoryl oxygen. Our results with simulations on the nanoscale support these conclusions and predict a similar behavior for the transphosphorylation step of the reaction.
The interaction between imidazolium side chain of His119 and the O3′ equatorial oxygen increases as the reaction proceeds in the forward direction, from a hydrogen bond occupancy of 0.03 in the reactant model to 0.79 for the [Hyd]TS mimic. In the case of the axial O5′ oxygen, the interaction increases from a hydrogen bond occupancy of 0.81 for the reactant model to 1.0 for the [Trans]TS mimic, and it decreases slightly to 0.88 for the [Hyd]TS model. Finally, it is remarkable that the side chain of residue His119 remains in its active A conformation that promotes catalysis [42, 60] in each simulation. In this sense, His119 and the adenine rings form continuous π – π stacking interactions that contribute to the stabilization of the His119 A orientation and the adenine ring anti orientation, and these interaction therefore seems to be fundamental for catalysis.
On the other hand, there are important differences in the solvation of the two transition state mimics. The gP−OW RDF (Fig. 2) shows a higher degree of solvation (as reflected by the peak height of the RDF and first coordination number) for the [Hyd]TS mimic simulation than for the other two simulations. The O3T axial oxygen is clearly more accessible to solvent in the [Hyd]TS simulation. Its RDF maximum (2.1) is at 3.0 Å while [Trans]TS model's maximum (1.2) is at 4.1 Å. This is also seen if we analyze the running coordination number up to the first minimum in the oxygen-RDF:
| (1) |
In the case of gO5′/O3T−OW RDF, n(R) is 0.75 for [Trans]TS and 3.19 for [Hyd]TS. Except for O2P (see below) the rest of the atoms follow the same tendency with running coordination numbers up to the first shell (around 3.1-3.6 Å) larger for [Hyd]TS than for [Trans]TS, namely 1.59/1.20 (O1P), 0.55/0.00 (O2′) and 0.84/0.79 (O3′) for [Hyd]TS /[Trans]TS respectively. The only exception is found for O2P for which the same first-shell running coordination number is found at both transition state mimics, namely, 1.00.
Finally, we would like to highlight the behavior of the RDF's of O2P. In both transition state mimic models, its RDF is 0 after the large peak between 2.5 and 3.0 Å. Also remarkable, is the zero probability to find a water molecule between 3 and 4 A in the [Trans]TS model, indicative of a rigid structural solvation shell in the vicinity of this atom. Thus, based on these simulations it seems that this water molecule could play a structural role in the stabilization of oxyphosphorane species. In this sense, Pelmenschikov et al. [70] has demonstrated by DFT calculations that for the stabilization of the salt bridge between deprotonated DNA phosphate groups and protonated basic groups, such as histidines, requires the direct interactions of these groups with water molecules. In particular, the specific interaction of a water molecule with the phosphoryl oxygen is needed to stabilize the negative charge at this oxygen and avoid proton transfer from the positively charged histidine. In oxyphosphoranes this tendency is probably enhanced due to the built up of negative charge at the phosphoryl oxygens, and our results points to this interpretation of an enhanced necessity of stabilization of the salt-bridge between the histidine and the oxyphosphorane by a direct interaction of O2P with a water molecule.
V. Conclusions
In the present paper, we report the results of MD simulations of RNase A - 3′,5′-CpA complex and its transphosphorylation and hydrolysis transition state mimic models using recently developed force field parameters for phosphoryl transfer intermediates [35]. The aim of these studies is to determine structural relaxation, and differential solvation that occurs at discreet stages of the transesterification and cleavage reaction, in particular, at the CpA phosphate reactant, and at the two pentacovalent oxyphosphorane structures that represent the transition states or high-energy intermediates in the transphosphorylation and hydrolysis steps of the reaction. Simulations were performed with explicit solvation, with rigorous electrostatics, and for several nanoseconds, which allow to make a detailed analysis of the main changes in hydrogen bond patterns and interaction with the solvent among the three structures.
Based on our simulations we can conclude that there are no major differences between the backbone structure of the studied three structures. Besides, the relative orientation of the bases, denoted by their glycosyl dihedral angle conformations, is very stable and it is not affected by the nature of the substrate. In addition, it is quite remarkable that the active A conformation of His119 is maintained for the three structures studied and along the whole production run.
Analysis of the hydrogen bond occupancies between the substrates and RNase A shows that the residues directly interacting with the substrates are His12, His119, Lys41, Gln11, Phe120 and a variety of water molecules. However, there are important changes in the hydrogen bond pattern between the reactant and transition state analogs that shed light on the reaction mechanism and role of specific residues in transition state stabilization. The formation of pentacovalent phosphorane anchors His12 to interact with the equatorial O2P oxygen, especially in the case of the [Hyd]TS simulation, and causes Lys41 to loosen the interaction with the equatorial O2P oxygen and strengthen the interaction with the equatorial O1P oxygen while maintaining significant hydrogen bond occupancy with axial O2′ atom. This result suggests that the role of His12 and Lys41 in the transphosphorylation and hydrolysis reactions could be interchanged to the ones proposed in the classical mechanism, and is in qualitative agreement with conclusions of other theoretical calculations [19–22] in which Lys41 has been claimed to possibly act as the acid catalyst in the hydrolysis reaction.
Analysis of substrate interaction with water molecules has been accomplished by the calculation of hydrogen bond occupancies between the substrate oxygen atoms and specific water molecules and by the analysis of the radial distribution functions around key atoms of the phosphate and phosphorane moieties. Simulations results point to a higher solvation of the [Hyd]TS, compared to [Trans]TS or the reactant model. In all models, the equatorial O1P and O2P atoms are the most solvated phosphate/phosphorane atoms. It is remarkable that the formation of phosphorane structures leads to the encapsulation of a water molecule hydrogen bonded directly to O2P that shows no exchange with other water molecules in the time scale of the simulations, and suggests an important role of this water molecule in the stabilization of the negative charge accumulated at this equatorial phosphorane oxygen in both [Trans]TS and [Hyd]TS simulations [70].
The work presented in this paper could also be taken as the base for the future analysis of MD simulations of this type of oxyphosphorane transition state analogues bound to RNase A mutants that are known to affect the enzyme turnover rate, namely, H119N, H119A, H119D, H12A, H12E, H12D, K41R or K41A [71–74] which decrease kcat between two and four orders of magnitude. In addition, the present data could also be used as reference structures to analyze how chemical changes at the oxyphosphorane itself (like sulfur substitution, i.e., thio effects) affects their recognition by RNase A. Work along these lines is under progress.
Supplementary Material
Acknowledgments
This research was funded by the Spanish Ministerio de Ciencia e Innovación (grant BES2005-6803 to E.F.) and by the National Institutes of Health (grant GM62248 to D.M.Y.). The SGI/IZO-SGIker UPV/EHU (supported by Fondo Social Europeo and MCyT) and the Minnesota Super-computing Institute for Advanced Computational Research (MSI) are gratefully acknowledged for generous allocation of computational resources.
Footnotes
Supporting Information Available
Time evolution of ligand dihedral angles, phase angles, torsional dihedral angles and selected distances. This material is available free of charge via the Internet at http://pubs.acs.org
Contributor Information
Elena Formoso, Kimika Fakultatea, Euskal Herriko Unibertsitatea and Donostia International Physics Center (DIPC), P.K. 1072, 20080 Donostia, Euskadi (Spain).
Jon M. Matxain, Kimika Fakultatea, Euskal Herriko Unibertsitatea and Donostia International Physics Center (DIPC), P.K. 1072, 20080 Donostia, Euskadi (Spain)
Xabier Lopez, Kimika Fakultatea, Euskal Herriko Unibertsitatea and Donostia International Physics Center (DIPC), P.K. 1072, 20080 Donostia, Euskadi (Spain).
Darrin M. York, Department of Chemistry, University of Minnesota, 207 Pleasant St. SE, Minneapolis, Minnesota 55455-0431
References
- 1.Cho S, Beintema JJ, Zhang J. The ribonuclease A superfamily of mammals and birds: identifying new members and tracing evolutionary histories. Genomics. 2005;85:208–220. doi: 10.1016/j.ygeno.2004.10.008. [DOI] [PubMed] [Google Scholar]
- 2.Raines R, Ribonuclease A. Chem Rev. 1998;98:1045–1065. doi: 10.1021/cr960427h. [DOI] [PubMed] [Google Scholar]
- 3.Riordan JF. Angiogenin. Method Enzymol. 2001;341:263–273. doi: 10.1016/s0076-6879(01)41157-8. [DOI] [PubMed] [Google Scholar]
- 4.Fett JW, Strydom DJ, Lobb RR, Alderman EM, Bethune JL, Riordan JF, Vallee BL. Isolation and characterization of angiogenin, an angiogenic protein from human carcinoma cells. Biochemistry. 1985;24:5480–5486. doi: 10.1021/bi00341a030. [DOI] [PubMed] [Google Scholar]
- 5.Gleich GJ, Adolphson CR. The eosinophilic leukocyte: structure and function. Adv Inmunol. 1986;39:177–253. doi: 10.1016/s0065-2776(08)60351-x. [DOI] [PubMed] [Google Scholar]
- 6.Vescia S, Tramontano D, Augusti-Tocco G, D'Alessio G. In Vitro Studies on Selective Inhibition of Tumor Cell Growth by Seminal Ribonuclease. Cancer Res. 1980;40:3740–3744. [PubMed] [Google Scholar]
- 7.Richards FM, Wyckoff HW. The Enzymes. 3rd New York Academic; 1971. IV - Hydrolytic Cleavage. Part A0, chap. Bovine Pancreatic ribonuclease; pp. 647–907. [Google Scholar]
- 8.Nogués MV, Vilanova M, Cuchillo CM. Bovine pancreatic ribonuclease A as a model of an enzyme with multiple substrate binding sites. Biochim Biophys Acta. 1995;1253:16–24. doi: 10.1016/0167-4838(95)00138-k. [DOI] [PubMed] [Google Scholar]
- 9.Kelemen BR, Schultz LW, Sweeney RY, Raines RT. Excavating an Active Site: The Nucleobase Specificity of Ribonuclease A. Biochemistry. 2000;39:14487–14494. doi: 10.1021/bi001862f. [DOI] [PubMed] [Google Scholar]
- 10.D'Alessio G. Ribonucleases: Structure and functions. Academic Press; 1997. [Google Scholar]
- 11.Witzel H, Barnard EA. Mechanism and Binding sites in the Ribonuclease Reaction II. Kinetic studies on the first step of the Reaction. Biochem Biophys Res Commun. 1962;7:295–299. doi: 10.1016/0006-291x(62)90194-8. [DOI] [PubMed] [Google Scholar]
- 12.Blackburn P, Moore S. The Enzymes. 3rd New York Academic; 1982. XV- Nucleic Acids. Part B, chap. 12-Pancreatic Ribonuclease; pp. 317–433. [Google Scholar]
- 13.Eftink MR, Biltonen RL. Hydrolytic Enzymes. Elsevier; 1987. 16 of New comprehensive biochemistry; pp. 333–376. [Google Scholar]
- 14.Cuchillo CM, Vilanova M, Nogués MV. Ribonucleases: Structures and Functions. Academic Press; 1997. chap. 9- Pancreatic Ribonucleases; pp. 271–300. [Google Scholar]
- 15.Roberts G, Dennis E, Meadows D, Cohen J, Jardetzky O. The mechanism of Action of Ribonuclease. Proc Natl Acad Sci USA. 1969;62:1151–1158. doi: 10.1073/pnas.62.4.1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Findlay D, Herries D, Mathias A, Rabin B, Ross C. The active site and mechanism of action of Bovine Pancreatic Ribonuclease. Nature. 1961;190:781–784. doi: 10.1038/190781a0. [DOI] [PubMed] [Google Scholar]
- 17.Anslyn E, Breslow R. On the mechanism of catalysis by ribonuclease: cleavage and isomerization of the dinucleotide UpU catalyzed by imidazole buffers. J Am Chem Soc. 1989;111:4473–4482. [Google Scholar]
- 18.Haydock K, Lim C, Brünger A, Karplus M. Simulation Analysis of Structures on the Reaction Pathway of RNase A. J Am Chem Soc. 1990;112:3826–3831. [Google Scholar]
- 19.Wladkowski BD, Svensson LA, Sjolin L, Ladner JE, Gilliland GL. Structure (1.3 Å) and Charge States of Ribonuclease A-Uridine Vanadate Complex: Implications for the Phosphate Ester Hydrolysis Mechanism. J Am Chem Soc. 1998;120:5488–5498. [Google Scholar]
- 20.Wladkowski B, Ostazeski P, Chenoweth S, Broadwater S, Krauss M. Hydrolysis of cyclic phosphates by ribonuclease A: A computational study using a simplified ab initio quantum model. J Comput Chem. 2003;24:1803–1811. doi: 10.1002/jcc.10331. [DOI] [PubMed] [Google Scholar]
- 21.Lopez X, York D, Dejaegere A. Theoretical Studies on the hydrolysis of phosphate diesters in the Gas Phase, Solution, and RNase A. Int J Quant Chem. 2002;86:10–26. [Google Scholar]
- 22.Elsässer B, Valiev M, Weare J. A Dianionic Phosphorane Intermediate and Transition States in an Associative AN+DN Mechanism for the Ribonuclease A Hydrolysis Reaction. J Am Chem Soc. 2009;131:3869–3871. doi: 10.1021/ja807940y. [DOI] [PubMed] [Google Scholar]
- 23.Breslow R. How do imidazole groups catalyze the cleavage of RNA in enzyme models and in enzymes? Evidence from ”Negative Catalysis”. Acc Chem Res. 1991;24:317–324. [Google Scholar]
- 24.Cohen AJ, Mori-Sánchez P, Yang W. Insights into Current Limitations of Density Functional Theory. Science. 2008;321:792–794. doi: 10.1126/science.1158722. [DOI] [PubMed] [Google Scholar]
- 25.Wlodawer A, Miller M, Sjolin L. Active site of RNase: Neutron diffraction study of a complex with uridine vanadate, a transition-state analog. Proc Natl Acad Sci USA. 1983;80:3628–3631. doi: 10.1073/pnas.80.12.3628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wlodawer A, Borkakoti N, Moss DS, Howlin B. Comparison of Two Independently Refined Models of Ribonuclease-A. Acta Crystallogr B. 1986;42:379–387. [Google Scholar]
- 27.Borah B, wan Chen C, Egan W, Miller M, Wlodawer A, Cohen JS. Nuclear Magnetic Resonance and Neutron Diffraction Studies of the Complex of Ribonuclease A with Uridine Vanadate, a Transition-State Analogue. Biochemistry. 1985;24:2058–2067. doi: 10.1021/bi00329a038. [DOI] [PubMed] [Google Scholar]
- 28.Ladner JE, Wladkowski BD, Svensson LA, Sjölin L, Gilliland GL. X-ray Structure of a Ribonuclease A–Uridine Vanadate Complex at 1.3 Å Resolution. Acta Crystallographica Section D. 1997;53:290–301. doi: 10.1107/S090744499601582X. [DOI] [PubMed] [Google Scholar]
- 29.Messmore J, Raines R. Pentavalent Organo-Vanadates as Transition State Analogues for Phosphoryl Transfer Reactions. J Am Chem Soc. 2000;122:9911–9916. doi: 10.1021/ja0021058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Holloway DE, Chavali GB, Leonidas DD. Influence of Naturally-occurring 5′-Pyrophosphate-linked Substituents on the Binding of Adenylic Inhibitors to Ribonuclease A: an X-Ray Crystallographic Study. Biopolymers. doi: 10.1002/bi 21158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cole R, Loria JP. Evidence for Flexibility in the Function of Ribonuclease A. Biochemistry. 2002;41:6072–6081. doi: 10.1021/bi025655m. [DOI] [PubMed] [Google Scholar]
- 32.Beach H, Cole R, Gill ML, Loria JP. Conservation of μs-ms Enzyme Motions in the Apo- and Substrate-Mimicked State. J Am Chem Soc. 2005;127:9167–9176. doi: 10.1021/ja0514949. [DOI] [PubMed] [Google Scholar]
- 33.Kovrigin EL, Loria JP. Enzyme Dynamics along the Reaction Coordinate: Critical Role of a Conserved Residue. Biochemistry. 2006;45:2636–2647. doi: 10.1021/bi0525066. [DOI] [PubMed] [Google Scholar]
- 34.Kovrigin EL, Loria JP. Characterization of the Transition State of Functional Enzyme Dynamics. J Am Chem Soc. 2006;128:7724–7725. doi: 10.1021/ja061435a. [DOI] [PubMed] [Google Scholar]
- 35.Mayaan E, Moser A, Jr, M AD, York DM. CHARMM Force Field Parameters for Simulation of Reactive Intermediates in Native and Thio-Substituted Ribozymes. J Comput Chem. 2007;28:495–507. doi: 10.1002/jcc.20474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Brünger A, Brooks C, Karplus M. Active site dynamics of ribonuclease. Proc Natl Acad Sci USA. 1985;82:8458–8462. doi: 10.1073/pnas.82.24.8458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Seshadri K, Rao VSR, Vishveshwara S. Interaction of substrate uridyl 3′,5′-adenosine with ribonuclease a: A molecular dynamics study. Biophys J. 1995;69:2185–2194. doi: 10.1016/S0006-3495(95)80094-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Toiron C, Gonzalez C, Bruix M, Rico M. Three-dimensional structure of the complexes of ribonuclease A with 2′,5′-CpA and 3′,5′-d(CpA) in aqueous solution, as obtained by NMR and restrained molecular dynamics. Protein Science. 1996;5:1633–1647. doi: 10.1002/pro.5560050817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sanjeev B, Vishveshwara S. Protein-water interactions in ribonuclease A and angiogenin: A molecular dynamics study. Proteins: Structure, Function, and Bioinformatics. 2004;55:915–923. doi: 10.1002/prot.20114. [DOI] [PubMed] [Google Scholar]
- 40.Cotesta S, Tavernelli I, Di lorio EE. Dynamics of RNase-A and S-Protein: A Molecular Dynamics Simulation of the Transition Toward a Folding Intermediate. Biophys J. 2003;85:2633–2640. doi: 10.1016/s0006-3495(03)74686-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Esposito L, Daggett V. Insight into Ribonuclease A Domain Swapping by Molecular Dynamics Unfolding Simulations. Biochemistry. 2005;44:3358–3368. doi: 10.1021/bi0488350. [DOI] [PubMed] [Google Scholar]
- 42.Zegers I, Maes D, Dao-Thi M, Poortmans F, Palmer R, Wyns L. The structures of RNase A complexed with 3′-CMP and d(CpA): active site conformation and conserved water molecules. Protein Sci. 1994;3:2322–2339. doi: 10.1002/pro.5560031217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Brooks BR, Brooks CL, III, MacKerell AD, Jr, Nilsson L, P RJ, Roux B, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaris T, Ma J, Ovchninnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu W, Yang W, York DM, Karplus M. J Comput Chem. Vol. 30. 2009. CHARMM: The biomolecular simulation program; pp. 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Brooks B, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J Comput Chem. 1983;4:187–217. [Google Scholar]
- 45.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck J, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, III, R B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiórkiewicz-Kuczera J, Yin D, Karplus M. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 46.Foloppe N, MacKerell AD., Jr All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J Comput Chem. 2000;21:86–104. [Google Scholar]
- 47.MacKerell AD, Banavali NK. All-Atom Empirical Force Field for Nucleic Acids: II. Application to Molecular Dynamics Simulations of DNA and RNA in Solution. J Comp Chem. 2000;21:105–120. [Google Scholar]
- 48.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. The Journal of Chemical Physics. 1983;79:926–935. [Google Scholar]
- 49.Andersen HC. Molecular dynamics simulations at constant pressure and/or temperature. J Chem Phys. 1980;72:2384–2393. [Google Scholar]
- 50.Nosé S. A unified formulation of the constant temperature molecular dynamics methods. J Chem Phys. 1984;81:511–519. [Google Scholar]
- 51.Hoover WG. Canonical dynamics: Equilibration phase-space distributions. Phys Rev A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 52.Darden T, York DM, Pedersen L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 53.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. J Chem Phys. 1995;103:8577–8593. [Google Scholar]
- 54.Sagui C, Darden TA. Molecular Dynamics Simulations of Biomolecules: Long-Range Electrostatic Effects. Annu Rev Biophys Biomol Struct. 1999;28:155–179. doi: 10.1146/annurev.biophys.28.1.155. [DOI] [PubMed] [Google Scholar]
- 55.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Oxford University Press; 1987. [Google Scholar]
- 56.Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical Integration of the Cartesian Equations of Motion of a System with Constraints: Molecular Dynamics of n-Alkanes. J Comput Phys. 1977;23:327–341. [Google Scholar]
- 57.Neidle S, Schneider B, Berman HM. Structural Bioinformatics. Wiley-Liss, Inc., San Diego Supercomputer Center, Department of Pharmacology, University of California San Diego; La Jolla, CA, USA: 2003. 44 of Methods of Biochemical Analysis, chap. 3- Fundamentals of DNA and RNA structure; pp. 41–73. [PubMed] [Google Scholar]
- 58.Richardson JS, Schneider B, Murray LW, Kapral GJ, Immormino RM, Headd JJ, Richardson DC, Ham D, Hershkovits E, Williams LD, Keating KS, Pyle AM, Micallef D, Westbrook J, Berman HM. RNA backbone: Consensus all-angle conformers and modular string nomenclature (an RNA Ontology Consortium contribution) RNA Journal. 2008;14:465–481. doi: 10.1261/rna.657708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Altona C, Sundaralingam M. Conformational analysis of the sugar ring in nucleosides and nucleotides. New description using the concept of pseudorotation. J Am Chem Soc. 1972;94:8205–8212. doi: 10.1021/ja00778a043. [DOI] [PubMed] [Google Scholar]
- 60.Borkakoti N, Moss DS, Palmer RA. Ribonuelease-A: Least-Squares Refinement of the Structure at 1.45 Å Resolution. Acta Crystallogr B. 1982;38:2210–2217. [Google Scholar]
- 61.Saenger W. Principles of nucleic acid structure. chap. 17. Springer-Verlag; New York: 1984. pp. 368–384. [Google Scholar]
- 62.Bloomfield VA, Crothers DM, Tinoco I., Jr . Nucleic Acids: Structures, Properties, and Functions. University Science Books; Sausalito, CA: 2000. [Google Scholar]
- 63.Thompson JE, Venegas FD, Raines RT. Energetics of Catalysis by Ribonucleases: Fate of the 2′,3′-Cyclic Phosphodiester Intermediate. Biochemistry. 1994;33:7408–7414. doi: 10.1021/bi00189a047. [DOI] [PubMed] [Google Scholar]
- 64.Park C, Raines RT. Catalysis by Ribonuclease A Is Limited by the Rate of Substrate Association. Biochemistry. 2003;42:3509–3518. doi: 10.1021/bi026076k. [DOI] [PubMed] [Google Scholar]
- 65.Messmore JM, Fuchs DN, Raines R. Ribonuclease A: Revealing Structure-Function Relationships with Semisynthesis. J Am Chem Soc. 1995;117:8057–8060. doi: 10.1021/ja00136a001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Jentoft J, Gerken T, Jentoft N, Dearborn D. [13C]Methylated Ribonuclease A, 13C NMR studies of the interaction of lysine 41 with active site ligands. J Biol Chem. 1981;256:231–236. [PubMed] [Google Scholar]
- 67.Berisio R, Sica F, Lamzin VS, Wilson KS, Zagari A, Mazzarella L. Atomic resolution structures of ribonuclease A at six pH values. Acta Crystallogr D. 2002;58:441–450. doi: 10.1107/s0907444901021758. [DOI] [PubMed] [Google Scholar]
- 68.Nelson DL, Cox MM. Lehninger Principles of Biochemistry. 4th. W. H. Freeman; New York, NY: 2005. [Google Scholar]
- 69.Babu CS, Lim C. Theory of ionic hydration: Insights from molecular dynamics simulations and experiment. J Phys Chem B. 1999;103:7958–7968. [Google Scholar]
- 70.Pelmenschikov A, Yin X, Leszczynski J. Revealing the Role of Water in the Acid-Base Interaction between the Phosphate Groups of DNA and the Amino Acid Side Chains of Proteins: A Density Functional Theory Study of Molecular Models. J Phys Chem B. 2000;104:2148–2153. [Google Scholar]
- 71.Panov K, Kolbanovskaya E, Okorokov A, Panova T, Terwisscha van Scheltinga A, Karpeisky M, Beintema J. Ribonuclease A mutant His119Asn: the role of histidine in catalysis. FEBS Letters. 1996;398:57–60. doi: 10.1016/s0014-5793(96)01173-8. [DOI] [PubMed] [Google Scholar]
- 72.Park C, Schultz LW, Raines RT. Contribution of the Active Site Histidine Residues of Ribonuclease A to Nucleic Acid Binding. Biochemistry. 2001;40:4949–4956. doi: 10.1021/bi0100182. [DOI] [PubMed] [Google Scholar]
- 73.Tanimizu N, Ueno H, Hayashi R. Replacement of His12 or His119 of Bovine Pancreatic Ribonuclease A with Acidic Amino Acid Residues for the Modification of Activity and Stability. J Biosci Bioeng. 2002;94:39–44. doi: 10.1263/jbb.94.39. [DOI] [PubMed] [Google Scholar]
- 74.Trautwein K, Holliger P, Stackhouse J, Benner SA. Site-directed mutagenesis of bovine pancreatic ribonuclease: Lysine-41 and aspartate-121. FEBS Letters. 1991;281:275–277. doi: 10.1016/0014-5793(91)80410-5. [DOI] [PubMed] [Google Scholar]
- 75.Lisgarten J, Maes D, Wyns L. Structure of the Crystalline Complex of Deoxycytidylyl-3′,5′-guanosine (3′,5′-dCpdG) Cocrystallized with Ribonuclease at 1.9 A Resolution. Acta Crystallographica Section D. 1995;51:767–771. doi: 10.1107/S0907444995001570. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.