Feasible Stability Region in the Frontal Plane During Human Gait

Abstract

The inability to adequately control the motion of the center of mass (COM) in the frontal plane may result in a loss of balance causing a sideways fall during human gait. The primary purposes of this study were (1) to derive the feasible stability region (FSR) in the mediolateral direction, and (2) to compare the FSR with the COM motion state taken from 193 trials among 39 young subjects at liftoff during walking at different speeds. The lower boundary of the FSR was derived, at a given initial COM location, as the minimum rightward COM velocity, at liftoff of the left foot, required to bring the COM into the base of support (BOS), i.e. the right (stance) foot, as the COM velocity diminishes. The upper boundary was derived as the maximum rightward COM velocity, beyond which the left foot must land to the right of the right foot (BOS) in order to prevent a fall. We established a 2-link human model and employed dynamic optimization to estimate these threshold values for velocity. For a range of initial COM positions, simulated annealing algorithm was used to search for the threshold velocity values. Our study quantified the extent to which mediolateral balance can still be maintained without resorting to a crossover step (the left foot lands to the right of the BOS) for balance recovery The derived FSR is in good agreement with our gait experimental results.

Introduction

Falls are a serious medical and public health problem facing adults aged 65 and older⁸. Falling to the side has been identified as an important causal factor for hip fracture²¹, which is associated with up to a 20% chance of death⁴⁸. Aging appears to present particular problems for lateral balance related to falls³³. A better understanding of the mechanisms underlying falls, particularly sideways or lateral falls, would be a significant step in designing risk assessments or interventions towards lateral fall prevention. These same mechanisms for maintaining lateral balance would apply as well to the fields of prosthetic and bi-pedal robotic gait with similar control of resultant joint moments or joint actuators.

Human movement stability has long been correlated to falls among elders^31,32. Some advanced mathematical tools, such as Poincare mapping²⁹ and Lyapunov stability theory⁵⁴ have been used to investigate human movement stability. With the development of nonlinear dynamics theory, a method for evaluating body dynamic stability based on variability in kinematics and spatiotemporal gait parameters has also been established^15,18. Several indexes characterizing gait variability, such as the Approximate Entropy³⁶, Maximum Floquet Multipliers¹⁷, Lyapunov Exponents¹⁶, and simply the standard deviation of step length²⁴, have been employed to evaluate body stability. A basic assumption of these approaches is that an increased variability in walking patterns is indicative of impaired motor control. However, the extent to which this variability is equal to stability is not clear¹⁸; there might be a difference between variability and instability⁴. Dynamic stability describes the capacity of the neuromuscular system to restore or maintain function successfully despite naturally occurring disturbances and neuromotor control errors. Summary statistics of variability fail to account for the dynamic mechanisms underlying the variability⁴.

A person's ability to avoid a fall can also be characterized by the kinematic relationship between the center of mass (COM) and its base of support (BOS)⁹. In line with this conceptualization several methods have been developed to quantify dynamic stability. For example, some researchers use Time-to-Contact (TtC) to characterize dynamic stability^22,23,43. The TtC is a boundary-relevant measure that combines information about the instantaneous kinematics of the COM to predict a future time at which the COM will cross the BOS boundary or stability boundary. Stability is also calculated based on the Zero Moment Point which requires that the projection of the COM remain inside the support polygon during walking^28,52.

Similarly, an approach for calculating dynamic stability based on a Feasible Stability Region (FSR) was proposed^26,40. The FSR encloses all possible combinations of position and velocity of the COM for which a balance loss is preventable. The FSR in the anteroposterior (AP) direction has been derived by using computer simulation assisted by an optimization routine^40,55. This FSR provides a quantitative method for evaluating stability in the sagittal plane. If a COM motion state lies within the FSR, balance loss is unlikely to occur³⁷. An initial motion state further below the lower boundary of the FSR (i.e., a more negative AP stability) is more unstable and will be more likely to lead to a backward balance loss. This is due to an initial forward momentum that is insufficient to carry the COM forward to within the BOS. Conversely, when the motion state is further above the upper boundary (i.e. a more positive AP stability), a forward loss of balance would be more probable due to the excessive forward momentum³⁷.

Efforts have been undertaken in the past decade to verify this concept of the FSR with experimental data by ourselves^5,7,42,55,56 or those collected by different research groups^{26,35,39,41,44}. The conceptual framework does have very high capability (∼100% accuracy) in predicting balance loss in the AP direction when COM states reside outside of the FSR^7,56. This method for empirically verifying the necessary condition is less than perfect because a person can choose to step even when it is not biomechanically necessary. In addition, predictions on adaptive improvements in stability derived from the FSR indeed correlated highly with empirical observations of the reduction of balance loss incidence upon repeated exposure to slips induced during chair-rise and during walking⁷. The latter application underscores the merit of this conceptual framework, because it provides the rationale for quantifying and evaluating adaptation, retention, and transfer of motor skills for falls prevention.

An analogous FSR for assessment of dynamic stability in the mediolateral (ML) direction has not been defined. Yet, evaluation of dynamic stability in the frontal plane is an important aspect of the quantification of mechanisms of falls among elders. In fact, altered frontal plane COM and BOS control are associated with heightened fall risk, and lateral falls are associated with dangerous hip fractures^21,48. In addition, there is evidence that COM and BOS control in the ML direction may be equally or even more important in identifying or addressing fall risk among older adults than AP control⁴⁵. ML variables, but not AP parameters, have been found to be significantly associated with a history of falls³⁴ and future falls⁴⁵. Identification of the FSR in the frontal plane during locomotion would be invaluable in assessing dynamic stability in the ML direction.

Much of the current research in the area of human movement analysis and simulation relies on simplified human biomechanical models. For example, Scott and Loan developed a computational framework for simulating and analyzing human gait in which the human body was represented as a 12-link model^13,14. Other researchers have used a more simplified model, such as 10-link model², 5-link model^28,51, 2-link model²⁰, and 1-link pendulum system³⁰ to simulate human movement. In our present study, the 2-link model, composed of the right foot and the remaining body, was preferred because of its efficiency and robustness. In addition, it has been previously found that the boundary values of the FSR in the AP direction derived from a 7-link model and a 2-link model have comparable tendencies and values^38,56.

The primary purposes of this study were (1) to derive the FSR in the ML direction, and (2) to compare the results with the COM state taken at liftoff during walking. The derived FSR will offer a framework to evaluate stability in the ML direction and some guidance to develop effective interventions toward preventing falls.

Methods

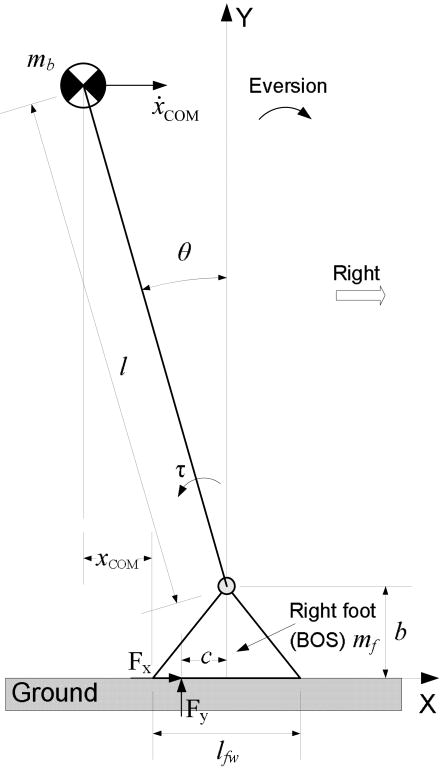
The human model used in computing the FSR for gait, in this case, was confined to the frontal plane (ML direction) and comprised the right foot and the rest of the body (Fig. 1). The right foot was the BOS to the human model in order to investigate the relative position of the COM to the BOS. To simplify the calculation of the boundary of the BOS, the shape of the sole was represented by a decagon (Fig. 2). The vertexes of the decagon were determined by the natural points of the foot¹. The coefficient of friction between the right sole and the ground was set at 1.41¹⁰, which is large enough to exclude slipping in the ML direction between the surfaces. The right ankle was actuated by a single resultant joint moment, τ, with peak evertor and invertor limits adopted from published data⁴⁶. Specifically, the joint moment was computed as⁵⁵:

Fig. 1.

Schematic of the 2-link (the right foot and the rest of the body), frontal-plane model of the human body. The right foot is the base of support (BOS) of the model. The ankle joint is modeled as a 1-degree-of-freedom hinge joint, and its angle θ represents the generalized coordinates of the model. The foot and body anthropometric parameters were determined based on a typical male with body height at 1.78m and body mass at 80kg⁵³. The positive X-axis is to the right, and the positive Y-axis is upward. Positive joint rotation is along the positive Z-axis (counterclockwise).

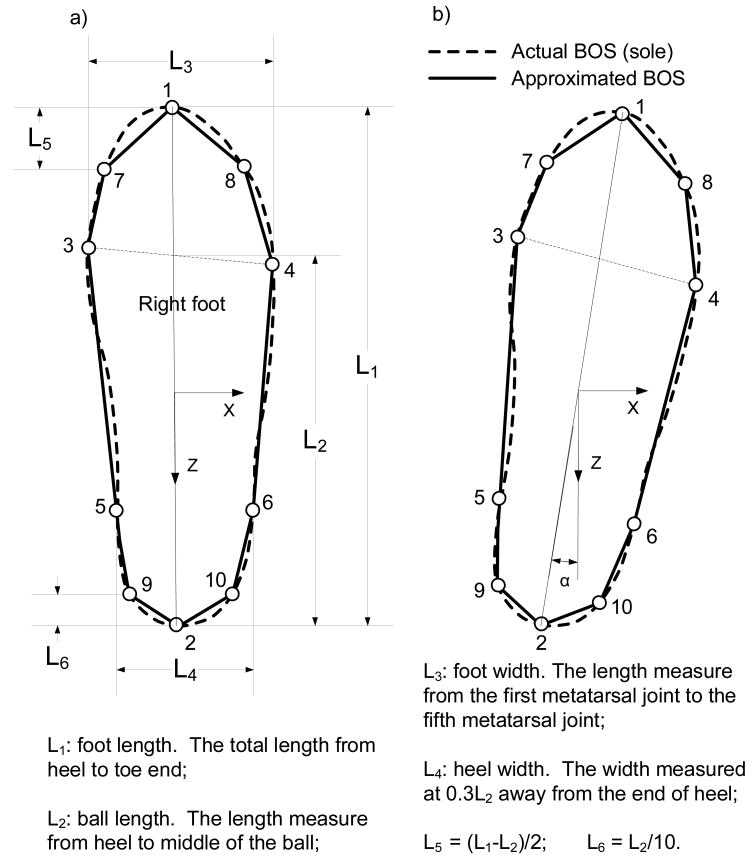
Fig. 2.

(a) The schematic for approximating the base of support (BOS, the sole) which is the right foot in this study. The BOS is represented by a decagon. Ten vertexes of the decagon, as indicated by the open circles, are the toe end (1), the heel (2), the first metatarsal joint (3), the fifth metatarsal joint (4), two ends of the heel width (5 and 6); vertexes of 7 and 8 are between 1 and 3, and between 1 and 4, respectively; vertexes of 9 and 10 are between 2 and 5, and between 2 and 6, respectively. The definitions of foot length, foot widths, and ball length were adopted from the literature¹. The reference point for calculating the relative position of the center of mass (COM) to the BOS is the most leftward point on the outline of the BOS. In all simulations, the reference point was the position of the first metatarsal joint because we assume that the foot is along the Z axis. When applying this BOS definition to experimental data, the reference point might be altered due to foot's orientation deviating from the Z asix, as shown in (b).

$$\tau =\{\begin{array}{cc}a(t){\text{T}}^E& a(t)\ge 0\\ a(t){\text{T}}^I& a(t)<0\end{array}$$ (1)

where τ, a, and T are the joint moment, activation level, and the physiological moment range of the joint, respectively. The superscripts E and I represent eversion and inversion respectively. A first order differential equation governed the change of the activation level in response to a joint actuator excitation (u):

$$\begin{array}{l}\dot{a}=\left(u-a\right)/t_{\text{act}}\\ u=u\left(t\right)\in [-1,1],a=a\left(t\right)\in \left[-1,1\right]\end{array}$$ (2)

The activation time constant, t_atc, was 10 ms.

Equations of motion for the model were derived by using Newton-Euler methods and were solved using a 4^th order Runge-Kutta integrator. Forward simulation of the right single-stance phase of the model started from the instant of left liftoff (i.e. toe-off). Simulation times, ranging from 0.28 to 0.52s, were set based on the duration from left liftoff to its touchdown (i.e. heel strike) averaged across all the experimental trials at the corresponding initial COM position (see below).

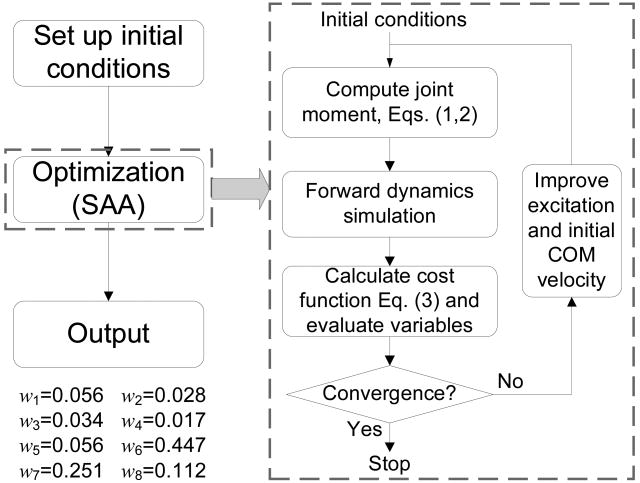
The thresholds of the FSR were computed through model simulations starting at six specific positions for the lower boundary and ten positions for the upper boundary (Fig. 3). For the first simulation of the lower boundary, the initial horizontal position of the COM relative to BOS $({\mathit{\text{x}}}_{\text{COM}}^{\text{initial}})$ was 0.25 foot widths (l_fw, i.e. L₃ in Fig. 2) to the left of the first metatarsal joint (point 3 in Fig. 2) of the right foot. (i.e., $({\mathit{\text{x}}}_{\text{COM}}^{\text{initial}})=-0.25$). Subsequent simulations started with the ${\mathit{\text{x}}}_{\text{COM}}^{\text{initial}}$ at increments of -0.25l_fw to the left, with the final starting position at ${\mathit{\text{x}}}_{\text{COM}}^{\text{initial}}=-\text{1}.50$. For the upper boundary, ${\mathit{\text{x}}}_{\text{COM}}^{\text{initial}}$ was 0.75 for the first simulation and -1.50 for the last simulation. The joint excitation time history, u(t), was discretized into control nodes at every 0.02s and each node was varied independently during the optimization procedure. The values for the activations in between nodes were determined by linear interpolation.

Fig. 3.

The flow chart of the simulation and optimization utilized in the present study to derive the feasible stability region boundaries. Simulated annealing algorithm (SAA) was adopted to conduct the optimization portion. The iteration was terminated when the improvement in the cost function was less than 10^-3 for 500 consecutive function evaluations. Also shown are the values of the weights employed in the cost function.

At each ${\mathit{\text{x}}}_{\text{COM}}^{\text{initial}}$, simulated annealing algorithm¹² was used to find the optimal rightward initial COM velocity ${\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}}$ (i.e., the maximum initial COM velocity for the upper boundary; and the minimum initial COM velocity for the lower boundary) and u(t), that would minimize the cost function,

$$minf=w_{1}e\left({\dot{x}}_{\text{COM}}^{\text{initial}}\right)+w_2\underset{t_0}{\overset{t_f}{\int }}\lfloor F_y\left(t\right)\rfloor dt+w_3\underset{t_0}{\overset{t_f}{\int }}h\left(\theta \left(t\right)\right)dt+w_4\underset{t_0}{\overset{t_f}{\int }}h\left(\dot{\theta }\left(t\right)\right)dt+w_5\underset{t_0}{\overset{t_f}{\int }}u{\left(t\right)}^{2}dt+w_6\left|x_{\text{COM}}^{\text{final}}\right|+w_7\left|{\dot{x}}_{\text{COM}}^{\text{final}}\right|+w_8\left|{\ddot{x}}_{\text{COM}}^{\text{final}}\right|$$ (3)

w_i is the weight of the i^th term. Symbols x/ẋ/ẍ respectively represent COM position/velocity/acceleration relative to the right foot. The function of $\mathit{\text{e}}({\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}})$ can be computed as,

$$e\left({\dot{x}}_{\text{COM}}^{\text{initial}}\right)=\{\begin{array}{cc}\left|{\dot{x}}_{\text{COM}}^{\text{initial}}\right|& \text{for the lower boundary}\\ \frac{1}{\left|{\dot{x}}_{\text{COM}}^{\text{initial}}\right|}& \text{for the upper boundary}\end{array}$$ (4)

The symbol ⌊⌋ has the following behavior:

$$\lfloor s\rfloor =\{\begin{array}{ll}0& s\ge 0\\ -s& s<0\end{array}$$ (5)

h(s) is computed using the equation,

$$h\left(s\left(t\right)\right)=\{\begin{array}{ll}{s}^{-}-s\left(t\right),& s\left(t\right)<s^{-}\\ 0,& s^{-}\le s\left(t\right)\le s^{+}\\ s\left(t\right)-s^{+},& s\left(t\right)>s^{+}\end{array}$$ (6)

$s_i^{-}$ and $s_i^{+}$ represent the lower and upper limits, respectively, of the feasible range of the ankle angle and angular velocity.

The first item ensured that ${\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}}$ would be the optimal rightward velocity. The second term required that the vertical ground reaction force (i.e. F_y) remain positive during the simulation period. The third and fourth terms constrained the ankle angular displacement/velocity to their corresponding physical ranges. The fifth term was used to minimize the integral of the square of the ankle moment⁴⁷. The sixth term required the COM to lie inside the BOS when the relative motion between the COM and BOS diminished at the termination of a simulation – a condition guaranteed by the last two terms. The expression of ${\mathit{\text{x}}}_{\text{COM}}^{\text{initial}}$ was:

$$x_{\text{COM}}^{\text{final}}=\{\begin{array}{cc}{\left(x_{\text{COM}}-x_{\text{BOS},1^{st}\text{metatarsal}}\right)}_{\text{final}}& \text{for the lower boundary}\\ {\left(x_{\text{COM}}-x_{\text{BOS},5^{th}\text{metatarsal}}\right)}_{\text{final}}& \text{for the upper boundary}\end{array}$$ (7)

The threshold values derived from the optimization routine were evaluated by comparing them to experimental gait data⁶ from 193 trials among 39 young, healthy adults (age in years: 27.0 ± 4.7). All subjects had given written informed consent to the experimental protocol as approved by the Institutional Review Board. These subjects were randomly divided into three speed groups: fast (n = 12), natural (n = 13), and slow (n = 14). Subjects in each group walked three blocks of 10 trials each at their self-selected fast, natural, or slow speed along a 7-m instrumented walkway. Full body kinematics, used to compute COM motion state, were gathered using a six-camera motion capture system (Motion Analysis, Santa Rosa, CA). In the present study, COM motion states in the frontal plane of the last 6 trials were analyzed for each subject. The trials with missing markers were excluded from the analysis.

To identify whether gait speed affected the COM motion state in the ML direction and step width, an one-way ANOVA with speed group as the factor was employed to analyze COM position/velocity/stability in the ML direction as well as gait speed at left liftoff, and step width. Post hoc analyses used t-tests with a Bonferroni correction. Analyses were performed using SPSS 16.0 (Chicago, IL). A significance level of 0.05 was used for all analyses.

Results

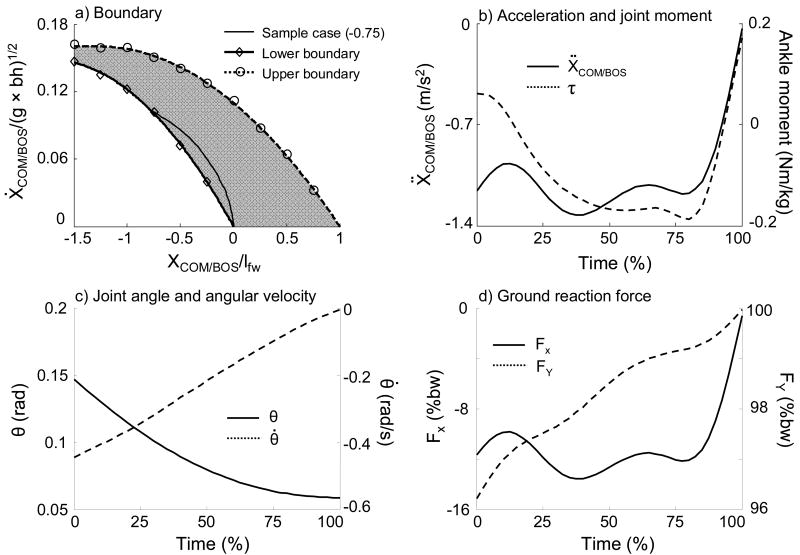
At left liftoff, a more leftward ${\mathit{\text{x}}}_{\text{COM}}^{\text{initial}}$ required a greater minimum rightward ${\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}}$ to bring the COM over the BOS or a greater maximum rightward ${\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}}$ to prevent the COM from moving outside the BOS when the COM velocity diminished. The lower boundary values, necessary to carry the COM within the BOS, required normalized horizontal COM velocities of 0.146, 0.137, 0.122, 0.101, 0.074, and 0.040 when the COM started 1.5, 1.25, 1, 0.75, 0.5, and 0.25 l_fw to the left of the first metatarsal joint of the BOS, respectively (Fig. 4-a). The upper boundary was derived as the maximum rightward COM velocity, beyond which the left foot must land to the right of the BOS in order to prevent a fall; it ranged from 0.161 at 1.5l_fw to the left of the first metatarsal joint of the BOS, to 0 over the fifth metatarsal joint of the BOS (Fig. 4-a).

Fig. 4.

A representative simulation result of the center of mass (COM) motion state trajectory for the lower boundary of the feasible stability region (FSR) in the frontal plane (a), horizontal acceleration of the COM and time history of ankle joint moment with positive as the inversion moment (b), ankle angle and angular velocity (c), and ground reaction force (d) of a successful lateral balance recovery with an initial COM position of -0.75 (normalized to foot width, l_fw). In (a), the open diamond marks the starting point of the COM motion state for this simulation sample. Also shown is the FSR (gray area) with the lower boundary (thick solid line) and the upper boundary (thick dashed line) to control the body balance. The COM position is relative to the BOS and normalized to foot width (l_fw). The velocity of the COM was normalized to $\sqrt{g\times bh}$, where g is the gravitational acceleration, and bh is body height. In (d), the ground reaction forces are normalized to body weight (bw).

Inspection of the results of a specific simulation for the lower boundary revealed that the optimization process resulted in a coordinated solution that enforced the various conditions expressed in the cost function (Eq.3). At the instant of simulation termination, the COM was just above the first metatarsal of the BOS, with a COM velocity and acceleration close to zero (Fig. 4-a, b). Ankle angle and angular velocity remained within physiological ranges (Fig. 4-c). The vertical ground reaction force was constantly positive and was very close to body weight at movement termination. The horizontal ground reaction force was close to zero at movement termination (Fig. 4-d).

As designed, gait speed differed significantly among these three speed groups during walking (p < 0.001, Table 1). Gait speed affected the COM motion states in the frontal plane. Specifically, subjects in the natural speed group demonstrated a more leftward ${\mathit{\text{x}}}_{\text{COM}}^{\text{initial}}$ than the other two groups (p < 0.01, Table 1). Subjects walking at high gait speeds exhibited a slower rightward ${\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}}$ than the other two groups (p < 0.001, Table 1).

TABLE 1.

Mean (SD) values of gait speed and the kinematic parameters in the mediolateral (ML) direction at left foot liftoff (across all subjects) and statistical comparisons for three speed groups. The parameters in the ML direction include the COM position and velocity relative to the base of support (BOS), the COM stability in the frontal plane, and step width. Gait speed is normalized to $\sqrt{g\times bh}$, where g represents the gravitational acceleration, bh is body height. COM position and velocity are relative to the first metatarsal joint of the right foot (the BOS) and normalized to foot width and $\sqrt{g\times bh}$, respectively. Step width is normalized to bh.

	Speed groups
Dependent variable	Fast (n = 61)	Natural (n = 69)	Slow (n = 63)	Statistical analysis p-valuea [t-testb]
Gait speed	0.470 (0.063)	0.345 (0.049)	0.227 (0.045)	< 0.001 [Fast > Natural > Slow]
COM position [ML]	-0.393 (0.260)	-0.462 (0.205)	-0.336 (0.206)	< 0.01 [(Natural & Fast) < Slow]
COM velocity [ML]	0.018 (0.009)	0.029 (0.011)	0.026 (0.010)	< 0.001 [Fast < (Natural & Slow)]
COM stability [ML]	-0.038 (0.031)	-0.037 (0.022)	-0.023 (0.025)	< 0.001 [Slow > (Fast & Natural)]
Step width	0.056 (0.030)	0.063 (0.026)	0.062 (0.026)	> 0.05

^a Results of ANOVA tests of the three groups.

^b Results of t-test (performed only when ANOVA, p < 0.05). Outcomes with comparable values (p > 0.05) are grouped within parentheses.

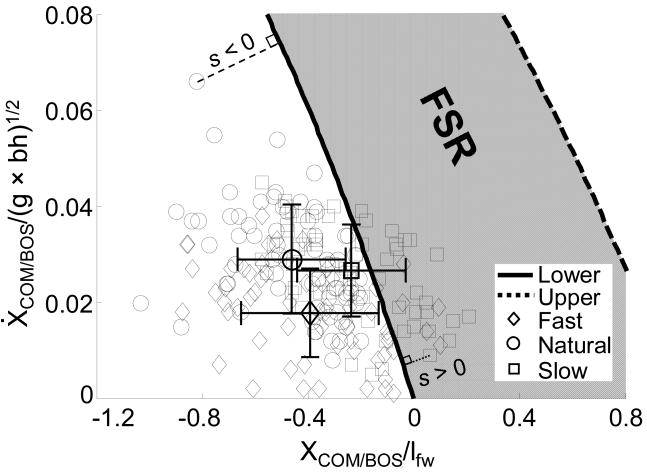
For all trials (n = 61) in the natural group, 56 of 61 (91.8%) in the fast group, and 40 of 63 trials (63.5%) in the slow group, the initial COM motion states were located below the lower boundary (Fig. 5). For the remaining trials, the initial COM motion state lay above the lower boundary but below the upper boundary (Fig. 5). The slow-speed group was the most stable group in the ML direction with the initial COM motion state closest to the FSR (Table 1, p < 0.001).

Fig. 5.

The feasible stability region (FSR) to control balance in the frontal plane and the initial COM motion state in the mediolateral (ML) direction during gait experiments. The COM motion state in the ML direction at the instant of left liftoff were from 193 trials among 39 young subjects walking at fast (n = 61), natural (n = 69), and slow (n = 63) speeds. Also shown are the corresponding mean ± SD values of the COM motion state for these subjects. The thin dashed lines indicate the ML stability, s, for given COM motion states. The stability magnitude (s) is defined as the shortest distance from the given COM motion state to the boundary.

Discussion

The FSR in the ML direction, which provides a quantitative tool to evaluate dynamic stability in the frontal plane during human movement, was derived by a reductionist approach based on an inverted pendulum model, with the aid of an optimization routine. The overall tendency of the derived boundary was the same as the FSR in the AP direction, i.e. a more leftward/posterior ${\mathit{\text{x}}}_{\text{COM}}^{\text{initial}}$ required a greater rightward/forward ${\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}}$ to bring the COM over the BOS. Conversely, excessive ${\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}}$ would carry the COM beyond the right/forward edge of the BOS, requiring a subsequent crossover step (the left foot landed to the right of the BOS (right foot)) in that direction to prevent a fall. No excessive ${\dot{\mathit{\text{x}}}}_{\text{COM}}^{\text{initial}}$ was found in the experimental verification. Correspondingly, no crossover step was found.

The magnitude of the stability in the ML direction can be defined as the shortest distance from a given COM motion state to the derived boundaries (thin dashed lines in Fig. 5)⁵⁸. Further below the lower boundary, stability values become more negative. A negative stability value predicts that the person would lose his/her balance in the ML direction at left foot touchdown. A leftward (to the left of the right foot) recovery step must be taken to keep the body from falling sideways. On the other hand, an initial COM motion state which is above the lower boundary, but still within the feasible stability region, holds a positive stability. Theoretically, a person with a positive initial ML stability could maintain balance in the frontal plane without taking a recovery step. An initial COM motion state which lies above the upper boundary predicts the need for a crossover step to prevent the body from falling aside.

The initial COM state at liftoff of the left foot for all subjects from the natural speed group (and 92% from the fast speed group) was below the lower boundary of the FSR (Fig. 5). Thus, according to model predictions, these subjects would be unstable at liftoff, and they would experience a leftward fall. All of them indeed took a step leftward to the stance foot, as predicted, for recovery of stability. This finding is also in accordance with reports that the COM is redirected waveringly in the ML direction and remains between the borders of both feet and does not typically move to a point above the stance foot during human gait¹¹. According to the model predictions, at no time during swing phase did the COM of any subject in the natural speed group cross the medial border of the BOS. This similarity further supports the derived lower threshold of FSR in the present study.

The COM states were located inside the FSR for less than 40% of the subjects walking slowly (Fig. 5). This only means that these subjects could in fact have remained stable thereafter in single stance, if they so chose, from the perspective of lateral stability. Apparently, this is not what they wanted to do in order to achieve forward progression. The most important prediction of all, however, is that all subjects, regardless of their speeds, were stable (below the upper boundary of the FSR) against falling towards the right side of the stance foot. The experimental results correctly verified this prediction that none of them took a rightward step.

It is noteworthy that COM motion state and stability in the ML direction vary with gait speed (Table 1, Fig. 5). Our results agreed with previous findings that gait speed does affect some gait parameters in the frontal plane, including lateral COM sway³ and trunk acceleration²⁵, rather than step width²⁷. These altered gait parameters might further influence lateral balance control. Our results indicated that the slow group was the most stable in the frontal plane (Fig. 5).

It has been found previously that recovery touchdown during gait-slip is the most important event in predicting a fall that would take place ∼400 ms later⁵⁷. Although the instability at liftoff of the recovery step is a precursor of an actual fall, the control of stability and the causes of falls have some distinguishable differences. Not all those who had instability at liftoff of the recovery step ended in an actual fall. In fact, our findings indicate only 25% of the young adults who were unstable at liftoff ultimately fell⁵⁷, whereas this rate increased to >50% among older adults during gait-slip⁵⁰. The focus of our current study is to predict the outcome (balance loss or no balance loss) at touchdown (i.e. the end of the single stance phase) by using the COM motion state at liftoff (i.e., the beginning of the single stance phase).

The usefulness of the FSR is to predict, from the COM motion state at liftoff, where a step must be taken to prevent a loss of balance medial or lateral to the stance foot. Liftoff represents an abrupt transition from double stance phase to single stance phase in gait. This type of transition in itself represents a dynamic disruption and a discontinuity from a large BOS to a smaller one. Anterior instability and medial instability as a result of this abrupt transition are in fact a necessity during locomotion in association with forward displacement of the body. Such instability is always followed by transient stability³⁷. The control of the COM and BOS motion state allows both mobility and stability. Mobility in walking is accomplished through periods of controlled loss of balance in both the AP and ML directions. Each of these transient losses of balance must be interrupted through stepping before they proceed to an actual fall. In contrast, a lateral or backward loss of balance is highly uncommon in regular gait. If either should occur and a lateral (or backward) recovery step would fail to be properly executed, such as through foot misplacement or inability to provide sufficient support and generate momentum, a fall would take place.

One limitation of the present study was that, beyond the right foot, we used a single segment to represent the human body. This assumption might limit the predictive capacity of the threshold. Given the fact that the difference in the prediction accuracy of slip outcomes from a 7-link human model⁵⁶ and from a 2-link model³⁸ is small, we anticipated that the improvement gained by using a complicated human model against our current model might be limited. Additionally, the model used here was confined to the frontal plane. The interactive effect of the movement in the sagittal plane on current boundaries is unknown. Future studies should also explore the extent to which the current FSR can be applied to quantify the stability of subjects with high risk of falls and individuals with neurological impairments, such as Parkinson's disease or stroke.

It also should be noted that the basic assumption for deriving the FSR is that the COM velocity diminishes when the COM arrives at the BOS. This quasi-static terminal condition is different from normal gait wherein a person does not usually operate utmostly near the limits of stability, successfully redirected their COM in ML direction, and kept walking forward.⁴⁹ However, this assumption, representing an extreme case, is important for deriving the utmost initial velocity for stability. Furthermore, the extensive effort in verifying the FSR conceptualization has proven that such an assumption is accurate.

In conclusion, the present study determined the FSR, inside which an initial COM motion state should keep the body balanced in the frontal plane during human gait. This FSR provides, for the first time, a quantitative basis for assessing dynamic stability in the ML direction during gait (Fig. 5), which is important to the development of effective interventions aimed at fall prevention among elders. The findings in this study could also provide some theoretical guidance to humanoid robotics design¹⁹. In addition, the FSR derived in the present study could be further extended to guide the design of prosthetics and gait training programs for amputees to facilitate independent ambulation²⁷. Although the right foot was chosen as the BOS in the present study, the analysis could be easily applied to the left foot as the BOS due to the symmetry of the human body.