Low Pore Connectivity Increases Bacterial Diversity in Soil

Abstract

One of soil microbiology's most intriguing puzzles is how so many different bacterial species can coexist in small volumes of soil when competition theory predicts that less competitive species should decline and eventually disappear. We provide evidence supporting the theory that low pore connectivity caused by low water potential (and therefore low water content) increases the diversity of a complex bacterial community in soil. We altered the pore connectivity of a soil by decreasing water potential and increasing the content of silt- and clay-sized particles. Two textures were created, without altering the chemical properties or mineral composition of the soil, by adding silt- and clay-sized particles of quartz to a quartz-based sandy soil at rates of 0% (sand) or 10% (silt+clay). Both textures were incubated at several water potentials, and the effect on the active bacterial communities was measured using terminal restriction fragment length polymorphism (TRFLP) of bacterial 16S rRNA. Bacterial richness and diversity increased as water potential decreased and soil became drier (P < 0.012), but they were not affected by texture (P > 0.553). Bacterial diversity increased at water potentials of ≤2.5 kPa in sand and ≤4.0 kPa in silt+clay, equivalent to ≤56% water-filled pore space (WFPS) in both textures. The bacterial community structure in soil was affected by both water potential and texture (P < 0.001) and was correlated with WFPS (sum of squared correlations [δ²] = 0.88, P < 0.001). These findings suggest that low pore connectivity is commonly experienced by soil bacteria under field conditions and that the theory of pore connectivity may provide a fundamental principle to explain the high diversity of bacteria in soil.

Soil bacteria are among the most diverse groups of organisms on earth (47), and 4 × 10⁶ taxa may coexist in a single tonne of soil (13). One of soil ecology's most intriguing puzzles is how so many different bacterial species can coexist when competition theory predicts that less competitive species should decline and eventually disappear (45). Many mechanisms have been proposed to explain the extraordinarily high diversity of bacteria in soil, including high mutation rates, trophic interactions, temporal change in environmental conditions, and spatial heterogeneity, but the causes remain unclear (27). It has been suggested that soil ecology lacks a set of unifying principles to explain ecological interactions in this habitat, including high bacterial diversity (4). Others have observed that for soil ecologists to develop a set of fundamental theories to explain ecological interactions in soil, they must first identify common properties of the soil habitat (22, 52). A recently proposed theory links a physical property common to many soils, low pore connectivity, to the high bacterial diversity of this habitat (44).

The theory of pore connectivity predicts that bacterial diversity is increased by low water potential (low water content) and high silt and clay content (44). Under these conditions, the water-filled pores in which active bacterial communities exist are poorly connected to each other by thin, tortuous water films, decreasing bacterial motility and decreasing the rate of substrate diffusion by 1 to 4 orders of magnitude compared to the rates in bulk liquids (31, 38). Low pore connectivity in soil may hinder the capacity of competitive organisms to decrease substrate availability to competitors and create opportunities for diffusional and spatial “sheltering” of less competitive organisms (30, 48). In modeling studies of bacterial competition, slow diffusion of substrates and low motility were thought to explain the coexistence of competing bacteria on rough surfaces (30, 31) and in solid foods (17). The theory of pore connectivity may provide a fundamental theory to explain the high diversity of bacteria in soil.

There is evidence to support the prediction of pore connectivity theory that when water potential decreases (i.e., soil becomes drier), bacterial diversity increases. Field studies using rRNA cloning approaches have shown that bacterial communities in unsaturated surface soils had higher evenness than those in saturated subsurface soils, which were dominated by a few species (54, 56). In an artificial soil matrix containing a single substrate, two bacterial species were able to coexist at low water potentials (dry soil) but not at high water potentials (48). In a model system which mimicked soil, slower substrate diffusion improved the survival of noncompetitive species (16). However, the effect of water potential on bacterial diversity has not been tested in a soil collected from the field and having a complex bacterial community and a variety of naturally occurring substrates.

Fewer studies have examined the hypothesis that bacterial diversity is increased by increasing the content of silt- and clay-sized particles. Studies have used terminal restriction fragment length polymorphism (TRFLP) to show that bacterial richness was higher in the clay-sized fraction than the sand-sized fraction (37, 41, 47). However, the size fractions may have influenced bacterial communities because they had different chemical properties or were composed of different mineral types, which is known to alter bacterial community structure in soil (9). To test the hypothesis that bacterial diversity is increased by increasing the content of silt- and clay-sized particles in soil, it would be necessary to alter soil texture without altering its chemical properties or mineral composition.

In this study, we tested two hypotheses based on the theory of pore connectivity, these being that the diversity of a complex, indigenous bacterial community in soil is increased by (i) decreasing water potential (decreasing water content) and (ii) increasing the content of silt- and clay-sized particles. Silt-and clay-sized particles of quartz were added to a quartz-based sandy soil at rates of 0% (sand) or 10% (silt+clay). Each texture was incubated for 7 days at water potentials between −1.0 kPa (high water content, pores of <306 μm are water filled) and −6.0 kPa (low water content, pores of <51 μm are water filled). The effects of water potential and texture on bacterial diversity and structure were assessed using TRFLP of bacterial 16S rRNA. TRFLP based on RNA may more accurately reflect the active component of the bacterial community than that based on DNA because RNA transcription is correlated to microbial activity (21, 28, 51).

MATERIALS AND METHODS

Soil.

Soil was collected from the 0- to 10-cm layer of an Albic Arenosol (20) with parent material of wind-blown siliceous marine sand (33). The 0- to 10-cm layer (<2 mm) had 99% sand, 1.0% organic carbon (vario Macro CNS; Elementar, Germany), and a pH of 5.8 (water), and the mineral particles in the soil were >99% quartz. Because the soil was composed of >99% quartz, it was possible to modify its texture using quartz particles without altering the mineral composition of the soil or its chemical properties. The site had been planted with Eucalyptus maculata for 8 years and was previously a managed pasture. Prior to incubation, the soil was sieved (<2 mm), adjusted to 10% water content (wt/wt), and preincubated for 5 days at 24°C in plastic bags that enabled gas diffusion.

Incubation.

The incubation experiment consisted of two factors, texture and water potential. The two texture treatments were 0% silt+clay (sand) and 10% silt+clay (silt+clay) and were achieved by mixing the quartz-based sandy soil with quartz particles that were either sand sized or silt and clay sized. Quartz was used to alter the texture of the soil without altering its chemical properties (34, 50) or its mineral composition, as this is known to influence the structure of the bacterial communities (10). The silt+clay treatment consisted of soil with ground quartz added at the rate of 10% (wt/wt). The ground quartz was 51% clay-sized particles (0.5 to 2 μm) and 49% silt-sized particles (2 to 10 μm) (silicon dioxide; Sigma-Aldrich). The sand treatment consisted of soil with sand-sized particles of quartz (>106 μm, 99.9% SiO₂; Rocla Quarry Products, Australia) added at the rate of 10% (wt/wt). Since both textures contained the same proportion of soil, they contained the same concentrations of soil, organic matter, and soil bacteria. Before being mixed with soil, the sand-sized quartz and silt- and clay-sized quartz were sterilized by autoclaving three times at 121°C for 20 min to ensure that they were not a source of microorganisms.

A hanging water column (14, 26) was used to create soil with a spectrum of pore connectivity from highly connected to spatially isolated. The two textures were packed into columns made from polyvinyl chloride (PVC) pipe 55 cm in length and with an inner diameter of 2.8 cm. To allow soil to be sampled from 5-cm lengths of each column, they were constructed by connecting 5-cm segments of pipe. A 20-μm porous membrane (air entry value, >2.5 m) was sealed into the base of each column to prevent air invasion. An outlet at the base of each column was connected to a free water reservoir by flexible tubing from which all the air had been removed. The bulk density of each texture was kept constant by packing the same weight of soil into each segment of the columns. Sand was packed to achieve a constant bulk density in each segment of 1.49 g cm⁻³, and silt+clay to a bulk density of 1.65 g cm⁻³. The bulk densities of the textures differed from each other as a consequence of their different textures (50), and it was not possible to increase the bulk density of the sand or decrease the bulk density of the silt+clay. The bulk density of each segment was not significantly affected by its position in the column (P = 0.571).

Water potential treatments were achieved by controlling the height of the water reservoir connected to the soil column. The water reservoir was initially held level with the top of the soil column until soil was saturated from below and was then lowered to 10 cm below the base of the soil column. Under these conditions, the potential applied to the soil water ranged from −1.0 kPa (wet) at the base of the soil column to −6.5 kPa (dry) at the top of the soil column. Applying a potential to soil water ensured that water was always located in the smallest pores, which was essential to obtain soils along a gradient of pore connectivity. It also made it possible to calculate the size of the largest pore that contained water and to identify the critical pore size where bacterial diversity decreased. As water potential decreased from −1.0 kPa to −6.5 kPa, water was sequentially drained from smaller pores. Therefore, in the segment at the base of the column (wet), only pores of >306 μm were drained, and in the segment at the top of the column (driest), all pores of >51 μm were drained.

The soil columns were incubated at 25°C for 7 days to decrease the possibility of soils becoming anaerobic. At the end of the incubation, the segments in the columns were separated from each other while still containing soil. In total, there were eight replicate soil columns. From all eight replicates, the moist soil in each segment was weighed, after which 10 g of soil was dried at 105°C and used to calculate the gravimetric water content and bulk density. From four replicate soil columns, subsamples of soil were immediately frozen with liquid nitrogen for extraction of nucleic acids.

Water release curve and pore size distribution.

To determine the water release curves, the volumetric water content (cm³ cm⁻³) was calculated for eight replicates of each water potential using the gravimetric water content of soil and the volume of the segment. The replicates of volumetric water content at each potential were used to fit water release curves to each texture with the equation θ = r + {(s − r)/[1 + (a·h)ⁿ]^{(1 − 1/n)}}, where θ is the volumetric water content of soil (cm³ cm⁻³), h is the potential applied to soil water (cm), and r, s, a, and n are constants (listed in Results) (49). The pore size distributions were calculated from the water release curves and the Kelvin equation. First, the volume of water released with each 0.5-kPa decrease in water potential was calculated from the water release curves. Then, the Kelvin equation was used to determine the size of the pores from which the volume of water was removed. The Kelvin equation, or capillary law for perfectly wettable soils, describes the constant relationship that exists between the water potential applied to a soil and the size of the largest pore containing water and reduces to the following equation: diameter of the largest water-filled pore (μm) = 300/water potential (kPa).

Scanning electron microscopy was used to visualize the differences in the pore structure of the two textures. Each texture was packed into a column 13.5 mm long and 7 mm in inner diameter and embedded in resin. Embedding was achieved by slowly passing solutions through each column according to the following protocol. Initially, columns were dehydrated using acetone at 70% (3 changes over ∼24 h), 90% (∼12 h), and 100% (2 changes over ∼24 h). The columns were then infiltrated with increasing concentrations of Araldite resin (Proscitech) in acetone at 33% (∼12 h), 66% (∼12 h), and 100% (∼12 h under vacuum without resin accelerator). The columns were then placed in fresh 100% resin (∼60 h under vacuum with accelerator) and then oven polymerized at 60°C for 36 h. (Note that all resin was degassed under vacuum without accelerator for ∼60 h prior to use.) Polymerized columns were then cut in transverse sections to a thickness of ∼4 mm and then reembedded in aluminum support rings with Araldite resin such that the transverse face of the column was presented for polishing. Grinding and polishing were achieved using increasing grades of SiC paper (to 4,000 grit; Struers), followed by diamond suspensions (to 1 μm, MD-Nap; Struers), respectively. The polished columns were then coated with ∼30 nm of carbon (Speedivac; Edwards) prior to imaging with a scanning electron microscope (JEOL 6400) at 15 keV.

Bacterial diversity and community structure analyses using 16S rRNA-TRFLP.

Total soil RNA was extracted from soil incubated at 6 water potentials in each texture with four replicates of each. To ensure that RNA was extracted from soil at a range of water contents for each texture, RNA was extracted from sand incubated at −1.5, −2.0, −2.5, −3.0, −4.0, and −5.5 kPa and from silt+clay incubated at −1.5, −2.5, −3.5 −4.0, −4.5, and −5.5 kPa. The extraction and reverse transcription of RNA were performed using the method of Griffiths et al. (25) with slight modifications as follows. Soil was lysed for 2 min, and nucleic acids were pelleted by centrifugation at 16,000 × g for 15 min and resuspended in H₂O. DNA was digested by adding 1 μl DNase (1 U μl⁻¹; Promega) and 1 μl of the supplied reaction buffer to 8 μl of nucleic acids and incubating at 37°C for 30 min. One microliter of RNA was denatured by mixing with 0.5 μl of the primer 926r (100 μM) and 13.5 μl H₂O and heating to 70°C for 5 min. This mixture was added to a reaction mixture containing 1.25 μl 10 mM deoxynucleoside triphosphate mix, 2.5 μl 10× KCl buffer (Bioline), 0.25 μl avian myeloblastosis virus reverse transcriptase (10 U μl⁻¹; Promega), and 6 μl H₂O. Reverse transcription was carried out at 50°C for 30 min, followed by 5 min at 95°C.

PCRs were performed in duplicate using 2 μl of cDNA diluted 1:10 in a 50-μl reaction mix (24), the PCR conditions of Sessitsch et al. (40), and the primer set 8f (AGAGTTTGATCCTGGCTCAG) and 926r (CCGTCAATTCCTTTRAGTTT) (29). The forward primer was labeled with the fluorescent dye FAM (6-carboxyfluorescein). After amplification, 5 μl of purified PCR product (Wizard SV gel and PCR cleanup system; Promega) was quantified on a 2% agarose gel using Total Lab (Nonlinear Dynamics, United Kingdom). Aliquots containing approximately 100 ng of PCR product were restricted using 20 units of HhaI (Promega, United States) according to the manufacturer's instructions (29). Digests were incubated at 37°C for 3 h and were subsequently desalted.

The lengths of the terminal restriction fragments (T-RFs) were determined by electrophoresis using a capillary electrophoresis system (Applied Biosystems). Profiles were generated for each sample based on the relative heights of the peaks which indicated the relative abundance of that T-RF within the sample. T-RFs were assigned to phylotypes using the program RiboSort (39) and the statistical software R (36) (both available free from www.cran.r-project.org). T-RFs in different profiles that differed by less than 0.5 bp were considered identical (19). For each sample, bacterial TRFLP profiles were standardized by total fluorescence and fragments contributing <0.1% to the total fluorescence of that sample were removed and the samples standardized again. Applying a relative abundance threshold of 0.1% has been shown to result in strong correlations between true community diversity and that estimated from TRFLP data (7) without altering ordination plots (5). The richness, evenness, and diversity of bacterial TRFLP profiles were determined using the following indices described by Blackwood et al. (7): richness (S), Shannon effective richness (e^H′), Shannon's diversity index (H′), Simpson's index (1/D), and Shannon evenness (J′).

Statistical analysis.

The experiment consisted of two factors: water potential and texture. Two-way analysis of variance (ANOVA) was used to determine whether water potential and texture significantly affected indices of bacterial community diversity. To determine whether water potential and texture affected bacterial TRFLP profiles, multivariate statistical analyses were performed in Primer 6 (Primer-E Ltd., United Kingdom). Multivariate analyses of bacterial TRFLP profiles were performed on data that had been standardized by total fluorescence and 4th root transformed. Fourth-root transformation was chosen to balance the advantages of using untransformed data, which preserves relative abundance information, and binary data, which down-weights abundant groups (43). Bray-Curtis similarity was used as a measure of similarity because, unlike some other measures of similarity, it is not affected by ribotypes that are jointly absent between samples, which is common in TRFLP data (11).

To visualize the effects of water potential and texture on TRFLP profiles, ordination plots were constructed using nonparametric multivariate multiple regression (DISTLM) (2) and distance-based redundancy analysis (dbRDA) (32). In DISTLM, the variation in bacterial communities was explained and modeled using all specified soil variables without covariance. dbRDA was then used to construct an ordination plot of the variation in bacterial communities modeled by soil variables in DISTLM. dbRDA plots are constrained ordinations of the fitted values from a multivariate regression model. The soil variables used in the DISTLM and dbRDA were water-filled pore space (percentage of total pore volume), silt+clay content (% [wt/wt]), porosity (cm³ cm⁻³), largest water-filled pore (μm), and volume of water contained in pores in the size ranges 56 to 61 μm, 61 to 68 μm, 68 to 77 μm, 77 to 88 μm, 88 to 102 μm, 102 to 122 μm, 122 to 153 μm, and 153 to 204 μm (water volume as percentage of total pore volume).

To determine whether the effects of water potential and texture on bacterial TRFLP profiles seen in the dbRDA were significant, permutational multivariate analysis of variance (PERMANOVA) was performed (1). PERMANOVA constructs an F ratio from sums of squared distances within and between groups that is analogous to Fisher's F ratio (1). Pairwise comparisons were performed to determine whether bacterial communities differed significantly (P < 0.05) between different water potentials. To provide a further test of the theory of pore connectivity, we used canonical correlation analysis to determine the extent of the relationship between bacterial community structure and WFPS. Unlike water potential, whose relationship with connectivity differed between the two textures, WFPS provided a single variable that indicated the degree of pore connectivity in both textures. Canonical correlation analysis finds the canonical axis that maximizes the relationship with a quantitative environmental variable (in this case, WFPS). The significance of the relationship was assessed using the sum of squared correlations (δ²) and obtaining a P value by permutation (3).

RESULTS

Water release curve and pore size distribution.

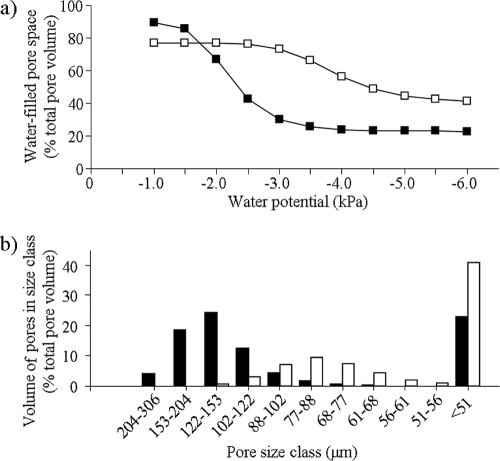
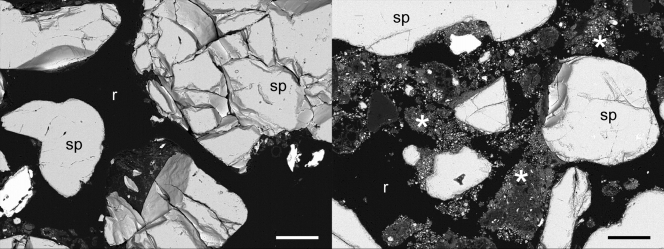
The water release curve fitted to sand had the following constants: s = 0.39, r = 0.10, a = 0.05, and n = 7.22. The constants for silt+clay were s = 0.29, r = 0.15, a = 0.03, and n = 8.49. Between water potentials of −1.0 and −6.0 kPa, the water-filled pore space (WFPS, % total pore volume) decreased from 90 to 23% in sand and from 77 to 41% in silt+clay (Fig. 1 a). The pore size distributions show that pores of <102 μm were 30% of the total pore volume in sand and 73% of the total pore volume in silt+clay (Fig. 1b). Scanning electron micrographs show the differences in particle and pore size in sand and silt+clay (Fig. 2).

FIG. 1.

Fitted water release curves (a) and pore size distributions (b) for sand (▪ and black bars) and silt+clay (□ and white bars). Water release curves show the water-filled pore space at each water potential. Pore size distributions show the percentage of total pore volume occupied by each pore size class. At a given water potential, pores in the corresponding size class and all smaller pores contain water.

FIG. 2.

Back-scattered scanning electron micrographs demonstrating the variation in particle and pore size in sand (left) and silt+clay (right). Sand-sized quartz particles (sp) are visible in both treatments, while ground quartz particles (indicated with an asterisk) are only present within the resin (r)-infiltrated pore spaces in silt+clay. Scale bars = 100 μm.

Bacterial community diversity and structure analyses using TRFLP.

Water potential affected the richness (S, e^H′) and diversity (H′, 1/D) of bacterial communities (P <0.012), but texture did not (P > 0.553). In both textures, the richness and diversity of bacterial communities was higher at WFPS values of <56% (dry) than at WFPS values of >56% (wet) (Table 1). In terms of water potential, this corresponded to higher richness (S, e^H′) and diversity (H′, 1/D) of bacterial communities in sand at −2.5 kPa (43% WFPS, all pores <122 μm are water filled) than at −2.0 kPa (67% WFPS). In silt+clay, the richness values (S, e^H′) of bacterial communities were significantly higher at −4.0 kPa (49% WFPS, all pores of <76 μm are water filled), −4.5 kPa, and −5.5 kPa than at −2.5 kPa (76% WFPS) and their diversity (1/D) was significantly higher at −4.5 than at −2.5 kPa.

TABLE 1.

Mean richness, evenness, and diversity values of bacterial RNA TRFLP profiles following incubation in sand and silt+clay^a

Texture	Water potential (kPa)	WFPS (% pore vol)	S	eH′	H′	1/D	J′
Sand	−1.5	90	105	58	4.05	43	0.871
	−2.0	69	102	56	4.03	40	0.870
	−2.5	40	116	73	4.28	54	0.901
	−3.0	33	115	66	4.18	47	0.882
	−4.0	26	112	66	4.19	47	0.888
	−5.5	21	119	71	4.26	50	0.891
Silt+clay	−1.5	78	101	60	4.09	46	0.886
	−2.5	74	100	56	4.03	42	0.875
	−3.5	67	107	65	4.17	50	0.892
	−4.0	56	111	70	4.24	54	0.901
	−4.5	48	111	71	4.25	55	0.903
	−5.5	42	118	70	4.24	50	0.890
LSD			11	14	0.23	13	0.036

^aIncubations were performed at a range of water potentials whose corresponding mean WFPS values are shown. S, richness; e^H′, Shannon effective richness; H′, Shannon's diversity index; 1/D, Simpson's index; J′, Shannon evenness; LSD, least significant difference (P < 0.05). LSD was determined by two-way analysis of variance. WFPS, n = 8; TRFLP profiles, n = 4.

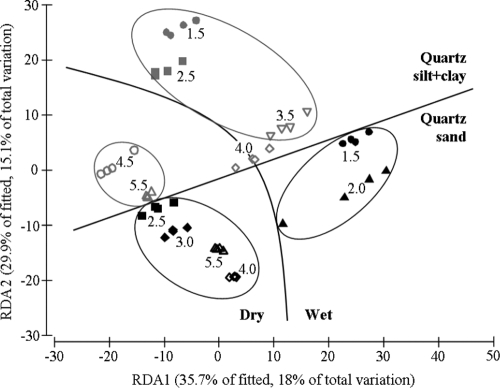
Both water potential and texture significantly affected the structure of bacterial communities (P < 0.001). A total of 381 bacterial T-RFs were identified across all samples. In dbRDA plots, bacterial communities clustered together into four groups depending on whether they were incubated in sand or silt+clay and whether they were incubated at water-filled pore spaces corresponding to dry or wet soil (Fig. 3). Separate clusters were formed by bacterial communities incubated in silt+clay at >4.0 kPa, silt+clay at <4.0 kPa, sand at −1.5 and −2.0 kPa, and sand from −2.5 to −5.5 kPa. At a significance level at a P of <0.05, there were no differences in bacterial communities within each of the four clusters except between those in silt+clay at −2.5 and −3.5 kPa (P = 0.017) and between those in sand at −2.5 and −4.0 kPa (P = 0.047). However, at a P value of <0.1, there were some differences within clusters, i.e., between bacterial communities in silt+clay at −1.5 and −3.5 kPa (P = 0.065) and between bacterial communities in sand at −2.5 and −5.5 kPa (P = 0.097). Between each of the four clusters, all bacterial communities differed at a P value of <0.05, with the exceptions of (i) bacterial communities in silt+clay at −3.5 kPa and in sand at −1.5 kPa (P = 0.217) or −2.0 kPa (P = 0.080) and (ii) those in silt+clay at −5.5 kPa and in silt+clay at −1.5 kPa (P = 0.082) and dry sand (−2.5 to −5.5 kPa, P > 0.095).

FIG. 3.

Distance-based redundancy analysis (dbRDA) of bacterial communities incubated in either sand (black symbols) or silt+clay (gray symbols, separated by straight line) at the water potentials (cm) shown by the values. Circles surround data for bacterial communities that did not differ from each other (P > 0.05). The curved line separates data for bacterial communities incubated in wet and dry soils (water-filled pore space more than or less than 56%, respectively). All pairwise comparisons across the curved line were significantly different (P < 0.05), except for silt+clay at −1.5 and −5.5 kPa, which did not differ. The soil variables used to generate the dbRDA were water-filled pore space (% total pore volume), silt+clay content (% [wt/wt]), porosity (cm³ cm⁻³), largest water-filled pore, and the volume of water in pore size classes 68 to 77 μm, 77 to 88 μm, 88 to 102 μm, 102 to 122 μm, 122 to 153 μm, and 153 to 204 μm. The values in parentheses indicate the percentages of the fitted and total variations explained by each axis.

Canonical correlation analysis revealed that bacterial community structure was significantly correlated with WFPS across both soil textures (δ² = 0.88, P < 0.0001). In silt+clay at −4.0 kPa, the water-filled pore space was 56% and bacterial communities were positioned centrally in the dbRDA plot. The bacterial communities in silt+clay at −4.0 kPa did not differ (P < 0.05) from those in either texture or any water potential except those in sand at −2.5 kPa (P = 0.038). However, at a P value of <0.1, the bacterial communities in this treatment differed from those in sand at −4.0 kPa (P = 0.082) and in silt+clay at −4.5 kPa (P = 0.074).

DISCUSSION

This study showed that low pore connectivity contributed to high bacterial diversity in soil. Using a 16S rRNA community fingerprinting approach, we showed that bacterial diversity in soil increased as water potential decreased (water content decreased) (Table 1). Previous studies have shown that the coexistence of different bacterial species is favored by low water potential (16, 17, 30, 31, 48). However, these studies measured competition between only two bacterial species for a single substrate and were either modeling studies (17, 30, 31) or laboratory studies using agar or artificial soil (16, 48). In contrast, we studied a complex, indigenous bacterial community in a field soil with a variety of naturally occurring substrates and found that decreasing water potential increased bacterial diversity. Further evidence for the theory of pore connectivity is provided by the finding that bacterial community structure was correlated to WFPS across both textures. In contrast with water potential, whose relationship with connectivity varies with soil texture, WFPS provides a single variable that indicates the degree of pore connectivity in soils with different textures. Previous field studies using rRNA cloning approaches showed that bacterial communities in saturated subsurface soils were dominated by a few species (competitive diversity pattern) and had lower evenness than those in unsaturated surface soils (55, 56). Our results suggest that as pore connectivity decreases, a bacterial community that displays a competitive diversity pattern can be shifted to one that lacks the same level of competition.

Greater bacterial diversity at low pore connectivity is likely to be mediated by a number of interacting factors which decrease the strength of competitive interactions and favor coexistence. In unsaturated soils, low water potential limits substrate diffusion to bacterial cells and can inhibit bacterial growth and activity. These conditions may hinder the capacity of more competitive bacteria to decrease the substrate availability for less competitive bacteria, allowing both to coexist (30, 48). Unsaturated soils can also limit bacterial movement, preventing highly motile bacteria from exploiting substrate-rich patches and protecting less motile species from competition and extinction.

The effects of low pore connectivity are likely to contribute to high bacterial diversity in soil under field conditions, where water potential (and water content) is usually <5 kPa (field capacity). In the present study, bacterial diversity increased when water potential was close to field capacity. In sand, bacterial diversity increased between water potentials of −2.0 and −2.5 kPa, i.e., when WFPS decreased from 69 to 40% and 122- to 153-μm pores became air filled (Table 1). In silt+clay, bacterial diversity increased between water potentials of −3.5 and −4.0 kPa, i.e., when WFPS decreased from 67 to 56% and 77- to 88-μm pores became air filled. These water potentials (and water contents) represent those most likely to occur in the field. A previous study showed that two bacterial species competing for a single substrate were able to coexist at −10 kPa but not at −8 kPa (48). In a simulation study, the relative motility of two bacterial species did not affect their coexistence at −100 kPa, but at ≥10 kPa, increasing the motility of the less competitive bacterium increased the time it coexisted with the more competitive species (31). In addition, the present study found that bacterial communities incubated at 56% WFPS (silt+clay at −4.0 kPa) were centrally positioned in the dbRDA plot (Fig. 3), and they did not differ significantly from most other bacterial communities. This suggests that the threshold at which water-filled pores in soil switch from being spatially isolated to highly connected occurs near 56% WFPS. These findings suggest that low pore connectivity is commonly experienced by soil bacteria under field conditions and contributes to their high diversity.

This study also found that bacterial community diversity was not higher in silt+clay than in sand, which does not support the theory of pore connectivity (Table 1). This may have been due to the relatively minor change in the soil textures that were compared. Although bacterial community diversity did not differ between textures, bacterial community structure differed significantly (Fig. 3), even without associated changes in the soil's chemical properties and mineral composition. Previous studies using TRFLP showed that bacterial communities associated with silt- and clay-sized soil particles had higher richness and different structures than those associated with sand-sized particles (37, 41, 47). However, in field soils, sand- and clay-sized particles are generally different mineral types, a factor which can alter the chemical properties of soil and has been shown to alter the structure of microbial communities in soil (10) and other microbial habitats (8, 23, 53). In this study, the soil texture was altered using mineral particles with the same composition as the mineral particles in soil (quartz). Thus, it was possible to attribute the effects of silt- and clay-sized particles on the structure of bacterial communities to their influence on physical properties of soil.

TRFLP has been widely used for the study of microbial community dynamics; however, indices of diversity and evenness of bacterial communities estimated from TRFLP profiles need to be interpreted with caution. TRFLP has been criticized as underestimating the true diversity of bacterial communities because different phylotypes can be represented by the same fragment length and because methods to remove “noise” from the data can delete rare species (6, 7, 18). In addition, biases may be introduced during DNA extraction and PCR amplification (12). Although the diversity of TRFLP profiles reported here is not interpreted as an exact prediction of true community diversity, relative abundance thresholds of 0.1% (as used in this study) have been shown to give higher correlations between the true diversity of the bacterial communities and estimates based on TRFLP (7) and to produce similar ordination plots (5) in comparison to the results for relative abundance thresholds of 0.5% and 1%. In this study, all samples were subject to the same biases and only relative (rather than absolute) data are presented. Additionally, it is likely that the proportion of technique-induced changes in diversity constitutes a relatively small proportion of the observed changes in diversity. It is also worth noting that molecular fingerprinting techniques represent a significant improvement in estimating diversity over culture-based techniques, which exclude >95% of soil microorganisms and alter selective conditions (15, 42, 46), and these techniques are useful for comparisons within an experiment (35).

We have demonstrated that low pore connectivity caused by low water potential (low water content) increased the diversity of a complex bacterial community in soil. Bacterial diversity was greater when water potential was less than field capacity (−5 kPa and <56% WFPS), suggesting that low pore connectivity increases bacterial diversity in most soils under field conditions. Future changes in climate may have implications for soil biodiversity since changing rainfall patterns will alter the frequency of periods of high pore connectivity, thus affecting competitive interactions between bacterial species. This study also demonstrated that texture influenced bacterial community structure (although not bacterial diversity) even when the change in texture was relatively small and when there was no change in the soil's mineral composition (and therefore its chemical properties). These findings show that bacterial diversity and community structure in soil are linked to the basic physical properties of the soil matrix and suggest that the theory of pore connectivity may contribute to a theoretical framework for soil ecology.