Abstract
Objective
During phonation, energy is transferred from the subglottal airflow through the air/mucosa interface which results in the propagation of the mucosal wave in the vocal fold. The vocal fold is soft, and the subglottal mucosa is stiff. We hypothesize that it is highly improbable that there is a rigid boundary between the tissue structures, with a sudden drop in stiffness; and that a gradual change would be more likely to support the efficient transfer of energy from the air-flow to the mucosal wave. Our objective is to test this hypothesis by quantifying the change in mucosa stiffness with respect to anatomical position.
Study Design
In this initial study, using 5 pig larynges, a series of point specific measurements of mucosa stiffness were taken in a line from the midpoint of the vocal fold towards the trachea.
Methods
A modified linear skin rheometer (LSR) adapted for laryngeal elasticity measurement applied shear stress to a series of 7 positions at 2mm intervals starting from the mid-membranous vocal fold medial surface. A sinusoidal shear force of 1g was applied at each point, and resultant displacement curve logged. Using a regression algorithm the stiffness of the tissue was derived in units of grams force per mm displacement. 5 readings were taken at each position.
Results
The results indicate that there is a linear increase in stiffness with respect to position, increasing as the measurements are taken further from the vocal fold.
Conclusion
There is a gradual change in stiffness of the subglottal mucosa of a pig larynx.
Keywords: mucosa, stiffness, mucosal wave, energy
INTRODUCTION
Energy derived from the subglottal air flow is required to power the oscillation of the vocal folds during phonation. To achieve this, the energy associated with the sub-glottic pressure transfers to the vocal fold soft tissue, by a complex process described by the cover-body theorem of Hirano. It is our hypothesis that there is a gradual change in tissue stiffness from the stiff mucosa inferior to the vocal fold to the substantially less stiff vocal fold. This gradation may support a more efficient transfer of energy across the air/tissue boundary, by supporting lamina as opposed to turbulent flow.
The physiology of phonation is best explained by Hirano’s cover-body theorem [Hirano 1985]. Hirano describes a process reliant on air-flow causing a drop in air pressure due to Bernoulli’s theorem. The soft vocal fold cover is pulled up, leading to closure that cuts of the airflow, enabling the tension in the underlying body to pull the cover back down. This process has been superbly modelled mathematically by Ingo Titze [Tize 1994], and forms the basis of our understanding of the dynamics of voice production today. What remains unknown is whether or not the sub-glottal mucosa also plays a role in this process, and there is recent evidence that this may the case from a study by Smith, Roy, Stoddard & Barton [Smith 2007] which examined the change in pitch in 14 female patients (mean age 53) following a cricotracheal resection. In all cases the mean fundamental frequency fell significantly, typically by 21Hz. Whilst this is most likely to have been caused by the transection of cricothyroid muscle, the removal of part of the sub-glottal mucosa may also be partly responsible for the resultant pitch reduction. Other evidence that the sub-glottal mucosa could be important for the dynamics of current myoelastic thinking is a study by Sundberg, Iwarsson & Billström [Sundberg, 1995], which determined that voice quality deteriorated after the anaesthetisation of the subglottal mucosa.
Visualisation of the subglottal region, and direct measurements of air pressure, during phonation are difficult and invasive. This may explain why this region, and its’ role in phonation, has been rarely studied. The subglottal mucosa will be subject to compression during closure, and will also be uplifted by the same aero-dynamic principles that apply to the vocal fold cover. Simply because it is almost impossible to visualise this region during phonation does not mean that it does not play a role in the overall process. As we are currently unable to visualise this region using stroboscopy or imaging without an invasive procedure, we must rely on inferring the biomechanical behaviour using other techniques. Using excised larynges it is possible to measure the elastic properties of the subglottal mucosa, but standard material methods such as a Bohlin parallel plate rheometer may not necessarily be able to determine differences in tissue elasticity with respect to anatomical position, and it is the variation of subglottal mucosa stiffness that is of importance for this study. Therefore we chose to use a Linear Skin Rheometer (LSR) which is able to take point specific measurements with respect to anatomical position, enabling us to determine the gradation in subglottal stiffness mucosa
In this initial study a series of point specific measurement of mucosa stiffness were taken using 5 excised pig larynges. 7 sets of 5 values were taken at 2mm intervals starting at the midpoint of the vocal fold in the mid-musculo-membranous portion inferior of the vocal fold. The results show that there is a linear relationship between distance from the vocal fold and tension. This supports our hypothesis that the energy transfer between the subglottal air flow through the tissue membrane to form the mucosal wave will be more efficient with a smooth transition. This observed phenomena will be examined in more detail in future studies using human larynges.
MATERIALS AND METHODS
5 freshly excised pig larynges were divided in the mid-sagittal plane to reveal the vocal folds. The pigs had been previously sacrificed for another study not involving the larynx. The larynges had been kept refrigerated for 4 days at 4 degrees C and were allowed to slowly warm up to room temperature. The study was carried at room temperature, and the surface of the larynges were kept moist using saline solution. They were mounted to ensure that there was no source of external tension. A Linear Skin Rheometer (LSR) was used to take a series of readings inferior to the vocal fold at 2mm intervals [Hess 2006, Goodyer 2007, Dailey 2007]. 5 readings were taken at each point, and the results averaged to obtain a mean value. The probe was attached using suction, with a 2mm ID cannula and a vacuum pressure of approximately 50mbar. A cyclical shear force of +-1g was applied to the probe such that it tensioned the mucosa in a transverse direction, being the same direction as the subglottal air flow. The experimental setup can be seen in figure 1. The displacement was logged, and the Dynamic Spring Rate (DSR) derived. The DSR is a measure of shear stiffness expressed as grams force required to achieve a displacement of 1 mm. For this study our interest is relative change in stiffness, therefore all results were normalised, with the stiffness at the mid-membranous point of the vocal fold defined as 1. The study was carried out post-mortem, which will result in different readings being obtained from a similar study carried out in-vivo. However as we are interested in determining the relative differences in tissue elasticity with respect to anatomical position, and not absolute values, we are of the opinion that any post-mortem changes will equally affect all sample points.
Figure 1.
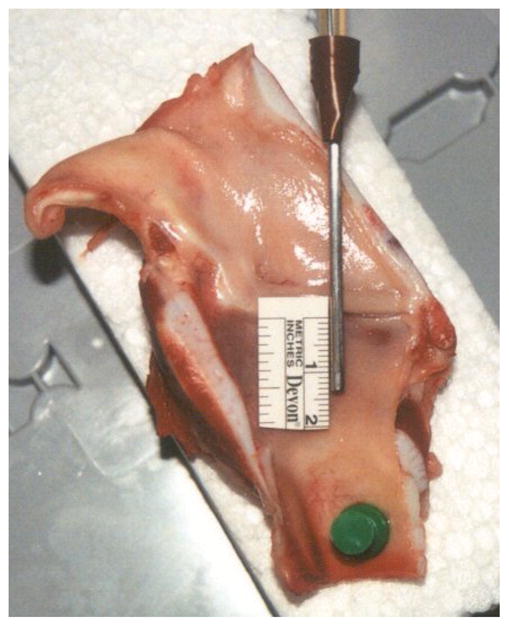
Experimental Setup showing attachment of measuring probe
RESULTS
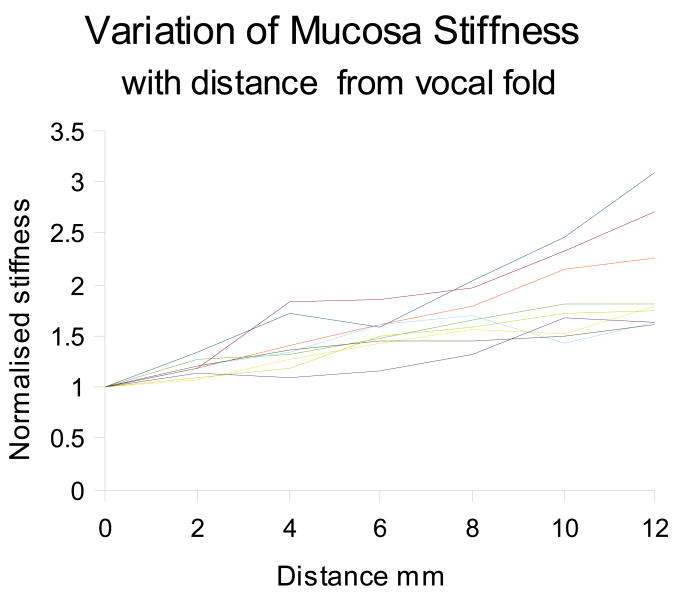
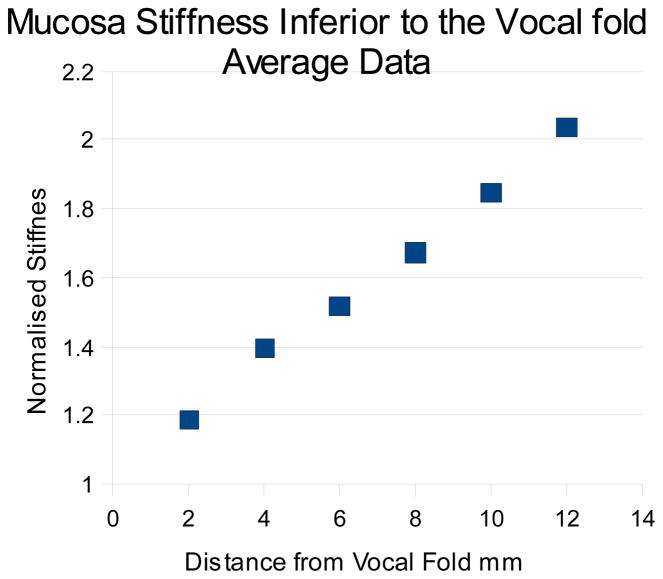
Usable data was obtained from 9 hemi larynges, and are given in table 1, the 10th hemi larynx was damaged during preparation. The results are expressed as normalised stiffness with respect to the reading obtained from the midpoint of the vocal fold. All data was obtained in a transverse direction. The results are also presented graphically in figure 2, and are averaged to produce the line shown in figure 3. For each hemi-larynx there are 7 test points, equally spaced by 2mm, and 5 measurands were taken at each point; giving a set of 35 data points in total for each side. The correlation coefficients (CC) obtained when comparing the left hand side data to the right hand side for the 4 larynges for which usable data was obtained from both sides are respectively –
Table 1.
Normalised shear stiffness with respect to distance from the vocal fold
| Distance mm | Hemi Larynx | Hemi Larynx | Hemi Larynx | Hemi Larynx | Hemi Larynx | Hemi Larynx | Hemi Larynx | Hemi Larynx | Hemi Larynx |
|---|---|---|---|---|---|---|---|---|---|
| Right 1 | Left 2 | Right 2 | Left 3 | Right 3 | Left 4 | Right 4 | Left 5 | Right 5 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1.34 | 1.19 | 1.07 | 1.26 | 1.18 | 1.21 | 1.21 | 1.1 | 1.13 |
| 4 | 1.72 | 1.42 | 1.28 | 1.31 | 1.84 | 1.33 | 1.36 | 1.18 | 1.09 |
| 6 | 1.6 | 1.6 | 1.42 | 1.46 | 1.86 | 1.61 | 1.46 | 1.49 | 1.16 |
| 8 | 2.03 | 1.78 | 1.55 | 1.66 | 1.96 | 1.7 | 1.46 | 1.59 | 1.32 |
| 10 | 2.47 | 2.15 | 1.52 | 1.81 | 2.34 | 1.44 | 1.5 | 1.72 | 1.68 |
| 12 | 3.1 | 2.27 | 1.8 | 1.82 | 2.71 | 1.63 | 1.62 | 1.74 | 1.64 |
Figure 2.
Variation of mucosa stiffness with respect to distance from the vocal fold
Figure 3.
Mucosa stiffness inferior to the vocal fold
larynx 2 CC of 0.95
larynx 3 CC of 0.93
larynx 4 CC of 0.91
larynx 5 CC of 0.89
Where a CC of 1 is a perfect match.
If we define the stiffness at the vocal fold as 1, the mean stiffness increases linearly with distance from the vocal fold such that is doubles to 2 after approximately 12mm.
DISCUSSION
The data clearly shows that there is a relationship between mucosa stiffness and distance from the vocal fold, thus supporting our original hypothesis. The CC results give us a high degree of confidence in the data. The averaged data shown in figure 3 implies that this relationship is linear, but this cannot be determined from such a small sample as is demonstrated by the spread of slopes observed in the graph in figure 2.
According to Wyke and Kirchner [Wyke 1976] mechanoreceptors in the subglottal mucosa play a significant role in the control of laryngeal muscle activity in response to changes of subglottal pressure during phonation. Sundberg’s study confirmed that voice quality deteriorated when this region is anaesthetised, thus impairing the operation of the mechanoreceptors. The implication of this study is that scarring of the mucosa inferior to vocal fold could result in poor energy transfer into the vocal fold, resulting in a weaker mucosal wave. This would explain why the mechanoreceptors described by Wyke are important, in that they are are used to sense the transfer of energy from the subglottal airflow into the vocal fold in advance of the mucosal wave. Further evidence to support this hypothesis can be found in the study by Smith which demonstrated that the resection inherently changes the dynamic biomechanical processes of the larynx. In addition the removal of part of the gradated mucosa, and the resultant scar, could both contribute to a lessened ability to transfer energy from the subglottal airflow into the mucosa wave. Less energy will result in a lower frequency.
Another point of interest is the shape of the subglottal mucosa during the myoelastic cycle. By applying a simple mathematical model of the extension of the subglottal mucosa when subjected to the uplift due to the air flow we can make a reasonable prediction. The basis of this model is the standard Young’s Modulus formulae for extension.
| 1 |
| 2 |
| 3 |
where
x = extension
L = initial thickness of the mucosa
E = Young’s Modulus
F = Force
A = the surface area that the force acts over
P = the uplift pressure
The purpose of this model is to predict the shape of the mucosa due to a drop in pressure, therefore we are not attempting to derive any absolute values at this time. In the absence of any aerodynamic models for the uplift pressure in the subglottal region we can only assume that is it constant over the surface. If we define the the stiffness at the vocal fold as 1, and the stiffness 12mm inferior as 2, the change in stiffness and length is given by
| 4 |
| 5 |
| 6 |
Where
Ey is the Young’s Modulus at a distance y from the vocal fold
y is the distance from the vocal fold in mm
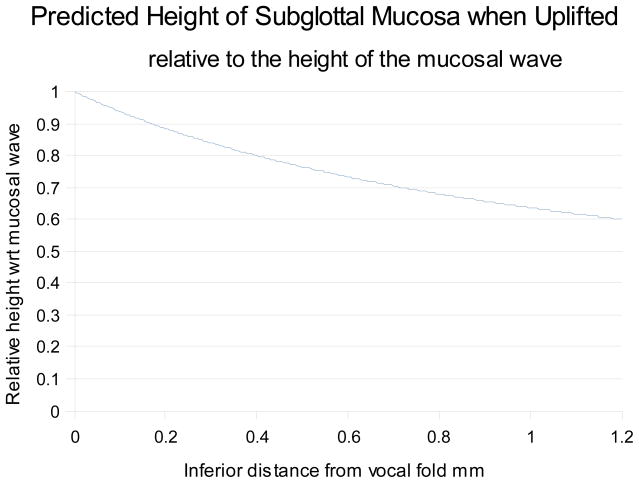
If we assume an initial thickness of 1mm we can predict the resultant shape under uplift pressure in terms of relative change. This shape is shown in figure 4. Of interest is the curve shape that gradually compresses the airflow as it approaches the vocal fold, and will thus be more likely to produce lamina flow over the vocal fold itself.
Figure 4.
Predicted shape of the subglottal mucosa when uplifted
It would therefore be of interest for a future study to determine if there is a relationship between dysphonia and scarring in this region. It is also necessary to widen the study to use more larynges, and to carry out a similar study with donor human tissue. If it is demonstrated that subglottal scarring impairs energy transfer into the mucosal wave, then this region could benefit from current research examining tissue engineering and augmentation techniques being developed for the vocal fold itself.
CONCLUSION
There is a linear relationship between mucosa tension and distance from the vocal fold; with stiffness increasing towards the trachea in pig larynges. The purpose of this gradation remains unknown. Our theory is that it enhances the probability of lamina flow in this region, and is necessary to ensure an efficient transfer of energy from the air-flow into the vocal fold. This theory requires more in depth study.
As this study was carried out using pig larynges, not human, the study needs to be repeated using human larynges to determine if the theory also applies to human phonation.
Acknowledgments
This project received financial support from the Engineering Physics & Science Research Council (EPSRC) of Great Britain EP/E04087X/1, The Royal Academy of Engineering and The National Institutes of Health (NIH) 5R01DC004428-07.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Dailey SH, Tateya I, Montequin D, Welham N, Goodyer EN. Viscoelastic Measurements of Vocal Folds Using the Linear Skin Rheometer (LSR) Journal of Voice (on-line) 2007 May; doi: 10.1016/j.jvoice.2007.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodyer EN, Hemmerich S, Muller F, Hess M. The shear modulus of the human vocal fold, preliminary results from 20 larynges. European Archives of Oto-Rhino-Laryngology. 2007;264:45–50. doi: 10.1007/s00405-006-0133-8. [DOI] [PubMed] [Google Scholar]
- Hirano M, Kakita Y. In: Cover-body theory of vocal fold vibration. Daniloff RG, editor. Speech Science; San Diego: 1985. [Google Scholar]
- Hess M, Muller F, Kobler JB, Zeitels S, Goodyer EN. Measurements Of Vocal Fold Elasticity Using The Linear Skin Rheometer. Folia Phoniatrica. 2006 April;58(3):207–216. doi: 10.1159/000091734. [DOI] [PubMed] [Google Scholar]
- Smith ME, Roy N, Stoddard K, Barton M. How does cricotracheal resection affect the female voice? Annals of Oto Rhino Laryngology. 2008 Feb;117(2):85–9. doi: 10.1177/000348940811700202. [DOI] [PubMed] [Google Scholar]
- Sundberg J, Iwarsson J, Billström AH. Significance of mechanoreceptors in the subglottal mucosa for subglottal pressure control in singers. Journal of Voice. 1995 Mar;9(1):20–6. doi: 10.1016/s0892-1997(05)80219-x. [DOI] [PubMed] [Google Scholar]
- Titze IR. Principles of voice production. Prentice-Hall, NJ; Englewood Cliffs, NJ: 1994. [Google Scholar]
- Wyke B, Kirchner J. Neurology of the larynx. In: Hinchcliffe R, Harrison D, editors. Scientific foundation of otolaryngology. London: William Heinemann Medical Books; 1976. pp. 546–66. [Google Scholar]