Auditory Sensitivity to Formant Ratios:Toward an Account of Vowel Normalization

Abstract

A long-standing question in speech perception research is how do listeners extract linguistic content from a highly variable acoustic input. In the domain of vowel perception, formant ratios, or the calculation of relative bark differences between vowel formants, have been a sporadically proposed solution. We propose a novel formant ratio algorithm in which the first (F1) and second (F2) formants are compared against the third formant (F3). Results from two magnetoencephelographic (MEG) experiments are presented that suggest auditory cortex is sensitive to formant ratios. Our findings also demonstrate that the perceptual system shows heightened sensitivity to formant ratios for tokens located in more crowded regions of the vowel space. Additionally, we present statistical evidence that this algorithm eliminates speaker-dependent variation based on age and gender from vowel productions. We conclude that these results present an impetus to reconsider formant ratios as a legitimate mechanistic component in the solution to the problem of speaker normalization.

Introduction

The perceptual and biological computations responsible for mapping time-varying acoustic input onto linguistic representations are still poorly understood (Fitch et al. 1997; Hickok and Poeppel 2007; Phillips 2001; Scott and Johnsrude 2003; Sussman 2000). The speech signal includes not only the content of an utterance but also cues that allow listeners to infer sociolinguistic and physical characteristics about the speaker (Ladefoged and Broadbent 1957). These cues, however, also serve to introduce significant variation, obscuring any straightforward one-to-one mapping between acoustic features and phonetic or phonological representations. Some of the most compelling demonstrations of this variability in the speech signal have been presented in acoustic analyses of vowel distributions across different talkers (Peterson and Barney 1952; Potter and Steinberg 1950). Given their tractable nature and well-understood spectral properties, vowels have played a central role in understanding the mechanisms that underlie speaker variation and normalization (Rosner and Pickering 1994). The primary acoustic characteristic of spoken vowels is their formants: resonant frequencies of particular vocal tract configurations superimposed on the harmonic resonances of the glottal pulse source during production (Fant 1960). Within speakers, the first (F1) and second (F2) formants are the principal determinants of vowel type—F1 varies as a function of vowel height and F2 varies as a function of vowel backness (the third formant (F3) primarily cues rhoticity, Broad and Wakita 1977). F1 and F2 can secondarily be affected by other articulatory gestures, such as tongue root position and lip posture (Stevens 1998).

While the relative pattern of formants remain approximately constant across speakers for a given vowel type (Potter and Steinberg 1950), the absolute formant frequencies for a given vowel token vary as a function of vocal tract length (Huber et al. 1999). Using magnetic resonance imaging of the vocal tract, Fitch and Giedd (1999) demonstrate that vocal tract length positively correlates with age, and within adults, gender. Despite these differences, however, listeners are quite good at recognizing phonemes across a number of different speakers (Strange et al. 1983), and can reliably categorize vowel tokens synthesized with varied vocal tract lengths, both within and outside the normal range (Smith et al. 2005) and, furthermore, can estimate speaker size from modulations of vocal tract length with a minimal amount of speech input (Ives et al. 2005; Smith and Patterson 2005). It seems, then that auditory cortex segregates the incoming speech signal into information that allows listeners to recover both the vocal tract size (formant scales) and vocal tract shape (formant ratios) contemporaneously with one another (Irino and Patterson 2002; Smith et al. 2005). In addition to this ability to cope with significant variation due the physical characteristics of a talker, listeners can reliably identify the sociolinguistic background of a speaker with as little information as `hello', as has been documented in cases of housing discrimination (Purnell et al. 1999). Moreover, prelinguistic infants ignore speaker-dependent acoustic variation and successfully categorize vowels across different talkers (Kuhl 1979, 1983). Thus, whatever normalization procedures are available to listeners are deployed without significant linguistic experience or exposure to novel speakers, and consequently, accumulating a large amount of speaker-dependent information is unnecessary to adequately normalize across speakers. In order for a vowel normalization algorithm to be plausible, it must, at least, normalize the vowel space and be computable by the auditory system during online speech perception.

Recent functional neuroimaging and electrophysiological work has identified different cortical networks subserving the processing separation of speaker dependent (“who” is speaking) from speaker invariant (“what” is being said) features in vowel perception (Bonte et al. 2009; Formisano et al. 2008). Specifically, Formisano, et al. (2008) showed that the cortical networks responsible for distinguishing vowel categories independent of speaker were more bilaterally distributed in superior temporal cortex and involved the anterior-lateral portion of Heschl's gyrus, planum temporale (mostly left lateralized) and extended areas of superior temporal sulcus (STS)/superior temporal gyrus (STG) bilaterally. In contrast, the networks underlying speaker identification independent of vowel category were far more right lateralized and included the lateral part of Heschl's gyrus and three regions along the anterior-posterior axis of the right STS that were adjacent to areas in vowel discrimination. The conclusion that the neurobiology segregates the processing of speaker and vowel are consistent with recent perceptual learning (McQueen et al. 2006; Norris et al. 2003) and neurophysiological work (see Obleser and Eisner 2009) arguing that listeners construct abstract prelexical representations of phonological categories that are independent of particular speakers and that episodic traces (e.g., Bybee 2001; Goldinger 1996; Johnson 1997, 2005; Pierrehumbert 2002; Pisoni 1997) cannot be the only representational schema employed in speech perception.

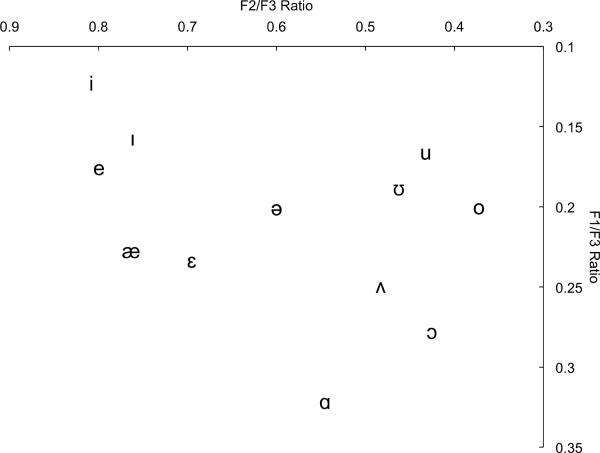
The primary goal of this paper is to revisit an idea that has received sporadic attention within the literature in attempting to solve the speaker normalization problem: formant ratios, or the calculation of relative log differences between formants in vowel perception (Lloyd 1890; Miller 1989; Peterson 1951, 1961; Potter and Steinberg 1950; Syrdal and Gopal 1986; see Johnson 2005 for criticisms). We pursue here a specific instantiation of formant ratios: namely, information in higher formants, specifically the third formant (F3), acts as the normalizing factor (Deng and O'Shaughnessy 2003; Peterson 1951). (Insert Figure 1 about here.) A consequence of this proposal, then, is that the appropriate dimensions for the vowel space are the ratios F1/F3 and F2/F3 (or logarithmic-like transforms of these quantities, such as Mel (Stevens and Volkmann 1940) or Bark (Zwicker 1961) difference scores) as opposed to the traditional F2 by F1 vowel space. In this article, we calculate the extent to which this particular hypothesis (F1/F3 by F2/F3) removes inter-speaker variation based on age and gender of the talkers from the Hillenbrand, et al. (1995) corpus of American English vowels. Subsequently, we present data from two magnetoencephalographic (MEG) experiments that suggest that auditory cortex is sensitive to modulations of the F1/F3 ratio. Additionally, our findings indicate that the perceptual system displays heightened sensitivity to formant ratios in more densely populated regions of the vowel space (in English, this would be for front and back vowels and not central vowels).

Figure 1. Vowel Space Normalized Against F3.

Traditional vowel space plotted in the proposed normalized vowel space (F3 as the normalizing factor). Formant values from which ratios were computed are from Hillenbrand et al. (1995) and averaged across age and gender per vowel category (except for /ə/ which was not collected in Hillenbrand, et al. (1995); instead, those values were computed from the frequency values used in the experiments reported here (before F3 modulation)).

The Third Formant in Perception and Normalization

The center frequency of F3 appears to vary correlationally with a given speaker's fundamental frequency and remains fairly constant across vowels for that speaker (Deng and O'Shaughnessy 2003; Potter and Steinberg 1950). Given that F3 appears to be relatively stable across vowel tokens within a given speaker, but varies as a function of vocal tract length inter-talker, and is present in different types of speech (e.g., whispered, non-phonated speech), a possible solution to vowel normalization would be to take the ratio of the first and second formants against the third. Consequently, the vowel space would not be best represented as F2 plotted against F1 or the difference between F2 and F1 plotted against F1 (Ladefoged and Maddieson 1996: 288), but rather as the ratio of F1 to F3 plotted against the ratio of F2 to F3. The third formant (F3) is useful in the identification and discrimination of a variety of speech contrasts (e.g., rhoticization on vowels (Broad and Wakita 1977), /l/-/r/ discrimination (Miyawaki et al. 1975), stop consonant place of articulation identification (Fox et al. 2008)), has been shown to affect the perception of vowels (Fujisaki and Kawashima 1968; Nearey 1989; Slawson 1968), provides a good estimate of vocal tract length in automatic speech recognition (Claes et al. 1998), is useful in normalizing whispered vowels (Halberstam and Raphael 2004; although their data on the role of F3 in normalizing phonated vowels was inconclusive), and has also been shown that the higher formants are as important, if not more so, than pitch in normalizing noise-excited vowels (Fujisaki and Kawashima 1968). Given these results, we can be confident that listeners are able to use and exploit information contained within this frequency range.

Peterson (1951) converted vowel frequencies into Mel space and plotted F1/F3 against F2/F3 in the final two pages of his article. Taking vowel productions from one man, one woman and one child, he showed that, impressionistically, these ratios remove much of the variation seen when F2 is plotted against F1. Unfortunately, little discussion or further results are provided, and it seems that this particular algorithm has not been pursued subsequently in the formant ratio literature. A similar solution was echoed in Deng and O'Shaughnessy (2003), where they write: “Since F3 and higher formants tend to be relatively constant for a given speaker, F3 and perhaps F4 provide a simple reference, which has been used in automatic recognizers, although there is little clear evidence from human perception experiments.” One of half of the algorithm we propose (F2/F3) is present in previous formant ratio algorithms (Miller 1989; Syrdal and Gopal 1986). Therefore, in the experiments reported here, we concentrate on finding neurophysiological evidence for the more novel ratio, the F1/F3 ratio.

While the objective of this paper is to demonstrate human perceptual sensitivity to formant ratios, it is useful to assess how well our proposed algorithm eliminates variance due to speaker differences. The corpus data used to test our model is from Hillenbrand, et al. (1995). In a replication of Peterson and Barney (1952), Hillenbrand, et al. (1995) collected the productions of twelve American English vowels from 45 men, 48 women and 46 children in an /hVd/ frame. In an acoustic analysis of the data, they identified a point centrally located in the steady-state portion of the vowel and measured the fundamental frequency (f0), as well as the center frequencies for the first through fourth formants (F1–F4) for each token. Prior to the analysis reported here, vowel tokens missing a value for one of their formants (F1–F4) in the corpus were eliminated from subsequent calculations (16.3% of the data).

To assess the amount of inter-speaker variation in the data as a function of speaker age and gender, we performed Linear Mixed Effects modeling (Baayen 2008) using the nlme package in R (R Development Core Team, 2006) with Subject as a Random Variable on the Hillenbrand, et al. (1995) data comparing the effects of Age (`adult', `child') and Gender (`male', `female') on the raw frequency values for f0–F3 and subsequently on the transformed F1/F3 and F2/F3 ratios. Given previous results on differences in the fundamental frequency and formant frequencies of vowels across men, women and children, we predict to find reliable main effects of Gender and Age for the untransformed data for all four measures (f0–F3).

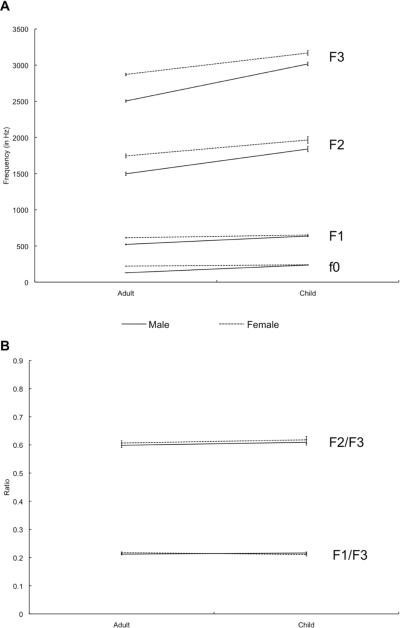
For f0, we found a significant Age × Gender interaction (F(1,135) = 133.4, p < 0.0001) and significant main effects for both Age (F(1,135) = 255.0, p < 0.0001) and Gender (F(1,135) = 302.4, p < 0.0001). For F1, we found a significant Age × Gender interaction (F(1,135) = 19.8, p < 0.0001), as well as significant main effects of both Age (F(1,135) = 70.8, p < 0.001) and Gender (F(1,135) = 66.6, p < 0.0001). For F2, we again found a marginal Age × Gender interaction (F(1,135) = 3.4, p = 0.07), and significant main effects of Age (F(1,135) = 64.6, p < 0.0001) and Gender (F(1,135) = 45.3, p < 0.0001). Finally, for F3, we also find a significant Age × Gender interaction (F(1,135) = 24.0, p < 0.0001) and significant main effects of both Age (F(1,135) = 306.5, p < 0.0001) and Gender (F(1,135) = 211.1, p < 0.0001). These results confirm that the raw, untransformed values of formants across men, women and children are highly variable, and effects of age and gender contribute greatly and interactively to this variability. Thus, a simple mapping between frequency information and speaker-independent representations is inadequate.

To provide an initial demonstration as to how well our proposed algorithm eliminates speaker variation, we ran the same model above on the transformed (F1/F3; F2/F3) corpus data. The significant main effects of age and gender, as well as the significant interactions of age and gender were completely eliminated. For F1/F3, there were no main effects of Age (F(1,135) = 0.08, p = 0.78) or Gender (F(1,135) = 0.3, p = 0.57) and no Age × Gender interaction (F(1,135) = 2.3, p = 0.12). For F2/F3, we also find no main effects of Age (F(1,135 = 1.0, p = 0.32) or Gender (F(1,135) = 0.77, p = 0.38) and no Age × Gender interaction (F(1,135) = 0.001, p = 0.97). (Insert Figure 2 about here.)

Figure 2. Comparison of Mean Formant Values.

(A) Comparison of the untransformed formant values for fundamental frequency (f0), first formant (F1), second formant (F2), and third formant (F3) by age and gender of speaker. Mean formant values by group calculated from Hillenbrand et al. (1995). (B) Comparison of the transformed values for F1/F3 and F2/F3 by age and gender of speaker. Error bars represent one standard error of the mean.

The results of the Linear Mixed Effects models on the transformed Hillenbrand, et al. (1995) data demonstrates that our proposed algorithm, whereby F1 and F2 are ratioed against F3 successfully eliminates the variance due to effects of age and gender found in productions of vowel tokens across different speakers. The question we now focus on, and the primary aim of this paper, is to demonstrate that auditory cortex is sensitive to one of the two dimensions of our proposed formant ratio algorithm, namely F1/F3. To do this, we present data from two MEG experiments on vowel perception. Our findings confirm that auditory cortex appears to be sensitive to modulations of the F1/F3 ratio (the more novel of the two computations in the proposed algorithm).

The Contribution of Magnetoencephalography

Magnetoencephalography (MEG) is an electrophysiological recording technique that measures fluctuations in magnetic field strength caused by the electrical currents in neuronal signaling (Frye et al. 2009; Hari et al. 2000; Lounasmaa et al. 1996) and is particularly adept at recording potentials from auditory cortex (Roberts et al. 2000). Combining its excellent temporal resolution (1 ms; and fair spatial resolution ~2–5 cm) and aptitude for recording from auditory cortex, it provides a powerful tool in understanding how humans process speech in real-time, whose temporal properties are both fast and fleeting. In the two experiments reported below, we exploit the response latency of an early, evoked neuromagnetic potential, the M100 (or N1m), which is the MEG equivalent of the N1 ERP component (Eulitz et al. 1995; Virtanen et al. 1998). The electrical N1 in EEG is a negative-going potential comprising several subcomponents, with a primary sub-component localizing to primary auditory cortex (A1, Picton et al. 1976). It is an exogenous response evoked by any auditory stimulus with a clear onset, and is found regardless of the task performed by participant, or his/her attentional state (Näätänen & Picton, 1987). Its MEG counterpart, the N1m or M100, appears to be the magnetic equivalent of the primary sub-component that localizes to A1 in supratemporal auditory cortex (Hari et al. 1980; Eulitz et al. 1995; Virtanen et al. 1998), thereby making it a more focused dependent measure for use in understanding auditory processing (Roberts et al. 2000). (Insert Figure 3 about here.) The dependent measures of the evoked M100 (latency, amplitude) typically reflect spectral properties of the acoustic stimulus (frequency, loudness, fine-structure of the waveform, etc.), as opposed to later evoked components (e.g., MMNm), and integrates only over the first 40 ms of the auditory stimulus (Gage et al. 2006). Given its robustness and replicability, the M100 has been used extensively to study early auditory cortical processing, and we have a fair understanding of the types of stimulus dependent factors to which the M100 is sensitive (Roberts et al. 2000). Sinusoids closest to 1 KHz elicit the shortest evoked M100 response latency, while moving outward from 1 KHz in either direction (both lower and higher in frequency) elicit longer evoked latencies (Roberts and Poeppel 1996). Relevant to the current work, the M100 response properties to vowels have been fairly well characterized. In particular, the M100 seems to be sensitive to F1 (Diesch et al. 1996; Govindarajan et al. 1998; Poeppel et al. 1997; Roberts et al. 2000; Roberts et al. 2004; Tiitinen et al. 2005) independent of differences in fundamental frequency (Govindarajan et al. 1998; Poeppel et al. 1997). Diesch, et al. (1996) compared the evoked latencies of the M100 to four different synthesized German vowels (/a/, /i/, /u/, /æ/) and found that /a/ and /æ/, having higher F1 values, elicited reliably shorter latencies than /u/. Poeppel, et al. (1997) synthesized three English vowels (/i/, /u/, /a/) and also report a reliable difference in the evoked M100 latency between /a/ and /u/, with /a/ eliciting a shorter M100 latency, and do not report a difference between /i/ and /u/. This finding was replicated in Govindarajan, et al. (1998), who also found that both one and three formant synthesized tokens of /a/ elicit reliably faster M100 evoked latencies in English listeners than one and three formant synthesized tokens of /u/, respectively. Moreover, Tiitinen, et al. (2005) replicated these findings in Finnish speakers, showing again that /a/ elicits faster M100 latencies than /u/ using semi-synthetic speech. The interpretation for the directionality of these effects, namely that /a/ elicits reliably shorter M100 evoked latencies than /u/, is that the spectral energy in F1 is driving the M100 response (Govindarajan et al. 1998; Poeppel et al. 1997; Roberts et al. 2000), and /a/ elicits shorter latencies because the F1 in /a/ (~ 700 Hz) is considerably closer to 1 KHz than the F1 in /u/ (~ 300 Hz), consistent with the sinusoidal data (Roberts and Poeppel 1996). This effect does not seem to be speech specific, however (Diesch et al. 1996; Govindarajan et al. 1998).

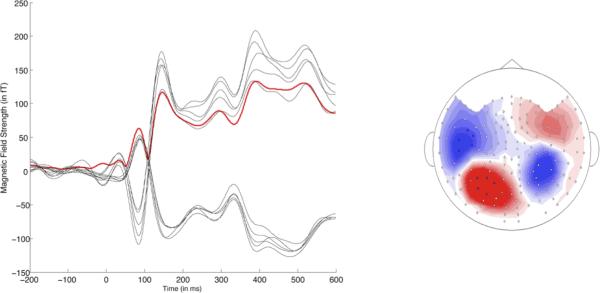
Figure 3. Evoked M100 Temporal Waveform and Magnetic Field Contour.

Temporal waveform from ten left hemisphere channels (RMS: solid red line superimposed) and the magnetic field distribution at peak latency of the M100 for a representative subject. For the magnetic field distributions, red indicates outgoing magnetic field source and blue indicates ingoing magnetic field sink.

These findings have been confirmed and extended in more recent work. Roberts, et al. (2004) showed that unlike responses to sinusoids, where the M100 response latency follows a smooth 1/frequency function (at least up to approximately 1000 Hz, above that point the latency again increases), the latency of the M100 to vowels (F1, in particular) seems to respect vowel category boundaries. They synthesized tokens of /a/ and /u/ and modulated F1 in 50 Hz increments between 250 Hz and 750 Hz while keeping the values for F2 (1000 Hz) and F3 (2500 Hz) constant, albeit with broader than normal formant bandwidths. Instead of following the smooth 1/f function, M100 latencies clustered into three distinct bins, the lowest F1 values (250 – 350 Hz) elicited the longest latencies, the middle F1 values (400 – 600 Hz) elicited reliably shorter latencies and the high F1 values (650 – 750 Hz) elicited even shorter M100 latencies. The bin with the lowest F1 values also represent the natural range of F1 in /u/ and the bin with the highest F1 values represent the natural range of F1 in /a/ tokens. Roberts, et al. (2004), therefore, concluded that the latency of the M100 is sensitive to information about the F1 frequency distributions of different vowel categories. In summary, the primary conclusion drawn from these results is that the M100 is sensitive to F1 in vowel perception, as vowel categories with a higher F1 (closer to 1000 Hz) consistently elicit shorter evoked latencies of the M100.

Experiment 1

The goal of the following experiments is to determine if the auditory system is sensitive to formant ratios, and in particular, if it is sensitive to the F1/F3 ratio. Given our hypothesis regarding the algorithm that is (at least partly) responsible for vowel normalization, combined with previous MEG findings on vowel perception (Diesch et al. 1996; Govindarajan et al. 1998; Poeppel et al. 1997; Roberts et al. 2000; Roberts et al. 2004; Tiitinen et al. 2005), we propose that the M100 is actually sensitive to the ratio of the first formant (F1) against the third (F3), instead of F1 alone. In order for us to test this representational and normalization hypothesis with the M100, the M100 must be able to index more complex auditory operations performed on the input and not solely reflect surface properties of the stimulus. The results from Roberts, et al. (2004) and work on inferential pitch perception that has shown that the M100 is modulated by a missing fundamental component (Fujioka et al. 2003; Monahan et al. 2008) demonstrate that the M100 can index more complex and abstract auditory operations that integrate information from across the acoustic spectrum.

In the first experiment, we presented participants with synthesized tokens of the mid-vowel categories /ɛ/ and /ə/, holding F1 (and F2) constant while manipulating the value of F3 for each type. We modulated F3 both higher and lower by 4% in Mel space from the mean/standard F3 value (8% overall difference between the two tokens for a given vowel type). We predict that vowels with a lower F3 (larger F1/F3 ratio) should elicit faster M100 latencies than vowels with a higher F3 value (smaller F1/F3 ratio). This directional prediction is derived from recalculating the formant values of Poeppel, et al. (1997). Converting their vowel tokens (for the male fundamental frequency) into F1/F3 Mel space, we find that the token of /a/ used in their experiment had a larger F1/F3 ratio than the token of /u/ and that these two tokens are 20% apart in this transformed space. Given that /a/ elicits an M100 latency than /u/ (Diesch et al. 1996; Govindarajan et al. 1998; Poeppel et al. 1997; Roberts et al. 2000; Roberts et al. 2004; Tiitinen et al. 2005), we therefore predict that tokens with a larger F1/F3 ratio should elicit shorter M100 latencies than tokens with a smaller F1/F3 ratio.

Methods

Materials

Vowel tokens were synthesized using HLSyn (Stevens and Bickley 1991) with a sampling frequency of 11,025 Hz and an intensity of approximately 70 dB SPL (range: 69.2 – 71.2 dB SPL). Two tokens for each vowel type (mid-vowels /ɛ/ and /ə/) were synthesized, for a total of four tokens. A fundamental frequency of 150 Hz was used for all tokens. Using an f0 between typical male and female speaker values allowed for greater flexibility in possible F3 values. Moreover, a fundamental frequency of 150 Hz is not outside the possible range for either male or female speakers.

As previously mentioned, the values of F1 and F2 remained consistent across the tokens within each type. The Hertz (Hz) values were converted into Mel space, and we modulated the F3 value 4% higher and 4% lower in the transformed Mel space. Each token was 250 ms in duration with a 10 ms cos² on- and off-ramp. The values for F1, F2 and F3, and their respective bandwidths are presented in Table 1 and a comparison of the LPC-based spectral envelopes of the vowel tokens are presented in Figure 4. (Insert Table 1 and Figure 4 about here). The F1, F2 and F3 values for [ə] are standard values (Stevens 1998). The F1 and F2 values (and the F3 value for which we computed from) for [ɛ] are taken from a corpus of American English vowel formant frequencies (Hillenbrand et al. 1995) extracted from the steady state portion of the vowel in [hVd] syllables. For present purposes, we used the average formant values for male speakers.

Table 1. Spectral characteristics of the four vowel tokens used in Experiment 1.

The center frequency and bandwidth for each of the first three formants are provided in Hertz. The stimuli were synthesized using KLSyn (Stevens and Bickley 1991), a user interface for the HLSyn speech synthesizer. The formant ratio calculations were performed in Mel frequency space and then converted back into Hertz for the speech synthesis.

		F1		F2		F3
Vowel Type	F3 Height	Center Frequency	Bandwidth	Center Frequency	Bandwidth	Center Frequency	Bandwidth
/Ə/	Low	500	80	1500	90	2040	150
/Ə/	High	500	80	1500	90	3179	150
/□/	Low	580	80	1712	90	2156	150
/□/	High	580	80	1712	90	3247	150

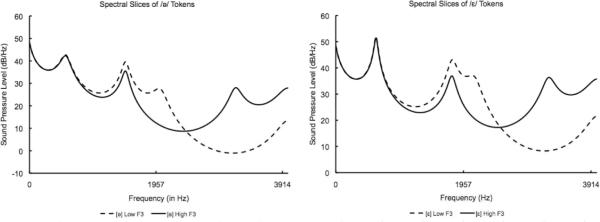
Figure 4. Experiment 1: Spectral Slices of Vowel Tokens.

LPC-based spectral envelopes of the vowel sounds used in Experiment 1. The solid line indicates the token with a higher F3 (smaller F1/F3 ratio) and the dashed line indicates tokens with a lower F3 (larger F1/F3) ratio. Spectral envelopes smoothed with six pole LPC filter.

Participants

Thirteen monolingual English participants (5 female; mean age: 20 yrs old) participated in the experiment. Two participants were excluded from statistical analysis: for one participant, the evoked waveform did not show a reliable M100; the other participant showed exceptionally fast M100 responses (< 80 ms). Consequently, the data from 11 participants was analyzed. Participants reported no hearing deficits. All participants provided written informed consent approved by the University of Maryland Institutional Review Board (IRB) and scored strongly right-handed on the Edinburgh Handedness Survey (Oldfield 1971). Each participant was compensated $10/hour. The typical session lasted approximately 1 ½ to 2 hours.

Procedure

Participants lay supine in a dimly lit magnetically shielded room, as stimulus evoked magnetic fields were passively recorded by a whole-head 157-channel axial-gradiometer magnetoencephalography system (Kanazawa Institute of Technology, Kanazawa, Japan). The stimuli were delivered binaurally into the magnetically shielded room via Etymotic ER3A insert earphones that were calibrated and equalized to have a flat frequency response between 100 and 5000 Hz. Prior to the experiment, a hearing test was administered to the participants within the MEG system to ensure normal hearing and that the auditory stimuli were appropriately delivered by the earphones. Subsequently, a pretest localizer was performed. Participants were presented with roughly 100 tokens each of four pure sinusoids: 125Hz, 250Hz, 1000Hz and 4000Hz. The neuromagnetic-evoked responses to the sinusoids were epoched and averaged online. The pretest was done to ensure good positioning of the participant's head within the system, as well as guaranteeing that he/she would show a reliable M100 response. The experiment began subsequent to the hearing test and pretest localizer.

For the experiment itself, participants listened to both vowel tokens and pure sinusoids. The four vowel tokens (/ə/: high F3, low F3; /ɛ/: high F3, low F3) were each presented 300 times in pseudo-randomized order (1200 vowel tokens in total), ensuring a good signal-to-noise ratio in the MEG signal. Sinusoids of 250Hz and 1000Hz were pseudo-randomly presented 50 times each throughout the experiment. Participants were asked to listen passively to the vowel tokens and discriminate between the 250 Hz and 1000 Hz sinusoids by pressing one of two labeled buttons depending on the sinusoid they heard. The inter-trial interval pseudo-randomly varied between 700ms and 1300ms.

Recording and Analysis

Neuromagnetic signals were acquired in DC (no high pass filter) at a sampling frequency of 1 KHz. An online Low Pass Filter of 200 Hz and a 60 Hz notch filter were applied during recording. Noise reduction was performed on the MEG data using a multi-shift PCA noise reduction algorithm (de Cheveigné and Simon 2007). We extracted epochs of 800 ms intervals, including 200 ms of prestimulus baseline with the zero point set at stimulus presentation onset, from the continuous, noise-reduced data file. During the averaging process, any trials with artifacts exceeding 2.5 pT in amplitude during their epoch were removed from the analysis (6.2% of the total data). Off-line filtering (digital Band Pass Filter with a Hamming window, range: 0.03 – 30 Hz) and baseline correction (100 ms prior to onset of the vowel) were performed on the averaged data.

a. Evoked Waveform Analysis

Ten channels from each hemisphere that best correlated with the sink (ingoing magnetic field; 5 channels) and source (outgoing magnetic field; 5 channels) of the signal were selected for statistical analysis on a participant-by-participant basis. The same channels were used across the four conditions for the within subjects analysis. The peak latency and amplitude of the root mean square (RMS) of the evoked M100 component in the MEG temporal waveform for each hemisphere were carried forward for statistical analysis.

b. ECD Source Location Analysis

In addition to the latency and amplitude analyses of the RMS of the evoked M100, the equivalent current dipole (ECD) solution for the four distinct vowel tokens was calculated. First, we defined an orthogonal left-handed headframe; x projected from the inion through to the nasion and z projected through the 10–20 Cz location. Thus, the lateral-medial dimension was defined by x coordinates, the anterior-posterior dimension was defined by y coordinates, and the superior-inferior dimension was defined by z coordinates. Then, a sphere, whose center position and radius were calculated in headframe coordinates, was fit for each participant covering the entire surface of his/her digitized head-shape. A single ECD model in a spherical volume conductor was used for source modeling analysis (Sarvas 1987; Diesch and Luce 1997) of the neuromagnetic data. For a source analysis of the data, sensors were selected from each hemisphere for each vowel token within each participant (mean number of channels per hemisphere = 25). The ECD was calculated based on a single point in time located during the final 30 ms of rise-time to peak amplitude of the RMS waveform. The minimum goodness of fit (GoF) for inclusion in the analysis was 90% (mean GoF = 95.8%). We, thus, obtained the x, y and z coordinates for each vowel token (/ɛ/ high F3, /ɛ/ low F3, etc.) in each hemisphere for each participant. From the 11 participants included in the evoked waveform analysis, one additional participant was excluded due to an inability to calculate a GoF > 90% (statistics on ECD source location, n = 10). Given that we do not have access to structural MRIs for each of our participants, we are unable to anatomically localize our findings; instead, our comparisons are based on the relative source location positions for each ECD fit for each vowel token.

Results

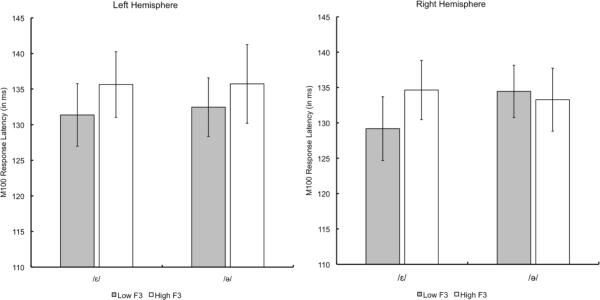
We conducted a linear mixed effects model on the M100 latencies and amplitudes for each vowel type with the factors Hemisphere (Left Hemisphere & Right Hemisphere) and F3 (High & Low) with Subject as a random effect using the lme() package in R statistical software. For the M100 latencies to the vowel type /ε/, only the main effect of F3 had an F-value greater than 1 (Hemisphere and Hemisphere × F3: F < 1). Given that neither Hemisphere or the interaction with Hemisphere approached significance, we conducted a one-tailed (given our directional prediction: larger F1/F3 ratios should elicit shorter latencies) paired t-test comparing the latencies to the token of /ε/ with a high F3 to the token of /ε/ with a low F3. As predicted, the /ε/ token with the lower F3 (larger F1/F3 ratio) elicited a significantly shorter M100 latency than the /ε/ token with the higher F3 (smaller F1/F3 ratio; t(21) = 3.05; p < 0.005). When the hemispheres are compared independently of one another, we also find the reliable differences in the predicted directions (one-tailed paired t-tests; LH: t(10) = 1.88, p < 0.05; RH: t(10) = 2.35, p < 0.05). (Insert Figure 5 about here.) Comparing the tokens of /ə/ using the same model as above, we did not obtain reliable differences in the latency of the RMS of the M100 response (all Fs < 1). Analyzing the amplitude of the RMS M100 waveform, we again modeled the data using a linear mixed effects model with Subject as a random effect and the factors Hemisphere (Left Hemisphere & Right Hemisphere) and F3 (High & Low). We find a main effect of Hemisphere for each vowel type (right hemisphere showing significantly larger amplitudes than the left hemisphere; /ε/: F(1,30) = 143.3, p < 0.0001; /ə/: F(1,30) = 181.7, p < 0.0001), but no main effects F3 or interactions of Hemisphere × F3 (all Fs < 1). At this point in time, we do not have an explanation for why the right hemisphere shows reliably larger amplitudes than the left hemisphere.

Figure 5. Experiment 1: M100 Response Latencies by Vowel Type.

Mean M100 response latencies across participants to the vowel tokens in Experiment 1. Gray bars refer to tokens with a Low F3 (large F1/F3 ratio) and white bars refer to tokens with a high F3 (small F1/F3 ratio). Error bars represent one standard error of mean.

To summarize, we found a reliable difference in the latency of the evoked M100 component in the predicted direction, vowel tokens with a larger F1/F3 ratio elicit a shorter M100 latency than tokens with a smaller F1/F3 ratio, which is consistent with our reinterpretation of the previous M100 results on F1 (Diesch et al. 1996; Govindarajan et al. 1998; Poeppel et al. 1997; Roberts et al. 2000; Roberts et al. 2004; Tiitinen et al. 2005). We only find this effect for the front vowel /ε/, however, and not the central-vowel /ə/. In the discussion, we speculate on some potential explanations for this pattern of results. In general, however, we take these results to suggest that the perceptual system is sensitive to formant ratios, and the F1/F3 ratio in particular.

M100 ECD Source Location

The primary aim of this study was to determine if the auditory perceptual system is sensitive to formant ratios in general, and moreover, if manipulations of the F1/F3 ratio would modulate the response latency of the RMS of the evoked auditory M100 component. In addition to the latency and amplitude analysis of the M100, we also conducted a source analysis on the data to determine if there were any localization differences between the vowels. Obleser, et al. (2004), using MEG, calculated the ECD source location for seven distinct German vowels. They found that front vowels tend to map onto a more anterior portion of auditory cortex, while back vowels map onto a more posterior region, retaining the front/back distinction of vowel categories on the anterior/posterior dimension of auditory cortex. It should be noted that Obleser, et al. (2004) did not include mid-vowels in their experiment; however, given the directionality of their effects, we might expect to find reliable differences between the tokens of /ɛ/ and /ə/, with the front vowel /ɛ/ localizing to more anterior regions than the mid vowel /ə/. We performed a linear mixed effects model on each coordinate axis (i.e., x, y, z) in each hemisphere independently with the factors Vowel (/ə/ and /ɛ/) and F3 (High and Low) and Subject as a random effect. In the left hemisphere, along the lateral-medial dimension, we find no main effects or Vowel × F3 interaction (all Fs < 1) and along the superior-inferior dimension, we again find no main effects (all Fs < 1), but we do find an interaction of Vowel × F3 (F(1,27) = 5.38, p < 0.05). Finally, along the inferior-posterior dimension, the dimension in which Obleser, et al. (2004) found reliable differences in the ECD source location between front and back vowels, we also find no main effects of Vowel or F3 and no interaction of Vowel × F3 (all Fs < 1).

In the right hemisphere, along the lateral-medial dimension, we again find no main effects and no interaction of Vowel × F3 (all ps < 0.1), and along the superior-inferior dimension, we also find no main effects and no interaction of Vowel × F3 (all Fs < 1). Finally, along the anterior-posterior dimension, we again find no main effects and no interaction of Vowel × F3 (all ps < 0.2). Finally, we performed a one-tailed sign test on the values in the anterior-posterior dimension across vowel type for each hemisphere to determine whether the front vowels (the two tokens of /ɛ/) were located more anterior than the mid-vowels (the two tokens of /ə/). In the left hemisphere, we found no difference between the tokens with a high F3 (S = 6; p = 0.5) or between the tokens with a low F3 (S = 4; p = 0.89), and in the right hemisphere, we find no difference between vowel types for the tokens with a high F3 (S = 4; p = 0.89) or with a low F3 (S = 4; p = 0.89) along the anterior-posterior dimension.

Discussion

These findings suggest that auditory cortex (minimally, the neurobiological generators of the M100) is sensitive to formant ratios, and in particular, to modulations of the F1/F3 ratio. The latency difference was robust across participants for the /ɛ/ vowel and was in the predicted direction for nearly all subjects for the vowel type /ɛ/ (Sign Test: S=16; p < 0.05). Any more concrete conclusions, however, should be taken cautiously, given that we did find such an effect for the mid-central vowel /ə/.

The immediate question is why we found an effect of F3 manipulation for /ɛ/ but not for /ə/. The lack of a result for /ə/ is not likely due to a lack of power in the experiment, given that 300 tokens of each vowel is more than sufficient to obtain a good signal-to-noise ratio. Moreover, the fact that we found an effect with /ɛ/ suggests that this asymmetry is due to some intrinsic properties of the vowels or their location in vowel space. It is this latter possibility that we explore in the second experiment. In particular, the asymmetry found in Experiment 1 could be a consequence of the location in vowel space that /ɛ/ and /ə/ occupy. The front mid-vowel /ɛ/ occupies a more crowded portion of the vowel space relative to that occupied by /ə/ (i.e., there are many more phonetic categories in close proximity to the distribution of /ɛ/ as opposed /ə/ in the vowel space), where categorization might be more critical than the middle of the vowel space.

In Experiment 2, we test the hypothesis that the asymmetry found in Experiment 1 is due to the location in vowel space of each vowel. Consequently, we test two hypotheses. First, we aim to replicate the null effect with /ə/ that we found in Experiment 1. To accomplish this, we test the same /ə/ tokens with a different set of participants. Second, to test whether it is the demands for categorization that drive the perceptual system's sensitivity to formant ratios in more crowded portions of the vowel space, we test two tokens of /o/ with the same manipulations we performed on /ɛ/ in the first experiment. The back vowel /o/, like /ɛ/, also occupies a more crowded portion of the vowel space than /ə/.

Experiment 2

The second experiment was nearly identical to Experiment 1; however, instead of testing tokens of /ɛ/, we tested synthesized tokens of /o/, a vowel produced in the back of the vocal tract. The back mid rounded vowel /o/, like /ɛ/, resides in a more crowded portion of the vowel space, at least when compared with the central vowel /ə/. Practically speaking, our hypothesis predicts that we should find M100 latency differences for vowels located in more crowded portions of the vowel space. Therefore, we should find effects for /o/ and replicate our null effects for /ə/. We speculate that the reason for this particular pattern is likely due to greater competition within the category space, which drives the perceptual system's heightened sensitivity to the formant ratios in these more densely populated regions.

Methods

Materials

For the /ə/ stimuli, we used the same tokens used in Experiment 1. For the /o/ stimuli, we synthesized two new tokens using HLSyn (Stevens and Bickley 1991) with a sampling frequency of 11,025 Hz and an average intensity level of 70 dB SPL (range: 69.5 – 71.2 dB SPL). The F1 and F2 values were taken from Hillenbrand et al. (1995). Again, we converted the Hz frequency values into Mel space. Using the F3 value (transformed into Mel space) from Hillenbrand, et al. (1995) as the standard, we computed the new F3 values for our experimental tokens by moving 4% in either direction of the F1/F3 ratio space. Therefore, the overall distance in F1/F3 ratio space between the tokens was 8%. As before, we predict a M100 latency facilitation for the token with the smaller F3 (the larger F1/F3 ratio). The F1, F2 and F3 values for the four tokens used in Experiment 2 are presented in Table 2 and a comparison of the LPC-based spectral envelopes of the vowel tokens are presented in Figure 6 (Insert Table 2 and Figure 6 about here).

Table 2. Spectral Characteristics of the Vowel Tokens used in Experiment 2.

The center frequency and bandwidth for each of the first three formants are provided in Hertz. The stimuli were synthesized using KLSyn (Stevens and Bickley 1991), a user interface for the HLSyn speech synthesizer. The formant ratio calculations were performed in Mel frequency space and then converted back into Hertz for the speech synthesis.

		F1		F2		F3
Vowe 1 Type	F3 Height	Center Frequency	Bandwidth	Center Frequency	Bandwidth	Center Frequency	Bandwidth
/Ə/	Low	500	80	1500	90	2040	150
/Ə/	High	500	80	1500	90	3179	150
/o/	Low	497	80	938	90	2011	150
/o/	High	497	80	938	90	3118	150

Figure 6. Experiment 2: Spectral Slices of Vowel Tokens.

LPC-based spectral envelopes of the vowel sounds used in Experiment 2. The solid line indicates the token with a high F3 (smaller F1/F3 ratio) and the dashed line indicates the token with a low F3 (larger F1/F3) ratio. Spectral envelopes smoothed with six pole LPC filter.

Participants

Fifteen monolingual English participants (9 female; mean age: 20 yrs old) participated in the experiment. Six participants were excluded from analysis on various grounds: two participants were not included in the analysis, as there were no discernable M100 in the data; two participants were excluded from the analysis because the source distribution of the component did not match that of an M100; one participant was excluded because the peak latency of their M100 was over 200 ms; and finally, one participant was excluded due to hardware failure. Consequently, for the analysis, the data from nine participants (5 females) was analyzed. All participants had normal hearing. All participants provided written informed consent approved by the University of Maryland Institutional Review Board (IRB) and scored strongly right-handed on the Edinburgh Handedness Survey (Oldfield 1971). Each participant was compensated $10/hour. The typical session lasted approximately 1 ½ to 2 hours.

Procedure

The procedure was identical to Experiment 1.

Recording and Analysis

The recording parameters and analysis procedures used in Experiment 2 were identical to those used in Experiment 1. All trials with artifacts above 2.5 pT in the noise-reduced data were eliminated from analysis (5.2% of the total data). The filtering and baseline correct parameters are identical to those used in Experiment 1.

a. Evoked Waveform Analysis

The methods for channel selection and calculation of the RMS of the evoked waveform carried forward for statistical analysis were identical to those used in Experiment 1.

b. ECD Source Location Analysis

The methods used for calculation of the ECD source locations in Experiment 2 are identical to those in Experiment 1. The mean number of channels per hemisphere across participants for each measurement was 28. The minimum goodness of fit (GoF) for inclusion in the analysis was 90% (mean GoF = 95%). From the 9 participants included in the evoked waveform analysis, one additional participant was excluded due to an inability to calculate a GoF > 90% (statistics on ECD source location, n = 8). Again, given that we do not have access to structural MRIs for each of our participants, we are unable to anatomically localize our findings; instead, our comparisons are based on the relative source location positions for each ECD fit for each vowel token.

Results

Given the results from Experiment 1 and our hypothesis that the perceptual system displays a greater sensitivity to formant ratios for vowels located in more densely populated regions of the vowel space, we predict to find a reliable difference between the two tokens of /o/, with the token with a lower F3 (larger F1/F3) eliciting a shorter M100 latency, while we expect to replicate the null difference for the two tokens of /Ə/ that we found in Experiment 1. (Insert Figure 7 about here.) We again conducted a linear mixed effects model on the M100 latencies and amplitudes for each vowel type with the factors Hemisphere (Left Hemisphere & Right Hemisphere) and F3 (High & Low) with Subject as a random effect using the lme() package in R statistical software. For the M100 latencies to the vowel type /o/, we find main effects of F3 (F(1,24) = 15.36, p < 0.001) and Hemisphere (F(1,24) = 4.95, p < 0.05) but no Hemisphere × F3 interaction (F < 1). The response latencies of the RMS of the M100 temporal waveform were approximately 6 ms shorter than those in the left hemisphere (paired two-tailed t-test: t(17) = 2.93, p < 0.01). We did not have a hypothesis regarding hemispheric differences in latencies, a finding not reported in other similar experiments (e.g., Diesch et al. 1996; Tiitinen et al. 1999), and consequently, we are hesitant to draw any significant conclusions based on this result. The main effect of F3 motivates our planned comparison: a comparison of the latencies to the token of /o/ with a high F3 to the token of /o/ with a low F3 using a paired one-tailed t-test. Our findings demonstrate that the /o/ token with the lower F3 (larger F1/F3 ratio) elicited a reliably faster M100 latency than the /o/ token with the higher F3 (smaller F1/F3 ratio; t(17) = 3.81; p < 0.001). Subsequently, we compared the hemispheres independently of one another, and we again find reliable differences in the predicted directions (one-tailed paired t-tests; LH: t(8) = 2.93, p < 0.01; RH: t(8) = 2.33, p < 0.05). In order to assess whether we were able to replicate the null finding for the tokens of /Ə/ from Experiment 1, we used the same model as above. As expected, consistent with the hypothesis that there is an influence on location in vowel space with sensitivity to formant ratios, we did not find reliable differences in the latency of the RMS of the M100 response between the tokens of /Ə/ (all Fs < 1). Next, we turn to an analysis of the amplitudes of the RMS of the M100 temporal waveform. We modeled the data using a linear mixed effects model with Subject as a random effect and the factors Hemisphere (Left Hemisphere & Right Hemisphere) and F3 (High & Low) on each vowel type separately. We found no main effects or interactions for either vowel type (i.e., /o/ and /Ə/; all Fs < 1). The findings from Experiment 2 confirm that the auditory perceptual system (at least the neurobiological generators of the M100) is sensitive to formant ratios, and in particular at least the F1/F3 ratio, and that the perceptual system shows greater sensitivity to formant ratios in regions of the vowel space that are more densely populated.

Figure 7. Experiment 2: M100 Response Latencies by Vowel Type.

Mean M100 response latencies across participants to the vowel tokens in Experiment 2. Gray bars refer to tokens with a Low F3 (large F1/F3 ratio) and white refer to tokens with a high F3 (small F1/F3 ratio). Error bars represent one standard error of mean.

M100 ECD Source Localization

To assess whether the vowels presented to participants in Experiment 2 elicited differences in their source localization as well as the latency of the evoked M100, we calculated the ECD solution for the four distinct vowel tokens on an intra-subject and intra-hemispheric basis. Identical to the statistical analysis performed for the ECD source data in Expeirment 1, we performed a linear mixed effects model on each coordinate axis (i.e., x, y, z) in each hemisphere independently with the factors Vowel (/Ə/ and /o/) and F3 (High and Low) and Subject as a random effect. We first report our findings from the left hemisphere. Along the lateral-medial dimension, we find no main effects or interaction (all ps < 0.15). Moreover, along the superior-inferior dimension, we again find no main effects or interaction (all ps < 0.1). Finally, along the inferior-posterior dimension, we again find no main effects and no interaction (all ps < 0.1). In the right hemisphere, along the lateral-medial dimension, we also find no main effects and no interaction (all Fs < 1), and along the superior-inferior dimension, we again find no main effects and no interaction (all ps < 0.15). Finally, along the anterior-posterior dimension, there are no main effects and no interaction of (all ps < 0.25). To determine if there are directional differences in the location of the ECD between the vowels along the anterior-posterior dimension, we performed a sign test on the different vowels types within each hemisphere. In the left hemisphere, we find a strong directional difference for the tokens with a High F3 (S = 1; p < 0.05), in the opposite direction, with the ECD source location of the token of /o/ with a High F3 localizing to a more anterior position along the anterior-posterior dimension than the token of /Ə/ with a High F3. We find no difference between the tokens with a Low F3 (S = 5; p = 0.86). In the right hemisphere, we found no effect between /Ə/ and /o/ with Low F3s (S = 6; p = 0.14), nor did we find an effect between /Ə/ and /o/ with High F3s (S = 4; p = 0.64).

Discussion

The motivation for Experiment 2 was to determine if the density of speech sound categories in perceptual space affects the sensitivity of the perceptual system to formant ratios. Recall that in Experiment 1, we found a significant M100 latency difference for the /ɛ/ token with a larger F1/F3 ratio but not for the /Ə/ token with a larger F1/F3 ratio. If an adequate explanation for the findings in Experiment 1 is that the sensitivity of our perceptual system to the F1/F3 ratio is a function of how dense the space is, and consequently, how much more competitive categorization is, then we also predict to find a significant difference for tokens of /o/ that vary on the F1/F3 ratio. As predicted, the token of /o/ with a larger F1/F3 ratio elicited a shorter M100 latency than the token of /o/ with a smaller F1/F3 ratio. And equally important, we replicated the null effect for /Ə/. This reaffirms our findings from Experiment 1 that the auditory system is sensitive to F1/F3 ratios, lending further support to using ratios in normalization algorithms. And moreover, it demonstrates that formant ratios are psychologically plausible computations that can be exploited in the course of speaker normalization.

An alternative explanation of the results we report is that the M100 response latency is sensitive to the entire spectrum, and therefore is also sensitive to modulations of F3 or perhaps even to differences in the power spectral density (PSD) of the vowel tokens (see Roberts et al. 2000 for results that suggest the M100 is sensitive to PSD). However, given that the differences in F3 between the tokens for each category (/ε/: Δ = 1091 Hz; /Ə/: Δ = 1139 Hz; /o/: Δ = 1107 Hz) are roughly equivalent in raw Hz space and moreover, the differences between tokens within each category are equivalent in Mel space (8% difference in the Mel space), this alternative does not adequately account for the M100 latency findings. Additionally, differences in the central moment of the power spectral density of the tokens (PSD; /ε/: Δ = 11 Hz; /Ə/: Δ = 14 Hz; /o/: Δ = 10 Hz) cannot account for the differences either, as /o/ has a smaller difference than /Ə/ and yet, we found a reliable difference in the M100 response latency for /o/ and not for /Ə/. While we accept that the overall power spectral density may contribute considerably to the response (differences in formant ratios lead to differences in power spectral densities), our results suggest that this alternative is insufficient as the sole property responsible for our findings.

General Discussion

Understanding how listeners normalize the highly variable speech signal across different talkers has been a long-standing problem in speech perception research (see Johnson 2005 for an overview of the various approaches to speaker normalization). Within the domain of vowel perception, a variety of different proposals have been offered to account for how listeners cope with this variation (Adank et al. 2004; Disner 1980; Irino and Patterson 2002; Miller 1989; Nearey 1989; Rosner and Pickering 1994; Strange 1989; Zahorian and Jaghargi 1993). Here, we revisited an idea that has been sporadically proposed in the literature: listeners are sensitive to the relative differences between formants (formant ratios) and not their absolute values (Lloyd 1890; Miller 1989; Peterson 1951, 1961; Peterson and Barney 1952; Syrdal and Gopal 1986). We put forward a (relatively) novel formant ratio algorithm in which the first (F1) and second (F2) formants are ratioed against the third formant (F3). Higher formants, such as F3, may act as an adequate normalizing factor (Deng and O'Shaughnessy 2003) and have been, at least impressionistically, judged to eliminate speaker-dependent variation (Peterson 1951), the sort of variation that exists in vowel productions between men, women and children. Previous work on formant ratios have employed algorithms that require large corpora to adequately eliminate speaker variation (e.g., Miller 1989). One of the advantages to the algorithm we propose here is that it appears to be an efficient computation for online speaker normalization that can be performed with little exposure to a given speaker, which is consistent with what we know about dialect identification (Purnell et al. 1999), the perceptual abilities of infants (Kuhl 1979, 1983), and listeners' abilities to make speaker size estimates (Ives et al. 2005; Smith et al. 2005).

In this paper, we investigated whether the perceptual system is sensitive to the F1/F3 ratio (the less novel of the two ratios; F2/F3 has appeared in previous ratio algorithms (Miller 1989; Syrdal and Gopal 1986)). We reported data from two MEG experiments that demonstrate that the neurobiological generators of the M100, an early, auditory evoked neuromagnetic component is sensitive to modulation of the F1/F3 ratio. The M100 had been previously reported to show sensitivity to the frequency of F1 in vowel perception (Diesch et al. 1996; Govindarajan et al. 1998; Poeppel et al. 1997; Roberts et al. 2000; Roberts et al. 2004; Tiitinen et al. 2005). Given our hypothesis regarding the algorithm involved in vowel normalization and the consequential representational nature of the vowel space (F1/F3 by F2/F3), we reinterpreted the previous MEG findings to conclude that the M100 is actually sensitive to the F1/F3 ratio and not F1 alone. The frequency of the third formant (F3) was not typically modulated in the previous MEG experiments, only F1. Therefore, we hypothesized that if we varied the value of the F3, and consequently, the F1/F3 ratio, we should be able to modulate the latency of the M100 in a predicted direction if the neurobiological generators of the M100 are sensitive to the F1/F3 ratio.

Our findings suggests the perceptual system can calculate formant ratios (or something substantially equivalent), lending further support to the notion that this is a plausible normalization algorithm, and moreover, that the M100 is sensitive to the F1/F3 ratio and not F1 alone. Furthermore, we calculated the statistical effectiveness of this algorithm in eliminating variance that is a function of the age and gender of a speaker on a large corpus of productions of American English vowels (Hillenbrand et al. 1995). While the statistical analysis was perfunctory in many respects (e.g., we did not calculate how well the vowel space categorizes or how well particular tokens are classified as is normally done), which was beyond the scope of this paper, the calculations demonstrate that speaker dependent variation, when we compare vowel utterances across different talkers, as a function of age and gender was eliminated.

While we found that auditory cortex is sensitive to modulations of the F1/F3 ratio, the pattern of effects suggest a more nuanced conclusion. In the first experiment, we found a reliable difference in the predicted direction only for the front-mid vowel /ε/, but no difference between in the response latency of the M100 for the two tokens of /ə/. As a result of this asymmetric result and the direction of the pattern, we hypothesized that the perceptual system displays heightened sensitivity to modulations of the F1/F3 ratio only when mapping acoustic information into more crowded regions of the vowel space. Experiment 2 was designed to test this hypothesis. As predicted, we found a reliable difference in the latency of the M100 between the two tokens of /o/ in the predicted direction and we replicated the null effect for /ə/, demonstrating that the sensitivity of auditory system is not equal across the vowel space. To place these findings within a theoretical framework, in English, the front and back portions of the vowel space are more densely populated and therefore, categorization can be though of as being “more competitive”. In other words, the acoustic distribution of a vowel can afford to be more diffuse in central portions of the vowel space where no other categories exist, as compared to more densely populated regions of the space, where more different vowel categories are located. This provides an intuitive explanation for why we might find a greater sensitivity of the neurobiological generators of the M100 to vowels located in the front and back of the vowel space as compared with vowels located in the center of the space.

As a point about the M100 component itself, we can be confident that the M100 is sensitive not only to F1, but that higher regions of the frequency space also play a role in modulating its latency. In particular, we conclude that the response latency of the M100 indexes more abstract computations that have been performed on the stimulus and in fact reflect complex representational schemas in auditory cortex. This conclusion is consistent with other work done on the relation between the M100 and F1 (Roberts et al. 2004) and findings that demonstrate that the M100 is sensitive to differences in the inferred pitch of complex tone stimuli that are missing a fundamental component (Fujioka et al. 2003; Monahan et al. 2008).

The question of how the brain computes formant ratios is a tractable one; and one that we believe is a point where biology and psycholinguistics can fruitfully combine to provide a fairly complete account of a perceptual linguistic phenomenon. Since Delattre et al. (1952) presented participants with synthetic one- and two-formant vowels and showed that listeners were able to reliably judge vowel category based on this information alone, the working hypothesis within the field is that listeners extract formant information from vowel tokens (i.e., the “formant extraction” principle). One of the possible ways in which the brain encodes formant information is via rate encoding at various characteristic frequencies (CF) of auditory nerve fibers (Sachs and Young 1979; Young and Sachs 1979). For example, Sachs and Young (1979) recorded the rate response properties of populations of neurons with different CF in auditory nerve fibers in anaesthetized cats to the steady-state synthetic vowels /ɪ/, /ɛ/ and /ɑ/. For stimulus presentations below 70 dB SPL, they report increases in the normalized rate of auditory nerve fibers whose CF matches the formant peaks of the synthetic vowels; for the vowels /ɪ/ and /ɛ/, they show a clear separation between the peaks of discharge rates of nerve fibers with CF corresponding to F1 and F2 of the synthesized vowel (the separation of discharge rates of the CF between F2 and F3 was not as clear – it should be noted, however, that the distance between F2 and F3 in the spectral envelope of their synthetic vowels was not particularly large for these two vowel types). For the vowel /ɑ/, which has the most closely spaced F1 and F2 of all English vowels (and thus, the most distanced F2 and F3 of the vowels they tested), they report what appears to be a separation in the peak discharge rates at CF corresponding to F1, F2 and F3 separately at the lower presentation levels. At higher presentation levels (> 70 dB SPL), the distinct peaks appear to rate saturate. Provided these results, one could conclude that the auditory representation of vowel spectra is in terms of place (CF) and rate encoding. Given the inability to find reliable distinct peaks in the discharge rate at sound intensity levels greater than 70 dB SPL, however, in a follow-up paper, Young and Sachs (1979) replaced normalized rate and instead measured the temporal response patterns (defined as the amount of synchronization between the peak of a harmonic in the Fourier transform of the vowel and the discharge rate at that particular harmonic) of the nerve fibers, again at different CF along the auditory nerve. They find a better representation of the vowel spectra (including separation of F1, F2 and F3) throughout the range of sound levels used in the experiment. It seems, then, that a combination of rate, place and temporal coding provides an interpretable representation of vowels in auditory nerve fibers. Delgutte and Kiang (1984) report similar findings using two-formant steady state synthesized vowels, whereby the CF of the auditory nerve fibers closest to the spectral peaks of the auditory stimulus dominated the responses; subsequently, they delineate the tonotopically arranged fibers into five distinct CF regions centered around the largest spectral peaks in the vowel stimuli. Much of the work on vowel perception, however, has demonstrated the need for a transformation of the vowel space (i.e., a simple F2 by F1 coordinate system is an inadequate representation of the vowel space; see the formant ratio literature cited above and Rosner and Pickering 1994 for an overview).

Ohl and Scheich (1997) measured cortical patterns in response to vowels using FDG (2-Fluro-2-Deoxy-D-[¹⁴C(U)]Glucose Autoradiography) in euthanized gerbils. They found a vertical stripe of activity caused by vowel excitation along consecutive horizontal slices of A1 in auditory cortex. Boundaries of activity along the dorsal-ventral direction appeared to correlate with the distance between the first two formants; that is, the vowel /i/, which has a larger F2–F1 distance showed stripes that extended further dorsally than vowels with a smaller F2–F1 distance (e.g., /o/). Single formant vowels produced maximal vertical excitation across the cortical slices, suggesting neuronal inhibition in the calculation of relative differences between formants. These results provide support for the notion that auditory cortex calculates the relative differences between formant peaks as a means toward vowel perception, a result consistent with the central intuition of formant ratios as a mechanism in solving speaker normalization. Recent electrophysiological work is also consistent with this result. For example, Diesch and Luce (1997), using MEG, showed that the properties of the N1m/M100 (latency, ECD moment, ECD location) differed between responses to composite (two-formant vowel tokens) and the linear sum of its components, suggesting that the component spectral properties of a vowel (e.g., formants, harmonics, etc.) interact. Additionally, also using MEG, Mäkelä et al. (2003) showed that vowels having equal F2–F1 differences elicited equally strong N1m/M100 responses – again, suggesting that the calculation of differences between formants is a plausible algorithm employed by auditory cortex. It seems then, that the neurophysiological evidence supports the extraction of formant peaks in the auditory nerve and, with additional evidence from human electrophysiology, sensitivity to relative differences between formant peaks can be found in cortical responses. Whether these calculations occur prior to cortex remains to be seen. While the particular algorithm proposed in this paper has not been tested using such methods, the general notion that listeners are calculating relative differences between spectral peaks gains considerable evidence from this work – and provides support for the idea that work of this sort provides a tractable bridge between linguistics/psychology and neuroscience.

Conclusion

The goal of this paper was to test whether auditory cortex, and in particular the neurobiological generators of the M100 located in auditory cortex, were sensitive to formant ratios. In a pair of experiments using MEG, we found that the latency of the M100 is modulated by the F1/F3 formant ratio. These results also suggest, however, that the auditory system shows differential sensitivity to formant ratios depending upon where in vowel space the vowel categories are located. In particular, we found significant M100 latency differences to modulations of the F1/F3 ratio for tokens of the vowel categories /ɛ/ and /o/ but not /ə/. While we are hesitant to conclude that this is the algorithm wholly responsible for successfully eliminating variance based on inter-speaker variation in vowel perception, we suggest that the exploitation of higher formants in vowel normalization, in particular F3, could provide valuable insight into furthering our understanding of the perceptual and neurobiological mechanisms underlying speaker normalization.