Role of Computational Simulations in Heart Valve Dynamics and Design of Valvular Prostheses

Abstract

Computational simulations are playing an increasingly important role in enhancing our understanding of the normal human physiological function, etiology of diseased states, surgical and interventional planning, and in the design and evaluation of artificial implants. Researchers are taking advantage of computational simulations to speed up the initial design of implantable devices before a prototype is developed and hence able to reduce animal experimentation for the functional evaluation of the devices under development. A review of the reported studies to date relevant to the simulation of the native and prosthetic heart valve dynamics is the subject of the present paper. Potential future directions toward multi-scale simulation studies for our further understanding of the physiology and pathophysiology of heart valve dynamics and valvular implants are also discussed.

INTRODUCTION

The human heart consists of two pumps in series: the right heart pumping the blood to the pulmonic circulation; and the left heart to the systemic circulation. The valves in the human heart ensures that the blood flows only in the forward direction by opening during the forward flow phase and closing very efficiently minimizing regurgitation of blood to the chamber it came from. In the right heart, the tri-cuspid valve opens during ventricular diastole filling the right ventricle and closes during the beginning of the ventricular contraction preventing blood back into the right atrium. The pulmonic valve opens after isovolumic contraction for the blood to flow into the pulmonary artery and closes efficiently at the beginning of ventricular relaxation. The mitral valve between the left atrium and the left ventricle and the aortic valve between the left ventricle and the aorta play similar roles in the left heart. Since the valves in the left heart are subject to higher pressures than those in the right heart, valvular diseases such as stenosis and incompetency are more common with the mitral and the aortic valves. Valves open and close for more than 100,000 times per day and the leaflets undergo complex deformation during a cardiac cycle. The time-dependent blood flow past these valves is also highly three-dimensional. There is a general consensus that the mechanical stresses induced on the valvular structures during its function as well as the flow-induced stresses during a cardiac cycle play a significant role in the etiology of valvular diseases. Treatment for diseased valves includes valvular repair or replacement with prosthetic heart valves. At present, the commercially available valvular prostheses include mechanical heart valves (MHV) or bioprosthetic heart valves (BHV). Bioprostheses are either preserved porcine aortic valves or valves made from preserved bovine pericardial tissue. Durability of these implants is still a significant problem with the average life of about 12 years for a BHV before a replacement surgery is necessary. The failure of the preserved tissue in these valves can also be related to the regions of stress concentration in the leaflets during its function. MHV made with artificial material such as pyrolytic carbon are strong and durable. However, thrombus deposition on the structures of the valves and ensuing embolic complications with the rupture of the thrombus is the major problem with the MHV and patients with these implants require long-term anticoagulant therapy. Regions of abnormal flow past the MHV inducing relatively high shear stresses activating platelets is considered to be a major factor resulting in thrombus deposition with these types of valves. Thus a detailed analysis of the dynamics of the heart valves is of interest in our understanding of the complex function of the healthy native heart valves, etiology of valvular diseases, alterations in the valve dynamics with congenital malformation, as well as the problems associated with replacement valves.

During the past four decades, numerous studies have been reported on the valve dynamics providing valuable information on the functional analysis of native and prosthetic heart valves and the relationship between mechanical stresses and etiology of diseases. These studies have included in vivo and in vitro experimental measurements as well as computational analysis. In general, in vivo experimental studies require acquisition of data from human subjects or in animal models, and they are more expensive and only limited data can be obtained due to experimental limitations. In vitro experiments require use of expensive and sophisticated equipment for the measurements and once again the measurements are limited particularly near the valvular structures due to optical accessibility. Nevertheless, experimental data play an important role in our understanding of the valve dynamics in realistic conditions and complement simulations in addition to providing data for validation of the computations. Computational simulations are rapidly gaining importance in the research in the understanding of the complex physiology of the native and prosthetic valve dynamics. With the advent of high speed computational capabilities and developments in advanced computational techniques for biological soft tissue and blood flow, computational simulations are providing more detailed results on the dynamics of the valvular structures and flow across the valves in a range of spatial and temporal scales. In recent years, computational analyses are also being employed for initial optimization of design of implants before the prototypes are built and expensive experimental evaluations are conducted. In general, detailed and realistic computational analyses for native and prosthetic heart valves require: (1) morphologically realistic three-dimensional geometry of the valvular apparatus; (2) constitutive relationships for the valvular structures and blood; and (3) appropriate boundary conditions and physiological loads that the valves are being subjected to in a cardiac cycle. Once a simulation for a particular application is developed, the validation of the results with measured data under similar conditions cannot be over emphasized before the simulations are applied for specific problems to be addressed. In this article, some of the most recent computational studies that have been reported in the literature on the native and prosthetic heart valve dynamics are reviewed and potential future areas of computational developments are discussed. The first part of the article includes studies performed on the aortic and mitral valve dynamics as well as BHV and the simulations performed on the dynamics of MHV are discussed in the second part.

SIMULATION OF NATIVE HEART VALVES AND BHV

The human aortic valve¹²⁶ apparatus consists of the aortic root, the three leaflets, and the aortic sinuses. The aortic root is a fibrous annular ring separating the aorta from the left ventricular outflow tract. The details of the anatomy of the aortic valve and the microstructure of the three semicircular (semilunar) leaflets have been described in detail previously.^114,126 The leaflets undergo complex deformation pattern during the opening and closing phases of the cardiac cycle and are subjected to tensile and compressive in-plane and bending stresses during a cardiac cycle. The mitral valve apparatus consist of a saddle-shaped valve annulus, anterior and posterior leaflets inserted to the connective tissue of the annulus, and the chordae tendinae attached to the free edges of the leaflets at several locations on one end and to the papillary muscles on the other end.⁶² The tethering of the chordae plays an important role in the deformation of the leaflets and also prevents the leaflets from prolapsing into the left atrium during ventricular systole.

The dynamic simulation of tissue heart valves can be divided into two categories. The first is the finite-element (FE) structural analysis in which the interest is on the deformation pattern and stress distribution on the leaflets. In such an analysis, the pressure exerted by the fluid on the leaflets at the appropriate surface of the leaflet is specified with uniform pressure boundary condition and the simulation does not involve the solution of the blood flow dynamics past the valve prostheses. The assumption of uniform pressure boundary condition on the leaflet surface ignores any variation in the pressure load as well as the effect of flow-induced shear stresses on the leaflets due to the three-dimensional flow in the vicinity of the valve. The second category of the dynamic simulations involve a detailed fluid–structure interaction (FSI) analysis in which both the structural analysis of the valve apparatus and the fluid dynamic analysis of blood flow past the valve are coupled at the interface between the fluid and biological soft tissue. In addition to the computation of leaflet deformations and stress patterns, FSI analysis will also enable the computation of detailed flow dynamics past the valves.

Finite Element (FE) Structural Analysis

FE analyses have been employed to describe the deformation pattern and stress distribution on the leaflets since the regions of stress concentration have been suggested as a factor leading to leaflet calcification and subsequent structural failure^126,127 and through non-calcific deterioration of the leaflet structures.¹¹² Such an analysis can also be employed to perform parametric studies on the valve geometry and dimensions in order to optimize the design of prosthetic valves as well as in valve repair strategies. The requirements for the FE analyses include the detailed 3D geometry as well as the material description of the valvular structures.

3D Geometry

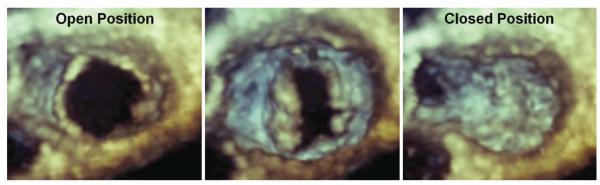
Even though earlier FE analyses employed valve geometry based on mathematical models^41,44,59 and geometry constructed based on the typical dimensions of the human aortic valve,^42,126 more recently, advent of several imaging modalities such as ultrasound, computed tomography (CT), and magnetic resonance (MR) imaging have afforded reconstruction of morphologically realistic 3D geometry of the valvular apparatus for detailed structural analysis. Ultrasound imaging has the advantages of being relatively inexpensive and non-invasive. Echocardiographic images can capture the rapid motion of the valve structures during a cardiac cycle and functional information on blood flow and regurgitation can also be obtained by the use of color Doppler ultrasound. However, disadvantages of this modality include a restricted window for imaging in some patients, low signal-to-noise ratio compared to CT and MR imaging, and acoustic reflection and ultrasound attenuation. Echocardiographic data have been employed to analyze the shape and motion of the mitral annulus in cardiomyopathic patients,³⁴ annular shape changes with mitral valve regurgitation,⁶⁹ and 3D volumetric reconstruction of the mitral valve geometry.¹³² More recently real time 3D echo imaging has afforded morphologically realistic 3D geometrical reconstruction of the mitral valves at various times in the cardiac cycle. Non-planarity of the mitral valve annulus,¹⁰⁸ and the effect of annular shape on leaflet curvature and leaflet stresses¹¹⁵ have been reported with 3D echocardiographic imaging. Applications have also included the assessment of mitral valve function in normal subjects and with valvular pathology.^20,109 An example of a reconstructed image of the human mitral valve from 3D echocardiographic image data is shown in Fig. 1.

FIGURE 1.

An example of reconstructed human mitral valve from 3D echocardiographic data (Courtesy of Dr. Hyunggun Kim, Ph.D., University of Texas Medical Center at Houston, Texas).

The advantage of CT and MR imaging for valvular studies is the relatively clearer images with a high signal-to-noise ratio. However these imaging modalities suffer from difficulties in capturing the moving leaflets and the cost of imaging equipment and data acquisition. In addition, CT imaging also involves risks associated with radiation exposure and contrast injection. Multi-slice CT imaging has been employed to obtain volumetric data on aortic valve leaflet calcification.⁹⁸ Annular geometry of the mitral valve with valvular regurgitation has been analyzed with MR images⁶⁸ and a motion compensated MR valve imaging²⁸ has been reported to overcome the problem of valve motion in the capturing of images. Further advancements in imaging data acquisition and processing techniques will enable us to obtain morphologically realistic 3D geometric data of aortic and mitral valves for the simulation of heart valve dynamics.

Material Property Description for the Valvular Structures

The second important component of the analysis of dynamics of native and bioprosthetic tissue heart valves is the realistic material property specification. During the opening and closing phases, the leaflets of the aortic and mitral valves undergo large and complex deformations and realistic simulations require knowledge on the mechanical behavior of the leaflets. The aortic valve leaflet is a tri-layered structure consisting of a spongiosa layer sandwiched by fibrosa (on the aortic side) and ventricularis (on the ventricular side) layers.^114,126 Ventricularis layer is composed of a dense network of collagen and elastin fibers, and the fibrosa layer consists of a network of predominantly collagen fibers. The fibrosa layer is thought to be the main load bearing layer of the leaflet. The spongiosa layer consists of mainly proteoglycans and apparently does not bear the mechanical load on the leaflet. Numerous interconnecting structures are present in this layer that couple the fibrosa and the ventricularis layers. The collagen fibers are generally oriented in the circumferential direction of the leaflet while the elastin fibers are oriented in the radial direction. The collagen fibers can withstand high tensile stresses and have low torsional and bending stiffness. Hence the orientation of the collagen fibers also represents the direction in which the leaflet withstands high tensile stresses. Orientation of the collagen fibers in aortic valves has been determined with the aid of small angle light scattering technique.¹¹³ At lower transvalvular pressures, the collagen is in a crimped state and the fibers straighten out with increasing load on the leaflets.¹¹⁴ Due to the specific fiber orientations, the leaflets exhibit mechanical anisotropy and non-linear stress–strain relationships. A number of studies have been reported in the last two decades on the experimental determination of the load-deformation behavior of heart valve leaflets and are succinctly summarized elsewhere.¹¹⁴ Earlier tests on valvular tissues were restricted to uniaxial load-deformation behavior and these studies have been able to demonstrate the alterations in mechanical behavior of the leaflets after chemical fixation for bioprosthetic valves. More recently biaxial testing has been performed toward constitutive modeling of the leaflets. Even though some bi-axial tensile behavior of the mitral valve leaflets have been reported in the literature,^55,56,93,94 most of the detailed mechanical analysis have been reported with the aortic valve leaflets. These studies have included biaxial testing and constitutive model development,^9,10 biaxial testing of the individual load bearing fibrosa and ventricularis layers,¹²³ and flexural response of the leaflets.^32,95 Such detailed experimental studies have made it possible to specify physiologically realistic constitutive relationship for the leaflets in the biomechanical simulations of heart valves. Even though the leaflets undergo larger and complex deformations compared to the other structures within the valvular apparatus, the importance of the shape and deformation of the annulus on the valvular function has been reported particularly for the mitral valves.^69,115 Hence experimental determination of the constitutive relationship for other structures of the valvular apparatus will also aid in more realistic simulation of the complex interaction among the structures in the normal valve dynamics and in valvular diseases.

Even with the dynamic analysis of the leaflet dynamics with experimentally determined constitutive relationships, validation of the resulting leaflet deformation with experimental data is necessary. One of the common comparisons for validation is the computed local regional strain on the leaflets with those measured experimentally. Thubrikar et al.^128,129 pioneered such studies with radiopaque markers sutured directly to the leaflets and capturing the motion of the leaflets in vivo using biplane fluoroscopy. They were able to measure the dimensions of the leaflets and local strains in the circumferential and radial directions. More recently, three-dimensional motion of the surface markers have been tracked to compute the local strain on the leaflets in vitro for the mitral valves.^60,61,110 Sonomicrometry technique has been employed to measure the local strains of mitral valve leaflets in vivo in animal models.^43,86 Measurement of local strains with such techniques will be invaluable in comparing the results with dynamic simulations in order for validation of the computational results.

FE Analysis

Earlier FE studies employed idealized models of the aortic valve,⁴⁴ bioprosthetic heart valves,^58,59 and synthetic valve designs^18,41 and the analyses were mostly performed with the leaflets in the closed position since the larger pressure loads on the leaflets occur with the valves in the fully closed position. Linear isotropic material property specifications were employed for the synthetic leaflet material while for the biological tissue valves, analyses included non-linear stress–strain relationship employing a step-wise linear analysis. With the leaflets in the closed position, with increasing pressure loads, coaptation area between leaflets also increases and hence with each increment in loading, nodes were checked for potential contact with neighboring leaflet and contact boundary conditions were specified. Generally the valve annulus was assumed to be rigid relative to the flexible leaflets where as the effect of flexibility of the stents for the bioprosthetic valves were considered in the analysis. Resulting regions of stress concentration are generally correlated with regions of calcification and/or leaflet tear with implanted valves. Rousseau et al.¹⁰⁷ incororated the fiber reinforcement and the viscoelastic properties of a porcine bioprosthetic valve leaflet in their FE analysis with time-varying pressure load on the leaflets. Due to the large and complex deformations of the leaflets during a cardiac cycle, the use of membrane elements in the analysis does not account for the effect of leaflet bending. The importance of the incorporation of the non-linear material property of the leaflets in the analysis was also pointed out¹⁰⁰ and hence subsequent stress analysis of tissue valve leaflets incorporated shell elements in the analysis with non-linear isotropic material specification for the leaflets.^11,63,64,100 Li et al.⁸⁵ and Sun et al.¹²⁴ have reported on the use of non-linear anisotropic model for the leaflet tissues in the FE models.

Grande et al.⁴⁹ have reported on a FE analysis of the human aortic root and the valves with the geometry of the valve–root complex obtained from MR images of human valve specimens preserving the asymmetric geometry and the regional thickness variations in the geometry were also incorporated. They employed higher order elastic shell elements and incorporated anisotropic material behavior coinciding with the collagen fiber alignment. Subsequently they extended the analysis to study the effect of aging, aortic root dilatation and Marfan syndrome on valvular incompetence.^50,51,53 That group also have reported on an aortic valve structural analysis to study the effect of graft shape and stiffness as well as the geometry of the sinus on aortic valve sparing.^52,54

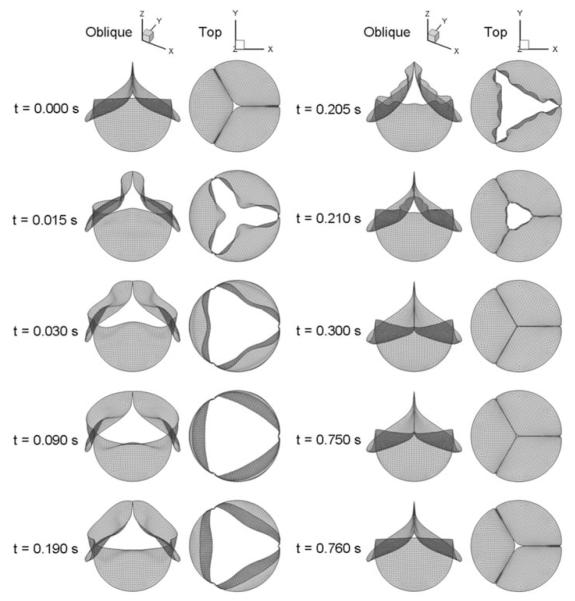
More recently several studies have been reported on the dynamic simulation of the aortic valve throughout the cardiac cycle including the opening and closing phases of the valve function.^42,122 These studies employed a computer-aided design model of the human aortic valve and the root and performed a dynamic analysis employing shell elements with linear elastic properties for the valve and the root. Contact elements were used to simulate the coaptation of the leaflets during the closing phase of the valve dynamics and the importance of the use of the flexible model for the aortic root and the interaction between the root and the valve in the proper functioning of the valves were emphasized in this study. Kim et al.^70,71 have reported on a dynamic simulation of a pericardial bioprosthesis with the geometry of a commercially available valve. Experimentally determined in-plane biaxial loading¹²⁵ and three-point bending⁹⁶ data for the glutaraldehyde treated pericardial tissue specimen were specified with pressure boundary conditions on the leaflets during the opening and closing phases. These studies emphasized the use of experimentally determined material property for the leaflets for more realistic simulation of the native and bioprosthetic heart valve dynamics. Figure 2 shows an example of the sequence of leaflet displacements for a pericardial bioprosthetic valve from a dynamic FE simulation with experimentally determined material property specification for the leaflets.

FIGURE 2.

Sequence of displacements of the leaflets of a pericardial bioprosthetic valve during a cardiac cycle (Reprinted from Kim et al.⁷¹ with permission from Springer Science + Business Media).

Complicated anatomical structure of the mitral valve including a non-planar saddle-shaped annulus and the presence of chordae tendinae at the free edge of the leaflets presents additional challenges in the structural analysis. Salgo et al.¹¹⁵ employed a linearly elastic, orthotropic model for mathematical models of the mitral valve leaflets under static loading in order to analyze for the effect of the saddle-shaped annulus in reducing the leaflet stress. Lim et al.⁸⁸ performed a quasi-static FE analysis with linear isotropic material model for the leaflet of a mathematically derived model of a mitral valve to analyze the effect of asymmetry. Kunzelman et al.⁷⁸ developed a geometry of the mitral valve from an excised porcine specimen and employed a dynamic FE model with a linear elastic and anisotropic material properties for the leaflets. They further exploited the model to analyze the effect of tissue thickness, annular circumference and rigid or flexible annuloplasty ring on the stresses on the leaflets.^80–82 This FE model has been further exploited to analyze for the optimal annuloplasty ring prosthesis geometry for the treatment of mitral regurgitation.^90,136 Edge-to-edge surgical repair of the mitral valve leaflets is a common treatment to correct mitral valve prolapse. The effect of suture size and position on the repair technique has been analyzed with FE models.^8,23,137 The above studies represent the effective use of FE structural analysis on objective evaluation of surgical repair techniques and implant geometries on the optimal treatment for the complex organ such as the mitral valve.

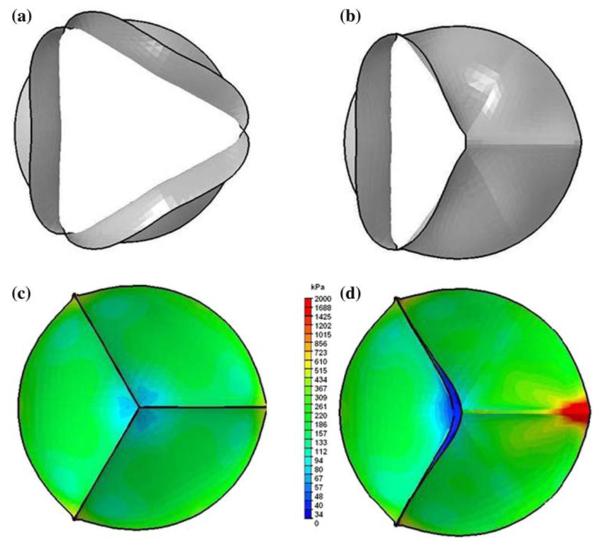
Another important application of mechanical analysis of valve dynamics is for the congenital bicuspid aortic valves (CBAV). CBAV is prevalent in 1–2% of the population and occurs twice as often in males.¹⁴¹ About one third of those patients with CBAV will face clinical complications including aortic regurgitation, infective endocarditis, coarctation of the aorta, aortic dissection, and ascending aortic dilatation requiring surgical interventions.³³ The geometry of the CBAV is generally the result of fusion of two leaflets and varies among patients. Mechanically the dynamics of the CBAV can be anticipated to be significantly different from that of a normal healthy tri-leaflet aortic valve and details of the structural analysis of CBAV dynamics is lacking in the literature. Figure 3 is an example of the valve orifice for a simulated CBAV compared with that of normal aortic valve geometry and it can be observed that the orifice in the fully open position for the CBAV is about 30% of that for the tri-leaflet valve.⁶⁶ The preliminary dynamic analysis of the results presented in this figure employed a non-linear anisotropic material description of the leaflets.⁷¹ The shape of the orifice in the open position for the bicuspid valve is qualitatively similar to that observed by Robicsek et al.¹⁰⁶ with cryopreserved and then thawed valves inserted in a pulse duplicator. Weinberg et al.^138,139 have presented a multi-scale simulation of the aortic valve dynamics. FE analyses were performed for the aortic valve dynamics at the organ level, at the tissue level with the three layers of the leaflet, and at the cell-level to analyze for the cellular deformation with the external load. The need for multi-scale simulations is further discussed in a subsequent section below.

FIGURE 3.

Comparison of the valve orifice in the fully open position (a: Normal tri-leaflet valve geometry; b: simulated bicuspid valve geometry where the two leaflets on the right are fused) and the von Mises stress distribution on the leaflets in the fully closed position (c: tri-leaflet aortic valve; and d: simulated bicuspid aortic valve) from dynamic FE analysis from Jermihov et al.⁶⁶.

FE analysis has been successfully employed hitherto in quasi-static and dynamic 3D analysis of the complex deformation of the leaflets and for the identification of regions of stress concentration that can be correlated with leaflet calcification and structural failure. With the advent of 3D imaging and image processing techniques, use of patient-specific morphologically realistic 3D geometry of the heart valves for the structural analysis is becoming a reality. Experimental techniques for the determination of the bi-axial in-plane force deformation as well as flexural properties of the leaflets have been reported in the literature. However, it is not feasible to determine the patient-specific material behavior of the leaflets and other valvular structures for the analysis and material property specifications need to depend on published data from experimental studies. The boundary conditions employed in the dynamic analysis is the time-dependent pressure difference across the leaflet and hence ignores the local variations on the pressures and fluid shear stresses due to the blood surrounding the leaflets during the cardiac cycle. It can be anticipated that the pressure difference across the leaflet is the principal load inducing the leaflet deformation and assuming a uniform pressure distribution on the leaflet surface should yield reasonably accurate results and the accuracy of such an analysis can be verified by comparing the computer-predicted local strains with experimentally measured magnitudes. It can be anticipated that patient-specific dynamic analysis will be routinely employed toward optimal valve repair techniques. Dynamic simulations will also play a larger role in designs of bioprosthesis with improved durability and in the development of engineered tissue valve prostheses.

More accurate dynamic analysis of tissue leaflet heart valves need to incorporate the blood flow during the valvular function and will require an accurate fluid–structure interaction (FSI) analysis. Such an analysis will find applications on our understanding of the flow development past the valves in the ascending aorta. As an example, it is known that in a significant percentage of patients with bicuspid aortic valves, dilatation and dissection of the ascending aorta is also commonly observed. As can be observed from Fig. 3, substantial changes in the valve orifice area in patients with bicuspid valves may lead to abnormal flow past the valve during the opening phase of the valves. The effect of any potential impingement of the flow on the wall of the ascending aorta on the problems encountered in the ascending aorta of patients with bicuspid aortic valves has not been explored and will require a detailed and accurate fluid–structure interaction analysis. In addition, our increased understanding of the effect of vortical flow in the aortic sinuses on the closing dynamics of aortic valves, the interaction between the mitral valvular structures and the ventricular chamber flow during the filling and ejection phases, the effect of valvular repair and/or annuloplasty implants on regurgitation with aortic and mitral valves also require a detailed FSI analysis.

FSI Analysis

In the dynamic function of the heart valves, the valvular structures such as the leaflets move due to the fluid forces (hydrostatic pressure and flow-induced shear stresses on the leaflets at the interface between the leaflets and the blood). In turn, as the leaflets undergo large deformations both during the opening and closing phases, the fluid dynamics is also constantly changing due the motion and forces exerted on the fluid by the valvular structures and also the change in the geometry of the flow domain. FSI analyses of tissue heart valve dynamics presents several challenges in the computational simulation. The leaflet material exhibits a highly non-linear, anisotropic behavior and undergoes large and complex deformation and the flow past the valvular structures results in a complex three-dimensional time-dependent flow and both the solid and fluid dynamics must be accurately resolved.

Three-dimensional time-dependent reconstruction of the valve geometry during a cardiac cycle will also provide the instantaneous leaflet position at any time. One method for detailed fluid dynamic analysis is to prescribe the kinematics of the leaflets as moving boundary in the unsteady flow problem¹¹⁴ and thus avoid the leaflet structural analysis. Such an analysis demonstrated the presence of instability of the shear layers emanating from the leaflets resulting in complex vortex shedding distally. Important differences in the shear stress field on the ventricular and aortic side surfaces of the leaflets were also pointed out in this analysis. However, such an analysis will not provide any information on the stress distribution on the leaflets.

In order to enforce kinematic compatibility (i.e. no slip and no penetration for viscous fluids) and the dynamic equilibrium at the interface, FSI analysis requires the solution for the fluid domain using an Eulerian formulation and for the solid structures employing a Lagrangian formulation and these two formulations are incompatible.²⁵ The details of the approaches to coupling at the interface between the solid and the fluid employed in the FSI analysis of heart valve dynamics, including the immersed boundary method, immersed interface method, finite element method, fictitious domain method and the arbitrary Lagrangian–Eulerian (ALE) methods are described in Vigmostad.¹³⁴ Sotiropoulos and Borazjani¹²¹ also discuss the problems encountered in the treatment of the interfaces with respect to mechanical valve dynamics simulation. Peskin and colleagues pioneered the immersed boundary method for the FSI analysis of the left ventricular chamber and valvular prostheses in the mitral position.^101–104 Problems encountered in this method include smearing of the interfaces and time-step limitations due to the high structural force combined with low fluid viscosity. Makhijani et al.⁹¹ have reported on a 3D FSI analysis of a generic pericardial bioprosthesis in the aortic position. Pericardial tissue was modeled as an isotropic hyperelastic material and coaptation of the leaflets was modeled with contact of the leaflets with a symmetry plane. Influence coefficient technique was used to couple the structural and flow solvers and the results on the valve opening orifice area was compared with experimental results. Velocity vectors during the valve opening phase are presented even though detailed validation of the results is lacking in this work. ALE method in which the fluid mesh is continuously adapted without modifying the mesh topology has been successfully employed in the analysis of arterial flow dynamics. However, in valve dynamics, where the leaflets undergo large deformations, mesh adaptation is difficult without loss of mesh quality or without changing the mesh topology. Alternately remeshing can be performed and this procedure may result in artificial diffusivity and the computations are extremely difficult for 3D analysis. De Hart et al.^24–26 have treated the coupling between the solid and the fluid at the interface with a fictitious domain method. In a 2D FSI analysis with a single leaflet in a rigid channel with a simulated aortic sinus, the leaflet was assumed isotropic with a linear elastic behavior and the mass of the leaflet was neglected in the dynamic analysis.²⁵ The analysis was extended to study the dynamics of a fiber-reinforced stentless aortic valve prosthesis²⁴ and for a 3D analysis of the aortic valve.²⁶ In this study the valve leaflets were assumed to behave in a linear elastic and isotropic Neo-Hookean constitutive model. The same group also reported on a FSI analysis to demonstrate that the collagen fibers on the aortic valve leaflet reduce the stresses and stabilize the motion of the leaflets during the opening phase of the valve dynamics.²⁷ These studies encountered numerical instabilities for analysis with physiologically realistic Reynolds numbers.¹³⁴ The accuracy of the treatment of the interface boundaries with the fictitious domain method is lower and hence its usefulness in the detailed computation of stresses on the leaflets is also limited.²⁹ A partitioned strongly-coupled method has also been proposed for the FSI analysis of valves with flexible leaflets¹³³ and the leaflets were modeled with segments connected with frictionless pivots and torsional springs. Carmody et al.¹⁷ have presented a two-stage approach for the FSI analysis of the aortic valve. In the first stage, the flow dynamics in the left ventricular outflow tract is computed employing the LV geometry and wall motion from experimental data. The computed flow velocities are prescribed as inflow data for the FSI analysis of the aortic valve in the second stage. A 2D FSI analysis of the mitral valve dynamics has been presented by van Loon et al.¹³¹ in which a Lagrangian multiplier based contact algorithm is incorporated for the interaction of fluid boundaries with solid surfaces. Kunzelman et al.⁷⁹ have presented on a 3D FSI analysis of the mitral valve. In this study, anisotropic non-linear material property was specified for the leaflets while the blood was assumed to be compressible and thus employing an artificial compressibility approach in the analysis. However, the bulk modulus was modified to be representative of that of air for computational efficacy and hence the simulations were not representative of the physiological flow conditions. The FSI analyses reported to date have encountered numerous numerical challenges and the solutions have been generally restricted to non-physiological flows and with inadequate grid resolutions.

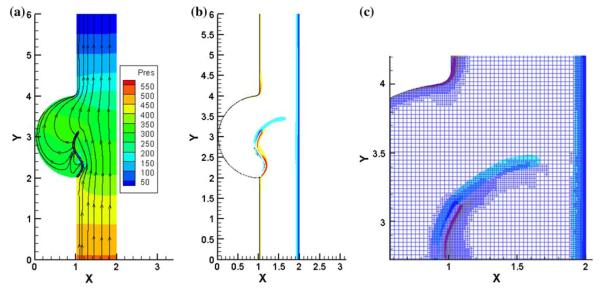
In order to overcome the challenges faced in the FSI analysis of heart valve dynamics, Vigmostad^134,135 has employed a fixed Cartesian grid flow solver in order to avoid remeshing that becomes necessary with the complex motion of the leaflets. The material property specification for the leaflets was based on experimentally determined in-plane and flexural load-deformation characteristics for pericardial valve prosthesis. The solid interfaces in the computational domain are identified accurately employing a sharp-interface level-set technique and updating the level-set field with the leaflet deformation. Strong coupling is employed for the treatment at the interfaces and a local mesh refinement technique is incorporated in the flow solver in order to resolve the flow accurately at the leaflet interface. The method has been successful in the simulation of the flow past the aortic valve in a 2D model with physiologically realistic leaflet material properties and Reynolds numbers for flow. Figure 4 shows an example of a 2D FSI analysis with physiologically realistic material property for the leaflet⁷¹ and the vorticity distribution plot on the leaflet surface with the valve in the fully open position. The leaflet in the fully open position exhibits an ‘s’ shaped geometry compared to the deformation with a stiffer fiber-reinforced artificial prosthesis leaflet deformation reported in de Hart et al.²⁵ In order to extend this analysis for 3D valve dynamics with physiologically realistic flow conditions, the code is currently being parallelized and validated rigorously.

FIGURE 4.

Results from a 2D FSI analysis of an aortic valve¹³⁴: (a) pressure contours and stream line plots with the leaflet in the fully open position; (b) and (c): Vorticity plots on the leaflet surfaces. Physiologically realistic material property was employed for the leaflets and the fluid dynamic analysis included physiologically realistic Reynolds numbers (Courtesy of Sarah Vigmostad, Ph.D. of the University of Iowa).

For a realistic simulation of the heart valve dynamics and in increasing our understanding of the details of the leaflet deformation and stresses as well as the fluid induced stresses on the leaflets, 3D FSI analysis with physiologically realistic leaflet material specification and solutions incorporating physiological flow conditions is necessary. With innovative experimental techniques, it is now becoming possible to incorporate structural material properties for the valvular structures and hence compute the local deformation characteristics more accurately. With rapid advancement of the FSI analysis by several groups, more realistic simulations should be realized in the near future and these simulations will be very valuable in our understanding of the biomechanics of the native heart valves, relationship between the mechanical forces and valvular diseases, and as an objective assessment of interventional techniques.

SIMULATIONS OF MHV DYNAMICS

Mechanical heart valves are being implanted as replacement of diseased valves in more than 50% of the patients undergoing valve replacement therapy.¹ The commercially available tilting disc and bi-leaflet mechanical heart valves (MHV) have occluders made of pyrolytic carbon and for the bi-leaflet valves, even the housing is made of the same material. Pyrolytic carbon is chemically inert and highly durable and hence mechanical valves can be functional in a patient for several decades. However, a significant problem encountered with the MHV implants is the propensity for thrombus deposition on the valvular structures and subsequent embolic complications. Hence patients with MHV require long-term anticoagulant therapy. Since the geometry of the commercially available MHV are drastically different from the native or bioprosthetic heart valves, non-physiological flow past these valves can be anticipated and there is a general consensus that the tendency for thrombus initiation with MHV is related to the flow dynamics past the valve prostheses. Over the past five decades a vast number of in vitro experimental studies and computational simulations have been reported in the literature on the measurement and computation of the flow dynamics past the MHV and correlation of the flow-induced stresses with platelet activation and aggregation subsequently resulting in thrombus deposition.

Unlike with tissue valve prostheses, the leaflets of MHV are relatively rigid and due to the relatively strong material that the leaflets are made of, there is very little interest in the stress distribution on the leaflets. Hence experimental and computational studies concentrate on the detailed flow dynamics including regions of high viscous and turbulent shear stresses and also regions of flow stagnation where activated platelets may further aggregate and attach to the valve structures. FSI analysis of MHV dynamics will generally employ a single equation of motion for the leaflet. The flow passes through gaps of relatively small dimensions through the hinge regions where the leaflets interact with the valve housing in the case of bi-leaflet MHV and also through narrow gap width between the leaflet edge and the valve housing in both the bi-leaflet and tilting disc MHV prostheses. The flow in these regions needs to be resolved very accurately in order to identify magnitudes of high shear stresses that the formed elements in the blood can be subjected to in these regions. In developing the FSI analysis for MHV, the rapid changes in the geometry during a cardiac cycle need to be taken into account and the problems associated with the treatment at the interface between the boundaries of the moving leaflets and the blood is discussed in detail in Sotiropoulos and Borazjani.¹²¹

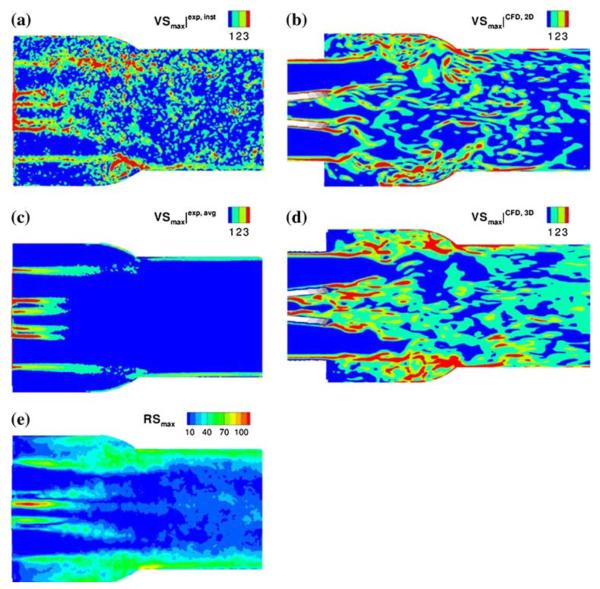
In flow past the MHV during the acceleration and deceleration phases of forward flow past the fully open MHV in the aortic position, flows with relatively large Reynolds numbers can be anticipated resulting in high shear flows past the valve leaflets and housing and turbulent shear stresses downstream from the valve in the ascending aorta. Avoiding the complications of a FSI analysis, earlier studies have generally analyzed the detailed flow past the tilting disc and bi-leaflet valves with the leaflets in the open position modeling the tilting disc^75,117,118 and bi-leaflet valves.^38,39,73,74 Ge et al.³⁹ reported on an unsteady laminar 3D flow simulation with the leaflets in the fully open position, Subsequently they reported³⁸ on a steady flow analysis employing direct numerical simulation (DNS) with a laminar flow model and with unsteady Reynolds-averaged Navier-Stokes (URANS) simulation as well as a detached eddy simulation (DES) approaches to model turbulent flow past a bi-leaflet valve geometry. King et al.^72,74 have reported on the simulation of unsteady flow past two bi-leaflet valve models with the leaflet fixed in the fully open position and the prime motivation of these studies was to analyze for the effect of leaflet angular position on the flow development downstream from the valve. Their results showed that with increasing opening angle of the leaflet, the wake downstream from the leaflet decreased in size, and yet the maximum velocity and shear stresses increased. Bluestein et al.¹² employed a Wilcox k × ω turbulence model for transient turbulent flows past bi-leaflet valves with the leaflets in the open position to investigate the effect of valve placement in the orifice and implantation techniques on free emboli formation distal to the valve. Vortex shedding in the flow past the open leaflets has been suggested as a mechanism for free emboli formation with the implanted mechanical valves.¹³ Shi et al.¹¹⁶ employed a moving boundary analysis for the simulation of moving leaflets for the analysis of laminar flow past bi-leaflet valves during the opening phase. Alemu and Bluestein⁶ have proposed a platelet activation and damage accumulation model coupled with a 3D flow analysis through a fully open bi-leaflet valve to quantify the thrombogenic potential for cardiovascular implants. Ge and Sotiropoulos⁴⁰ have reported on a curvilinear immersed boundary method for FSI analysis of heart valve dynamics. They reported on the flow dynamics past mechanical valve prostheses³⁷ and the study is focused on the acceleration and deceleration phases during the forward flow past the valve in the aortic position. They discuss the relative importance of the viscous shear stresses in the aortic root during the acceleration phase and the turbulent shear stresses present during the deceleration phase measured with DPIV experiments. They propose that the Reynolds shear stresses do not contribute to the mechanical load on formed elements of blood and the instantaneous viscous shear stresses are more appropriate measure for damage to blood cells. Plots of the experimentally measured viscous and Reynolds shear stresses in flow past a bi-leaflet valve during the deceleration phase and comparison of the computed viscous shear stresses from this work is shown in Fig. 5.

FIGURE 5.

Comparison of experimentally measured (left column) viscous shear stresses (a and c) and Reynolds shear stresses (e) with computational results (b and d) of viscous shear stresses (Reprinted from Ge et al.³⁷ with permission from Springer Science + Business Media).

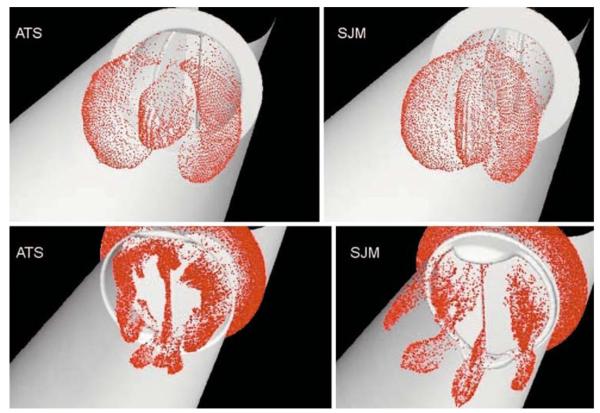
More recently, numerous studies employing FSI analysis for the flow past mechanical valves with moving leaflets have been reported. Dumont and colleagues^29–31 have presented a FSI analysis of flow past bi-leaflet valve employing a laminar flow analysis. Particle dynamics analysis was employed³⁰ to simulate platelets and platelet shear histories were calculated during the forward flow phase with the leaflet in the fully open position and in the regurgitation phase with the leaflets in the fully closed position. The results indicated that shear stresses to the level exceeding the threshold for platelet activation are present only during the regurgitation phase. However, the platelet shear history calculations were performed with the leaflets fixed in the fully open and fully closed positions and hence these calculations ignored the fluid dynamic alterations due to the rapid closure of the leaflets during the closing phase of the cardiac cycle. Figure 6 shows the dispersion patterns of particles simulating platelets for the stress accumulation computations with fixed leaflets in the open and closed positions for two different bi-leaflet valve models.³⁰ Borazjani et al.¹⁴ have reported on the FSI analysis with the curvilinear immersed boundary method for high resolution flow analysis for valve dynamics. Morbiducci et al.⁹⁷ have reported on a computational analysis of blood damage safety with prosthetic heart valves. Computing the shear stress–time history of particles simulating the blood platelets in the flow simulation, they predict that platelet activation is more in late systole of the forward flow phase and span wise vorticity has more influence in the activation compared to the stream wise vorticity.

FIGURE 6.

Disperson of particles simulating platelets during forward flow phase (top row) and during the regurgitant flow phase with the leaflets in the fully closed position (bottom row) are compared for open pivot (left column) and recessed hinge (right column) bi-leaflet valve models (Reprinted from Dumont et al.³⁰ with permission from ASME Press).

The simulations described above have concentrated on the details of the flow dynamics past the valve prostheses in the aortic position and have described in detail the complex flow pattern resulting from shed vortices from the leaflets during the acceleration phase and the turbulent flow that develops during the deceleration phase. Some studies have also looked into the nature of the regurgitant flow past the valve with the leaflets in the fully closed position. The viscous shear stresses and Reynolds shear stresses have been either measured or computed employing transient turbulent flow models and it is suggested that platelets being subjected to high shear stresses will be activated. Hemolysis and platelet activation and aggregation can be anticipated as the blood cells pass through such complex flow regimes, but blood is moving away from the valvular structure during the forward flow phase of the cardiac cycle and hence the damage to formed elements of blood can be anticipated to affect the physiology downstream. Furthermore, the details of the flow dynamics in the small gap widths in the hinge region of bi-leaflet valves and between the leaflet edge and the valve housing in the peripheral edge adjacent to the valvular structures has not been examined in detail in these studies.

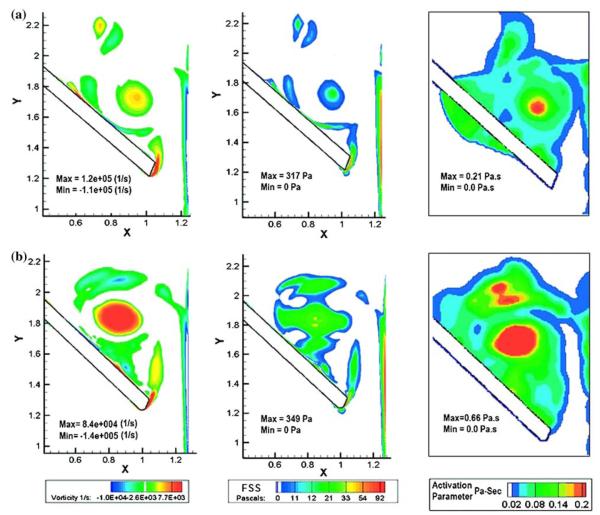
With reports of structural failure with one model of a bi-leaflet valve,^67,76 experimental and computational simulations have also been reported addressing the complex fluid dynamics in the vicinity of the valvular structures during the closing phase of mechanical valves.^19,83 The closing phase dynamics will be more significant with the valve in the mitral position since the leaflets close due to higher pressures on the leaflets from the left ventricular contraction compared to that in the aortic position. Risk of embolism has also been reported to be higher with mechanical valves in the mitral position compared to that in the aortic position.¹⁶ During the closing phase of the mechanical valve dynamics, the leaflets move from the fully open position to the closing position with a high angular velocity and come to a sudden stop on impact with the valve housing. Due to the water hammer effect, large positive pressure transients are present on the ventricular side of the leaflet and negative pressure transients are present on the atrial side.¹⁹ The potential for cavitation exists if the magnitudes negative pressure transients fall below the vapor pressure for blood either during the initial leaflet closure or during the subsequent rebound and closure. Incidences of cavitation of implanted MHV resulting in structural failure have not been reported except with the Edwards-Duromedics valve that was withdrawn from the market. However, the instantaneous high pressure developing across the leaflet at the instant of valve closure and subsequent rebound can be anticipated to force high velocity flows through the narrow gap width as well as through the hinge region during the leaflet closing and rebound phases. Highly resolved computation of the flow dynamics through the peripheral gap width at the instant of valve closure in the peripheral gap width has been reported by Krishnan et al.⁷⁷ In this 2D FSI analysis, a fixed Cartesian grid was employed for the flow solver and the moving leaflet boundary was identified with a level-set algorithm. A local mesh refinement was incorporated in the flow solver that will refine the mesh in regions with high velocity and vorticity gradients and hence the flow through the gap width is highly resolved. Particle dynamics computation was also incorporated to compute the viscous shear stress–time history on particles representing platelets passing through the high shear flow region. Results suggested that particles that are subjected to high shear flows through the gap width are trapped in the vortical flow on the atrial side in the vicinity of the leaflets and hence these studies suggest that potential for thrombus deposition on the leaflet structures exists during the closing phase of the valves where platelets that may be activated due to the high viscous shear will stay for a longer time in the vortical flow with potential to aggregate and stick to the surface of the valve structures. This analysis has been extended to study the design parameters of bi-leaflet valve models⁴⁷ and this study suggested that larger angle of traverse of the leaflet from the fully open to the fully closed position is detrimental due to higher potential for platelet activation. Figure 7 shows an example of vorticity and shear stress distribution as well as platelet activation parameter (computed as the integral of the shear stress–time history of particles incorporated in the flow analysis) for two different valve models. It can be observed that the simulation indicates that the potential for platelet activation with the valve model in which the leaflets traverse an angle of 55° is significantly less compared to a model with a leaflet traverse angle of about 64°. Furthermore, this study showed that the local design parameters such as the geometry of the leaflet edge did not play a significant role in the flow dynamics at the instant of valve closure. A comparison of the closing dynamics between the bi-leaflet and tilting disc valve⁴⁸ demonstrated major differences between the two models. In the case of the tilting disc valve, our simulations show that the major shear flows occur in the major orifice region with potential for platelet activation, but the vortical flow forming on the atrial side migrates toward the minor orifice region during the leaflet rebound phase. These results correlate well with the minor orifice being the probable site for thrombus deposition with tilting disc valves. These 2D simulations have also been further extended to study the details of the flow dynamics in the hinge region of a bi-leaflet valve⁴⁵ and the results showed that the potential for platelet activation in the hinge region is comparable to that in the peripheral gap region for the bi-leaflet valve designs. In addition, our analysis also demonstrated that the potential for platelet activation is smaller with the open pivot valve design compared to the recessed hinge designs.⁴⁶

FIGURE 7.

Plots of vorticity contours (left column), viscous shear stress (middle column), and platelet activation parameter (right column) on the atrial side of the leaflet during the first rebound after closing of the leaflet with two bi-leaflet heart valve models.⁴⁷ The leaflet traverse angle from the fully open position to the fully closed position was 55° (for valve model plots in the top row) and 64° (for valve model plots in the bottom row) (Reprinted from the J. Heart Valve Dis.⁴⁷ with permission from ICR Publishers).

The 2D simulations described above need to be extended to 3D analysis for a more realistic study of valve dynamics. Local mesh refinement is an important feature in our flow solver that enables high resolution of the flow field in the small gap widths near the valvular structures. However, extension of this detailed dynamic analysis to 3D requires parallelization of the code and we are currently validating the code before initiating detailed 3D analysis. Since numerous 3D dynamic analyses have been published in literature, one can question the validity on studies involving 2D analyses. However, the 3D analyses reported to date have not incorporated the details of the flow structure in the gap width or the hinge region particularly during the closing phase of the cardiac cycle. In addition, the use of computational analyses for initial design of implantable devices before a prototype is made and tested is becoming increasingly popular. The 2D analyses presented above employ the maximum leaflet dimensions and hence represents the region where the flow velocity will be anticipated to be the highest and can be employed for initial analysis and design decisions before the prototypes are manufactured. Our previous 2D and 3D simulations^21,22 have shown that 2D analysis captures the important flow phenomena in the gap width and hence is valid for initial design process and in the identifications of regions of flow features that are critical for potential platelet activation.

Validation of Simulations

Validation of the simulations being developed with appropriate experimental data is a very important step in gaining confidence in the results of the simulations. Numerous experimental studies on the heart valve dynamics have been published in the literature and have provided valuable information on our understanding of the complex dynamics of the heart valve function and discussion of those results are beyond the scope of this article. However, the experimental studies provide data on velocity fields and data on viscous and turbulent shear stresses with flow past MHV and BHV particularly during the opening and closing phases and also the deformation of the tissue leaflets with tissue leaflet heart valves. Laser-based flow visualization technique has been employed to map the velocity field past MHV in a simulated ventricular chamber.^2,4 Laser Doppler point velocity measurement has also been employed to analyze for the velocity profiles and turbulent shear stresses distal to MHV.^5,57,84,89 More recently, digital particle image Velocimetry (DPIV) technique has been exploited for the detailed analysis of the flow fields in the vicinity of BHV and MHV.^{3,15,87,92,105} In the case of tissue valves, dual camera stereo photogrammetry,³⁶ and structured light projection technique⁶⁵ have been employed to quantify the leaflet motion. Thubrikar et al.^128,129 pioneered the technique of implantation of radiopaque markers on the leaflets and bi-plane fluoroscopy imaging to capture the leaflet motion in vivo for the aortic valves. Implantation of Sonomicrometry transducers on the leaflets and valve rings has also been a viable technique for dynamic three dimensional imaging of the valve leaflets in vivo.⁴³ The data presented from such experimental studies among others will be very valuable in comparing the results obtained from computational simulations.

NEED FOR MULTI-SCALE COMPUTATIONAL ANALYSIS

From the review of the several publications to date on the computational simulations of heart valve dynamics, it is apparent that rapid advancements are being made on sophisticated structural, fluid dynamic, and FSI simulations of heart valve dynamics that includes realistic geometry of the valvular structures, experimentally determined material property description, and physiologically realistic boundary conditions. One of the challenges in the modeling of heart valve dynamics is in dealing with the wide disparity in length scales. The valvular structures undergo large scale motions with length scales of the order of the size of the valve (~25 mm). In the case of mechanical valves, the flow through the leaflet edge gaps and in the hinge region are through dimensions of the order of 1 mm or less. The red blood cells (RBC) and platelets flowing through these small gaps have dimensions in the order of micrometers. Similarly in the case of tissue valves, the stresses developed on the leaflets affect the fibers and the interstitial cells at the micrometer level. Local changes in the tissue microstructure or activation of platelets in blood will occur in time scales of the order of fractions of a second where as tissue calcification or thrombus deposition will occur at larger time scales. Hence, multi-scale simulations accounting for both temporal and spatial scale variations need to be developed for the description of the mechanisms for these events.

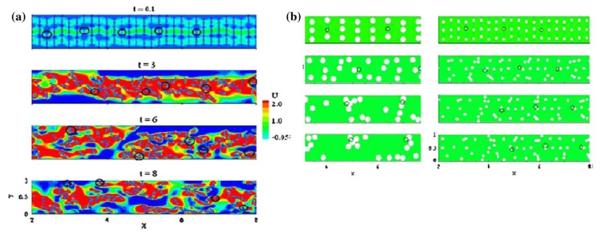
In the case of mechanical valves, the fluid has been generally treated as a continuum with Newtonian or with non-Newtonian constitutive relationship in flow through these small gap widths. Particle dynamics is incorporated with the fluid dynamic analysis in which platelets are assumed to be point particles with appropriate dimensions and the lift and drag computed around each particle for analyzing the particulate flow within the flow domain. The effect of alterations of the flow in the presence of particles is neglected in this one-way coupling analysis. The particles in flow are assumed to be subjected to the bulk fluid shear stresses and the shear stress–time history for the particles is computed. From experimental data on platelet activation with platelet rich plasma, a threshold magnitude for the shear stress–time integral is specified beyond which the platelets are assumed to be activated. These results are generally correlated with experimental studies with mechanical valves in which the platelet activation is measured and correlated with the computational results. There are several limitations in such simulations for platelet activation. In gap widths where the gap dimensions are of the same order as the blood cells, two phase analysis will become necessary. Furthermore, in introducing particles for simulated particles, the analysis ignores the presence of larger RBCs in much higher concentration than platelets and the effect of interaction among the blood cells including collision among cells, and cell and the wall are ignored. Previous experimental studies have shown that in blood flow through small vessels such as in arterioles, the platelets move toward the wall and the red blood cells are moving toward the core region.^130,140 A micro-scale computational analysis of simulated interaction of interaction among simulated RBC and platelets has been reported recently.⁷ In this study RBC was assumed to be semi-rigid ellipsoid particles while platelets were assumed to be rigid cylindrical discs and the 2D analysis included collision among particles as well as the rotation and translation of particles in flow. As shown in Fig. 8a, as the time progressed, the platelets were shown to marginate toward the wall and red blood cells move toward the core region as was observed experimentally. Furthermore, it was also shown (Fig. 8b) that when the shape of the red blood cell is changed to a discoid shape, the same behavior was observed. However, when the size of the RBC was decreased, the platelet margination toward the wall was not predicted. These simulations indicated that the relative size of the RBC and platelets are important in the platelets moving toward the wall rather than the shape of the red blood cell. Furthermore, this analysis also showed that the shear stress experienced by the platelets in the flow was much higher than the bulk viscous shear stress and the magnitude of the shear stress on the surface of the platelets also increased with increasing number of RBCs (increasing hematocrit). Previous studies have assumed that the computed bulk viscous and Reynolds shear stresses are experienced by the platelets present in that region and the effect of Reynolds shear stress in such computations has also been questioned. However, the micro-scale analysis has demonstrated that the actual shear stress experienced by the platelets depend upon the hematocrit and the source of the increased shear on the platelets were shown to be the fluid streaming effect between adjacent particles rather than the forces of collision between particles. Another relevant study on platelet behavior in flow is that of Nesbitt et al.⁹⁹ In this study performed in mouse mesenteric arterioles, the results suggest that platelet aggregation is primarily governed by shear stress gradients and only secondarily by blood-soluble agonists. Experiments in the mesenteric arteriole with a constriction–expansion geometry representing a stenosis demonstrated the aggregation of platelets on the wall of the expansion region where reduced shear stresses can be anticipated. The constriction–expansion geometry is also present in the mechanical heart valves in the hinge region as well as in the peripheral gap region with the leaflets during the closure and rebound phases. The two works cited above emphasize the importance of developing detailed micro-scale analysis of local flow dynamics in the regions of interest in MHV geometry and relating the same to the organ level dynamic analysis through the development of appropriate multi-scale analysis algorithm. FSI analyses cited above for MHV analysis have suggested that the shed vortices may play an important role in the formation of free emboli distal to the valves. However, detailed micro-scale analysis is also warranted in those flow regions of interest in order to delineate the effect of interaction between RBCs and platelets in such complex flow environments and the stresses imparted on the platelets toward activation.

FIGURE 8.

Micro-scale 2D analysis of red blood cell–platelet interaction with red blood cells (RBCs) assumed as semirigid 8 μm elliptical particles and platelets as rigid 2 μm discoids (highlighted in circles) at a Reynolds number of 1 and hematocrit of 15%: (a) Plot of velocity contours and RBC/platelet distribution at various time intervals. It can be observed that RBCs move toward the core region and the platelets are marginated to the channel surfaces at t = 8. (b) The analysis with RBCs assumed to be 8 μm discoids (left column) shows similar margination of platelets to the channel surface where as when reduced in size to 4 μm (right column), platelet margination is not observed indicating that the relative size between the RBCs and platelets are more important than the shape of the cells (Reprinted from AlMomani et al.⁷ with permission from Springer Science + Business Media).

In the case of tissue leaflet valves, FSI simulations have enabled detailed computations of the deformation patterns of the leaflets and in the identification of regions of stress concentrations. Correlations are reported between the computed regions of stress concentrations on the leaflet and morphologically observed regions of calcification and/or structural failure of leaflets. The computational simulations are performed at the organ level scale. The aortic valve leaflets consist of several layers as discussed earlier, and the collagen and elastin fibers have specific orientations and the fibers are stronger along the axial direction. An understanding of the effect of local stresses on the fiber architecture and function of the fibers require detailed structural analysis at the micro-scale level. In addition, within the three layers of the leaflet tissue is a heterogeneous population of interstitial cells¹¹¹ and an understanding of the mechanical behavior and function at the cellular level requires a analysis with cellular dimensions. In order to link the effect of regions of stress concentration identified with the organ level continuum analysis, with the effect of such a stress environment at the cellular and sub-cellular level and the long-term effect of behavior at the cellular and fiber level on structural failure or calcification, need for the development of multi-scale analysis is necessary.¹¹¹ Efforts on the development of multi-scale simulations for the valve dynamics has been recently reported in the literature.^138,139 In addressing the frequent occurrence of calcified aortic stenosis in bicuspid aortic valves, the multi-scale approach¹³⁹ employs a FE analysis at the organ level. Subsequently FE analysis is conducted at the tissue levels at selected regions of interest employing the experimentally determined material properties of the layers of the aortic valve leaflet and then at the cellular level.

In summary, computational simulations play a significant role in the understanding of the normal physiology and etiology of valvular diseases, in objective decision making for interventions such as valvular repair, and in the design of prosthetic valves and tissue-engineered valve prostheses. There are significant challenges and yet opportunities present for researchers in the development of more realistic simulations. Some of the potential and important areas of advancements in the modeling efforts include: (1) further improvements in the FSI algorithm development in order to overcome some of the restrictive assumptions invoked to overcome the difficulties encountered in the computational techniques employed; (2) innovations on the development of multi-scale analysis linking both the spatial and temporal scales to simulate the development of pathological events; and (3) in coupling the mechanical aspects of the simulation with biochemical interactions of platelet activation and aggregation.^35,119,120