Synthesis, Characterization, and Microwave Absorption Property of the SnO₂Nanowire/Paraffin Composites

Abstract

In this article, SnO₂nanowires (NWs) have been prepared and their microwave absorption properties have been investigated in detail. Complex permittivity and permeability of the SnO₂NWs/paraffin composites have been measured in a frequency range of 0.1–18 GHz, and the measured results are compared with that calculated from effective medium theory. The value of maximum reflection loss for the composites with 20 vol.% SnO₂NWs is approximately −32.5 dB at 14 GHz with a thickness of 5.0 mm.

Introduction

In recent years, electromagnetic (EM) wave absorbing materials have aroused great interest because of more and more civil, commercial, and military applications in electromagnetic interference (EMI) shielding and radar cross section (RCS) reduction in the gigahertz (GHz) band range [1, 2]. Traditionally, EM wave absorbing materials, which are composed of magnetic metals or alloys particles, are restricted in application because of high specific gravity and formulation difficulty. It is hence desirable to have microwave absorbing materials that are lightweight, structurally sound, and flexible and show good microwave-absorbing ability in a wide frequency range. In terms of these criteria, one-dimensional nanostructures, which have a tremendous surface area and more dangling bond atoms on surface, appear to be good candidates [3]. Recently, carbon nanotubes (CNTs) [4–6], magnetic-particle-doped CNTs [7], magnetic nanowires (NWs) [8], nanostructured ZnO [9, 10], and Mn₃O₄[11] were intensively studied and found to be promising microwave absorbing materials. Many groups found ZnO nanomaterials with different morphologies show excellent microwave absorption behavior, and partly attributed to its semiconductor character [9, 10, 12]. Microwave absorption property of ZnO has been investigated thoroughly in previous reports. In this work, microwave absorption behavior of another important semiconductor SnO₂ was investigated in detail.

SnO₂ has been paid attention in a variety of applications in chemical, optical, electronic, and mechanical fields, due to its unique high conductivity, chemical stability, photoluminescence, and gas sensitivity [13–16]. However, the research on its dielectric property and microwave absorption has not been reported. Here, both the complex permittivity (ε_r = ε′ − j ε″) and permeability (μ_r = μ′ − j μ″) of the SnO₂ NWs/paraffin composites with different loading proportion were studied, and the measured results are compared with calculation results from effective medium theory (EMT). The effective permittivity of composite has linear increase with increment of SnO₂ NWs proportion. Their microwave reflection loss curves were simulated according to transmission line theory. The excellent absorbing properties of the NW–paraffin were revealed, and the relationship between absorption property and the proportion between SnO₂ NWs and paraffin were also investigated.

Experimental Section

SnO₂NWs were prepared by a normal chemical vapor deposition (CVD) method. Briefly, a small amount of Sn powder (purity: ≥99%, about 3 g) was placed in an alumina crucible. A porous aluminum oxide (AAO) template coated with Au film of about 10 nm was used as substrate, which was positioned about 5 cm downstream from the precursor. Then, the crucible was put into a quartz tube that was located at the center of an electronic resistance furnace. One end of the quartz tube was connected with a mass-flow controller, which introduces a constant mixed carrier gas flow of Ar and O₂at a flow rate of 100 and 10 sccm, respectively; the other end of the quartz tube was evacuated by a pump. The furnace was heated to 1,000 °C and kept for 1 h. After the furnace was cooled naturally down to room temperature, white wool-like products in high yield were found on the substrate.

The powder samples were characterized by high resolution transmission electron microscopy (TEM) and selected-area electron diffraction (SAED) on a JEM-2010 transmission electron microscope operated at 100 kV. Field emission scanning electron microscopy (FESEM) observation was performed on a Hitachi S-4800 field emission scanning electron microscope. The products were mixed with paraffin wax with different volume fraction and pressed into toroidal-shaped samples (φ_out = 7 mm, φ_in = 3. 04 mm) for microwave absorption tests. The real part and imaginary part of the complex permittivity and permeability of the samples were measured using the transmission/reflection coaxial method by an Agilent E8363B vector network analyzer working at 0.1–18 GHz.

Results and Discussion

Figure 1shows the SEM and TEM images of the as-synthesized SnO₂NWs. The diameters of the SnO₂NWs are about 100 nm, and the lengths are up to micron scale. From TEM image (Fig. 1c) and HRTEM image (Fig. 1d), as-synthesized SnO₂NWs are well crystallized and have smooth surfaces.

Figure 1.

a and b Different magnification FESEM images of SnO₂NWs.c TEM image andd HR-TEM image of SnO₂NWs, the inset is the SAED pattern

Figure 2is the typical SEM image of the SnO₂NWs/paraffin composite with 50 vol.% loading. From Fig. 2a, it is clear that the inclination angle of these NWs (indicated with arrows) in the composites is different, leading to the randomly oriented NWs in the composites, and the volume proportion of NWs close to the surface is much lower than 50%, which is lower than that inside the composites (indicated with ellipse in a gap). As paraffin is EM wave transparent, EM waves can easily penetrate into the microwave absorbing materials with this structure.

Figure 2.

a,b The SEM images of the SnO₂NWs–paraffin composite with 50 vol.% loading

We independently measured the relative complex permittivity and permeability of the SnO₂NWs/paraffin composites in a frequency range of 2–18 GHz (Fig. 3a–c) using theT/R coaxial line method as described in the experimental section. The complex permittivity of composite versus frequency is shown in Fig. 3a. One can see a decrease of ε′ and an increase of ε″ with frequency rise. It reveals that the real part ε′ exhibits an abrupt decrease from 23 to 18 at the 0–4-GHz range, an approximate constant over 4–12 GHz and a broad peak at 12–18 GHz. Meanwhile, the imaginary part increases from 0.1 to 0.5 in the whole frequency range. As shown in Fig. 3b of complex permeability, a decrease of μ′ from 1.2 to 1 and an imaginary part close to 0 can be related to the absence of ferromagnetic components in the sample. The tangent of dielectric and magnetic loss can be expressed as tan δ_E = ε″/ε′ and tanδ _M = μ″/μ′, respectively. From Fig. 3a-b, it can be seen that tan δ_Eincreases from 0.1 to 0.5 in the whole frequency range, while tan δ_Mis below 0.1. It suggests that microwave absorption enhancement of composite results mainly from dielectric loss rather than magnetic loss.

Figure 3.

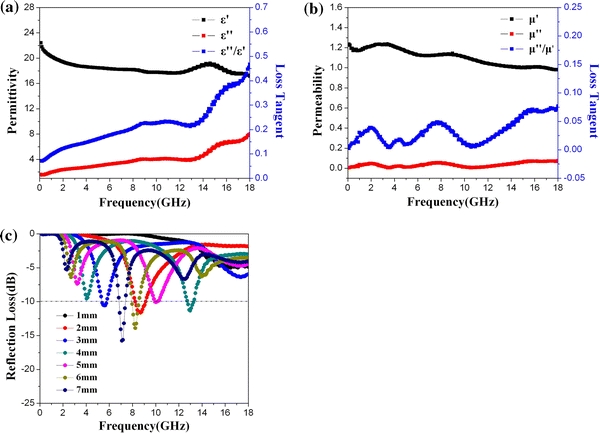
a The real part ε′,b the imaginary part ε″ of the permittivity, andc reflection loss of the composite samples with 50 vol.% of SnO₂NWS

According to the transmission line theory [17], the normalized input impedance Z _in of a microwave absorber is given by

1

where μ_r and ε_r are the relative permeability and permittivity of the composite medium, c the velocity of EM waves in free space, f the frequency of the microwave, and d the thickness of the absorber. The reflection loss is related to Z _in as

2

where 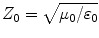is the characteristic impedance of free space.

Figure 3c shows the microwave reflection loss of composite with 50 vol.% loading at different composite thicknesses. With matching thicknesst _m = 7 mm, the maximum reflection lossR _maxis ca. −16 dB at 7 GHz. Att = 2 mm, the bandwidth corresponding to reflection loss below −10 dB (i.e., over 90% microwave absorption) is higher than 1.5 GHz.

It can be seen that the sample of 50% proportion does not exhibit good ability of microwave absorption compared with the results of ZnO and CNTs [5–11], in order to find optimal loading proportion and to investigate the intrinsic reasons for the absorption. Figure 4a, b show the real part ε′ and the imaginary part ε″ of the permittivity of the composite samples with different contents of SnO₂ NWs. It can be seen that the values of both real part ε′ and imaginary part ε″ of the permittivity increase significantly with SnO₂ NWs loading increasing, and the variation curve of every contents has the similar shape with that of 50 vol.%. Figure 4c–f shows the microwave reflection loss of composite with different loading proportion at different composite thicknesses. Composite of 10, 20, 30, and 40 vol.% loading proportion have their matching thickness t _m = 7, 5, 7, 7 mm and the approximate maximum reflection loss R _max = −27.5, −32.5, −25, −18 dB. It can be found that the microwave absorption property of the SnO₂ NW/paraffin composites becomes better with the decrease of proportion of SnO₂ NWs and get optimal proportion at 20% when the best EM parameter matching realizes. In particular, the composite sample of 40 vol.% exhibits enhanced microwave absorption with an absorber thickness of 2 mm, which is same as that of 50 vol.% shown in Fig. 3c.

Figure 4.

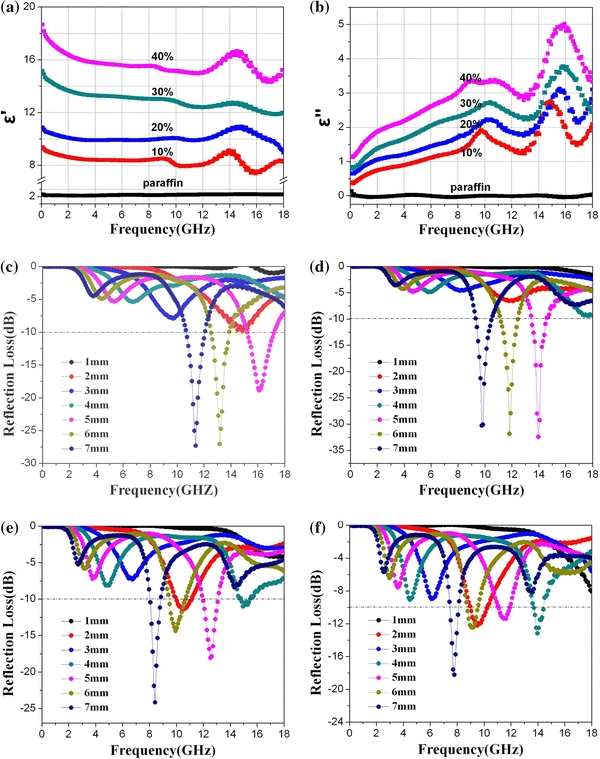
a The real part ε′ andb the imaginary part ε″ of the permittivity andc–f reflection loss of the composite samples with different content of SnO₂NWs

The dominant dipolar polarization and the associated relaxation phenomena of SnO₂ constitute the loss mechanisms. Composite materials, in which semiconductor NWs are coated with a dielectric nanolayer, introduce additional interfaces and more polarization charges at the surface [18, 19]. The interfacial polarization is an important polarization process and the associated relaxation will also give rise to a loss mechanism. It is reasonable to expect that the dielectric loss may be due to significant contributions of the interfacial polarization. It is well known that SnO₂ NWs have excellent gas sensitivity and can form space charge layer of several nanometers on the surface. Molecular dipoles formed at the NWs surface interact with the microwave field, leading to some absorption losses through heating [18].

From Fig. 4c–f, it can be seen that composite of 10, 20, 30, 40 vol.% loading proportion have their approximate reflection loss R _max at 11.5, 10, 8.5, 8 GHz at thickness t = 7 mm. With the increase of proportion in the nanocomposites, the matching frequency tends to shift to the lower frequency region, and similar results have been gained on CNTs [1, 2] and ZnO NWs [9]. Fan et al. pointed out that with an increase of CNT content in composite, the electric field of short-distance resonance multipoles leads to dominance of reflection property rather than absorption property. They reported that ε increase with increasing CNT concentration, resulting in a shift of reflectivity peak toward lower frequency [2]. The revelation is important because it suggests that the range of absorption frequency can be easily tuned by changing the SnO₂ NWs content of composites. Thus, wideband absorption could be achieved by coupling SnO₂ NWs/paraffin layers of different SnO₂ NWs contents. So, it is of great significance to calculate real and imaginary part of complex permittivity at different loading proportion of SnO₂ NWs.

Composites consisting of metallic or semiconductor particles embedded in a dielectric matrix have been widely used and studied for years [20–22], but their physical properties are still not fully understood or unveiled. It would be extremely useful to predict the properties of composites once the properties of constituent components are known and extract the properties of constituents from the measured composite properties. If the composites are isotropic and homogeneous, this work could be done with EMTs. Classical EMTs are usually based on an equivalent dipole representation of the composite. The effective macroscopic EM properties of the composites are modeled on the effective dipole moments per unit volume, which is determined by the intrinsic dipole moment contributions of each constituent and their relative volume concentration [23]. Among EMTs, the Bruggeman (BG) formula is the most commonly used. In this work, the complex permittivity ε of SnO₂ NWs/paraffin composites at microwave frequencies has been studied in the framework of the BG formula.

3

From formula (3), one can calculate Φe, Φm as follows:

4

5

Φ is either of the real part and imaginary part of the complex permittivity ε and complex permeability μ. Φe, Φi, Φm correspond to the parameter of the effective medium, the insulator, and the semiconductor particles, respectively. p is the volume fractions of SnO₂ NWs in the components. The insulator is paraffin in our experiment, real part and imaginary part of the complex permittivity are 2 and 0.01, respectively, as shown in Fig. 4a, b

Using the BG equation, the effective permittivity of the SnO₂NWs/paraffin composite at 100 MHz was calculated over a wide particle volume fraction range of 10–50% and was compared to the measured values in Fig. 5. Prior to the calculation, the permittivity of SnO₂NWs at 100 MHz was extracted from the measured effective permittivity of a mixture sample with SnO₂NWs of 40 vol.% using Eq. 4.

Figure 5.

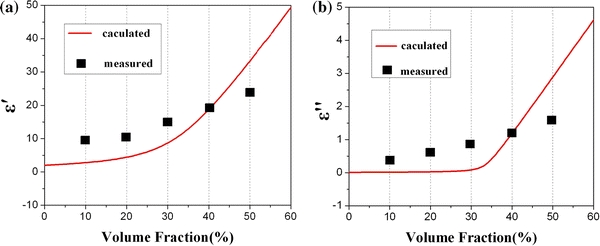
Comparison between the calculated and measured effective permittivity:a real part andb imaginary part of the composite at 100 MHz versus the volume fraction of SnO₂NWs

The real and the imaginary parts of the permittivity increase with the volume concentration. Our measured results show approximately a homogeneous increase across different proportion. BG formula predicts a distinct increase happening at around 30 vol.%, which results from the semiconductor–insulator transition at the percolation threshold [3], and a linear increase after percolation, which is the same as measured results but with a different slope. BG formula is often used in the case of spherical inclusions whose diameter d is much smaller than the incident wavelength λ. In our experiment, SnO₂ NWs are around 100 nm in width and up to micron scale in length; the aspect ratio is so large that error may be brought and result in the difference in slope. As BG formula has difficulty in dealing with composite with percolation, we find that EMT can be only used in qualitative analyses, and leads to large error in quantitative analyses.

Conclusion

In conclusion, SnO₂NWs have been prepared by a CVD method and their microwave absorption properties have been investigated in detail. Complex permittivity and permeability of the SnO₂nanostructures and paraffin composites have been measured in a frequency range of 0.1–18 GHz, the value of both real part ε′ and imaginary part ε″ of the permittivity increase significantly with increasing SnO₂NWs loading, and the variation curve of every content has the similar shape. The value of maximum reflection loss for the composites with 20 vol.% SnO₂NWs is −32.5 dB at 14 GHz with a thickness of 5.0 mm. The measured results are compared with results calculated with EMT. We find that BG equation can be only used in qualitative analyses, and leads to large error in quantitative analyses.