Silencing of glycolysis in muscle: experimental observation and numerical analysis

Abstract

The longstanding problem of rapid inactivation of the glycolytic pathway in skeletal muscle after contraction was investigated using ³¹P NMR spectroscopy and computational modeling. Accumulation of phosphorylated glycolytic intermediates (hexose-mono-phosphates) during cyclic contraction and subsequent turnover during metabolic recovery was measured in vivo in human quadriceps muscle using dynamic ³¹P NMR spectroscopy. Hexose-mono-phosphates concentration in muscle peaked 40s into metabolic recovery from maximal contractile work at 6.9±1.3 mM (mean±SD; n=8) and subsequently declined at a rate of 0.009±0.001 mM/s. It was next tested if current knowledge of the kinetic controls in the glycolytic pathway in muscle integrated in the Lambeth and Kushmerick computational model of skeletal muscle glycolysis, explained the experimental data. It was found that the model underestimated the magnitude of deactivation of the glycolytic pathway in resting muscle resulting in depletion of glycolytic intermediates and substrate for oxidative ATP synthesis. Numerical analysis of the model identified phosphofructokinase and pyruvate-kinase as the kinetic control sites involved in deactivation of the glycolytic pathway. Ancillary 100-fold inhibition of both phosphofructokinase and pyruvate-kinase was found necessary to correctly predict glycolytic intermediate and ADP concentrations in resting human muscle. Incorporation of this information in the model resulted in highly improved agreement between predicted and measured in vivo hexose-mono-phosphates dynamics in muscle following contraction. We concluded that silencing of the glycolytic pathway in muscle following contraction is most likely mediated by phosphofructokinase and pyruvate-kinase inactivation on a timescale of seconds and minutes, respectively, and necessary to prevent depletion of vital cellular substrates.

INTRODUCTION

Excitable cells like skeletal muscle fibres may undergo rapid and large (up to two orders of magnitude) transitions in ATP turnover rate upon activation (Walter et al., 1999;Blei et al., 1993). To buffer and balance this large dynamic capacity for ATP utilization, excitable cells contain multiple ATP synthetic pathways including glycolysis and mitochondrial oxidative phosphorylation (Walter et al., 1999;Blei et al., 1993). These pathways and their kinetic controls have been extensively investigated and characterized to the point that detailed in silico models are now available (Lambeth & Kushmerick, 2002;Dash et al., 2008;Selivanov et al., 2008;Beard, 2005;Magnus & Keizer, 1997;Vicini & Kushmerick, 2000). Conversely, these computational models offer powerful quantitative tools for rigorous testing of the sufficiency and consistency of current understanding and formulation of cellular ATP synthesis and its regulation (Beard et al., 2005). A specific concern is the fact that the majority of the information captured by these models has come from in vitro determinations of enzyme kinetics (Beard et al., 2005;Teusink et al., 2000). However, in the living cell, ancillary interactions (e.g. protein-protein interactions (Frieden, 1971) or substrate channelling (Winkel, 2004)) may greatly influence pathway behavior. For example, it has been documented that the activity of phosphofructokinase (PFK), a key regulatory enzyme in the glycolytic pathway, is regulated by attachment to the cellular cytoskeletal matrix in addition to classic metabolic regulation by AMP, ADP and inorganic phosphate (Pi) (Lilling & Beitner, 1991;Marinho-Carvalho et al., 2006;Marinho-Carvalho et al., 2009). Any incorporation of this information in the available computational models of glycolysis, however, has been lacking (Lambeth & Kushmerick, 2002;Dash et al., 2008;Selivanov et al., 2008). As such, it remains to be tested if and how much the latter type of ‘physiological’ metabolic regulation (as opposed to ‘biochemical’ regulation by metabolite concentrations) contributes to pathway flux and concentration control in vivo.

In the case of glycolysis, there is, in fact, a clear and pressing need for such a test. It has been long known that glycolytic flux in skeletal muscle is arrested in non-contracting muscle even in the presence of elevated concentrations of the classic metabolic regulators AMP, ADP and Pi. This observation was first made almost 30 years ago (Dawson et al., 1980), and has since been independently confirmed (Taylor et al., 1983;Quistorff et al., 1993;Wackerhage et al., 1998;Crowther et al., 2002a;Crowther et al., 2002b). Hypotheses explaining this surprising finding all invoke inactivation of key glycolytic enzymes like PFK via some relaxation-related mechanism (e.g., a drop in cytoplasmic Ca²⁺) (Dawson et al., 1980;Crowther et al., 2002a;Crowther et al., 2002b). However, biochemical details, including sites, magnitude and mechanism of pathway inactivation as well as the physiological significance for the resting skeletal muscle state all remain yet to be discovered.

Here, the kinetic controls involved in shutting down glycolysis in non-contracting skeletal muscle and its physiological significance for the resting skeletal muscle state are investigated using a combination of experimental and computational investigative approaches. First, we performed high time resolution dynamic in vivo measurements of the turnover of phosphorylated glycolytic metabolites (hexose monophosphates; HMP) in human leg muscle after exhaustive exercise using ³¹P NMR spectroscopy. Next, the Lambeth & Kushmerick computational model of glycolysis in muscle was used as a platform to investigate if current knowledge of glycolytic flux and concentration control incorporated in the model was sufficient to explain the measured HMP dynamics (Lambeth & Kushmerick, 2002). Finally, computational strategies, including network analysis, were used to identify the kinetic control sites in the glycolytic pathway involved in shutting down glycogen turnover in the post-exercise state and to investigate its significance for the resting skeletal muscle state. It was found that inactivation of both PFK as well as pyruvate kinase (PK) are necessary components of the metabolic regulation underlying silencing of glycolysis in resting skeletal muscle to prevent depletion of vital cellular substrates.

METHODS

NMR experiments

Ethical Approval

Eight normally active, healthy male subjects (mean age 26 yrs; range 22–45) participated in the study. The nature and the risks of the experimental procedures were explained to the subjects, and all gave their written informed consent to participate in the study, which conformed to the standards set by the Declaration of Helsinki and was approved by the local Medical Ethical Committee of the Máxima Medical Center, Veldhoven, The Netherlands. All subjects wore shorts and athletic shoes during the examination.

³¹P NMR spectroscopy

All measurements were performed on a 1.5T whole body scanner (Gyroscan S15/ACS, Philips Medical Systems, Best, The Netherlands) equipped with a custom-built non-ferrous, mechanically-braked bicycle ergometer. Details of the ergometer, its interfacing with the spectrometer for gated acquisition during bicycling exercise, subject positioning and familiarization with the exercise are described in detail elsewhere (Jeneson et al., 2009). A single-turn 31P surface coil (diameter: 6 cm) supplied by the manufacturer was positioned over the medial head of the quadriceps muscle of the right leg and fastened with velcro. The magnet was shimmed using a custom-built rectangular ¹H surface coil (20×10 cm) positioned over the quadriceps muscle as described elsewhere (Jeneson et al., 2009). All ³¹P NMR spectra were acquired using a 90° adiabatic excitation pulse. Prior to the exercise bout, two ³¹P spectra (16 summed free induction decays (FIDs); 1024 points; sweep width 2 kHz) were obtained from the resting muscle in resting position under fully relaxed (TR 15s) and partly-saturated (TR 3s), actual experimental conditions to determine saturation correction factors for each resonance. Next, subjects performed a bicycling ramp exercise bout consisting of three incremental workloads including maximal (1, 2 and 3 kg braking load, respectively). The pedalling rate was 80 rpm set by a metronome. Each workload was maintained for 144s during which four ³¹P NMR spectra (12 summed FIDs) were collected from the muscle. During the first 108s of metabolic recovery after completion of the exercise test, ³¹P NMR spectra consisting of four summed FIDs were serially collected yielding a time resolution of 12s. In the second phase of recovery, the time resolution was decreased to 36s (12 summed FIDs per spectrum). The total scan time was 846s (432s during exercise and 414s during recovery, respectively). 15 minutes after exercise had ended the subjects performed a second, less intense incremental workload of which the data was not used, except for the first spectrum that provided an additional data point in the hexose-monophosphates (HMP) recovery dynamics.

Data processing

Spectra were fitted in the time domain by using a nonlinear least-squares algorithm (AMARES) in the jMRUI software package (Vanhamme et al., 1997). Phosphate-mono-esters (PME), Pi, PCr and ATP signals were fitted to lorentzian line shapes. The three ATP peaks were fitted as two doublets and one triplet, with equal amplitudes and line widths and prior knowledge for the J-coupling constant (17 Hz). Maximal line widths were constrained at 30Hz. Absolute concentrations of the metabolites were calculated after correction for partial saturation and assuming that the ATP concentration ([ATP]) is 8.2 mM at rest (Taylor et al., 1986). Intracellular pH was calculated from the chemical shift difference between the P_i and PCr resonances (8δ measured in parts per million) according to eqn (1) (Tobin et al., 1972):

$$pH=6.75+\text{log}(\frac{\delta -3.27}{5.63-\delta })$$ (1)

Computational modelling

Design of the numerical analysis

The primary purpose of the computational part of this study was to investigate the mechanisms involved in the observed HMP dynamics during metabolic recovery form exercise. The analysis also required information that was obtained by performing simulation under two additional conditions: high ATP demand flux and rest, respectively. The glycolytic pathway substrate supply flux was assumed to be different for each of these three conditions: 1.) under the metabolic recovery conditions, substrate for the glycolytic pathway supply was provided by glucose phosphorylation by hexokinase concomitant with net glycogen synthesis. The model for this particular condition will be referred to as the ‘recovery condition model’ (Figure 1A). 2.) under the condition of high ATP demand (i.e., during exercise), pathway substrate supply was assumed to be provided by net glycogen breakdown; the relative contribution of glucose phosphorylation by hexokinase was assumed to be negligible. The pathway model under this particular condition is the original Lambeth and Kushmerick model (Figure 1B). 3.) under steady state rest conditions (i.e., with respect to ATP metabolism), it was assumed as a first approximation that no net glycogen production occurred and pathway supply was provided by glucose phosphorylation through hexokinase. The pathway model under this particular condition will be referred to as the ‘resting condition model’ (Figure 1C).

Figure 1. Schematic representation of the computational model.

Recovery condition model (A), original Lambeth and Kushmerick model (B), resting condition model (C).

The Lambeth and Kushmerick model of muscle glycolysis (Lambeth & Kushmerick, 2002) was used as platform to perform the numerical analyses. This model was parameterized with data of mammalian skeletal muscle origin, except for the phosphoglycerate mutase parameters which were obtained from chicken skeletal muscle. Minor adaptations were made to model conditions 1 and 3 described above. A schematic representation of the adapted models is shown in Figure 1A,C. The flux equations, initial conditions and parameter values have been described previously by Lambeth and Kushmerick (Lambeth & Kushmerick, 2002); in the sections below we restrict the description to the details of model adaptations. The computational models were implemented using Matlab 7.5.0 (the Mathworks Inc., Natick, US). Differential equations were numerically solved using ODE15s. The model did not take mitochondrial dynamics into account. The ATPase flux that was set in the model therefore corresponded only to the part that was matched by glycogenolytic ATP production.

The Lambeth and Kushmerick model of glycogenolysis mammalian skeletal muscle was parameterized using information on rabbit and pig muscle enzyme kinetics reported by Scopes et al. (Scopes, 1973). Here, the model was applied to analyze human muscle data. The effect of possible differences in kinetic properties and concentrations of glycolytic enzymes in human muscle versus rabbit and pig muscle on model predictions was probed by performing model simulations in a Monte Carlo approach.

Estimation of ATPase flux rate

Under resting conditions, ATP is mainly produced by mitochondria, whereas the glycolytic pathway accounts for only a minor part of the total ATP production flux. The ATPase flux in resting human skeletal muscle tissue was reported by Blei et al.: 8 ± 2µM/s (n=5) (Blei et al., 1993). The part of the ATPase flux that was accounted for by glycolytic ATP production was calculated. Assuming mitochondria synthesize 30 moles of ATP per mole of glucose and glycolysis has a net yield of 2 moles ATP per mole glucose (Brand, 2005), glycolytic flux would account for 1/15 part of the total ATPase flux under the conditions mitochondria rely solely upon pyruvate as substrate. However, under resting conditions muscle mitochondria also oxidize significant amounts of fatty acids. Reported values for the percentage of fatty acid utilization vary between 30 and 60 percent (Bradley et al., 1999;Jensen et al., 1998;Bergman et al., 1999a). To include this effect and take into account some additional uncertainties due to unknown fluxes through other pathway branches, the glycolytic ATP production flux at rest was estimated to be within the range of 0.1 and 0.75 µM/s. This range is in accordance with literature values of leg glucose uptake (0.05 – 0.35mM/min per limb (Katz et al., 1986;Bergman et al., 1999b;Enevoldsen et al., 2005;Durham et al., 2004;Snyder et al., 1975)), that were converted by assuming a leg has between 7–10 kg of muscle mass(Snyder et al., 1975).

Blei et al. reported the ATPase rate in resting skeletal muscle; it remained however unknown to which extend this value is also valid for skeletal muscle during recovery conditions. To include this uncertainty in the analysis the ATPase during recovery was estimated to be within a range of 0.1– 10 times the normal resting muscle ATPase activity, which sets the range for ATPase during recovery conditions to 0.0001–0.01 mM/s.

Model analysis of recovery dynamics

Model adaptations

The model used to simulate recovery conditions featured a net glycogen production and glucose phosphorylation by hexokinase (recovery condition model, Figure 1A). Developing a kinetic model of the glycogen production pathways was beyond the scope of this study. Instead, net glycogen production was modelled by deleting glycogen phosphorylase flux and substituting it with a net glycogen production flux. Glucose phosphorylation is inhibited at high [G6P]. As a consequence, G6P supply flux by hexokinase could not be modelled as a constant during recovery period, therefore a kinetic model of hexokinase was included. Hexokinase was modelled according to the description of (Gerber et al., 1974), eqn 2. Although this model was developed for a different cell type, i.e. human erythrocytes, this description was used, since in skeletal muscle tissue the same isozyme is predominant too (Wilson, 1995).

$$H{K}_{\mathit{\text{flux}}}=\frac{V_{\text{max}}^{\mathit{\text{HK}}}\frac{[\mathit{\text{ATP}}][\mathit{\text{Glc}}]}{K_{\mathit{\text{ATP}}}{K}_{\mathit{\text{ATP}},\mathit{\text{Glc}}}}}{1+\frac{[\mathit{\text{ATP}}]}{K_{\mathit{\text{ATP}}}}+\frac{[\mathit{\text{Glc}}]}{K_{\mathit{\text{Glc}}}}+\frac{[\mathit{\text{ATP}}][\mathit{\text{Glc}}]}{K_{\mathit{\text{ATP}}}{K}_{\mathit{\text{ATP}},\mathit{\text{Glc}}}}+\frac{[G6P]}{K_{G6P}}+\frac{[\mathit{\text{Glc}}][G6P]}{K_{\mathit{\text{Glc}}}{K}_{\mathit{\text{Glc}},G6P}}}$$ (2)

The ATPase flux equation was simplified compared to the original model. The mass action equation used by Lambeth and Kushmerick was substituted by a single, parameter (unit mM/s) which effectively clamped ATPase flux at a certain, adjustable level.

Model parameterization

The model adaptations introduced a few new parameters: kinetic parameters of hexokinase, glycogen production flux and ATPase flux. All other parameters were left unchanged from the original paper of Lambeth and Kushmerick.

Hexokinase kinetic parameter values are listed in Table 1. Intracellular glucose concentration was clamped at 3mM, according to measurements of Katz et al, who reported glucose concentration remained stable during at least the first 10 minutes of recovery following an exhaustive bicycle exercise bout (Katz et al., 1986). V_maxHK was calculated by assuming for [ATP], [Glucose], [G6P] and steady state HK_flux,, 8.2mM, 3mM, 0.4mM and 2.5µM/s respectively.

Table 1.

Kinetic parameters of hexokinase model, according to (Gerber et al., 1974).

Parameter	Value	Unit
VmaxHK	0.0078	mM/s
Katp	1.76	mM
Kglc	0.040	mM
KATP,Glc	0.051	mM
Kg6p	0.334	mM
KGlc,G6P	0.069	mM

The glycogen production flux (unit µM/s) after a glycogen depleting exercise bout was measured by Price et al. (Price et al., 1994). From these results the glycogen production flux was estimated to be within a range of 0 – 0.75 µM/s.

The ATPase during recovery was estimated to be within a range of 0.1– 10 times the normal resting ATPase activity, which sets the range for ATPase during recovery conditions to 0.0001–0.01 mM/s.

The model V_max parameters were set by Lambeth and Kushmerick according to the Scopes et al. data (Scopes, 1973). As these parameters were not specifically set for human quadriceps muscle uncertainties with respect to these values were also taken into account. V_max values of glycolytic enzymes were assumed to be within a range of 25 – 175 percent of the value determined by Scopes et al. This range was set based upon comparison of glycolytic enzyme activities determined for multiple species: rabbit, pig, rat and human respectively (Scopes, 1973;Shonk et al., 1964;Shonk & Boxer, 1964).

Lactate efflux was modelled by a mass action flux, eqn 3, with parameter K_lac set to 0.01s⁻¹.

$${\text{LAC}}_{\text{eff}}={\mathrm{K}}_{\text{Lac}}[\text{Lac}]$$ (3)

Initial conditions

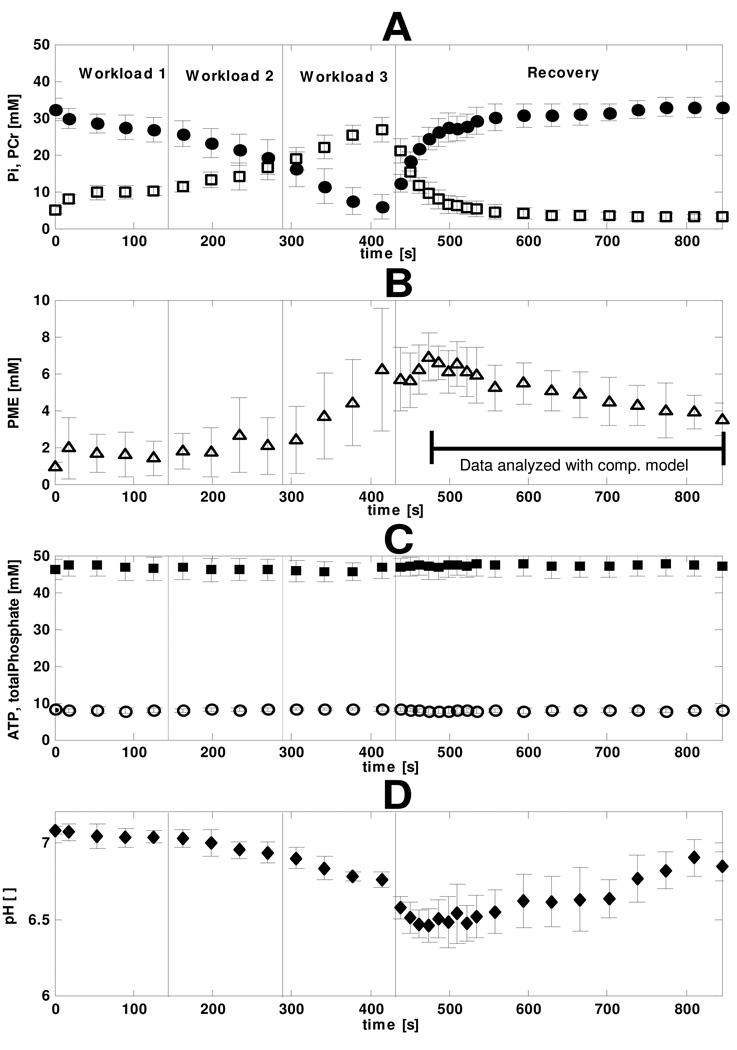
During the first phase of recovery PCr was re-synthesized by mitochondrial function. These dynamics were accompanied by Pi, ADP and AMP concentrations that dropped to resting levels. Pi, ADP and AMP are important substrates and regulators of the glycolytic pathway. The mitochondria exert control on the Pi, ADP and AMP dynamics and thus indirectly on the dynamics of the glycolytic pathway. Modelling glycolysis during the full recovery period would therefore require including a model of mitochondrial function. However, instead of including even more complexity to the model, we choose a different solution. The first 60 seconds of data were excluded, which restricted our analysis to the part of the data were PCr, Pi, ADP and AMP were close to resting levels. The part of the data analyzed with the computational model is indicated in figure 3.

Figure 3. Quantified metabolite dynamics during the rest – exercise – recovery protocol.

The vertical solid black lines separate the data points of the three different workloads and recovery period. The error bars indicate the standard deviation (n=8). The [PCr] • and [Pi] □ (A), [PME] Δ (B), [ATP] ○ and [total phosphate pool] ▪ (C), pH ♦ (D), are shown. The part of the data analyzed with the computational model is indicated by a black bar.

All initial conditions were left unchanged from the paper by Lambeth and Kushmerick, except for the initial conditions of [G1P], [G6P] and [F6P] which were set according to the experimental NMR data. The PME detected in the NMR spectra was used to calculate the concentration of HMP, which represent the sum of G1P, G6P and F6P (Walter et al., 1999;Dawson et al., 1980). Individual G1P, G6P and F6P concentrations were calculated by assuming phosphoglucomutase and phosphoglucoisomerase were close to equilibrium (Rolleston & Newsholme, 1967;Eanes et al., 2006). Calculated values for initial concentrations of G1P, G6P and F6P were 0.26mM, 4.37mM and 1.96mM, respectively.

Model simulations

For both the glycogen production flux as well as the ATPase rate and glycolytic enzyme V_max values we determined a range rather than a precise value. We used a Monte Carlo approach to perform simulations for these parameter distributions. Uniform distributions were assumed within the determined range. 5000 simulations were run, randomly drawing parameter values from the distributions. As a result the computational model predicted a solution space (mean +/− standard deviation of 5000 simulations) indicating the influence of the width of the distributions on the accuracy of the model predictions. It was tested if 5000 simulations were enough to obtain stable predictions for the models solution space. To this end, the solution space calculated based upon 5000 simulations was compared to the result obtained with 1000 simulations. These results were similar indicating 5000 simulations were enough to provide stable predictions.

Maximal glycolytic ATP production capacity

We calculated the maximal glycolytic ATP production capacity, which was defined as the maximal ATP production flux the model can generate while state variables remaining within a physiological domain. During maximal activation of the glycolytic pathway, pathway substrate supply is primarily provided by glycogen breakdown. These conditions were modelled by the original Lambeth and Kushmerick model (Figure 1B). Therefore, the Lambeth and Kushmerick model was used to calculate the maximal pathway flux (pathway V_max).

Maximal pathway flux was calculated by performing a series of simulations, incrementally increasing the ATPase rate with a step size of 0.01mM/s. All simulations were run until glycolytic ATP production and ATPase fluxes were balanced and steady state was reached. The free energy of cytoplasmic ATP hydrolysis (ΔG_p) was calculated according to eqn 4, (Jeneson et al., 1996):

$$\mathrm{\Delta }{G}_p=\mathrm{\Delta }{G}_p^{o\text{'}}+RT\text{ln}([ADP][P_i]/[ATP])$$ (4)

Where $\mathrm{\Delta }{G}_p^{o\text{'}}$ is −32.8kJ/mol at 37°C, (Rosing & Slater, 1972).

Previous studies indicated that if ΔG_p increased beyond −48kJ/mole, excitation-contraction coupling failed (Hancock et al., 2005). This information was used to constrain the computational dynamic range of the model: if ΔG_p increased beyond −48kJ/mole, simulations went out of physiological range and the incremental increase of ATPase flux was ended. The ATPase flux at which the simulations were ended was then defined as the maximal glycolytic ATP production capacity.

Identification of control points

We analyzed which enzymes exerted most of the concentration control under resting conditions. To this end, resting state model predictions (resting condition model, Figure 1C) were compared to literature data of the skeletal muscle resting concentration of a selected subset of metabolites relevant to the model: [ADP], [G6P] and [F-1,6P₂].

Under resting state conditions it was assumed no net glycogen production or consumption was present. This was modelled by deleting the glycogen phosphorylase flux from the original Lambeth and Kushmerick model. The resting state ATPase flux that was met by glycogenolytic ATP production was, as described in the section ‘Estimation of ATPase flux rate’, estimated between 0.1 and 0.75 µM/s. Under steady state conditions, glycolytic pathway substrate supply, glycolytic ATP production and ATPase flux are in balance. Glycolysis yields 2 moles of ATP per glucose molecule. This stochiometry, combined with the requirement of steady state conditions determine that glucose phosphorylation flux is balanced to ATPase flux according to eqn 5. This relation was used to set the G6P supply flux in these steady state simulations.

$$\mathrm{G}6{\mathrm{P}}_{\text{supply}}=½\text{ATPase}$$ (5)

The concentration control of individual glycolytic enzymes on the concentration of selected metabolites [ADP], [G6P] and [F-1,6P₂] was calculated by performing a series of simulations. For each simulation a different glycolytic enzyme was inhibited, by multiplying the V_max of that specific enzyme with 0.05 and differences in steady state values of glycolytic intermediates were compared.

RESULTS

³¹P MRS

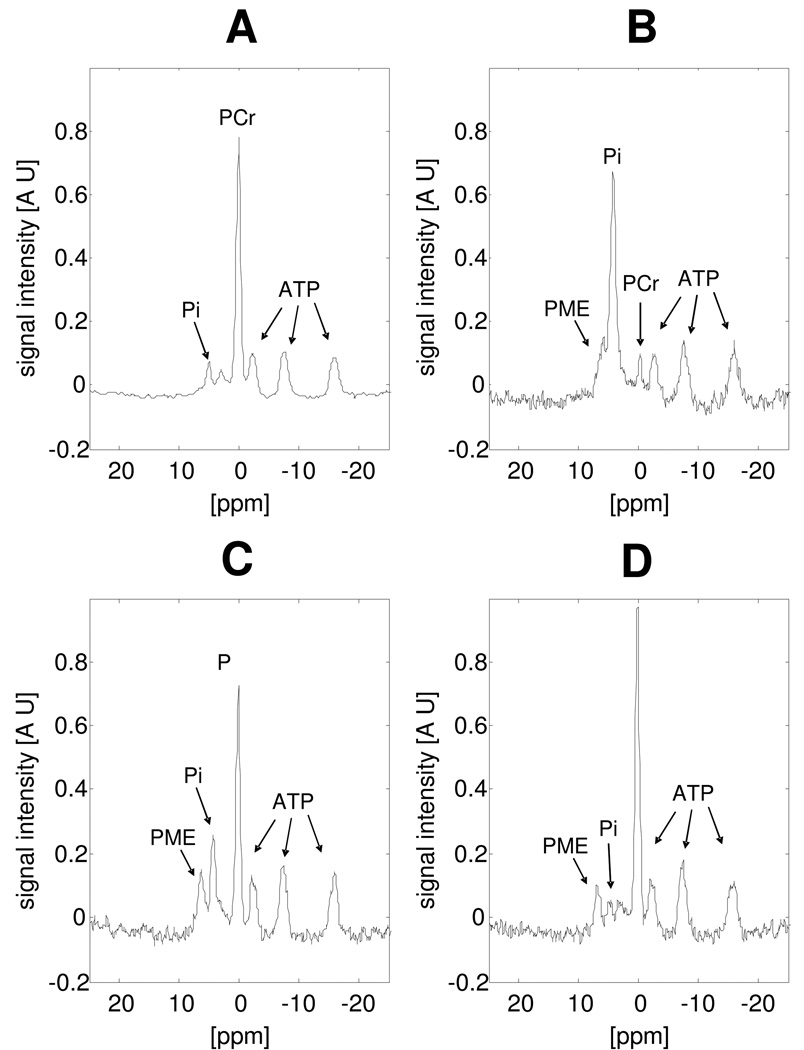
Figure 2 shows a selection of ³¹P NMR spectra from a large dynamic set acquired from the quadriceps muscle at rest (Figure 2A), during exercise at maximal workload (Figure 2B) and during metabolic recovery (Figures 2C and D). At the end of the incremental exercise bout, the phosphocreatine (PCr) pool was near-depleted and accompanied by complementary increase in Pi. During bicycling at the maximal workload, a significant phosphate-monoester (PME) resonance appeared up-field of the Pi resonance that was attributed to accumulating phosphorylated glycolytic intermediates (hexose-mono-phosphates; HMP) in contracting muscle fibres (Walter et al., 1999;Dawson et al., 1980). During subsequent metabolic recovery, Pi and PCr returned to resting levels within 60s. The PME resonance, however, exhibited much slower dynamics and was still clearly observed 240s into recovery. The striking accumulation of HMP is most clearly observed during recovery due to the downfield shift of the Pi resonance as a result of rapid ancillary muscle acidification (Figures 2C and D).

Figure 2. Selection of ³¹P NMR spectra recorded during the rest - exercise – recovery protocol.

The spectrum at rest (A), end of exercise (B), 40s into recovery (C) and 240s into recovery (D) are shown. Spectra were apodized with a 10Hz lorentzian function. Signal intensity is expressed in arbitrary units.

The quantified, pooled results of the ³¹P NMR measurements in eight muscles are shown in Figure 3. The PCr concentration decreased from 32.2 ± 3.0mM (mean ± SD; n=8) at rest to 5.9 ± 3.2mM at the end of the high intensity exercise bout, while Pi increased from 4.8 ± 0.8 to 26.8 ± 3.5mM (Figure 3A). Accumulation of HMP started during exercise at the highest workload and peaked at 6.9 ± 1.3mM 42s into recovery, after which a slow, but steady consumption (0.009 ± 0.001 mM/s) was observed (Figure 3B). The HMP concentration, quantified from a spectrum obtained 15 minutes after the end of exercise had returned to resting level (1.1 ± 0.4mM; data point not shown in figure 3). ATP and total phosphate pool levels remained stable within 10% of resting values throughout the entire protocol (8.2 mM and 47 mM, respectively; Figure 3C). Intramuscular pH decreased 0.3 units during the exercise bout from 7.08 ± 0.02 at rest to 6.75 ± 0.05 at maximal workload (Figure 3D). This moderate drop in muscle pH during exercise indicated that the muscle remained well perfused during the entire exercise protocol and lactate and CO₂ were to a high extend washed out of the muscle tissue (Jeneson & Bruggeman, 2004). During the initial phase of recovery, pH dropped another 0.3 units to 6.46 ± 0.11 as a result of rapid consumption of proton buffer (i.e., Pi; (Jeneson & Bruggeman, 2004)) and recovered slowly towards resting value (Figure 3D).

Model simulations of recovery dynamics

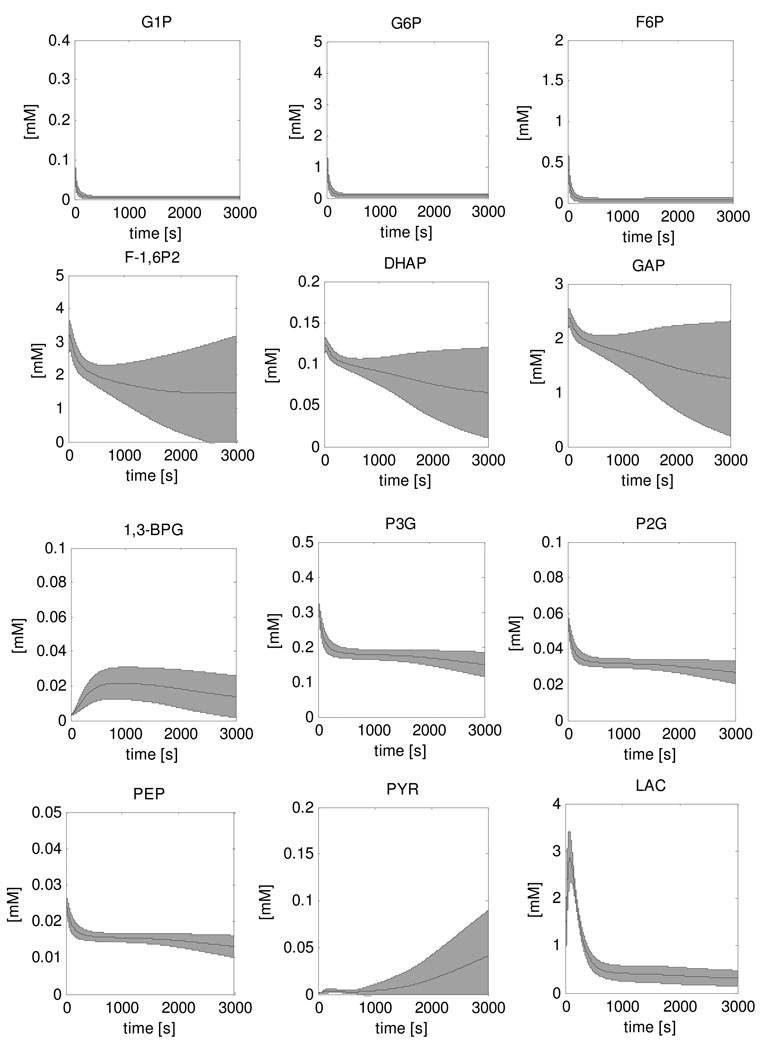
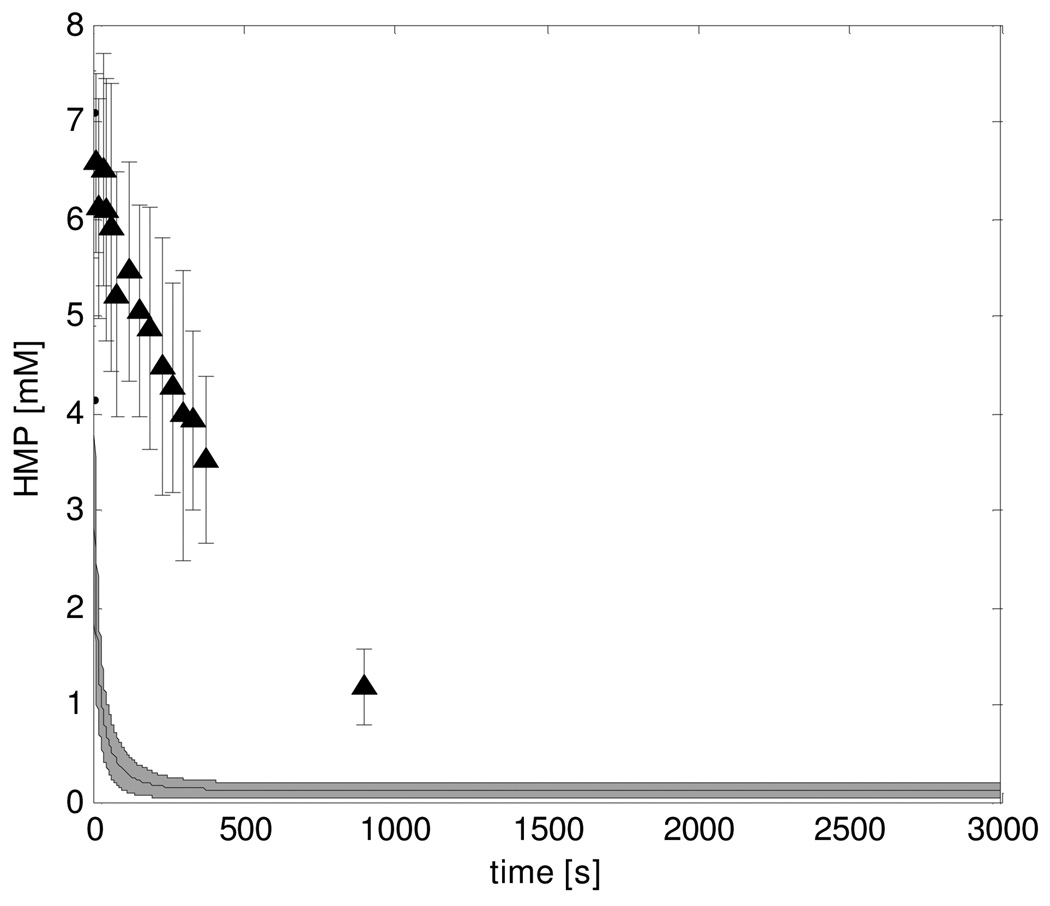
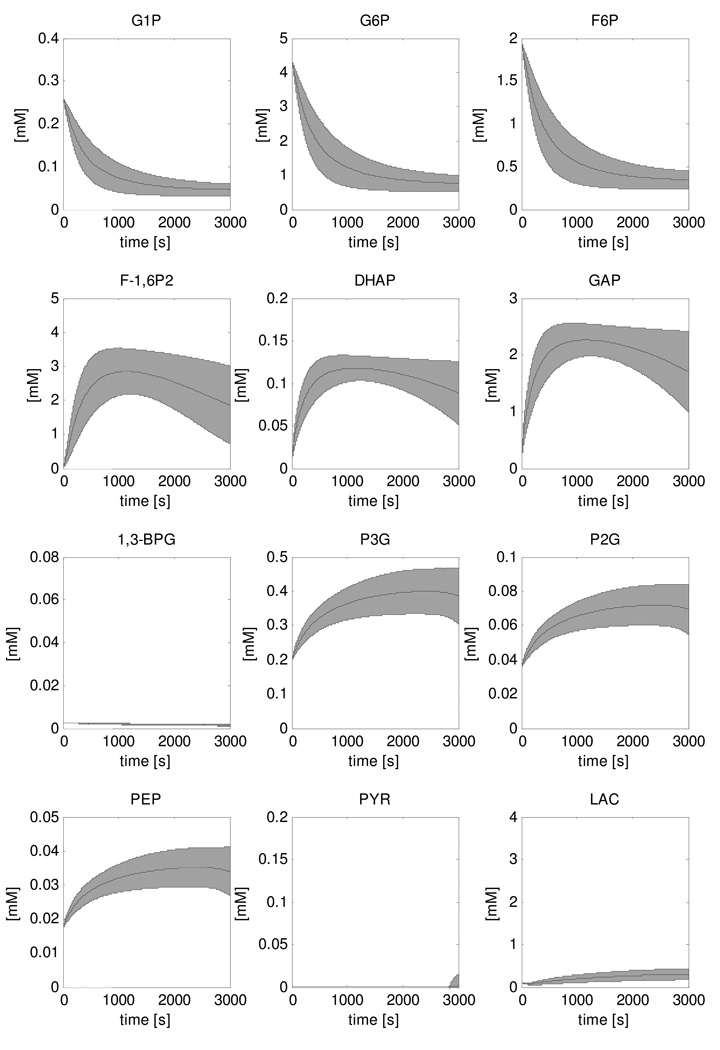
Figure 4 shows the result of the simulation of the recovery dynamics of all twelve glycolytic intermediate metabolites of the model. The results show the mean +/− standard deviation of the 5000 simulations that were performed in the Monte Carlo approach to account for uncertainties in the model parameter values. In this approach, parameter values for the ATPase rate, the glycogen consumption and V_max parameters of glycolytic enzymes were selected randomly from a uniform distribution with ranges 0.0001mM/s – 0.01mM/s, 0 – 0.75µM/s and 25% – 175% of the value reported by Scopes et al. respectively. HMP dynamics (sum of glucose-1-phosphate (G1P), G6P and fructose-6-phosphate (F6P) (Walter et al., 1999;Dawson et al., 1980)) were calculated from the model simulations and compared to the experimental data (Figure 5). The predicted HMP consumption rate was two orders of magnitude faster than the experimentally determined rate (0.57 mM/s versus 0.009 ± 0.001 mM/s, respectively). This HMP consumption rate was accompanied by a rapid accumulation of fructose-1,6-phosphate (F-1,6P₂) and glyceraldehyde-3-phosphate (GAP) to levels of 3.4mM and 2.5mM, respectively, and a peak in lactate production. All other state variables remained at relatively stable levels.

Figure 4. Simulations of recovery dynamics of glycolytic intermediate metabolites performed with the original model.

The solution space is indicated by the mean ± SD of the 5000 simulations that were run in a Monte Carlo approach.

Figure 5. HMP recovery dynamics according to predictions of the original model and experimental data ▲.

Model predictions of HMP dynamics were calculated by summation of G1P, G6P and F6P dynamics. The solution space is indicated by the mean ± SD of the 5000 simulations that were run in a Monte Carlo approach. Experimental data represent the pooled results of all eight subjects, error bars indicate standard deviation (n=8).

Maximal glycolytic ATP production capacity

It was next tested if the overly fast kinetics of the recovery conditions model were the trivial result of the maximal glycolytic ATP production capacity of the model exceeding reported experimental values. The maximal glycolytic ATP production of the computational model was calculated to be 1.4 mM/s as described in the Methods section. This value agreed well with the rate reported for a type I muscle fibre and was about half the value reported for a type II muscle fibre (1.5 and 3.0mM/s, respectively (Greenhaff et al., 1994)). From these results we concluded that two orders of magnitude faster consumption of HMP predicted by the model (Figure 5) was not a trivial result.

Identification of control points

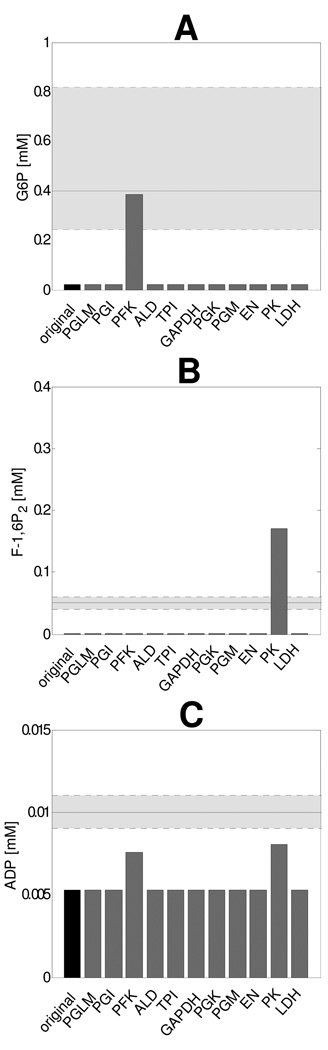
It was next investigated if concentration control in the model was sufficient to reproduce reported experimental values of steady state [ADP], [G6P] and [F-1,6P₂] (Table 2). Figure 6 shows the effect of inhibition of individual glycolytic enzymes by 95% (individual enzyme V_max value was set to 5% of original value) on steady state [ADP], [G6P] and [F-1,6P₂]. Measurements of human skeletal muscle resting state metabolite concentrations reported in literature are listed in Table 2 and indicated as shaded areas in Figure 6. From these results, it followed that the model converged at a non-physiological steady state without additional enzyme inhibition, indicating inadequate concentration control. Model simulations predicted a nearly full depletion of G6P and F-1,6P₂ to levels of 0.0094mM and 0.00028 mM respectively, whereas reported values range between 0.24mM – 0.82mM and 0.04mM – 0.06mM, respectively (Katz et al., 1986;Essen & Kaijser, 1978;Greenhaff et al., 1994;Katz & Lee, 1988). Likewise, [ADP] fell to a twofold lower value than the consensus value in absence of additional flux inhibition (0.0050mM versus 0.010mM (Walter et al., 1999;Roef et al., 2002;Chen et al., 1999;van den Broek et al., 2007), respectively). Steady state metabolite concentrations calculated for the case of selective ancillary enzyme inhibition by 95% showed that [G6P] was increased by inhibition of PFK and [F-1,6P₂] was increased by inhibition of PK. The steady state [ADP] was affected both by 95% inhibition of PFK and PK.

Table 2. Physiological values of metabolite concentrations in resting skeletal muscle.

Mean value as well as the range are listed. The range represents the lowest and highest reported values.

State Variable	Mean value	Range	Unit	Reference
ADP	0.010	0.09 – 0.011	mM	(Walter et al., 1999;Roef et al., 2002;Chen et al., 1999;van den Broek et al., 2007)
G6P	0.40	0.24 – 0.82	mM	(Katz et al., 1986;Essen & Kaijser, 1978;Greenhaff et al., 1994;Sahlin et al., 1987)
F-1,6P2	0.050	0.040 – 0.060	mM	(Essen & Kaijser, 1978;Katz & Lee, 1988)

Figure 6. Effect of inhibition of individual enzyme activity on resting muscle steady state [G6P] (A), [F-1,6P₂] (B) and [ADP] (C).

Inhibition of the enzyme activity was modeled by setting V_max values to 5%. The predictions of the original model are shown as a darker bar. The shaded area represents the physiological range and the horizontal solid black line indicates the mean value, as listed in table 2.

Parameterization of PFK and PK inhibition factors

We next hypothesized that additional inhibition of PFK and PK in electrically-silent skeletal muscle must be present. Hereto, inhibition factors in the form of V_max scalars for PFK and PK were introduced into the model. Parameterization of these inhibition factors was performed based upon reported values of [G6P], [F-1,6P₂] in resting skeletal muscle tissue (Table 2): first, steady state [G6P] was used to fine tune the PFK inhibition factor, next, [F-1,6P₂] was used to fine tune the PK inhibition factor. [ADP] was used only for verification: for the identified inhibition factor values, steady state [ADP] was within the physiological range. The magnitude of the inhibition factors were estimated for two conditions: the upper and lower values of the estimated ATP consumption rate. This yielded an upper and lower bound on the estimate of the PFK and PK inhibition factor. The values of the inhibition factors and the corresponding steady state metabolite concentrations ([G6P], [F-1,6P₂] and [ADP]) are listed in Table 3.

Table 3. Estimated PFK and PK inhibition factor.

PFK and PK inhibition factors were estimated for two conditions: the upper and lower boundary of the ATP consumption rate at rest, 0.75µM/s and 0.1µM/s, respectively, yielding an upper and lower boundary for the estimated PFK and PK inhibition factors. Steady state metabolite concentrations ([G6P], [F-1,6P₂] and [ADP]) predicted by the model that included the inhibition factors are also listed.

	PFK inhibition	PK inhibition	[G6P] [mM]	[F-1,6P2] [mM]	[ADP] [mM]
Upper bound	0.030	0.021	0.38	0.056	0.009
Lower bound	0.0037	0.0027	0.40	0.052	0.010

It was then tested if introduction of the PFK and PK inhibition factors caused other state variables to go out of their physiological range. Hereto, the steady state metabolite concentrations were calculated for four cases: (i) no additional inhibition; (ii) inhibition of PFK and PK; (iii) inhibition of PFK; (iv) inhibition of PK. Steady state metabolite concentrations were determined using a Monte Carlo approach. Parameter distributions were assumed for PFK inhibition factor (0.0037 – 0.030, Table 3), PK inhibition factor (0.0027 – 0.021, Table 3) and ATPase rate (0.1 – 0.75 µM/s, see section Methods). The results represented by the mean ± SD of the solution space of 5000 simulation runs and initial model conditions are listed in Table 4. Initial model conditions were set by Lambeth and Kushmerick and represent consensus literature values. Adding PFK and PK inhibition resulted in improved predictions of steady state [G1P], [G6P], [F6P] and [F-1,6P₂]. PFK inhibition was responsible for the changes observed in [G1P], [G6P], [F6P], whereas PK inhibition was responsible for the changes observed in [F-1,6P₂]. Predictions of other state variables were not dramatically improved or distorted compared to model simulations without inhibition.

Table 4. Model predictions of resting steady state metabolite concentrations.

Steady state metabolite concentrations calculated for four cases: (i) no additional inhibition (original model); (ii) PFK and PK inhibition; (iii) PFK inhibition; (iv) PK inhibition.

State variable	Initial conditionsa, b [mM]	Original model [mM] (mean±sd)	PFK and PK inhibition [mM] (mean±sd)	PFK inhibition [mM] (mean±sd)	PK inhibition [mM] (mean±sd)
G1P	0,059a	0,00056± 0,00024	0,025±0,011*	0,025±0,012 $	0,00057±0,00025
G6P	0,75a	0,0094±0,0040	0,41±0,19*	0,41±0,20 $	0,0094± 0,0041
F6P	0,23a	0,0042±0,0018	0,18±0,086*	0,19±0,089 $	0,0042±0,0018
F-1,6P2	0,072a	0,00028± 0,00020	0,18±0,30*	2,46e-5±1,42e-5	0,41±0,46 #
DHAP	0,076a	0,0011± 0,00045	0,020±0,022	0,00027±0,00011	0,037±0,026
GAP	0,036a	0,021±,0087	0,39±0,43	0,0053± 0,0021	0,71±0,50
13BPG	0,065b	0,0043± 3,97e-5	0,0032±0,00071	0,0025± 0,00058	0,0037±0,0010
P3G	0,052a	0,13±0,00021	0,20±0,042	0,12±0,0074	0,21±0,042
P2G	0,0050b	0,024±3,69e-5	0,036±0,0076	0,021±0,0013	0,039±0,0076
PEP	0,019a	0,012±1,45e-5	0,018±0,0037	0,010±0,00066	0,019±0,0037
PYR	0,099a	0,065±5,05e-5	0,012±0,015	0,088±0,010	0,0051±0,0096
LAC	1,3a	0,84±0,36	0,84±0,36	0,84±0,36	0,84±0,36
ATP	8,2a	8,20±5,0e-5	8,20±0,0046	8,21±0,0013	8,20±0,0051
ADP	0,013a	0,0045±5,0e-5	0,0098±0,0046	0,0070±0,0013	0,0095±0,0051
AMP	2,0e-05a	1,13e-6±2,5e-8	6,49e-6± 6,94e-6	2,82e-6±1,11e-6	6,47e-6±7,75e-6
Pi	4,1a	1,82±0,022	3,79±1,35	3,02±0,60	3,36±1,43
PCr	34,7a	38,26±0,037	34,85±2,56	36,49±0,89	35,09±2,89
NAD	0,50a	0,50±0,00017	0,47±0,044	0,50±0,00011	0,46±0,048

^*indicates improved model prediction as a result of PFK and PK inhibition.

^$indicates improved model prediction as a result of PFK inhibition.

^#indicates improved model prediction as a result of PK inhibition.

^aSee Refs: (Arnold & Pette, 1968;Cheetham et al., 1986;Harris et al., 1974;Sahlin, 1985)

^bConcentration unreported for skeletal muscle. Estimated values are based upon orders of magnitude seen in other cell types.

Effect of PFK and PK deactivation on recovery dynamics

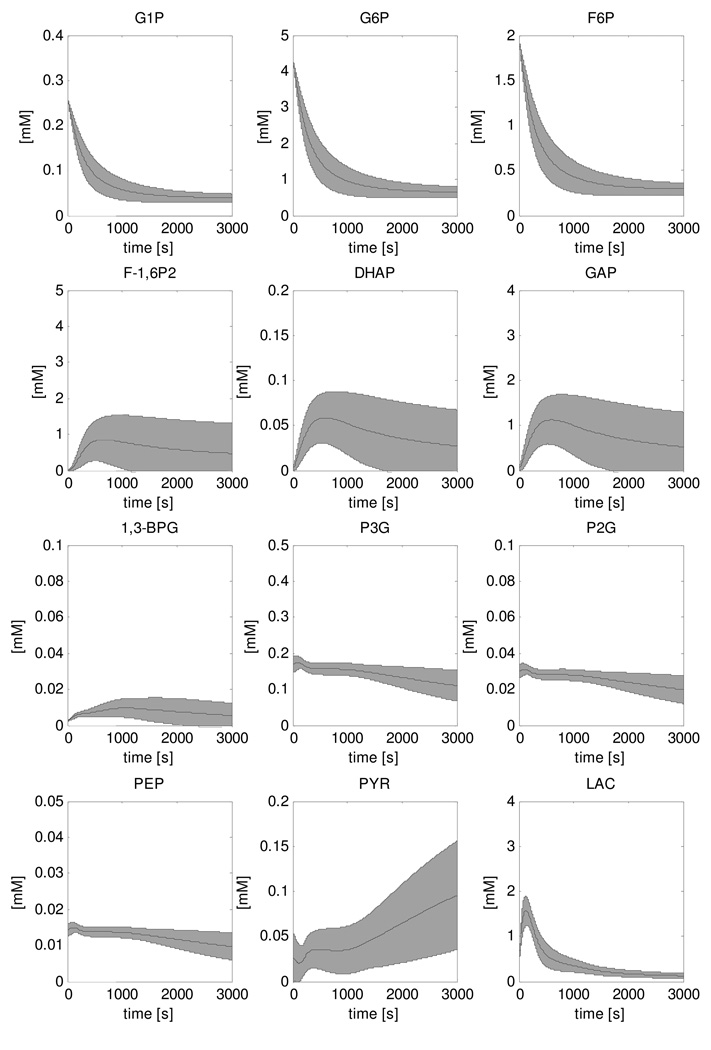
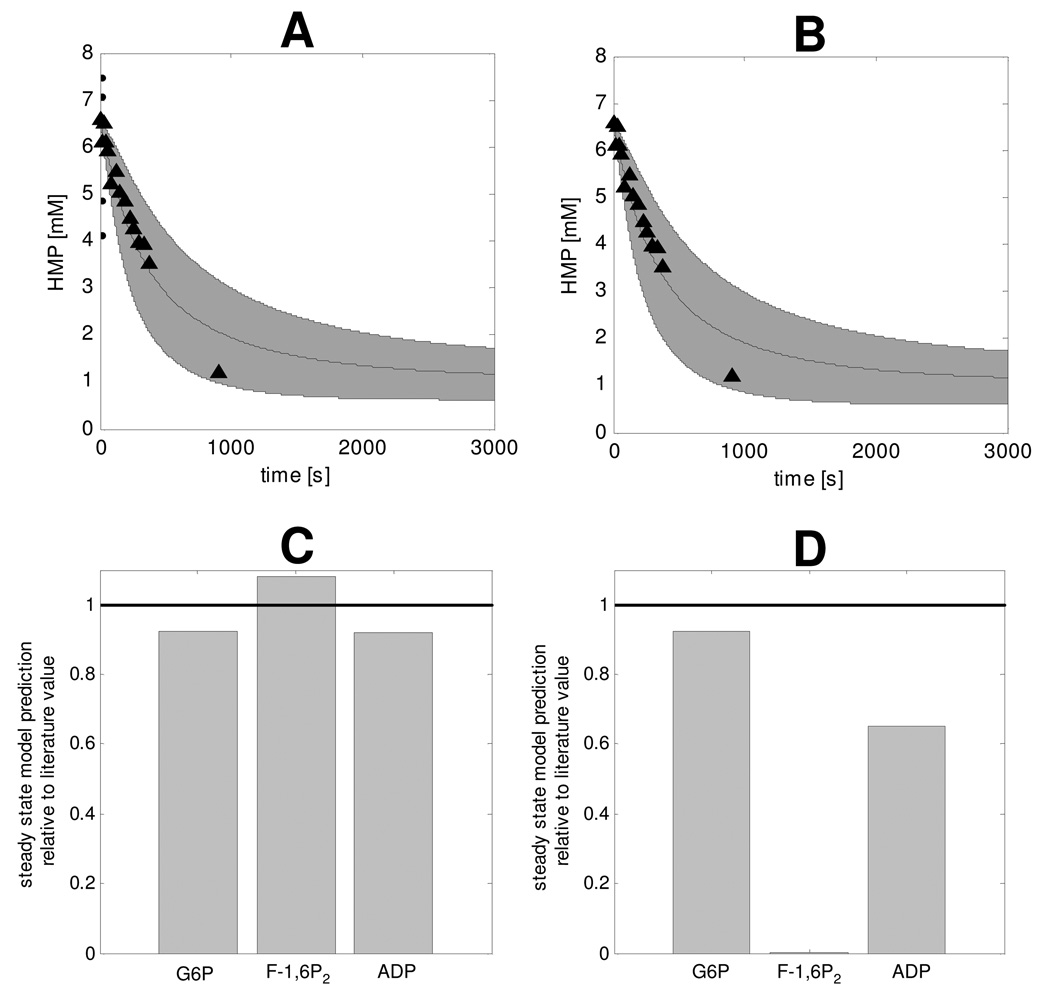
Metabolite concentration dynamics during recovery were calculated for the adapted model featuring PFK and PK deactivation mechanisms and are shown in Figure 7. The shaded area represents the mean +/− standard deviation of 5000 simulations that were run in a Monte Carlo approach. Parameter distributions were assumed for glycogen production flux (0 – 0.75µM/s), ATPase rate (0.01 – 0.0001mM/s), PFK inhibition factor (0.0037 – 0.030, Table 3), PK inhibition factor (0.0027 – 0.021, Table 3) and V_max parameters of glycolytic enzymes (25% – 175% of the value reported by Scopes et el.). Recovery dynamics were calculated for the case of both PFK and PK inhibition (Figure 7) and PFK inhibition only (Figure 8). The corresponding HMP dynamics for each case were calculated by summation of [G1P], [G6P] and [F6P] and are shown in Figures 9A and B, respectively. These results showed that model predictions of HMP dynamics in both cases agreed well with the experimental data. Compared to predictions of HMP dynamics according to the model without inhibition (Figure 5) a clear improvement between simulated HMP dynamics and experimental HMP data was observed. Figures 9C and D show the model predictions of steady state [G6P], [F1,6P₂] and [ADP] relative to the literature value, in case of PFK and PK deactivation (Figure 9C) and only PFK inhibition (Figure 9D). The results were normalized by dividing model predictions by the reported literature value. The black line represents the target value of 1, which corresponds to ideal situation of a perfect agreement between literature value and model prediction. The results show that in case of only PFK deactivation, the model failed to correctly predict [F-1,6P₂] at steady state indicating both PFK and PK deactivation must be present in resting skeletal muscle. Finally, it was investigated if inhibition of all glycolytic enzymes other than PFK and PK by 99% or reduced inhibition of PFK and PK (80%) could produce similar results. In either case, the HMP dynamics were similar to the original model and did not agree with experimental data (data not shown).

Figure 7. Simulations of recovery dynamics of glycolytic intermediate metabolites performed with the model that included PFK and PK inhibition.

The solution space is indicated by the mean ± SD of the 5000 simulations that were run in a Monte Carlo approach.

Figure 8. Simulations of recovery dynamics of glycolytic intermediate metabolites performed with the model that included PFK inhibition.

The solution space is indicated by the mean ± SD deviation of the 5000 simulations that were run in a Monte Carlo approach.

Figure 9. HMP recovery dynamics (A, B) and steady state G6P, F-1,6P₂ and ADP relative to literature values (C, D), predicted for the case of both PFK and PK inhibition (A, C), and only PFK inhibition (B, D).

Model predictions of HMP dynamics were calculated by summation of G1P, G6P and F6P dynamics. The solution space is indicated by the mean ± SD of the 5000 simulations that were run in a Monte Carlo approach. Experimental data (▲) represent the pooled results of all eight subjects (n=8), error bars were omitted for clarity of presentation. The value of the steady state G6P, F-1,6P₂ and ADP relative to literature values were calculated by dividing steady state model predictions by the mean value reported in literature as listed in table 2.

DISCUSSION

The main and novel result of the present investigation of muscle glycolysis was the identification of a principal role for the regulation of PFK and PK activity in silencing of glycolytic flux in non-contracting muscle. Below, these results and possible biochemical viz. physiological regulatory mechanisms that may be involved in PFK and PK activity control are discussed together with several methodological aspects of the study.

Experimental observations

The dynamics observed in the PME domain of the NMR spectrum were attributed to G6P, F6P, G1P conform to previous studies (Walter et al., 1999;Dawson et al., 1980). The accumulation of G6P observed during the high intensity in-magnet exercise protocol agreed with measurements based upon the analysis of muscle biopsy samples obtained after high intensity dynamical exercise (Katz et al., 1986;Essen & Kaijser, 1978;Greenhaff et al., 1994;Sahlin et al., 1987). Essen and Kaijser collected five biopsy samples during the first 180s of the recovery period (Essen & Kaijser, 1978) to determine the [G6P] dynamics. They also reported [G6P] peaks after about 30s (Essen & Kaijser, 1978). Moreover, the measured rate of G6P consumption (0.007 ± 0.001mM/s) agreed well with the rate that we determined non-invasively by ³¹P MRS (0.006 ± 0.001mM/s). The G6P consumption rate was obtained by applying the computational model to decompose the measured HMP consumption rate (0.009 ± 0.001mM/s) by predicting individual G6P (0.007 ± 0.001 mM/s), G1P (0.0004 ± 0.0002 mM/s), F6P (0.003 ± 0.002 mM/s) consumption rates.

Model parameterization

The Lambeth and Kushmerick model of muscle glycogenolysis, like the majority of computational models of metabolism (e.g.,(Beard, 2005;Dash et al., 2008)), contains specific values for all model parameters. The lack of information on the exact value of the ATP consumption and glycogen synthesis rates in human quadriceps muscle during recovery following exhaustive exercise as well as the postulated PFK and PK inhibition factors, however, warranted the use of an alternative approach in the present study. Instead of single values, simulations of our adapted model of muscle glycogenolysis were performed using a range of values for this particular subset of the model parameters. This allowed investigation of the sensitivity of the model predictions to uncertainties in the value of each of these model parameters. Indeed, the predictions of HMP dynamics by the tested adaptations of the Lambeth and Kushmerick model that included additional PFK and PK inhibition were sensitive to these uncertainties (Figure 9A, B). However, the resulting solution space was still sufficiently narrow to allow for detection of any improvement of the model predictions after inclusion of the postulated additional strong PFK and PK inactivation in non-contracting muscle. Conversely, it allowed for validation of the model adaptations by comparison of the simulations to the recorded in vivo HMP dynamics. On basis of these findings, we conclude that, in this particular case, the limited incorporation of uncertainties in parameter values in a deterministic computational model of a biological network through the use of parameter value ranges instead of single parameter values was beneficial. Any generic value of this particular model parameterization strategy in computational biology remains to be established.

Model adaptation: PFK inhibition

Instead of rather arbitrarily changing model parameters in order to reproduce the HMP dynamics, we used model predictions of steady state [ADP], [G6P] and [F-1,6P₂] in combination with measurements of the concentrations of these metabolites in resting human skeletal muscle tissue to identify and parameterize the inhibition factors. As the HMP dynamics were not used in this methodology, they provided an independent dataset that could be used for testing the model adaptations. Comparison of Figures 5 and 9 shows the clear improvement of model predictions as a result of addition of the deactivation mechanisms. This improvement was attributed to the addition of the PFK inhibition factor; not e including PK inhibition did not affect predicted HMP dynamics, Figure 9A,B. The comparison of HMP model predictions and experimental data provides validation of the model adaptations with respect to PFK inhibition.

Previous studies of silencing of glycolysis in resting muscle have proposed direct or indirect (i.e., via a kinase / phosphatase network) inactivation of key glycolytic enzymes by a drop in intracellular Ca²⁺ to explain their experimental observations. Alternatively, PFK deactivation may be explained by detachment from the cytoskeleton (Lilling & Beitner, 1991;Marinho-Carvalho et al., 2006;Marinho-Carvalho et al., 2009). Yet another possible mechanism may be related to pH. Specifically, Hand and Somero measured PFK activity as a function of pH at different temperatures in Spermophilus beecheyi (Hand & Somero, 1983). They found that at pH 6.8 (temperature 37 °C), there was no inhibition of pH on PFK (PFK activity 95% of V_max), whereas at pH 6.5 PFK activity was nearly fully inhibited (PFK activity 5% of V_max). During the initial phase of recovery, pH dropped from 6.8 to 6.5 within seconds (Figure 3). As such, pH may have a regulatory function in the work to rest transitions. However, it can not explain the deactivation of PFK in a normal resting skeletal muscle (pH: 7.05) and therefore we concluded that a pH related mechanism of PFK deactivation cannot be the primary mechanism.

Model adaptation: PK inhibition

Predictions of resting steady state [F-1,6P₂] according to the model with only PFK inhibition were over ten thousand times smaller than experimentally determined. Computational analysis of inhibition of individual glycolytic enzymes indicated PK inactivation must be present in resting skeletal muscle tissue to rise resting [F-1,6P₂]. However, no Ca²⁺ mediated PK inactivation mechanism has been reported. Model simulations of recovery dynamics of both PFK and PK inhibition and only PFK inhibition showed no difference in predicted HMP dynamics. [F-1,6P₂] dynamics were however more affected. These predictions provide valuable information about the mechanisms of PK inhibition. Analysis of muscle biopsy samples taken after intense exercise showed only a twofold increase in [F-1,6P₂] from 0.05mM to 0.1mM respectively (Essen & Kaijser, 1978;Katz & Lee, 1988). Immediate inactivation of both PFK and PK predicted a solution space of [F-1,6P₂] accumulation larger than experimentally observed, whereas only PFK inhibition predicted a solution space more consistent with experimental data. These results indicated that PK inhibition is not present at the onset of the recovery period and the deactivating mechanisms is not as fast as PFK inhibition and thus probably also not Ca²⁺ mediated. Feed forward regulation of PK activity by [F-1,6P₂] is a well known mechanism (Hall & Cottam, 1978;Valentini et al., 2000;Fothergill-Gilmore & Michels, 1993) that can explain the PK inhibition at rest. All mammalian PK iso-enzymes are sensitive for allosteric regulation of F-1,6P₂ except for isoenzyme M1 (Hall & Cottam, 1978;Valentini et al., 2000;Fothergill-Gilmore & Michels, 1993), which is the iso-enzyme found in mammalian skeletal muscle tissue (Hall & Cottam, 1978;Valentini et al., 2000;Fothergill-Gilmore & Michels, 1993). However, there is also evidence that a single amino acid substitution in the M1 isoenzyme can turn it into an allosteric regulated enzyme (Ikeda et al., 1997). It is not inconceivable that under in vivo conditions other factors, e.g. metabolites, signalling molecules, cause a small conformation change which activates the allosteric regulation in the M1 isoenzyme. This investigation indicated PK inhibition must occur in parallel to PFK inhibition, albeit at a much slower timescale. The underlying mechanism, however, remains to be determined.

Silencing of glycolysis in muscle: hypothesis

The present finding of a slow HMP consumption rate in muscle in the post-exercise state agreed well with the observation that in spite of high substrate (ADP, Pi) and activator (AMP) levels, glycolytic flux is silenced in non-contracting muscle (Dawson et al., 1980;Taylor et al., 1983;Quistorff et al., 1993;Wackerhage et al., 1998;Crowther et al., 2002a;Crowther et al., 2002b). Quistorff et al. did not detect any accumulation of HMP during ischemic recovery from which they concluded glycogen phosphorylase must be regulated in concert with glycolysis (Quistorff et al., 1993). This hypothesis was later refuted by results reported by Crowther et al. who found that glycolytic flux was silenced despite a significant increase in HMP (>3mM) (Crowther et al., 2002a;Crowther et al., 2002b). Instead, these results indicated that the deactivation of glycolytic flux is controlled at one or more sites downstream of glycogenolysis. Our results confirm the findings of Crowther et al. (Crowther et al., 2002a;Crowther et al., 2002b). Moreover, our computational analysis of metabolite concentrations in resting skeletal muscle, validated by reproduction of the HMP dynamics, has for the first time identified the most likely sites of this regulation (i.e., PFK and PK) as well as the physiological significance of these controls for the skeletal muscle resting state. Specifically, the simulations suggest that the inactivation of PFK and PK in non-contracting muscle is necessary for cellular metabolite concentration control by preventing depletion of ADP and Pi and associated negative effects on other cellular processes including mitochondrial ATP synthesis. Furthermore, glycolytic intermediates like G1P, G6P, F6P, F-1,6P₂ and DHAP would also be depleted affecting fluxes through other branches of the glycolytic pathway (e.g. glycogen production, glycerophospholipid metabolism; glycine, serine and threonine metabolism; fructose and mannose metabolism). The precise mechanisms involved in the rapid deactivation of PFK and the slower deactivation of PK in skeletal muscle indicated by the present study to occur in the post-exercise state remain, however, to be elucidated.

Model limitations

All of the above should be viewed in the context of the limitations of the model simulations. In the process of developing computational models very often model parameterization is based upon data obtained from different species and or cell types (e.g. (Wu et al., 2007;Cortassa et al., 2003;Nguyen & Jafri, 2005 )). Here, we have dealt with this problem numerically by performing Monte Carlo simulations to probe the effect of small changes in parameter values on simulation results. A further improvement can be made by determining the glycolytic enzyme kinetic parameters of human quadriceps muscle. In addition, incorporation of knowledge on the pH dependency of these enzyme kinetics (Vinnakota et al., 2006) would also further improve the basis for the generated hypothesis. Specifically, the NMR data provides quantitative information on in vivo muscle pH dynamics that can be used in the computations. With the current model we were not able to exploit this data. Finally, the numerical analysis indicated that additional PFK and PK deactivation must be present to explain the recorded HMP dynamics. The current model could not be used to reveal the precise biochemical implementation of this deactivation. As discussed above, the numerically identified hypothesis relates to the work of others indicating a potential role for Ca²⁺ mediated binding of PFK to the cytoskeleton. It can, however, not be ruled out that other (unknown) metabolic feedback loops not included in the model, may also contribute to the predicted magnitude of PFK and PK deactivation. Experimental identification of these control loops and addition of this information into future models can be used to gain quantitative insight in relative contribution of these feedback loops to the deactivation mechanisms.

In summary, in vivo magnetic resonance spectroscopy revealed a large accumulation of hexosemono-phosphates during exercise and a subsequent slow turnover during metabolic recovery. Computational modelling was used to relate these experimental observations to the control mechanisms of the underlying metabolic pathways. Following this approach, the experimental observations were translated into a new hypothesis that silencing of glycolysis in skeletal muscle tissue involves inactivation of both PFK as well as PK