Pooling Data from Multiple Longitudinal Studies: The Role of Item Response Theory in Integrative Data Analysis

Abstract

There are a number of significant challenges encountered when studying development over an extended period of time including subject attrition, changing measurement structures across group and developmental period, and the need to invest substantial time and money. Integrative data analysis is an emerging set of methodologies that overcomes many of the challenges of single sample designs through the pooling of data drawn from multiple existing developmental studies. This approach is characterized by a host of advantages, but this also introduces several new complexities that must be addressed prior to broad adoption by developmental researchers. In this paper we focus on methods for fitting measurement models and creating scale scores using data drawn from multiple longitudinal studies. We present findings from the analysis of repeated measures of internalizing symptomatology that were pooled from three existing developmental studies. We describe and demonstrate each step in the analysis and we conclude with a discussion of potential limitations and directions for future research.

By definition, the empirical study of developmental processes requires repeated assessments of individuals over time (e.g., Nesselroade & Baltes, 1979). Despite the efficiency of more recent developmental research methods (e.g., accelerated longitudinal and cohort designs; Mehta & West, 2000; Miyazaki & Raudenbush, 2000; Raudenbush & Chan, 1992), multi-wave longitudinal studies remain time-intensive, expensive, and methodologically challenging. Beyond the obvious problem that extensive time is needed for individuals to mature through the developmental period under study before comprehensive results are available, longitudinal studies also introduce classic sources of potential inferential bias such as selective subject attrition and the confounding of cohort, historical, and maturational effects (e.g., Shadish, Cook, & Campbell, 2002). To overcome such methodological challenges often requires intensive resources and, in many cases, these challenges continue to limit the final contributions of these studies. In addition, longitudinal studies must consider changing measurement structures across development to produce reliable and valid assessments that appropriately capture the changing expression of developmentally salient constructs from childhood through adolescence and into adulthood. Taken together, substantial difficulties must be surmounted in the successful empirical study of developmental processes over an extended period of time.

Offering the potential to address many of these challenges, integrative data analysis (or IDA) is an emerging set of methodological techniques that involves the simultaneous analysis of multiple independent samples (e.g., Curran, Edwards, Wirth, Hussong, & Chassin, 2007; Hussong, Flora, Curran, Chassin, & Zucker, in press; Hussong, Wirth, Edwards, Curran, Zucker, & Chassin, 2007; McArdle & Horn, 2002). In contrast to meta-analysis, in which multiple parameter estimates are pooled from previously fitted models, IDA literally pools the raw data drawn from two or more existing studies and then fits models directly to the aggregated data set. The strategy of pooling data drawn from separate investigations holds many benefits including increased statistical power, greater sample heterogeneity in important subject demographics, the broader psychometric assessment of constructs, and the ability to estimate a variety of models that would not be possible within any single data set. Moreover, IDA offers the potential for built-in study replication that might yield a more systematic integration of findings within the literature and in turn foster a more cumulative approach to the psychological sciences. In the study of developmental processes, IDA may hold additional advantages when age-heterogeneous, longitudinal studies are combined. Not only is this approach more time- and cost-efficient than a single longitudinal study, but the appropriate pooling of longitudinal samples also permits the study of a longer maturational period than was assessed within any single investigation.

However, IDA also introduces challenges in determining appropriate methods for pooling independent samples, particularly with longitudinal data. A central challenge is how to appropriately pool measures of key constructs across independent, developmental studies for the purpose of simultaneous analysis. Often independent studies differ in their assessment of key constructs. Variations in the developmental period under study, the historical timing of the study, and the target populations may all drive resulting measurement differences as each study attempts to select instruments that are maximally valid for the developmental period and population under study based on the state of knowledge at the time. Adapting measures to maximize developmental relevance avoids the administration of items that become less valid over a long period of time and allows for the inclusion of new items that become more salient with maturation. Thus, measures of central constructs may differ over studies and even across assessment periods within study. Although this presents an obvious challenge in the calculation of scale scores that are anchored to a common metric, it does allow for maximally valid assessment instruments to be used for the specific developmental period under study. Moreover, greater heterogeneity in demographic representation resulting from pooling independent studies also increases the ability to conduct important tests of measurement invariance over development and across sub-group.

In the current paper, we attempt to highlight the many potential advantages of IDA by focusing specifically on the challenges associated with the pooling of multiple measures from multiple independent longitudinal studies. Our overarching goal is to develop and implement an analytic strategy that will allow for the calculation of a set of individual- and time-specific scale scores based on a pool of dichotomously scaled items drawn from two different established scales assessing internalizing symptomatology as reported by individuals drawn from one of three developmental studies. To meet this goal, we must address four central challenges.

First, because we are focused on the presence or absence of discrete symptoms, we must incorporate a measurement model that is appropriate for dichotomously scored response scales.¹ Second, because we are drawing items from different established scales that assess the same underlying theoretical construct, we must use a technique that does not require the same item set to be administered to all individuals in the sample. Third, because we anticipate potential measurement differences across both development and sub-group, we must incorporate a methodology that provides formal inferential tests of measurement invariance. Finally, to create maximally valid scale scores that share a common underlying metric, we must use an analytic method to create individual- and time-specific scores that reflect any differences in the psychometric properties of items across development or group.

We begin with a review of two existing analytic methods that can be used to create person- and age-specific scale scores based on a set of dichotomously scored items: the proportion score model and the item response theory (IRT) model. Next, we focus on the ability to conduct tests of differential item functioning over age and across sub-groups within the IRT framework. We then present a detailed empirical analysis in which we apply IRT models to pooled data sets drawn from three developmental studies that track trajectories of internalizing symptomatology from ages 10 to 33. Finally, we conclude with potential limitations of these techniques and directions for future research.

Measurement Models for Categorical Data

Our ultimate goal is to fit a series of growth models to a single pooled sample that consists of data drawn from three, separate developmental studies to examine individual variability in trajectories of internalizing symptomatology. To accomplish this, we must first create composite scale scores for internalizing symptomatology that are valid, reliable, and anchored to the same underlying metric regardless of the study from which the data were drawn. Although there are several analytic approaches that can be used to create scale scores based on a set of items that are discretely scored (e.g., Curran et al., 2007), here we will focus on two: the proportion score and the item response theory model.

Proportion scores

The application of the proportion score model to create scale scores is ubiquitous in many areas of developmental research, both past and present. Indeed, we have used this approach profitably ourselves (e.g., Curran, Bauer, & Willoughby, 2004; Curran & Bollen, 2001; Curran & Hussong, 2003). There are a number of reasons for this ubiquity, including the straight forward method of scoring and the long history of using this approach in many other scientific disciplines. However, as we will see, there are a number of salient limitations that make the proportion score less viable for our purposes here.

We will define y_jti to represent the observed binary response (i.e., 0 or 1) of item j assessed at time-point t for individual i. The number of items endorsed by a given individual at a given time-point is denoted j_i=1,2,…,J_ti; this potentially cumbersome notation has the advantage of allowing for a different number of items to be endorsed across individuals within the same time-period. The proportion score is then defined as

$${\widehat{p}}_{ti}=\frac{\sum _{j=1}^{J_{ti}}{y}_{jti}}{J_{ti}}$$ (1)

where pˆ_ti represents the proportion of J_ti dichotomous items that were endorsed at time-point t for individual i. In words, Equation (1) is simply adding up the number of positively endorsed items and dividing by the total number of available items for each person within each time point. This score is then used as the dependent variable in subsequent analyses.

The proportion score offers several potential advantages: it is calculated in an easily understandable way; the calculation is non-iterative so that convergence problems are never encountered; and the resulting metric is often directly interpretable. For example, a proportion score of .70 unambiguously reflects that 70% of the presented items were positively endorsed. However, there are several potentially critical disadvantages to the proportion score as well. First, all endorsed items are weighted equally, and there is no allowance for differences in either salience or severity across items within a scale. For example, endorsement of an item about feeling sad and an item about suicidal ideation both contribute equally to the overall scale score. Second, all items are assumed to equivalently define the construct both over time and across group. This precludes the ability to either assess or incorporate information about differential item functioning across critically important groups such as gender, ethnicity, developmental status, and study group membership. For example, an item assessing cries easily is treated as an equally valid indicator of depression for individuals who are 10, 20 and 30 years of age. Finally, proportion scores that are calculated based on different numbers of items across time (e.g., six items at one age and 12-items at another) can artifactually deflect a developmental trajectory because of changes in the underlying metric of the score. Taken together, although the proportion score has been widely used for decades in developmental research, more comprehensive analytical techniques exist that overcome many of these limitations. One particularly promising set of analytic methods is the item response theory model.

Item Response Theory Models

There is a long and rich history in the development and application of IRT models, a comprehensive review of which is beyond the scope of our paper; see Chang & Reeve (2005), Embretson & Reise (2000), McDonald (1999), and Thissen and Wainer (2001) for excellent treatments of this topic. Briefly, the term IRT is used to refer to a broad set of nonlinear statistical models designed to empirically examine the psychometric structure of a set of discretely scaled items. IRT models were primarily developed within the field of education, and many past applications have tended to focus on topics related to academic testing. However, IRT models have become increasingly used in many areas of social science research, and these techniques have much to offer the field of developmental psychology.

We focus our attention here on the two parameter logistic IRT model, or 2PL. The 2PL is one of the most widely used forms of the IRT model for dichotomously scored items. This model is typically written as:

$$P(y_{jti}=1\mid {\theta }_{ti})=\frac{1}{1+e^{-1.7a_{jt}({\theta }_{ti}-b_{jt})}}$$ (2)

where P represents probability, y_jti is the observed binary response for item j at time-point t for individual i, θ_ti is the latent construct that is hypothesized to underlie the observed item response patterns, a_jt and b_jt are the slope (or discrimination) and intercept (or severity)² parameters for item j at time-point t, respectively, and −1.7 is a constant that scales the logistic distribution that of the normal ogive. The a and b parameters are quite similar to the factor loading and threshold parameters in a dichotomous factor analysis, and in many conditions these are isomorphic (Takane and de Leeuw, 1987).

The typical application of the IRT model is in academic or achievement testing. For example, say that a sample of 12th grade students were administered a set of 25-items assessing mathematics ability. The underlying construct θ represents latent math ability; this is the theoretical construct of interest. The intercept term (i.e., b) would represent the value on θ that is needed to have a probability of .50 of endorsing a given item correctly; larger intercepts reflect items that are more difficult because higher values of the underlying trait are needed to obtain a probability of .50 to correctly respond to the item. The slope term (i.e., a) would represent the strength of the relation between the item and the underlying distribution of θ; steeper slopes reflect items that better discriminate among individuals as a function of latent math ability. These intercept and slope values can then be used in a variety of ways, including understanding the psychometric properties of a test, retaining and omitting items for future tests, and calculating scale scores that estimate an individual’s latent mathematics ability.

Given the multitude of strengths of the IRT models, these have been increasingly used in applications outside of education and testing. Instead of 25-items assessing mathematics ability, consider 25-items assessing internalizing symptomatology. Now the latent construct θ reflects individual variability in underlying levels of anxiety and depression. The intercept term now reflects the level of θ that is needed to have a probability of .50 of endorsing a given symptom; larger values of b reflect that higher levels of θ are needed to positively endorse the item, so the item is considered more severe. Finally, the slope term now reflects the strength of the relation between the symptom items and the underlying distribution of θ; larger values of a reflect a stronger relation between the item and the latent construct, so the item is considered more discriminating. Thus, unlike the proportion score that treats all items equivalently, the IRT model allows items to differ along two dimensions.

There are two additional advantages that are of particular interest to us here. The first is that we can use the IRT model to conduct tests of differential item functioning, or DIF. This allows for a formal inferential test of the equality of the intercept and slope parameters for each item across one or more discrete groups (e.g., gender, study membership, developmental status, etc.). In other words, we can test whether the sample estimate of the slope value for a given item is equal across sub-groups, or whether unique values for the estimate of the slope must be allowed within each group. This provides critically needed information about whether the test is operating differently across key sub-groups within the sample. The second advantage is that, once DIF testing is completed, the full set of item parameters (including those that reflect DIF) can be used to calculate a person- and time-specific estimate of the underlying construct θ, denoted θˆ_ti. Importantly, these scores are scaled as a standard normal variate (i.e., mean=0, sd=1) which in turn provides a clear metric for interpretation. Continuing our example, if a slope estimate for a given item were found to significantly differ within each sub-group, these sub-group-specific values would be retained in the calculation of the individual scores. This second step is often called IRT scoring, and these estimates of θˆ_ti can then be taken to other modeling applications (e.g., growth models, mixture models, etc.).

A remarkable characteristic of the IRT model is that items need not come from the same scale, nor even from the same study. For example, in the empirical application we present below, we drew internalizing items from two separate scales: the Child Behavior Checklist (CBCL; Achenbach & Edelbrock, 1981) and the Brief Symptom Inventory (BSI; Derogatis & Spencer, 1982). Some individuals have responded only to the former, some only to the latter, and some have responded to both. Further, some subjects who responded to items drawn from the same scale participated in separate developmental studies. As such, only a subset of individuals responded to all possible items, one subset responded to just the BSI items, one subset responded to just the CBCL items, and no subject participated in more than one of the three studies. As such, this is fundamentally a missing data problem. The IRT model will provide us with the analytic methods needed to pool data drawn from three separate developmental studies; to evaluate a set of items assessing internalizing symptomatology drawn from two separate psychometric scales; to conduct formal tests of DIF as a function of developmental status, gender, and study membership; and to create individual scale scores that are anchored to the same metric over all time-points and all three studies.

Empirical Example: Developmental Trajectories of Internalizing Symptomatology

Our next goal is to demonstrate the use of a series of IRT models to combine data from multiple developmental studies and create psychometrically sound scale scores that reflect potential differences in item functioning across gender, study, and developmental status. Our motivating research question of interest relates to the evaluation of individual variability in developmental trajectories of internalizing symptomatology spanning from childhood through adolescence and into young adulthood. Our goal is to determine the optimal functional form of the developmental trajectory for the entire group (the fixed effects), and to evaluate the individual differences of each subject around this group trajectory (the random effects). More comprehensive analyses would then attempt to predict these individual differences as a function of important child- and family-specific measures, but space constraints preclude us from pursuing this further here. To empirically evaluate our research question, we consider data drawn from three existing longitudinal studies of the development of children with and without an alcoholic parent: the Michigan Longitudinal Study (Zucker et al., 2000), the Adolescent/Adult Family Development Project (Chassin, Rogosch, & Barrera, 1991), and the Alcohol and Health Behavior Project (Sher, Walitzer, Wood, & Brent, 1991).

Michigan Longitudinal Study (MLS)

The MLS assessed three cohorts of children using a rolling, community-based recruitment (Zucker et al., 2000). In cohort one, 338 males (aged 2–5; 262 children of alcoholics [COAs] and 76 matched controls) and their parents completed in-home interviews. COA families were identified through fathers’ court-arrest records and community canvassing and inclusion criteria were that fathers meet Feighner (1972) diagnostic criteria for adult alcoholism by diagnostic interview, reside with their biological sons aged 3–5, be in intact marriages with their sons’ biological mothers at the time of first contact and that sons show no evidence of fetal alcohol syndrome. Contrast families were recruited through community canvassing in the neighborhoods in which COA families resided and were matched to COA families on the basis of age and sex of the target child; both parents of controls had to be free of lifetime adult alcoholism and drug abuse/dependence diagnoses. Seventy percent of eligible court families and 93% of community canvassed families agreed to participate (overall participation rate was 84%).

Cohort two was girls (aged 3–11) from the cohort one families who were recruited when cohort one boys were at Wave 2.³ Cohort three contained all additional siblings (aged 3–11) of the male target children in cohort one across subsequent waves of assessment. A total of 152 girls (from 152 families) comprised cohort two and an additional 106 siblings (from 84 families) comprised cohort three. Across all three cohorts, 596 children from 338 families provided four waves of data, separated by three-year intervals, with those (across cohorts) aged 3–5, 6–8, 9–11 and 11–14 receiving batteries for Waves 1–4, respectively. A total of 399, 339, 402, and 418 participants had reports on their functioning available at waves 1–4, respectively, yielding an overall participation rate of 73% for those with at least two waves of data in the sample. In addition, adolescents completed abbreviated annual assessments beginning at age 11. Each family completed a primarily in-home assessment conducted by trained staff that was blind to family diagnostic status. Although protocol length varied by wave of assessment, assessments were typically 9–10 hours for parents and 7 hours for children, each spread over seven testing sessions.

Adolescent/Adult Family Development Project

In the AFDP (Chassin, Flora, & King, 2004; Chassin, Rogosch, & Barrera, 1991), a community sample of 454 families (246 COAs and 208 match controls) completed three annual interviews when the target child was an adolescent (at ages 10–15 at Time 1). At a young adult follow-up (Time 4), full biological siblings were included if they were in the age range of 18–26, and all of these siblings were again invited to participate at Time 5, five years later. A total of 327 siblings (78% of eligible participants) were interviewed at Time 4, while 350 siblings (83%) were interviewed at Time 5 (n=378 interviewed at either wave). The combined sample of original targets and their siblings was n=734 at Time 4 (M age=21.1), n=762 at Time 5 (M age=26.6) and n=817 with at least one wave of measurement. Retention in young adulthood was excellent, with 407 (90%) of the original target sample interviewed at Time 4 and 411 (91%) interviewed at Time 5 (96% had data at either time point). Details of sample recruitment are reported elsewhere (Chassin, Barrera, Bech, & Kossak-Fuller, 1992). Alcoholic parents were identified through court records, HMO wellness questionnaires, and telephone surveys. Inclusion criteria for COA families were: living with a biological child aged 11–15, non-Hispanic Caucasian or Hispanic ethnicity, English speaking, and a biological and custodial parent who met DSM-III lifetime criteria for alcohol abuse or dependence. Control families were matched to these COA families on the basis of ethnicity, family structure, SES and the adolescent’s age and sex. Data were collected with computer-assisted interviews either at families’ homes or on campus, or by telephone for out-of-state participants.

Alcohol and Health Behavior Project

In the AHBP (Sher, Walitzer, Wood, & Brent, 1991), 489 college freshmen (250 COAs and 237 controls) completed four annual assessments (Years 1−4) as well as two additional post-college follow-ups (at 3 and 4 year intervals, or Years 7 and 11, respectively). Participants were recruited through a screening of 3,156 first-time freshmen at the University of Missouri who reported on paternal alcoholism using the father-SMAST (Crews & Sher, 1992; Sher & Descutner, 1986). Of these, 808 were selected for more intensive assessment using the Family History Research Diagnostic Criteria interview (FH-RDC; Endicott, Andreason, & Spitzer, 1978) to confirm reports of parent alcoholism, with the remainder of participants excluded due to a surplus of non-COA participants, but some were discarded for other reasons (e.g., they were adopted, they were non-native English speakers). An additional 319 participants were subsequently excluded due to questionable data, refusal to participate, inconsistent reports of family alcoholism, and psychopathology in first-degree relatives that violated exclusion criteria for FHN membership. At each follow-up, diagnostic interviews and questionnaires were primarily completed in person, but telephone interviews (and mailed questionnaires) were used more commonly as increasing numbers of participants relocated over time (1%, 4%, 13%, 27%, and 42% of the diagnostic interviews at Years 2, 3, 4, 7, and 11, respectively, were conducted by phone). The sample has excellent retention with 84% of the original participants completing the Year 11 interview.

Final pooled sample

The final pooled sample consisted of a total of 1827 subjects, 512 of which were drawn from the MLS (age ranging from 10 to 17 years); 830 from the AFDP (age ranging from 10 to 33 years); and 485 from the AHBP (age ranging from 17 to 23 years). Each subject was assessed between one and five times resulting in a total of 7377 person-by-time observations. Of the total sample, chronological age ranged from 10 to 33 years with a modal age of 19 years, 56% of the subjects were male, and 57% had one or both parents diagnosed as alcoholic.

Measures of internalizing symptomatology

We began with 27-dichotomous self-report items to define internalizing symptomatology for the IRT analyses.⁴ A total of 12-items were drawn from the anxiety and depression scale of the Brief Symptom Inventory (BSI) and 15-items were drawn from anxiety and depression subscale of the Child Behavior Checklist (CBCL).⁵ Of the total pool of 27-items, six items were unique to the BSI, nine items were unique to the CBCL, and six items were identical between the BSI and CBCL (i.e., precisely the same item content appeared on both scales). For the six shared items, a pooled item was created that was scored zero if both the BSI and CBCL items were scored zero, and was scored one otherwise. Given the six common items appearing on both scales, there were 21-unique items assessing internalizing symptomatology. Of these 21-items, all were administered in the MLS; 10 of the 15 CBCL items but none of the BSI items were administered in the AFDP; and all 12 BSI items but none of the CBCL items were administered in the AHBP.⁶ Table 1 presents a summary of item content, scale source, and study source (as well as additional information that we will discuss later).⁷

Table 1.

Item content, scale source, study source, proportion endorsed, and IRT item parameters for the 21 internalizing symptomatology items

#	Item	Scale	Study Source	Proportion Endorsed	IRT Discrimination	IRT Severity
1	hopeless about future	BSI	MLS / AHBP	.16	2.19	1.26
2	scared for no reason	BSI	MLS / AHBP	.08	2.00	1.86
3	blue	BSI	MLS / AHBP	.34	1.92	0.55
4	no interest in things	BSI	MLS / AHBP	.24	1.65	1.00
5	terror / panic	BSI	MLS / AHBP	.03	2.09	2.43
6	restless	BSI	MLS / AHBP	.21	1.15	1.41
7	Cries a lot	CBCL	MLS / AFDP	.17	1.41	1.47
8	might think / do something bad	CBCL	MLS	.17	1.31	1.56
9	have to be perfect	CBCL	MLS / AFDP	.36	1.06	0.64
10	no one loves me	CBCL	MLS / AFDP	.10	2.70	1.53
11	feel guilty	CBCL	MLS / AFDP	.15	1.45	1.60
12	Unhappy / sad / depressed	CBCL	MLS / AFDP	.25	2.96	0.79
13	Worried	CBCL	MLS / AFDP	.35	1.83	0.52
14	others out to get me	CBCL	MLS	.11	1.65	1.79
15	suspicious	CBCL	MLS	.39	1.21	0.49
16	lonely	CBCL / BSI	MLS / AFDP / AHBP	.32	2.13	0.60
17	worthless / inferior	CBCL / BSI	MLS / AFDP / AHBP	.13	3.26	1.27
18	Nervous / tense	CBCL / BSI	MLS / AFDP / AHBP	.44	1.52	0.22
19	Fearful / anxious	CBCL / BSI	MLS / AFDP / AHBP	.19	1.80	1.21
20	Self-conscious / easily embarrassed	CBCL / BSI	MLS / AHBP	.39	1.51	0.43
21	Thinks about killing self	CBCL / BSI	MLS / AHBP	.06	2.04	2.07

note: MLS=Michigan Longitudinal Study; AFDP=Adolescent / Adult Family Development Project; AHBP=Alcohol and Health Behavior Project; Total sample size for proportion endorsed and IRT parameters N = 1827; MLS N = 512; AFDP N =830; AHBP N = 485; for items 16 through 19, AFDP items were drawn from the CBCL, AHBP from the BSI, and MLS from both the CBCL and BSI;

Calculating Scale Scores

Our analytic strategy consisted of four sequential steps. First, we estimated a dichotomous exploratory factor analysis model to evaluate the dimensionality of the 21 internalizing symptomatology items; this is the dimensionality step. Second, we fitted a standard 2PL IRT model to a single randomly selected assessment for each of the 1827 individuals in the pooled sample; this is the calibration step. Third, we estimated a series of multiple group IRT models as a function of developmental status, gender, and study group membership to provide formal tests of differential item functioning across group; this is the DIF step. Finally, using the full set of item parameters estimated under the DIF step, we calculated individual- and time-specific scale scores for every subject at every time-point at which they were assessed; this is the scoring step. We describe each of these in turn.

Step 1: Dimensionality

A core assumption underlying the IRT model defined in Equation (2) is that a single dimension (denoted θ) underlies the set of observed items (e.g., Embretson & Reise, 2000; Stout, 1990). Violation of this assumption introduces local dependence among the items and can bias resulting sample estimates in unpredictable and sometimes substantial ways. To empirically evaluate the dimensionality of the set of items assessing internalizing symptomatology, we estimated a dichotomous exploratory factor analysis (EFA) within each study separately.⁸ The purpose of the EFAs were to determine the optimal number of factors to extract based on a set of traditional measures including Eigenvalues, scree plots, and estimates of incremental variance (e.g., Gorsuch, 1983). Because the items were dichotomous, we used a robust weighted least squares estimator based on polychoric correlations (see, e.g., Flora & Curran, 2004, for a recent review).⁹ All of the relevant indices within each of the three studies clearly supported the existence of a single factor underlying the 21-items. For example, the first four Eigenvalues within AFDP were 9.68, 1.65, 1.32, and 1.25, with explained variance of 46%, 7.8%, 6.2%, and 5.9%, respectively. These values indicated that only modest unique information is gained with the extraction of more than a single factor. Precisely the same pattern of Eigenvalues was found in the MLS and AHBP studies. Taken together, the empirical evidence strongly suggests that the IRT assumption of unidimensionality is adequately met.

Step 2: Calibration

After establishing the unidimensionality of our set of dichotomous items, we next fitted a 2PL IRT model to the pooled sample ignoring all possible sub-groups. The purpose of this model is to obtain initial estimates of the intercept and slope parameters for the set of 21-items which will then be extended in Step 3 (the DIF step) to determine if these pooled estimated item parameters hold across the full sample or if unique item parameter values must be estimated within each sub-group. To estimate this model, we first randomly selected a single observation from the set of available observations for all N=1827 individuals. For example, if a given individual was assessed a total of five times, we randomly selected one of these five assessments; if another individual was assessed two times, we randomly selected one of these two assessments. This randomization procedure ensured that all possible subject ages were represented in the calibration sample. If some other strategy were used (e.g., selecting the assessment at age of first entry into the study), then by definition we would have omitted individuals from the older range of ages given that no one had aged into that developmental period yet.

A standard 2PL IRT model using maximum marginal likelihood (MML) estimation was fitted to the 21-dichotomous items drawn from the pooled calibration sample using the software package MULTILOG (Thissen, 1991).¹⁰ The raw endorsement rates and the IRT intercept and slope estimates for each of the 21-items are presented in the last three columns of Table 1. These initial results indicate that there are clear differences in both the severity and the discrimination parameters across the set of items. This alone is a substantial improvement over the proportion score method of scoring in which the relation of all items to the underlying construct are treated identically.

For example, the item nervous or tense shows the lowest severity (item 18, b=.22) whereas the item spells of terror or panic shows the highest (item 5, b=2.43). This implies that a much lower level of latent internalizing is needed to endorse the first item (.2 standard deviations above the mean) whereas a much higher level is needed to endorse the second (nearly 2.5 standard deviations above the mean). Further, the item feel that I have to be perfect shows the lowest discrimination (item 9, a=1.06) whereas the item feel worthless or inferior shows the highest (item 17, a=3.26). This implies that the first item is less strongly related to (or less reflective of) latent internalizing compared to the second item. In other words, there is a smaller increase in the probability of endorsing item 9 with a 1-unit increase in latent internalizing than in the probability of endorsing item 17 with the same 1-unit change; the former item is thus a weaker indicator of the underlying construct than is the latter item.

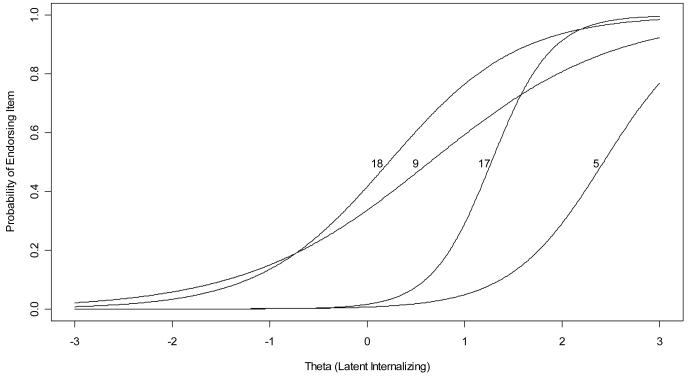
A key advantage of the IRT model is that the item parameters can be presented graphically in which the underlying latent construct is mapped onto the probability of endorsing each item; this graphical mapping is called an item traceline or item characteristic curve. Figure 1 presents the item tracelines for the four items described above (items 5, 9, 17, and 18). The x-axis represents the value of the underlying latent internalizing, and the y-axis represents the probability of endorsing that particular item at any given value of the latent construct. The discrimination parameter is the slope of this traceline, and the severity parameter is the point at which the traceline crosses a probability of precisely .50. The tracelines for the items reflecting greater severity (e.g., items 5 and 17) are shifted to the right reflecting that higher values of latent internalizing are needed to endorse that item. The tracelines for the items reflecting greater discrimination (e.g., also items 5 and 17) are defined by a steeper slope reflecting that the item is more strongly related to latent internalizing compared to items with less steep slopes.

Figure 1. IRT trace lines for four of the 21 internalizing symptomatology items for the N=1827 subjects in the calibration sample.

note: Item 5 = spells of terror or panic; Item 9 = feel that I have to be perfect; Item 17 = feel worthless or inferior; Item 18 = nervous or tense;

Considering all of the IRT model results, the item parameters and the associated tracelines reflect that the 21-dichotomous items provide an excellent assessment of latent internalizing symptomatology. However, there is an important caveat to this conclusion. Namely, the reliability and validity of the measurement of latent internalizing symptomatology is wholly dependent on the extent to which the item parameters are equal across all individuals in the sample. There are of course many applications in which this is a perfectly reasonable assumption. However, we anticipate that the severity and discrimination item parameters may differ as a function of gender, age, and study group membership.¹¹ To formally evaluate the degree to which the item parameters are equal over these sub-groups, we expand the single group IRT model to multiple groups so that we can conduct tests of differential item functioning across discrete groups.

Step 3: DIF

Current methodology allows for the testing of DIF as a function of two or more discrete groups. Although in principle more than two groups could be considered simultaneously, large sample sizes within each group are required for stable model estimation. Because we did not have the necessary sample sizes required for simultaneous estimation across all groups and all ages, we conducted our tests of DIF in a sequential manner.¹² We first formed two groups based on age: young (10 to 17 years of age) and old (18 to 33 years of age). We then formed two groups based on gender: male and female. Finally, we formed three groups based on study membership: MLS, AFPD, and AHBP.

For our DIF testing, we first estimated a two-group IRT model based on age, and we conducted likelihood ratio tests (LRT) of each item parameter for young versus old. Using the Benjamini-Hochberg adjustment for multiple tests to control for alpha-inflation (Benjamini & Hochberg, 1995), we identified eight items that showed differences in either severity or discrimination as a function of age (items 3, 4, 10, 13, 16, 18, 19, and 20 from Table 1). We then created “sub-items” for these eight items that allowed for the estimation of unique item parameters within each age group; in other words, separate sample estimates were allowed for these eight items in terms of severity, discrimination, or both, within the young and the old age groups.

Next, we took this set of 29-items (13-invariant items and 16-sub-items) and repeated the DIF testing as a function of gender. These results identified three additional items that showed DIF as a function of gender (items 7, 12, and 15). We again created sub-items within each gender, and took this set of 32-items and repeated the DIF testing as a function of study group membership. These results identified three additional items that showed DIF as a function of study group membership (items 16, 17, and 18). We thus created sub-items within each unique study to reflect this DIF. This procedure resulted in a set of 9-items that were fully invariant across all groupings, and 12-items that showed evidence of DIF across one or more groups. Combining across the invariant items and the group-specific sub-items, there were 38-total items used to assess internalizing symptomatology. The item parameters for these 38-items are presented in Table 2.

Table 2. IRT item parameters after DIF testing.

#	Wording	Sub-group	IRT Discrimination	IRT Severity
1	hopeless about future		2.06	1.22
2	scared for no reason		2.07	1.76
3	blue	Adult Youth	3.19 1.41	0.11 1.05
4	interest in things	Adult Youth	2.23 1.22	0.88 0.99
5	terror / panic		2.11	2.35
6	restless		1.15	1.33
7	Cries a lot	Male Female	1.24 1.62	2.45 0.84
8	might think / do something bad		1.31	1.53
9	have to be perfect		1.07	0.68
10	no one loves me	Adult Youth	2.75 2.80	1.84 1.44
11	feel guilty		1.49	1.62
12	Unhappy / sad / depressed	Male Female	2.94 2.97	0.90 0.76
13	Worried	Adult Youth	2.12 1.80	0.40 0.65
14	others out to get me		1.64	1.78
15	suspicious	Male Female	1.15 1.44	0.38 0.64
16	lonely	Adult – AFDP Adult – AHBP Youth – MLS Youth – AFDP	2.85 2.96 2.08 1.27	0.84 0.13 0.73 0.72
17	worthless / inferior	MLS AFDP AHBP	3.18 3.44 2.95	1.21 1.32 1.26
18	Nervous / tense	Adult – AFDP Adult – AHBP Youth – MLS Youth – AFDP	1.73 1.68 1.50 1.90	0.51 −0.25 −0.02 0.83
19	Fearful / anxious	Adult Youth	2.33 1.60	1.32 1.02
20	Self-conscious / easily embarrassed	Adult Youth	1.85 1.42	0.63 0.05
21	Thinks about killing self		2.05	1.99

note: MLS=Michigan Longitudinal Study; AFDP=Adolescent / Adult Family Development Project; AHBP=Alcohol and Health Behavior Project; Total sample size for proportion endorsed and IRT parameters N = 1827; MLS N = 512; AFDP N =830; AHBP N = 485; Youth N=807; Female N=808.

The item parameters provide much information about the utility of the items in the assessment of internalizing symptomatology across age, gender, and study group membership. For example, the item feeling hopeless about the future is invariant across all possible groups; in other words, the sample estimates for the intercept and slope for this item are equal across age, gender, and study membership. In contrast, the item feel that no one loves me operates differently for young versus old, but holds equally across gender and study group membership; examination of the item parameters indicates that the item is slightly more discriminating for young versus old (2.80 and 2.75, respectively) but is less severe for young versus old (1.44 versus 1.84, respectively). Finally, the item nervous or tense shows differences in both discrimination and severity across age and study group membership (see item 18 in Table 2 for detailed parameter estimates). Interestingly, no item shows differences across all three groupings. It is clear that much valuable information would have been lost had we not extended the single group IRT model to these more comprehensive tests of DIF. The potential for lost information is even greater had we only considered the proportion score approach in which tests of DIF are not even possible due to the fact that the set of items are assumed equally indicative of the underlying construct for all individuals regardless of age or group.

We have now developed a detailed and thorough understanding of how the 21-items jointly define the underlying construct of internalizing symptomatology. However, we still only have estimates of the item parameters that define the relation between each item and the latent construct (e.g., the item-specific values presented in Table 2). Our ultimate goal is to use this information to obtain sample estimates of the unobserved latent construct for each individual and at each time point that we can then take to other types of analysis (e.g., growth models, mixture models, etc). To accomplish this, we turn to our fourth and final step: IRT scoring.

Step 4: Scoring

The calculation of IRT scale scores is analytically quite challenging in that estimates must be obtained for the posterior distribution of theta as a function of the set of item parameters for each unique observed pattern of responses. There are two primary methods for computing these IRT scores: expected a posteriori (EAP) and modal a posteriori (MAP). A comprehensive comparison of these two approaches is beyond the scope of our paper, but drawing on the recommendations of Thissen and Wainer (2001), we used the MAP method to obtain scores here. The MAP score is denoted θ ˆ_ti and represents an estimate of internalizing symptomatology for each individual at each time point as operationalized by the nine-invariant items and 29-sub-items. Importantly, these scores are anchored to a shared underlying standard normal metric despite the fact that we are combining three separate developmental samples in which some individuals responded to the CBCL only, some to the BSI only, and some to both. These IRT scores are now ready for secondary analysis.

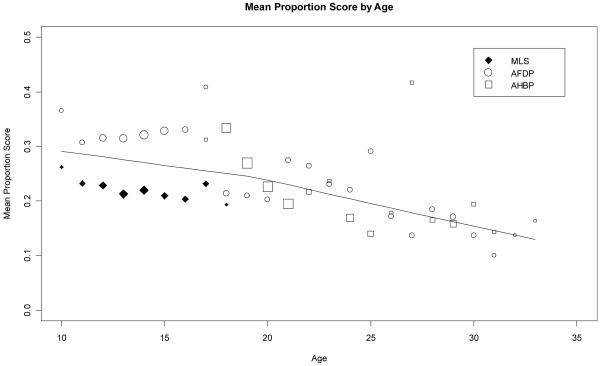
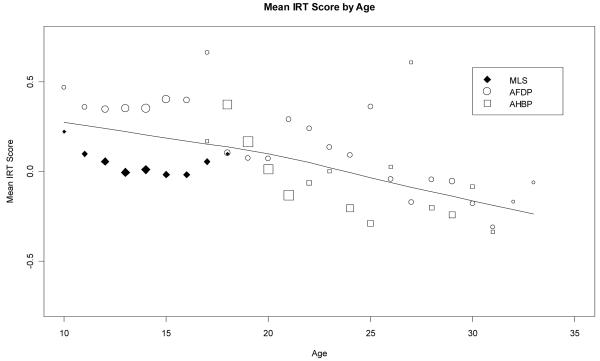
Table 3 presents the means and standard deviations of the IRT and proportion scores across all of the ages of study; this same information is graphically presented in a bubble plot in Figure 2 where the bubbles represent the available sample sizes at each age of measurement. Of greatest salience is the apparent downtrend in the mean trajectory of internalizing symptomatology with increasing age; this mean trend is modestly decreasing from age 10 to about age 20, but then accelerates downward through age 33. This trend appears similar between the IRT and proportion scores, although formal differences can be tested using random effects growth models. Further, this is only a mean trend, and important individual differences likely exist around this mean trajectory (e.g., critical differences in mean trajectories for males versus females, particularly at transition to adolescence).

Table 3.

Means and standard deviations of the IRT and proportion scores within each age

		IRT Score	Proportion Score
Age	N	Mean (SD)	Mean (SD)
10	51	0.38 (0.86)	0.33 (0.25)
11	283	0.20 (0.79)	0.26 (0.22)
12	477	0.17 (0.82)	0.26 (0.24)
13	613	0.15 (0.84)	0.26 (0.24)
14	639	0.17 (0.87)	0.27 (0.25)
15	481	0.20 (0.86)	0.27 (0.25)
16	359	0.16 (0.83)	0.26 (0.24)
17	266	0.21 (0.90)	0.28 (0.25)
18	560	0.30 (0.78)	0.30 (0.24)
19	587	0.15 (0.79)	0.26 (0.24)
20	558	0.03 (0.77)	0.22 (0.22)
21	562	−0.04 (0.74)	0.21 (0.22)
22	202	0.06 (0.78)	0.24 (0.24)
23	94	0.11 (0.79)	0.23 (0.24)
24	385	−0.13 (0.77)	0.18 (0.22)
25	242	−0.05 (0.78)	0.19 (0.22)
26	117	−0.04 (0.71)	0.17 (0.21)
27	105	−0.14 (0.69)	0.15 (0.20)
28	203	−0.13 (0.76)	0.17 (0.22)
29	365	−0.17 (0.70)	0.16 (0.19)
30	142	−0.15 (0.69)	0.16 (0.19)
31	69	−0.31 (0.61)	0.10 (0.17)
32	20	−0.11 (0.67)	0.16 (0.20)
33	12	−0.05 (0.63)	0.16 (0.16)

Figure 2. Age-specific means from 10 to 33 years of age for IRT scores with nonlinear spline superimposed.

note: Area of the plotted symbol is directly proportion to the sample size within that study at that age (i.e., larger symbols denote larger sample sizes).

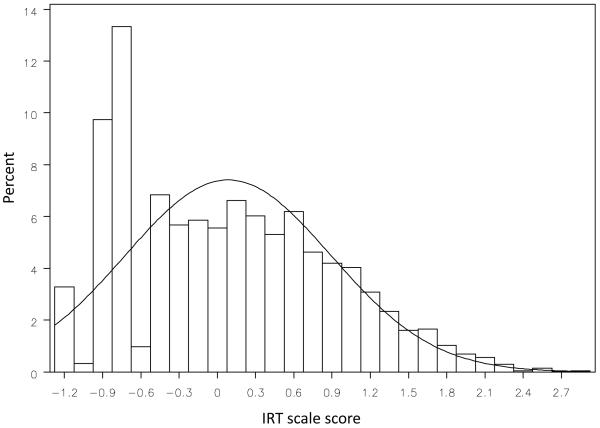
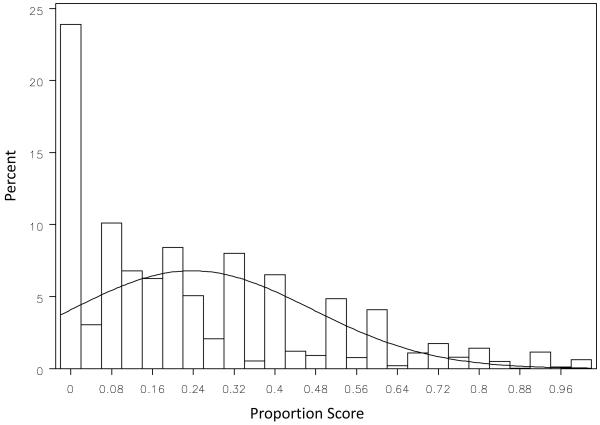
It is also important to consider the distributions of the IRT and proportion scores. The histograms for the IRT and proportion scores are presented in the top and bottom panels of Figure 3, respectively. It is immediately clear that the proportion scores are, by definition, bounded between zero and one. Further, for the pooled data the modal value for the proportion scores is at zero; there is thus a “piling up” of observations at the lowest value of the scale. In contrast, although the IRT scores similarly shows a spike at zero, the overall distribution is much more even and appears to better approximate a continuous and normal distribution. These differences are critically important when fitting statistical models to these scale scores. Many (but not all) methods of estimation used to fit models assume continuously and normally distributed dependent measures that are not characterized by upper or lower boundaries (e.g., bounded between 0 and 1). Whereas the IRT scores represent a reasonable approximation to a normal distribution, the proportion scores clearly do not. Thus taking the proportion scores to a modeling framework that assumes continuity and normality could lead to biased conclusions.

Figure 3. Histogram with superimposed normal distribution for the IRT scores (top panel) and proportion scores (bottom panel).

Fitting Growth Curve Models to Test Trajectories of Internalizing Symptomatology

To conclude our demonstration, we fitted a multilevel growth model to the IRT scores to obtain estimates of the fixed and random effects of the trajectories of internalizing symptomatology from ages 10 to 33.¹³ As noted earlier, here we focus on several initial growth models with the understanding that much more comprehensive models would be tested to more thoroughly evaluate the joint effects of time- invariant and time-varying predictors of development; see Curran et al. (2007), Hussong et al. (in press; 2007) and Flora et al. (in press) for more detailed presentations of growth models fitted to different sets of predictors and outcomes drawn from this same project.

We fitted a series of linear and non-linear three-level growth models using restricted maximum likelihood estimation in Version 9.1 of SAS PROC MIXED (SAS Institute, 2000-2004). A three-level model was required to properly account for the multiple siblings nested within the MLS and AFDP families (resulting in the nesting of time within child within family). We rescaled our metric of time so that the intercept was defined at age 21; this had the dual advantage of being the median age and also the age at which there were a large number of observations (N=562). Following the recommendations of Bollen and Curran (2006), we fitted a series of nested and non-nested growth models (intercept-only, linear, quadratic, piecewise) and concluded that the three-piece linear model was the most parsimonious and best fitting for our purposes here. The first piece was tied at age 18 and the second piece at age 21 (where age 21 also served as the intercept of the trajectory). The parameter estimates are presented in Table 4, and a graphical plot of the fixed effects and a random selection of individual trajectories are presented in Figure 4.

Table 4. Fixed and random effects for the three-level piecewise-linear growth model fitted to the IRT scale scores.

Random Effects Estimates
Effect	Estimate	Standard Error	Z Value	Pr Z
Intercept	0.258	0.030	8.57	<.0001
Piece #1	0.010	0.002	5.89	<.0001
Piece #2	0.025	0.005	4.80	<.0001
Piece #3	0.002	0.001	3.12	0.0009
Family	0.081	0.015	5.48	<.0001
Residual	0.294	0.007	40.53	<.0001

Fixed Effects Estimates
Effect	Estimate	Standard Error	DF	t Value	Pr > |t|
Intercept	−0.034	0.024	1224	−1.40	0.1618
Piece #1	0.001	0.006	6164	0.18	0.8605
Piece #2	−0.092	0.010	6164	−9.30	<.0001
Piece #3	−0.019	0.004	6164	−5.39	<.0001

note: Piece #1 spans ages 10 to 18; Piece #2 spans ages 18 to 21; Piece #3 spans ages 21 to 33. Intercept defined at age 21. Only variance components are presented, although the full matrix of variance and covariance terms were estimated in the growth model.

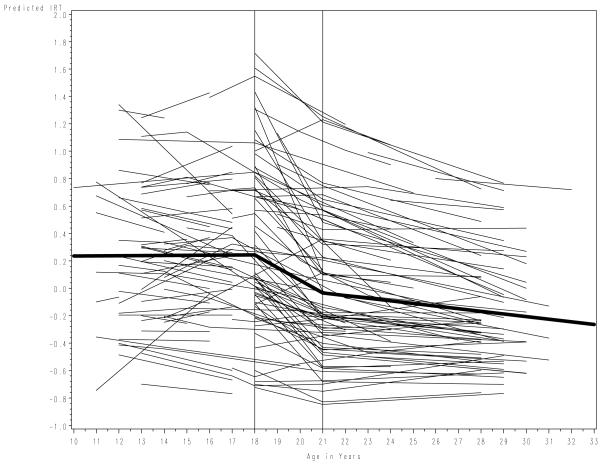
Figure 4. Fixed effects and a random sampling of individual trajectories drawn from the final three-piece linear growth model fitted to the 7392 observations drawn from 1827 individual subjects.

note: dark line represents fixed effects for the three linear pieces; the vertical reference lines at age 18 and 21 denote the points at which the pieces are tied; the intercept is defined at age 21; the individual trajectories are empirical Bayes estimates of a random subset of individuals drawn from all three studies.

Considering the fixed effects first, the intercept term did not significantly differ from zero (γˆ = −0.3,p = 1.6); given the scaling of the IRT scores, this reflects that the mean reported level of internalizing symptomatology at age 21 was at the mean of the underlying distribution of the latent construct (given that the IRT scores are scaled to a standardized mean of zero). Further, the slope of the first piece also did not significantly differ from zero (γˆ =0.01, p = 8.6), although the slopes of the second and third pieces did (γˆ = −0.9, p < 0.01, and γˆ = -0.2, p < 0.01 respectively). These values reflect that, on average, there is not systematic change in internalizing symptomatology between ages 10 and 18, but there is a significant negative drop between ages 18 and 21, and a less steep but still significant drop between ages 21 and 33.

The fixed effects only reflect the average trajectory pooling over all individuals and the random effects reflect individual variability around these mean values. All five random effects significantly differed from zero (the intercept, the three linear pieces, the level-1 residual, and the level-3 family variance component; see Table 4). These random effects are also graphically depicted in Figure 4 in terms of the variability among the individual trajectories around the overall mean trajectory. These significant random effects suggest that there is evidence of potentially meaningful individual variability around all components of the development trajectory as well as within individuals and between families. However, we have still not considered the potential impact of study group membership, and this must be incorporated into the model prior to evaluating other measures of theoretical interest.

To formally test for potential study group differences, we created two dummy-coded variables to represent the three study groups. Because the AFDP study provided subjects over the full 24-year developmental span, we chose this as the reference group. The main effects of the two dummy codes thus compared the AHBP to the AFDP, and the MLS to the AFDP. However, the main effects only consider overall mean differences in internalizing symptomatology across the three studies. To test for potential study differences in rates of change over time we also included all possible interactions between study group membership and each of the three linear pieces of the developmental trajectory. The addition of these five fixed effects (i.e., two main effects and three interactions) led to a significant improvement in model fit (likelihood ratio test χ² =158, df=5, p<.0001) indicating that study differences need to be incorporated into the model. The final fixed-effects estimates are presented in Table 5. These results indicate that the MLS and AHBP participants reported significantly lower overall levels of internalizing symptomatology compared to the AFDP participants. Further, there were no study differences in the magnitude slope of the first linear piece. However, the slope of the second linear piece was significantly more negative for the AHBP compared to the AFDP, and the slope of the third linear piece was significantly less negative for the AHBP compared to the AFDP.¹⁴

Table 5. Fixed effects for the three-level piecewise-linear growth model fitted to the IRT scale scores including main effects and interactions with study membership.

Fixed Effects Estimates
Effect	Estimate	Standard Error	DF	t Value	Pr > |t|
Intercept	.234	.037	1222	6.35	<.0001
Piece #1	−.038	.009	6161	−4.08	<.0001
Piece #2	.007	.017	6161	0.43	.667
Piece #3	−.043	.005	6161	−8.08	<.0001
MLS	−.240	.065	1222	−3.71	.0002
AHBP	−.388	.048	1222	−8.01	<.0001
MLS*Piece #1	.021	.013	6161	1.65	.1
AHBP*Piece #2	−.183	.021	6161	−8.56	<.0001
AHBP*Piece #3	.034	.007	6161	4.78	<.0001

note: Piece #1 spans ages 10 to 18; Piece #2 spans ages 18 to 21; Piece #3 spans ages 21 to 33. Intercept defined at age 21. MLS=Michigan Longitudinal Study; AHBP=Adolescent Health and Behavior Project; symbol “*” reflects interaction. Model estimated with random effects at all three levels, but these are not presented here.

Taken together, these results reflect that there are differences in both overall level and rates of change in internalizing symptomatology as a function of study group membership. A key strength of this modeling framework is that these study group influences can be formally incorporated and subsequently controlled in the growth model. Given space constraints, we do not elaborate on this model further here. However, this model could be expanded to include a variety of important time-specific measures at level-1 (e.g., time-varying covariates such as externalizing symptomatology or substance use), child-specific measures at level-2 (e.g., child gender or child pubertal status), or family-specific measures at level-3 (e.g., parental alcoholism status or family size). Regardless of specifics, all of these additional measures would be assessed above and beyond the estimated differences across the three studies. Detailed examples of these various model extensions are presented in Curran et al. (2007), Hussong et al. (in press; 2007) and Flora et al. (in press).

Are the Complexities of the IRT Model Worthwhile?

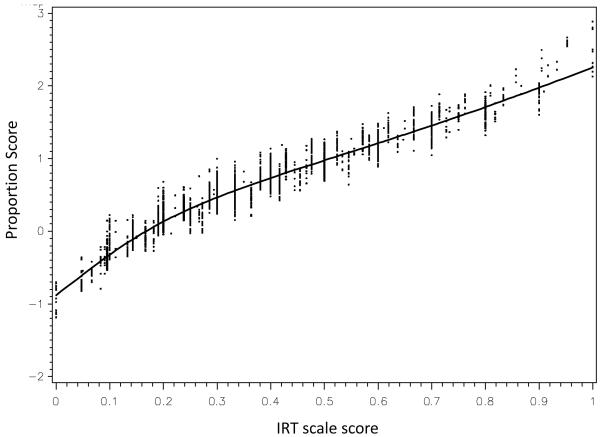
A very reasonable question can be raised as to whether the IRT modeling strategy that we have described here is worth the effort relative to using the (much) simpler proportion score model. To better understand the relation between the proportion scores and IRT scores, we estimated the bivariate correlations between the proportion and IRT scores within each age; the correlations ranged from .96 to .98 with a median value of .97. These extremely high values raise obvious concerns about the added value stemming from the more complex IRT models. However, the high bivariate correlations between the IRT and proportion scores can be quite deceiving in that the correlation coefficient is a test of rank and not variance. As such, although relative rank is quite similar between the IRT and proportion scores, the estimated scale score variance most certainly is not. This is most clearly demonstrated in Figure 5 in which the bivariate relation between the proportion scores (plotted on the x-axis) and the corresponding IRT scores (plotted on the y-axis) is presented. The near-linear relation between the two types of scores reflects the high correlation presented earlier. However, it is also clear that at any given value of the proportion score there is an entire distribution of values of the IRT scores.

Figure 5. Scatterplot of observed proportion scores with calculated IRT scores pooled over age and study.

note: x-axis values are proportion scores and y-axis values are corresponding 2PL IRT scale scores ; total sample size is N=1827

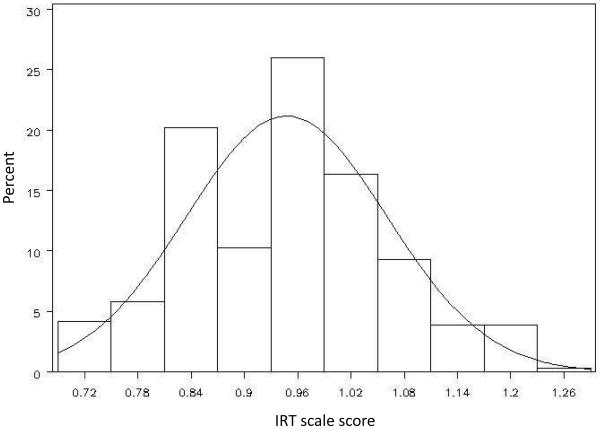
For example, consider a proportion score of .50. Pooling over all individuals and all ages, there were 312 subjects who endorsed precisely one-half of the presented items at any given age. However, for this very same proportion score of .50 there were literally 149 unique IRT scores, any specific value of which was dictated by the pattern of endorsed items as well as the age, gender, and study membership of the individual. This is further highlighted in Figure 6 in which these 149 unique values are plotted as a histogram; again, in the proportion score approach, every individual would have received a scale score equal to .50, yet in the IRT approach there is an entire distribution of scores. The existence of this distribution of scores is due to the fact that the IRT model does not simply consider how many items were endorsed (as is done with the proportion score), but also considers precisely which items were endorsed. As we have demonstrated in prior work (Curran et al., 2007), this greater variability in score estimation in turn allows for the more rigorous testing of potentially important individual differences in subsequent growth curve modeling.

Figure 6. Distribution of IRT scores for the N=312 subjects who reported proportion scores equal to .50.

Potential Limitations and Recommendations

Our goal has been to highlight the many advantages of pooling data from multiple developmental studies to which IRT models and multilevel growth curve models can be fitted that would not otherwise have been possible within any single data set. Despite a large number of advantages, there are two clusters of potential limitations encountered in such an endeavor: limitations when pooling the data and limitations when fitting the models.

With respect to pooling the data, IDA is a nascent methodology and much is yet to be learned about how to best use these techniques in practice. Several issues are clearly evident, though. First, it is important that there be overlap in ages between adjacent studies to allow for the linking of measurement across study and over time. In our example the three studies ranged in age from 10 to 17, from 17 to 23, and from 10 to 33; we thus had full coverage of all ages from 10 to 33. However, it would not be possible to use the methods we describe here if there were to be coverage from say 10 to 17 and from 18 to 25, since no data are available to link the two studies together at a shared age. Second, an important topic that we have not discussed in detail is that of sampling. We were fortunate in that the three studies we considered here were all designed to sample the same general population (e.g., children of non-institutionalized alcoholic parents). We believe it is thus reasonable to assume that the aggregate sample is representative of this targeted population. It is not currently known what the implications would be when combining data sets that were obtained under more discrepant sampling frameworks, nor is it known if the use of sampling weights might offset any potential bias when generalizing to some unknown aggregate population. Finally, even when samples overlap with respect to age, there must also be sufficient overlap in measurement to allow for the calculation of valid scale scores. Measurement might be considered the most important link in the chain, and inferences drawn from subsequent growth models are only as valid as the measures to which they are fitted.

With respect to fitting the models, the initial limitation that is immediately encountered is the requirement of relatively large sample sizes. The IRT uses a likelihood-based method of estimation in which all parameters are estimated simultaneously and large sample sizes are required to achieve proper convergence and efficient estimation. How large is large is an inherently unanswerable question; this depends on the number of items, the distribution of the responses, and the values of the item parameters. However, at least several hundred individuals are likely required for typical applications in the developmental sciences. A second potential limitation is the assumption of unidimensionality. In the current application there was strong evidence that the 21-items were characterized by a single dimension. However, there are other situations in which this would not be expected to hold (e.g., a set of items assessing multiple personality traits). Although modeling strategies do exist that allow for multidimensional IRT (e.g., Fox & Glas, 2001; Rabe-Hesketh, Skrondal, & Pickles, 2004), these tend to require even larger sample sizes, excessive computing time, and are sometimes computationally intractable (that is, there is simply no obtainable solution). A categorical confirmatory factor analysis might be used in these situations (e.g., fitting a CFA to polychoric correlations), but these models require massive numbers of parameters (e.g., in our application we would estimate 21-indicator latent factors at each of 24-assessments across 12 groups) and not all of the same information that is provided in the IRT model is available in the CFA (e.g., test information and scale measurement error). Although much future promise holds for multidimensional IRT models, current methods require unidimensionality.

Finally, the methods that we describe above can be considered a “two-step” procedure in which the scale scores are estimated via the IRT model in the first step, and these scores are then taken to other analytic frameworks in a separate second step. From a statistical standpoint, it would be ideal to simultaneously estimate the IRT part of the model in the presence of the corresponding secondary analysis (e.g., fitting a growth curve model directly to the IRT measurement model). An important example of a one-step approach was recently proposed by Raudenbush, Johnson, and Sampson (2003). This method is characterized by several key strengths, but at the same time certain restrictions must be imposed on the measurement model to achieve identification (i.e., to conform to a Rasch IRT model; Rasch, 1960). Other one-step procedures do not impose these restrictions (e.g., GLLAMM; Rabe-Hesketh et al., 2004), but these currently require very large sample sizes and sometimes do not result in obtainable solutions. Although simultaneous estimation is ideal from a statistical standpoint, we believe the two-step approach based on the 2PL IRT model is a highly practical strategy that is readily available today.

In conclusion, we strongly recommend that the simultaneous integration of multiple developmental data sets be closely considered for testing a broad range of theoretically derived research hypotheses. This approach is characterized by a host of advantages including marked increases in statistical power; greater heterogeneity in subject demographics; broader psychometric assessment of theoretical constructs; longer longitudinal windows of study; the opportunity to test hypotheses not considered in the original studies; and increased efficiency in both time and money. Because of these advantages, integrative data analysis has come under increasing demand by both researchers and funding agencies. Despite the many advantages that are offered by IDA, there are a number of complexities that remain to be overcome. Here we have focused on just one of these: the implementation of a measurement model that can be used to calculate scores anchored to a common metric over age and across study. We have presented a detailed empirical demonstration of these methods in hopes that future researchers will consider the IDA of pooled multi-sample data in the future.