Aging Effects on Cardiac and Respiratory Dynamics in Healthy Subjects across Sleep Stages

Abstract

Study Objectives:

Respiratory and heart rate variability exhibit fractal scaling behavior on certain time scales. We studied the short-term and long-term correlation properties of heartbeat and breathing-interval data from disease-free subjects focusing on the age-dependent fractal organization. We also studied differences across sleep stages and night-time wake and investigated quasi-periodic variations associated with cardiac risk.

Design:

Full-night polysomnograms were recorded during 2 nights, including electrocardiogram and oronasal airflow.

Setting:

Data were collected in 7 laboratories in 5 European countries.

Participants:

180 subjects without health complaints (85 males, 95 females) aged from 20 to 89 years.

Interventions:

None.

Measurements and Results:

Short-term correlations in heartbeat intervals measured by the detrended fluctuation analysis (DFA) exponent α₁ show characteristic age dependence with a maximum around 50–60 years disregarding the dependence on sleep and wake states. Long-term correlations measured by α₂ differ in NREM sleep when compared with REM sleep and wake, besides weak age dependence. Results for respiratory intervals are similar to those for α₂ of heartbeat intervals. Deceleration capacity (DC) decreases with age; it is lower during REM and deep sleep (compared with light sleep and wake).

Conclusion:

The age dependence of α₁ should be considered when using this value for diagnostic purposes in post-infarction patients. Pronounced long-term correlations (larger α₂) for heartbeat and respiration during REM sleep and wake indicate an enhanced control of higher brain regions, which is absent during NREM sleep. Reduced DC possibly indicates an increased cardiovascular risk with aging and during REM and deep sleep.

Citation:

Schumann AY; Bartsch RP; Penzel T; Ivanov PC; Kantelhardt JW. Aging effects on cardiac and respiratory dynamics in healthy subjects across sleep stages. SLEEP 2010;33(7):943-955.

IN PHYSIOLOGY, LONG-RANGE POWER-LAW CORRELATIONS HAVE BEEN STUDIED FOR MANY YEARS, E.G., IN HEARTBEAT DYNAMICS,^1,2 RESPIRATION dynamics,^3–5 brain waves,^6–8 and gait time series.^9–11 Such correlations characterize a persistent variation of the given signal on many time scales. For example, the probability of persistently larger (or smaller) values over extended periods of time is characteristically increased. Long beat-to-beat or breath-to-breath time intervals are more likely to be followed by longer intervals than by shorter ones, and vice versa.

This correlation structure of the data can be classified by fractal or multifractal scaling analysis.^12–15 Calculated scaling exponents are affected by pathologic conditions, sympathovagal balance, cardiopulmonary regulation, and circadian rhythm, paving the way towards an identification and discrimination of physiologic states, such as exercise versus rest,^16,17 wake versus sleep,¹⁸ across circadian phases¹⁹ or different sleep stages,^13,20,21 and for the development of diagnostic markers for diseases or physiologic risks, such as cardiac risk.²² In particular, short-term scaling exponents were shown to be more powerful predictors of mortality than standard measures of heart-rate variability.²³

Another parameter characterizing short-term variations of heartbeat intervals is the recently introduced deceleration capacity (DC) index. It is calculated by applying the phase rectified signal averaging (PRSA) technique²⁴ to heartbeat interval time series, and describes how quickly the heart rate decelerates. DC has been shown to be a powerful risk predictor of mortality in patients surviving an initial myocardial infarction,²⁵ as it is characteristically diminished in high-risk patients.

There have been very few studies of aging effects on these characteristic measures,^26,3,27,28 and there is a recent study comparing a group of young with a group of elderly subjects during different sleep stages.²⁹ However, no study has systematically examined how these scaling measures change across a wide range of age groups during different sleep stages. Heart rate variability, and in particular parasympathetic autonomic regulation, significantly decrease with aging^30–32 and with pathology. In addition, the deteriorating impact of aging on sleep quality, sleep quantity, sleep efficiency, and sleep structure is generally accepted. For reviews on sleep-related consequences of normal aging see Bliwise³³ and Espiritu³⁴ and references therein. Aging manifests itself in many ways, including a declined ability to initiate and maintain sleep, shorter total time of sleep, and decreased deep sleep (slow wave sleep) and REM sleep. It is accompanied by increased light sleep (stages 1 and 2), as well as a larger number and frequency of arousals, and an elevated wake duration after sleep onset.^35–37 Sleep disorders and diseases have been identified with an increased cardiovascular probability of morbidity and mortality in the elderly. It has been reported that nocturnal changes in respiratory function occur with age and lead to sleep apnea, hypopnea, and respiratory arousals. Besides, age-related changes in the thalamocortical regulatory mechanisms³⁶ and the neuroendocrine system³⁸ have been reported and associated with the deterioration of health and quality of sleep. Interestingly, at the age of 50 years cortisol levels suddenly rise, accompanied by a worsening of sleep fragmentation and a decline in REM sleep.³⁹ Here, we systematically study the effect of aging and sleep stages upon cardiovascular oscillations and correlations, as well as respiratory correlations in a large cohort and for a wide range of ages.

METHODS

Subjects and Protocol

This paper studied the data of 180 healthy subjects (85 males and 95 females) at ages from 20 to 89 years. Within the SIESTA project^37,40 196 healthy subjects (94 males and 102 females) underwent full-night polysomnography and were monitored for 2 subsequent nights, resulting in a total of 392 polysomnographic recordings. All subjects gave informed consent, and the study was approved by the local ethics committees of all sleep laboratories involved. General exclusion criteria were a history of drug abuse or habitation (including alcohol), psychoactive medication or other drugs, e.g., β-blockers, or night-shift work. All subjects reported no symptoms of neurological, mental, medical, or cardiovascular disorders. Additional exclusion criteria for healthy subjects comprised: (1) significant medical disorders, (2) a Mini Mental State Examination (MMSE) score < 25,41 (3) a Pittsburgh Sleep Quality Index (PSQI) global score > 5,⁴² (4) a usual bedtime before 22:00 or after 00:00, (5) a Self-rating Anxiety Scale (SAS) raw score ≥ 33,⁴³ and (6) a Self-rating Depression Scale (SDS) raw score ≥ 35.⁴⁴ During the study the consumption of coffee, alcohol, and cigarettes was limited to each subject's habitual rate.

We excluded one 95-year-old female (the only subject above 90 years of age) and one 69-year-old male whose ECG exhibits clear signs of pacemaker interventions. We also removed 37 single-night recordings due to an apnea-hypopnea-index (AHI) ≥ 10 per hour and another 5 recordings due to missing or damaged sleep stage annotations. Altogether, this left us with 346 full-night polysomnographic recordings from 180 disease-free subjects (161 from males and 187 from females). Note that only one night was used for some subjects. The typical duration of the recordings was 7 to 8 hours. Therefore we analyzed approximately 2,500 hours of heartbeat data and the same for respiration. The data sets were binned in 7 age groups (Figure 1). For some of the calculations males and females were separated.

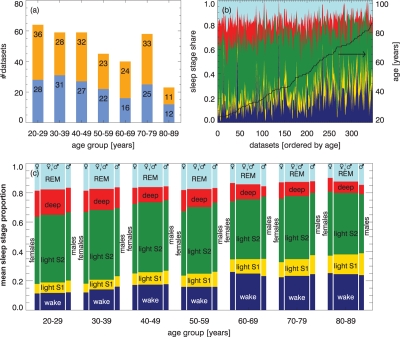
Figure 1.

(a) Age and gender characteristics of the considered study cohort of disease-free humans (males blue, females orange). The total numbers of data sets (nights) are shown for each age group. (b) Proportion of sleep stages on total time in bed for all subjects sorted by age (from left to right). The colors indicate the states, from bottom to top: wake state - dark blue, light sleep stage 1 - yellow, light sleep stage 2 - green, deep sleep stages 3 and 4 - red, and REM sleep - light blue. (c) Sleep stage distribution averaged over 10 years for all subjects (large bars in the center), and separately for females (left) and males (right); colors and order as in (b).

Measurements

Full-night polysomnographic data was obtained within the EU project SIESTA at 7 sleep laboratories located in 5 European countries.^37,40 Each recording consisted of an electroencephalogram (EEG) using at least 6 leads, a 2-lead electrooculogram (EOG), a 2-lead electromyogram (EMG, chin and leg), oronasal airflow, respiratory body movements (belts around chest and abdomen), snoring (microphone), oxygen saturation, and a single-channel electrocardiogram (ECG, modified V1 lead as typical for polysomnographic recordings). Sleep stages were identified according to the sleep scoring system of Rechtschaffen and Kales⁴⁵ by 3 trained technicians (2 independent scorers and 1 adjudicator) familiar with polysomnographic data. In this study we concentrate on ECG and oronasal airflow data. ECG was sampled at 100 Hz, 200 Hz, or 256 Hz; while airflow was sampled at 16 Hz, 20 Hz, 100 Hz, or 200 Hz, depending on the laboratory and the equipment. The detailed experimental setup has been reported elsewhere.⁴⁰

Data Preparation

In order to study correlations and oscillations within respiratory data and heartbeat data for different sleep stages, as well as night-time wake, we split all recordings into segments corresponding to wake, light sleep (stage 1), light sleep (stage 2), deep sleep (stages 3 and 4 joined),⁴⁶ and REM sleep. Since sleep stage determination during transitions is sometimes complicated and possibly unreliable, we removed the first and last 30 s from each segment. We omitted the results of light sleep stage 1 in this paper because of insufficient statistics (see Figure 1).

Heartbeat time positions (R-peaks) were extracted from the ECG data using the semi-automatic peak detector Raschlab developed by the cardiology group of Klinikum Rechts der Isar, Munich Germany.⁴⁷ A beat classification (normal beat, ventricular beat, artifact) was assigned to each R-peak by the detector. Then we calculated the series of RR time intervals between each pair of consecutive heartbeats. An RR interval was excluded from our calculations if (1) the beat at the beginning or at the end of the interval was not normal, (2) the calculated interval was shorter than 330 ms or longer than 2000 ms, or (3) the interval was more than 30% shorter or more than 60% longer than the preceding interval. The purpose of the last filter was to eliminate extrasystoles and ectopic beats unnoticed by the peak detector. We discarded all sleep stage segments that contained less than 100 normal intervals or had more than 5% of the intervals excluded.

Recorded oronasal airflow data were processed by determining the times and values of the signals’ maxima and minima, representing expiration and inspiration, respectively. Since noise in the data mainly consists of spikes (outliers), a simple threshold filter is sufficient. All data points exceeding a threshold of 95% of the maximum value or dropping below 95% of the (negative) minimum value within a moving time window are set to the corresponding threshold values. Data was resampled at 4 Hz before identifying maximum and minimum values. As well, we employed a classification scheme assigning to each event a measure of reliability depending on (1) the length of the identified breathing cycle, (2) the difference between cutoff threshold and extremal point, and (3) a comparison with averages over 3 preceding and 3 following breathing cycles.

All methods were applied separately for each subject and each night, taking into account all reliable segments for the same sleep stage. Preceding detrended fluctuation analysis (DFA, see below) all excluded intervals were cut and the gaps were joined. This procedure has been shown to not affect the DFA results, even if as much as 50% of the data is removed.⁴⁸ For phase-rectified signal averaging (PRSA, see below), the excluded data points were skipped in the averaging step because a removal of data points could disturb the timing.

Detrended Fluctuation Analysis (DFA)

DFA, first introduced by Peng et al. for studying DNA sequences, has been intensely applied to studies of correlations in noisy, non-stationary time series.⁴⁹ Bunde et al. improved the method describing higher-order detrending.¹³ It has been validated on surrogate (control) time series with additional correlations and trends.^50,51,48

The method quantifies fluctuations on different time scales, s, i.e., different numbers of heartbeat or respiratory intervals. For each s the integrated (cumulated) signal, of length N, is split into non-overlapping pieces (segments) of length s. For each segment an n-th order polynomial fit is subtracted, and the remaining mean-square fluctuations are averaged. Repeating the procedure for many scales s yields the square of the fluctuation function, which scales according to a power-law with exponent α, F²_DFAn ∼ s^2α. The exponents, α, can easily be extracted by linear fits of log(F_DFAn(s)) versus log(s). Uncorrelated fluctuations lead to α = 1/2, while α > 1/2 indicates positive temporal correlations, and α < 1/2 anti-correlations.

Fluctuation functions obtained from heartbeat data usually exhibit a crossover between 2 scaling regimes. Thus, we define 2 slopes, α_RR,1 for small scales (6 ≥ s ≥ 16 heartbeats) and α_RR,2 for larger scales (50 ≥ s ≥ 200 heartbeats). Since there is no clear crossover, respiration can be characterized by just one fluctuation exponent α_RES. Under the assumption of an average breath cycle spanning 4 heartbeats⁵² we have defined an associated fitting range of 12 ≥ s ≥ 50 breaths to allow comparison with α_RR,2.

Short-term correlations quantified by α_RR,1 are related to the HF-band as can be derived in a simple approximation (see footnote following acknowledgments). Scaling exponents α_RR,2 and α_RES, on the other hand, describe long-range correlations associated with the VLF band. Thus they reflect cerebral dynamics rather than autonomic control. Hence, DFA results for large scales elucidate additional features of cardiopulmonary control and coupling.

Phase-Rectified Signal Averaging (PRSA) Method

PRSA is a powerful tool for extracting and displaying quasi-periodic oscillations in noisy, non-stationary signals.²⁴ It allows for the identification of complex control leading to nearly periodic oscillations despite phase resetting and noise. Focusing on particular time scales, it is complementary to the DFA procedure, which analyzes the scaling behavior by comparing variations on different time scales and characterizing the underlying noise. In addition, PRSA can be employed to study causal relationships between events, such as deceleration or acceleration of heartbeat.

The algorithm is rather simple. In the first step, anchor points are selected in the time series. In the standard form of the algorithm, anchors are defined for moderate increases in heart beat intervals, i.e., when the current heartbeat interval is longer than the preceding one, x(t) > x(t − 1). Here, we neglect very large changes (> 10%) in consecutive heartbeat intervals, which are most likely associated with artifacts in the data. We note that in the original version of the PRSA method²⁵ the limit for large changes was set to > 5% because this earlier study was designed to analyze data from post-infarction patients. Since healthy subjects have a large heart rate variability, we found that increases in consecutive heartbeat intervals between 5% and 10% are rather common and normal. Thus, in this study we used a > 10% cutoff. In addition, we carefully removed all ventricular beats prior to the PRSA analysis.

The anchors are related to deceleration events, and thus, parasympathetic activation. Surroundings of length 2L are then defined around each anchor point, including the data from L previous points and L − 1 future points. Finally, all windows are aligned at the anchor positions and the PRSA curve x_PRSA(j) is obtained by calculating the arithmetic average over all windows separately for each point j, j = − L,…,0,…, L −1.

Taking 4 points from the center of the PRSA curve, which is equivalent to choosing L = 2, is sufficient to define the parameter deceleration capacity

DC = (1/4)[x̄_PRSA(0) + x̄_PRSA(1) – x̄_PRSA(–1) – x̄_PRSA(–2)]

DC has been shown to be a superior predictor of mortality in post-infarction patients, compared with the current gold standard, left ventricular ejection fraction (LVEF).²⁵

Artifacts or outliers in the data can easily be handled by disregarding them in the selection of anchor points and in the averaging procedure. Note that a different number of data points might contribute to the PRSA averages at different locations.

Data Analysis and Statistics

For each data recording, and for each sleep stage, we calculated the values of α_RR,1, α_RR,2, α_RES, and DC, taking into account all reliable segments. In addition, we determined, for each α, the sum of squared residuals χ² for the linear fit in the double logarithmic plots, as well as the sum of squared deviations from the mean (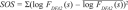). The coefficient of determination, r² = 1 − χ² / SOS, indicates the reliability of the fits; r² = 1 for a perfect fit and r² << 1 for significant deviations from a power-law behavior in the corresponding fitting regime. The α values were considered to be reliable if (1) F_DFA2(s) could be calculated for the whole regime and (2) r² ≥ 0.98. For deceleration capacity (DC) we only considered values in the range 0 ≥ DC ≥ 40 ms to be reliable. Within each age group we obtained statistical properties (mean, standard error, median, quartiles Q25 and Q75) based on reliable α and DC values only. However, we also present the distributions of the α values for unreliable fits for comparison.

RESULTS

Distribution of Sleep Stages

Figure 1a reports the study cohort with age and gender distribution. Figure 1b shows the share of the total time in bed for all states, separately for each record; and it is horizontally ordered by increasing age of the subjects. Each individual's age is indicated by the black curve, referring to the right axis. For Figure 1c, these data have been binned in age groups amounting to 10 years each. Separate results for males and females are also shown. Since effects of aging upon quantitative sleep parameters based on the SIESTA database (but without considering gender differences) were studied and reported earlier,³⁷ we will not discuss this in detail here.

However, in Figure 1b, it can be seen that inter-individual sleep notedly fluctuates, even within the same age class. Nevertheless, when considering group averages, total wake and total light sleep percentage obviously increase with age, while percentages of deep sleep and REM sleep decrease as shown in Figure 1c. Young females seem to have less wake and light sleep S1, but more REM sleep, when compared with males. For elderly (> 60 years) the behavior appears to be the opposite. While young males and females exhibit almost the same percentage of deep sleep, it decreases much more rapidly in males upon disease-free aging.

Correlation Properties of Heartbeat Intervals

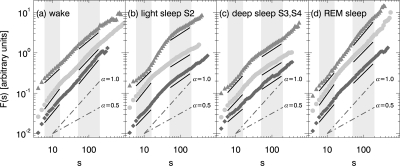
Figure 2 shows the heartbeat fluctuation functions, F_DFA2 (s), of 3 representative subjects from different age groups: (1) young (20–39 years, lowest curves in each panel), (2) intermediate age (40–69 years, center), and (3) elderly (70–89 years, top) in a double logarithmic plot. The fitting regimes for α_RR,1 (characterizing short-term correlations) and α_RR,2 (characterizing long-term correlations) are indicated by gray bars. The slopes of the straight solid lines are identical with the fitted values of α_RR,1 and α_RR,2.

Figure 2.

Examples of DFA2 heartbeat fluctuation functions for different sleep stages and representative subjects from three age groups, from bottom to top: young - dark gray diamonds, intermediate age - light gray circles, and elderly - gray triangles up. Gray shaded bars indicate the fitting regimes for α_RR,1 (6 ≥ s ≥ 16 heartbeats) and α_RR,2 (50 ≥ s ≥ 200 heartbeats). The slopes of the solid black lines are identical with these fitted exponents. For comparison gray dash-dotted lines indicate slopes of α = 1/2 (uncorrelated behavior) and α = 1 (1 / f noise). Fluctuation functions and fits are vertically shifted for clarity.

There are two important observations. First, one clearly sees the presence of long-range correlations (α_RR,2≈ 1 >> 1/2) during wakefulness and REM sleep, while long-term correlations are weak or absent during light sleep and deep sleep (α_RR,2 ≈ 1/2). This finding is consistent with earlier results.^13,21 Secondly, age differences in the scaling behavior are apparent, especially when comparing α_RR,2 for young and elderly subjects during wakefulness and REM sleep, and when comparing α_RR,1 for young and intermediately aged, as well as intermediately aged and elderly during all sleep stages.

To study these age dependences systematically we calculated DFA2 fluctuation functions for all data sets and fitted α_RR,1 and α_RR,2 in the scaling regimes shaded in Figure 2. To monitor the quality of the fits, we also calculated the coefficient of determination r² and disregarded fits with r² < 0.98, since the fluctuation functions are not sufficiently close to a power-law in these cases. Note that “healthy” subjects with unrecognized sleep apnea often exhibit deviations from the power scaling law, as the duration of the apneas is a characteristic time scale. This leads to a crossover in the DFA scaling function at this time scale.²⁸ Most data for such subjects are automatically disregarded by our r² < 0.98 criterion.

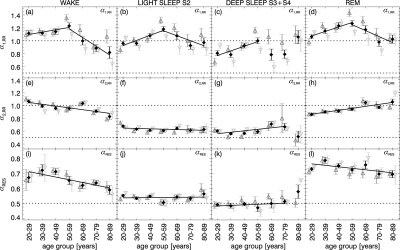
Figure 3 shows our main findings. Mean values and standard error of the means for α_RR,1, α_RR,2, and α_RES were calculated from the data of all subjects separated into 7 age groups spanning time periods of 10 years each. Results for men and women are shown separately. We have also compared the results for first and second nights (not shown) and found no systematic differences.

Figure 3.

Age dependence of (a-d) heartbeat short-term fluctuation exponents α_RR,1, (e-h) heartbeat, and (i-l) respiration long-term fluctuation exponents α_RR,2 and α_RES for wakefulness, light sleep S2, deep sleep S3 and S4, and REM sleep. The mean values for all subjects (black diamonds), men (dark gray open triangles up), and women (light gray open triangles down) are shown with error bars representing the standard errors of the means. Black solid lines indicate linear fits to the means based on all age groups, except for α_RR,1, where 2 separate fit regimes (20–59 and 50–89 years) were chosen and for deep sleep, where insufficient statistics in elderly did not allow fitting. Note that α values with r² < 0.98 or incomplete fitting regimes were disregarded. The dotted lines mark α = 1/2 (uncorrelated behavior) and α = 1 (1 / f noise).

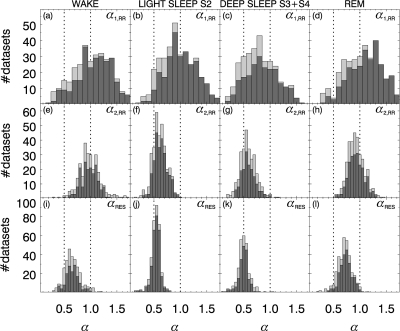
The corresponding distributions of individual scaling exponents for all data sets are shown in Figure 4, combining all age groups. The dark gray histograms are associated with the data included in Figure 3, while the additional light gray histogram bars include the results of non-reliable fits. One can see that the distributions are very close to Gaussian so that a Student t-test can be applied for checking the significance of differences.

Figure 4.

Histograms of (a-d) α_RR,1, (e-h) α_RR,2, and (i-l) α_RES in wake state, light sleep S2, deep sleep S3 and S4, and REM sleep. Light gray histograms show the distributions for all 348 data sets considered in this study, while the α values from fits with r² < 0.98 or incomplete fitting regimes were excluded for the dark gray histograms. Dotted lines indicate random uncorrelated behavior α = 1/2 and strongly correlated behavior α = 1. Note that the bins were chosen twice as wide for (a-d) compared with (e-l).

Table 1 reports the numerical means and standard deviations (instead of standard errors of the means, as in Figure 3) for the 3 α parameters and the 4 states in young, intermediately aged, and elderly subjects. The significance of the differences between these 3 age groups is indicated in the table by different symbols that were defined according to different P-values obtained from a t-test.

Table 1.

Measure	αRR,1	αRR,2	αRES
Wake
Young	1.12 ± 0.25†	1.02 ± 0.15†∘	0.69 ± 0.16*
Middle	1.13 ± 0.33∘	0.98 ± 0.15	0.66 ± 0.12
Elderly	0.87 ± 0.35†	0.89 ± 0.14‡	0.62 ± 0.10
Light sleep S2
Young	0.96 ± 0.26	0.65 ± 0.11	0.54 ± 0.07
Middle	1.12 ± 0.29†	0.62 ± 0.13	0.53 ± 0.08
Elderly	0.95 ± 0.35‡	0.60 ± 0.14	0.54 ± 0.10
Deep sleep S3 and S4
Young	0.80 ± 0.29	0.59 ± 0.13	0.49 ± 0.09
Middle	0.93 ± 0.29‡∘	0.60 ± 0.15	0.49 ± 0.11∘
Elderly	0.84 ± 0.35	0.60 ± 0.15	0.52 ± 0.07
REM sleep
Young	1.11 ± 0.28	0.88 ± 0.13†	0.75 ± 0.11*
Middle	1.23 ± 0.33‡∘	0.95 ± 0.15†	0.74 ± 0.12∘
Elderly	1.00 ± 0.36†	1.00 ± 0.13	0.69 ± 0.12

Mean values and standard deviations for fluctuation exponents α during wakefulness, light sleep stage S2, deep sleep S3 and S4, and REM sleep distinguishing 3 cohort subsets: young (age 20–39), intermediately aged (age 40–69), and elderly (age 70–89). The null-hypothesis that values for a pair of cohort subsets are drawn from distributions with identical mean was checked by a 2-sided heteroscedastic Student t-test. Three significance levels are indicated by symbols, P < 0.001 (†), P < 0.01 (‡), and P < 0.03 (*). The symbols (†, ‡, *) in the line for young subjects refer to the test comparing young and elderly, the symbols in the line for intermediately (middle) aged subjects to comparing them with young, and the test in the line for elderly refers to comparing elderly with middle aged. Additionally, the symbol ∘ indicates significant differences (P < 0.03) between males and females in the same age group.

A very interesting age dependence is observed in heartbeat correlations on short time scales, i.e., in the exponent α_RR,1. We find a systematic and significant increase, in the age range from 20 to 59 years, for each sleep stage, but not during wake (where our analysis shows no significant difference between the 20–29 year and the 50–59 year group, t–test: P > 0.05). This increase is almost independent of gender (Figures 3a-d and Table 1). Above 60 years of age, a systematic and significant decrease in α_RR,1 occurs with further aging, except during deep sleep, where statistics are insufficient in the elderly groups. Note that the total time spent in deep sleep is reduced in elderly subjects (Figure 1), and is usually accompanied by an increased occurrence of ectopic beats. In our analysis this results in the rejection of whole segments of data during deep sleep when dealing with elderly subjects (thus, the average α_RR,1 value for the 80–89 year old group during deep sleep as shown in Figure 3c is based on only 8 α_RR,1 values from 6 subjects). The general picture of a maximum in α_RR,1 in the age regime of 50–60 years is, nevertheless, independent of the considered sleep stage (or wake). This is the same for both, males and females, indicating a high reliability. However, in the intermediate age group of 40–69 years, the values for females are lower than those for males, at a P < 0.03 significance level during wakefulness, deep sleep, and REM sleep (see Table 1). These differences might be an indication of an earlier decay in α_RR,1 for females.

Besides the most interesting age dependence, our analysis showed significant differences in α_RR,1 values across sleep stages for all age groups (except the 80–89 year group, where the statistics are not sufficient). These differences are comparable to the age difference within each sleep stage. Specifically, for the 20–29 year group, we find a significant difference between sleep stages, with the lowest α_RR,1 values during deep sleep, higher values during light sleep and highest values during REM and wake (Figures 3a-d, P < 0.01 for deep sleep versus light sleep and light sleep versus wake, and P < 0.001 for deep sleep versus REM sleep). For the 50- to 59-year-old group, where the maximum in α_RR,1 occurs, our results show a similar pattern of lowest values during deep sleep and higher values during light sleep, REM sleep, and wake (Figures 3a-d), with P < 0.01 for deep sleep versus light sleep; P < 0.001 for deep sleep versus REM sleep; and no significant differences between wake, REM sleep, and light sleep. Comparing the 20–29 year-old group with the 50–59 year-old group, we find statistically significant age related differences within each sleep stage (deep sleep P < 0.01, light sleep P < 0.001, REM sleep P < 0.001) but not wake (P > 0.05). These age differences are statistically similar to the differences across sleep stages for each of the 2 groups. These observations indicate that the effect of sleep regulation on α_RR,1 in heartbeat intervals is comparable to the effect of aging.

For larger time scales α_RR,2≈ 0.9 > > 1/2 indicates that there are long-term correlations in both, wake and REM sleep that are almost absent in NREM sleep (light sleep and deep sleep, α_RR,2 ≈ 0.6). This confirms the scaling behavior observed previously in a much smaller cohort of young subjects,^13,21 as well as in a group of elderly subjects,²⁹ suggesting a common dependence of α_RR,2 on sleep stages for all age groups. Note that data from the 2 oldest groups must be disregarded during deep sleep because of insufficient statistics (also indicated by large error bars).

Looking at the age dependence of α_RR,2, we observe significant changes during REM and wake (see Figures 3e, h). During REM sleep, α_RR,2 increases from α_RR,1= 0.86 for young adults (aged 20–29) up to values α_RR,2 = 1.05 in the very elderly (aged 80–89). This increase is statistically significant for the young and middle age groups, while we find no significant difference when comparing intermediate age and elderly subjects (see Figure 3h and Table 1). For wakefulness α_RR,2 decreases from α_RR,2= 1.06 to α_RR,2= 0.83 in the course of normal disease-free aging. This decrease is statistically significant both when comparing intermediate age and the elderly as well as young and elderly subjects, while we found no significant difference when comparing the young and the intermediate age groups (see Figure 3e and Table 1). During light sleep and deep sleep, no significant age dependence is observed in α_RR,2 (see Figures 3f and g and Table 1).

Correlation Properties of Respiration

Regarding respiration we present results for inter-breath intervals obtained from maxima in the oronasal-airflow signal. We have also checked other respiration proxies (inter-breath intervals from belt recordings and based on signal maxima or minima), but found the differences too small to warrant a separate reporting in this paper. Neglecting age dependence, one finds similar scaling behavior as for heartbeat, i.e., α_RES> 1/2 for wake states and REM sleep, as well as α_RES≈ 1/2 for deep sleep (Figures 3i-l and Table 1). This is consistent with earlier observations in a much smaller cohort.⁴ Furthermore, it seems that weak long-term correlations are present in respiration during light sleep and absent during deep sleep (see also the histograms in Figure 4). The overall correlations are much weaker than those observed for heartbeat data. Given that the histograms are almost identical for males and females (not shown), during all studied sleep stages and wakefulness, we conclude there are hardly any gender effects. Although we note that intermediately aged females have (weakly significant) smaller and larger averages during deep sleep and REM sleep, respectively (Figures 3k-l).

Looking at the age dependence, one recognizes an opposite aging effect during REM sleep when compared with heartbeat: α_RES decreases with age while α_RR,2 increases (Figures 3h, 3l). For wakefulness, both exponents α_RES and α_RR,2 decrease (Figures 3e, 3i). Note, however, that the observed age dependences in α_RES during wake and REM are weakly significant (see Table 1). No significant age dependencies in respiratory correlations are observed during NREM sleep.

Influence of Tobacco and Alcohol on Cardiac and Respiratory Dynamics

To asses the influence of smoking on the correlation properties of cardiac and respiratory dynamics across different sleep stages and how they change with aging, we separately analyzed and compared smokers and nonsmokers. In the SIESTA database, 39 of the healthy subjects were identified as smokers and 136 as nonsmokers. There is no information available for 5 subjects in the database. For the subjects that were identified as smokers there is no information recorded in the database on the number of cigarettes per day or on the period (years) over which subjects have been actively smoking prior to the SIESTA study. We have tested whether any of the scaling exponents (α_RR,1, α_RR,2, α_RES), characterizing cardiac and respiratory dynamics for smokers, are significantly different from the values observed for non-smokers. By differentiating 3 age groups (age: 20–39 years, 40–69 years, and 70–89 years) and 4 sleep stages (wake, light sleep, deep sleep, and REM sleep), we found significant changes with smoking in 2 cases: (1) in young subjects during wake, the scaling exponent α_RR,1, characterizing short-term correlations in heartbeat fluctuations, decreases when compared with nonsmokers (P < 0.01); and (2) in intermediately aged subjects during REM sleep, the scaling exponent α_RES of respiratory dynamics also decreases when compared with nonsmokers (P < 0.03). The number of smokers among the elderly (n = 4) was insufficient to assure meaningful statistics. We did not find effects of smoking upon the scaling exponent α_RR,2, characterizing the long-term heartbeat correlations. The observed differences related to smoking are smaller when compared with the age-dependent and sleep-stage dependent differences presented in Figure 3 and Table 1.

Regular alcohol intake in a certain period of their life prior to the recordings was reported by 31 subjects (out of 180 subjects; no information is available on 2 subjects). Combining all age groups, we find that the short-term scaling exponent α_RR,1 of heartbeat dynamics is significantly larger for the subjects with regular alcohol intake across all sleep stages – with 19% increase during wake (P < 0.001) when compared with subjects without a history of regular alcohol intake; 12% increase during REM sleep (P < 0.01), 13% increase during NREM sleep (P < 0.01). For the respiration scaling exponent α_RES, we found a 5% increase for the alcohol group during NREM sleep (P < 0.01). We observed no significant changes in the long-term scaling exponent α_RR,2 of heartbeat dynamics. By considering separate age groups, we found a significant increase in α_RR,1 during REM and in α_RES during NREM sleep (both with P < 0.03) for the group of younger subjects (age: 20–39 years) who had regular alcohol intake. For the group of intermediately aged subjects (age: 40–69 years) who had episodes of regular alcohol intake, we found a significant increase in the short-term scaling exponent, α_RR,1, of cardiac dynamics only during wake. The number of elderly subjects (age: 70–89 years) in our database who reported episodes of regular alcohol intake is insufficient for a meaningful statistical analysis.

Alcohol consumption on the day before the recordings was reported only by 30 subjects (38 night recordings). Combining all age groups, we find a slight increase (below significance level) in the exponent α_RR,1 during REM and NREM sleep, and a significant increase in α_RES during NREM sleep.

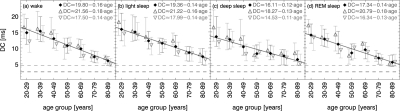
Deceleration Capacity of the Heart

Figure 5 shows our results for the deceleration capacity of the heart (DC parameter) as a function of age, shown separately for the sleep stages and wake. A significant decay from younger subjects towards older subjects is obvious in all states. The slope of the decay is, however, smaller for females than for males (see different symbols and fits printed in the figure but not shown). In particular young females (age 20–29) exhibit surprisingly low DC values, especially during wake. If one excluded this age group from the study, the DC slope for males and females during wakefulness would be the same. In general, DC values for males and females become more similar with aging for all states.

Figure 5.

Deceleration capacity (DC) versus age for (a) wakefulness, (b) light sleep S2, (c) deep sleep S3 and S4, and (d) REM sleep for all subjects (black filled diamonds), males (dark gray open triangles up), and females (light gray open triangles down). We plotted median values and both quartiles Q25 and Q75 as lower and upper errors bars, respectively. Solid straight lines are linear fits to the medians for all subjects; the formulas of the separate fits for males and females are printed in the top right corner. Black and gray dashed lines indicate risk levels previously defined for infarction patients: high cardiac risk DC < 2.5 ms and low cardiac risk DC < 4.5 ms.

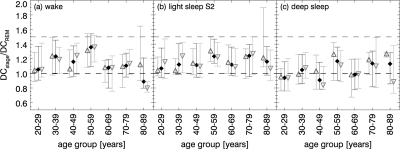
When exploring individual DC values we recognized for most subjects, lower values during REM sleep and deep sleep than during light sleep and wakefulness. To test this observation, Figure 6 shows the mean ratios over DC_REM and their standard deviations. In the case of a lower DC during REM sleep, the ratios are larger than 1. This is observed for young subjects during wake, and for all age groups during light sleep S2, i.e., DC_REM < DC_wake and DC_REM < DC_{light sleep}. The results during deep sleep were inconclusive. Employing a paired t–test comparing all DC-value combinations we found highly significant differences (P < 0.0001) for the combinations wake vs. REM sleep, light sleep vs. REM sleep, wake vs. deep sleep, and light sleep vs. deep sleep. Marginally significant differences (P < 0.05) were found for wake vs. light sleep. The DC values during deep sleep and REM sleep were not significantly different.

Figure 6.

Age dependence of DC ratios: (a) DC_wake / DC_REM, (b) DC_{light sleepS2} / DC_REM, and (c) DC_{deep sleep S3&S4} / DC_REM for all subjects (black filled diamonds), males (dark gray open triangles up), and females (light gray open triangles down).

DISCUSSION

Our study leads to the following four main observations: (1) There is a significant aging effect on the short-term correlation properties of heartbeat time series, since a maximum in α_RR,1 occurs around 50–60 years of age. We also observe comparable differences across sleep stages for the young and intermediate age groups. (2) The long-term correlation properties of heartbeat and respiration data exhibit similar characteristic dependencies on sleep stages and wake: long-term correlations and effects of aging are observed only during wakefulness and REM sleep. Heartbeat correlations increase with age in REM sleep and decrease during wake, while respiratory correlations decrease with age both during REM and wake. (3) Differences between males and females of the same age are not significant for most scaling parameters in the studied cohort, except for a significantly lower average in α_RR,1 for intermediately aged females. (4) Deceleration capacity (i.e., the ability of the heart to slow down) decreases linearly with age and reduces significantly during deep sleep and REM sleep when compared with light sleep and wakefulness.

Previous studies have also analyzed the short-term and long-term correlation behavior of heartbeat and breathing intervals in healthy subjects. However, previous studies considered much less data (approx. 500 h, compared to our 2,500 h), did not distinguish sleep stages, and only compared a single group of young with a single group of elderly subjects.^26,3,27,28 Others distinguished sleep stages but did not study age dependencies and focused mainly on healthy young subjects (age ≈ 25 years).^13,20,21,4 Only one study so far has considered the effect of aging across different sleep stages based on a group of young subjects (age ≈ 33 years) and a group of elderly subjects (age ≈ 78 years).²⁹ Since intermediate age groups of 50–60 year-old subjects have not been studied, the pronounced maximum in short-term heartbeat correlations has not been previously observed.

Short-Term Correlation Properties of Heartbeat

While earlier studies have suggested that multi-scale complexity and fractal scaling behavior break down with healthy aging,^53,26 a recent work,²⁸ utilizing the same data sets as in Iyengar et al.²⁶ as well as a second independent database, did not find significant differences between young and elderly healthy subjects in the heartbeat scaling behavior after carefully excluding artifacts. Iyengar et al. found α_RR,1 = 0.90 for young (age ≈ 27 years) and α_RR,1 = 1.12 for elderly (age ≈ 74 years) subjects based on 40 hours of data recorded from 20 subjects during wake in a resting semi-recumbent position. Their results show the opposite trend when compared with our results of α_RR,1 = 1.12 for the 20–29 year-old group and α_RR,1 = 0.88 for the 70–79 year-old group during wake (see Figure 3a). This is perhaps due to apnea-related artifacts in the data from elderly subjects which were not taken into account in Iyengar et al.²⁶ but significantly alter the scaling exponent at both short and long time scales as demonstrated by Schmitt et al.²⁸

However, our results for young subjects are consistent with recent studies. Penzel et al.²¹ found α_RR,1 = 1.21 during wakefulness, 1.18 during REM sleep, 1.00 during light sleep, and 0.82 during deep sleep in a data set of 14 healthy subjects with an average age of 33 years (220 hours of data). Guzman-Vargas and Angulo-Brown²⁷ studied 36 hours of data from ten young and eight elderly subjects during wake using a different technique; their results correspond to α_RR,1 ≈ 1.13 and 1.48, respectively. Clearly, the values for young subjects are consistent with ours, but the values for elderly subjects are higher than ours. We speculate that the unexpectedly large value 1.48²⁷ might be due to outliers among their eight elderly subjects. In addition, slightly larger α values are usually found when different states are not analyzed separately due to non-stationarities at the transitions between the states. Recently, Schmitt et al.²⁸ found α_RR,1 = 1.09 for 19 young subjects (age ≈ 26 years) and α_RR,1 = 1.22 for 16 elderly subjects (age ≈ 74 years) during wake in a resting semi-recumbent position. In addition they found α_RR,1 = 1.12 for an independent group of 29 elderly subjects (age ≈ 76 years) during sleep and α_RR,1 = 1.09 for the same subjects five years later (altogether ≈ 550 hours of data), reporting no significant age differences. Our results show no significant difference in α_RR,1 between young (age 20–39 years) and elderly (age 70–89 years) for deep sleep, light sleep, and REM, and a significant difference only during wake (see Table 1).

As mentioned before, none of the previous studies looked at intermediate age groups and therefore the pronounced maximum in α_RR,1 around 50–60 years of age, for all sleep stages as well as wakefulness, was missed. We suggest that the underlying effect of healthy aging could be an increase in α_RR,1 as indicated by the trend present from 20 to 55 years of age (see Figure 3). If the increase continued for the next 35 years, i.e., up to 90 years of age, the values of α_RR,1 would reach 1.4 or 1.5, i.e., values typical for an uncorrelated random walk. This usually does not happen, though, because another effect leads to a drop of α_RR,1 for subjects of ages above 50–60 years. The drop seems to start somewhat earlier in women. A satisfying explanation of this observation would seem to require a change in the related control mechanisms which is sufficiently fundamental to affect all sleep stages and wakefulness. We speculate that this change might be related to the rise in evening cortisol levels associated with increased sleep fragmentation and a decline in REM sleep. Such a rise was reported to begin at the age of 50 years.³⁹ High cortisol levels have been associated with physiological stress and increased cardiac risk. We note that reduced short-term correlation exponents were shown to be better indicators than standard HRV parameters for predicting mortality in post-infarction patients.^23,22 However, we also note that the α_RR,1 values for the elderly subjects are comparable to the α_RR,1 values for the young subjects during all sleep stages except for wake, where α_RR,1 is significantly lower in elderly (see Figures 3a-d, Table 1). We cannot exclude that the age-related drop in α_RR,1 might be a reflection of a detrimental effect of this endpoint on individual survival. This means that the study of older subjects might favor individuals who had particularly favorable lower α_RR,1 values throughout their entire life, whereas those with less favorable larger values had a lower probability of survival and were less likely to be included.

Regarding only the elderly subjects, there is a relevant technical point affecting the mean values of α_RR,1. We observed an additional decrease in α_RR,1, down to values even close to 0.5, in the oldest subjects if bad fits with coefficient of determination r² < 0.98 were not disregarded in our analysis and ectopic beats were not carefully removed (ectopic beats have the effect of random spikes in the positively correlated heartbeat interval time series that leads to a decrease in the scaling exponent on short time scales resulting in α_RR,1 ≈ 0.5⁴⁸). This indicates that an increasing number of ectopic beats and effects of sleep apnea (leading to deviations from the power-law scaling behavior of the fluctuation function²⁸) might be partly responsible for the decrease in α_RR,1 in clinically healthy, elderly subjects with possibly increased cardiac risk. We note that the coefficient of determination is usually not checked in instances where α_RR,1 is used as an indicator for predicting cardiac risk and mortality in post-infarction patients.^23,22,54 In general, the aging characteristics of α_RR,1 should be taken into account when using it for diagnostic purposes in post-infarction patients.

Long-Term Correlation Properties of Heartbeat and Respiration

Similar to the case for the short-term correlations in heartbeat intervals, previous studies regarding the age dependence of long-term correlation properties of heartbeat and respiration in healthy subjects have not yielded a consistent picture. Early works found significant differences between young and elderly subjects, see, e.g., α_RR,2 = 0.99 versus 0.75 in Iyengar.²⁶ More recent studies reported no significant difference in α_RR,2 between young and elderly during wake, see, e.g., α_RR,2 = 1.13 versus 1.17²⁷ and α_RR,2 = 0.76 versus 0.78.²⁸ The latter study also reported α_RR,2 = 0.88 during sleep for elderly subjects (age ≈ 76 years) and α_RR,2 = 0.97 for the same individuals five years later (P = 0.01).

For respiration during wake, Peng et al.³ reported a gender difference, finding α_RES = 0.68 (0.70) versus 0.60 (0.67) for males (females) and, again, young versus elderly subjects. Although we found similar results when comparing young and elderly during wake, we did not find a significant gender difference. However, all these studies did not distinguish between physiologically different states like sleep stages, and thus, these values cannot be directly compared with ours. For both heartbeat and inter-breath intervals, we found that there is a stark contrast between the clearly long–term correlated behavior observed during wakefulness and REM sleep and the nearly uncorrelated behavior observed during NREM sleep. We also observed significant changes, with aging, during wakefulness and REM, but not during light sleep and deep sleep (see Figures 3e-l).

Most studies separating sleep stages looked at healthy young (age ≈ 25 years) subjects only.^4,13,21,55 A comparison of scaling and other characteristics of heartbeat intervals between young and elderly subjects, during different sleep stages, was presented in Schmitt et al.,²⁹ reporting a similar stratification pattern for both young and elderly across sleep stages. These earlier studies yielded results consistent with our findings, e.g., α_RR,2 = 0.94 (wake), 0.60 (light sleep), 0.55 (deep sleep), and 0.81 (REM sleep) for a group of young (age 25 years old) subjects²¹; and α_RR,2 = 0.97 (wake), 0.74 (light sleep), 0.61 (deep sleep), and 0.89 (REM sleep) for a group of 13 young (age 33 years old) subjects.²⁹ These results can be compared with the corresponding values α_RR,2 = 1.06 (wake), 0.68 (light sleep), 0.60 (deep sleep), and 0.86 (REM sleep) for the 20–29 year-old group in this paper for heartbeat, as well as α_RES = 0.57 (NREM sleep) versus 0.85 (REM sleep)⁴ compared with α_RES = 0.55 (light sleep) versus 0.73 (REM sleep) for respiration in our study. Schmitt et al.²⁹ also studied 24 elderly subjects (age ≈ 78 years) finding α_RR,2 = 1.03 (wake), 0.63 (light sleep), 0.57 (deep sleep), and 1.02 (REM sleep), compared with α_RR,2 = 0.91 (wake), 0.61 (light sleep), 0.67 (deep sleep), and 0.97 (REM sleep) in this paper for the corresponding age group of 70–79 years. This indicates a very similar stratification pattern in α_RR,2 across sleep stages for elderly subjects in both studies. Moreover, this stratification pattern in α_RR,2 is robust, as we observe it also for young subjects in agreement with Schmitt et al.²⁹ Clearly, it is not possible to find age dependencies by comparing these values with those for young subjects. Schmitt et al.²⁹ correctly conclude that there are no significant effects of aging observed in their data when comparing α_RR,2 for young (≈ 33 years old) and elderly (≈ 78 years old) across different sleep stages. We observed a similar behavior when comparing α_RR,2 for the 30–39 year-old group with the 70–79 year-old group, with P = 0.02 during REM and P > 0.02 for the other sleep stages and wake (see Figure 3). However, when we included the 20–29 year-old group and the 80–89 year-old group, we found a significant difference in α_RR,2 with age during REM and wake. In contrast, we did not find an age dependence in the long-term scaling behavior of the heartbeat and breathing intervals during light sleep and deep sleep. Moreover, while we observed a significant increase with age in the strength of the long-term correlations for heartbeat intervals during REM (Figure 3h), we found the opposite trend of decreasing α_RR,2 with age during wake (Figure 3e). We currently do not have a physiological explanation for the decrease in α_RR,2 with age during wake, considering that α_RR,2 reflects predominantly sympathetic tone, which was previously found to increase with age.

The pronounced long-term correlations, i.e., larger α_RR,2 for heartbeat and α_RESfor respiration we observe during REM sleep and wakefulness, indicate an enhanced control of higher brain regions on these autonomic functions when the brain is in a more active state. The enhanced control causing long-term correlations is obviously absent during NREM sleep, in agreement with earlier hypotheses.^4,13,55 This interpretation is strengthened by the observation of long-term correlations in the fluctuations of brain wave amplitudes and frequencies studied based on EEG data for wakefulness,⁵⁶ as well as separately for different sleep stages,⁸ since the latter study revealed that long-term brain-wave correlations exist during REM sleep and wakefulness only.

Deceleration Capacity of the Heart

The decay of DC with age observed in this study is in full qualitative agreement with previously published results obtained from 24-h Holter-ECG recordings in 1455 post-infarction patients.⁵⁷ In that study we found DC_all[ms] = 12.2−0.10·age[y], DC_males[ms] = 12.4−0.11·age[y], DC_females[ms] = 12.2–0.07·age[y] but did not distinguish between wakefulness and sleep or sleep stages. These findings are in accordance with the general understanding that there is a loss in total vagal output with normal aging. A suppressed parasympathetic tone leads to a lower DC value, which is a measure of parasympathetic efficiency. A recent study revealed a significant gender difference in sympathovagal balance with higher vagal tones in females during all sleep stages.⁵⁸ Assuming DC is directly correlated with parasympathetic outflow, this should lead to a larger DC value in females than males. However, we found the opposite dependence here and in the independent study of 24-h Holter ECGs.⁵⁷ We can imagine two possible interpretations of this finding. Either the ability of the heart to decelerate quickly is not directly associated with the amplitude of parasympathetic output, or less parasympathetic output in males is more efficiently transcribed into actual deceleration than in females.

Furthermore, it is known that during REM sleep HF power, a proxy for parasympathetic tone, is diminished relative to other sleep stages and wakefulness. Concordantly, we found slightly lower DC values during REM sleep than during light sleep for most subjects. A lower DC has been associated with an increased mortality in post-infarction patients.^25,57 Increases in sympathetic output accompanied by reduced vagal activity were related to ventricular arrhythmias that may cause sudden cardiac death.⁵⁹ Assuming these physiological conclusions are also applicable to healthy subjects, our findings suggest an increased cardiac risk during REM sleep when compared with light sleep or quiet wake. Together with the observation that most time spent in REM sleep takes place in the early morning hours the results of our analysis suggest an increase in cardiovascular risk during the morning hours. This is in agreement with earlier empirical observations based on hourly counts of sudden cardiac deaths and myocardial infarctions throughout the sleeping hours.⁶⁰

Very few subjects had DC values exceeding the intermediate risk or the high risk limits (indicated by the dashed lines in Figure 5)²⁵ Note, however, that the risk limits have been determined for 24-h ECG recordings sampled at 128 Hz, and thus, it remains unclear whether the same limits apply to our sleep study of healthy subjects.

Limitations

In this study we concentrated on the effects of chronological age on short-term and long-term fluctuations of heartbeat and respiration. Although many risk factors and declining health have been associated with chronological age, it is a rather rough estimator for physiological age (i.e., functional age). It still remains to be explored how chronological and physiological age are correlated and to what extent chronological age is an indicator of physiological condition and function.

Another important issue is the definition of the term “healthy” especially in aged subjects. To our knowledge there is no general agreement on inclusion and/or exclusion parameters for healthy subjects. We are convinced that “healthy” should also consider biological age. During this study we realized that even supposedly healthy middle-aged and elderly subjects, without reported health complaints, show, to some extent, altered (relative to young healthy subjects) patterns in heartbeat and respiration. For instance, we found several short apnea-like episodes in data from disease-free elderly subjects. These episodes did not, however, lead to an exclusion of the subjects, because the all-night AHI index remained below 10 per hour. As well, an enhanced occurrence of ectopic beats and reduced heart rate variability is observed in several elderly subjects. Again, we have not excluded these subjects, only removed the ectopic beats from the data. However, from cardiological studies we know that some of the older subjects that were declared healthy, in full agreement with the SIESTA protocol would not be considered healthy in a more restrictive study protocol concentrating specifically on cardiac conditions. The results shown here present a retrospective analysis, and we had to accept recordings with some cardiac disturbances. Based on our experience with beat-detection and artifact removal, we suggest recording data from more ECG leads in full-night polysomnographic studies.

Summary and Outlook

In conclusion we have investigated and quantified the effects of normal aging on heartbeat-to-heartbeat and breath-to-breath variability during wakefulness, light sleep, deep sleep, and REM sleep. Our study is based on 2,500 hours of full-night recordings in a large group of 180 disease–free (“healthy”) subjects ranging in age from 20 to 89 years.

We found that age significantly and systematically influences the short-term correlations of heartbeat, for all sleep stages and wakefulness. A striking maximum of the short-term correlation parameter α_RR,1 occurs at around 50–60 years of age. The observed behavior is very similar for males and females. We speculate that the effect of healthy aging is an increase of α_RR,1 with age that is reversed by a rise in evening cortisol levels reported to begin at the age of 50 years. Alternatively, the reduced α_RR,1 could also be related to extrasystoles and ectopic beats in young and elderly subjects, respectively. Including fluctuation functions that exhibit problematic scaling behavior (often associated with sleep apnea episodes) further reduces the effective α_RR,1 in elderly subjects. We believe that the aging characteristics of α_RR,1 should be taken into account when using this parameter for diagnostic purposes in post-infarction patients. However, full-night data can be used without limitations, since sleep stage only weakly effects α_RR,1.

Studying the auto-correlation behavior of heartbeat and respiration on longer time scales, we observed a clear difference between wakefulness and REM sleep on one hand and NREM sleep on the other. Pronounced long-term correlations occur during REM sleep and wakefulness only. They are probably related to an enhanced control of higher brain regions on these autonomic functions when the brain is in a more active state. In the case of heartbeat, we observed a slight decay of these long-term correlations with age, during wakefulness, and a slight increase during REM sleep. In the case of respiration we observed only a slight decay during both wakefulness and REM sleep.

Thus, the age dependence of heart rate and breathing rate correlations may be significantly more complex than a mere breakdown of multi-scale complexity and fractal scaling with aging.

Fluctuation characteristics have already been successfully applied to generate surrogate heartbeat data that is statistically indistinguishable from real recordings.⁶¹ The age-related effects on short- and long-range variability discovered in this study might allow for further improvements, and ultimately lead to a more realistic model of cardiorespiratory regulation during sleep. We believe that the results should also be taken into account when developing novel scoring parameters to enhance the detection specificity for sleep related disorders.

The observed sleep-stage related changes in deceleration capacity (DC) can be compared with changes in long-term heartbeat correlations during different sleep stages to improve the understanding of cardiovascular regulation during sleep. In addition, the results could be applied to make ECG-based detection of sleep stages possible, instead of using more complicated brain recordings. Another possible application is the identification of anomalous autonomic regulation associated with certain disorders. We recently suggested a generalization of the PRSA method (bivariate phase rectified signal averaging = BPRSA) enabling multivariate studies of quasi-periodicities.⁶² For example, one can separately analyze the behavior of heartbeat intervals at the phases of inspiration and expiration, or tackle the question how increases or decreases in heartbeat intervals affect respiratory rhythms and/or blood pressure. We are planning to apply BPRSA to heartbeat and respiration to further study cardiorespiratory control mechanisms during sleep and investigate respiratory gating.⁶³

DISCLOSURE STATEMENT

This was not an industry supported study. Dr. Penzel has received research support from Actelion, Resmed, Respironics, Sanofi, and Weinmann; is shareholder of The Siestagroup and of the CRO Advanced Sleep Research; and has received travel support from Respironics, Weinmann, and Hoffrichter.

FOOTNOTE FROM PAGE 945

A scale correction depending on the detrending-order has to be applied,⁵⁰ since observed crossovers are larger than real ones: DFA2 s_real ≈ s_observed / 2.5. A considered scaling range [6,16] heartbeats hence transforms to a real scaling range of [2.4,6.4] heartbeats corresponding to the frequency band [0.156,0.417] Hz under the simplified assumption of an average heartbeat interval of 1s. The HF band is usually associated with [0.15,0.4] Hz.