Abstract
Cooperative behavior that increases the fitness of others at a cost to oneself can be promoted by natural selection only in the presence of an additional mechanism. One such mechanism is based on population structure, which can lead to clustering of cooperating agents. Recently, the focus has turned to complex dynamical population structures such as social networks, where the nodes represent individuals and links represent social relationships. We investigate how the dynamics of a social network can change the level of cooperation in the network. Individuals either update their strategies by imitating their partners or adjust their social ties. For the dynamics of the network structure, a random link is selected and breaks with a probability determined by the adjacent individuals. Once it is broken, a new one is established. This linking dynamics can be conveniently characterized by a Markov chain in the configuration space of an ever-changing network of interacting agents. Our model can be analytically solved provided the dynamics of links proceeds much faster than the dynamics of strategies. This leads to a simple rule for the evolution of cooperation: The more fragile links between cooperating players and non-cooperating players are (or the more robust links between cooperators are), the more likely cooperation prevails. Our approach may pave the way for analytically investigating coevolution of strategy and structure.
Introduction
Cooperation is ubiquitous in the real world ranging from genes to multicellular organisms [1]–[4]. Most importantly, human society is based upon cooperation. However this cooperative behavior apparently contradicts natural selection [5]: Selfish behavior will be rewarded during competition between individuals, because selfish individuals enjoy the benefits from the cooperation of others, but avoid the associated costs. Therefore, the puzzle how natural selection can lead to cooperation has fascinated evolutionary biologists since Darwin.
Evolutionary game theory is an intuitive and convenient framework to study this puzzle. As a metaphor, the Prisoner's Dilemma (PD) has been widely used to investigate the origin of cooperation. In this game, two players simultaneously decide whether to cooperate (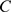 ) or to defect (
) or to defect (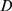 ). They both receive
). They both receive  upon mutual cooperation and
upon mutual cooperation and 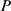 upon mutual defection. A defector exploiting a cooperator receives
upon mutual defection. A defector exploiting a cooperator receives 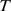 , and the exploited cooperator gets
, and the exploited cooperator gets 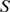 . This can be formalized in the form of a payoff matrix,
. This can be formalized in the form of a payoff matrix,
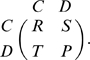 |
(1) |
The PD is characterized by the payoff ranking 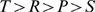 . For repeated games, the additional requirement
. For repeated games, the additional requirement 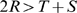 ensures that alternating between strategies is less lucrative than repeated mutual cooperation. In the one shot PD, it is best for a rational individual never to cooperate irrespective of the co-player's decision. Thus, defection is the Nash Equilibrium [6]. However, the two players would be better off if they both cooperated, hence the dilemma. In an evolutionary setting, where payoff determines reproductive fitness, defectors can reproduce faster based on their higher payoff and cooperation diminishes - defection is evolutionary stable [7], [8]. Several mechanisms have been proposed to explain the persistence of cooperative behavior, including kin selection [9], direct [10], [11] and indirect reciprocity [12], [13], group selection [14], [15] as well as the network reciprocity [16]–. Furthermore, the relationship between these mechanisms receives an increasing attention [25]–[28].
ensures that alternating between strategies is less lucrative than repeated mutual cooperation. In the one shot PD, it is best for a rational individual never to cooperate irrespective of the co-player's decision. Thus, defection is the Nash Equilibrium [6]. However, the two players would be better off if they both cooperated, hence the dilemma. In an evolutionary setting, where payoff determines reproductive fitness, defectors can reproduce faster based on their higher payoff and cooperation diminishes - defection is evolutionary stable [7], [8]. Several mechanisms have been proposed to explain the persistence of cooperative behavior, including kin selection [9], direct [10], [11] and indirect reciprocity [12], [13], group selection [14], [15] as well as the network reciprocity [16]–. Furthermore, the relationship between these mechanisms receives an increasing attention [25]–[28].
Both in animal and human societies, individuals interact with a limited number of individuals. The interactions of individuals are often captured based on the network of contacts. Therefore, there has been an increasing interest in the influence of population structure on the evolution of cooperation.
Nowak and May first studied the PD game on regular lattices [16]. Subsequently, social dilemmas on regular graphs have been investigated [19]–[21], [29]. Many authors have also considered more complex networks, such as scale-free and small-world afterwards [17], [18], [24]. It has been well recognized that network topologies can play a crucial role in the evolution of cooperation, in addition to the payoff matrix and the update mechanism.
The network topology is assumed to be static in the above work. However, social relationships between individuals are not eternal, but are continuously changing in the real world. Therefore, the coevolution of strategy and network receives increasing attention [30]–[47].
Dynamical networks can significantly boost cooperation compared to static networks. On the one hand, cooperation thrives if individuals are able to promptly adjust their social ties, because this allows cooperators to escape from defectors [38]. Similarly, cooperation is more likely to occur if the favored relationships between cooperators (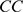 links) tend to be less fragile than adverse social ties (
links) tend to be less fragile than adverse social ties (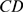 links) [37], [43]. The latter result is consistent with our empirical intuitions and is widely observed in the real world. However, most of the works on this issue are investigated only by numerical methods and not by analytical approaches. This is mainly because it is difficult to describe the coevolution of strategy and structure of a network analytically.
links) [37], [43]. The latter result is consistent with our empirical intuitions and is widely observed in the real world. However, most of the works on this issue are investigated only by numerical methods and not by analytical approaches. This is mainly because it is difficult to describe the coevolution of strategy and structure of a network analytically.
Pacheco et al. approximate their linking dynamics by ordinary differential equations [39]–[41], [43]. They found that fast linking dynamics leads to a transformation of the payoff matrix, such that e.g. cooperation in a Prisoner's Dilemma can be stabilized. This approach does not keep the total number of links constant. Moreover, the analytical approach does not take stochastic effects into account.
Here, we consider a linking dynamics described by a discrete stochastic model. The evolution of links can be described as a Markov chain, which is the starting point for our analytical considerations. We specify the conditions required for the payoff matrix to make cooperation stable. A simple rule is obtained when the linking dynamics proceeds sufficiently fast, which reveals quantitatively how the link breaking probabilities have to be chosen such that cooperation may gain a foothold. Furthermore, we show how our stochastic linking dynamics also results in a transformation of the payoff matrix as in [39].
Analysis
We consider the coevolution of strategy and structure in the PD game. Each player's strategy  can either be cooperation (C) or defection (D), denoted by
can either be cooperation (C) or defection (D), denoted by 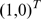 and
and 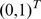 , respectively. Initially, the whole population of size
, respectively. Initially, the whole population of size 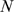 are situated on vertices of a regular graph with degree
are situated on vertices of a regular graph with degree 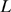 , where nodes indicate individuals while edges denote the pairwise partnerships between individuals. We consider the case where the total number of agents
, where nodes indicate individuals while edges denote the pairwise partnerships between individuals. We consider the case where the total number of agents 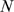 is much larger than the average degree
is much larger than the average degree 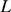 . The payoff of each individual is obtained by playing the PD game with all of its immediate neighbors:
. The payoff of each individual is obtained by playing the PD game with all of its immediate neighbors:
| (2) |
where 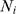 represents the neighborhood set of player
represents the neighborhood set of player  and
and 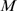 is the payoff matrix. Instead of the general matrix of the Prisoner's Dilemma Eq. (1) with four parameters, we consider a simpler payoff matrix,
is the payoff matrix. Instead of the general matrix of the Prisoner's Dilemma Eq. (1) with four parameters, we consider a simpler payoff matrix,
| (3) |
where the parameter  , measuring how profitable unilateral defection is, ranges from zero to one. Note that this payoff matrix recovers the payoff ranking described above,
, measuring how profitable unilateral defection is, ranges from zero to one. Note that this payoff matrix recovers the payoff ranking described above, 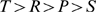 .
.
We emphasize that Eq.(3) describes a special case of general PD games, but it is widely used in biology and sociology [1].
In each time step, an agent has the opportunity to change its strategy with probability 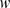 . With probability
. With probability  , a link in the network can be changed. For
, a link in the network can be changed. For 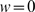 , no strategy update takes place, hence the cooperation level stays unchanged and only the dynamical organization of cooperators and defectors can be observed [45]. For
, no strategy update takes place, hence the cooperation level stays unchanged and only the dynamical organization of cooperators and defectors can be observed [45]. For  , this model degenerates to a PD game on a static regular graph, which has been studied in great detail [16], [19], [22], [29], [48].
, this model degenerates to a PD game on a static regular graph, which has been studied in great detail [16], [19], [22], [29], [48].
Let us first consider the dynamics of links (which occurs with probability  ). In each rewiring step, a link
). In each rewiring step, a link 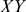 is selected from the network at random (
is selected from the network at random (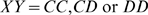 ). The link remains intact with probability
). The link remains intact with probability 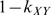 . With probability
. With probability 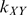 , the link is broken. In this case, one of the two adjacent players is picked at random and switches to a random player who is not its immediate neighbor in the population (see Fig. (1)). In this way, link
, the link is broken. In this case, one of the two adjacent players is picked at random and switches to a random player who is not its immediate neighbor in the population (see Fig. (1)). In this way, link  is broken and a new link
is broken and a new link 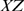 or
or 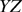 is introduced.
is introduced.
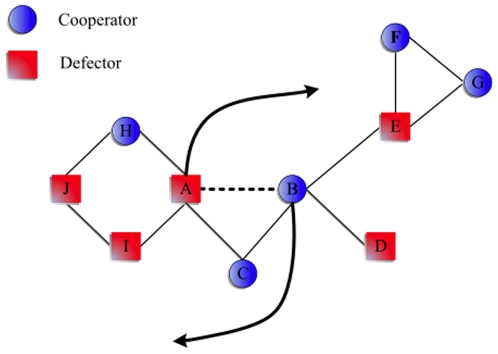
Figure 1. Linking dynamics.
If the dashed link is selected in the topological evolution, it will be broken off with probability 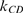 . If the dashed link is broken, then either A or B is selected to establish a new link. If A is chosen, then he switches to a random individual of the population who is not his current neighbors (B, D, E, F, G or J). Otherwise, B is chosen, then he also switches to a random individual of the population who is not his current neighbors (A, F, G, H, I or J).
. If the dashed link is broken, then either A or B is selected to establish a new link. If A is chosen, then he switches to a random individual of the population who is not his current neighbors (B, D, E, F, G or J). Otherwise, B is chosen, then he also switches to a random individual of the population who is not his current neighbors (A, F, G, H, I or J).
We consider the case of 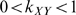 . In this case, linking dynamics does not assume rationality of agents: Adverse
. In this case, linking dynamics does not assume rationality of agents: Adverse 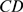 links may be kept and advantageous
links may be kept and advantageous 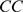 links may sometimes be broken.
links may sometimes be broken.
In contrast with previous analytical work focusing on a dynamical number of links [39], here the total number of links 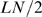 is constant in the evolution process as in [33], [38]. This constraint can imply a limited resource and avoids that all individuals are linked to all others (for generic parameter choices).
is constant in the evolution process as in [33], [38]. This constraint can imply a limited resource and avoids that all individuals are linked to all others (for generic parameter choices).
In the beginning, each link is assigned a name 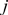 , where
, where  . In each time step, we choose a link
. In each time step, we choose a link 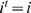 at random, where the superscript denotes the time. If the selected link
at random, where the superscript denotes the time. If the selected link 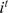 does not break, we have
does not break, we have 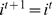 . If the link breaks, a new social tie is introduced, denoted as
. If the link breaks, a new social tie is introduced, denoted as 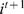 . We denote the type of link
. We denote the type of link 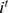 by
by 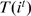 , where
, where 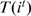 can be
can be 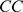 ,
, 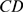 or
or 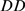 . Herein, we investigate how
. Herein, we investigate how 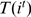 changes with time
changes with time  .
.
The dynamics of 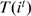 can be captured by a Markov chain with transition matrix
can be captured by a Markov chain with transition matrix 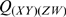 , which is the probability that an
, which is the probability that an  link transforms to a
link transforms to a 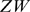 link in one time step. According to the linking dynamics, the probability of moving between
link in one time step. According to the linking dynamics, the probability of moving between 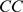 and
and 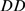 is zero. So, we only have to calculate
is zero. So, we only have to calculate 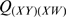 or
or 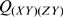 .
.
For instance, 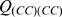 is the probability that
is the probability that 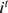 of type
of type 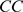 transforms to
transforms to 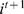 of type
of type 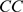 . This occurs in the following cases:
. This occurs in the following cases:
When
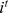 is not selected in the linking dynamics (with probability
is not selected in the linking dynamics (with probability 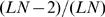 );
);- When
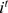 is selected (with probability
is selected (with probability 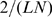 ), this happens either when the original
), this happens either when the original 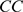 link is not broken off (with probability
link is not broken off (with probability 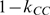 ) or when the selected player of the original link switches to another cooperator provided the link is broken (with probability
) or when the selected player of the original link switches to another cooperator provided the link is broken (with probability 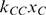 where
where 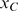 is the frequency of cooperators). Hence,
is the frequency of cooperators). Hence,
Similar considerations for other links lead to the transition probability matrix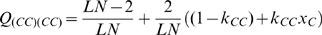
(4)
where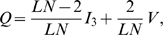
(5) 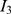 is the identity matrix and the matrix
is the identity matrix and the matrix 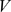 is given by
is given by
and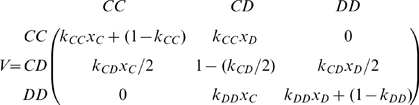
(6) 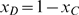 is the frequency of defectors. We emphasize that the transition matrix is only an approximation, because it does not exclude the case that a player establishes a second link with one of its immediate neighbors. However, the approximation is very good when the degree of all links is much smaller than the population size.
is the frequency of defectors. We emphasize that the transition matrix is only an approximation, because it does not exclude the case that a player establishes a second link with one of its immediate neighbors. However, the approximation is very good when the degree of all links is much smaller than the population size.
Note that this Markov chain is irreducible and aperiodic when 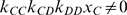 , hence there exists a unique stationary distribution
, hence there exists a unique stationary distribution 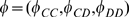 determined by equation
determined by equation 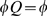 [49]. We find that
[49]. We find that
| (7) |
where 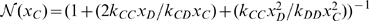 is a normalization factor. Here,
is a normalization factor. Here, 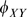 represents the probability that a link
represents the probability that a link 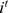 is of type
is of type  in the stationary regime. Therefore, the average number of
in the stationary regime. Therefore, the average number of  links
links 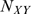 is given by:
is given by:
| (8) |
Thus, 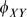 also represents the average fraction of
also represents the average fraction of  links in the whole population in the stationary regime of the linking dynamics.
links in the whole population in the stationary regime of the linking dynamics.
Let us now consider the dynamics of strategies (which occurs with probability 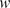 ). A player
). A player  with strategy
with strategy 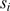 is selected at random, subsequently player
is selected at random, subsequently player 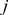 with strategy
with strategy 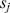 is randomly selected among
is randomly selected among  's current neighbors. Player
's current neighbors. Player  compares the payoff with that of player
compares the payoff with that of player 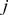 and takes strategy
and takes strategy 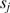 with probability [48], [50]
with probability [48], [50]
| (9) |
where 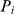 and
and 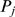 are the accumulated payoffs for
are the accumulated payoffs for  and
and 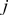 , respectively. The parameter
, respectively. The parameter 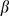 denotes the intensity of selection. For
denotes the intensity of selection. For 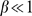 , selection is weak and strategy changes are almost random. For
, selection is weak and strategy changes are almost random. For 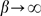 , selection is strong and strategies of more successful agents are always adopted, whereas less successful agents are never imitated. In large, well mixed populations the dynamics can be approximated by [51]
, selection is strong and strategies of more successful agents are always adopted, whereas less successful agents are never imitated. In large, well mixed populations the dynamics can be approximated by [51]
| (10) |
where  is the Gaussian white noise with variance
is the Gaussian white noise with variance  ,
, 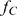 and
and 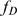 denote the average fitness of a cooperator and a defector, respectively. For large population size
denote the average fitness of a cooperator and a defector, respectively. For large population size 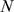 , the stochastic term vanishes [51] and we obtain
, the stochastic term vanishes [51] and we obtain
| (11) |
Note that this equation has the same equilibrium properties as the usual replicator dynamics [8]
| (12) |
If 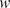 is sufficiently small, the structure of the system is close to the stationary state when strategies change. In this case, the stationary distribution of linking dynamics determines the average fitness of individuals [39]. Then, we can employ the strategy dynamics from well mixed populations for our structured system. The average payoff of cooperators is given by
is sufficiently small, the structure of the system is close to the stationary state when strategies change. In this case, the stationary distribution of linking dynamics determines the average fitness of individuals [39]. Then, we can employ the strategy dynamics from well mixed populations for our structured system. The average payoff of cooperators is given by
| (13) |
The average payoff of defectors is
| (14) |
Equating 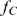 and
and 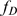 or, equivalently, substituting them into Eq. (12), we find that an unstable equilibrium
or, equivalently, substituting them into Eq. (12), we find that an unstable equilibrium 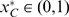 emerges when
emerges when
| (15) |
It is located at
| (16) |
This critical value 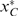 determines the attraction basin of cooperation
determines the attraction basin of cooperation 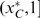 : Cooperators take over when their initial frequency
: Cooperators take over when their initial frequency 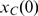 is larger than this critical value, whereas defectors take over when
is larger than this critical value, whereas defectors take over when 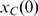 is less than this critical value. In other words, the evolutionary PD game with linking dynamics is similar to that of the coordination game in well mixed population where both cooperation and defection are best replies to themselves.
is less than this critical value. In other words, the evolutionary PD game with linking dynamics is similar to that of the coordination game in well mixed population where both cooperation and defection are best replies to themselves.
Let us show how the PD game transforms into a coordination game under linking dynamics. Substituting Eqs. (13)(14) into Eq. (12) yields
| (17) |
where the first factors are always positive and 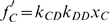 and
and 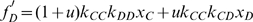 are the payoffs of cooperators and defectors in a modified game with payoff matrix
are the payoffs of cooperators and defectors in a modified game with payoff matrix
| (18) |
In other words, the coevolution of strategy and structure transforms the original PD game into another one. In particular,  turns to a coordination game when
turns to a coordination game when  , i.e.,
, i.e., 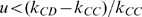 . Thus, the PD game with linking dynamics corresponds to a coordination game in a well mixed population [39], [40]. Cooperation is stable only when
. Thus, the PD game with linking dynamics corresponds to a coordination game in a well mixed population [39], [40]. Cooperation is stable only when
| (19) |
where 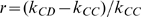 .
.
The quantity  measures the propensity for cooperators to form clusters that supports cooperation [16]. Indeed, remembering that
measures the propensity for cooperators to form clusters that supports cooperation [16]. Indeed, remembering that 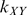 indicates the probability with which an
indicates the probability with which an  link breaks,
link breaks, 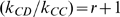 characterizes the fragility ratio between
characterizes the fragility ratio between 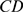 and
and 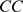 link. In particular,
link. In particular, 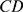 link are more fragile than
link are more fragile than 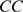 links if
links if  exceeds zero. In other words, a cooperator is more likely to play with cooperators than defectors and to sustain the social relationship when
exceeds zero. In other words, a cooperator is more likely to play with cooperators than defectors and to sustain the social relationship when  is greater than zero. Therefore
is greater than zero. Therefore  also illustrates how likely a cooperator is to interact with a cooperator. The greater
also illustrates how likely a cooperator is to interact with a cooperator. The greater  , the more likely it is for cooperators to form clusters.
, the more likely it is for cooperators to form clusters.
Increasing  allows cooperators to spread more effectively and can allow them to invade from initially small clusters [52]. The quantity
allows cooperators to spread more effectively and can allow them to invade from initially small clusters [52]. The quantity  characterizes the propensity of cooperators to form clusters. Cooperation gains a foothold when
characterizes the propensity of cooperators to form clusters. Cooperation gains a foothold when  is sufficiently large. Precisely,
is sufficiently large. Precisely,  is sufficiently large when
is sufficiently large when 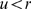 by Eq. (19). In this case, cooperator clusters expand and take over the whole population.
by Eq. (19). In this case, cooperator clusters expand and take over the whole population.
We have explained intuitively how  enhances cooperation level. In addition, we can also show analytically that large
enhances cooperation level. In addition, we can also show analytically that large  leads to cooperation by enlarging the cooperation attraction basin:
leads to cooperation by enlarging the cooperation attraction basin:
Substituting 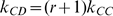 to Eq. (16), we obtain:
to Eq. (16), we obtain:
| (20) |
The quantity 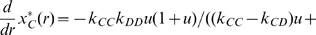
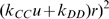 is always negative for all permitted parameters. Hence,
is always negative for all permitted parameters. Hence, 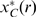 is a decreasing function of
is a decreasing function of  . Since
. Since 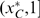 is the attraction basin of cooperation. Accordingly, increasing
is the attraction basin of cooperation. Accordingly, increasing  enlarges the attraction basin of cooperation. In other words, it requires fewer cooperators to take over the whole population with larger
enlarges the attraction basin of cooperation. In other words, it requires fewer cooperators to take over the whole population with larger  .
.
So far, it has been shown that the simple rule gives us an insight on how cooperation comes into being with linking dynamics. Furthermore, it can also be revealed that 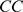 links should be less fragile [39] while
links should be less fragile [39] while 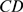 ones should be easy to break in order to promote cooperation. Since
ones should be easy to break in order to promote cooperation. Since 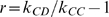 , the larger
, the larger 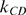 or the smaller
or the smaller 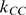 , the greater
, the greater  is. Thus cooperation is promoted when the probability to break
is. Thus cooperation is promoted when the probability to break 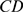 links
links  is large or the probability to break
is large or the probability to break 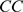 links
links 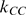 is small. This is in line with previous numerical consideration [37], [38]. However,
is small. This is in line with previous numerical consideration [37], [38]. However,  is independent of
is independent of 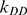 . Does this mean that
. Does this mean that 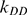 has no impact on cooperation? In fact, it is not the case. On the contrary,
has no impact on cooperation? In fact, it is not the case. On the contrary, 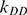 plays an important role in promoting cooperation when
plays an important role in promoting cooperation when 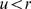 holds. Actually, this simple rule only guarantees that the equilibrium
holds. Actually, this simple rule only guarantees that the equilibrium 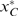 of Eq. (16) lies between zero and one, where it is defined. However it is not sufficient to make cooperation advantageous. Besides, the initial frequency of cooperators should lie in the attraction basin of cooperation
of Eq. (16) lies between zero and one, where it is defined. However it is not sufficient to make cooperation advantageous. Besides, the initial frequency of cooperators should lie in the attraction basin of cooperation 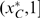 to make cooperators gain a foothold in the population. Nevertheless, notice that Eq. (16) can be rewritten as:
to make cooperators gain a foothold in the population. Nevertheless, notice that Eq. (16) can be rewritten as:
| (21) |
hence, 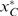 is a decreasing function of
is a decreasing function of 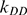 provided
provided 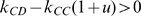 , i.e. the simple rule holds. In this way, increasing
, i.e. the simple rule holds. In this way, increasing 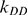 augments the attraction basin of cooperation
augments the attraction basin of cooperation 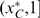 (See Fig. (2)). Thus it is easier for cooperators to gain a foothold when
(See Fig. (2)). Thus it is easier for cooperators to gain a foothold when 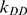 is larger.
is larger.
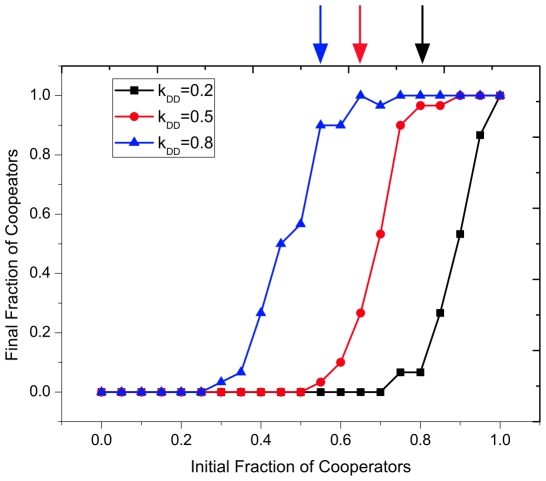
Figure 2. Final fraction of cooperators as a function of initial fraction of cooperators.
The symbols indicate the simulation while the arrows represent the analytical results. Both simulation and the analytical results show that fewer cooperators can invade a population of defectors when the 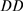 ties are more fragile, which validates the analytical prediction.
ties are more fragile, which validates the analytical prediction. 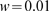 ,
, 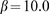 ,
, 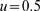 ,
, 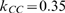 ,
, 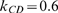 ,
, 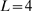 and
and 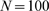 for all the three lines in the plot. In addition, each data point for all the plots from Fig. (2) to
Fig. (6) is averaged over
for all the three lines in the plot. In addition, each data point for all the plots from Fig. (2) to
Fig. (6) is averaged over 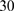 independent runs. And in each run, we set the mean value over time window of
independent runs. And in each run, we set the mean value over time window of 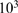 generations to be the final fraction of cooperators, after a transient time of
generations to be the final fraction of cooperators, after a transient time of 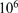 generations.
generations.
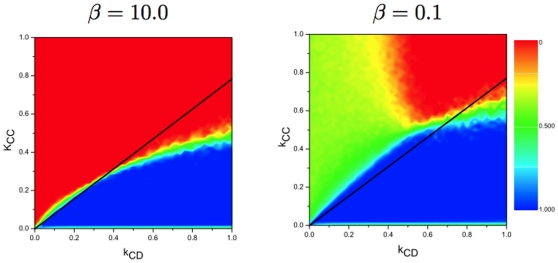
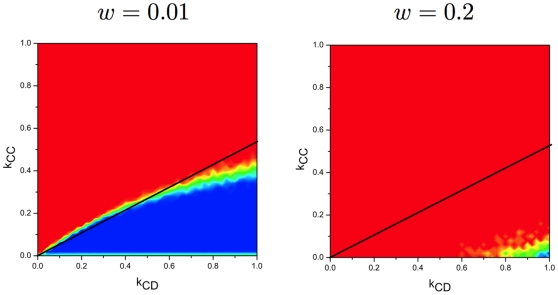
In Fig. (3), we show that the simulation results are in agreement with our analytical predictions when the selection pressure is high, while the simulations deviate from the analytical results when the selection pressure is low. For strong selection, we find above the line 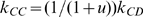 , the cooperation level is low, which is consistent with our theoretical predictions. For weak selection, however, the cooperation level is almost
, the cooperation level is low, which is consistent with our theoretical predictions. For weak selection, however, the cooperation level is almost 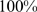 for the parameter region closely above the line for
for the parameter region closely above the line for 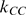 between
between  and
and 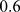 , where the cooperation level should be low based on our the simple rule.
, where the cooperation level should be low based on our the simple rule.
Figure 3. Results for the final fraction of cooperators for different selection pressure 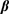 .
.
It shows how the selection pressure affects the analytical prediction. The black line is our analytical condition 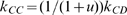 . Initially, all the individuals are situated on a regular graph of degree
. Initially, all the individuals are situated on a regular graph of degree 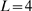 and size
and size 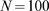 . Each individual is assigned to be a cooperator or a defector with the same probability. All plots from Fig. (3) to
Fig. (6) share the same color code and initial condition. Analytical results predict that higher cooperation level can emerge only below the black line. Simulation results show that the analytical result is more accurate for strong selection than weak selection as expected. The error is induced by the finite population size effect. (other parameters
. Each individual is assigned to be a cooperator or a defector with the same probability. All plots from Fig. (3) to
Fig. (6) share the same color code and initial condition. Analytical results predict that higher cooperation level can emerge only below the black line. Simulation results show that the analytical result is more accurate for strong selection than weak selection as expected. The error is induced by the finite population size effect. (other parameters 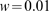 ,
, 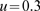 , and
, and 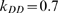 ).
).
These deviations are due to both the finite population effect and the approximation of linking dynamics by Eq. (5). On the one hand, as mentioned above, the transition matrix Eq. (6) is only an approximation based on the global frequency of cooperators, while they are also influenced by local frequencies in the simulations. On the other hand, we use the replicator equation to describe the strategy evolution. But the replicator equation is only an approximation of the strategy evolution when the population size is sufficiently large, which implies that small fitness differences can influence the dynamics. This explains why our theoretical predictions are less accurate for weak selection. Therefore, we focus on strong selection in the following.
We first investigate how  affects the evolution of cooperation. For each plot in Fig. (4), above the line
affects the evolution of cooperation. For each plot in Fig. (4), above the line 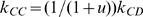 , there is nearly no cooperation, while below the line, cooperation is possible. This is consistent with our simple rule. Furthermore, compared with the three plots in Fig. (4), we observe a decrease of the parameter region to sustain the cooperation when
, there is nearly no cooperation, while below the line, cooperation is possible. This is consistent with our simple rule. Furthermore, compared with the three plots in Fig. (4), we observe a decrease of the parameter region to sustain the cooperation when  increases. It indicates that only a small temptation to defect can sustain cooperation.
increases. It indicates that only a small temptation to defect can sustain cooperation.
Figure 4. Results for the final fraction of cooperators for different values of the payoff parameter  .
.
The slope of the critical line is increasing when  is decreasing, indicating that cooperators are more likely to emerge when the parameter
is decreasing, indicating that cooperators are more likely to emerge when the parameter  is small. (
is small. (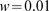 ,
, 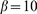 and
and 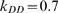 . )
. )
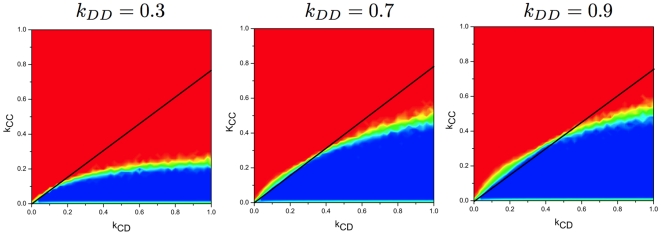
Let us further examine the role of 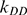 in the evolution of cooperation by simulation. It is observed clearly in Fig. (5) that the more fragile
in the evolution of cooperation by simulation. It is observed clearly in Fig. (5) that the more fragile 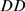 ties are, the easier it is for cooperators to wipe out defectors. Intuitively, for greater
ties are, the easier it is for cooperators to wipe out defectors. Intuitively, for greater 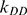 ,
, 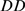 links are more likely to break and defectors are no longer trapped in their fruitless interactions and can instead seek new cooperators to exploit. Thus, it seems less likely to promote cooperation for large
links are more likely to break and defectors are no longer trapped in their fruitless interactions and can instead seek new cooperators to exploit. Thus, it seems less likely to promote cooperation for large 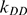 . However, both analytical and simulation results show that high
. However, both analytical and simulation results show that high 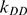 promotes cooperation (See Eq. (21) and Fig. (2)). This is counter-intuitive. In fact, in this case, the quick partner-switching between defectors induces the heterogeneity of the population, which results in cooperation. Similar results have been reported in [43].
promotes cooperation (See Eq. (21) and Fig. (2)). This is counter-intuitive. In fact, in this case, the quick partner-switching between defectors induces the heterogeneity of the population, which results in cooperation. Similar results have been reported in [43].
Figure 5. Results for the final fraction of cooperators for different values of 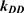 .
.
It shows that quick partner switching between defectors, i.e., high 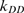 , promotes cooperation. (
, promotes cooperation. (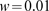 ,
, 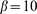 and
and 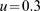 .)
.)
Finally, we turn to investigate the role of 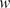 on the coevolution. Fig. (6) shows that for small
on the coevolution. Fig. (6) shows that for small 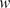 , the result is in good agreement with the theoretical prediction, while deviates from the simple rule for large
, the result is in good agreement with the theoretical prediction, while deviates from the simple rule for large 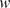 , as expected. Similar results have been reported in the analytical approach of Pacheco et al. [39]. Both analytical approaches are based on the time scale separation, i.e., all the links are almost in the stationary states when the strategy update occurs.
, as expected. Similar results have been reported in the analytical approach of Pacheco et al. [39]. Both analytical approaches are based on the time scale separation, i.e., all the links are almost in the stationary states when the strategy update occurs.
Figure 6. Results for the final fraction of cooperators for different values of  .
.
Our analytical results are only valid under time scale separation, as shown in this plot. (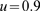 ,
, 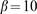 and
and 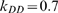 )
)
Results and Discussion
To sum up, we have established a discrete model to describe the stochastic linking dynamics analytically in terms of a Markov chain. Based on this linking dynamics, we have studied the coevolution of strategy and network structure. A simple condition for the evolution of cooperation is obtained analytically that becomes more accurate when selection is stronger. The rule shows that the less fragile 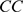 links are, the easier cooperation emerges. The more fragile
links are, the easier cooperation emerges. The more fragile 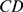 links are, the easier cooperation prevails.
links are, the easier cooperation prevails.
Compared to Pacheco et al.'s work, time scales separation also plays an important part in our analysis. In Pacheco et al.'s work, time separation is used to ensure that the linking dynamics is in the stationary regime when the strategy evolution happens. But in contrast to Pacheco et al.'s work, our analytical approach explicitly considers stochastic effects in the linking dynamics. Further, when the population size is sufficiently large, this Markov chain describing the linking dynamics can be approximated by a different system of differential equations. Since the total number of links is constant in our approach, there are only two independent variables describing the different kinds of links. In Pacheco et al.'s method, however, all the three variables are independent. In general, both methods lead to very similar qualitative results.
Regarding the coevolution of strategy and network, previous numerical work with constant number of links has assumed that dissatisfied ties are more likely to break off than satisfied ones. In this case, cooperation is more likely to be sustained. However, it has not been shown analytically that to what extent satisfied links are more stable than adverse ones to make cooperation gain a foothold. The simple rule 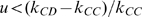 reveals such a relation between the payoff matrix and the parameters of the linking dynamics. It shows under which conditions cooperation may prevail, provided the linking dynamics is sufficiently fast. Furthermore, we have provided a series of numerical results to validate the analytical results. We find that numerical results are in agreement with the analytical results for strong selection, yet may deviate from the analytical results for weak selection.
reveals such a relation between the payoff matrix and the parameters of the linking dynamics. It shows under which conditions cooperation may prevail, provided the linking dynamics is sufficiently fast. Furthermore, we have provided a series of numerical results to validate the analytical results. We find that numerical results are in agreement with the analytical results for strong selection, yet may deviate from the analytical results for weak selection.
Acknowledgments
We thank C.S. Gokhale and W. Huang for help.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: B.W. gratefully acknowledges the financial support from China Scholarship Council (2009601286). D.Z. acknowledges support by the Natural Science Foundation of China (10625101) and 973 Fund (2006CB805900). L.W. acknowledges support by the National Natural Science Foundation of China (10972002 and 60736022). A.T. acknowledges support by the Emmy-Noether program of the Deutsche Forschungsgemeinschaft. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Nowak MA. Evolutionary Dynamics. Cambridge, MA: Harvard University Press; 2006. [Google Scholar]
- 2.Sigmund K, editor. The calculus of selfishness. Princeton, New Jersey: Princeten University Press; 2010. [Google Scholar]
- 3.Axelrod R. The Evolution of Cooperation. New York: Basic Books; 1984. [Google Scholar]
- 4.Levin SA, editor. Games, Groups and the Global Good. Springer Series in Game Theory. Springer; 2009. [Google Scholar]
- 5.Nowak MA. Five rules for the evolution of cooperation. Science. 2006;314:1560–1563. doi: 10.1126/science.1133755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nash JF. Equilibrium points in N-person games. Proc Natl Acad Sci USA. 1950;36:48–49. doi: 10.1073/pnas.36.1.48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Maynard Smith J. Evolution and the Theory of Games. Cambridge: Cambridge University Press; 1982. [Google Scholar]
- 8.Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge: Cambridge University Press; 1998. [Google Scholar]
- 9.Hamilton WD. The genetical evolution of social behavior I. J Theor Biol. 1964;7:1–16. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- 10.Trivers RL. The evolution of reciprocal altruism. Q Rev of Biol. 1971;46:35–57. [Google Scholar]
- 11.Ohtsuki H, Nowak MA. Direct reciprocity on graphs. J Theor Biol. 2007;247:462–470. doi: 10.1016/j.jtbi.2007.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wedekind C, Milinski M. Cooperation through image scoring in humans. Science. 2000;288:850–852. doi: 10.1126/science.288.5467.850. [DOI] [PubMed] [Google Scholar]
- 13.Nowak MA, Sigmund K. Evolution of indirect reciprocity. Nature. 2005;437:1291–1298. doi: 10.1038/nature04131. [DOI] [PubMed] [Google Scholar]
- 14.Wilson DS. A theory of group selection. Proc Natl Acad Sci USA. 1975;72:143–146. doi: 10.1073/pnas.72.1.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wilson DS, Wilson EO. Rethinking the theoretical foundation of sociobiology. Q Rev of Biol. 2007;82:327–348. doi: 10.1086/522809. [DOI] [PubMed] [Google Scholar]
- 16.Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. [Google Scholar]
- 17.Santos FC, Pacheco JM, Lenaerts T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations. Proc Natl Acad Sci USA. 2006;103:3490–3494. doi: 10.1073/pnas.0508201103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Santos FC, Pacheco JM. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys Rev Lett. 2005;95:098104. doi: 10.1103/PhysRevLett.95.098104. [DOI] [PubMed] [Google Scholar]
- 19.Szabó G, Hauert C. Phase transitions and volunteering in spatial public goods games. Phys Rev Lett. 2002;89:118101. doi: 10.1103/PhysRevLett.89.118101. [DOI] [PubMed] [Google Scholar]
- 20.Szabó G, Fáth G. Evolutionary games on graphs. Physics Reports. 2007;446:97–216. [Google Scholar]
- 21.Ohtsuki H, Hauert C, Lieberman E, Nowak MA. A simple rule for the evolution of cooperation on graphs. Nature. 2006;441:502–505. doi: 10.1038/nature04605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Perc M. Transition from gaussian to levy distributions of stochastic payoff variations in the spatial prisoner's dilemma game. Phys Rev E. 2007;75:022101. doi: 10.1103/PhysRevE.75.022101. [DOI] [PubMed] [Google Scholar]
- 23.Tomassini M, Luthi L, Giacobini M. Hawks and doves on small-world networks. Phy Rev E. 2006;73:016132. doi: 10.1103/PhysRevE.73.016132. [DOI] [PubMed] [Google Scholar]
- 24.Chen X, Fu F, Wang L. Promoting cooperation by local contribution under stochastic win-stay-lose-shift mechanism. Physica A. 2008;387:5609–5615. [Google Scholar]
- 25.Nowak MA, Tarnita CE, Antal T. Evolutionary dynamics in structured populations. Phil Trans Roy Soc London B. 2010;365:19–30. doi: 10.1098/rstb.2009.0215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Taylor C, Nowak MA. Transforming the dilemma. Evolution. 2007;61:2281–2292. doi: 10.1111/j.1558-5646.2007.00196.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Traulsen A. Mathematics of kin-and group-selection: Formally equivalent? Evolution. 2009;64:316–323. doi: 10.1111/j.1558-5646.2009.00899.x. [DOI] [PubMed] [Google Scholar]
- 28.Bshary R, Grutter AS. Punishment and partner switching cause cooperative behaviour in a cleaning mutualism. Biology Letters. 2005;1:396–399. doi: 10.1098/rsbl.2005.0344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lindgren K, Nordahl MG. Evolutionary dynamics of spatial games. Physica D. 1994;75:292–309. [Google Scholar]
- 30.Skyrms B, Pemantle R. A dynamical model of social network formation. Proc Natl Acad Sci USA. 2000;97:9340–9346. doi: 10.1073/pnas.97.16.9340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bala V, Goyal S. Conformism and diversity under social learning. J Econ Theory. 2001;17:101–120. [Google Scholar]
- 32.Ebel H, Bornholdt S. Evolutionary games and the emergence of complex networks. 2002. cond-mat/0211666.
- 33.Zimmermann MG, Eguluz VM. Cooperation, social networks, and the emergence of leadership in a prisoner's dilemma with adaptive local interactions. Phys Rev E. 2005;72:056118. doi: 10.1103/PhysRevE.72.056118. [DOI] [PubMed] [Google Scholar]
- 34.Poncela J, Gómez-Gardeñes J, Traulsen A, Moreno Y. Evolutionary game dynamics in a growing structured population. New Journal of Physics. 2009;11:083031. [Google Scholar]
- 35.Hanaki N, Peterhansl A, Dodds PS, Watts DJ. Cooperation in evolving social networks. Management Science. 2007;53:1036–1050. [Google Scholar]
- 36.Biely C, Dragosit K, Thurner S. Prisoners dilemma on dynamic networks under perfect rationality. Physica D. 2007;228:40–48. [Google Scholar]
- 37.Fu F, Hauert C, Nowak MA, Wang L. Reputation-based partner choice promotes cooperation in social networks. Phy Rev E. 2008;78:026117. doi: 10.1103/PhysRevE.78.026117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Santos FC, Pacheco JM, Lenaerts T. Cooperation prevails when individuals adjust their social ties. PLoS Comput Biol. 2006;2:1284–1291. doi: 10.1371/journal.pcbi.0020140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pacheco JM, Traulsen A, Nowak MA. Co-evolution of strategy and structure in complex networks with dynamical linking. Phys Rev Lett. 2006;97:258103. doi: 10.1103/PhysRevLett.97.258103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pacheco JM, Traulsen A, Nowak MA. Active linking in evolutionary games. J Theor Biol. 2006;243:437–443. doi: 10.1016/j.jtbi.2006.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Pacheco JM, Traulsen A, Ohtsuki H, Nowak MA. Repeated games and direct reciprocity under active linking. J Theor Biol. 2008;250:723–731. doi: 10.1016/j.jtbi.2007.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Segbroeck SV, Santos FC, Lenaerts T, Pacheco JM. Reacting differently to adverse ties promotes cooperation in social networks. Phy Rev Lett. 2009;102:058105. doi: 10.1103/PhysRevLett.102.058105. [DOI] [PubMed] [Google Scholar]
- 43.Segbroeck SV, Santos FC, Nowé A, Pacheco JM, Lenaerts T. The evolution of prompt reaction to adverse ties. BMC Evolutionary Biology. 2008;8:287. doi: 10.1186/1471-2148-8-287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zschaler G, Traulsen A, Gross T. A homoclinic route to full cooperation on adaptive social networks. 2009;arXiv:09100940. [Google Scholar]
- 45.Do AL, Rudolf L, Gross T. Patterns of cooperation: fairness and coordination in self-organized networks of interacting agents. New Journal of Physics. 2009 (in press) [Google Scholar]
- 46.Gross T, Blasius B. Adaptive coevolutionary networks - a review. J R Soc Interface. 2008;5:259–271. doi: 10.1098/rsif.2007.1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Perc M, Szolnoki A. Coevolutionary games - a mini review. Biosystems. 2010;99:109–125. doi: 10.1016/j.biosystems.2009.10.003. [DOI] [PubMed] [Google Scholar]
- 48.Szabó G, Töke C. Evolutionary Prisoner's Dilemma game on a square lattice. Phys Rev E. 1998;58:69. [Google Scholar]
- 49.Karlin S, Taylor HMA. A First Course in Stochastic Processes. London: Academic, 2nd edition edition; 1975. [Google Scholar]
- 50.Blume LE. The statistical mechanics of strategic interaction. Games and Economic Behavior. 1993;5:387–424. [Google Scholar]
- 51.Traulsen A, Nowak MA, Pacheco JM. Stochastic dynamics of invasion and fixation. Phys Rev E. 2006;74:011909. doi: 10.1103/PhysRevE.74.011909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Helbing D, Yu W. The outbreak of cooperation among success-driven individuals under noisy conditions. Proc Natl Acad Sci USA. 2009;106:3680–3685. doi: 10.1073/pnas.0811503106. [DOI] [PMC free article] [PubMed] [Google Scholar]