Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2010 Feb 17;7(49):1219–1227. doi: 10.1098/rsif.2009.0514

Stochasticity in staged models of epidemics: quantifying the dynamics of whooping cough

Andrew J Black 1, Alan J McKane 1,*
PMCID: PMC2894870  PMID: 20164086

Abstract

Although many stochastic models can accurately capture the qualitative epidemic patterns of many childhood diseases, there is still considerable discussion concerning the basic mechanisms generating these patterns; much of this stems from the use of deterministic models to try to understand stochastic simulations. We argue that a systematic method of analysing models of the spread of childhood diseases is required in order to consistently separate out the effects of demographic stochasticity, external forcing and modelling choices. Such a technique is provided by formulating the models as master equations and using the van Kampen system-size expansion to provide analytical expressions for quantities of interest. We apply this method to the susceptible–exposed–infected–recovered (SEIR) model with distributed exposed and infectious periods and calculate the form that stochastic oscillations take on in terms of the model parameters. With the use of a suitable approximation, we apply the formalism to analyse a model of whooping cough which includes seasonal forcing. This allows us to more accurately interpret the results of simulations and to make a more quantitative assessment of the predictions of the model. We show that the observed dynamics are a result of a macroscopic limit cycle induced by the external forcing and resonant stochastic oscillations about this cycle.

Keywords: epidemics, stochastic modelling, whooping cough

1. Introduction

Traditionally deterministic models have formed the bedrock of mathematical epidemiology. The standard approaches such as the susceptible–infected–recovered (SIR) and the susceptible–exposed–infected–recovered (SEIR) models (Anderson & May 1991; Keeling & Rohani 2007) have shaped much of our present day understanding of recurrent epidemics. Stochasticity has long been recognized as an important factor within epidemic modelling, but there is still much debate as to its precise dynamical role and how it can be understood from a theoretical point of view (Bjornstad & Grenfell 2001; Coulson et al. 2004).

The first stochastic simulations of an epidemiological system were carried out by Bartlett (1957) on the then new Manchester electronic computer. He was primarily interested in extinction dynamics (Nasell 1999), but also recognized that the simple deterministic models of Hamer (1906) and Soper (1929) would give recurrent dynamics with the addition of stochasticity; in other words, that noise could maintain oscillations by constantly perturbing the system away from its steady state (Aparicio & Solari 2001). The recognition that external forcing is also important to the dynamics of many diseases adds an extra complication (London & York 1973; Bjornstad et al. 2002; Altizer et al. 2006); trying to understand how this interacts with stochastic effects and thus shapes the dynamics of recurrent epidemics is a challenging problem.

In larger populations, noise has tended to be regarded as a small perturbation to the underlying deterministic dynamics, or as something which can cause switching between different deterministic states (Schwartz 1985; Earn et al. 2000). However, the idea that stochasticity plays a more critical role in large populations has been growing over the past few years (Higgins et al. 1997; Rohani et al. 1999; Alonso et al. 2007). For instance, the noise due to demographic stochasticity (noise at the individual level owing to chance events; Nisbet & Gurney 1982) can excite the system's natural frequency, creating a resonance and giving rise to large structured oscillations, even in large populations. The signature of this effect has been detected in real time series data (Bauch & Earn 2003a; Grassly et al. 2005).

1.1. Models

The challenge in epidemic modelling is to form a model which captures the observed dynamics but also elucidates the mechanisms behind them. The most popular approach tends to have two steps: first to create a suitable population-level model (PLM), usually in terms of ordinary differential equations which are deterministic. Next, the corresponding individual-based model (IBM) is formed, and then simulated, to investigate any stochastic properties. Logically, the procedure should be reversed: real populations are finite and the PLM is always an approximation to the underlying IBM. Usually, it is assumed that the PLM will be accurate in the limit of large populations, but what is meant by large must first be defined (Nasell 2002).

Clearly, the IBM, rather than the PLM, should be adopted as the starting point of an investigation. Once an IBM has been defined, it is usually studied using computer simulations. However, simulations are still inferior in at least one respect to the analysis that can be carried out on PLMs: general results valid over a wide range of models and parameters cannot in general be established. In addition, many insights and a deeper understanding can frequently be more readily obtained from analytical studies than from computer simulations. Knowledge of the mathematics required to analyse stochastic models has lagged behind that used to study nonlinear differential equations. Recently, more effort has been put into this area (Nasell 2002; Alonso et al. 2007; Kuske et al. 2007; Keeling & Ross 2008; Ross et al. 2009), although the lack of analytical studies of IBMs has held back the study of stochastic and other effects in models of epidemics.

The modelling of whooping cough provides a good illustration of these points. Whooping cough is a childhood disease (Cherry 2005; Crowcroft & Pebody 2006), which can be described by the SEIR formalism (Hethcote 1997). In England and Wales, before mass vaccination, the time series of case reports shows dynamics which are strongly multiennial, but after vaccination in the 1950s quite regular 3.5–4 year epidemic cycles occur (Fine & Clarkson 1986; Rohani et al. 1999). All suitably parametrized deterministic PLMs fail to capture the correct dynamics, but IBMs produce qualitatively correct patterns (Hethcote 1998; Rohani et al. 1999). Stochasticity is therefore important, but its precise role has been hard to quantify (Coulson et al. 2004). The work which has been carried out has been an amalgam of analytical work on the PLM and simulations of the IBM (Keeling et al. 2001; Rohani et al. 2002). While this has yielded valuable insights, fundamentally one is left with the problem of interpreting stochastic simulations in terms of deterministic results. More recently, Nguyen & Rohani (2008) have proposed that an SEIR model, with realistically distributed exposed and infectious periods, can capture the qualitative dynamics of whooping cough. The mechanism behind the dynamics is multiple coexisting attractors (Earn et al. 2000); noise plays a secondary role of switching the system between these different deterministic states.

1.2. Methodology

A method which begins from a mathematical formulation of the IBM, and, through a simple and straightforward procedure, gives analytical results would be a valuable tool in the investigation of the SIR, SEIR and related models. Such a method exists, and was developed by van Kampen (1992) in statistical physics nearly 50 years ago. It has been applied to understand stochastic amplification and other effects in ecological models (Alonso & McKane 2002; McKane & Newman 2005), while other authors have used similar methods in a more mathematically rigorous context to investigate population dynamics (Pollett 1990; Ross 2006). Within epidemiology, it has only been used for investigating relatively simple models (Nasell 1999; Alonso et al. 2007; Black et al. 2009; Dangerfield et al. 2009).

In this paper, we apply the van Kampen method to the SEIR model with distributed exposed and infectious periods (Lloyd 2001; Keeling & Grenfell 2002; Wearing et al. 2005), which has recently been employed as a more realistic model of epidemics (Conlan & Grenfell 2007; Ferrari et al. 2008; Nguyen & Rohani 2008). The essence of van Kampen's method is an expansion in 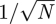Inline graphic, where N is the number of individuals in the population. In the limit where N is very large, stochastic fluctuations become unimportant and the equations describing the model approach the PLM. The method determines these, rather than postulating them phenomenologically, but it also provides a stochastic correction to the equations of the PLM which takes the form of a set of linear stochastic differential equations. It is the analysis of these equations which allows one to accurately interpret the results of simulations and to trace back the effects seen to the mechanisms involved, something which has previously proved difficult to do.

This method is especially powerful when studying the staged SEIR model. By deriving the theoretical power spectrum, we can distinguish the effects of the more realistically distributed periods from the other factors such as immigration and finite size effects. This allows us to give quantitative results for a broad range of parameters very quickly and easily, which would otherwise need large amounts of simulation time to achieve.

The rest of this paper is split into four sections: in §2, we give an overview of the stochastic SEIR model with distributed exposed and infectious periods and our method of analysis. Section 3 details our results and we discuss the impact of the effect of changing the variances of the distributions on the form of the power spectrum. In §4, we use our methods to reinterpret the dynamics of a seasonally forced model of whooping cough studied by Nguyen & Rohani (2008), and we conclude in §5.

2. The staged SEIR model

In the standard SEIR model, each individual within the population belongs to one of four classes: susceptible, exposed (infected but not yet infectious), infectious and recovered (Anderson & May 1991; Keeling & Rohani 2007). The usual assumption is that the exposed and infectious periods are exponentially distributed; thus, the probability of moving from one class to another is independent of the time spent in that class. This is unrealistic and in general the probability of recovery will depend quite strongly on the time since infection (Hope-Simpson 1952; Bailey 1956). This can be remedied by splitting the exposed and infectious classes into a number of subclasses or stages, which are traversed sequentially (Andersson & Britton 2000; Lloyd 2001; Keeling & Grenfell 2002; Nguyen & Rohani 2008). If the number of stages is M and L in the exposed and infectious classes, respectively, with rates Mσ and Lγ between them, then we obtain gamma-distributed periods (Cox & Miller 1965; Anderson & Watson 1980; Wearing et al. 2005).

The gamma distribution is convenient as, with this particular formulation, the mean exposed and infectious periods remain fixed at 1/σ and 1/γ, while the variances can be changed with the parameters M and L. If we set M = L = 1, we regain the exponential distributions of the standard SEIR model. As the number of stages is increased, the gamma distribution becomes more central (smaller variance) and an individual remains on average exposed/infectious for a more constant amount of time. For large values of M or L, the gamma distribution is approximately normal, and the periods approach fixed duration as M, L → ∞ (Grossman 1980).

Birth and death rates are set equal to μ, and these events are linked, so that the total population N remains constant. This allows for the elimination of the variable relating to recovered individuals. Frequently, birth and death processes are assumed to happen at the same rate, but remain as distinct events. This still results in fluctuations in the total population size for finite systems. By linking these events at the stochastic level, the population size remains constant at any system size, so that we can still eliminate the variable relating to recovered individuals. This only has an effect on the dynamics for very small populations.

In the analytical approach, seasonal forcing is not explicitly included (Fine & Clarkson 1982; Aron & Schwartz 1984; Keeling et al. 2001) and β, the contact rate between individuals, is taken as a constant. In §4, we show how a model with forcing can be analysed using a suitable approximation scheme. We also include a small immigration term η, allowing for infectious imports (Hagenaars et al. 2004; Alonso et al. 2007). The formulation we use corresponds to a commuter model, where a susceptible has the possibility of catching the disease while away from the main population, and then returning (Engbert & Drepper 1994). Vaccination is simple to incorporate, as it can be shown in the deterministic version of the model that vaccinating a proportion p of the population at birth scales β by (1 − p), and this remains true for the stochastic version (Earn et al. 2000). The processes which define the stochastic system are given in table 1.

Table 1.

The reactions defining the staged SEIR model, where a = 1, … , L and α = 1, … , M. The full rates and equations are given in the electronic supplementary material.

event transition
infection 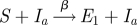Inline graphic
immigration 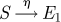Inline graphic
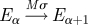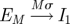incubation Inline graphic
Inline graphic
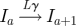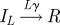recovery Inline graphic
Inline graphic
birth/death 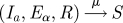Inline graphic
Open in a new tab

The model can now be investigated by two methods: simulation with Gillespie's (1976) algorithm, and analytically by constructing the master equation corresponding to the processes given in table 1 and performing van Kampen's system-size expansion (van Kampen 1992; Black et al. 2009). Both methods allow the power spectrum of the fluctuations of the infective time series to be found. Full technical details of the model and analysis are given in the electronic supplementary material.

3. Results

3.1. The power spectrum

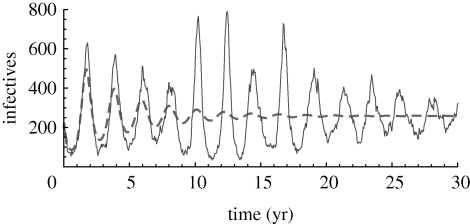
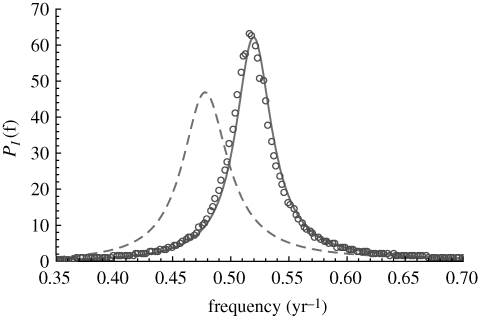
For orientation, we first show in figure 1 a typical simulation of the stochastic model with parameters corresponding to measles as given by Keeling & Grenfell (2002). We see strong stochastic oscillations caused by the amplification of the demographic stochasticity. The theoretical power spectrum for the same parameters is shown in figure 2. The effect of using the more realistic gamma distributions, as compared with the exponentially distributed model, is to shift the peak frequency and increase the amplitude of the spectrum. These effects were first described for the SIR model with realistic recovery profiles by Simoes et al. (2008) and Black et al. (2009).

Figure 1.

Figure 1.

Open in a new tab

A typical stochastic realization of the staged SEIR model. The dashed curve shows the deterministic result; see the electronic supplementary material for these equations. Parameters are β = 3.4 d−1, σ = 1/8 d, M = 8, γ = 1/5 d, L = 5, μ = 5.5 × 10−5 d−1, η = 10−6 d−1 and N = 106.

Figure 2.

Figure 2.

Open in a new tab

Theoretical power spectrum (solid curve) for the staged SEIR model parametrized for measles, with results from simulations (open circles). The dashed curve is the standard SEIR result, assuming exponentially distributed exposed and infectious periods. The shift in period is from 1.9 to 2.1 years. Transient periods are discarded before evaluating the numerical spectrum; parameters are as in figure 1.

The deterministic version of this model (derived in the limit N → ∞) shows weakly damped oscillations tending to a stable fixed point (Hethcote & Tudor 1980; Lloyd 2001; see figure 1). A linear stability analysis yields equations for the eigenvalues which allows for the approximate calculation of the damping time and frequency of these oscillations (Grossman 1980; Lloyd 2001). By contrast, the van Kampen method gives exact analytical expressions (in terms of the frequency, ω) for the power spectrum, allowing precise calculation of the peak frequency and amplification. It is possible to give these expressions explicitly in terms of the original parameters of the model, but they would be so unwieldy when given in this way that they would be of little use. They can be constructed from the information given in the electronic supplementary material, but we prefer to represent them graphically where the nature of the oscillations is clearer to see.

Although the eigenvalues of the deterministic system, to a large extent, determine the form (peak frequency and amplitude) of the power spectrum of the fluctuations (see the electronic supplementary material), this is not exact, as the demographic stochasticity can shift the peak frequency away from that predicted from the deterministic equations (Alonso et al. 2007; Keeling & Ross 2008). It does, however, form a good approximation for epidemic models of this kind.

The spectrum is normalized so that square root of the amplitude is equal to the root mean square of the fluctuations. Essentially, the spectrum is seen to be very similar to that of the SIR model; the parameter range for which large peaks in the power spectrum occur is also where the deterministic model shows large transients (Alonso et al. 2007).

3.2. Effect of the variance of the distributions on the power spectrum

In this section, we examine the effect of the parameters M and L on the form of the power spectrum, which control the variances of the gamma distributions. The behaviour is obviously parameter dependent, but, if we hold the intrinsic parameters {β, σ, γ, δ, η} fixed, then we can make a number of observations.

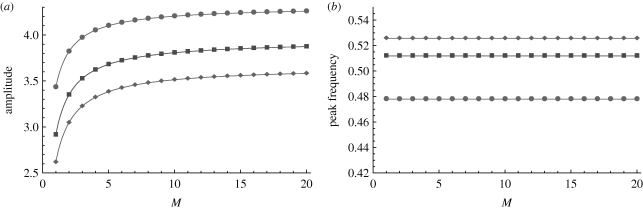
Independent of the other parameters, changing M has a simple effect on the power spectrum. Increasing M (decreasing the variance of the exposed period distribution) increases the amplitude of the spectrum with a negligible change to its frequency. This is illustrated in figure 3. The longer the exposed period, as compared with the infectious period, and the larger L, the larger the increase in amplitude. The largest changes happen for the smaller values of M, typically less than 10, where the exposed period distribution changes the most.

Figure 3.

Figure 3.

Open in a new tab

The (a) amplitude and (b) peak frequency of the analytical power spectrum as a function of M, the exposed period variance parameter. Increasing M (decreasing the variance of the exposed period distribution) increases the amplitude of the spectrum, while having negligible effect on the peak frequency. The intrinsic parameters are typical of measles as given in figure 1. In this example, the exposed period is longer than the infectious period so the spectra with larger L have smaller amplitudes. Filled diamond, L = 10; filled square, L = 3; filled circle, L = 1.

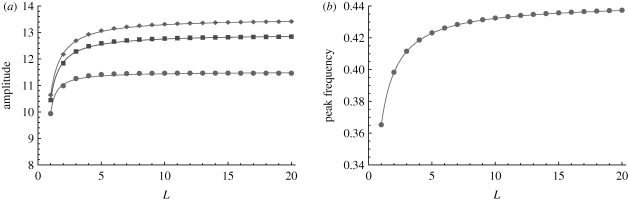
The effect of L on the power spectrum is more complicated and can change both the peak frequency and amplitude. Firstly, independent of M, increasing L shifts the peak frequency of the spectrum to higher values. The effect on the amplitude depends on whether the infectious period is longer than, approximately equal to or shorter than the exposed period. When the infectious period is longer than the exposed period (σ > γ), then the results are similar to that of the SIR model with gamma-distributed infectious periods (Lloyd 2001; Black et al. 2009). Thus, increasing L increases both the amplitude and the peak frequency of the spectrum (figure 4). Again, the largest changes are seen for smaller values of L.

Figure 4.

Figure 4.

Open in a new tab

The (a) amplitude and (b) peak frequency of the analytical power spectrum as a function of L, where the infectious period is longer than the exposed period. Increasing L leads to an increase in the peak frequency and amplitude of the spectrum. The change in frequency is independent of M. Parameters are typical of whooping cough: β = 1.2 d−1, σ = 1/8 d, γ = 1/14 d, μ = 5.5 × 10−5 d−1 and η = 10−6 d−1. Filled diamond, M = 10; filled square, M = 3; filled circle, M = 1.

If the exposed period is longer than the infectious period (γ > σ), as with measles (Anderson & May 1991), then there is still an increase in frequency with increasing L, but a decrease in amplitude (figure 3). When the two average periods are approximately equivalent (γ ≈ σ), the behaviour is not as easy to quantify and the amplitude is not necessarily an increasing function of L (Lloyd 2001); however, any shifts tend to be small.

4. Whooping cough model

In this section, we apply our analysis to the seasonally forced, staged SEIR model, proposed by Nguyen & Rohani (2008) as an explanation for the long-term dynamics of whooping cough before and after mass vaccination. Their model includes seasonal forcing by assuming that the contact rate, β(t), follows a term-time pattern (Schenzle 1985; Keeling et al. 2001),

4. 4.1

where β0 is the baseline contact rate, β1 the magnitude of forcing and term(t) is a periodic function that switches between 1 during school terms and −1 during holidays. We use the England and Wales term dates as set down by Keeling et al. (2001). The problem now explicitly includes time dependence, which is simple to include in simulations with appropriate changes to the Gillespie algorithm (Anderson 2007). It is also possible to include time dependence in the master equation, but this introduces considerable complications in the derivation of the power spectrum, which we will consider in a forthcoming publication. Instead, here we replace β(t) in the master equation with the average effective β, defined as

4. 4.2

where ps is the fraction of the time spent in school, as opposed to on holiday; for the term dates, we use ps = 0.75. As we show later, simulations confirm this is a good approximation.

All other parameters are taken from Nguyen & Rohani (2008). Before vaccination R0 = 17, from which we find 〈β〉 ≈ γR0 = 1.21. After vaccination, p=0.6 so 〈β〉vac ≡(1 − p)〈β〉 = 0.48 (Earn et al. 2000). Assuming β1 = 0.25 and using equation (4.2), we find that β0 = 1.075 pre-vaccination and 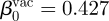Inline graphic. These are lower than 〈β〉 because children spend more time in school when β(t) is higher. The intrinsic parameters, estimated from household incubation data, are 1/σ = 8 days, M = 1, 1/γ = 14 days, L = 4 and μ = 5.5 × 10−5 per day. Note that there is a typographical error in the caption of fig. 6 of Nguyen & Rohani (2008), which should read n = 4, m = 1. These authors assume a small rate of infectious imports of δ = 10 per million per year. We can convert this to our commuter model formulation of immigration by noticing that to a good approximation η ≈ (δ/N)R0 (Keeling & Rohani 2007, p. 210). This gives η = 5 × 10−7 per day.

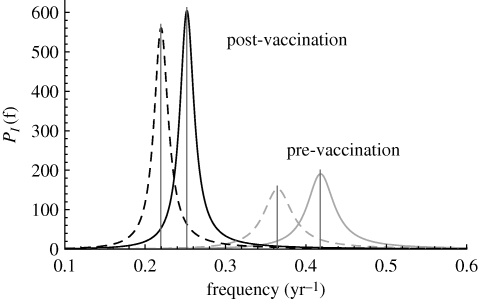
Figure 5 shows the predicted analytical spectra before and after vaccination. The results of using a gamma-distributed infectious period, as compared with a standard exponential, is to shift the peak frequencies, while only slightly increasing the amplitudes of the power spectra. Further increases in L have much smaller effects on the power spectrum (figure 4). Figure 5 also shows the peak frequencies from simply carrying out a deterministic analysis. As can be seen for this choice of parameters, demographic stochasticity causes only very small shifts in frequency away from those predicted by the deterministic theory (Alonso et al. 2007).

Figure 5.

Figure 5.

Open in a new tab

Comparison of the analytical power spectra for whooping cough using the SEIR (dashed curves) and staged SEIR (solid curves) models. Parameters are given in the main text. Using the staged version shifts the peak periods from 2.7 to 2.4 years pre-vaccination and from 4.5 to 4 years post-vaccination. The vertical lines show the peak frequencies from an analysis of just the deterministic model.

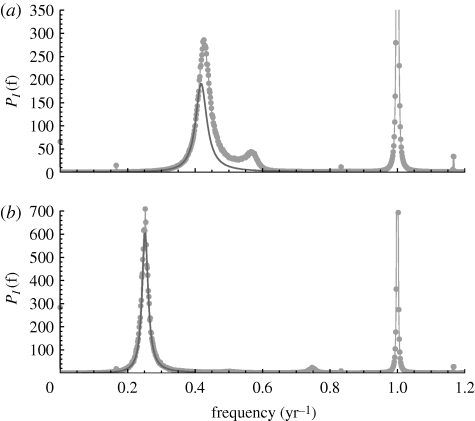
Figure 6 shows power spectra from simulations of the staged SEIR model which include the time-dependent β, along with the analytical predictions. The simulations were initialized near to the fixed point of the unforced system, and transients were allowed to damp down before the data for the power spectra were collected. Other initial conditions were tried, but it was found that the dynamics always settled into the annual attractor. As the transients have essentially the same frequency as the stochastic oscillations, it is important to make sure these have damped down, otherwise the stochastic peak in the power spectrum will appear enhanced. The length of each time series was about 700 years; this is certainly very large, but was chosen to facilitate a good resolution on the power spectrum without aliasing (Priestley 1982). The simulations show an annual peak at 1 year, which comes from the macroscopic limit cycle induced by the external seasonal forcing, and a stochastic peak at lower frequencies. In general, there are more peaks at 1/2, 1/3, etc. years, but for clarity these are not shown.

Figure 6.

Figure 6.

Open in a new tab

Theoretical and numerical power spectra for the whooping cough model: (a) pre-vaccination and (b) post-vaccination. The filled circles are the average of 2000 realizations of the stochastic simulation, including seasonal forcing. The dark curves are the theoretical predictions. The forcing slightly shifts the frequency and amplitude of the stochastic peaks from the analytical prediction, but is otherwise good. The value of N is 5 × 106, with other parameters being given in the main text. The spectra are normalized to N1/2 as we are predominantly interested in the stochastic parts and comparing with analytical calculations. The annual peaks in the numerical spectra are cropped for clarity in the comparison.

Pre-vaccination, the analytical prediction is good at lower frequencies, but there is enhancement, giving a higher amplitude and very slight shift in frequency. This is in contrast to the post-vaccination model where the analytical curve provides a very good fit, but still somewhat enhanced. The amount of power under each peak depends on the population size. The annual macroscopic peak scales with N, while the stochastic part scales with N1/2. In the post-vaccination case, the stochastic peak is larger and the annual peak is smaller by a factor of a third than in the pre-vaccination simulations.

In the time series, the dominant period can appear to change. This is due to the superposition of the macroscopic limit cycle and stochastic fluctuations. The power of the stochastic oscillations is spread out over a range of frequencies. Although there is a dominant frequency, at certain times the stochastic oscillations will be of a much longer/shorter frequency, with a much reduced amplitude. This allows the macroscopic signal to be seen more strongly, thus generating the effect of a changing period.

Simulating the system at smaller population sizes results in small shifts to the peak frequencies (Simoes et al. 2008), but does not alter the qualitative picture. For the whooping cough model, significant shifts occur at N < 106. Taking a smaller forcing magnitude (e.g. β1 = 0.15) results in significantly better agreement with the analytical predictions at lower population sizes.

5. Discussion

We have applied the van Kampen method to the more realistic staged SEIR epidemic model. The ability to derive the exact power spectrum gives considerable insight, especially with regards to the effects of the parameters M and L on the form of the spectrum. Both Lloyd (2001) and Keeling & Grenfell (2002) show that gamma-distributed models are much more sensitive to seasonal forcing, in the sense that the bifurcation to biennial dynamics happens at lower forcing magnitudes, than the basic exponential model. Lloyd (2001) attributes this increased sensitivity to a destabilization of the model, but our analysis goes further to show that a distributed infectious period also tends to increase the natural frequency of the system. We conjecture that it is this effect rather than the decreased stability that makes these models more sensitive to seasonal forcing. This should be easy to test within this framework as, with the appropriate choice of parameters, we can tune the size and frequency of the power spectrum. It should be possible to see whether a model with only a distributed exposed period is more sensitive to forcing, as this would be destabilized but with the same natural frequency.

It should also be feasible to include other heterogeneities such as spatial structure (Hagenaars et al. 2004; Lloyd & Jansen 2004) or age structure (Schenzle 1985; Hethcote 1997), or further complications such as waning immunity (Grenfell & Anderson 1989). The method does start to break down for smaller values of N, where deviations from the predicted spectrum are seen. This is due to the proximity of the fade-out boundary at I = 0. This could be overcome by going to the next order in the expansion, which would give corrections to the spectrum which depend on the population size (van Kampen 1992).

The review article by Coulson et al. (2004) defines two categories for the role of noise: active and passive. These have been characterized as follows (Nguyen & Rohani 2008). Active noise is where ‘stochasticity interacts with the nonlinearity in the deterministic clockwork producing patterns that cannot result from either factor alone’. Passive noise is where ‘stochasticity influences the transition among different deterministic states’. Previous work on whooping cough models formulated with the basic SEIR model (Rohani et al. 1999, 2002; Keeling et al. 2001) concludes that the noise is of the ‘active’ type and plays a major role in the observed dynamics. This is largely due to the failure of the deterministic model to predict anything other than annual dynamics. In contrast, Nguyen & Rohani (2008) conclude that a realistic deterministic staged SEIR model can account for the qualitative patterns, due to the existence of multiple coexisting attractors, which are not present in the basic SEIR model. This explanation reverts to a passive interpretation of noise, which kicks the system between deterministic states. All these models have been shown to be consistent with the observed whooping cough dynamics, but a persuasive explanation for the mechanisms has been lacking.

Our approach, which allows us to be much more quantitative, can encompass both older SEIR results and the newer staged SEIR model of Nguyen & Rohani (2008). For the unforced system, there are strong stochastic oscillations about a macroscopic fixed point. External forcing creates a macroscopic annual limit cycle with stochastic oscillations about it. For the case of whooping cough, the oscillations about the limit cycle are very similar to those of the unforced model and the two components of the power spectrum, the macroscopic (from the limit cycle) and the stochastic, can be viewed as approximately independent of each other. Using the staged SEIR model changes this picture only in that it shifts the frequency of the stochastic oscillations; it does not change the basic nature of the dynamics.

Our results argue against multiple coexisting attractors in the stochastic whooping cough system. Preliminary results show that the bifurcation diagrams of Nguyen & Rohani (2008) are not robust to the inclusion of immigration. Even small amounts as used in the simulations depress the onset of period 3 attractors which only appear at significantly higher magnitudes of forcing. This effect, whereby immigration can destroy longer period attractors, has been reported before (Engbert & Drepper 1994; Ferguson et al. 1996; Alonso et al. 2007). One can speculate that the lack of immigration in the deterministic analysis of Nguyen & Rohani (2008) might explain their findings; alternatively there may be other stable solutions of the deterministic equations, but that the noise is never strong enough to move the system towards them.

Our interpretation, in many ways, echoes the findings of Bauch & Earn (2003b). They find resonant and non-resonant peaks in their power spectra of real time series which correspond to what we term the stochastic and macroscopic peaks. They also show that the natural damping period of the transients near the annual attractor is well approximated by the damping period from the unforced deterministic model (Bauch & Earn 2003a). Our analysis goes further to show that the power spectra are also well approximated by their unforced counterparts.

At the heart of the van Kampen approach is a splitting of the dynamics into two components: a macroscopic part and a stochastic correction to this. In the case of the seasonally forced model, the macroscopic part is a limit cycle and the stochastic corrections are oscillations about this limit cycle. Firstly, we must ask whether the macroscopic part is really a limit cycle, that is, whether the stable solution of the deterministic equations is a limit cycle or whether the multiple attractors, unstable limit cycles, invasion orbits, etc. found or postulated by previous authors have a role or appear in the fully stochastic model. One has to begin from a finite-event-driven model to study these questions, but the problem of disentangling these effects in the time series and power spectra remains. This is where the systematic approach of the system-size expansion is invaluable, because it allows us to separate out the different structures which are seen in the power spectrum. So, for instance, one would expect to see a 3 year peak in the power spectrum if there was a stable 3 year attractor in the model. We also note that the van Kampan expansion frees us from the need to introduce concepts such as invasion orbits (Rand & Wilson 1991; Rohani et al. 2002), which reflect the local geometry around an attractor. Such structure is automatically encoded into the van Kampen expansion and so there is no need to explicitly consider it.

It is surprising that the predictions from the unforced model remain so good in the presence of forcing—there is no a priori reason to expect this to be true. There are some deviations when the forcing is large, but we expect these would be explained by a theoretical treatment in which the time dependence of β(t) given by equation (4.1) was not replaced by the effective value (equation (4.2)). This more complete theory would tell us whether these deviations are from stochastic oscillations about the limit cycle or due to some macroscopic effect such as the presence of an unstable multiennial limit cycle (Boland et al. 2009). The fact that we get such a good fit using approximation (4.2) suggests the former explanation. We do not expect the current approach to provide a good fit to forced measles spectra, as in that case there is almost certainly a more complex macroscopic dynamics, namely a biennial limit cycle, to take into account. A completely systematic approach to stochastic perturbations of forced systems, which is currently being developed, should be able to elucidate these points. However, we believe that the good agreement which we have found in this paper between the simulations of the fully time-dependent model and the van Kampen expansion using the effective contact rate (4.2) shows the essential correctness of our approach. It also clarifies several aspects of the dynamics of epidemic models of the SEIR type.

Acknowledgements

A.B. would like to thank the EPSRC for the award of a postgraduate grant.

References

  1. Alonso D., McKane A. 2002. Extinction dynamics in mainland-island metapopulations: an N-patch stochastic model. Bull. Math. Biol. 64, 913–958. ( 10.1006/bulm.2002.0307) [DOI] [PubMed] [Google Scholar]
  2. Alonso D., McKane A. J., Pascual M. 2007. Stochastic amplification in epidemics. J. R. Soc. Interface 4, 575–582. ( 10.1098/rsif.2006.0192) [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Altizer S., Dobson A., Hosseini P., Hudson P., Pascual M., Rohani P. 2006. Seasonality and the dynamics of infectious diseases. Ecol. Lett. 9, 467–484. ( 10.1111/j.1461-0248.2005.00879.x) [DOI] [PubMed] [Google Scholar]
  4. Anderson D. F. 2007. A modified next reaction method for simulating chemical systems with time dependent propensities and delays. J. Chem. Phys. 127, 214 107 ( 10.1063/1.2799998) [DOI] [PubMed] [Google Scholar]
  5. Anderson D., Watson R. 1980. On the spread of a disease with gamma distributed latent and infectious periods. Biometrika 67, 191–198. ( 10.1093/biomet/67.1.191). [DOI] [Google Scholar]
  6. Anderson R. M., May R. M. 1991. Infectious diseases of humans: dynamics and control. Oxford, UK: Oxford University Press. [Google Scholar]
  7. Andersson H., Britton T. 2000. Stochastic epidemics in dynamic populations: quasi-stationarity and extinction. J. Math. Biol. 41, 559–580. ( 10.1007/s002850000060) [DOI] [PubMed] [Google Scholar]
  8. Aparicio J. P., Solari H. G. 2001. Sustained oscillations in stochastic systems. Math. Biosci. 169, 15–25. ( 10.1016/S0025-5564(00)00050-X) [DOI] [PubMed] [Google Scholar]
  9. Aron J. L., Schwartz I. B. 1984. Seasonality and period-doubling bifurcations in an epidemic model. J. Theor. Biol. 110, 665–679. ( 10.1016/S0022-5193(84)80150-2) [DOI] [PubMed] [Google Scholar]
  10. Bailey N. J. T. 1956. On estimating the latent and infectious periods of measles. I. Families with two susceptibles only. Biometrika 43, 15–22. ( 10.1093/biomet/43.1-2.15) [DOI] [Google Scholar]
  11. Bartlett M. S. 1957. Measles periodicity and community size. J. R. Stat. Soc. Ser. A 120, 48–70. ( 10.2307/2342553) [DOI] [Google Scholar]
  12. Bauch C. T., Earn D. J. D. 2003a Interepidemic intervals in forced and unforced SEIR models. Fields Inst. Commn. 36, 33–44. [Google Scholar]
  13. Bauch C. T., Earn D. J. D. 2003b Transients and attractors in epidemics. Proc. R. Soc. Lond. B 270, 1573–1578. ( 10.1098/rspb.2006.3495) [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Bjornstad O. N., Grenfell B. T. 2001. Noisy clockwork: time series analysis of population fluctuations in animals. Science 293, 638–643. ( 10.1126/science.1062226) [DOI] [PubMed] [Google Scholar]
  15. Bjornstad O. N., Finkenstadt B. F., Grenfell B. T. 2002. Dynamics of measles epidemics: estimating scaling of transmission rates using a time series SIR model. Eco. Monogr. 72, 169–184. [Google Scholar]
  16. Black A. J., McKane A. J., Nunes A., Parisi A. 2009. Stochastic fluctuations in the susceptible–infectious–recovered model with distributed infectious periods. Phys. Rev. E. 80, 021 922 ( 10.1103/PhysRevE.80.021922) [DOI] [PubMed] [Google Scholar]
  17. Boland R. P., Galla T., McKane A. J. 2009. Limit cycles, complex Floquet multipliers and intrinsic noise. Phys. Rev. E 79, 051 131 ( 10.1103/PhysRevE.79.051131) [DOI] [PubMed] [Google Scholar]
  18. Cherry J. D. 2005. The epidemiology of pertussis: a comparison of the epidemiology of the disease pertussis with the epidemiology of bordetella pertussis infection. Pediatrics 115, 1422–1427. ( 10.1542/peds.2004-2648) [DOI] [PubMed] [Google Scholar]
  19. Conlan A. J. K., Grenfell B. T. 2007. Seasonality and the persistence and invasion of measles. Proc. R. Soc. B 274, 1133–1141. ( 10.1098/rspb.2006.0030) [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Coulson T., Rohani P., Pascual M. 2004. Skeletons, noise and population growth: the end of an old debate? Trends Ecol. Evol. 19, 359–364. ( 10.1016/j.tree.2004.05.008) [DOI] [PubMed] [Google Scholar]
  21. Cox D. R., Miller H. D. 1965. The theory of stochastic processes. London, UK: Chapman and Hall. [Google Scholar]
  22. Crowcroft N. S., Pebody R. G. 2006. Recent developments in pertussis. Lancet 367, 1926–1936. ( 10.1016/S0140-6736(06)68848-X) [DOI] [PubMed] [Google Scholar]
  23. Dangerfield C. E., Ross J. V., Keeling M. J. 2009. Integrating stochasticity and network structure into an epidemic model. J. R. Soc. Interface 6, 761–774. ( 10.1098/rsif.2008.0410) [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Earn D., Rohani P., Bolker B., Grenfell B. 2000. A simple model for complex dynamical transitions in epidemics. Science 287, 667–670. ( 10.1126/science.287.5453.667) [DOI] [PubMed] [Google Scholar]
  25. Engbert R., Drepper F. 1994. Chance and chaos in population biology—models of recurrent epidemics and food chain dynamics. Chaos Soliton Fract. 4, 1147–1169. ( 10.1016/0960-0779(94)90028-0) [DOI] [Google Scholar]
  26. Ferguson N. M., Anderson R. M., Garnett G. P. 1996. Mass vaccination to control chickenpox: the influence of zoster. Proc. Natl Acad. Sci. USA 93, 7231–7235. ( 10.1073/pnas.93.14.7231) [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ferrari M. J., Grais R. F., Bharti N., Conlan A. J. K., Bjornstad O. N., Guerin P. J., Djibo A., Grenfell B. T. 2008. The dynamics of measles in sub-Saharan Africa. Nature 451, 679–684. ( 10.1038/nature06509) [DOI] [PubMed] [Google Scholar]
  28. Fine P. E. M., Clarkson J. A. 1982. Measles in England and Wales. I. An analysis of underlying seasonal patterns. Int. J. Epidemiol. 11, 5–14. ( 10.1093/ije/11.1.5) [DOI] [PubMed] [Google Scholar]
  29. Fine P. E. M., Clarkson J. A. 1986. Seasonal influences on pertussis. Int. J. Epidemiol. 15, 237–247. ( 10.1093/ije/15.2.237) [DOI] [PubMed] [Google Scholar]
  30. Gillespie D. 1976. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Compt. Phys. 22, 403–434.( 10.1016/0021-9991(76)90041-3) [DOI] [Google Scholar]
  31. Grassly N., Fraser C., Garnett G. 2005. Host immunity and synchronized epidemics of syphilis across the United States. Nature 433, 417–421. ( 10.1038/nature03072) [DOI] [PubMed] [Google Scholar]
  32. Grenfell B. T., Anderson R. M. 1989. Pertussis in England and Wales: an investigation of transmission dynamics and control by mass vaccination. Proc. R. Soc. Lond. B 236, 213–252. ( 10.1098/rspb.1989.0022) [DOI] [PubMed] [Google Scholar]
  33. Grossman Z. 1980. Oscillatory phenomena in a model of infectious disease. Theor. Pop. Biol. 18, 204–243. ( 10.1016/0040-5809(80)90050-7) [DOI] [PubMed] [Google Scholar]
  34. Hagenaars T., Donnelly C., Ferguson N. 2004. Spatial heterogeneity and the persistence of infectious diseases. J. Theor. Biol. 229, 349–359. ( 10.1016/j.jtbi.2004.04.002) [DOI] [PubMed] [Google Scholar]
  35. Hamer W. H. 1906. Epidemic disease in England—the evidence of variability and of persistency of type. Lancet 1, 733–739. ( 10.1016/S0140-6736(01)80340-8) [DOI] [Google Scholar]
  36. Hethcote H. W. 1997. An age-structured model for pertussis transmission. Math. Biosci. 145, 89–136. ( 10.1016/S0025-5564(97)00014-X) [DOI] [PubMed] [Google Scholar]
  37. Hethcote H. W. 1998. Oscillations in an endemic model for pertussis. Can. Appl. Math. Quart. 6, 61–88. [Google Scholar]
  38. Hethcote H., Tudor D. 1980. Integral equation models for endemic infectious diseases. J. Math. Biol. 9, 37–47. ( 10.1007/BF00276034) [DOI] [PubMed] [Google Scholar]
  39. Higgins K., Hastings A., Sarvela J. N., Botsford L. W. 1997. Stochastic dynamics and deterministic skeletons: population behavior of dungeness crab. Science 276, 1431–1435. ( 10.1126/science.276.5317.1431) [DOI] [Google Scholar]
  40. Hope-Simpson R. E. 1952. Infectiousness of communicable diseases in the household (measles, chickenpox and mumps). Lancet 260, 549–554. ( 10.1016/S0140-6736(52)91357-3) [DOI] [PubMed] [Google Scholar]
  41. Keeling M. J., Grenfell B. T. 2002. Understanding the persistence of measles: reconciling theory, simulation and observation. Proc. R. Soc. Lond. B 269, 335–343. ( 10.1098/rspb.2001.1898) [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Keeling M., Rohani P. 2007. Modelling infectious diseases in humans and animals. Princeton, NJ: Princeton University Press. [Google Scholar]
  43. Keeling M. J., Ross J. V. 2008. On methods for studying stochastic disease dynamics. J. R. Soc. Interface 5, 171–181. ( 10.1098/rsif.2007.1106) [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Keeling M., Rohani P., Grenfell B. 2001. Seasonally forced dynamics explored as switching between attractors. Physica D 148, 317–335. ( 10.1016/S0167-2789(00)00187-1) [DOI] [Google Scholar]
  45. Kuske R., Gordillo L. F., Greenwood P. 2007. Sustained oscillations via coherence resonance in SIR. J. Theor. Biol. 245, 459–469. ( 10.1016/j.jtbi.2006.10.029) [DOI] [PubMed] [Google Scholar]
  46. Lloyd A. L. 2001. Destabilization of epidemic models with the inclusion of realistic distributions of infectious periods. Proc. R. Soc. Lond. B 268, 985–993. ( 10.1098/rspb.2001.1599) [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Lloyd A. L., Jansen V. A. A. 2004. Spatiotemporal dynamics of epidemics: synchrony in metapopulation models. Math. Biosci. 188, 1–16. ( 10.1016/j.mbs.2003.09.003) [DOI] [PubMed] [Google Scholar]
  48. London W. P., York J. A. 1973. Recurrent outbreaks of measles, chickenpox and mumps. I. Seasonal variation in contact rates. Am. J. Epidemiol. 98, 453–468. [DOI] [PubMed] [Google Scholar]
  49. McKane A. J., Newman T. J. 2005. Predator–prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 94, 218 102 ( 10.1103/PhysRevLett.94.218102) [DOI] [PubMed] [Google Scholar]
  50. Nasell I. 1999. On the time to extinction in recurrent epidemics. J. R. Stat. Soc. B 61, 309–330. ( 10.1111/1467-9868.00178) [DOI] [Google Scholar]
  51. Nasell I. 2002. Stochastic models of some endemic infections. Math. Biosci. 179, 1–19. ( 10.1016/S0025-5564(02)00098-6) [DOI] [PubMed] [Google Scholar]
  52. Nguyen H. T. H., Rohani P. 2008. Noise, nonlinearity and seasonality: the epidemics of whooping cough revisited. J. R. Soc. Interface 5, 403–413. ( 10.1098/rsif.2007.1168) [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Nisbet R., Gurney W. 1982. Modelling fluctuating populations. New York, NY: Wiley. [Google Scholar]
  54. Pollett P. K. 1990. On a model for interference between searching insect parasites. J. Austral. Math. Soc. Ser. B 32, 133–150. ( 10.1017/s0334270000008390) [DOI] [Google Scholar]
  55. Priestley M. B. 1982. Spectral analysis and time series. London, UK: Academic Press. [Google Scholar]
  56. Rand D. A., Wilson H. B. 1991. Chaotic stochasticity—a ubiquitous source of unpredictability in epidemics. Proc. R. Soc. Lond. B 246, 179–184. ( 10.1098/rspb.1991.0142) [DOI] [PubMed] [Google Scholar]
  57. Rohani P., Earn D. J. D., Grenfell B. T. 1999. Opposite patterns of synchrony in sympatric disease metapopulations. Science 286, 968–971. ( 10.1126/science.286.5441.968) [DOI] [PubMed] [Google Scholar]
  58. Rohani P., Keeling M. J., Grenfell B. T. 2002. The interplay between determinism and stochasticity in childhood diseases. Am. Nat. 159, 469–481. ( 10.1086/339467) [DOI] [PubMed] [Google Scholar]
  59. Ross J. V. 2006. Stochastic models for mainland–island metapopulations in static and dynamic landscapes. Bull. Math. Biol. 68, 417–449. ( 10.1007/s11538-005-9043-y) [DOI] [PubMed] [Google Scholar]
  60. Ross J. V., Pagendam P. E., Pollett P. K. 2009. On parameter estimation in population models. II. Multi-dimensional processes and transient dynamics. Theor. Popul. Biol. 75, 123–132. ( 10.1016/j.tpb.2008.12.002) [DOI] [PubMed] [Google Scholar]
  61. Schenzle D. 1985. An age-structured model of pre- and post-vaccination measles transmission. J. Math. Appl. Med. Biol. 21, 347–361. ( 10.1093/imammb/1.2.169) [DOI] [PubMed] [Google Scholar]
  62. Schwartz I. B. 1985. Multiple stable recurrent outbreaks and predictability in seasonally forced nonlinear epidemic models. J. Math. Biol. 21, 347–361. ( 10.1007/BF00276232) [DOI] [PubMed] [Google Scholar]
  63. Simoes M., Telo da Gama M. M., Nunes A. 2008. Stochastic fluctuations in epidemics on networks. J. R. Soc. Interface 5, 555–566. ( 10.1098/rsif.2007.1206) [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Soper H. 1929. The interpretation of periodicity in disease prevalence. J. R. Stat. Soc. 92, 34–73. ( 10.2307/2341437) [DOI] [Google Scholar]
  65. van Kampen N. 1992. Stochastic processes in physics and chemistry. Amsterdam, The Netherlands: Elsevier. [Google Scholar]
  66. Wearing H., Rohani P., Keeling M. 2005. Appropriate models for the management of infectious diseases. PLoS Med. 2, 621–627. ( 10.1371/journal.pmed.0020174) [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES