Scaling and mechanics of carnivoran footpads reveal the principles of footpad design

Abstract

In most mammals, footpads are what first strike ground with each stride. Their mechanical properties therefore inevitably affect functioning of the legs; yet interspecific studies of the scaling of locomotor mechanics have all but neglected the feet and their soft tissues. Here we determine how contact area and stiffness of footpads in digitigrade carnivorans scale with body mass in order to show how footpads’ mechanical properties and size covary to maintain their functional integrity. As body mass increases across several orders of magnitude, we find the following: (i) foot contact area does not keep pace with increasing body mass; therefore pressure increases, placing footpad tissue of larger animals potentially at greater risk of damage; (ii) but stiffness of the pads also increases, so the tissues of larger animals must experience less strain; and (iii) total energy stored in hindpads increases slightly more than that in the forepads, allowing additional elastic energy to be returned for greater propulsive efficiency. Moreover, pad stiffness appears to be tuned across the size range to maintain loading regimes in the limbs that are favourable for long-bone remodelling. Thus, the structural properties of footpads, unlike other biological support-structures, scale interspecifically through changes in both geometry and material properties, rather than geometric proportions alone, and do so with consequences for both maintenance and operation of other components of the locomotor system.

1. Introduction

The structural properties of an object are a product of its size, geometry and material composition (table 1); however, for the structures most often examined in biomechanical studies of scaling, the effects of geometry predominate (Schmidt-Nielsen 1984; Currey 2002; Biewener 2005). In these structures, mechanical properties typically vary with size as a result of changes in the shapes (Ker et al. 1988), proportions (Alexander et al. 1979) or arrangement (Biewener 1989) of elements, while material composition varies little, if at all, and that variation appears uncorrelated with size. For example, for the bony elements of skeletal support systems of terrestrial mammals and birds, interspecific scaling differs only slightly from geometric similarity (Alexander et al. 1979) so stress should increase with increasing body size. However, the more erect limb bone posture of larger mammals increases muscle mechanical advantage and thus ensures that peak bone and muscle stress remain fairly uniform across a broad size range (Biewener 1989, 2000, 2005).

Table 1.

Definitions of variables and terms.

symbol	definition	units	relation to other variables
M	body mass	kg
F	compressive load on footpad	N
A	ground contact area of a footpad	mm2
P	foot pressure	N m−2 or Pa	F/A
y	thickness of footpad	mm
Δy	compressive deformation of footpad	mm
σy	compressive stress on the footpad tissue: load on the pad standardized by contact area	N m−2 or Pa	F/A
εy	compressive strain in the footpad tissue: deformation of the pad standardized to its original thickness	(dimensionless)	Δy/y
Ey	compressive modulus of footpad tissue (a material property)	N m−2 or Pa	σy/εy
ky	compressive stiffness of the whole pad (a structural property)	N m−1	F/Δy
U	strain energy storage, the area under load–deformation curvea	J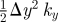
u	strain energy density, i.e. strain energy stored per unit volume, which can be calculated as the area under stress–strain curvea	J m−3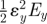
bY	regression coefficient (or ‘scaling factor’) for the log-transformed value of a given variable, log Y, on log M (see equation (2.3))	(dimensionless)
scaling	of a variable, the pattern or manner of change that is associated with changes or differences in size. (Here, animal body size is measured as body mass, M.)
geometry	shape: the spatial arrangement of components. (Distinct from both size and material.)
material	of or relating to the substance of which an object or component is composed.
structural	of or relating to an entire object. (Structural properties of an object are a consequence of its size, geometry and material.)

^aIf allowance is made for curvature in the load–deformation (or stress–strain) curve the maximum total energy storage will be (slightly) lower than the quantity shown here, which assumes linearly elastic material.

Despite their key role in transmitting locomotory forces during foot–ground contact and the attention human heel pads have received in previous studies (Sokolov 1982; Alexander et al. 1986; Aerts et al. 1995; Ker 1996, 1999), feet and footpads have been all but neglected in interspecific studies of the scaling of locomotor mechanics. (The few exceptions include Chi & Roth 2004; Chi 2005; Michilsens et al. 2009; for an example of intraspecific ontogenetic scaling see Miller et al. 2008.) If in the footpads, as in the skeleton, geometric similarity applies, and if the material properties of the fibrous adipose composing the pads are constant, plantar pressure should increase with increasing size. Thus stress (and strain) should be greater within the pad tissue of large animals, putting plantar tissues at greater risk of failure. How, then, can footpads maintain structural integrity and function effectively across a broad range of body sizes? Do they achieve this by a change in geometry or material?

The mechanical variables of particular concern are (i) the loading situation of the material—i.e. stress (from plantar pressure) and strain, and (ii) the resistance to deformation—i.e. compressive modulus of the material and the stiffness of the structure (table 1). Both for dimensional reasons and to maintain the footpads’ functional integrity if safety factors are insufficiently high, some of these variables must change with changing body size (see table 2). Given that the mechanical behaviour of a footpad as a structure under load is determined both by the pad's physical dimensions and by the material of which it is made, what features do footpads appear to maintain across the range of body masses? In other words, what are the principles of footpads’ mechanical design?

Table 2.

Predictions for various scaling factors (b) for fore- and hindpads according to different hypotheses. Derivations of these values, keyed to superscripts used here, are summarized in footnotes below or in the electronic supplementary material, §1. All variables (except y) are calculated under the load to which the pad is subjected when the animal is standing.

hypotheses	area (bA)	thickness (by)	stiffnessa (bky)	foot pressureb (bP)	Young's modulusb (bEy)	strainb (bεy)	deformationb (bΔy)	strain energy densityb (bu)	strain energy storageb (bU)
H1	1c			0d
H2	0.67e	0.33e	0.33f	0.33	0d	0.33	0.67	0.67	1.67
fore	0.65g	0.40h	0.25f	0.35	0d	0.35	0.75	0.70	1.75
	0.89i	0.40h	0.49f	0.11	0d	0.11	0.51	0.22	1.51
hind	0.58g	0.40h	0.18f	0.42	0d	0.42	0.82	0.84	1.82
	0.89i	0.40h	0.49f	0.11	0d	0.11	0.51	0.22	1.51
H3	0.67e	0.33e	0.67j	0.33	0.33	0d	0.33	0.33	1.33
fore	0.65g	0.40h	0.60j	0.35	0.35	0d	0.40	0.35	1.40
	0.89i	0.40h	0.60j	0.11	0.11	0d	0.40	0.11	1.40
hind	0.58g	0.40h	0.60j	0.42	0.42	0d	0.40	0.42	1.40
	0.89i	0.40h	0.60j	0.11	0.11	0d	0.40	0.11	1.40
H4	0.67e	0.33e	1d	0.33	0.67	−0.33	0	0	1.0
fore	0.65g	0.40h	1d	0.35	0.75	−0.40	0	−0.05	1.0
	0.89i	0.40h	1d	0.11	0.51	−0.40	0	−0.29	1.0
hind	0.58g	0.40h	1d	0.42	0.82	−0.40	0	0.02	1.0
	0.89i	0.40h	1d	0.11	0.51	−0.40	0	−0.29	1.0

^aValues of the scaling factor shown here are based upon the specific hypothesis and the scaling relationship (either isometry (see footnote e) or derived from empirical data (footnotes g–i)) assumed for areas and thicknesses. The values predicted for scaling factors are calculated by expressing each variable in terms of M (raised to the appropriate exponent) within the formulae indicated in footnote f or j, and then combining terms, as explained in the text.

^bFor derivation of predictions for other parameters see the electronic supplementary material, §1.

^cIf H1 is true, prediction can be made only for area (according to definition of P in table 1 and equation (2.4)).

^dValues shown in bold indicate the scaling factor that each hypothesis implies for the log-transformed values of, respectively, foot pressure (H1: constant pressure), Young's modulus (H2: constant material), strain (H3: constant strain) or stiffness (H4: scaled stiffness) with log(body mass).

^eValue of scaling factor assuming area and thickness scale isometrically with mass.

^fFrom equation (2.5).

^gLower bound for scaling factor of A versus M, with data from broad taxonomic sample (all available data for A: n = 47). The interval between lower and upper bound includes the 95% CIs for least squares (LS) and reduced major axis (RMA) slopes of log A versus log M, as well as the minimum and maximum values of the scaling factor obtained from RMA of their phylogenetically independent contrasts (see the electronic supplementary material, table S1.1 and §4).

^hScaling factor obtained from RMA slope of log y versus log M with data from specimens (all available data for y: n = 14). See the electronic supplementary material, table S1.2; taxa are indicated in figure S4.2. Because b_y for forepad and hindpad did not differ significantly for individuals for which both the fore- and the hindpads were available (n = 12, p > 0.05, 2-tailed test), data for fore- and hindpads were pooled and the average y was used. To extend the size range of the specimens to estimate b_y, we included two other individuals with only forepads available. For all specimens available (n = 14 individuals), RMA b_y = 0.40.

ⁱUpper bound for scaling factor of A versus M, with data from broad taxonomic sample (n = 47; see footnote g).

^jFrom equation (2.6).

2. Hypotheses and predictions

2.1. Hypotheses proposed

In order to discern the most general principles of footpad construction as it relates to compressive loading, we considered four hypotheses. Two (H₁, H₂) entail variation in the size or geometry but not the material properties of the pads, whereas two others (H₃, H₄) involve changes in the material that produce specific patterns of scaling in structural properties (for definitions see table 1). Here we do not aim to approximate any specific type of locomotion; instead, we focus on footpad mechanics under dynamically similar locomotion, in which peak vertical ground reaction force relative to body weight is independent of animal size (Alexander & Jayes 1983; Farley et al. 1993). Therefore, the only forces exerted on the footpads that we consider in this study are vertical (i.e. compression). In H4, we specifically consider vertical impact forces that occur immediately after foot strike. The hypotheses and their rationales are as follows.

H₁: According to the ‘constant pressure hypothesis’, plantar pressure (P) remains constant across a wide range of body sizes. The rationale for this prediction is that structural integrity of the footpads can more readily be maintained if pressure is constant despite the larger loads imposed by animals of larger mass.

If, on the contrary, pressure does rise with body size, safety factors of the footpads must decline with body size when the following hypothesis holds true.

H₂: The ‘hypothesis of constant material properties’ posits that the pads' compressive modulus (E_y) remains unchanged, irrespective of body mass.

Otherwise, footpads may accommodate the rising pressure with differences in the material of which they are composed. Material properties can change in various ways that help preserve the structural integrity of the pad. Through H₃ and H₄ we considered two possibilities.

H₃: With the ‘constant strain hypothesis’, the properties of footpad tissue vary in such a way that strain (ε_y) within the footpad tissue when loaded in proportion to the animal's mass remains constant with change in body size. This hypothesis is consistent with scaling patterns observed for bones and other load-bearing biological structures (McMahon 1973; Ker et al. 1988; Biewener 1989, 2000, 2005; Currey 2002).

H1–H3 were proposed within the same conceptual framework as most limb-scaling studies, that is, to suggest that the footpad functions in a way similar to the rest of the limb in structural support. However, we also propose that footpads, as the interface during foot–ground contact, can contribute importantly to the functioning of the foot. It is well accepted that the ratio between effective foot mass and the structural property of pad stiffness determines the loading frequency during foot–ground impact (Alexander et al. 1986; Whittle 1999; Chi 2005; Chi & Schmitt 2005). Because the observed frequency of this impact (Alexander & Vernon 1975; Bryant et al. 1987; Chi & Schmitt 2005) is similar to the loading frequency viewed as optimal for bone formation in various animals of different body sizes (Rubin et al. 1990; Turner 1998; Fritton et al. 2000), it has been proposed that foot–ground impact during normal activities is a crucial mechanical stimulus for bone remodelling (Chang et al. 2001; Currey 2002). One mechanism through which similar impact loading regimes could be maintained at different body sizes is for footpad stiffness to scale in direct proportion to effective foot mass.

To date, there are no empirically obtained data on effective foot mass except in humans (e.g. Chi & Schmitt 2005); however, Chi & Schmitt (2005) suggested that limb postures prior to foot–ground contact would determine this mass. It has been reported that during dynamically similar locomotion, limb postures at footfall remain similar among digitigrade carnivorans of different sizes (Day & Jayne 2007); we could therefore expect a similar portion of the leg (i.e. ‘effective foot mass’) to contribute to the initial impact in a given type of locomotion. If among digitigrade carnivorans of different sizes the leg mass maintains a similar relationship to body mass (Grand 1977), we could also expect a similarity between effective foot mass and body mass.

For these reasons, we considered another hypothesis.

H₄: With the ‘scaled stiffness hypothesis’, tissue properties vary instead in such a way that compressive stiffness of the footpad as a whole (k_y) scales in proportion to effective foot mass and body mass.

If safety factors for footpads are sufficiently high, we would not expect their material properties to vary systematically with body mass (H2). But if, on the contrary, safety factors are not high enough, the mechanical properties of footpads must change with changing body size to maintain the footpads’ functional integrity (H3 or H4).

2.2. Predictions

Consistency with H₁ can be evaluated with data for contact area of the footpads (A) and body mass (M) from animals spanning a broad range of body sizes. H₂, H₃ and H₄ each focus on the scaling of different parameters of footpad mechanics—E_y, ε_y and k_y—which by definition (and with certain simplifying assumptions about similarities in pad shape, homogeneity in the composition of a pad, and uniformity in its loading) are interrelated mathematically (Wainwright et al. 1976; Currey 2002; Vogel 2003):

2.1

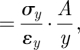2.2

where σ_y is the compressive stress on the footpad when it is loaded, and its value is the same as P. Consistency with H₂, H₃ or H₄ can therefore be assessed empirically by measuring the stiffness (k_y) of entire footpads of known sizes (A and y, where y is pad thickness), solving for the particular variable of interest, and establishing the scaling relationship of that variable with body mass.

Scaling relationships are described using a power function, Y = aM^b, in its log-transformed linear form:

2.3

where Y is the particular variable of interest, M is body mass, and a and b are empirically determined constants, with b being the scaling factor or slope of this relationship and the variable of interest is specified by a subscript. For example, for the special case of isometry in the relationship between mass and area, b_A = 0.67, and between mass and thickness, b_y = 0.33.

Assuming that during dynamically similar locomotion the load (F) is proportional to body mass (M; Alexander & Jayes 1983; Biewener 1989; Farley et al. 1993), and with P defined as F/A, specific predictions for the scaling of area (A, for H1) and stiffness (k_y, for H2, H3, H4) are thus derived in the following way.

H₁ (constant pressure P, or P ∝ M⁰):

2.4

H₂ (constant material property E_y, or E_y ∝ M⁰):

2.5

H₃ (constant strain ε_y, or ε_y ∝ M⁰):

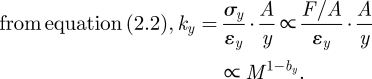2.6

H₄ (scaled stiffness):

2.7

3. Material and methods

We examined the consistency of scaling relationships with each of these hypotheses in the digitigrade carnivorans. The mammalian order Carnivora spans a wide range of sizes, and many of its members exhibit digitigrade foot posture. In digitigrady, the heel is raised off the ground and the metacarpo- (or metatarso-) phalangeal (m-p) joints are the primary joint of flexure in the foot in a standing position (Carrano 1997). The toes that contact the ground each rest upon small digital pads, and the foot itself is supported by a large main (m-p) paw pad located beneath the m-p joints. Of particular value for the current study are findings from kinetic and kinematic analyses (Chi 2005) documenting that during normal locomotion in cats and dogs the m-p pad of each foot is loaded mainly in compression.

Histological studies (Chi 2005) indicate that digitigrade footpads are composed of adipose tissue subdivided into compartments by collagenous membranes; therefore these footpads can be viewed as a hydrostatic support (Ker 1999). The m-p pad is well defined and as reported by Alexander et al. (1986) it can readily be dissected and removed from the foot of a cadaver for mechanical testing. A membrane-like structure found on the dorsal portion of the m-p pad allows the pad to be removed intact without perforation of it (Chi 2005). Within the Carnivora the existence of both plantigrade and digitigrade forms within several lineages also suggests that digitigrady has evolved convergently multiple times (Carrano 1997, 2001; see the electronic supplementary material, figure S4.1). This situation facilitates phylogenetically independent comparison.

To assess whether pressure on the pads changes with body mass (H1) we collected body mass (M), the ground-contact area of the pads (i.e. total foot area, of m-p plus digital pads), and total m-p pad area (alone) from a broad sampling of species representing six families of carnivorans (47 species, 0.27–167 kg). Areas of fore and hind m-p pads were summed rather than treated separately for this broad interspecific sample because the distribution of body mass between fore and hind limbs varies among taxa. Whereas the measurement whose scaling is most relevant to the ‘constant pressure hypothesis’ (H1) is total foot area, measuring total m-p pad area permitted comparison of the broad interspecific sample with mechanically tested specimens (described below). Classification of foot posture as digitigrade followed guidelines by Taylor (1988) and Carrano (1997).

To obtain the area data (A) for pads of each species, we used the image analysis software SigmaScan Pro 4.0 (SPSS, Inc.) to calculate pad areas from digital images of footprints. The images were taken from two major sources: (i) tracks photographed in a zoo (Bronx Zoo, courtesy of Patrick Thomas, PhD) or illustrated in published sources (as noted in the electronic supplementary material, table S2.1) and (ii) images of plantar views of the feet taken directly from live animals (whenever possible) or preserved specimens that were either (a) frozen, (b) fluid or (c) skin preparations (i.e. pelts). Comparison of areas obtained in these ways is discussed in the electronic supplementary material, §2.

To obtain the body mass (M) for each species, we used data from two sources: (i) for known subjects, M was measured directly using a balance or obtained from their caretaker and (ii) for those whose footprint data were obtained from the literature, M was estimated as the mean for an adult female. If mean body mass data of adult females were unavailable from these sources, we consulted Silva & Downing (1995) and Stuart & Stuart (2000). Female body size was chosen to represent the species because in mammals adult males often show great variation in their body size (Cumming & Cumming 2003). For a list of species and sources of data see the electronic supplementary material, table S2.1.

To assess whether mechanical properties of the pads change with body mass (H2, H3, H4), we conducted compressive tests on isolated m-p pads. The more limited sample of tissues that was available for mechanical testing—specimens from 10 adult individuals of five species from three carnivoran families—provided data representative for a broad and densely occupied region of the body mass distribution (figure 1a). For calculating relationships between footpad strain (ε_y) or deformation (Δy) and body mass, the scaling of footpad thickness (y) was assessed from measurements obtained for eight species from 14 individual animals, including the 10 that were available for mechanical tests (see the electronic supplmentary material, table S1.2; the species are noted in figure 1a). The results we illustrate and compare with predictions of the hypotheses here represent the patterns of scaling observed specifically within the set of subjects that were mechanically tested; accordingly, in calculating those results we used the b_y and b_A obtained for those subjects. As an alternative set of assumptions for extrapolating our conclusions to the digitigrade Carnivora more generally, we also consider (illustrated in the electronic supplementary material and briefly discussed) the results that would obtain using b_y and b_A from the largest samples of individuals available.

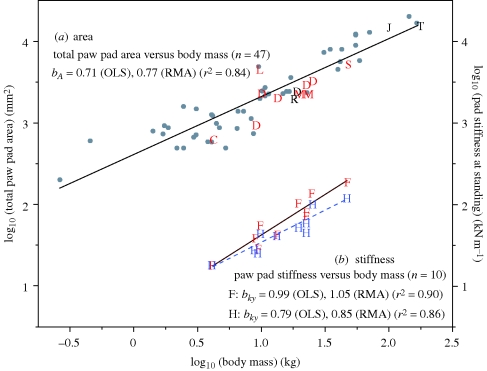
Figure 1.

Scaling of total m-p (paw) pad area and stiffness with body mass. (a) Across the range of body size in digitigrade carnivorans, m-p pad area increases more slowly than body mass (slope less than 1; OLS, ordinary least squares; RMA, reduced major axis). Although scaling of total foot area is not shown here it shows a very similar pattern, with b = 0.76, CI: 0.70–0.83. Analyses of phylogenetically independent contrasts using a variety of models and assumptions also yielded values for the slope that fell within the CI of the slopes for phylogenetically un-transformed data; see the electronic supplementary material, table S1.1 and §4. These scaling relationships would lead to an increase in tissue stress and strain in large animals if material properties remain unchanged (i.e. according to H2). Superimposed on area data from 47 digitigrade carnivoran species (grey circles) are data for individual specimens that were available for measurements of thickness (n = 14 adults; C: cat; D: dogs (n = 6); J: jaguar; L; clouded leopard; M: maned wolves (n = 2); R: caracal; S: spotted hyena; T: tiger) or for both thickness and mechanical testing (n = 10 adults, in red). For the tiger specimen, only the fore m-p pad was available and total area shown here is the species mean. (b) In fact, however, fore (F) and hind (H) m-p pad stiffnesses scale differently from each other (ANCOVA, p = 0.04), and both have scaling factors greater than those predicted by H2 (figure 3a and table 2). In the forepad, the scaling factor ≈ 1 maintains similar impact loading regimes among animals of all sizes.

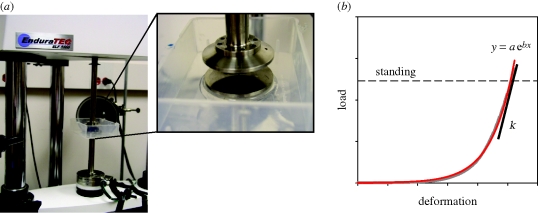
Compressive tests were conducted using a universal mechanical test machine (EnduraTEC ELF3200; figure 2a). The load cell used for this study has a maximal capacity of 250 N at a precision of 0.01 N. The software WinTest (EnduraTEC) was used to control the motion of the test machine and simultaneously record the load and displacement data. Each complete m-p pad, isolated carefully with its skin intact from the fore or hind foot, was placed between two platens. The upper platen contacted the dorsal side of the pad, which originally connected to the foot skeleton and the surrounding skin; while the lower platen contacted the ventral surface of the m-p pad skin. No slip was found between the pad and either platen, which indicated that the specimen was loaded in compression. The original thickness of each pad was measured under a pre-load of 0.01 N. Each specimen was subjected to quasi-static compression (strain rate = 0.01 mm s⁻¹) to a maximal strain of 0.5, except those of the spotted hyena, which were compressed to a strain of 0.25. In order to allow a slope of the force–displacement curve to be calculated for an appropriate load (see below), these strains exceeded the deformation the pad would undergo under approximately the load of a standing animal. The tolerance of the load cell limited testing to animals less than or equal to the size of the hyena. Each specimen was kept moist by spraying Ringer's solution throughout the test.

Figure 2.

Mechanical testing. (a) Equipment setup (in the Guilak Laboratory, Duke University) for compressive tests on the whole m-p pad. (b) Load–deformation plot obtained from one m-p pad. The data (shown in grey) were first curve-fitted as a two-parameter exponential function (red line). The compressive stiffness for the sample was calculated as the derivative of the fitted curve at a load under which the particular pad would be subjected when the animal is standing.

To calculate the compressive stiffness (k_y), force–displacement data were first curve-fitted using SigmaPlot 8.0 (SPSS). A single, two-parameter exponential function (y = a e^bx) was chosen because it provided the best fit for all data (r² > 0.98, p < 0.0001). Because the mechanical behaviour of most biological materials is load-dependent, as indicated by the J-shaped curve (figure 2b), for the purpose of comparison and due to the capacity of our load cell, the loading condition considered in our analyses is the load to which the particular pad would be subjected when the animal is standing. Therefore, k_y was calculated as the derivative of the fitted curve under that specific load (figure 2b).

In this study, we considered dynamically similar locomotion, and assumed (as did Alexander et al. 1986) that in a moving animal the ratio of peak vertical forces on fore and hind feet remains the same as when the animal is stationary. Extrapolating the fitted force–displacement curves from our mechanical tests to the load of trotting (= 4 × supported body weight) considered by Alexander et al. (1986) predicts a change in stiffness equivalent to what they obtained empirically; therefore, the general trends found in our study are applicable to other types of locomotion as long as the animals of various sizes move in a dynamically similar manner. The method for calculating the distribution of load between fore and hind limbs in a stationary animal is described in the electronic supplementary material, §3.

From empirically obtained compressive stiffness k_y, the modulus E_y and strain ε_y at specific loads can be calculated from equations (2.1) and (2.2). In addition, we also considered the footpad properties from the perspective of energy storage: the strain energy storage (U) is the total elastic energy stored in the whole pad and can be calculated as the area under the load–deformation curve, while the strain energy density (u) is the strain energy stored per unit volume of pad and can be calculated as the area under the stress–strain curve (table 1).

Scaling relationships or slopes (b in equation (2.3)) were first calculated as reduced major axis (RMA) regressions of log-transformed A, y or k_y on log M, with 95% CI as described by Rayner (1985). The variables were also examined for phylogenetic patterning (see the electronic supplementary material, §4). Patterning was significant for all variables in the broad interspecific sample and so RMA slopes were also calculated for phylogenetically independent contrasts of log A and log M for several alternative phylogenetic topologies and several branch-length transformations. Phylogenetic patterning was notably absent in the subsample of specimens used in mechanical testing (see the electronic supplementary material, §4) and therefore phylogenetically independent contrasts were not used for data from these specimens.

Two methods were used to obtain CIs for b_ky: calculation (Rayner 1985) and bootstrapping (see the electronic supplementary material, table S1.3). Bootstrap distributions of b_FOREky and b_HINDky were each produced from 1000 replicates of (i) sampling, with replacement, 10 individuals from our mechanically tested specimens and then (ii) calculating the RMA b_ky for each of these samples of 10. Bootstrap CIs were obtained from the range of b_ky, with the 25 largest and smallest b_ky values excluded from the tails of each distribution.

4. Results and interpretation

From the scaling of pad areas in digitigrade carnivorans (figure 1a; see also the electronic supplementary material, table S1.1 and §4), whether raw data or phylogenetically independent contrasts for total foot area or total m-p area are used, we find that b_A < 1, which indicates that H₁, the ‘constant pressure’ hypothesis, is rejected. Neither total foot area nor total m-p pad area keeps pace with increasing body mass, and the 95% CIs of the RMA slopes exclude a value of 1. Rather than remaining constant, foot pressure under static loads evidently rises as body mass is increased. In principle, this conclusion could be tested in vivo (Michilsens et al. 2009) with direct measurements from experiments on this set of species.

Each of the remaining three hypotheses (H₂, H₃, H₄) makes a specific prediction for the scaling of a different variable (E_y, ε_y and k_y, respectively; equations (2.4)–(2.7)), and values of that variable predicted by other hypotheses are derived algebraically. (The predicted values are shown in table 2, and notes and derivations are provided there and in the electronic supplementary material, §1.) For example, whereas the ‘scaled stiffness’ hypothesis, H₄, predicts that b_ky = 1 (represented by a green dot in figure 3a), the predictions for b_ky under H₂ and H₃ are calculated using equations (2.5) and (2.6), respectively, and these equations in turn involve estimates of b_A and b_y.

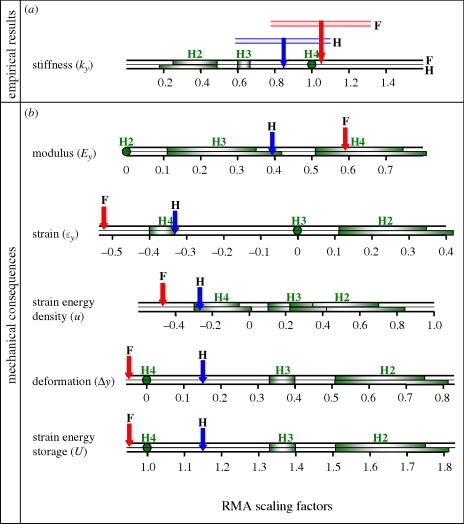
Figure 3.

Hypotheses and results, schematic summary. RMA scaling factors (red or blue arrows; F: forepad; H: hindpad; n = 10 adults) were (a) obtained empirically for m-p pad compressive stiffness (each is shown here with its CI; see the electronic supplementary material, table S1.3), or (b) derived algebraically for the modulus, strain, strain energy density, total deformation and strain energy storage of the pad as indicated in the electronic supplementary material, §1. Calculations were obtained for each pad under the load to which it would be subjected when the animal is standing. Each result is compared to the predicted ranges of values for the proposed hypotheses (green dot or bar; ranges of green bars span values given in table 2, which as noted there were obtained using different regression models and assumptions) for fore (upper bar of each pair) or hind (lower bar) pads. Results (see also table 4) indicate that stiffness of forepads scales directly with body mass (t-test: p ≫ 0.5; H4 accepted), but that of hindpads has a scaling factor between and overlapping predictions made by both H3 and H4.

In generating predictions we used the broadest available samples to estimate b_A and b_y: the value of b_A used for calculating predictions is that obtained for the scaling of m-p pads in the broad interspecific sample (n = 47); the value used for b_y was obtained for the 14 individuals from which we had specimens (see the electronic supplementary material, tables S1.1 and S1.2). To account for statistical variance in these estimates we represent predictions that depend algebraically upon them as intervals (in green in figure 3; for values see table 2). The upper and lower bounds of each prediction interval encompass all values predicted using b_A assessed from a variety of models for phylogenetically independent contrasts, as well as the 95% confidence limits of both RMA and least-squares slopes for the original data. (For these values see the electronic supplementary material, table S1.1.) Whereas the value we used for b_y was b_y = 0.40, which we obtained from our measured specimens, the case of isometry (b_y = 0.33, b_A = 0.67) was also considered (table 2; for values of b_y see the electronic supplementary material, table S1.2). Using the values of b_A, b_y and b_ky, we then made predictions for the scaling factors (b) of other variables (table 2).

To assess whether the mechanically tested sample was representative, we compared patterns of scaling of pad areas and thicknesses in the tested subjects (n = 10, raw data given in table 3) with those found for the broader samples (n = 14 and n = 47 for thicknesses and areas, respectively) and found them to be similar: fore and hind m-p pad thicknesses of the tested subjects did not differ significantly, and the RMA slope for their means was b_y = 0.48 (table 4), which falls within the 95% CIs of the RMA slopes for the larger sample of 14 individuals (0.32 < b_y < 0.48; see the electronic supplementary material, table S1.2). For scaling of total m-p pad areas, the RMA slope for the tested subjects (b_A = 0.94, n = 10; table 4) falls outside the 95% CIs for the 47 species (0.68 < b_A < 0.89; see the electronic supplementary material, table S1.1), but their least-squares estimates are indistinguishable: b_A = 0.71 for both datasets (figure 1a, see the electronic supplementary material, table S1.1).

Table 3.

Data on ten subjects whose m-p pads were available for mechanical testing. Total m-p pad areas are calculated as twice the sum of the areas of fore- and hindpads. Stiffness of each pad specimen is estimated under the load to which the pad is subjected when the animal is standing.

				thickness, y (mm)		stiffness, ky (kN m−1)
mechanically tested specimensa	ID	body mass, M (kg)	total m-p pad area, A (mm2)	fore	hind	fore	hind
Canis familiarisb (domestic dog)	D06	10.0	2412	12.0	9.5	56.2	45.7
	D09	25.0	3419	12.6	12.5	139.8	103.1
	D10	13.6	2145	14.0	13.7	44.3	42.2
	D12	9.1	947	10.6	7.0	39.8	28.8
	D13	22.7	3005	17.0	16.2	76.2	60.5
Chrysocyon brachyurusc (maned wolf)	M26	20.0	2335	10.3	13.8	108.1	54.0
	M40	22.7	2340	13.5	17.8	82.7	46.6
Felis catusb (domestic cat)	C10	4.2	641	6.5	6.5	18.7	18.5
Neofelis nebulosac (clouded leopard)	L01	9.4	4576	9.9	11.6	29.2	25.8
Crocuta crocutad (spotted hyena)	S50	48.0	5326	21.0	n.a.	194.0	122.7

^aSources of cadaveric specimens.

^bDurham Animal Protection Society.

^cUS National Museum of Natural History.

^dSteve Glickman at the University of California, Berkeley.

Table 4.

Results: summary of scaling factors (b) obtained for fore- and hindpads from mechanically tested specimens. A, y and k_y were obtained empirically (n = 10 subjects) and the scaling factors reported here are RMA slopes; values for the rest of the variables are derived in the same way they were for the hypotheses (see table 2 and see the electronic supplementary material, §1). All variables (except A and y) are calculated under the load to which the pad is subjected when the animal is standing.

mechanically tested specimens (n = 10 subjects)		area (bA)a	thickness (by)a	stiffness (bky)	foot pressure (bP)	Young's modulus (bEy)	strain (bεy)	deformation (bΔy)	strain energy density (bu)	strain energy storage (bU)
fore	b (s.e.)			1.05 (0.12)	0.06	0.59	−0.53	−0.05	−0.47	0.95
	95% CI			0.78–1.31e
	r2			0.90
fore and hinda	b (s.e.)	0.94 (0.22)	0.48b (0.06)
	95% CI	0.44–1.44	0.34–0.63
	r2	0.56c; 0.86d	0.87
hind	b (s.e.)			0.85 (0.11)	0.06	0.39	−0.33	0.15	−0.27	1.15
	95% CI			0.59–1.10e
	r2			0.86

^aEstimates of b_ky for fore- and hindpads differ significantly (p = 0.04), but fore- and hindpads do not differ for b_A (p = 0.10; n = 10 subjects) or b_y (p = 0.32; n = 9 subjects because hindpad thickness data for hyena were unavailable). In calculations of b for the other mechanical parameters, total area of m-p pads was used for estimates of b_A, average of fore and hind thicknesses was used for estimates of b_y, and separate estimates of b_ky were used for fore- and hindpads.

^bn = 10 subjects; forepad thickness of hyena was used in place of average of fore + hind in calculating this b_y.

^cIn the sample of n = 10 mechanically tested subjects the correlation of log A with log M is relatively low.

^dThe value of r² for log A and log M rises dramatically if the clouded leopard, which has relatively large feet, is removed, leaving n = 9. By contrast, removal of the clouded leopard changes r² for b_y and b_ky by at most 0.01 (not shown here). For alternative estimates of b_A and its CIs for this sample, see the electronic supplementary material, table S1.1 and figure S1.1.

^eThese RMA CIs were obtained by calculation; for CIs obtained by bootstrap or for phylogenetically independent contrasts see the electronic supplementary material, table S1.3.

We present here as results the values we obtained for scaling of compressive stiffness (b_ky) of fore- (‘F’) and of hindpads (‘H’) of the 10 mechanically tested subjects (raw data given in table 3 and plotted in figure 1b) along with values for b_A, b_y and the other scaling factors derived from them for this same set of subjects (table 4). These results are also presented schematically in figure 3 for comparison with predicted values for different hypotheses (H2, H3, H4).

Figure 3a shows the RMA scaling factors for pad stiffness with their 95% CIs calculated for fore (‘F’ and in red), b_FOREky = 1.05 (CI_p>0.05: 0.78–1.31), and for hind (‘H’ and in blue), b_HINDky = 0.85 (CI_p>0.05: 0.59–1.10) limbs. Conclusions based on these estimates are robust to alternative regression models and assumptions: these RMA-calculated CIs include the least-squares (LS) estimates for b_ky, and are similar both to the LS 95% CIs (but shifted slightly higher) and to the RMA 95% CIs that were obtained by bootstrapping (but shifted slightly lower; see the electronic supplementary material, table S1.3). None of these alternative methods of estimation changes which of the hypotheses the results favour (cf. figure 3a).

We used the b_ky, b_A and b_y obtained directly from the same 10 tested subjects to calculate the scaling factors for the other mechanical variables—modulus, strain, deformation, etc. (see table 4)—on the supposition that patterns of scaling for these individuals are more generally representative of a full sampling of digitigrade carnivorans. Although, as noted above, this appears to have been the case, among the tested specimens the CI for the RMA b_A was extremely wide and the coefficient of determination between log A and log M was relatively low. A major reason for this wide CI is that the pads of one subject, the clouded leopard, are relatively large in area, though this animal's pads are not unusual in thickness or stiffness (tables 3 and 4). There appear to be several values of b_A other than the RMA estimate that also provide a plausible description of the relationship between log A and log M for the tested subjects, and these were also considered (see the electronic supplementary material, figure S1.1).

In the electronic supplementary material, figure S1.2, we illustrate results of an alternative approach: instead of suggesting that the 10 tested subjects were representative in all respects and extrapolating from them to a full sampling of digitigrade carnivorans, we use the largest samples of individuals available—i.e. n = 10 for b_ky, n = 14 for b_y and n = 47 for b_A—for estimating each scaling coefficient used in calculating the scaling factors for the other mechanical variables. Doing this produces a shift in the numerical values obtained for the variables, but these results do not change the conclusions based on them.

Our results and analyses of scaling from mechanical testing show the following.

• — Among our test subjects, the scaling factors for compressive stiffness (b_ky) of fore- and of hindpads are significantly greater than values predicted by H2 (figure 3a)—i.e. structural stiffness of entire footpads scales with body mass in a way that indicates that material properties, specifically, compressive modulus E_y and strain energy density u, are not constant: in both fore- and hindpads b_Ey ≠ 0 and b_u ≠ 0 (figure 3b).

• — Unlike other load-bearing biological structures (which often conform to H3; McMahon 1973; Ker et al. 1988; Biewener 1989, 2000, 2005; Currey 2002) footpads not only change material properties with body size, they also experience reduced strain in larger animals (b_εy < 0; figure 3b).

• — Although further mechanical study and comparison could improve our understanding of the differences in function of fore- and hindpads, some interesting (i) differences and (ii) implications emerge from calculations based on our results.

  1. For each individual, compressive stiffness (k_y) of forepads is equal to or greater than that of hindpads, and across individuals it increases more rapidly for forepads (RMA b_ky = 1.05) than for hindpads (b_ky = 0.85; ANCOVA p = 0.04; figure 1b, see the electronic supplementary material, table S1.3). Fore- and hindpads also differ in that the total strain energy stored in the hindpads (U) increases disproportionately with body mass (i.e. b_U > 1), whereas forepads show the opposite trend (b_U < 1; figure 3b).
  2. The increasing difference in strain energy storage between fore- and hindpads as body size increases may reflect both the greater importance of elastic energy return in hindpads of larger animals and the greater role of hindpads in providing propulsion (Alexander 1988; Biewener 2005). By contrast, as noted above, forepads have greater stiffness than hindpads and their stiffness increases more rapidly with body size (i.e. b_ky is larger) than H2 or H3 would predict. Forelimbs touch ground before hindlimbs during a stride and are therefore subjected to greater forces of impact (Bryant et al. 1987; Lee et al. 1999; Usherwood & Wilson 2005), especially in larger animals. Compared to a very soft pad that easily reaches its limits of compression (i.e. ‘bottoms out’), a pad of appropriate stiffness can provide resistance as it deforms to decelerate the mass of the foot and hence reduce these impact forces. Under a given load, a very soft pad deforming to a greater extent would pull directly at other soft tissues, causing tendons, ligaments and other soft tissues of the limb to stretch to a greater extent as they assist in deceleration, heightening the risk of joint dislocation. Our calculations suggest that in forepads, deformation is less in larger animals (b_Δy = −0.05), whereas in hindpads of larger animals deformation increases slightly (b_Δy = 0.15; figure 3b).

• — Patterns in the comparison of fore- and hindpads are similar at structural and material levels: the scaling factors for both compressive modulus (b_Ey) and the compressive stiffness of entire pads (b_ky) are higher for forepads than for hindpads (figure 3)—but this need not have been the case. The structural property of compressive stiffness of the pads is influenced importantly not just by their material composition but also by their size and geometry, and in principle, with countervailing patterns in the pads' sizes and shapes, scaling patterns at material and structural levels could be decoupled.

• — Stiffnesses of fore- and hindpads scale in a way that is consistent with H4: stiffness of forepads scales directly with body mass (t-test: p≫ 0.5; H4 accepted), while the scaling factor for hindpad stiffness falls between the predictions made by H3 and H4, with a CI that overlaps both (figure 3a). As we described above in the rationale proposed for H4, we infer that this scaling of footpad stiffness with body size allows similar impact loading regimes (Alexander & Vernon 1975; Alexander et al. 1986; Bryant et al. 1987; Whittle 1999; Chi 2005; Chi & Schmitt 2005) favourable for bone remodelling (Rubin et al. 1990; Turner 1998; Fritton et al. 2000; Chang et al. 2001; Currey 2002) to be maintained among mammals of different sizes.

• — The extent to which loading regimes in hindpads deviate from strict similarity (i.e. away from H4 and toward H3; figure 3a) may reflect a compromise: one that allows, as previous studies have suggested for other systems (Bennett & Taylor 1995; Lee et al. 1999; Usherwood & Wilson 2005), larger animals to have greater elastic energy storage to assist the hind limbs in efficient propulsion (Alexander 1988; Biewener 2005). Though it would not contribute directly to propulsion, the energy stored from vertical compression may prepare the foot for the propulsive phase by helping elevate the m-p joint.

In conclusion, carnivoran footpads provide an example of a soft-tissue element in which both geometry and material properties vary with size, scaling in a manner that has mechanical consequences not only for the maintenance of their own structural integrity and locomotor function, but additionally for those of associated tissues and bony elements.