Simulation of lung alveolar epithelial wound healing in vitro

Abstract

The mechanisms that enable and regulate alveolar type II (AT II) epithelial cell wound healing in vitro and in vivo remain largely unknown and need further elucidation. We used an in silico AT II cell-mimetic analogue to explore and better understand plausible wound healing mechanisms for two conditions: cyst repair in three-dimensional cultures and monolayer wound healing. Starting with the analogue that validated for key features of AT II cystogenesis in vitro, we devised an additional cell rearrangement action enabling cyst repair. Monolayer repair was enabled by providing ‘cells’ a control mechanism to switch automatically to a repair mode in the presence of a distress signal. In cyst wound simulations, the revised analogue closed wounds by adhering to essentially the same axioms available for alveolar-like cystogenesis. In silico cell proliferation was not needed. The analogue recovered within a few simulation cycles but required a longer recovery time for larger or multiple wounds. In simulated monolayer wound repair, diffusive factor-mediated ‘cell’ migration led to repair patterns comparable to those of in vitro cultures exposed to different growth factors. Simulations predicted directional cell locomotion to be critical for successful in vitro wound repair. We anticipate that with further use and refinement, the methods used will develop as a rigorous, extensible means of unravelling mechanisms of lung alveolar repair and regeneration.

1. Introduction

Acute lung injury and associated respiratory conditions often result in denudation of alveolar epithelia and impairment of the oxygen–blood barrier function (Ware & Matthay 2000; Gropper & Wiener-Kronish 2008). Denudation damages the alveolar type I cells providing most of the respiratory surface. Following injury, surviving alveolar type II (AT II) cells act to reestablish the alveolar epithelia using mechanisms that resemble aspects of lung development (Warburton et al. 2001). To gain insight into the epithelial repair process, AT II cells have been studied in two-dimensional in vitro wound healing assays (Kheradmand et al. 1994; Garat et al. 1996). Albeit simplistic, the cultures mimic an epithelial wound: a confluent cell monolayer is scraped to cause denudation and the surviving cells are left to heal (i.e. close) the denuded site. For AT II cells, cell migration plays a predominant role; cell spreading also contributes to the process. Cell proliferation plays no significant role during the initial closure (Kheradmand et al. 1994). Early evidence also suggests that similar repair processes might engage in a more complex, three-dimensional environment (Yu et al. 2007). However, little is known about mechanisms underpinning these processes. Identifying, characterizing and understanding those mechanisms represent an important step toward elucidating alveolar repair process in vivo.

A number of modelling methods have been developed to better understand mammalian wound repair (see the electronic supplementary material, table S1). Most are mathematical models based on Fisher's equation, a single reaction–diffusion equation, which characterizes propagating waves of an invariable form (Fisher 1937). When applied to wound closure, the equation describes a migrating cell front in terms of cell motility, or diffusivity, and the rate of proliferation (Kobayashi et al. 2000; Maini et al. 2004; Savla et al. 2004). Adaptations have been made to further characterize two-dimensional wound healing in vitro or in vivo (Sherratt & Murray 1990; Sheardown & Cheng 1996; Olsen et al. 1998; Dallon et al. 1999; Haugh 2006). More recently, a discrete lattice approach was used to model cell level dynamics of two-dimensional fibroblast wound healing (Cai et al. 2007). Using parameters fitted to experimental data, the model produced reasonable predictions of mouse fibroblast monolayer formation and wound closure in vitro. For additional, related examples, see Sherratt & Dallon (2002) and Murray (2003) and references therein.

In a previous study (Kim et al. 2009), we introduced an AT II cell-mimetic software analogue that validated for key cystogenesis features. The analogue is an example of what Fisher & Henzinger (2007) called executable biology. It is a multi-agent (Grimm et al. 2005), discrete event system (Law & Kelton 2000) composed of quasi-autonomous cell agents within an experimentation framework supported by other agents (Hunt et al. 2009). We constructed basic mechanisms for random and directed migration, cell–cell attachment and cluster remodelling actions governed by a small set of axiomatic operating principles. Axioms map to cell level phenomena (behaviours) that emerge from more detailed (fine-grained) subcellular mechanisms. By strictly adhering to the axiom set, the analogue developed structures resembling alveolar-like cysts (ALCs) in vitro. Here we used, refined and extended that analogue to discover and characterize possible mechanisms underlying in vitro AT II wound healing. The methods used share similarities with those described in two-dimensional wound healing studies of human urothelial cells (Walker et al. 2004) and mouse fibroblasts (Bindschadler & McGrath 2007). Recent studies of foot ulcer (Mi et al. 2007) and injured vocal folds (Li et al. 2008) also adapted similar agent-based methods for modelling wound repair in vivo.

We targeted two conditions: cyst repair in three-dimensioanl cultures and two-dimensional cell monolayer wound healing. For simulated cyst repair, we speculated that a wound creates a local depolarizing condition. We introduced an additional axiom enabling simulated cells to automatically respond to and close a wound. The new axiom used a depolarization algorithm from Grant et al. (2006). For two-dimensional culture simulation, we further extended the analogue with a control mechanism enabling the cell-mimetic agents to automatically switch to a repair mode in the presence of an abstract distress signal. In repair mode, the simulated cells were given an option to migrate or rearrange based on local signal gradients.

For both repair mechanisms, the simulated cells closed wounds by adhering to essentially the same axioms used for simulated ALC morphogenesis. Simulated cyst repair completed within a few simulation cycles but required a longer recovery time for large or multiple wounds. In two-dimensional simulations, cell migration mediated by a diffusive signal led to repair kinetics and patterns that were comparable to those observed in cell cultures exposed to different growth factors. Simulated cells migrating randomly produced low closure rates that roughly matched in vitro control conditions. Consistent with the experimental findings, in silico cell proliferation was not needed to achieve initial wound closure. Overall, the results predicted directional cell migration to be a critical determinant of AT II wound healing in vitro.

2. Material and methods

2.1. Agent-based and discrete event simulation methods

We employed agent-based modelling (ABM; Grimm et al. 2005), discrete event simulation (DES; Law & Kelton 2000) methods grounded on the synthetic method of modelling and simulation; see Hunt et al. (2009) for a detailed description of the synthetic method and approach. In ABM, a system is comprised of quasi-autonomous, decision-making entities called agents. Each agent follows a set of rules that governs its actions and interactions with other system components. ABM facilitates creating systemic behaviours and attributes that arise from purposeful component interactions. Agent-based models have advantages when attempting to understand and simulate phenomena produced by systems of interacting components. We used quasi-autonomous agents to represent AT II cells. We also employed quasi-autonomous components outside of the simulated biological system, but still within the computational framework. They played procedural, observational and data analysis roles analogous to those performed by researchers conducting experiments. In DES, system operation is represented as a temporal sequence of events, each occurring within a discrete time interval. System state evolves during those discrete time intervals. Using DES methods facilitated encapsulating system operations and conceptualizing complex dynamics. The methods provided a rigorous formalism for managing modularity and hierarchy. In AT II simulations, cellular activities were represented as being discrete. Operations of all analogue components were represented as discrete events. Stochasticity, which is natural to both ABM and DES, was introduced mostly in the form of probabilistic parameters that regulated agent actions and execution order. Hereafter, we use small capitals to distinguish analogue components and properties from their wet-laboratory counterparts.

2.2. System architecture and components

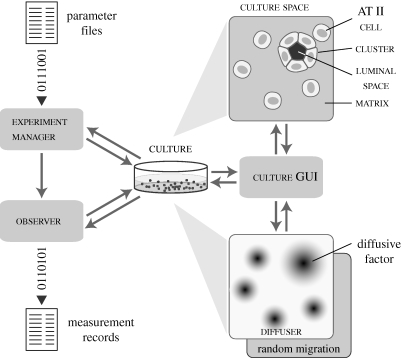
The model is a self-contained experimental system that comprises the core AT II cell-mimetic analogue and support components for experimentation and analysis (figure 1). The core analogue is composed of cell, cluster, matrix, free space and culture. Support components are experiment manager, observer, culture graphical user interface (GUI), and diffuser. Detailed descriptions of the system architecture and individual components are provided in Kim et al. (2009). An abridged description follows.

Figure 1.

AT II analogue components and system architecture. Experiment manager is a system-level agent that prepares parameter files, manages experiment execution and processes output data for analysis and summary. Observer is an agent that tracks individual cell activities and measures culture attributes. Culture represents an arbitrary section of an in vitro cell culture. It maintains a two-dimensional hexagonal grid within which cells, matrix and free space objects interact. Those three object types correspond to, respectively, AT II cells, extracellular matrix and the region (e.g. cyst lumen) devoid of cells and extracellular matrix. Matrix and free space are passive objects. Cells are quasi-autonomous agents with a set of axioms and decision logic that determine their action based on their internal state and neighbouring object configurations. Cluster represents a coherent aggregate of two or more cells and can include free space. Cells and clusters can call on different migration modes: random and factor-responsive. Diffuser is an extension to the culture space to simulate factor diffusion. It uses a second hexagonal grid. Culture graphical user interface (GUI) provides features to visualize and probe culture during simulation. The system was implemented using MASON, which provides standard libraries, object classes and methods for multi-agent, discrete event simulation (Luke et al. 2005).

Discrete objects with eponymous names represent the essential AT II culture components: cells, matrix and free space. Cells have decision logic and axiomatic operating principles (figure 2) for interacting with the neighbouring environment. Cells have the same relative size. Matrix and free space map to units of extracellular matrix (ECM) and matrix-free material. For simplicity, matrix maps to any cell-sized volume containing sufficient ECM to which AT II cells can attach. Free space maps to similarly sized regions devoid of ECM and cells. Free space also represents luminal material and the material in pockets enclosed by cells. The latter are called luminal space when distinction from free space is useful.

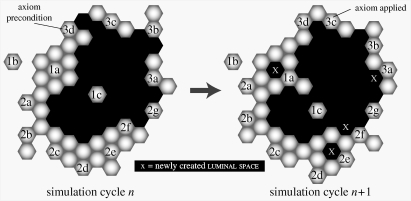
Figure 2.

AT II cell axiomatic operating principles. Culture space and all objects within are hexagonally discretized. Simulation time advances in steps corresponding to simulation cycles. Each simulation cycle maps to an identical interval of wet-laboratory time. During a simulation cycle, every cell, in a pseudo-random order, decides what action to take based on the composition of its adjacent neighbourhood. For clustered cell rearrangement, a set of axioms determines what action is taken for each possible neighbourhood configuration. Objects represented: cell (grey), matrix (off-white) and luminal space (black). To the left, selected decision-making cells at the start of simulation cycle n are numbered to indicate each of 14 axiomatic preconditions being satisfied. For purpose of this illustration, the unnumbered cells are inactive. To the right, the system at the start of simulation cycle (n + 1) shows the consequences of applying all 14 axioms. Axiom 1a: if all neighbours are cells, then push an adjacent cell and move to its location, leaving behind a luminal space. Axiom 1b: if all neighbours are matrix, do nothing. Axiom 1c: if all neighbours are luminal spaces, then exchange places with an adjacent luminal space. Axiom 2a: if there are matrix plus one cell or two adjacent cells, then exchange places with an adjacent matrix that is next to a neighbouring cell. Axiom 2b: if there are matrix and two nonadjacent cells, then remove an adjacent matrix that is next to a cell neighbour and move to that location while dragging the other attached cell. Axiom 2c: if there are matrix and three cells, do nothing. Axiom 2d: if there are matrix and four cells, then exchange places with either adjacent matrix. Axiom 2e: if there are matrix and five cells, then remove the matrix and move to its location, leaving behind a luminal space. Axiom 2f: if there are cells and luminal space only, then push an adjacent cell and move to its location, leaving behind a luminal space. Axiom 2g: if there are matrix and luminal space only, do nothing. Axiom 3a: if there are cells, luminal space and a single matrix, then remove the matrix and move to its location, leaving behind a luminal space. Axiom 3b: if there are matrix, luminal space and a single cell located next to a matrix neighbour, then remove a luminal space and move to that location while dragging an attached cell. Axiom 3d: if there are cells, luminal space and matrix mixed in a depolarizing configuration (Grant et al. 2006), then exchange places with an adjacent free space. Axiom 3c: for all other neighbourhood configurations, do nothing.

Cluster is an agent and a composite object containing member cells and associated luminal space. It represents a cohesive aggregate of cells that can act quasi-autonomously, independent of individual cell activities. A cluster is created when two or more cells attach. A cluster schedules its own events, which run at the same frequency of cell events. Their execution ordering is pseudo-random. Each cluster uses an identical step function to determine its action. A cluster can either migrate a certain distance or do nothing. Similar to a cell, a cluster can adopt different migration modes. For simplicity, it adopts the majority migration mode of its member cells. To further simplify design, cluster movement maintains overall shape and relative positions of the composing cells. Cluster movement stops when the movement is blocked by non-member cells or other clusters.

A culture maps to an arbitrary section of an in vitro cell culture. It has a master event schedule, pseudo-random number generators, and its own start and end methods that are called automatically at simulation's start and end. Simulation time advances discretely, which is maintained by the master event schedule. Event ordering within a simulation cycle is pseudo-random. Culture uses two-dimensional hexagonal grids to represent spaces in which cells, matrix and free space objects are placed. Grids have toroidal topologies. For simplicity, each grid position is occupied by one object. That condition can be easily changed when the need arises. A culture GUI provides visualization and user interaction.

Diffuser is a culture extension for simulating dispersion of soluble, extracellular substances. A diffuser object is created only when factor-responsive migration mode is enabled. It contains a grid, which contains diffusive factors (described below). The same hexagonal two-dimensional grid type is used and aligned with the culture grid; however, the grid contains only numerical values that correspond to specific factor levels. The diffuser object is stepped and its diffusion algorithm executed a parameter-specified number of times within each simulation cycle. The algorithm provides a simple discrete approximation of diffusion in a continuous space using parametrically defined diffusion and loss rates.

Experiment manager is the top-level agent. It manages experiment setup, execution and data processing. Observer is responsible for recording measurements. Its probe method is called at the end of every culture simulation cycle. The probe method scans the culture internals and performs measurements that are recorded as time series vectors.

2.3. AT II cell analogue design

Cells mimic specified behaviours of AT II cells in cultures. Their behaviours are governed by a set of rules—axioms—that reflect observed in vitro behaviours. The term ‘axiom’ emphasizes that computer programs are mathematical, formal systems and the initial mechanistic premises within simulations are analogous to axioms in formal systems. For this study, an axiom is an assumption about what conclusion can be drawn from what precondition for the purposes of further analysis or deduction. Cell action is dictated by internal cell state and neighbouring object composition. Within a simulation, every cell carries out exactly one action during each simulation cycle. Available cell actions are: migrate, attach to an adjacent cell and rearrange within a cluster.

When stepped, a cell first determines the types and arrangement of neighbouring objects. If it has no cell neighbours, it classifies itself as single and migrates to a neighbouring non-cell location. Migration modes used are random motility and factor-responsive movement. Random cell migration implements a simple, unbiased random walk. In factor-responsive mode, a cell detects the level of cell-produced factor in its local environment and moves either towards or away from spaces having higher levels. Any number of factors may be introduced to represent one or more soluble, diffusive factors that mediate epithelial cell migration or wound closure. When one or more cell neighbours are in contact, the decision-making cell attaches to each neighbour with a parametrically controlled probability, p, to form a cluster. Following attachment, cells switch to clustered state. Clustered cells follow the axioms illustrated in figure 2 to rearrange their relative positions within the parent cluster, a process that is essential for cystogenesis.

Achieving targeted attributes along with envisioned, future uses and capabilities dictated model design. Our goal has been to first discover plausible cell level mechanistic details that account for a variety of targeted attributes. Thus we approached the problem from a cell level perspective, with an understanding that molecular and biophysical details, as well as other subcellular information, conflate into the cell level mechanisms and events. So doing allowed us to focus on aspects that directly map to available biological information and obviated the need to reduce the cellular phenomena into more detailed molecular or physico-chemical representations. For the attributes targeted, high-resolution chemical or physical mechanisms were not needed. However, cell and system design features make it easy to replace coarse-grained components with finer-grained components when that is needed.

2.4. AT II analogue revision for cyst wound repair simulation

We first tested the final, validated AT II analogue from Kim et al. (2009) for cyst wound repair simulation. The target attribute was: the cells must repair a cyst wound and do so by cell movement only. Starting with a preformed cyst, a wound was created by replacing one or more cells with luminal space. No other interventions were made after wounding. Using the set of axioms discussed above, the cells failed to detect the wound and repair the cyst. The cells' neighbouring object configurations all met the precondition for axiom 3c (do nothing), so the cells remained stable throughout the simulation.

For the additional target attribute, we devised, tested and screened candidate axioms to enable the cells to automatically detect and repair the wounded cyst, while validating for the original targeted attributes from Kim et al. (2009). Final validation required achieving the cystogenesis similarity measures (SMs) described in Kim et al. (2009) and an additional SM for wound repair. The new SM was that more than 98 per cent of cysts recover from a wound of one cell-width; 95 per cent for 2 cell-widths; and 90 per cent for three cell-widths. Variations of different axioms were tested, and those that moved the analogue closer to validation were selected for further refinement. In its validated form, the revised analogue used one additional axiom (axiom 3d), which adapted the depolarization algorithm from Grant et al. (2006) as follows.

Axiom 3d. Cells, free space and matrix mixed in a depolarizing configuration (i.e. all other configurations containing cells, matrix and free space): exchange places with an adjacent free space.

The axiom preempted axioms 3a–c illustrated in figure 2. Detailed descriptions of the depolarization algorithm and supporting biological observations are provided in O'Brien et al. (2002) and Grant et al. (2006).

2.5. Revision for AT II monolayer wound healing simulation

For AT II cultures, cell migration plays a predominant role in monolayer repair (Kheradmand et al. 1994; Garat et al. 1996). No significant proliferation occurs during wound closure. We defined a new, simple target attribute based on the study findings. The attribute was: when a patch of cells is removed from a preformed cell monolayer and replaced with free space, the remaining cells must close the wound and do so by cell migration only. Cell division and death were not allowed.

The cell axioms were revised further for two-dimensional culture simulation. We assumed that in two-dimensional in vitro environment, cells have cell–matrix contact at all times with the underlying substrate. We also assumed that the cells interface non-matrix medium on the opposite cell surface. With those assumptions, the cell axioms were revised iteratively to achieve the target SM values discussed below. For axiom 1a, no cell movement was needed (do nothing) because its precondition satisfied the three-surfaces mandate (O'Brien et al. 2002). For axiom 1c, the cell was allowed to move directionally (versus random). Axiom 2f corresponded to configurations consisting of cells and free space. The revised axiom directed the cell to move to a randomly or directionally selected adjacent free space. Axioms 1b, 2a–e, and 3a–d corresponded to configurations containing matrix, so were not used in two-dimensional monolayer simulation. The revisions represent what we determined as a minimal change that was required for validation. Revisions that were more elaborate also enabled the AT II analogue to achieve the target attribute. However, they were rejected because they were not parsimonious.

Culture details were revised to enable additional cells to enter the culture grid during simulation. The feature abstractly maps to intact populations of cells present beyond the relatively small, wounded section being simulated. Some of these cells near the boundary move into the observed area as the wound closes. To mimic that, we provided a spatially localized boundary source: cells were placed in newly vacant grid sites at the boundary. The same result can be obtained by increasing the width of the simulation space by a factor of 10 or more.

The initial, least stringent SM, SM-1, was that wound healing achieve more than 25 per cent closure in the first 24 h (42 simulation cycles). When that was achieved, we enforced a stricter threshold (SM-2) of more than 50 per cent wound coverage. SM-3 increased the stringency further; it required more than 90 per cent wound coverage within 12 h after wounding. SM-4 required that SM-3 be achieved and that mean, simulated wound healing be within 10 per cent of in vitro values. The final, most stringent SM-5 was that SM-4 be achieved and mean, simulated wound coverage be within 5 per cent of in vitro values obtained from cultures treated with 10 per cent foetal calf serum (FCS). SM-5 was achieved by an analogue that used the factor-responsive migration mode.

2.6. Simulation experiment design

For cyst repair experiments, we used a hexagonal cyst with a radius of five grid units. A total of 24 cells enclosed the luminal space. Replacing randomly selected cells with free space objects created cyst wounds. The culture grid width and height were set to 50. All other parameters and system variables were set to values used in the cystogenesis experiments (Kim et al. 2009).

To the extent possible, two-dimensional simulation design followed the experimental protocols described in Kheradmand et al. (1994) and Liang et al. (2007). First, the culture grid was filled completely with cells that collectively formed a cell monolayer. The culture grid width and height were set to 150 and 100, respectively. Next, vertical columns of cells in the middle of the culture grid were replaced with free space that abstractly mapped to non-matrix medium in vitro. The wound width was set to 50 grid units. For factor-responsive migration diffuser grid area corresponding to cell locations was initialized with the maximum concentration specified in Kim et al. (2009). The diffusion rate was set to 0.2, and the evaporation (loss) rate was set to 0.1. Each experiment consisted of 100 Monte Carlo runs executed for 50 simulation cycles.

2.7. Implementation tools

The model framework was implemented using a discrete event, multi-agent simulation library, MASON (Luke et al. 2005). Batch simulation experiments were performed on a small-scale Beowulf cluster system. For model development, testing, analysis, simulation image processing and video production, we used personal computers. Computer codes and project files are available at http://biosystems.ucsf.edu/research_epimorph.html.

3. Results

We conducted cystogenesis simulations to compare behaviours of the revised and earlier analogues for cross-model validation. The following represent a standard cystogenesis simulation design and execution. First, a new culture was instantiated with the specified grid dimensions; the new culture's grid was filled completely with matrix. The culture grid represents the observed xy-plane of an AT II cell culture. Next, cells were initialized (represented by a concrete instance) and randomly distributed on the culture's grid. The initial cell population was specified parametrically. Simulation started when the initialization of culture grid contents was completed. After simulation, the recorded measurements were written to files and the culture was destroyed. A new culture was created for each repetition or experiment.

The results were indistinguishable (not shown): following the axioms shown in figure 2, cells aggregated into clusters and subsequently rearranged into cysts having luminal space surrounded by a cell monolayer. As before, cyst size increased with the initial cell density and was comparable to the values obtained in Kim et al. (2009). Cell movement patterns for the different migration modes tested were visually indistinguishable from those from the previous study. The revised analogue met the most stringent SM described in Kim et al. (2009).

3.1. Revised cell axioms enabled cyst wound repair

A cyst wound was created by replacing one or more cells with free space. Replacement with matrix made no substantive differences in the repair phenotype (not shown). As in the case of cystogenesis simulations, the cells had fixed shape and size. Cell proliferation and death were not allowed.

When a small wound of one cell-width was created, the cells closed the wound within a few simulation cycles (figure 3a; electronic supplementary material, video S1). The wound led to a locally depolarizing condition, which triggered cell response at the wound interface. Some cyst remodelling was observed as the cells drew in closer and rearranged their positions to restore a single-layered, convex formation. The cells became stable, and the lumen fully enclosed once the wound closed completely. Multiple wounds of the same size led to mostly similar repair phenotypes (figure 3b,c; electronic supplementary material, video S2) but tended to cause more extensive cyst remodelling and a longer time for recovery. Some cysts failed to regain a stable morphology and managed to recover only partially from as little as three wounds (electronic supplementary material, video S3). Further increase in wound count often led to a complete collapse of the cyst structure followed by cyst regeneration.

Figure 3.

Simulated wound healing of preformed alveolar-like cysts. The cell axioms and a sensing mechanism for depolarizing local environment, shown in figure 2, enabled analogues to repair preformed cysts. Replacing one or more cells in a preformed cyst with free space objects simulated a cyst wound. (a) Shown are sample repair images of a wounded cyst following infliction of a single, one cell-width wound. Objects with white centres are cells. Black spaces represent free (or luminal) space. (b,c) Shown are successful cyst repairs upon infliction of multiple wounds. (d,e) AT II cyst repair of large wounds are shown. For a wound of 3 cell-widths (d), the cyst regained its structure without significant remodelling. In the case of a larger wound of 5 cell-widths (e), the composing cells failed to heal the wound and the cyst collapsed, but remodelled itself into a new, stable cyst.

We observed generally similar increases in recovery time and cyst remodelling when a larger wound was inflicted (figure 3d,e; electronic supplementary material, videos S4 and S5). Increasing wound size frequently caused the cyst to collapse into a disorganized cell cluster, which regenerated a new cyst. With larger wounds, the cells at the wound edge and behind initially moved rapidly into the wound region. The rapid movements resulted in a partially closed wound with smaller luminal space. The structure appeared to stabilize after the initial repair but subsequently collapsed rapidly. The remaining cells often failed to reorganize into a cyst before the simulation's end.

3.2. Quantitative similarities achieved for AT II monolayer wound healing

The two-dimensional in vitro scratch assay is a common method for studying wound repair and cell migration (Liang et al. 2007). Starting with the above AT II analogue, we revised the cell axioms to simulate the two-dimensional culture condition. We tested two cell migration modes. In the simple mode, cells moved randomly; in factor-responsive mode, cells moved away from a wound-produced factor, which maps to one or more distress signals. For in vitro comparison, we used wound healing assay data from Kheradmand et al. (1994) and Garat et al. (1996).

Typical wound healing patterns are shown in figure 4 and in the electronic supplementary material, videos S6 and S7. Additional cells from the boundary source filled newly vacant boundary grid sites. Indistinguishable results were obtained using a 10× wider simulation space absent the boundary source. In factor-responsive mode (figure 4a–d; electronic supplementary material, video S6), cells moved rapidly into the wound area and closed most of the wound within 12 h. One simulation cycle mapped to 35 min in vitro. The results shown in figure 5a were comparable to AT II cultures treated with 10 per cent FCS. The closure rate remained roughly constant during the first 4 h, followed by an asymptotic decrease. The cells achieved over 97 per cent closure by 24 h (figure 5b). With fibronectin, in vitro cultures had approximately 83 per cent closure by 24 h. A similar closure was achieved when cell migration speed was reduced from 1 to 0.6 grid unit per cycle. Obvious differences were noted in cell movements and wound closure when cells migrated randomly (figure 4e–h; electronic supplementary material, video S7). Cells migrating randomly dispersed slowly into the wound area, which led to 28 per cent closure over the 24 h period.

Figure 4.

Simulated AT II cell monolayer wound healing. In scratch wound healing assays, a confluent cell monolayer is scratched with a probe to inflict a denuding wound. Following injury, surviving cells move into the denuded area and eventually restore monolayer confluence. We simulated that protocol by creating a confluent cell monolayer, and then removing contiguous columns of cells across the middle. We explored two different cell migration modes: random and factor-responsive. (a–d) Shown are simulated wound healing images of factor-responsive cells, which migrated away from a wound-induced, diffusive factor. Objects with white centres are cells. The dashed line indicates wound margin; to its right is the denuded area. As simulation progressed, an increasing number of cells migrated into the wound area and closed most of the wound within 12 h post-wounding. One simulation cycle mapped to approximately 35 min in vitro. (e–h) Cells migrating randomly exhibited poor wound healing characteristics, and failed to close the wound within 12 h.

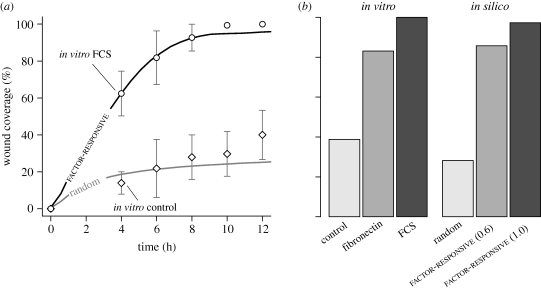
Figure 5.

Simulated and in vitro wound closure of AT II cell monolayer. See Kheradmand et al. (1994) and Garat et al. (1996) for details on in vitro assays and wound healing data. Briefly, AT II cell monolayers grown in the presence of different factors such as FCS and fibronectin were scraped once with a 23-gauge probe, and images captured at regular intervals over a 24 h period. Wound width was 50 cell-widths, which maps to 0.5 mm in vitro. We used two migration modes: random and factor-responsive. In factor-responsive mode, cells migrated away from a wound-induced factor. (a) Shown are wound closure of two in vitro conditions, and simulated wound healing using the two migration modes. Factor-responsive cells closed wounds at rates comparable to the in vitro condition with FCS, and regained monolayer confluence by 12 h. Randomly migrating cells failed to close the wound, and exhibited kinetics somewhat similar to the in vitro control condition. One simulation cycle mapped to approximately 35 min in vitro. Bars: ± s.d. (b) Shown are in vitro and simulated wound closures after 24 h. Compared with FCS, fibronectin was a less potent wound-healing agent. Cells migrating at 1.0 grid unit per cycle closed 97% of the wound. Reducing cell speed to 0.6 grid units per cycle led to 86% partial closure, which roughly matched the in vitro condition with fibronectin. The simulation data represent mean values of 100 Monte Carlo runs.

Individual cell movements showed markedly different patterns between randomly migrating and factor-responsive cells (figure 6). In the former case, cells at or near the wound margin initially had semi-persistent trajectories but soon lost the directionality. Total displacement from the initial position remained low. Cells far away from the wound exhibited mostly random trajectories, and their total displacements were close to zero. Sample migration paths for 12 h post-wounding confirmed the observations (figure 6a). In comparison, factor-responsive cells showed persistent, directional movements, which led to large displacements over the 12 h period. By 12 h post-wounding, cells up to 10 rows away from the wound margin had reached the centre region. Shown in figure 6b are sample migration paths starting at various distances from the margin. All exhibited a persistent direction into the denuded area.

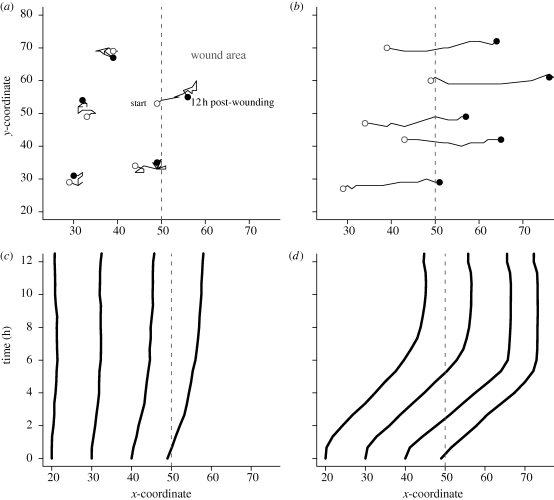
Figure 6.

Cell movement tracked during simulated wound healing. Simulations are the same as in figure 5. (a,b) Shown are typical movements for 12 h post-wounding by cells migrating (a) randomly or (b) directionally. Randomly migrating cells closer to the wound margin (dashed line) initially exhibited semi-persistent directionality towards the wound area, but soon lost the direction. Factor-responsive cells had persistent trajectories towards the wound area. (c,d) Shown are patterns of cell displacement from their initial positions. (c) Displacement of randomly migrating cells at specific distances away from the wound margin was small. Cells at the wound margin showed modest displacement over the 12 h period. (d) Factor-responsive cells had large displacements, which were consistent regardless of the initial distance away from the wound margin. Each curve represents mean displacement of cells initially at the same distance away from the wound.

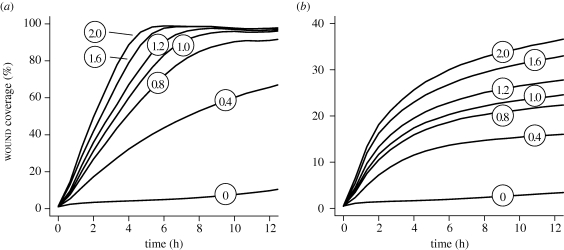
Changes in cell speed had observable effects on wound closure. In factor-responsive mode, initial wound closure rates decreased monotonically with cell speed (figure 7a). For example, decreasing cell speed from 1 to 0.4 grid unit per cycle led to approximately 50 per cent reduction in wound closure. However, allowed sufficient time, the more slowly migrating cells eventually closed most of the wound. Over 24 h, cells migrating at 0.4 grid unit per cycle closed 83 per cent of the wound. Increasing cell speed accelerated wound closure. Smaller but similar changes were observed for cells migrating randomly (figure 7b). However, the cells failed to reach 50 per cent closure within the 24 h period at any speed tested.

Figure 7.

Changes in cell speed and their effect on simulated wound closure. Simulation details and measurement mappings are the same as in figure 5. (a) Shown are wound closures by factor-responsive cells at different migration speeds. Circled numbers represent cell speed in grid unit per cycle. Wound closure results in figures 5 and 6 used cell speed of 1 grid unit per cycle. Increasing that speed led to more rapid wound closure. Decreasing cell speed slowed the closure. (b) Wound closures by randomly migrating cells at different speeds are shown. Increasing cell speed improved wound healing but failed to reach 50% closure in 12 h. Individual curves represent mean values of 100 Monte Carlo runs.

Wound closure rate constants (k) and half times (t_1/2) were computed using a nonlinear least squares fitting. Table 1 summarizes the derived measures for in vitro and simulated wound healing under varying conditions. Wound closure measures (k = 0.26% h⁻¹; t_1/2 = 2.66 h) for factor-responsive cells migrating 1 grid unit per cycle were comparable to the in vitro measures with 10 per cent FCS (k = 0.28% h⁻¹; t_1/2 = 2.4 h). Wound closure kinetics matching other in vitro conditions was possible by adjusting cell speed. For example, reducing cell speed to 0.4 grid unit per cycle led to wound closure kinetics (k = 0.10% h⁻¹; t_1/2 = 6.8 h) that matched in vitro cultures treated with transforming growth factor (TGF)-α. In the case of random cell migration, increasing cell speed led to repair kinetics (k = 0.04% h⁻¹; t_1/2 = 16 h) that matched the in vitro control (k = 0.04% h⁻¹; t_1/2 = 17 h). However, the cells failed to match closure kinetics of non-control conditions in Kheradmand et al. (1994) and Garat et al. (1996).

Table 1.

Wound healing rate constants and half times. FCS, foetal calf serum (10%); TGF-α, transforming growth factor-α (10 ng ml⁻¹); t_1/2, half time. Calculations of the rate constant and half time of wound healing of alveolar epithelial type II cells. The rate constant (k) for each condition was calculated by using a nonlinear least squares fitting equation (5 data points at 4, 6, 8, 10 and 12 h in vitro; every 40 min up to 12 h in silico) of % wound closure (W = 100(1 − e^kt)), where W is % wound closure and t is the time. The t_1/2 was derived from t_1/2 = ln 2/k.

conditions	rate constant (% h−1)	t1/2 (h)
in vitro
control (Kheradmand et al. 1994)	0.04	17.5
FCS (Kheradmand et al. 1994)	0.28	2.4
TGF-α (Kheradmand et al. 1994)	0.10	7.2
fibronectin (Garat et al. 1996)	0.14	4.9
in silico
random migration (0.4 grid unit per cycle)	0.019	36.48
random migration (1.0 grid unit per cycle)	0.030	22.79
random migration (1.6 grid unit per cycle)	0.043	16.08
random migration (2.0 grid unit per cycle)	0.049	14.05
factor-responsive (0.4 grid unit per cycle)	0.102	6.80
factor-responsive (1.0 grid unit per cycle)	0.261	2.66
factor-responsive (1.6 grid unit per cycle)	0.376	1.84
factor-responsive (2.0 grid unit per cycle)	0.436	1.59

4. Discussion

Alveolar epithelial damage is a key indicator of acute lung injury, which contributes to more systemic manifestations such as inflammation and fibrosis that are critical to prognosis. Repair of the damaged epithelia, by AT II cells in particular, plays an important role in whether the injury progresses to recovery or evolves into pulmonary fibrosis and organ failure (Ware & Matthay 2000). Rapid alveolar reepithelialization by AT II cells helps suppress fibrotic derangement in the alveolar, interstitial and vascular spaces for restoration of a functioning alveolar–capillary barrier. Delayed or impaired AT II repair activities on the other hand may precipitate alveolar obliteration and permanent loss of functional alveolar capillary units. Cell migration and spreading are thought to play a major role in the early, critical phase of alveolar epithelial repair, followed by proliferation of AT II cells and their differentiation into type I cells (Dos Santos 2008). In vitro studies also have shown that cell migration and spreading are primarily responsible for AT II epithelial wound healing (Kheradmand et al. 1994; Garat et al. 1996). The mechanisms that enable and regulate AT II repair process remain largely unknown and need further elucidation.

Recently, it has been suggested that the same regulatory mechanisms of lung morphogenesis are centrally implicated in alveolar repair and regeneration (Warburton et al. 2001). A number of regulatory factors and pathways are common to both processes, including fibroblast growth factor (FGF), epidermal growth factor (EGF) and TGF-β signalling that control critical events in embryonic and postnatal lung modelling (Warburton & Bellusci 2004). Likewise, key mediators of epithelial–mesenchymal interaction during embryonic airway morphogenesis are implicated in alveolar epithelial repair activities; an example is β-catenin, a key regulatory protein in the Wnt signalling pathway involved in spatial and temporal control of pulmonary development (Douglas et al. 2006). From those findings, we can reasonably theorize that common cell biological operating principles govern AT II morphogenesis, repair and regeneration.

Using the computational approach described in Kim et al. (2009), we extended the AT II cystogenesis analogue with wound healing features to help develop insight into the AT II repair mechanisms in vitro. The approach is based on the concept that when two model systems—an in vitro AT II cell culture and an in silico analogue—consist of components for which similarities can be established, and the two systems exhibit multiple attributes that are similar, then there may also be similarities in the generative mechanisms responsible for those attributes. In mature form, the analogue's mechanisms and operating principles can stand as working, explorable hypotheses—a theory—for those of AT II cells.

The analogue developed is a synthetic, biomimetic systems model that differs in important ways from the more familiar inductive mathematical models. As detailed in Hunt et al. (2009), synthetic analogues are ideal for discovering plausible mechanisms, relations between components and mechanism–phenotype relationships where knowledge of the referent wet-laboratory systems is insufficient to support precise predictions. They are best for exercising abductive reasoning and representing current knowledge. They are good at explanation. Because of the uncertainties reflected in stochastic parameters and mappings to the referent, they are not as good as inductive, equation-based models at precise, quantitative prediction; their predictions will be ‘soft’. However, they can make effective relational predictions. Synthetic models make predictions about component relations, and inductive models make predictions about variable relations and patterns in data. Both model types are needed for achieving deeper biological, mechanistic insight.

We started with theoretical AT II cyst wound healing in vitro. Adhering to the guideline of parsimony, which is important when building a complex model, we sought the simplest plausible mechanism(s) that would achieve targeted repair properties. For cyst wounds, successful repair required an additional axiom. The axiom imbued cells with an ability to automatically detect a wound based on neighbouring object configurations. Upon detection, cells closed the wound using the same actions available for cystogenesis. To the extent that the mappings described above are valid, the axioms theorize cell biological principles of AT II alveolar modelling and repair. We conjecture that comparable mechanisms in vivo might play a role in the early exudative phase of a lung injury (Dos Santos 2008). Additionally, the wound response mechanism raises an interesting possibility: depolarization might contribute to AT II repair in three-dimensional environment. Disruption of three surfaces—apical, basal and lateral—at the wound margin would create locally depolarizing conditions (O'Brien et al. 2002) that may prime or activate AT II repair processes. At a phenomenological level, similar observations have been made in branching morphogenesis, which involves transient depolarization and subsequent remodelling of the branching layer (Chung & Andrew 2008). We anticipate that further definition of the tubulogenesis control mechanisms such as those mediated by hepatocyte growth factor (Montesano et al. 1991; O'Brien et al. 2002) may help further unravel the mechanistic basis of alveolar epithelial repair (Ware & Matthay 2002).

Additional simulations showed that with large or multiple wounds, the wounded cyst often collapsed (i.e. lost luminal space) during repair, and the resulting disorganized cell cluster regenerated into a new cyst. While the simulations map only abstractly to an in vitro culture condition, they are reminiscent of fibrosis-type and destruction-type tissue alterations following a severe acute lung injury, which result in collapsed alveoli and profound rearrangement and disorganization of the acinar architecture (Bachofen & Bachofen 1997). However, the de novo cyst formation is abiotic at least relative to an in vivo context where the fibrotic and destructive lesions are irreversible. Furthermore, after severe alveolar denudation, AT II repair becomes ineffective due to increased rates of alveolar cell ‘dropout’ resulting from apoptotic or necrotic death (Dos Santos 2008). We speculate that three-dimensional AT II cell cultures may exhibit similar phenotypes. The current AT II analogue has no mechanism for cell death, but that can be added: simple self-deletion to mimic cell death. So doing would help make the analogue behaviours more realistic. On the other hand, defining conditions under which cell death takes place is not straightforward. As further insight from wet-laboratory studies becomes available we can proceed with the iterative refinement protocol (Kim et al. 2009) to expand the current set of axioms to include cell death option.

For two-dimensional AT II monolayer condition, previous in vitro studies have shown that a complete wound closure can be achieved by cell migration and spreading (Kheradmand et al. 1994; Garat et al. 1996). The studies also have identified a number of soluble and insoluble factors, including EGF, TGF-α and fibronectin, which enhanced wound closure rates. However, control mechanisms governing AT II cell migration in vitro are virtually unknown. One plausible mechanism, contact-mediated motility, has been identified and studied extensively in the wound repair context (Abercrombie & Heaysman 1954; Sherratt & Murray 1990; Ohtera et al. 2001; Bindschadler & McGrath 2007; Cai et al. 2007; Tremel et al. 2009). For our study, we considered additional, alternative mechanisms that could explain AT II cell patterns observed in vitro. One was simple random movement. Another was a form of chemotaxis, called fugetaxis or chemorepulsion (Vianello et al. 2005), by which cells migrated away from an abstract, wound-induced distress factor. As described in §3, differences between the two migration modes were obvious in cell patterns and wound closure kinetics (figures 5 and 6). Cells migrating randomly produced low closure rates that mapped to in vitro control, and had narrow trajectories. Increasing cell speed enhanced movement but failed to produce rapid closure (figure 7b). In comparison, factor-responsive cells were able to close the wound as efficiently as the AT II cells treated with growth factors. Cell proliferation was not needed for effective repair, which was consistent with the in vitro findings (Kheradmand et al. 1994; Garat et al. 1996; Farooqui & Fenteany 2005).

Taken together, the results suggest that random motility and the availability of an open space are not critical determinants of two-dimensional AT II wound closure in vitro. Directional cell locomotion is probably required for effective, sustained alveolar epithelial wound repair in vitro, which may be stimulated by growth factors such as those studied in Kheradmand et al. (1994), Lesur et al. (1995) and Garat et al. (1996). Boundary condition experiments of Madin-Darby canine kidney (MDCK) epithelial wound healing support the findings (Nikolić et al. 2006). In more complex, physiological conditions, additional factors might be involved including a number of cytokines, eicosanoids, oxygen radicals and other chemokinetic agents that have been identified for alveolar epithelial repair (Canonico & Brigham 1997; Matthay & Zimmerman 2005; Dos Santos 2008). Signalling mechanisms such as Ca²⁺ signals (Hinman et al. 1997) and ERK1/2 MAPK signalling (Nikolić et al. 2006) might also play roles. Articulating these mechanisms will be an important step towards better understanding the AT II epithelial repair process.

The results also highlight differences between AT II and a number of other cell types in wound healing context (Sherratt & Dallon 2002; Savla et al. 2004; Walker et al. 2004). Notably, it has been shown that cell proliferation plays a critical role in human peritoneal mesothelial cell wound closure (Maini et al. 2004) and chick-quail neural crest cell graft invasion (Simpson et al. 2006). In contrast, cell proliferation does not contribute significantly to in vitro AT II wound healing (Kheradmand et al. 1994; Garat et al. 1996). Thus, while reasonable mappings can be established from the analogue and simulations to AT II cell repair phenotypes, they are not intended to map to other cell types that require cell proliferation for effective wound healing.

Cell spreading has been shown to be an important mechanism in some studies (Garat et al. 1996; Geiser et al. 2001). For simplicity, cell spreading was not included as a targeted attribute. Cells having a fixed, uniform size managed to close the wounds at rates comparable to the in vitro conditions, but the closure rates diverged somewhat at later times (beginning approx. 8 h post-wounding) that are roughly coincident with increases in cell spreading in vitro. Differences were more obvious between the in vitro control and simulations where cells migrated randomly. Enabling cell spreading would trim those differences and further improve repair characteristics. For the level of similarity targeted, that additional capability was not needed. However, cell design features make it straightforward to implement cell spreading when it becomes necessary to do so.

As noted in §2, cell axioms are high level, low-resolution placeholders for more detailed representations of the actual complex mechanisms driving epithelial cell behaviour. Use of axioms precludes explicit representations of the abundant, detailed subcellular information that is available. However, we can elaborate the AT II analogue to include higher granularity components and mechanisms that map to subcellular details, such as life cycle pathways and intercellular signalling networks, when validation against an expanded set of targeted attributes requires doing so. From an engineering perspective, doing so can be accomplished by swapping the current cell component for a composite agent as illustrated in the electronic supplementary material, figure S1. Replacement could also occur at the intra-component level, for example by replacing cell axioms with more detailed logic based on interacting components. A challenging task will be to ensure cross-model validation between the different analogue variants, and to develop appropriate automated validation measures.

Further refinement of the AT II analogue is needed to explore additional mechanisms, which may proceed using the iterative, stepwise protocol described in Hunt et al. (2009) and Kim et al. (2009). That protocol is well suited for evolving any mechanistically focused, executable (Fisher & Henzinger 2007), agent-based, biomimetic analogue. The nature and organization of the AT II analogue components were designed to facilitate that process. As the process continues, following each round of refinement, more of what we know or think we know will become instantiated in the analogue. We anticipate that after many such rounds, the analogue will develop into a rigorous, dynamic platform, complementary with wet-laboratory approaches, for expanding our understanding of lung alveolar repair and regeneration.