Stance and swing phase costs in human walking

Abstract

Leg swing in human walking has historically been viewed as a passive motion with little metabolic cost. Recent estimates of leg swing costs are equivocal, covering a range from 10 to 33 per cent of the net cost of walking. There has also been a debate as to whether the periods of double-limb support during the stance phase dominate the cost of walking. Part of this uncertainty is because of our inability to measure metabolic energy consumption in individual muscles during locomotion. Therefore, the purpose of this study was to investigate the metabolic cost of walking using a modelling approach that allowed instantaneous energy consumption rates in individual muscles to be estimated over the full gait cycle. At a typical walking speed and stride rate, leg swing represented 29 per cent of the total muscular cost. During the stance phase, the double-limb and single-limb support periods accounted for 27 and 44 per cent of the total cost, respectively. Performing step-to-step transitions, which encompasses more than just the double-support periods, represented 37 per cent of the total cost of walking. Increasing stride rate at a constant speed led to greater double-limb support costs, lower swing phase costs and no change in single-limb support costs. Together, these results provide unique insight as to how metabolic energy is expended over the human gait cycle.

1. Introduction

The movements of humans and other animals have been a topic of scholarly interest for millennia. Evidence of a long-standing fascination with terrestrial locomotion is found in Upper Palaeolithic cave paintings (Windels & Laming-Emperaire 1949) and several early works by the likes of Aristotle, Borelli, the Weber brothers, and Braune and Fisher (Maquet 1989; Maquet & Furlong 1987, 1991; Preus 1981). Human walking has by far received the most attention, with tens of thousands of citations in the scientific and clinical literature. Walking is described and characterized in the context of the gait cycle (figure 1), with the start of the cycle traditionally coinciding with the heel striking the ground. In walking, the foot is on the ground for a little more than 60 per cent of the gait cycle. This interval is referred to as the stance phase. The stance phase begins and ends with both feet on the ground, which are known as periods of double-limb support. The intervening time, when only one limb is on the ground, is known as single-limb support. During the remainder of the gait cycle (i.e. slightly less than 40%), the foot is off the ground as the limb is swung forward to begin the next stride. This interval is referred to as the swing phase. As early as the 1830s, the swinging lower limb during walking was characterized by Wilhelm and Eduard Weber as a pendulum, acting mainly under the influence of gravity (Maquet & Furlong 1991). More recent evidence for this view has come from passive ballistic models of the swing phase that reproduce many of the gross features of walking (e.g. Mochon & McMahon 1980). However, these models do not predict the finer details of leg swing in walking (Whittlesey et al. 2000; Selles et al. 2001), suggesting that the swing phase is actually under some degree of active control by the neuromuscular system. This appears to be especially true during the early and late parts of the swing phase (Doke et al. 2005).

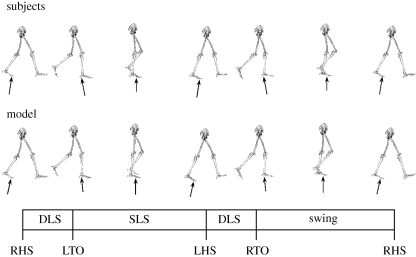
Figure 1.

Still-frame sequences for the simulation model and subjects walking at 1.3 m s⁻¹ at the preferred stride rate (54 stride min⁻¹). DLS, double-limb support; SLS, single-limb support; RHS, right heel strike; LTO, left toe off; LHS, left heel strike; and RTO, right toe off. The stance phase encompassed the two DLS periods and the SLS period. Animations of the model walking at all three stride rates are available in the electronic supplementary material.

If the swing phase in walking was essentially passive, then lower limb muscles would consume relatively little metabolic energy during this portion of the gait cycle. No contemporary researchers have suggested that the metabolic cost of the swing phase is nil, yet some lines of evidence indicate a relatively low cost of leg swing in walking. Experiments where loads were attached near the body centre of mass (Griffin et al. 2003) or leg swing was aided externally (Gottschall & Kram 2005) suggested that muscle energy consumption occurs mostly during the stance phase, with the swing phase representing only about 10–15% of the net cost of walking. Additional support for leg swing being relatively inexpensive comes from the comparative literature, where it has been shown that animals of similar size but different limb masses have similar locomotor costs (Taylor et al. 1974). If leg swing had a substantial influence on locomotor costs, one would expect animals with more massive limbs to incur greater costs than animals of the same total body mass, but with less massive limbs. However, contentions that leg swing costs are low are at odds with the results of studies which demonstrate that attaching additional mass to the lower limb increases the metabolic cost of walking by considerably more than attaching the same mass to the torso (e.g. Soule & Goldman 1969). This would indicate that the cost of swinging the legs in walking is not trivial. Further evidence comes from studies of isolated leg swinging in humans (Doke et al. 2005) and direct estimates of muscle blood flow in bipedal walking birds (Marsh et al. 2004). These studies suggest that leg swing may represent 25–33% of the net cost of walking. Interestingly, muscle mechanical work during the swing phase also appears to represent about the same proportion (25–29%) of total muscle work in walking (Neptune et al. 2008). However, it has been argued that muscle work may not be the primary determinant of leg swing costs (Doke & Kuo 2007; Rubenson & Marsh 2009). Thus, while the swing phase certainly has a lesser metabolic cost than the stance phase, it is not clear whether the cost of leg swing during walking is relatively low (e.g. approx. 10% of the net cost of walking), or relatively high (e.g. approx. 30% of the net cost of walking).

The metabolic costs associated with events that occur within the stance phase have also been the topic of recent debate (Kuo & Donelan 2009; Neptune et al. 2009). The results of one experimental study, motivated by predictions from an inverted pendulum model (Kuo 2002), led to the conclusion that step-to-step transitions may account for much of the metabolic cost of human walking (Donelan et al. 2002). Step-to-step transitions reflect the need to redirect the body centre of mass velocity between steps, and correspond closely with the double-limb support periods (Kuo et al. 2005). This line of research has led to estimates for the cost of performing work during step-to-step transitions that range from 45 per cent (Grabowski et al. 2005) to 65 per cent (Kuo et al. 2005) of the net cost of walking. If even the lowest of these estimates are correct, then performing step-to-step transitions would indeed be the major determinant of the metabolic cost of walking. However, results from a musculoskeletal modelling study indicate that muscles do considerable mechanical work to raise the body centre of mass during single-limb support, suggesting that this period of the stance phase is also quite costly (Neptune et al. 2004). This interpretation must be viewed cautiously, however, as it is difficult to infer the metabolic cost from mechanical work estimates alone. Inverted pendulum models predict that no work is needed except during the step-to-step transitions. The human body is not, in fact, a simple inverted pendulum, and if muscles are required to generate force and do mechanical work during single-limb support, then there would be a corresponding metabolic cost. The cost of generating muscle force to support body weight has been estimated to be 28 per cent of the net cost of walking (Grabowski et al. 2005). However, this estimate was rooted in the concept that muscles act nearly isometrically during single-limb support, in contrast to the findings of musculoskeletal modelling studies (Neptune et al. 2004, 2008).

Enhancing our understanding of the relative costs of the various phases of the bipedal gait cycle has implications both on the development of general theories of locomotion, and on more practical issues, such as treating gait disorders or designing lower limb prostheses. Muscle blood flow measurements currently provide the most direct estimates of muscle energy consumption during locomotion (Marsh et al. 2004), but this technique is not appropriate for use in humans. Creative experimental protocols (Donelan et al. 2002; Griffin et al. 2003; Doke et al. 2005; Gottschall & Kram 2005; Grabowski et al. 2005) can help set bounds on the expected ranges of costs, but do not allow the costs of individual phases to be fully isolated. Additional insights regarding the cost of walking can be gained by varying parameters of the gait cycle that affect the relative durations and intensities of the stance and swing phases (Donelan et al. 2002; Kuo 2002; Umberger & Martin 2007; Neptune et al. 2008; Sawicki & Ferris 2009). Speed, stride rate and stride length all affect the characteristics of the stance and swing phases, as well as the metabolic cost, and can be varied in many possible combinations, such as walking at a single speed using different stride rates and lengths. Some of the limitations of studying muscle function during locomotion experimentally in humans can be overcome by using musculoskeletal modelling and computer simulation techniques (Zajac et al. 2003). Musculoskeletal modelling studies of human walking have typically focused on the mechanics and control of locomotion; yet, it is also possible to predict the metabolic cost of muscle actions if an appropriate model is used (Umberger et al. 2003; Bhargava et al. 2004; Lichtwark & Wilson 2005).

Simple inverted pendulum models (e.g. Kuo 2002) have helped identify key determinants of the cost of walking that have been tested experimentally (Donelan et al. 2001, 2002). However, these simple models provide little insight as to which muscles are consuming energy across the gait cycle. Musculoskeletal modelling studies, on the other hand, have revealed much about the mechanical energetics of muscle function in the stance and swing phases (Neptune et al. 2001, 2004, 2008). Yet, there is still much uncertainty regarding the associated metabolic costs. Using a model of muscle energy expenditure (Umberger et al. 2003), it is possible to derive estimates of the metabolic cost incurred by the muscles during each phase of the gait cycle. Therefore, the purpose of this study was to estimate the metabolic costs of the stance and swing phases in human walking at a single speed and three different stride rates, using a modelling and simulation approach. Stance phase costs were considered both for the whole stance phase, as well as for the separate costs of double-limb and single-limb support.

2. Material and methods

Computer simulations of bipedal walking were generated using a forward dynamics model of the human musculoskeletal system. Dynamic optimization techniques were used to find a set of control parameters (i.e. muscle excitations) that produced human-like walking in the model. Experimental data obtained from healthy young adults were used both to define the initial conditions, and to evaluate the results obtained with the model. A model of muscle energy consumption was used to determine the relative metabolic costs of the stance and swing phases. The metabolic cost of the stance phase was further partitioned into double-limb and single-limb support costs.

2.1. Simulation model

A two-dimensional model of the human musculoskeletal system was created, with motions of the body segments constrained to occur only in the sagittal plane. The musculoskeletal geometry was based on an existing model used to study pedalling (Umberger et al. 2006), which was modified to account for the foot–ground interaction that occurs in walking. This resulted in a model that was conceptually similar to other musculoskeletal models that have been used to study the mechanics and energetics of human walking (e.g. Gerritsen et al. 1998; Neptune et al. 2001; Sellers et al. 2005). The present model consisted of seven rigid segments representing the trunk and lower limbs. The trunk segment included the mass and mass distribution of the pelvis, torso, head and arms. Each lower limb was modelled using three segments corresponding to the thigh, shank and foot. The mass of the model was 75 kg, and the standing height was 1.80 m. Parameter values for the individual body segments are provided in the electronic supplementary material, table A1. The hip, knee and ankle were modelled as frictionless revolute joints, which were maintained within the physiological range-of-motion limits by passive joint moments (Riener & Edrich 1999). The passive moments accounted for all of the anatomical structures that generate forces in parallel with the contractile parts of muscles (e.g. ligaments, joint capsule and parallel muscle elasticity). The vertical component of the ground reaction force was computed using a viscoelastic model (Gerritsen et al. 1995), with forces applied at the heel and toe of each foot segment. A ‘smooth’ friction model (Song et al. 2001) was used to compute the horizontal component of the ground reaction force. The combination of seven segments and six revolute joints resulted in the model having nine mechanical degrees of freedom. The closed-form equations of motion for the model were derived using the symbolic manipulator Autolev (OnLine Dynamics, Inc., Sunnyvale, CA, USA), which generated source code that was compiled and linked with a library of custom-written subroutines for the other model elements, such as the muscle and ground contact models. Motions of the model were visualized using the OpenSim software package (Delp et al. 2007).

The model was driven by 24 musculotendon actuators which represented the major muscles that produce movements at the hip, knee and ankle joints in the sagittal plane (Umberger et al. 2006). A Hill-type muscle model (van Soest & Bobbert 1993; Nagano & Gerritsen 2001) was used to model muscle contraction dynamics, along with an additional set of model equations that were used to predict muscle metabolic energy consumption (Umberger et al. 2003). The ‘standard’ muscle model parameters described in Umberger et al. (2006) were used in the present study, and represented population averages for muscle fibre type distribution in each muscle. The parameter values can be found in the electronic supplementary material, table A2. The length of each musculotendon actuator was modelled using polynomial equations that were fit to experimental tendon excursion data from the literature. Further details, as well as the polynomial coefficients, are provided in the electronic supplementary material, table A3. The magnitude of the moment arm of each muscle at any joint that it crossed was determined by taking the partial derivative of musculotendon length with respect to the joint angle (An et al. 1984). Given the musculotendon force computed from the Hill-type muscle model, and the moment arm computed from the polynomial equations, it was possible to determine the magnitude of the moments that each muscle applied to the model body segments (van Soest & Bobbert 1993).

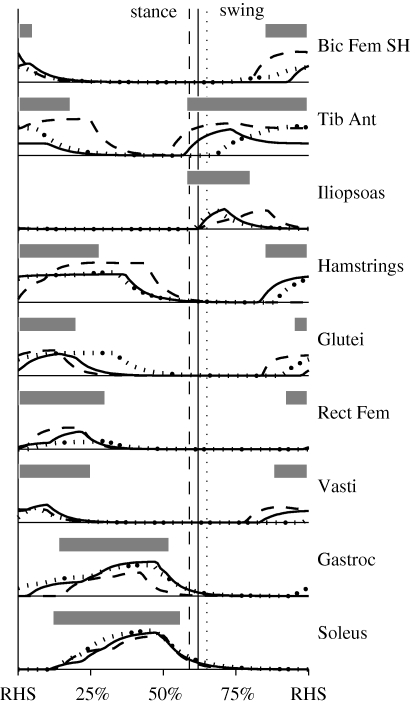
Each muscle in the model received an excitation signal (i.e. the control signal) that was transformed to muscle activation based on first-order dynamics (He et al. 1991). Each muscle excitation signal was described by seven parameters. The first two parameters denoted the time at which a muscle turned on, and the amplitude of excitation. After a muscle was turned on, the amplitude was allowed to change twice; the timing and amplitude of these changes in the excitation signal required four additional parameters. The final parameter indicated the time at which the muscle turned off, and the amplitude returned to zero. Thus, there were four excitation timing parameters and three excitation amplitude parameters per muscle. This approach provided more flexibility in controlling the model than using a single muscle excitation burst with a single amplitude (e.g. Gerritsen et al. 1998), at the expense of increasing the size of the solution space in the optimization problem. With the current approach, muscle excitation could ramp up or down gradually, or have two distinct periods of excitation (i.e. if the middle excitation amplitude was close to zero). Even with seven parameters per muscle, the dimension of the solution space was kept manageable by using the same excitation input for both the legs (shifted by 50% of the gait cycle), and by grouping synergistic muscles (Umberger et al. 2006). Together, these steps reduced the number of independent muscle excitation signals from 24 to 9, which corresponded to the nine muscle groups identified in figure 2 (also see electronic supplementary material, table A2).

Figure 2.

Muscle activation patterns for the walking simulation model at all three stride rates. Horizontal bars indicate on–off timing determined from electromyography data (Knutson & Soderberg 1995). In general, there was good temporal agreement between the bursts of muscle activation and the experimental data at the preferred stride rate (solid line). Most muscles showed some effects across stride rate in timing, amplitude or both. The transitions between stance and swing phases are shown by vertical lines that match the corresponding data line (solid (Pref SR), dashed (−20% SR) or dotted (+20% SR)) for each stride rate.

The initial conditions for the model were defined using the procedure described by Neptune et al. (2001). The initial positions and orientations of the body segments were set equal to the mean experimental values (described below). The initial velocities were also set equal to the experimental values, but were allowed to vary slightly by including them as parameters in the optimization. The initial muscle activations could not be determined from any experimental data, but could be found numerically. Given that walking is cyclic, the differential equations describing muscle activation dynamics were first integrated over the full gait cycle. Then, the initial values were set equal to the values at the end of the gait cycle. The initial muscle contractile element lengths also had to be determined numerically. The initial contractile element lengths were set such that, given the initial activations described above, the initial contractile element velocities were zero at the start of the simulations. While some muscles will clearly have non-zero contractile element velocities at the start of the gait cycle, this approach had little effect on the predicted muscle energy consumption for two reasons. First, the contractile element velocities approached the correct values within a few integration time steps (less than 0.01 s). Also, within normal operating ranges for walking, the predicted muscle energy consumption depends more heavily on activation than on contractile element length or velocity.

2.2. Experimental data

Experimental data were drawn from a subset (n = 6) of young (28.3 ± 3.7 years), healthy adult subjects from a prior study (Umberger & Martin 2007) who had the same average mass (75.2 ± 8.1 kg) and height (1.79 ± 0.04 m) as the simulation model. The experimental protocol was approved by the local Institutional Review Board, and all subjects provided informed consent. Complete details on the experimental data collection and processing can be found in Umberger & Martin (2007), and will be reviewed here for completeness. Subjects walked at 1.3 m s⁻¹ using their preferred stride rate (Pref SR condition), as well as stride rates 20 per cent higher than the preferred (+20% SR condition) and 20 per cent lower (−20% SR condition) than the preferred rates. Rates of oxygen consumption and carbon dioxide production were measured using a metabolic cart (TrueMax 2400, Parvo Medics, Sandy, UT, USA) as subjects walked on a motorized treadmill. Gross rates of metabolic energy consumption were computed from oxygen consumption and carbon dioxide production (Weir 1949). Net metabolic rates were determined by subtracting the rates of energy consumption during standing. Kinematic and ground reaction force data were collected during overground walking trials. Kinematic data were collected at 60 Hz with a S-VHS video camera (Panasonic, Secaucus, NJ, USA) and processed using Peak Motus software (Vicon, Centennial, CO, USA). Ground reaction forces were sampled at 600 Hz using a strain gage force platform (AMTI, Watertown, MA, USA). Care was taken to match both the speed and stride rates between the treadmill and overground trials. Subjects folded their arms across their chest during data collection, which emulated the mass distribution of the trunk segment in the simulation model. Walking without arm swing has been shown to have a relatively small effect on locomotor mechanics and energetics (Umberger 2008). Thus, the current simulation results should generalize to normal human walking.

2.3. Optimization and control

The procedures used to find muscle excitation control parameter that produced walking in the model at the three stride rates were based on Anderson & Pandy (2001). Given the symmetry of the model, full gait cycles were reconstructed from simulations of a single step (i.e. half of a full gait cycle). A parameter optimization problem was formulated (Pandy et al. 1992) to find the control parameters that minimized an energy-based objective function. Terminal equality constraints were used to ensure that the solution was cyclic; however, the motion of the model was unconstrained between the initial (t_I) and final (t_F) times. The terminal constraints were enforced using penalty terms. An additional penalty term was appended to the objective function to discourage large passive joint moments. The penalty on passive moments was necessary because the passive joint moment formulation (Riener & Edrich 1999) allowed for solutions where the knee joint was positioned at a few degrees of hyperextension during single-limb support. This allowed the model to use the passive knee moment to keep the knee from collapsing, which had a lower metabolic cost than using muscles to hold the joint in a few degrees of flexion. The penalty approach was effective at preventing final solutions that involved knee joint hyperextension. The objective function (J) was expressed as:

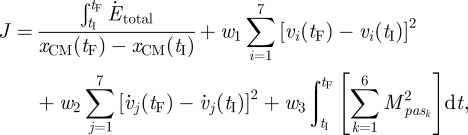where 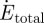is the total rate of metabolic energy consumption in the model, and x_CM(t_F) and x_CM(t_I) are the final and initial horizontal positions of the whole-body centre of mass. In the second term, on the right-hand side, v_j(t_F) and v_j(t_I) are the final and initial values of model segment angles (trunk angle and bilateral thigh, shank and foot angles). In the third term on the right-hand side, 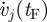and 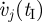are the final and initial values of model segment angular velocities (trunk angular velocity and bilateral thigh, shank and foot angular velocities). Given that only half of a gait was simulated, the final lower limb segment angles and angular velocities were actually compared with the initial values for the contralateral limb. In the fourth term on the right-hand side, 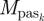is the passive moment applied at the kth joint (bilateral hip, knee and ankle joints). The constants w₁ (=0.005), w₂ (=0.0001) and w₃ (=0.001) were used to weigh the penalty terms against the energy term in the objective function, and were determined through trial-and-error to find the smallest values that resulted in acceptable solutions to the parameter optimization problem. The optimization problem was solved using a simulated annealing algorithm (Goffe et al. 1994; Neptune et al. 2001). Following the nomenclature used with that particular implementation, the simulated annealing algorithm parameter values used were RT = 0.75, NS = 20 and NT = 5, and the initial temperature (T) was 15. The optimization problem was solved 10 times for each stride rate condition, using different seeds in the random number generator. An optimization run was terminated after 100 simulations with less than 1 per cent reduction in the objective function value. The solution with the lowest objective function value for each stride rate condition was used for further analysis.

2.4. Analysis

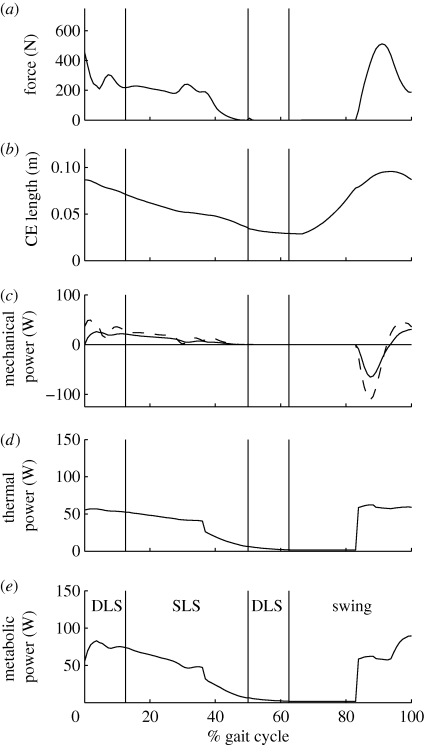
The muscle model used in this study provided the instantaneous mechanical power and rate of heat production over the duration of the simulation for each muscle. The mechanical and thermal energy rates were combined to yield the rate of metabolic energy expenditure, or metabolic power, for each muscle (Umberger et al. 2003). In this study, an updated version of the muscle model was used that was designed to provide better estimates of metabolic energy consumption during lengthening contractions. These modifications are described in the electronic supplementary material. The metabolic energy consumed by each muscle was determined by integrating the instantaneous metabolic power over the duration of the gait cycle. Summing over all muscles in both limbs yielded the total muscle energy consumption. Whole-body energy consumption was estimated by adding an additional energy term that represented the energy consumed by the rest of the body (Umberger et al. 2003). This was done for comparison with the gross metabolic power in the subjects. Total muscle energy consumption for a portion of the gait cycle (e.g. double-limb support, swing phase) was obtained by performing the numerical integration over the time corresponding just to that interval, rather than over the whole stride, and then summing across muscles. An example of the relevant outputs from the muscle model are shown in figure 3 for a single muscle, including metabolic power (figure 3e), which was integrated with respect to time to obtain the muscle metabolic energy consumption.

Figure 3.

Example muscle model outputs for a single muscle (medial hamstrings). Variables shown are (a) contractile element force, (b) contractile element length, (c) contractile element (CE) and musculotendon (MT) mechanical powers, (d) thermal power (i.e. rate of heat production) and (e) muscle metabolic power. CE mechanical and thermal powers were combined to determine metabolic power. Metabolic power was integrated with respect to time over various intervals of the gait cycle to compute muscle energy consumption. (c) Solid line, CE; dashed line, MT.

3. Results

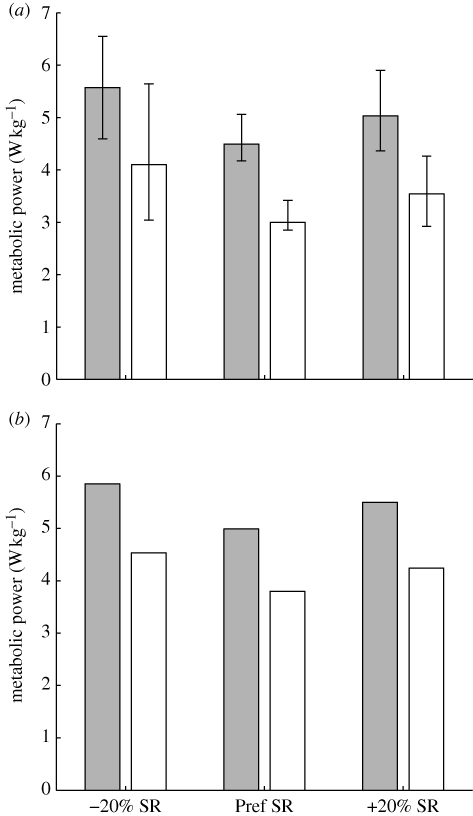
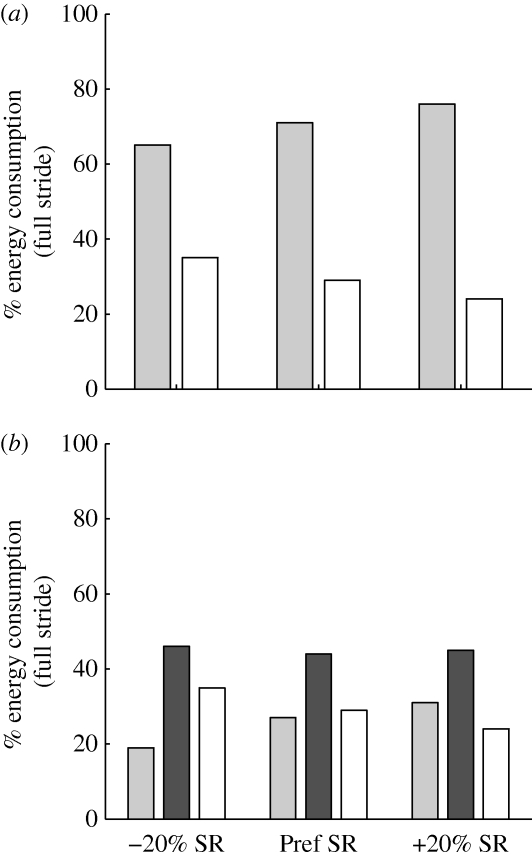
Following the optimization process, the musculoskeletal model was able to emulate human walking at the target speed (within ± 2%) for all three stride rate conditions. The positions of the body segments and the ground reaction force vectors at key points in the gait cycle are shown for the subjects and model for the preferred stride rate condition in figure 1. Animations of the model walking at all three stride rates are available in the electronic supplementary material. The root mean squares of the differences in initial and final segment angles were reduced to less than 5° (3.5–4.7°) for all three stride rate conditions. The model muscle activations for all three stride rates are shown in figure 2, along with on–off timing information derived from electromyography data (Knutson & Soderberg 1995). The timing of major gait cycle events was consistent to within about 1.5 per cent of the gait cycle between the subjects and model (table 1). The largest discrepancy was for the low stride rate condition (−20% SR), where the stance phase was 1.6 per cent shorter (and the swing phase 1.6% longer) in the model than the subjects. In both the subjects and the model, the stance phases, single-limb support periods and double-limb support periods represented smaller proportions of the total gait cycle at lower stride rates (table 1). The general trends in whole-body and total muscle energy consumption for the model were similar to gross and net metabolic power for the experimental subjects (figure 4). For both the model and the subjects, energy consumption was least at the preferred stride rate and greatest at the low stride rate (−20% SR). Total muscle energy consumption in the model was higher than the net energy expenditure in the subjects, and was less sensitive to stride rate (figure 4).

Table 1.

Relative timing of major gait cycle events for the subjects and model. Pref SR is the preferred stride rate condition; −20 per cent SR is the low stride rate condition; +20 per cent SR is the high stride rate condition. RHS, right heel strike; LTO, left toe off; LHS, left heel strike; RTO, right toe off. Stance phase is RHS to RTO and swing phase is RTO to RHS. First double-limb support phase is RHS to LTO, single-limb support phase is LTO to LHS and second double-limb support phase is LHS to RTO.

		gait cycle events
condition		RHS	LTO	LHS	RTO	RHS
		(percentage of the gait cycle)
−20% SR	subjects	0	10.3	50	60.9	100
	model	0	9.3	50	59.3	100
Pref SR	subjects	0	13.6	50	63.6	100
	model	0	12.5	50	62.5	100
+20% SR	subjects	0	15.2	50	65.2	100
	model	0	14.9	50	64.9	100

Figure 4.

(a) Average gross (shaded bars) and net (walking minus resting, open bars) metabolic power in the subjects across stride rates. Error bars indicate the range of experimental values. (b) Average whole body (shaded bars) and summed leg muscle (open bars) metabolic power in the simulation model across stride rates. The general trends in the data were the same between subjects (a) and the model (b). Metabolic power was lowest at the preferred stride rate (Pref SR) and highest at the low (−20% SR) stride rate. However, leg muscle energy expenditure was not as sensitive to stride rate as net metabolic power in the subjects.

At the preferred stride rate, the stance phase represented 71 per cent of the total muscle energy consumption and the swing phase accounted for 29 per cent (figure 5a). Swing phase energy consumption represented a greater percentage of the total (35%) for the low stride rate condition (−20% SR), and a lesser percentage (24%) for the high stride rate condition (+20% SR) (figure 5a). At the preferred stride rate, single-limb support represented 44 per cent of the total muscle energy consumption, and the two double-support periods combined accounted for 27 per cent (figure 5b). Single-limb support costs were a nearly constant percentage of the total (44–46%) across stride rates, but the double-limb support costs were a greater percentage of the total (31%) for the high stride rate condition (+20% SR), and a lesser percentage (19%) for the low stride rate condition (−20% SR) (figure 5b).

Figure 5.

(a) Percentage of total leg muscle energy expenditure consumed during the stance phase (shaded bars) and swing phase (open bars) across stride rates. (b) Same data as in panel (a), but with stance phase energy consumption partitioned into double-limb support (shaded bars) and single-limb support periods (black bars). The shaded and black bars in panel (b) for each stride rate sum to the shaded bar in panel (a) for the corresponding stride rate. Open bars indicate swing phase.

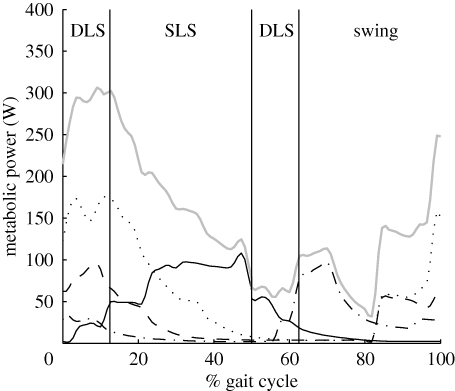
The rate of muscle metabolic energy consumption was not uniform across the gait cycle. Figure 6 shows the instantaneous metabolic power summed across all muscles in a single limb from heel strike (0% of the gait cycle) until the next heel strike of the same limb (100% of the gait cycle). Note that during the first double-limb support period in figure 6, the limb was in front of the body centre of mass, while for the second double-limb support period, the limb was behind the body centre of mass (see also figure 1). Instantaneous metabolic power was highest during the first double-limb support period and the early single-limb support period (0–20% of the gait cycle), and was lowest during the second double-limb support period and early swing phase (50–80% of the gait cycle). For ease of interpretation, the muscles in the model have been grouped for figure 6 into ankle extensors (AE: gastrocnemius, soleus and other plantarflexors), knee extensors (KE: vasti and rectus femoris), hip extensors (HE: glutei, medial hamstrings and biceps femoris longus) and flexors (FL: iliacus, psoas, biceps femoris brevis and dorsiflexors). While this simplifies the presentation of data, it should be recognized that some of these muscles act at more than one joint. Metabolic costs during the first double-support period were dominated by the HE and KE, with small contributions from the AE and FL. During the early portion of the single-limb support period, metabolic costs were incurred by a mix of HE, KE and AE. By the end of single-limb support, the total metabolic power was due almost entirely to the AE. Metabolic costs during the second double-limb support period were due to both the AE and the FL, with FL becoming the only major energy consumer during the first half of the swing phase. During the second half of the swing phase, energy consumption was due to a mix of HE, KE and FL.

Figure 6.

Instantaneous metabolic power for all of the muscles in a single limb across the gait cycle at the preferred stride rate. Heel strike of the ipsilateral limb corresponds to 0 and 100 per cent of the gait cycle. Therefore, during the first double-limb support period shown in this figure, the limb was in the front of the body centre of mass, while for the second double-limb support period, the limb was behind the body centre of mass (see also figure 1). AE (solid line, ankle extensors) is the sum of gastrocnemius, soleus and other plantarflexors; KE (dashed line, knee extensors) is the sum of vasti and rectus femoris; HE (dotted line, hip extensors) is the sum of glutei, medial hamstrings and biceps femoris longus; FL (dash-dotted line, flexors) is the sum of iliacus, psoas, biceps femoris brevis and dorsiflexors; and total (grey line) is the sum of all muscles.

4. Discussion

The primary findings of this simulation study were that leg swing, double-limb support and single-limb support all required a substantial expenditure of metabolic energy. Single-limb support costs were the greatest proportion of the total muscular metabolic cost at all three stride rates. The second largest component at the highest stride rate was double-limb support, but at the lowest stride rate the second largest component was the swing phase. At the preferred stride rate, double-limb support and swing phase costs were nearly the same. These results have implications on our basic understanding of human locomotion, and may also shed light on the recent discourse regarding the relative costs of various intervals of the human gait cycle (Donelan et al. 2002; Neptune et al. 2004; Doke et al. 2005; Gottschall & Kram 2005; Grabowski et al. 2005).

The cost of swinging the leg in walking has recently received much attention in the literature (e.g. Marsh et al. 2004; Doke et al. 2005; Gottschall & Kram 2005). For the current preferred stride rate simulation, the swing phase represented 29 per cent of the total metabolic energy consumed by the lower limb muscles. This is intermediate to the experimental estimates of leg swing cost obtained in humans performing isolated leg swinging (33%, Doke et al. 2005) and in guinea fowl walking on a treadmill (26%, Marsh et al. 2004). However, the present result is greater than predictions derived from torso loading (Griffin et al. 2003) and assisted leg swing (Gottschall & Kram 2005) studies, wherein leg swing costs were estimated to represent about 10–15% of the net cost of walking. The current results are also not consistent with ballistic swing phase models (e.g. Mochon & McMahon 1980), which implicitly assume that swing phase costs are zero. It should be noted, though, that proponents of ballistic swing phase models do not necessarily believe that the swing phase is completely passive with zero metabolic cost. The ballistic swing phase model, as with other ‘simple’ models may still be useful, even if some of its predictions are wrong (which is true of all models, regardless of complexity). Why then, did the swing phase represent a substantial proportion of the total cost of walking? The answer is that certain muscle groups were active and consumed energy during this part of the gait cycle. Energy consumption during the first half of the swing phase was dominated by the FL muscles (figure 6), with the uniarticular hip flexors and ankle dorsiflexors making the largest contributions owing to the timing of their activation (figure 2). During the second half of the swing phase, metabolic energy was consumed mostly by the HE and KE muscles (figure 6), with the biarticular hamstrings and the uniarticular knee extensors making the largest contributions (figure 2). The ankle dorsiflexors muscles also consumed energy during the second half of the swing phase, but at a lesser rate.

Within the stance phase, the relative metabolic costs of the double-limb and single-limb support periods have been a topic of contention (Kuo & Donelan 2009; Neptune et al. 2009). Some have argued that performing transitions between steps is a major determinant of the cost of walking (Donelan et al. 2002), perhaps representing 60–70% of the net cost (Kuo et al. 2005). Others have argued that muscles do considerable work to displace the body centre of mass during the first half of the single-limb support period, which suggests a major cost for this phase as well (Neptune et al. 2004). For the current preferred stride rate simulation, the two double-limb support periods combined represented 27 per cent of the total muscular cost, and the single-limb support period accounted for 44 per cent of the total muscular cost. This indicates that step-to-step transition costs during double-limb support are not the dominant energy-consuming event in the human gait cycle. However, this conclusion is subject to some qualification. Total muscle metabolic power (i.e. instantaneous rate of energy consumption) was indeed highest during the first double-limb support period (figure 6), with the HE and KE muscles expending metabolic energy at a high rate. The reason that double-limb support costs did not represent a greater percentage of the total is that double-limb support is relatively brief (table 1), and metabolic power was actually quite low during the second double-support period (figure 6). It might seem surprising that energy consumption was low during the latter part of the stance phase, which is typically associated with an active ‘push-off’ against the ground. The AE muscles actually do considerable mechanical work during the second double-support period. However, these are among the only muscles exhibiting substantial activation during this interval (figure 2), and they operate with little energy consumption owing to storage and release of elastic energy (Neptune et al. 2008; Sawicki & Ferris 2009). Thus, total muscular cost during the second double-limb support period was actually quite low.

An additional factor that affects the energy accounting is that step-to-step transitions may encompass more than just the double-limb support period (Donelan et al. 2002; Adamczyk & Kuo 2009). This would increase the percentage of total metabolic energy associated with the step-to-step transitions, and decrease the percentage associated with the rise and fall of the body centre of mass during the remainder of single-limb support. If the step-to-step transitions are assumed to begin 4 per cent of the gait cycle before, and extend 4 per cent of the gait cycle beyond the double-limb support periods at the preferred stride rate, then each step-to-step transition would represent 20 per cent of the gait cycle, which is consistent with recent estimates based on mechanical work considerations (Adamczyk & Kuo 2009). Under this scenario, the percentage of the total muscular cost associated with performing step-to-step transitions was increased to 37 per cent. This was nearly equal to the cost associated with what remained of the single-limb support phase, which accounted for 34 per cent of the total muscular cost. Thus, while performing step-to-step transitions are indeed demanding and places a high metabolic strain on the active muscles (figure 6), the relative cost was predicted to be less than other estimates (45–65%) in the literature (Grabowski et al. 2005; Kuo et al. 2005). Based on the present simulation results, total leg muscular energy consumption appears to be distributed across the gait cycle as follows: (i) performing step-to-step transitions account for a little more than one-third of the cost; (ii) controlling the rise and fall of the body centre of mass during the remainder of single-limb support represent about one-third of the cost; and (iii) swinging the leg forward for the next step represents a little less than one-third of the cost.

Changing stride rate at a constant speed affected the relative costs of the stance phase, swing phase and double-limb support, but had only a small effect on single-limb support costs (figure 5). These results can be explained in large part by the effects of stride rate on gait cycle interval durations (table 1), and the activation timing of certain muscles (figure 2). For example, relative double-limb support costs were greater at higher stride rates partly because the double-limb support was a greater percentage of the gait cycle. The two double-limb support periods combined spanned only 18.6 per cent of the gait cycle at the low stride rate (−20% SR) when compared with 29.8 per cent of the gait cycle at the high stride rate (+20% SR). In addition, gastrocnemius activation occurred earlier in the stance phase at higher stride rates, increasing the energy consumed by this muscle during the first double-limb support period. In contrast, relative swing phase costs were greater at lower stride rates due to the swing phase representing a greater proportion of the gait cycle. Swing phase comprised 40.7 per cent of the gait cycle at the low stride rate (−20% SR) when compared with 35.1 per cent of the gait cycle at the high stride rate (+20% SR). Vasti activation also occurred earlier in the swing phase at lower stride rates, which increased its swing phase energy consumption. These results may appear to be at odds with prior reports (Doke et al. 2005) that the cost of swinging the leg increases sharply with the frequency of oscillation. Doke et al. (2005) had subjects swing a single leg in isolation through a fixed amplitude at different frequencies. In contrast, leg swing amplitude is reduced as the stride rate is increased in actual walking. In a later study of isolated leg swinging, where amplitude was varied inversely with frequency (Doke & Kuo 2007), metabolic cost was found to increase with frequency by much less than in the earlier study (Doke et al. 2005). The remaining discrepancies with the current findings are likely owing to the many differences that exist between leg swing in walking and isolated swinging of a single leg. In interpreting the present result, it is also important to recall that they apply only to walking at a single speed with different stride rates and lengths, and may not generalize to other walking conditions where speed, stride rate and/or stride length are varied in other combinations (e.g. Donelan et al. 2002; Neptune et al. 2008; Sawicki & Ferris 2009).

Attributing metabolic costs to the stance and swing phases of walking in living organisms represent a great challenge (Marsh et al. 2004). In contrast, the present modelling approach provided for a precise demarcation between muscle energy consumption in stance versus swing, or double-limb support versus single-limb support, including the ability to easily split the cost for muscles that were active across two or more intervals. While this approach is unambiguous, one could easily argue that it is too simplistic in assigning the energy cost associated with a muscle action to one phase or the other. For example, the work done by gastrocnemius during the latter part of the stance phase has been shown to help propel the limb into the swing phase (Neptune et al. 2001). Therefore, part of the cost of activating this muscle should perhaps be associated with the swing phase, even though most of the energy consumption occurred during the stance phase. Such an approach could potentially change the accounting of stance and swing phase costs, but has the disadvantage of introducing a degree of subjectivity into the analysis. It is also easy to make counter-arguments, such as the energy consumed by muscles near the end of swing phase being associated with establishing the limb position for the subsequent stance phase. Thus, these effects would largely be offsetting, and do not affect the primary conclusions of this study. There were also some discrepancies in the timing of muscle activation (figure 2) that might affect the relative costs of the intervals of the gait cycle. Note that the electromyographic timing information in figure 2 should only be used to make general temporal comparisons with the preferred stride rate activations, as the electromyographic data were drawn from another source (Knutson & Soderberg 1995), and do not account for changes in timing that might occur across stride rates. The greatest timing discrepancy occurred in the biarticular hamstring muscles, with the period of activation in the model extending further into the gait cycle than suggested by the experimental data. This would increase hamstring muscle energy consumption during the stance phase, suggesting that the swing phase relative cost in the model (29% of the total) might actually be a slight underestimate. Regardless, the general concurrence of model and experimental muscle activation timing suggests that the metabolic cost values shown in figure 5 for the various intervals of the gait cycle provide reasonable estimates of the true values in humans during walking.

The present approach to estimating the relative contributions of the stance and swing phases to the metabolic cost of human walking has many advantages over prior experimental (Donelan et al. 2002; Marsh et al. 2004; Doke et al. 2005; Gottschall & Kram 2005; Grabowski et al. 2005) and modelling (Neptune et al. 2004, 2008) studies. Of primary importance is that the instantaneous metabolic power of each muscle was known over the full gait cycle. This allowed the metabolic cost of any interval of the gait cycle to be easily determined. However, outcomes of any modelling study are subject to the strengths and limitations of the underlying model. Thus, the present results should be viewed within the context of the other relevant data in the literature. Of particular importance is the model of muscle energy consumption. The muscle energy model employed in this study has been thoroughly evaluated at varying levels of complexity, and has been shown to provide reasonable estimates of locomotor costs in a range of applications (Umberger et al. 2003, 2006; Nagano et al. 2005; Sellers et al. 2005). The energy consumption predicted by the muscle model has been previously reported to be sensitive to the values assumed for specific tension (Umberger et al. 2003) and percentage of fast twitch muscle fibres (Umberger et al. 2006). In the present application, the primary effect of changing these model parameters was for the predicted energy consumption to increase or decrease quite uniformly across stride rates. Thus, there was no effect on the general trends shown in figures 4 and 5, or on the primary conclusions of this study. While this lends some confidence to the results, there is still a need for additional research using a number of different approaches. Particularly promising is the application of non-invasive techniques for measuring muscle metabolism in vivo, such as near-infrared spectroscopy (Colier et al. 1995; Praagman et al. 2003) and ³¹P-magnetic resonance spectroscopy (Chance et al. 2006; Prompers et al. 2006), which may provide for the development and validation of improved models of muscle energetics. This continued refinement of the modelling approach, combined with innovative experimental protocols, should ultimately lead to a deeper understanding of the determinants of the metabolic cost of walking, and how that cost is distributed across the gait cycle.

5. Conclusions

For a typical walking speed and stride rate, the single-limb support period of the stance phase was found to represent the greatest percentage of the total muscular cost, while double-limb support and the swing phase were found to have similar, but lesser, relative costs. Accounting for the duration of the transitions between steps led to the conclusion that performing step-to-step transitions accounted for a little more than one-third of the net cost of human walking. By comparison, controlling the displacement of the body centre of mass around midstance represented about one-third of the net cost, while the swing phase represented a little less than one-third of the net cost. Stride rate was found to have an effect on the double-limb support and swing phase costs, but not on the single-limb support costs. Varying stride rate at a constant speed changed the relative cost of the double-limb support period and the swing phase, in a manner consistent with changes in the relative durations of these two intervals. This study adds a unique perspective to the growing literature on the determinants of the metabolic cost of human locomotion. However, there is still much to be learned through the application of creative experimental and modelling techniques.