Invertebrate central pattern generator circuits

Abstract

There are now a reasonable number of invertebrate central pattern generator (CPG) circuits described in sufficient detail that a mechanistic explanation of how they work is possible. These small circuits represent the best-understood neural circuits with which to investigate how cell-to-cell synaptic connections and individual channel conductances combine to generate rhythmic and patterned output. In this review, some of the main lessons that have appeared from this analysis are discussed and concrete examples of circuits ranging from single phase to multiple phase patterns are described. While it is clear that the cellular components of any CPG are basically the same, the topology of the circuits have evolved independently to meet the particular motor requirements of each individual organism and only a few general principles of circuit operation have emerged. The principal usefulness of small systems in relation to the brain is to demonstrate in detail how cellular infrastructure can be used to generate rhythmicity and form specialized patterns in a way that may suggest how similar processes might occur in more complex systems. But some of the problems and challenges associated with applying data from invertebrate preparations to the brain are also discussed. Finally, I discuss why it is useful to have well-defined circuits with which to examine various computational models that can be validated experimentally and possibly applied to brain circuits when the details of such circuits become available.

1. Introduction

A rigorous understanding of the mechanisms underlying neural circuit function remains one of the most challenging problems in neuroscience. To study circuit function in the brain would involve characterizing billions of neurons and the trillions of synaptic connections that produce functional neural circuits. This is a long-term but worthwhile goal since it is highly likely that it is only by understanding such neural circuits that we will understand the sensory, cognitive and motor functions the brain performs. Because this is a task that seems overwhelming using the currently available technology, many have suggested that there are other ways to understand such complex interactions without having to get entangled in the weeds of cell and synaptic infrastructure, i.e. by making assumptions about the details. On the other hand, there is an enormous amount of cellular-level data that has not been incorporated into the study of neural circuits simply because there is no way to do so. We have an overload of reductionist data from brain research that is very solid but we do not as yet have the circuitry on which to hang it. This gap between systems and cellular-level knowledge has been written about extensively, but we cannot say that any workable methods to bridge the gap in the vertebrate central nervous system (CNS) have been put forward. Instead, systems biology has gone down a path that suggests this may not even be necessary. Computational neuroscientists have undertaken projects such as modelling one single cortical column (Markram 2006). The idea of building even a small ‘artificial brain’ is popular in the press and suggests that we have already sufficiently bridged the gap in a way that enough of the neural circuitry within a cortical column is known and can be modelled. The danger here is that the search for new technologies to actually describe cortical circuits is arrested (Dudai 2004). We have no idea how many inputs there are entering one cortical column, their nature or their targets. We do not know how many outputs are there or the transfer function between the inputs and the outputs. We do not know what kind of or how many synaptic connections exist between the neurons in the column, etc. One can construct a model in which assumptions are made about these parameters, but nothing informative about how the brain works will emerge, irrespective of how many colours and patterns are displayed by the simulation (even with musical accompaniment).

Although high-resolution data about cell-to-cell connectivity is sparse for brain microcircuits and single neurons can only be identified as a member of a class that can only be penetrated once, the considerable amount of invertebrate data on these subjects is hardly known to brain researchers. While I agree that to understand the brain one must study the brain, there are simply some questions that cannot be answered with contemporary techniques. This is especially true for attempts to fill the gaps in our knowledge between cellular data and systems performance. To ignore critical invertebrate data that can help bridge this gap is a shortcoming of the current efforts in brain research.

To study and to model neural circuits in an experimentally tractable way, invertebrate central pattern generators (CPGs) have proven to be extremely useful. They have not only helped us to define the issues involved, but they have also, because of their favourable experimental features, provided us with about as deep an understanding of neural circuits as we are going to get at the present time. For those whose original goal was not to study invertebrate systems as a model of the brain, but for the pure beauty of being able to explain animal behaviour in terms of nervous system function, the effort devoted to invertebrate CPGs has been successful. To examine the general usefulness of that idea more carefully, it is timely to evaluate whether or not invertebrate systems have also lived up to a parallel promise, helping to understand the vertebrate CNS. And if the answer is not much, then it should be asked whether what we have learned is worthwhile in its own right.

Despite some successes, thus far the application of invertebrate experimental methods to systems with vastly larger numbers of neurons has only been of limited value. For example, in circuits with 9 or 10 neurons, removing one using the photoinactivation technique has immediate and often dramatic effects on the remaining cells. Removal of one cell from a circuit containing thousands of cells will probably have no effect at all. More important however, is that despite the fact that invertebrate circuits use the same cell and molecular components that are found in all nervous systems, the arrangement of these components is uniquely suited to the neuromuscular plant and behaviour of each animal. So, even if different invertebrate circuits are idiosyncratic in their circuit topology and distribution of cellular properties, an understanding of any particular circuit will not have much value for understanding circuits in general. Nevertheless, it may be instructive to examine some of what we have learned from small circuits to see what might be applicable to the modelling of large-scale circuits. Are there particular combinations of ion channels or synaptic arrangements that are present in all CPGs even if the overall circuitry is different? What I would like to demonstrate is that the analysis of invertebrate CPGs illustrates more clearly than any other neural circuits how cell, synaptic and network properties can operate and be understood from the cellular to the behavioural level. I would also like to suggest some general principles such as consistency of circuit elements that apply to CPGs.

2. Some lessons learned from invertebrate circuit analysis

The last 40 years have seen a more or less complete description of several invertebrate CPG circuits. The initial rationale was that once the circuit was known, the mechanisms producing the rhythmic bursts of motor activity would follow in a relatively straightforward manner. In these circuits, where every neuron can be identified and studied repeatedly, we have learned that each uses a unique complement of voltage-gated ion channels to achieve an individual identity and function. Furthermore, each synaptic and electrical connection has individualized dynamical properties. To add further complexity, each ionic conductance, electrical connection and synaptic property can be modified by neuromodulatory substances that are plentiful in all nervous systems so that in the intact animal, we cannot even consider the values of the parameters constant from one day to the next. Nevertheless, if we consider each CPG in its most experimentally simplified condition, we can clearly explain the mechanisms for bursting and pattern formation in many cases. Such ‘canonical’ circuits can be studied in terms of sensory and other control inputs without having to treat the CPG as merely a black box with proscribed but unknown input–output relationships.

One of the principal advantages of small circuit analysis is that cellular conductances, which are easily studied in invertebrate neurons, can be linked to the role played by each neuron in the overall functioning of the circuit. That is, the gap between molecular–cellular data and the output of the circuit can be narrowed.

At a verbal level, we can say that we understand how the circuit oscillates and how bursts that directly or indirectly cause muscles to contract in behaviourally meaningful sequences are produced. To get at a more quantitative description of CPG mechanisms requires modelling. For this effort, it is probably less important to find the correct computational algorithm (there probably is not one), than to determine at what level to model. One of the biggest problems, as I have written previously (Selverston 1980), is that it is not trivial and immensely difficult to describe and predict multiple nonlinear interactions. Therefore, a model must be a representation that captures the nonlinear properties of each neuron and synapse and to do this we must know the properties of each voltage-gated conductance, in particular their activation and inactivation constraints.

Of all the circuits that have been examined thus far, only small invertebrate CPGs have come close to having enough data at the cellular level to model reasonably accurately. In some cases almost all of the cellular and synaptic properties, the network architecture and the nature of the chemical environment, including the effects of neuromodulators have been described. Using this data, computer simulations can be performed without the large number of assumptions necessary for large-scale modelling. We can describe when and why each neuron fires and its effects on other neurons in the circuit, that is, we can explain the source of the rhythm and the formation of the sequential activity. We cannot say however that first principles have emerged, as in the physical sciences, that can serve as the basis for understanding more complex brain circuits and I am not certain that they ever will. It may be timely therefore to assess why this may be the case and what future technological advances may offer.

The attractive features of invertebrate preparations, large cells, restricted numbers, identifiability, suggested to many that a complete deterministic explanation of rhythmic behaviour would be possible. It has been proposed for example that to fully understand a neural circuit, there are basically four problems that have to be solved (Yuste 2008).

• — What cells are involved?—their anatomy, physiology and molecular characteristics.

• — How are the cells connected to one another?

• — What is the computational algorithm they use?

• — How does the circuit behave as a dynamical system?

These terms suggest neurons behave like rigid computer parts and could use a fixed algorithm which of course is questionable.

To these problems I would add:

• — What is the behavioural function of the circuit?

• — What are the inputs and outputs of the circuit?

Can the circuit be isolated from the rest of the nervous system in such a way that its behaviour does not change fundamentally?

An early impetus for the study of invertebrate CPG circuits was that they seemed the most experimentally amenable for serving as a link between neural activity and behaviour. It was also clear that recurrent cyclic movements were more advantageous experimentally than behaviours that occurred once only or episodically. Motor systems also had the advantage of bypassing the question of how sensory information is coded by single neurons and by populations of neurons. How this code is employed by various centres in the CNS and finally decoded into representations that are meaningful to the animal is a much more difficult task than observing repetitive sequences of muscle contractions that underlie a specific rhythmic behaviour. Understanding the link between neural activity and particular behaviours is indeed still the primary goal of many comparative neurophysiologists.

Initially, the most important data for understanding these circuits was to obtain the microstructure by first physiologically identifying the neurons involved and then their synaptic connections. The neural correlates of a behaviour could be determined by recording from muscles or nerves in the intact animal while the behaviour was in progress and then comparing the output of the isolated CNS preparation (the fictive pattern) with the actual behavioural pattern. The general assumption was that by understanding the microscopic arrangement of the components we would understand their macroscopic behaviour. This approach would hopefully lead to the uncovering of the general principles applicable to the behaviour of complex brain circuits as well. It is certainly true that ball-and-stick models, though absolutely necessary, are not sufficient to explain the mechanisms that produce an output pattern because they are incomplete in terms of individual cell and synaptic properties. In this review, I will treat only basic or ‘canonical’ circuits and their outputs. In vivo, each is strongly affected by sensory feedback and by control mechanisms from higher centres or by connections to other CPGs. In addition, neuromodulation plays an important role in altering the functional connectivity of the circuits and therefore their outputs (Harris-Warrick 1988). However, all of the inputs act on the basic canonical circuit, a fundamental understanding of which is therefore indispensable.

3. Isolation of the cpg structure

Early debates about how rhythmic behaviour is produced by the nervous system centred on whether or not cyclic bursts of activity in motor nerves were the result of rhythmic sensory feedback elicited by movement, i.e. reflexes, or generated independent of rhythmic inputs, i.e. produced autonomously. The argument was definitively settled when de-afferentation experiments on locusts by Donald Wilson (Wilson 1961) and others showed all that was required was non-rhythmic activation of an ensemble of neurons that became known as the CPG. As the CPG represented a collection of neurons with a clearly defined function, it was apparent to many neurophysiologists that it could serve as a good preparation for electrophysiological analysis. Large cells, fewer cells and most importantly identifiable cells that could be found and recorded or stimulated in pairs using microelectrodes meant that the detailed circuit of the CPG was potentially discoverable. What were the characteristics of invertebrate systems that made a realistic analysis of CPGs and the behaviours they control possible? A short list would include the following:

• — the ability to find all of the CPG's component neurons;

• — knowing the nature of inputs that the CPG circuit receives;

• — knowing what the output looks like qualitatively and quantitatively and which muscles or effector organs are targeted;

• — mapping the circuitry by being able to stimulate and record from two or more identified neurons repeatedly;

• — being able to see sub-threshold as well as spiking activity.

Chemical synaptic transmission in invertebrates functions generally in the same way as in vertebrates, and in fact it was the easy access to pre- and postsynaptic recording sites that were the main attraction for early electrophysiologists who could not easily study synaptic transmission in the mammalian CNS. Peripheral inhibition of crustacean muscles was for a time one of the best preparations to investigate inhibitory mechanisms. So, it would not be far-fetched to consider invertebrate CPGs as models for vertebrate microcircuits (a term denoting small defined circuits with particular functions). There are differences however. Because invertebrate neuronal numbers are restricted, one neuron may take on the role of several vertebrate neurons. For example, inhibition in the vertebrate CNS is often thought of as a presynaptic property so that inhibitory interneurons have to be inserted into circuits between excitatory neurons and the neuron to be inhibited. We have known for many years that invertebrate neurons can have both excitatory and inhibitory outputs and in some cases both. For most CPGs, the temporal properties such as burst length and frequency must be flexible and modifiable by sensory receptors, inhibitory and excitatory inputs from other centres and by neuromodulators. Because these properties are similar to those of the brain, some suggested that such simple networks might serve as models for complex neural circuits (Welsh & Maynard 1951; Yuste et al. 2005).

The CPG however, should not be considered as an entity separate from the rest of the nervous system. We can think of the CPG as a collection of neurons that produces a fictive motor pattern when properly activated. There is little argument that CPGs form the basis of most rhythmic behaviours in animals (Delcomyn 1980). But in an intact animal, the CPG is simply part of the CNS. Looking at in this way, the CPG's control parameters are constantly modified by sensory feedback, descending fibres from higher centres and the effects of neuromodulatory substances. In the last case, it has been demonstrated that the neurons that are part of one CPG can, under appropriate conditions, be part of a different CPG or engage in motor behaviours separately from those controlled by the CPG. In fact neuromodulators can at least transiently change the functional connections of a CPG circuit in ways that can produce a totally different motor pattern, at least in the laboratory. Attempting to include all of these conditions when analysing a CPG produces a multi-fold increase in the complexity of the system. Adding them later, one at a time or in groups, after the canonical CPG itself has been defined, is a much more tractable experimental plan. It should also be noted that the influence of sensory feedback on various behaviours varies widely, with some behaviours relying almost entirely on sensory reflexes for patterning while others operate ballistically. This is especially true for some escape behaviours that once started are refractive to sensory control.

Of major importance in determining circuitry is the fact that the neurons of invertebrates are often identifiable from one preparation to another so that as the anatomical parameters and physiological characteristics of each neuron are identified, the neuron can be firmly placed within a functional circuit. There are often more than one of each identified cell and for some numerically restricted CPGs, it is possible to determine the exact number of copies for each cell type. Often CPG neurons are large and in some preparations can be found in the same location within the collection of neurons called a ganglion. There are some important differences however, between invertebrate and vertebrate neurons and circuits.

• — The somata of invertebrate neurons are often electrically inexcitable and the density of synaptic receptors on their surface is sparse or entirely absent. This means they often are a poor window into the integrative and spike-initiating parts of the cell.

• — Transmitter release can be graded, that is released in proportion to the degree of presynaptic depolarization rather than pulsatile (following a presynaptic action potential) although both types of release can occur at single terminals.

• — The pattern-forming function and the muscle-signalling function can be performed by the same group of neurons, that is, there is sometimes a complete absence of a premotor interneuron pool whose sole function is to produce the rhythm and the pattern and then trigger the motor neurons.

A few other points to mention when considering the cell identification problem. For a neuron to be considered part of a CPG, it has to actually participate in the formation of the pattern. Often neurons are found in the CNS that are coordinated with the firing pattern but are simply being driven by a CPG neuron. If these cells are removed by inactivation, they have no effect on the output pattern as they simply follow the activity of another cell. A more difficult question is raised when a CPG neuron is receiving rhythmic synaptic input whose source is not known. This suggests that some of the CPG neurons are yet to be found—that is, the circuit is incomplete, one of the most common and vexing problems encountered when identifying component neurons.

Perhaps, the key to unlocking neural circuit function is the ability to determine the precise influence of each neuron on the other neurons. In principle, the post-synaptic response of firing any neuron is measurable and when the circuit is operating, the effect of perturbing any one cell on the pattern can be observed. This phenomena of course can only occur if the circuit is relatively small.

4. What would constitute an ‘understanding’ of a cpg circuit?

A complete understanding would include the ability to explain how spatio-temporal patterns of behaviour are produced by circuits, how they are turned on and off, how they handle inputs from higher centres and sensory receptors, and how they are altered by neuromodulators. Being able to predict the response of a circuit to perturbations such as hyperpolarizing or depolarizing pulses to single neurons would also demonstrate an understanding of the mechanisms involved. To be able to say, we know how the rhythm and spatio-temporal pattern are formed by the circuit, we should know how the connectivity and the biophysics of the cellular and synaptic properties interact. In some cases, we may simply be able to describe these interactions as we do now for a small number of invertebrate CPGs. But since each is unique, the mechanisms involved are idiosyncratic.

One way to demonstrate an understanding of a system is to be able to build either a computer or robotic model of it. If a computational model not only mimics the normal output of a CPG, but is also able to predict the effects of perturbations, we probably understand the system, i.e. a model of the network performs like the biological network and therefore is explanatory (Calabrese & De Schutter 1992). At a deeper level, a more quantitative theoretical model, described as a set of fundamental principles that addresses questions of stability, variability and frequency, or an algorithm for how the computation of the output is produced in a general way would be a laudable goal. All rhythmic CPGs can be approximated mathematically as noisy limit cycles, but the limit cycle for each CPG is unique. The dynamical behaviour of CPGs also varies, with each having a unique orbit and set of bifurcations. So, while it may be possible to fully understand the dynamics of any single CPG, an inclusive theoretical simplification that covers all CPGs does not appear possible.

5. Fundamentals of cpg mechanisms—rhythmogenesis and patterning

Although the detailed analysis of invertebrate CPG circuits has not yielded the rules or general principles originally hoped for, they have demonstrated a wealth of new phenomena that can be useful in understanding the way more complicated circuits operate. These phenomena fall into three broad categories. First, we can consider the number of voltage-gated ionic channels expressed by each neuron, their density and their distribution. By using different combinations of these channels, each neuron defines its own signature profile for how it will behave in isolation and when it is embedded within a circuit. The total number of such channels is not known, but molecular genetic studies suggest that the number is large. If we consider just potassium channels, over 70 have been described thus far (Gutman et al. 2005). In the second category, the kinds of synapses, transmitters and neuromodulators used determine the parameters of cell-to-cell communication. Hundreds of substances have been described that are capable of acting as neurotransmitters or neuromodulators (Kaczmarek & Levitan 1987; Katz 1999). And third, the way the circuit is organized topologically determines the pattern produced in terms of robustness, stability and flexibility. One of the main lessons that can be drawn from invertebrate circuit chasing is that the details of the cell-to-cell connectivity matrix really matter. Connections do not exist as ill-formed or random but are extremely ordered from animal to animal. One can only speculate about how such defined circuits reached their final form, but it would not be unreasonable to suggest that the inhibition provided more stability than excitation and that antagonists were most effectively coupled with reciprocal inhibition. As the duties of the unit CPGs grew, so that instead of only two antagonists there developed a multi-sequential pattern in every cycle, then more neurons would be added. The pattern would be phase-controlled by mixtures of excitation, inhibition, feedback and special conductances that could fine-tune synaptic activity in order to precisely time the firing order of each cell.

We know a great deal about the types of channel proteins available at the molecular level in terms of their activation and inactivation properties. By knowing the details of how they are incorporated into CPG circuits, we can also see how they are used functionally. Despite the large numbers of channels potentially available, not all are expressed or appear to function under normal circumstances. This is also true of the many neuromodulators that have been described. These substances are often identified by immunohistochemistry or other relatively straightforward techniques that show a putative neurotransmitter or modulator is present, but determining under what circumstances it is released or used in vivo is a much more difficult question. Therefore, one cannot say if the description of the many variations of channel types, neuromodulators, etc., represent a triumph of modern technological classification or whether they are all actually used at one time or another during the lifespan of the animal. It is surprising that such questions are not raised even after the 75th potassium channel variant has been identified. In this respect, an understanding of CPG mechanisms may now require only incorporating the most common and robust channels and transmitters/modulators until it is demonstrated precisely just how the others are used.

6. Infrastructure components and modelling

For modelling neural circuits, the level of detail incorporated is crucial. Models can be constructed mathematically based solely on observable phenomena and still replicate many aspects of the behaviour being modelled. However, rigorous validation of the model will often demonstrate flaws in the computation that result from not incorporating sufficient biological detail. On the other hand, the inclusion of parameters which are not germane to the hypothesis being tested wastes computational energy and adds little value to the explanation. While it has been argued that the inclusion of all components into a multi-component system cannot explain macroscopic behaviour (Anderson 1972), the distinctiveness and function of individually identified neurons is tied closely to the kinds, amounts and locations of ion channel proteins they incorporate into their membranes. The direct role played by these channels in neurons making up invertebrate CPGs is now well documented. It is generally accepted that the biophysical parameters play a role in pattern formation that is as great as the elucidation of the circuit itself (Marder 1998; Arshavsky 2003; Toledo-Rodriguez et al. 2008). To understand each neuron's functional properties in a circuit, one can begin by considering each neuron as a tabula rasa to which channel and receptor proteins have been added. One of the primary advantages of working with identifiable neurons is that each has a constellation of proteins that gives them virtually identical properties in every animal. This is remarkable because it means that once the genome and whatever extra genomic directives have programmed the cell, other mechanisms must be able to keep these parameters constant (homeostasis) while allowing for changes in parameters necessary for learning and memory. Invertebrate CPGs do not demonstrate much flexibility of the type that may be related to learning and memory. Therefore, I will not deal with synaptic plasticity (LTP or STDP) or other important processes like development and growth that have to be considered in assessing the function of other parts of the CNS.

Although changes in synaptic function that may be related to learning and memory have not been found, CPG circuits, as discussed earlier, can be transiently affected by neuromodulators. As more infrastructure is added, each neuron assumes a personality that is appropriate to its role as a member of the circuit. Thus, it can burst autonomously or be silent, can fire strongly after it is hyperpolarized, etc. These channel functions can be further modified by neuromodulators making the personality of each cell variable and enabling one circuit to perform many different functions. But again, it is important to point out that although the fictive pattern can be altered by perfusion of neuromodulators, we know little about how this occurs in vivo. The kinetics of voltage-gated currents not only serves as the basis for individual cell function, it provides a good entryway into the pattern-forming process.

7. Voltage-gated channels

Because there has been such spectacular progress in the molecular biology and biophysical analysis of ion channels, the question of why there is so much complexity at this level is a legitimate one. To understand how they so beautifully explain the role of each individual neuron's function is to grasp one of the main successes of invertebrate circuit analysis. A detailed discussion of all known channels is beyond the scope of this paper but a logical clear summary can be found in Harris-Warrick (2002). Some of the more important channels and their currents are:

• — I_Na: A fast sodium current responsible for the depolarizing phase of the action potential.

• — I_K(V): A delayed rectifier current that repolarizes the membrane after a spike and is responsible for after-spike hyperpolarization that can limit the frequency of spiking.

• — I_L: A resting leak current, mostly potassium, which can set the level of threshold activity thus determining whether or not the resting neuron is silent or tonically active.

• — I_A: A large family of transient K currents, and depolarization-activated channels that can be used to delay the onset of bursting or further depolarization.

• — I_H: A hyperpolarization-activated inward current, which can act as a pacemaker current, responsible for the size of postinhibitory rebound (PIR).

• — I_Na(P): A persistent sodium current that keeps the membrane in up state, determines the length of plateau potentials, but can also play the role of a pacemaker in the vertebrate respiratory system (Smith et al. 2000).

8. Non-voltage-activated channels

• — I_K(M): Appears to be controlled by acetylcholine (Ach) in that its maximal conductance is decreased by muscarine.

• — I_K(Ca): A calcium-activated potassium current that can terminate bursts as internal Ca rises as a result of activity; therefore, a self-contained mechanism for burst termination.

• — I_CAN: A calcium-activated non-specific inward current

Ligand-gated channels: These are too many to include here, but glutamate-activated chloride channels and nicotinic potassium channels are common. There are also many examples of co-transmission—two or more transmitters released from the same presynaptic terminal and other cases where a conventional transmitter is released along with a neuromodulatory substance.

9. Synaptic properties

Polarity: generally inhibitory (I) or excitatory (E), but many examples of bimodal synapses (E–I) or (I–E) and even trimodal (E–I–E). The kinetic properties are generally the result of receptor channel properties.

Strength: the effectiveness of the synapse is often too difficult to measure quantitatively because the terminals are distant from the soma where the postsynaptic response is measured, and the resistance of the membrane between these points is unknown. The relative strength can be measured as a function of how effective the presynaptic cell is in terminating postsynaptic firing (if inhibitory) or in activating the postsynaptic cell (if excitatory).

Kinetics of postsynaptic response: the kinetics not only involve both the time course of the transmitter release, binding and release time, but also the direct effects of the transmitter on some channels and the triggering of some channel conductances as a result of the voltage response.

Nonlinear responses: facilitation and depression—in terms of function, these nonlinear changes in synaptic efficacy can play a key role in determining the firing pattern.

Electrical synapses: rectifying or Ohmic—found extensively in invertebrate circuits, these direct connections between cells are generally used to promote synchrony, but there are many examples where more complex interactions ensue.

Graded release: transmitter released as a smooth function of presynaptic terminal depolarization, especially important in oscillatory neurons and non-spiking presynaptic neurons.

10. Basic circuit properties—mechanisms of rhythmogenesis

(a). Intrinsic burst-driven oscillations

Ever since the elegant experiments of Barbara Alving on the completely isolated Aplysia neuron R15 (Alving 1968), we have known that single neurons have intrinsic bursting capability. In Aplysia, the burst-generating mechanisms appear to involve a high resting G_Na and a periodically varying G_K (Carpenter 1973; Smith et al. 1975), but other mechanisms abound. When such neurons are connected to other neurons appropriately, they can drive large networks of non-bursty cells or entrain other burster neurons. If a group of pacemaker neurons are connected with electrical and/or excitatory chemical synapses they will synchronize, forming an extremely reliable and robust CPG that is resistant to timing perturbations.

Intrinsic conductance properties that set frequency and other parameters:

• — Pacemaker potential–intrinsic self-generated potentials;

• — Pacemaker current, I_H, depolarizing current activated by hyperpolarization;

• — Burst length, I_Na-P, plateau potentials;

• — Spike frequency adaptation;

• — Spike threshold level (silent or tonic).

11. Network-driven bursting

• — Mutual excitation: termination by I_K-Ca or accumulated hyperpolarization. Yields in-phase synchronization;

• — Reciprocal inhibition: requires tonically firing cells or tonic excitation. Burst termination by synaptic depression. Yields out-of-phase synchronization;

• — Periodic inhibition of tonic firing;

• — Periodic excitation of silent cells.

12. Mechanisms to adjust phase relationships

• — In-phase synchronization

  1. Ohmic-resistive coupling;
  2. rectifying resistive coupling;
  3. reciprocal excitation.
• — Out-of-phase synchronization

  1. reciprocal inhibition;
  2. periodic inhibition of tonic firing.
• — Delay next phase

  1. increase I_A;
  2. I or E inputs to oscillator at the correct phase in the cycle.
• — Advance next phase

  1. increase I_H;
  2. I or E inputs to oscillator at the correct phase in the cycle.
• — Delay followed by synchronized burst

  • (i)reciprocal inhibition with one depressing synapse and electrical coupling.

• — feed-forward connections, feedback loops;

• — basic engineering control mechanisms for oscillatory circuits.

13. Concrete examples of invertebrate cpg circuits

To illustrate how the components just described are actually used by circuits to produce rhythmic motor patterns, we can briefly survey a few well-studied invertebrate CPGs. We will look only at the basic canonical circuits, independent of rhythmic inputs from sensory receptors. We start with a relatively simple single-phase rhythm, then move on to two- and three-phase patterns and finally describe several with multi-phasic patterns. These are all relatively small circuits where it is possible to study precisely the properties of individual identified neurons and the synaptic topology of their circuits. Given the extensive range of parameters that have evolved, it is interesting that the combinatorial complexity is still rather limited, with many of the circuits using almost identical conductance mechanisms.

14. The cardiac ganglion cpg

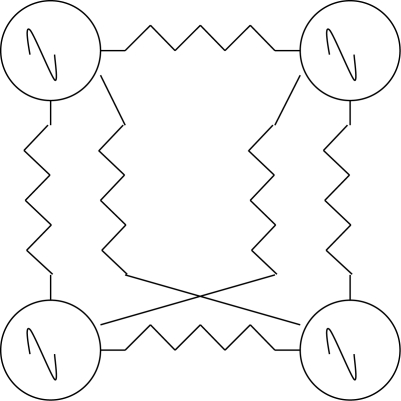
The crustacean cardiac ganglion (CG) delivers rhythmic bursts of action potentials to the heart muscles and is a superb example of a circuit with a grouped pacemaker configuration (Cooke 2002). The cardiac CPG circuit is composed of only four neurons in decapod crustaceans, although this number can be larger in other species (figure 1). These pacemaker neurons are small interneurons and the remaining five larger motor neurons together make up the CPG ensemble. When removed from the animal it will burst robustly for hours.

Figure 1.

Lobster cardiac ganglion. Four neurons with pacemaker properties drive five heart motor neurons. Tildes represent intrinsic burst properties. Resistors represent electrotonic coupling.

Pacemaker potentials originate in the smaller interneurons and their synchronized activity is transmitted to the larger neurons by excitatory synapses and electrical connections. The system, as can be seen in the diagram, is extremely simple and control inputs need only alter the duty cycle or the burst frequency. The ionic basis of the pacemaker potentials is not known but these potentials give rise to burst-forming driver potentials (DP) in the small and large cells. When the large cells are separated from the small cells and voltage clamped, the DP can be shown to consist of an I_Ca carrying inward current and three outward K⁺ currents, I_A, a slowly inactivating I_K and a calcium-activated I_K-Ca (Tazaki & Cooke 1986, 1990). Currents associated with pacemaking in other systems, I_H or the persistent Na current, I_Na-P have surprisingly not been found in large cells.

The presence of similar endogenously bursting neurons has now been found in almost all invertebrate CPGs. In many cases the intrinsically bursting properties are only expressed when neuromodulators are present, the so-called ‘conditional bursters’. It has been suggested that CPGs with such intrinsically bursting neurons were necessary for non-episodic or continuously active behaviours that were less flexible and required redundant fail-safe mechanisms (Getting 1989a,b). If we consider animals that require only two-phase patterns, circuits could evolve that require very few cells. In principle, a circuit in which one pacemaker neuron periodically interrupts another tonically firing neuron can produce alternating activity. The robustness of the output can be enhanced by adding PIR to the inhibited cell. A more common method is to use some form of reciprocal inhibition between two tonically firing neurons but these circuits usually require some form of generalized non-rhythmic excitatory drive. Although reciprocal inhibition is an extremely common form of cell interaction in invertebrate CPGs, it is not usually found to exist in CPGs by itself. More commonly, reciprocal inhibition is embedded into a CPG along with other neurons forming hybrid circuits that are very stable.

15. Tritonia swim circuit—a two-phase rhythm

The escape behaviour of the marine Mollusc Tritonia consists of 5–20 dorsal and ventral rhythmic flexions driven by the output of a well-studied CPG (figure 2). Interneurons in the CPG produce a series of alternating bursts to dorsal and ventral motor neurons (Getting 1989b). The behaviour is a fixed action pattern, i.e. once triggered, it runs to completion ballistically with little or no sensory control. Although there are only two phases to the behaviour, there are three main neuron types in the CPG which was originally described as a three-phase system (Getting 1989b) consisting of reciprocal inhibition with parallel delayed excitation. As with all CPGs, the pattern is a result of synaptic circuitry, properties of individual synapses and the biophysical properties of each cell. Getting had originally claimed that there were no intrinsic bursters in the circuit and that removal of any one cell type stopped the production of the pattern (Getting 1989a) but this idea has recently undergone revision (Katz et al. 2004). Because this CPG had no burster cells it was considered to be a true network oscillator whose mechanism could be understood by breaking it down into three phases (see figure 2):

• — When DSI starts to burst as a result of sensory and trigger neuron excitation the C2 and VSI neurons are silent. The DSIs excite themselves and C2 but because C2 has a high threshold it takes 1–4 s to start firing;

• — C2 starts to fire and re-excites DSI which keeps firing. It begins to depolarize VSI but this is delayed by the activation of an A current;

• — When VSI starts to fire, it terminates the DSI burst and C2 is also eventually inhibited. When VSI stops, the cycle repeats.

So although the reciprocal inhibition could in principle produce alternate flexions and extensions of the body, the third neuron (C2) inserts a particular delay that fine tunes the DSI–VSI antagonism in a way that promotes a more effective escape behaviour. It is likely that the circuit evolved in a way that took the neuromuscular plant and the effectiveness of the escape into consideration. However, recent work has provided a cautionary note to this analysis. Despite the fact that all of the known CPG neurons are necessary for the existence of the motor pattern, individual perturbations of any neuron are incapable of altering the periodicity of the output (Katz et al. 2004). Changes in synaptic dynamics as a result of G-protein signalling may also play a role in producing the pattern (Clemens & Katz 2003).

Figure 2.

Tritonia CPG. Symbols: dots, inhibitory synapses; triangles, excitatory synapses. DSI, dorsal swim interneuron; VS, ventral swim interneuron; C2 interneuron.

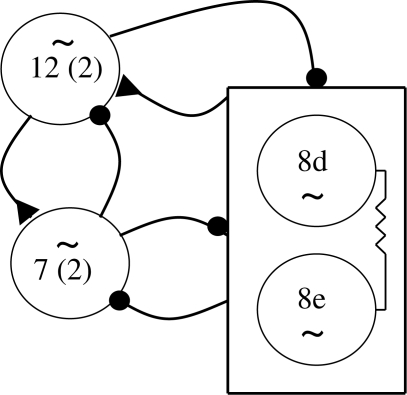
16. clione—a two-phase hybrid generator

Another two-phase CPG is found in the pteropod mollusc Clione limacine, the ‘sea angel’ (figure 3). Like Tritonia, two groups of premotor interneurons, type 7 and type 8, are connected by reciprocal inhibitory synapses and this circuit arrangement along with strong PIR excites the motor neurons that subsequently drive alternating dorsal and ventral movements of the wings (Arshavsky et al. 1985; Satterlie 1985). During slow wingbeat frequencies, these two groups are sufficient to drive the wings, however during higher frequencies, a third pair of neurons termed type 12 (figure 3) with strong plateau potentials are recruited so that as in Tritonia, three groups of neurons are involved in producing a two-phase rhythm. In this case, the function of the third group is to shorten the activation cycle of the ventral phase interneurons and to simultaneously excite the dorsal phase interneurons, the net effect being a shortening of the cycle time so that faster frequencies are possible. While the details of the individual cell conductances are not known for this CPG, it has been shown by transmitter blocking that they all have endogenous bursting properties represented by the tildes in the figure. This circuit therefore represents a third category of CPG structure.

• — In the first case, the cardiac ganglion, bursting was entirely a result of endogenous currents.

• — In the second case, Tritonia, no endogenously bursting neurons were found and the bursts were an emergent property of the network.

• — In Clione, we see the bursting mechanism assume a hybrid structure with both cell and network properties contributing to the rhythmogenic and pattern-formation function.

This theme is one that is widely emulated by other invertebrate CPGs.

Figure 3.

Swimming CPG in Clione limacine uses a mix of mostly inhibitory synapses (dots) and intrinsic burst-generating mechanisms. Resistors are electrical coupling. Triangle, excitatory chemical synapse.

17. lymnaea—a three-phase hybrid pattern

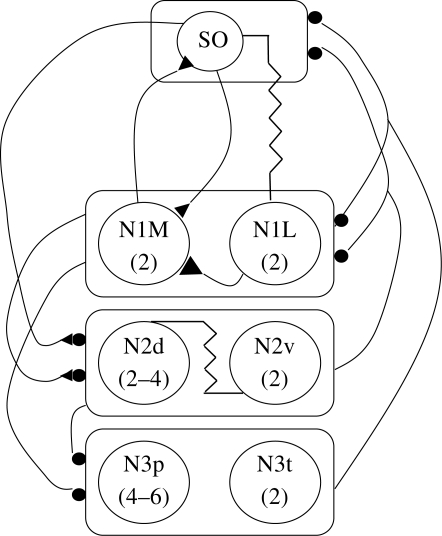
When we move to a consideration of CPGs that produce more than two phases of activity, the level of complexity and the analysis of the mechanisms involved can rise dramatically. For example, in the pond snail Lymnaea, the feeding CPG produces a three-phase rhythm that controls the protraction, rasp and swallowing phases of the feeding apparatus behaviour (figure 4).

Figure 4.

Lymnaea feeding CPG. Diagram showing known connections between SO, a modulatory feeding interneuron and the various CPG interneurons. Symbols as in previous figures (see text for details).

There are apparently only three groups of neurons making up the CPG, although this is based mainly on the observation of when they fire during the feeding cycle and in fact each of the three groups can be subdivided.

The CPG comprises the following neurons:

• — protraction phase: N1M and N1L;

• — rasp phase: N2d and N2v;

• — swallow phase: N3p and N3t.

The feeding cycle is activated when chemosensory neurons in the lips are activated and trigger a modulatory neuron called the slow oscillator (SO) and a protractor neuron N1M. Although N1s were originally thought to be endogenous bursters (Benjamin & Elliott 1989), more recent work on cultured neurons seems to suggests that N1M instead possesses endogenous plateau potential properties triggered by the depolarization from the SO input and excitation from N1L (Straub et al. 2002). The mechanism producing the feeding sequence is as follows:

• — When the N1s fire they initially inhibit and subsequently excite N2v, which triggers plateau potentials in N2v and N2d since they are electrically coupled to one another. This type of dual inhibitory–excitatory action is another form of synaptic interaction that is quite common in invertebrate synapses.

• — The activation of the N2s terminates the plateau potentials in the N1s and the SO since they are connected with reciprocal inhibitory synapses. The N2v plateau potential appears to terminate spontaneously and when this occurs it releases N3t and N3p from inhibition.

• — Because N3t has a large endogenous PIR current it fires strongly and recruits N3p via electrotonic connections with swallowing motor neurons. Inhibition from the N3s to the N1s acts to delay their recovery from N2 inhibition and when the N3s stop, a new cycle can begin.

So although the temporal firing sequences of the feeding CPG can be more or less described, many details of the actual mechanisms involved are not clear. The origin of the rhythm does not seem attributable to any single feature of the synaptic organization except possibly the reciprocal inhibition. Firing of the swallowing interneurons is simply the release of tonically firing cells from inhibition and the incorporation of PIR to strengthen the bursts. This circuit thus represents a pattern that truly ‘emerges’ from the network, its synaptic properties and two very important cellular phenomena—plateauing and PIR.

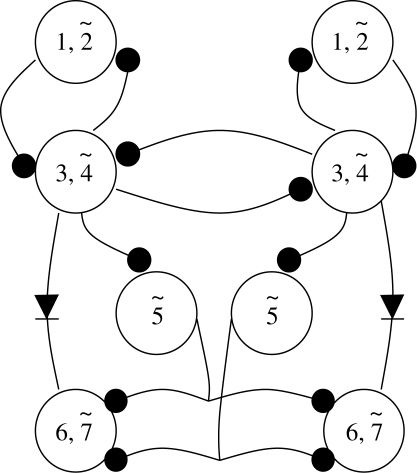
18. Leech heart cpg—a multi-phase multi-segment hybrid generator

Even more complex circuitry is found between the interneurons forming the leech heart CPG (figure 5). Like our own heart muscle, leech heart muscle has its own intrinsic rhythm, i.e. it is myogenic, but requires timed and patterned neural activity to function normally. The muscle surrounds two longitudinal heart tubes that are innervated by segmental ganglia along most of the animal's length. Instead of contracting synchronously like the crustacean heart, the heart tube on each side switches back and forth every 20–50 cycles from a peristaltic mode to a synchronous mode. The job of the CPG is to coordinate all of these activities.

Figure 5.

Leech heartbeat neuronal network. The numbers represent the segments in which the HN cell bodies are located, i.e. there is a left and right 1, 2, etc. Symbols as given previously.

Two kinds of neuron are used; the motor neurons (HE) that entrain the heart muscle but play no role in timing, and interneurons (HN) that make up the CPG. The timing derives from two pairs of HNs in ganglia 3 and 4 that are connected by reciprocal inhibition. As we have seen previously, this fundamental circuit can produce alternating bursts, but as we have also seen, this mechanism can be made more robust and regular if the neurons are also intrinsic bursters as they are in this case (Cymbalyuk et al. 2002). Two pairs of neurons in the first two ganglia (HN1 and HN2), make reciprocal inhibitory connections with HN3 and HN4 on each side and together all four pairs make up the timing network for the whole system. It should be immediately obvious that trying to determine the output of the circuit is not straightforward and is made even more complex by HN neurons in the fifth to the seventh ganglia that make up a ‘switching network’ that controls which heart tube is contracting in a peristaltic wave and which is contracting uniformly. The output of ganglia three to seven inhibits the tonically firing HE neurons in a way that can accomplish this. The currents underlying the bursting have been shown by voltage clamp experiments to consist of a fast I_Na for spikes, two low-threshold I_Cas, one with rapid and the other with slow inactivation times, an I_A, a persistent and a delayed rectifier type current, I_H, I_Na-P and a mixed Na⁺/K⁺ current (Kristan et al. 2005).

The exclusively inhibitory interactions between the timing interneurons are mediated via these currents. A graded inhibitory component is mediated by low threshold Ca⁺⁺ currents (Angstadt & Calabrese 1991) and a spike-mediated component carried by the high-threshold Ca⁺⁺ current (Ivanov & Calabrese 2000). Because the spike- mediated transmission continues during the burst and the low threshold currents are inactivated, modelling studies have shown that the reciprocal inhibition uses both escape and release (Rinzel & Ermentrout 1989) to sustain bursting. The escape is due to the slow activation of I_h and the release to the slow inactivation of the slowly inactivating I_Ca in the bursting neuron. The modelling studies also indicated that I_h could play a key role in regulating the cycle period by negative feedback. Anything that produced a longer cycle period increases I_h thus shortening the period and anything that shortened the period did the opposite.

The HN interneurons in ganglia 1 and 2 play an interesting coordinating role for the timing network. They do not activate the motor neurons but instead have their integrative components in the third and fourth ganglia where they form reciprocal inhibitory connections with HN3 and HN4. This allows them to couple the primary oscillators on each side together since they are otherwise independent.

The three other pairs of neurons, HN5–HN7, are part of the CPG and are also quite interesting in that HN5 can act as a switch for the two metastable states of the heart tubes while HN6 and HN7 are premotor and receive bilateral inhibitory input from both HN5 neurons. Although the exact mechanism is unknown, each HN5 will switch from an active to a totally silent state and this results in alternate peristaltic or synchronized behaviour of the heart tubes.

19. aplysia feeding—multi-phase switching behaviour

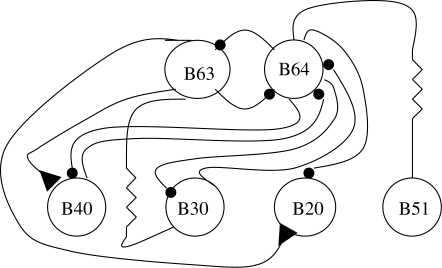
We have seen that by simple switching of the activity state in one neuron of the leech CPG, two separate behaviours can be generated. In the leech it has not yet been determined how this switching occurs except to say that it is probably owing to an input extrinsic to the CPG circuit. A somewhat more complicated form of behavioural switching can be found in the feeding behaviour of Aplysia (figure 6). It has been known for some time that the behaviour can be divided into at least three functionally different forms—biting, swallowing and rejection (Kupfermann 1974). These behaviours can be elicited by stimulating one of the two higher-order neurons, CBI-2 or CBI-4 (Jing et al. 2004). The main kernel of the CPG is made of two neurons, B63 and B64, connected together with reciprocal inhibitory synapses (Jing et al. 2004). Depending on which other neurons B40, B30 or B20 (all of those excite B8 the closer motor neuron) are involved, one of the three types of behaviour will be produced. If CBI-2 is stimulated, and B63 and B40 are activated, biting behaviour will be produced. If CBI-4 is stimulated, B63 and B30 are activated and swallowing will occur. And if both CBI-2 and CBI-4 are stimulated, B63 and B20 will fire and a rejection-like behaviour will ensue. The stimulation pattern can ‘code’ what are called behaviour-specific modules (B20, B30 and B40) to obtain an entirely different behaviour using the same groups of muscles, i.e. those controlling protraction, retraction and closure of the radula. Basically, there are only three phases of activity involved and it is the relative amount of time spent in each phase that determines what behaviour is produced.

Figure 6.

Aplysia feeding CPG circuit is capable of encoding three separate behaviour-specific modules. All symbols as previously described. Higher order neurons (not shown) can produce different cyclic behaviours depending upon which CPG interneurons receive excitatory input.

20. The stomatogastric ganglion—two rhythms with 11 phases

Two CPGs in the stomatogastric ganglion of crustaceans are arguably the most fully described neural circuits available (figure 7) and they are an excellent example of how the analysis of small systems has contributed to the study of the vertebrate CNS. There are two CPGs present in the ganglion, the pyloric and the gastric. The pyloric controls the operation of a filtering apparatus at the back of the stomach and the gastric that controls a set of three ‘teeth’ in the gastric mill portion. Unlike the muscles in the leech heart wall, the muscles are striated and require patterned input from the CNS in order to contract in the proper sequence. The behaviours per se are probably of interest to no more than a handful of zoologists around the world. Their usefulness lies largely in the fact that they possess exceptionally favourable experimental characteristics. The pyloric system is composed of 14 neurons that are connected with inhibitory and electrotonic synapses into a circuit whose topology has been known for over 30 years (Maynard & Selverston 1975). All of the neurons are conditional bursters (Nagy & Miller 1987; Bal et al. 1988), i.e. they have intrinsic bursting properties that are expressed when exposed to the neuromodulators which are normally present. This means that the system, which produces a five-phase motor rhythm at about 2 Hz can be treated as a network of coupled oscillators whose rhythm derives from the intrinsic properties of the neurons and whose spatio-temporal pattern is an emergent property of the network. Unlike some of the previous examples, the pyloric neurons are not only responsible for the rhythmic pattern but with the exception of one interneuron, also act as motor neurons for the pyloric musculature.

Figure 7.

(a) Pyloric and (b) gastric CPG circuits that comprise the lobster stomatogastric nervous system. Symbols as described previously except for diodes that represent rectifying electrotonic connections. The rectangles shown in some of the gastric synaptic connections represent delay lines between spikes in the presynaptic neurons and the postsynaptic excitatory response.

The gastric CPG comprises 11 neurons, one of which is an interneuron and the rest are motor neurons, sending axons to the gastric mill muscles as well as being part of the CPG. Note that in this system, pyloric and gastric cells are alike, i.e. most of the CPG neurons play a dual role, inhibitory within the ganglion and excitatory in the periphery. The overall rhythm is much slower than the pyloric rhythm, about 0.1 Hz in vitro. Some of the gastric neurons are intrinsic bursters while others fire tonically when isolated. The complex pattern of synaptic connectivity as well the properties of individual neurons contribute to the formation of a six-phase motor pattern. Although the two circuits control different parts of the stomach musculature, they are linked together synaptically by connections within the ganglion and by feedback loops from neurons with an efference copy function embedded in each CPG circuit that modulate cells in the paired commissural ganglia surrounding the oesophagus. These neurons provide patterned excitation to both gastric and pyloric circuits. Why the two circuits, each with a different frequency, are connected is not known. Both circuits employ many of the cellular and synaptic features that have already been discussed. In addition, both are heavily influenced by sensory feedback and command fibres. However, here, I want to treat the circuits as isolated but connected to the more anterior paired commissural ganglia. Under such conditions, both CPGs produce robust and regular canonical bursting patterns. As such, they form the basis for further studies concerning neuromodulation, sensory input, etc., but without having a complete description of the basic system, it would be difficult to analyse the role of these other inputs.

The pyloric rhythm frequency is determined by the fastest of the bursting neurons, the AB, which by virtue of its strong electrotonic connections to the two PDs, forms a pacemaking unit for the entire rhythm. The pattern is formed quite simply by simultaneously inhibiting all of the other neurons, especially the LP and the eight PY neurons. The LP neuron escapes from the inhibition first followed by the PYs, thus forming a basic three-phase pattern that produces a pumping action in the pyloric region of the stomach. The mechanisms by which the phasing of the LP and PYs is achieved is illustrative of how particular conductances (e.g. strong differences in the amount of their A-currents) can be used effectively in the patterning process. Despite the fact that AB and PD use different transmitters, their synaptic effects on LP and PY are the same (Rabbah & Nadim 2007). However, the larger the size of the IPSP the earlier the LP burst phase, which would be consistent with the presence of I_H. This current is prominent in the LP neuron and has been shown to be responsible for advancing the LP burst phase following hyperpolarization (Harris-Warrick et al. 1995). On the other hand, an increase in the size of the IPSP in the PY cells appears to delay the burst phase in an ongoing rhythm suggesting that the increased hyperpolarization removes the inactivation of I_A leading to its greater expression when the cell depolarizes. Together, these two currents could account for the difference in recovery times following AB/PD inhibition.

Two other pyloric neurons that have less well-defined actions are the VD and IC. Both are also inhibited by the PD-AB group and their burst timing is determined by their connections with other neurons in the CPG. If we include these two neurons, the pyloric CPG produces a five-phase rhythm.

The gastric mill CPG also uses a blend of intrinsic bursting and synaptic connections to produce a six-phase rhythm. There are three calcified ossicles in the gastric mill which act as teeth and open and close in a manner resembling chewing (Heinzel 1988). There are two lateral teeth controlled by the LG, MG and LPG neurons and one medial tooth controlled by the DG, AM and GM neurons. The single interneuron, Int 1, is shared by each subset of medial and lateral teeth motor neurons. The GMs and LPGs fire tonically when the mill is not operating thus holding the lateral teeth in an open position and the medial tooth forward and out of the way so that food can be squeezed into the gastric mill from where it is being stored in the cardiac sac (there is a separate CPG in the other ganglia for this behaviour). The chewing pattern consists of 3 s bursts at a frequency of about 0.1 Hz. The LG and MG fire slightly out-of-phase causing the lateral teeth to close followed by a resetting of the medial tooth by the DG and AM neurons. As the food is held by the closed lateral teeth, the four GM neurons fire, pulling the serrated surface of the medial tooth over the food. This cycle is then repeated. The overall coordination of both subsets is because of Int 1, which entrains spontaneous bursts in DG and AM while simultaneously inhibiting the tonic activity in the GMs. Int 1 first inhibits and then excites the LG and MG neurons (Selverston et al. 2009) and both of these inhibit the LPGs.

The circuit of each subset is quite different. The medial tooth subset has weak feedback loops and appears to be an almost pure feed-forward system, i.e. a delayed excitation from Int 1 to the DG/AM pair and simultaneous fast inhibition to the four GM neurons. The lateral teeth subset, however, is made up of two reciprocal inhibitory loops between Int 1 and the LG/MG pair and between the LG/MG pair and the LPGs. These feedback control loops can also exert some control back onto the medial tooth subset via Int 1 and an inhibitory synapse from MG to DG. A third set of reciprocal-inhibitory connections exists between MG and LG that are also linked by an electronic connection. This set of connections appears to be responsible for the small phase difference between LG and MG.

Another set of connections is present to synchronize the activity of the pyloric and gastric mill regions (Mulloney 1977). It is not immediately apparent why direct and indirect connections between the two CPGs are necessary, but it is possible to speculate that since the gastric mill empties directly into the pylorus, there may be some benefit in synchronizing the two rhythms. From a theoretical point of view however the fact that they are connected provides an experimentally tractable system for studying how oscillators with different frequencies can interact, a phenomenon that is widespread in the brain.

These examples of small networks are not exhaustive but they nevertheless are illustrative of the current state-of-the-art in the analysis of small circuits. There is a good deal more known about each of them than I have space to go into here. Nevertheless, we can first of all see that they all share many of the same elemental building blocks, but each is assembled in a unique way to perform a unique task. One fallacy that exists for the analysis of neural circuits is that a reductionist description of the components, a parts list, will lead to understanding of the operation of the system as a whole (Dudai 2004). Studying simple systems can in fact produce a very good parts list, but understanding how these are used to compute a motor pattern, i.e. what algorithm is used, is not always clear. Modelling small systems can at least compute how the many nonlinear interactions yield the correct pattern and begin to answer questions about frequency, burst length and other parameters that result from a circuits connectivity and cellular properties. At least for motor systems, the linkage between the CNS and the neuromuscular plant is, if not direct, easily accessible. Contrast this with what sensory receptor systems must represent to higher processing centres. How the total pattern of neural activity used to represent an object in the visual field is coded, bound together and computed is not known. The experimental fact that one can obtain only small samples of this activity during the acquisition of a sensory percept and that knowledge of the circuitry involved is minimal have nevertheless not prevented the modelling of complex sensory systems.

The systems I have discussed can all be understood at a fundamental level in terms of interactions between neurons. To get to this level of analysis would be a huge achievement for a brain microcircuit. Most of the systems I have discussed have been modelled and the models are able to reach the next level of understanding, the ability to predict the outcome of perturbations. In some cases single neurons have been removed from the circuit and replaced with electronic neurons that are able to rescue the pattern satisfactorily. This actually represents a high-level understanding of the system. Will it be possible to go even deeper, i.e. find a set of simplified equations that can generate a spatio-temporal time series for the neurons of a generalized CPG under different experimental conditions like the Hodgkin–Huxley equations do for the action potential? Probably not. The interactions of the few conductances underlying the action potential are much less complex than the many conductances that are operative during CPG activity.

21. How does functional circuit reorganization by neuromodulators affect the analysis?

The invertebrate circuits I have described are in their most elemental form. In some cases, the presence of neuromodulators or neurotransmitter analogues are necessary for the CPGs to produce robust fictive patterns. These agents either initiate bursting in particular cells or act globally on the entire circuitry. In so doing, the extent to which they have altered the normal output of the CPG can be determined by comparing the parameters of the in vitro ‘fictive’ pattern with the pattern observed in the intact animal. In general, the patterns are comparable except for the increased variability usually seen in vivo that results from sensory feedback. Some exogenously applied neuromodulatory substances can substantially alter CPG patterns in a consistently reliable manner. We know the actions of both intrinsic and extrinsic modulations are to functionally rewire CPG connectivity by changing synaptic strengths as well as alter the biophysical properties of individual cells (Harris-Warrick 1988). Immunohistochemistry has shown that these substances are present within or in close proximity to the CPG plant (Marder 1989). What is less well understood are the mechanisms controlling the release of these modulators or even if they are actually used by the animal during its normal activities. A strong case can be made that such small systems are ‘overmodulated’, but until we know more about how they are released in intact animals, we can only speculate. Since the actions of neuromodulators can fundamentally change spatio-temporal patterns and therefore behaviours, they obviously play an important part in trying to understand CPG mechanisms. A great deal of information has been obtained in terms of how neuromodulators function at the cellular level and this database has been applied to the identifiable neurons in small systems to great advantage. For example, if dopamine is applied to the pyloric CPG, each identifiable neuron in the circuit changes and the important conductance parameters in each cell can be determined (Harris-Warrick et al. 1998). I_A in AB, IC, LP and PY decreases but in the PDs it goes up. I_Ca in PD and VD goes down but in the IC, LP and the PY cells it goes up, etc. In some cells the action of modulators is excitatory and in others inhibitory (see a nice summary in Nusbaum & Beenhakker 2002). The G protein pathways for the action of these substances therefore must be different in terms of receptors and second messenger cascades. This has been demonstrated directly by a technique that allows visualization of changes in the c-AMP concentration of individually identified pyloric neurons (Hempel et al. 1996). It also makes it highly unlikely that individual neurons can use different conductance ratios in order to achieve equivalent biophysical properties. If this were true, each neuromodulator would produce different effects on each cell and the kind of pattern associated with a particular modulator would differ. This has not been shown to be the case by selectively blocking I_A in the same identified neurons taken from many different animals. If the amount of I_A varied, then blocking this channel alone would produce different burst patterns but they in fact show no statistical difference (Nowotny et al. 2007).

Work on the stomatogastric ganglion has shown that the effects of neuromodulators on the basic circuitry are substantial, effectively rewiring the circuit and leading to the generation of different patterns (Dickinson & Moulins 1992). Most of this work has been done by applying neuromodulators exogenously or by stimulating nerves known to contain neuromodulatory substances. In vitro preparations were generally used so that the precise loci of the changes to the synapses and neurons could be determined.

While it is not certain how many neuromodulators are actually used in a freely behaving animal, it is clear that their ability to drastically change the properties of a circuit means that a detailed knowledge of circuit anatomy is not of much value in determining functional mechanisms. The circuit is ‘rewired’ not in an anatomical sense, but mostly by weakening or strengthening synaptic connections. If a synapse is so weak it no longer transmits information from one cell to another; it essentially disappears functionally but not anatomically. The stomatogastric ganglion that contains a total of only about 30 neurons, has in the order of one million synaptic contacts within its neuropil, so it is likely that each functional synapse is represented anatomically by hundreds of discrete anatomical contacts. It has also been shown that the so-called silent synapses do not differ anatomically from those that are functioning normally (Atwood & Wojtowicz 1999). It remains to be seen if and when clear functional–anatomical studies of identified synapses in the brain are available, similar observations exist. But in interpreting the massive database that will result from such ambitious anatomical studies that are either planned or already underway and that have been touted as a route to unravelling brain circuits, functional studies should be complementary and of equal importance and not suggested only as an afterthought.

22. Small systems and understanding large-scale networks

The small networks of invertebrates have obvious experimental advantages that allow an in-depth analysis that would be impossible in the brain. Transferring what has been learned at the cellular level to more complex systems is relatively straightforward. Single-cell conductances and phenomena such as plateauing or PIR are likely to be the same in both small and large systems and much of what initially has been discovered at the cellular level in small systems has been useful to vertebrate brain research. While operational circuits have been fully or nearly fully described for many invertebrates, no such circuits have been described in vertebrates. We know the computational goal of invertebrate CPGs as well as vertebrate CPGs. But we cannot say that the computational algorithms are the same because we do not know what these are in either case. We can do a better job of modelling small systems because we know more about cell-to-cell connectivity and the properties of individual cells and synapses. But, despite the lack of vertebrate CPG detail, there are still many attempts to model them based on statistical sampling of the data. The question is that since we have to start somewhere, are large-scale models able to provide databases that could be expanded as we acquire more information? It is fair to ask that if assumptions have to be made about virtually all parameters of a complex CPG circuit, what is the explanatory value of the model even if it can replicate some aspects of the CPG output? In many large-scale models, neuronal properties are usually alike and synapses are modelled as excitatory or inhibitory without further elaboration. Most egregious however are assumptions about connectivity that are entirely fabricated. An argument could be made for such an approach if all synapse and cell types were equivalent biophysically and their synaptic connections were ill-defined. Even under these circumstances, it is not clear that a model of the cellular interactions could lead to a simulation of macroscopic behaviour. The emergent behaviour of networks that have uniform rules governing the interactions between elements can produce surprising behaviour that in some cases cannot be formally calculated (Binder 2009). If this is the case for homogeneous systems, how would it be possible to develop formal algorithms for networks in which not only is each element or finite group of elements different but the rules that govern their interactions are also different and even time-variant.

23. Some comments on the use of computer modelling

In any system with thousands of moving parts, a verbal description of the system's behaviour over time is impossible. Modelling such systems is a more rigorous way to explain the operation of the interactions. But it is important to keep in mind that a model is only a representation of the biological system. How accurately a model duplicates the biological system depends upon which parameters are incorporated into the model and how accurate the parameter values are. There are many additional questions that arise when constructing a mathematical model that can be implemented with a computer including the level and the structural accuracy (Webb 2001). Models, even with inadequate data and coarse-grain resolution, can simulate circuit function. But this does not imply at all that this is the way the biological system computes, i.e. a computer simulation cannot mimic biology without incorporating biological data. One should be extremely cautious about accepting as biological fact the results of computational analysis based on imaginary data. Furthermore, there are clear limits to reductionism. It is simply not possible to fully understand how a small circuit operates based on observation and intuition even if all parameters are known and assigned values. By understanding, we can simply mean the ability to predict the output of a CPG in terms of all measurable quantities following some specific input or perturbation. I believe we are close to being able to do that now for many of the small systems I have described both computationally and with straightforward verbal descriptions. But how will this ability scale up to very large systems without having to make assumptions about parameters not currently available experimentally or the possibility of obtaining them in the future? Some of the assumptions can be based on statistical sampling so they may not be completely determined intuitively. But sampling systems of unknown degrees of heterogeneity cannot produce reliable results. Sampling 100 cortical interneurons will provide a mean level of different conductances, but the standard deviation will be very large. This means we cannot use 100 model neurons with the same biophysical properties in the model because in actuality all of these parameters can vary over a wide range. What may turn out to be a far more difficult problem for modelling large systems is the inability to validate the simulated input and output patterns with experimental data. In the case of vertebrate CPGs, it should be possible to make some meaningful comparative studies between real and simulated motor output patterns (Grillner et al. 2007). However, there is no way I am aware of that similar comparisons can be made for non-motor areas of the brain.

The value of invertebrate work to those studying the brain is to show that every well-studied CPG uses essentially the same available building blocks to construct idiosyncratic circuits that have evolved along with the rest of the animal. This at least provides real-world knowledge that can be carried over to large systems in terms of what combinations of parameters have proven effective for particular tasks. But a realistic detailed analysis of brain circuits is still a long way off. The knowledge gained from the analysis of invertebrate CPGs might turn out to be more useful in robotic design than as a template for the brain. Robots that could mimic invertebrate locomotion and are constructed based on biological principles would be a feasible goal and are already being built.

24. Conclusions

Clearly the kind of experimental data obtained from small CPG circuits has produced a level of understanding far different from what we can expect to achieve for brain circuits. Since we know the infrastructure fairly completely in a number of cases, it is possible to explain verbally how these systems work in their simplest configuration, that is, without any more inputs than are sufficient to produce their basic rhythmic pattern. Furthermore, we can use this information to generate mathematical models which, when simulated, capture not only the features of the basic preparation but also responses to perturbations either experimentally induced or via natural pathways. In many cases, the models provide the deeper understanding for which we were originally searching. What the analysis of several small circuits has shown is that there are not many rules for how circuits have evolved and that all circuits investigated thus far use various combinations of cell and synaptic properties to construct individualized circuitry that parallels the evolved neuromuscular system unique to each animal. How could it be otherwise? While further progress in the study of small circuits will occur using standard neurophysiological techniques, it may play a greater role as a test bed for new methods that can be more easily applied to larger systems. But a further exposition of new invertebrate circuits will only be of interest for comparative studies that are valuable in their own right but will demonstrate a nearly endless combination of CPG components. Nevertheless, it should be clear that the basic building blocks of small systems are the same as for large systems and at lower hierarchical levels, information about mechanisms can and has been transferred usefully.

One definition of understanding something is that it is no longer necessary to ask more questions. We have come close to achieving that state as far as basic invertebrate CPG circuit mechanisms are concerned. While we have plenty to learn about the control of CPGs, there are few, if any, questions still being asked about their basic mechanisms. What remains to be understood is precisely how neuromodulators, sensory feedback and descending commands affect the canonical circuits. As a result, few new invertebrate CPGs are being brought forward to be explored. We may have seen the era of invertebrate circuit chasing come and go and it will require major new technological improvements before further new insights can be made. Right now, the analysis of additional circuits with current techniques would simply demonstrate the enormous diversity of CPG circuits in nature.