Potassium diffusive coupling in neural networks

Abstract

Conventional neural networks are characterized by many neurons coupled together through synapses. The activity, synchronization, plasticity and excitability of the network are then controlled by its synaptic connectivity. Neurons are surrounded by an extracellular space whereby fluctuations in specific ionic concentration can modulate neuronal excitability. Extracellular concentrations of potassium ([K⁺]_o) can generate neuronal hyperexcitability. Yet, after many years of research, it is still unknown whether an elevation of potassium is the cause or the result of the generation, propagation and synchronization of epileptiform activity. An elevation of potassium in neural tissue can be characterized by dispersion (global elevation of potassium) and lateral diffusion (local spatial gradients). Both experimental and computational studies have shown that lateral diffusion is involved in the generation and the propagation of neural activity in diffusively coupled networks. Therefore, diffusion-based coupling by potassium can play an important role in neural networks and it is reviewed in four sections. Section 2 shows that potassium diffusion is responsible for the synchronization of activity across a mechanical cut in the tissue. A computer model of diffusive coupling shows that potassium diffusion can mediate communication between cells and generate abnormal and/or periodic activity in small (§3) and in large networks of cells (§4). Finally, in §5, a study of the role of extracellular potassium in the propagation of axonal signals shows that elevated potassium concentration can block the propagation of neural activity in axonal pathways. Taken together, these results indicate that potassium accumulation and diffusion can interfere with normal activity and generate abnormal activity in neural networks.

1. Introduction

Known non-synaptic mechanisms such as osmolarity, ephaptic interactions and extracellular ionic waves are considered critical for neural network synchronization. They are essential in non-synaptic epileptogenesis, but also important in the generation of synaptic seizures (Yaari & Jensen 1988). More importantly, non-synaptic diffusion has been shown to be an energy efficient neurotransmission mechanism (Aiello & Bach-y-Rita 2000). Experimental studies have shown that a diffusion coupling signal can propagate in the hippocampus under normal extracellular calcium concentration (Perreault & Avoli 1992) and under low extracellular calcium concentration (Lian et al. 2001; see §2). Computational model studies have also confirmed that diffusive coupling can play an important role in the synchronization of oscillators (Hale 1996). Furthermore, the slow waveform and low frequency of ictal epileptiform activity are consistent with potassium dynamics known to underlie non-synaptic bursting (Bikson et al. 1999, 2001; Lian et al. 2003; Bihi et al. 2005). In most models of epilepsy, ictal activity originates almost exclusively in the CA1 and entorhinal cortex regions (Dreier & Heinemann 1990; Bragdon et al. 1992; Patrylo et al. 1994; Jensen & Yaari 1997) where the tight packing of cell bodies promotes non-synaptic interactions such as extracellular potassium build-up. In contrast, inter-ictal activity originates in the CA3 region where recurrent synaptic connections are abundant (Prince & Connors 1986). Traditionally, non-synaptic bursting was thought only to occur in the low-Ca²⁺ and zero-Ca²⁺ models. However, experimental data show that it is also possible to generate non-synaptic activity associated with increases in potassium concentration in the presence of normal synaptic transmission (Bikson et al. 2002). Therefore, besides synaptic transmission, potassium diffusion and its subsequent coupling effect can work together to modulate synchronization in neural networks.

(a). Potassium coupling

Although potassium coupling is best observed while synaptic transmission is blocked (low-calcium concentration), the effect of the synchronization by potassium diffusion has been observed in preparations with intact synaptic transmission (Perreault & Avoli 1992). These in vitro experiments using rat hippocampal slices perfused with potassium channel blocker 4-aminopyridine (4-AP) showed that γ-aminobutyric acid (GABA) released from interneurons activates postsynaptic GABA-A receptors that are located in the dendrites and this process produces a long-lasting depolarization (LLD) response. These LLDs are generated both in the CA1 and in the dentate gyrus (DG), and the LLD signals are synchronized across the hippocampus fissure. Synchrony is lost, however, when the two regions (CA1 and DG) are physically separated. Although it has been shown that GABAergic interneurons located in the CA1 region send both axonal and dendritic branches across the fissure towards the dentate granule cell layer (Lacaille & Schwartzkroin 1988), the speed of propagation of these events (4–17 mm s⁻¹) is similar to the activity generated in low-calcium potassium, suggesting that ‘non-synaptic mechanisms’ are probably involved in the propagation mechanism. These findings, taken together with the fact that potassium can cross a cut along a cell layer (Lian et al. 2001; §2), strongly suggest that potassium lateral diffusion can synchronize activity across two layers of neurons. Electrophysiology, pharmacology and computer simulations have been used to test this hypothesis further. Since it is not possible to remove lateral diffusion in experiments, computer simulations are essential to test the effects of lateral diffusion by adding and removing the mechanism.

(b). Potassium accumulation

Elevation of potassium concentration in the extracellular space has been shown to be a crucial factor in several types of epilepsy such as status epilepticus (SE). SE is the most severe form of epilepsy and it is often associated with considerable morbidity and mortality. The cause of SE is related in part to the failure of seizure termination (Coulter & DeLorenzo 1999). SE is very unlikely to be generated in in vitro normal extracellular medium, suggesting that the termination of seizure is robust (Coulter & DeLorenzo 1999). In recent in vivo low-Ca²⁺ experiments performed in the anaesthetized rat, SE-like activity (characterized by periodic double spikes) in the hippocampus has been observed (Feng & Durand 2005). Computer simulation studies have predicted that potassium lateral diffusion could explain this phase-synchronized state of individual cell activity leading to production of rhythmical SE-like activity (§4). Moreover, it has been shown in vitro (Lian et al. 2004) that phase synchrony could be destroyed by single site sub-threshold sinusoidal stimulation which is known to generate potassium accumulation. The mechanism underlying the control of phase synchronization is still unknown. However, it has to involve potassium diffusion coupling since this form of coupling is shown to be able to pass through a complete mechanical cut.

(c). Source of potassium

The source of the increasing extracellular potassium is often assumed to be intracellular compartment of neurons and glia. However, another important source of potassium resides within blood where potassium concentration (5 mM) is higher than that in cerebrospinal fluid (CSF; 2.9 mM). Normally, the blood–brain barrier (BBB) prevents potassium in blood from reaching the brain tissues. Advances in radiology have enhanced our ability to image and study the human BBB, and the persistent problem of multiple drug resistance to antiepileptic drugs has amplified the significance of the BBB's relationship to epilepsy (Oby & Janigro 2006). The same concept of BBB breakdown for therapeutic purposes (generally for the purpose of increasing drug delivery to the brain) has also revealed a previously unrecognized role for BBB breakdown (Oby & Janigro 2006) as a possible aetiologic mechanism in epileptogenesis. Several studies have shown that mechanisms such as the Na⁺/K⁺ pump and glial cell uptake play an important role in the regulation of [K⁺]_o (Janigro et al. 1997; D'Ambrosio et al. 1999; Ransom et al. 2000; Walz 2000).

(d). Neural network synchronization by diffusion

A first important question is: how can neurons be synchronized without synaptic transmission? Many studies on synchronization of oscillators in general and synchronization within networks of neurons in particular (Pikovsky et al. 2001) have been published. These studies show that coupling is a necessary but not sufficient condition for synchronization. In cases of globally coupled oscillators (all to all) with weak coupling, interesting behaviour between oscillators can emerge. An important contribution was made in 1975 whereby an analytical solution to the problem of globally coupled oscillators was obtained (Kuramoto 1975). One of the most publicized examples is that of fireflies which tend to fire in unison under certain conditions (Strogatz 2003). Analysis of global coupling showed that an arbitrary number of oscillators globally coupled would almost always synchronize (Mirollo & Strogatz 1990). However, the situation is not as simple for networks that are locally (nearest-neighbour) coupled. This type of coupling is also known as diffusive coupling. Diffusive coupling can be observed in chemical oscillators (Bar-Eli 1985) or in neural networks (Rossini et al. 2005). In some simulation studies, it has been shown that diffusively coupled neuronal oscillators are not necessarily completely synchronized but show various patterns of phase locking mode (Park et al. 1996). Diffusive coupling can also lead to dephasing of neuronal oscillators (Han et al. 1995). Noise has also been shown to enhance synchronization in coupled networks (a phenomenon known as coherence resonance; Stacey & Durand 2000, 2001; Balenzuela & Garcia-Ojalvo 2005). Therefore, it is difficult to predict the effect of a non-synaptic coupling mechanism on the synchronization of neural networks. The second important question to answer is: what is the coupling mechanism between cells when synaptic transmission is absent. There are several mechanisms to couple neurons non-synaptically within neural tissue, such as ephaptic transmission, gap junctions, field effect interactions and ionic and neurotransmitter diffusion. The diffusion coupling mechanism is to be distinguished from ephaptic interactions since it does not require the close apposition of the two membranes (ephapse). Diffusion of potassium ions between neurons is such a possible answer to this question in the hippocampus as shown by computer simulations and experiments.

2. Potassium diffusion as a coupling signal

Potassium ions can diffuse throughout neural tissue and could in principle couple neural networks not directly connected by axons or synapses. This effect was demonstrated with 4-AP preparation in which activity generated in the DG was found to cross the hippocampal fissure into the CA1 region (Perreault & Avoli 1992); this propagation was attributed to the accumulation and dispersion of potassium within the hippocampus. Therefore, one could predict that potassium diffusion should provide a coupling mechanism between two areas of the brain. To test this hypothesis, a complete mechanical cut of the CA1 region of the hippocampus was made and low-calcium solutions were applied to the slice to generate oscillations. Electrodes positioned within the CA1 layer of the hippocampus in the low-calcium concentration solution were able to record low-frequency periodic signals typical in this preparation as shown in figure 1a. The cross correlation between signals recorded by electrodes separated by a small distance (0.2 mm) was measured and found to be close to unity at t = 0 (figure 1), indicating a high level of correlation and synchronization. A complete cut through the tissue between the two electrodes did not destroy the correlation between the two signals (figure 1b). However, physical separation between the two sides did eliminate the coupling, which was restored by repositioning the two sides in close apposition (figure 1c,d). Ephaptic interaction between the two sides was eliminated as a possible mechanism since large evoked field potentials generated on one side did not elicit any response on the other. Gap junctions, synaptic and axonal transmission were also eliminated as possible coupling mechanisms since they were disrupted by the cut (Lian et al. 2001). These results indicate a novel coupling mechanism between the two pieces of slice and suggested that a diffusible coupling signal is responsible for the synchronization. Extracellular potassium concentration recordings did show that a wave of potassium was diffusing between the two sides (figure 2). From these experiments, it is clear that a diffusive coupling between cells exists and can contribute to the synchronization of neural activity.

Figure 1.

Synchrony of spontaneous low-calcium activity across a mechanical lesion. Neural activity is induced by a low-calcium solution in the hippocampal slice and recorded by two electrodes separated by 200 μm. (a) Before a cut: the cross variance between the activity recorded from the two electrodes indicates a high degree of synchrony between the two sites and periodicity. (b) After a cut (placed side-by-side): a cut is made between the two electrodes and the synchronization between the two sites is still present. (c) After a cut (separated by approx. 300 μm): the two sites are separated and the synchrony is lost. (d) After a cut (put two halves back together): the two cut sides are repositioned side by side and the synchrony is returned. These data indicate that a diffusible coupling mechanism exists between the two sides (Modified from Lian et al. 2001).

Figure 2.

Extracellular potassium measurements in low-calcium activity. (a) Before a mechanical cut: potassium concentration in the CA1 region of the hippocampus is oscillating between 7 and 9 mM. (b) After a mechanical cut (placed side-by-side): potassium recordings are made after a cut has been made and obtaned from an electrode located before the cut, within the cut and on the other side of the cut. The recording indicates that potassium concentration increases in the solution between the two sides. (c) After a mechanical cut (separated by approx. 300μm): when the two sides are separated, the potassium coupling signals disappears. These data suggest that a potassium wave is a possible coupling mechanism (Modified from Lian et al. 2001).

Can the local diffusion of potassium resulting from the excitation of a few neurons be sufficient to depolarize neighbouring cells and thereby generate propagation of diffusion-induced activity? This question is difficult to answer experimentally since it relies on the precise measurement of potassium in the small extracellular space between cells. Potassium-sensitive microelectrodes can measure the potassium concentration in the bulk extracellular space, but not without destroying tissue, and therefore cannot give a precise measurement of the interstitial value. Computer stimulations, however, are able to provide a possible answer to this question.

3. Computer simulation of lateral diffusion in neural networks

Several decades ago it was suggested that an accumulation of potassium ions [K⁺]_o in a very narrow interstitial space around neurons can serve as a potential mechanism for increasing neuronal excitability leading to seizure generation (Frankenhaeuser & Hodgkin 1956; Green 1964; Fertziger & Ranck 1970). Yet, the idea that elevated extracellular potassium concentration in the interstitial space is responsible for initiating seizure activity remains controversial. Some have concluded that [K]_o is not responsible for the initiation or the termination of the seizure activity (Lux 1974; Moody et al. 1974; Fisher et al. 1976; Heinemann & Lux 1977; Kager et al. 2000; Somjen 2004). Others have shown that [K]_o accumulation can initiate seizure activity (Zuckermann & Glaser 1968; Izquierdo et al. 1970; O'Connor & Lewis 1974). The latter is based on the fact that neurons sharing the same extracellular space were depolarized by the diffusion of high potassium concentration. Particularly, in several low-calcium experiments, the fluctuation of [K⁺]_o has been proposed as a key component for non-synaptic epileptogenesis (Jefferys & Haas 1982; Taylor & Dudek 1982; Yaari et al. 1983, 1986; Konnerth et al. 1986).

Computer models have been developed to test the role of lateral diffusion in the generation of seizure activity. Computer simulations are particularly valuable in this regard because manipulation of lateral diffusion (removing or adding the coupling) is not feasible in in vitro and in vivo experiments. The hypothesis is that sustained, spontaneous neuronal activity can be generated by potassium lateral diffusion coupling between neurons. To test this hypothesis, the effect of potassium lateral diffusion on the synchronization and generation of neuronal activity was examined using modified Hodgkin–Huxley (HH) type model neurons and more physiologically relevant CA1 pyramidal neurons (Park & Durand 2006).

(a). Model

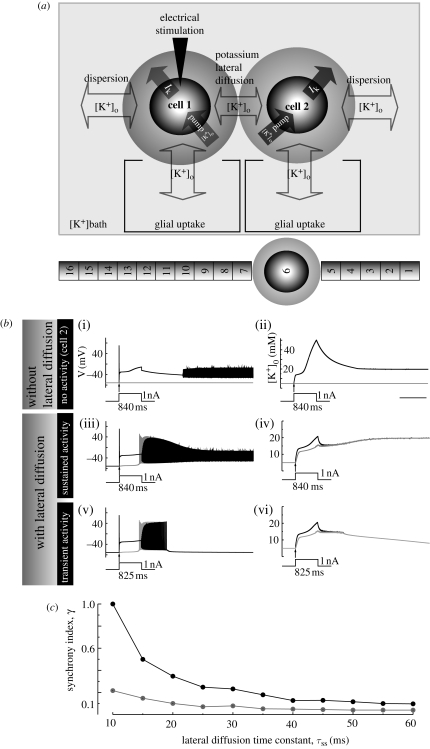
A diffusion model consisting of three compartments is shown in figure 3a for the cell, the interstitial space, and the bath. Two modified Hodgkin & Huxley (1952) type cells were juxtaposed in the potassium bathing solution. One of the cells was electrically stimulated. Each cell was surrounded by interstitial space where potassium ions accumulate. Potassium pump dynamics (Tuckwell & Miura 1978; Bazhenov et al. 2004) and a glial uptake mechanism (Kager et al. 2000; Bazhenov et al. 2004) were included in the model to remove the excess potassium ions from the interstitial space. Equations, variables, and parameters for each HH type cell can be found in Park & Durand (2006).

Figure 3.

Effect of potassium lateral diffusion on the generation and synchronization of neuronal activity in a two Hodgkin–Huxley (HH) type cell model system. Schematic of three compartment diffusion model where two HH type cells were embedded in the potassium bath is shown in (a). Each cell was inactive without electrical stimulation. Potassium ions released during neuronal firing were able to accumulate in the interstitial space (grey shadow around cells), diffuse to neighbouring interstitial spaces (lateral diffusion) and diffuse to the bath (dispersion). Excessive potassium concentration was cleared by potassium pump and glial buffer. Particularly, role of lateral diffusion in the generation of spontaneous sustained activity is shown in (b). In the absence of lateral diffusion, little activity in cell-1 (solid black line) but no activity in cell-2 (grey line) was observed during the supra-threshold stimulation (840 ms, 1 nA). Following the stimulation, self-regenerating activity was observed in cell-1 and still no activity was observed in cell-2; scale bar, 1 s (b(i,ii)). When lateral diffusion enabled excitation of cell-1 with the same supra-threshold current sustained activity was generated in both cells (b(iii,iv)). With sub-threshold current pulse (825 ms, 1 nA), however, the activation of cell-1 was able to generate transient activity in both cells. The parameter values used for the simulations were r_v = 0.15, [K⁺]_bath = 5 mM, τ_bs = 500 ms and τ_ss = 50 ms. For sustained activity of two non-identical neurons, effect of lateral diffusion time constant τ_ss on synchronization is shown in (c). Difference between cells was generated by varying g_KDR by 1–3%. The details on synchronization index and other methodologies can be found in the methods in Park & Durand (2006). For the simulation, r_v = 0.15, [K⁺]_bath = 5.0 mM and τ_bs = 500 ms were used. (Modified from Park & Durand 2006)

The mechanism for generating potassium lateral diffusion-induced activity was also applied to a more physiologically relevant zero-Ca²⁺ 16-compartment CA1 pyramidal neuron model initially developed for simulating non-synaptic epileptiform activity (Shuai et al. 2003). The 16-compartment neuron model includes a single compartment soma, 10 compartments for apical dendrites and five compartments for basal dendrites (figure 4a). In the simulation study, four CA1 pyramidal neurons were coupled through potassium lateral diffusion and each pyramidal model neuron was modelled by 25 variables. For integration of the differential equations, a Runge–Kutta fourth-order algorithm with time step of 0.01 ms (for HH type cell) and 0.005 ms (for CA1 pyramidal neuron) was used.

Figure 4.

Neuronal activity generated by potassium lateral diffusion in CA1 pyramidal neuronal network exposed to zero calcium solution. Schematic diagram of 16-compartment CA1 pyramidal neuronal network consisting of four neurons is shown in (a). The model neuron consists of five compartments for the basal dendrite, 10 compartments for the apical dendrite, and one compartment for the soma. Neuron-1 was excited by long pulse stimulation (40 s, 2 nA). With the volume ratio r_v = 0.15 and the radius of soma R = 8.9 μm, the distance between the first and the last was estimated as 74.56 μm. The membrane potential of each neuron plotted in three different time-frames (b). While the neuron-1 was inactivated during the stimulation, neuron-2 started firing first, and then neuron-3 and finally neuron-4 fired consecutively showing propagation in time. Immediately following stimulation, neuron-1 was activated and the activity for all neurons lasted about 50 s. The bursting patterns observed in experiments and in simulations are compared and shown in (c). The spontaneous triplet bursting observed from experiments (see fig. 3A in Shuai et al. (2003)) is shown on the right and the bursting pattern obtained from the simulation is shown on the left. (Modified from Park & Durand 2006)

To estimate the synchronization, a ‘synchronization index (γ)’ was calculated and γ is described as follows:

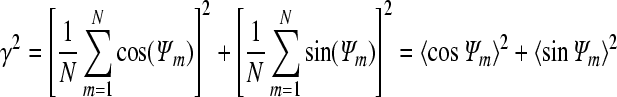
where Ψ indicates relative phase and 〈〉 denotes average over time (or a large number of firing events N; Pikovsky et al. 2001; Rosenblum et al. 2001; Park et al. 2005). The relative phase Ψ is the instantaneous phase of one cell at the time when the other cell fires and it is expressed as follows:

The synchrony index scales between phase-locked and phase-unlocked state (γ = 0) with γ =1 being the fully synchronized state.

(b). Sustained neuronal activity induced by potassium lateral diffusion

To examine the role of potassium lateral diffusion in the generation of neuronal activity, simulations with two HH type cells were performed in the presence and in the absence of the lateral diffusion process. One of the cells (cell-1) was electrically stimulated with a current pulse (1 nA for 840 ms) to initiate activity. During stimulation cell-1 stopped firing as [K⁺]_o increased (up to approx. 40 mM) due to sodium inactivation. Following the termination of stimulus cell-1 resumed firing but not until [K⁺]_o decreased to approximately 20 mM. In the absence of lateral diffusion coupling, no activity was generated in cell-2 (figure 3b(i,ii)). However, when lateral diffusion coupling was present, spontaneous sustained activity was generated in cell-1 and cell-2 with the same level of stimulation as previously injected to cell-1 (1 nA for 840 ms; figure 3b(iii,iv)). When the lower level of stimulation was applied (1 nA for 825 ms), the activity lasted about 1 s. This transient activity is shown in figure 3b(v,vi). The results suggest that potassium lateral diffusion is responsible for the generation of sustained neuronal activity in this model.

(c). Effect of potassium lateral diffusion on synchronization

Since the potassium lateral diffusion process mediates a coupling, the role of lateral diffusion on synchronization was quantified using a synchrony index (γ). To estimate the index, the relative phases extracted from the spike times across the threshold were used (see methods and fig. 5a in Park & Durand (2006) for details). Difference between cells was generated by varying potassium delayed-rectifier conductance (g_KDR) by 1 to 3 per cent: The index γ as a function of the lateral diffusion time constant (τ_ss) is shown in figure 3c. The synchrony index decreased as the lateral diffusion time constant was increased. Additionally, it has been shown that τ_ss can be expressed as the effective space constant and this space constant reflects a level of complexity of the path between cells (see appendix B in Park & Durand (2006) for details). The results show that an increase in the lateral diffusion time constant (or the space constant) weakens the coupling strength and decreases the synchrony level. Since the space constant depends on the extracellular space and therefore on the potassium concentrations, synchronization by potassium diffusion is a complex function of variables of the networks.

Figure 5.

In vivo non-synaptic SE-like activity and distribution of inter-event intervals. Thirty second long in vivo SE-like activity observed in the rat hippocampus exposed to EGTA, low extracellular calcium and high extracellular potassium solution is shown in (a). As shown in the inset, time intervals ΔT are estimated by the interval between consecutive two maximum peaks (events). (b) A distribution of the mean inter-event intervals for six other in vivo data sets including the data shown in (a) demonstrates that the structure of distribution with a local maximum around 0.25 s (4 Hz) is stable. Each dataset was recorded for 1 to 2 min with the sampling rate of 20 KHz following 60, 65, 70, 75, 80, 85 min the use of EGTA. (Modified from Park & Durand 2006)

(d). Spontaneous activity generated by potassium diffusive coupling

Since it has been shown that synchronization of non-synaptic epileptiform activity observed from low-calcium hippocampal slice experiments is due to potassium diffusion (Lian et al. 2001), a network of more physiologically relevant CA1 pyramidal neurons exposed to zero calcium solution was used to validate the simulation results obtained from the two-HH type cell model. A model consisting of four neurons with their surrounding network structure is shown in figure 4a. One of the neurons was stimulated by a 2 nA pulse for 40 s. In the absence of lateral diffusion only the stimulated cell was activated, whereas the other three neurons remained silent (data not shown). In the presence of potassium lateral diffusion, spontaneous activity was generated in neurons (neuron-2, neuron-3 and neuron-4) with a time delay in response to stimulation applied to neuron-1. The potassium-induced activity propagated with the velocity of approximately 1 mm s⁻¹ which is well within the physiological range (figure 4b). The simulated triple bursting shown in the grey inset of figure 4b is quite similar to the pattern observed in low-calcium experiments (Konnerth et al. 1986; Shuai et al. 2003).

(e). Model validation

• — An increase in potassium concentration to about 11 mM observed in the model is well within the physiological ‘ceiling level’ (9–12 mM; Moody et al. 1974; Heinemann & Lux 1977; Heinemann et al. 1983).

• — Spontaneous bursting activity can propagate throughout the network and corresponding potassium wave propagation velocity (74.56 µm (distance from neurons 1–4)/4 neurons/20 ms (lateral diffusion time constant) approx. 1 mm s⁻¹) falls within the range of experimentally obtained values: 0.44–4.2 mm s⁻¹ in Konnerth et al. (1984); 0.43–3.64 mm s⁻¹ in Lian et al. (2001); 0.2–5 mm s⁻¹ in Yaari et al. (1986) in low Ca²⁺. More importantly, in normal Ca²⁺, propagation velocity of seizure activity has been confirmed to be similar to that of potassium wave (0.18–0.83 mm s⁻¹; Weissinger et al. 2000).

• — The triplet spontaneous bursting pattern observed in experiments (Konnerth et al. 1986; Shuai et al. 2003) was also successfully reproduced by the model (Park & Durand 2006).

In this diffusive coupling model of a neural network without gap junctions or synaptic transmission, the results show that the potassium lateral diffusion process alone is necessary and sufficient to generate and synchronize sustained neuronal activity in a simple two-HH type cell model system. The synchronization level is dependent upon the lateral diffusion time constant. Additionally, neuronal activities are desynchronized as the time constant increased or as the space constant increased. The simulations performed with a CA1 pyramidal neuron network suggest that potassium lateral diffusion may serve as a potential mechanism to explain the non-synaptic activity observed in in vitro and in vivo experiments performed in low-Ca²⁺ solution (Feng & Durand 2003).

4. Diffusive coupling can induce periodic activity in neural networks

Consistent with the experimental observations, computer simulations with a three compartment diffusion model wherein two HH type cells are placed side by side and coupled through potassium diffusion have also shown that the synchronized activity could be attributed to potassium lateral diffusion (Park & Durand 2006). In general, synchronization is achieved through a mutual interaction due to a coupling between two or more oscillatory systems. One of the most extensively studied coupling mechanisms is global coupling (or all-to-all coupling) through which each individual oscillator interacts with equal strength with all the other oscillators in the system (Ostborn 2004). Another type of coupling mechanism in many physical systems is local coupling or diffusive coupling (or nearest-neighbour coupling). Diffusive coupling mediates a local interaction only between an individual component of the network and its nearest neighbours. Therefore, in the current context of computer model simulation studies, potassium dispersion where each cell is coupled with all other cells in the network through the same potassium bath can be characterized as global coupling. Potassium lateral diffusion through which each cell interacts only with its neighbouring cells can be characterized as local coupling or diffusive coupling.

Recently, extracellular potassium concentration has also been suggested as a causative factor in the generation of non-synaptic epileptiform activity in in vivo experiments with anesthetized rats (Feng & Durand 2006). The results showed that an increase of extracellular potassium concentration from 6 to 12 mM was responsible for a transformation from a typical non-synaptic burst (0.34 ± 0.14 Hz) into a regular type of epileptiform activity (3.77 ± 1.28 Hz), which lasted longer than 30 min. The physiological properties of the activity such as frequency and duration are consistent with those of SE reported in the literature (Coulter & DeLorenzo 1999).

However, a fundamental mechanism underlying the specific periodic activity (see figure 5) is not clear. Since synaptic transmission was blocked by lowering Ca²⁺ concentration in this in vivo experiment, a non-synaptic mechanism such as potassium lateral diffusion could explain the results. This experimental configuration includes both a potassium dispersion mechanism (global coupling) and a potassium lateral diffusion mechanism (diffusive coupling) since CA1 pyramidal cells are embedded in the same potassium bath and concurrently the cells are aligned and packed; thus, local cell-to-cell coupling is quite feasible. Computer simulation experiments were carried out to test the hypothesis that potassium diffusive coupling can promote network periodicity under low-calcium non-synaptic conditions in an in vivo rat preparation. To test this hypothesis a diffusively coupled network of 16-compartment CA1 pyramidal neurons was used.

(a). Two-dimensional diffusive coupling neural network model

Sixteen-compartment CA1 pyramidal neurons modelled for zero-Ca²⁺ solution were arranged in two-dimensional array (see figure 6a) and these neurons were coupled through the potassium lateral diffusion. At the macroscopic level, the diffusion process and potassium clearance mechanism (glial buffer and potassium pump) were implemented by the three compartment diffusion model (Park & Durand 2006). At the microscopic level, the kinetics of single cell for all channels was constructed based on the previous 16-compartment model developed for simulating low-calcium non-synaptic epileptiform activity (Shuai et al. 2003). The additional modifications were made to incorporate the diffusion process with each neuron (Park & Durand 2006). A 10 per cent reduced function of the potassium pump was used to generate spontaneous neuronal activity. Equations including variables, currents and the parameter values used in the simulations are given in tables 1–4 in Park et al. (2008). Among several parameters, potassium delayed-rectifier conductance (g_KDR) and sodium conductance (g_Na) were changed to generate the parameter disparity between the cells. Extracellular field potential periodicity was monitored by the inter-event interval distribution obtained from in vivo experiments (Feng & Durand 2006) and simulations. For intracellular neuronal activity, synchronized periodic behaviour was monitored by cyclic relative phase distribution. The relative phases were estimated from each pair of neurons of the network and synchronization was identified by phase locking of the neuronal activities (see methods in Park et al. (2008) for details).

Figure 6.

Extracellular field potential activity and intracellular activity using the neuronal network model with potassium lateral diffusion. Schematic diagram of zero calcium 16-compartment CA1 pyramidal neurons arranged in two-dimensional array embedded in the potassium bath is shown in (a). Two diffusion coupling processes were incorporated into the three compartment diffusion model: potassium dispersion (global coupling) and potassium lateral diffusion (diffusive coupling). For potassium clearance mechanisms, potassium pump and glial buffer uptake were used. To calculate the field potential, the distance (r) between the virtual recording location (solid circle) and the centre of each cell was used. Field potential activity and inter-event interval distribution in the presence and absence of diffusive coupling are shown in (b(i,ii)) and (c(i,ii)), respectively. With potassium lateral diffusion coupling, field potential activity shows a periodic pattern (b(i)) and the average inter-event interval distribution for 10 realizations reveals a clear local maximum around 0.25 s (b(ii)). Without diffusive coupling, no periodicity in field potential activity can be detected (c(i)) and no clear peak can be observed in the inter-event interval distribution for 10 different realizations (c(ii)). Intracellular activity and relative phase distribution in the presence and the absence of diffusive coupling are shown in b(iii,iv) and c(iii,iv), respectively. With potassium lateral coupling, phases of neuronal firings (activities of five neurons out of sixteen are shown here) are locked (b(iii)) and this locking is confirmed by preferred phases shown in the cyclic relative phase distribution (b(iv)). Without lateral diffusion coupling, however, phases of neuronal firings keep slipping (c(iii)) and this desynchronized state is confirmed by absence of a local maximum around the preferred phase value in the relative phase distribution (c(iv)). For the simulations, parameter values used were τ_ss = 5 ms and n = 16. The different types of lines indicate neuronal activity from different cells. (Modified from Park & Durand 2006)

(b). Periodic extracellular activity in in vivo preparation and in computational network model

By implementing diffusive coupling between each cell and its nearest neighbours, the network model simulations were able to generate neural activity similar to that observed in in vivo network lacking synaptic transmission. The network activity was estimated by the field potential. As indicated in figure 6a and as described previously in Park et al. (2008), the extracellular field potential was calculated by summing the electrical activity of each cell weighted by their distance (r) to the recording site. The network periodicity was monitored by the inter-event interval distribution for which simulations were performed in 10 separate trials, and the numbers falling into each bin of the histogram were averaged for all the trials.

In the presence of diffusive coupling, the network generated periodic field potential activity. The periodicity observed in this simulated model was confirmed by a clear peak around 0.25 s (4 Hz) in the inter-event interval distribution shown in figure 6b. As shown earlier in figure 5b, similar periodicity in in vivo experimental data was detected by a well-defined peak centred at approximately 0.25 s in the inter-event interval distribution obtained from six different in vivo data sets. When the potassium lateral diffusion (diffusive coupling) was removed while potassium dispersion (global coupling) remained intact, the network still generated activity (figure 6c(i)) but with no periodic pattern as indicated in figure 4c. As confirmed by the distributions shown in figure 6b,c, the emergence of periodic activity taking place in the presence of potassium diffusion coupling is robust. Therefore, the results suggest that diffusive coupling, but not global coupling, is responsible for generating periodic activity in the network lacking synaptic transmission.

(c). Synchronized periodic intracellular activity in the presence of lateral diffusion coupling

To understand the mechanism underlying extracellular periodicity appearing with potassium lateral diffusion, the effect of diffusive coupling on intracellular activity in the network was examined. Each cell in the network independently produced a periodic burst and the bursts are much more broadly distributed in the absence of lateral diffusion coupling (figure 6c(iii)) compared with those in the presence of diffusive coupling (figure 6b(iii)), suggesting that the lateral diffusion is necessary for synchronized activity.

The firing rate of a periodic burst was about 4 Hz which is similar to the rate of in vivo experimental activity. Therefore, the histogram of mean frequency values in the absence and in the presence of lateral diffusion coupling show about the same frequency distribution with a local maximum around 4 Hz (see fig. 4b,e in Park et al. (2008)). When the frequencies of the individual oscillators are only slightly different, frequency alone is not a sufficient basis for identifying true synchronization, since it is possible to falsely identify an uncoupled state as a synchronized state simply because individual frequencies of the elements in the network are similar. In this particular situation, synchronization can be revealed by a local maximum around a preferred phase in the distribution of the relative phase (Schäfer et al. 1999). In the presence of both diffusive coupling and global coupling, synchronization was detected by a well-defined peak in the phase distribution as shown in figure 6b(iv), but when diffusive coupling was removed and global coupling still remained the peak disappeared and no synchronization was observed. Therefore, the results show that lateral diffusion coupling is responsible for network periodicity based on phase locking of the intracellular activity in this model.

Taken together, these simulations indicate that potassium lateral diffusion (or diffusive coupling) is responsible for generating synchronized periodic activity in the absence of synaptic transmission in the network model and could explain the periodic non-synaptic epileptiform activity observed in the in vivo preparation.

5. Role of potassium diffusion in axon bundles

Neural networks are a collection of interconnected neurons, and axons are usually neglected in the simulation of the behaviour of networks. Yet the nervous system is composed of both grey and white matter, with white matter fibre tracts occupying a large portion of the brain. Previous experiments have shown that electrical stimulation of axons' tracts induced potassium elevation, membrane depolarization and excitation of adjacent fibres by potassium diffusion (Eng & Kocsis 1987). Therefore, the diffusion of potassium could have an important effect on the activity of the network if neuronal activity along the axons is also modulated by potassium coupling. High frequency electrical stimulation (HFS) of the central and peripheral nervous systems (CNS, PNS) can modulate both somatic and axonal activity in vitro, in vivo and in situ (Benabid et al. 1998; Garcia et al. 2003; Hashimoto et al. 2003; Kilgore & Bhadra 2006; Hung et al. 2007; Tai et al. 2007). Historically, studies have emphasized the effect of electrical stimulation on activity at the cell body, with suppression of somatic activity during stimulation predominating (figure 7a,b; D'Ambrosio et al. 1998; Beurrier et al. 2001; Bikson et al. 2001; Garcia et al. 2003; Lee et al. 2003; Richardson et al. 2003; D'Ambrosio 2004). Recent studies have shown that electrical stimulation also generates changes in axonal activity (Raastad & Shepherd 2003; Soleng et al. 2004; Meeks et al. 2005; Iremonger et al. 2006; De Col et al. 2008) including a depression of excitatory synaptic currents (Iremonger et al. 2006; Schiller & Bankirer 2007), and conduction blockade in the PNS (Kilgore & Bhadra 2006; Ragnarsson 2007; Tai et al. 2007) and in the CNS (figure 7c; Jensen & Durand 2007). Thus, changes in neural activity induced by electrical stimulation provide a means to modulate abnormal communication at several levels within the target network. In the case of somatic suppression and axonal conduction block, HFS is hypothesized to cause a non-specific suppression of target structures via depolarization blockade (Benazzouz et al. 1995; Garcia et al. 2003; Meeks & Mennerick 2004; Meeks et al. 2005). In general, excess potassium in the extracellular space is thought to mediate development of depolarization blockade (Benazzouz et al. 1995; Garcia et al. 2003; Meeks & Mennerick 2004; Meeks et al. 2005). Yet, it is unclear whether the blockade observed during electrical stimulation is the direct effect of: (i) potassium upon neural elements within the target (Jensen & Durand 2007; Bellinger et al. 2008b); or (ii) stimulation on voltage gated channel dynamics leading to impairment of action potential initiation and conduction (Diamond & Jahr 2000; Beurrier et al. 2001; Kilgore & Bhadra 2006).

Figure 7.

Electrical stimulation generates suppression of spontaneous and evoked somatic and axonal activity. (a) Local electric stimulation (suprathreshold 50 Hz sinusoidal) blocks spontaneous epileptiform activity (low-Ca²⁺). Bar indicates the duration of stimulation. Stimulation was applied to the CA1 somatic layer (filled circle; Lian et al. 2003). (b,c) Local stimulation (suprathreshold 50 Hz sinusoidal) blocked evoked potentials under physiological conditions (Jensen & Durand 2007). Blocking stimulation applied to the CA1 somatic layer in (b), and the alvear axon field in (c). Recording sites denoted by filled boxes. (Modified from Jensen & Durand 2007)

(a). Effect of potassium on axonal conduction

Repetitive stimulation has long been associated with increases in extracellular potassium that, in part, produce changes in neural excitability (Gutnick et al. 1979; Kocsis et al. 1983; Poolos et al. 1987; Benazzouz et al. 1995; Kaila et al. 1997; Beurrier et al. 2001; Garcia et al. 2003; Jensen & Durand 2007; Shin et al. 2007). Excess potassium alters brain function, generating abnormal network activity and modulating the efficacy of somatic and axonal communication. As potassium concentrations increase, neurons depolarize, leading to tonic inactivation of sodium channels. As a result, sustained inactivation of sodium channels could lead to suppression of somatic and axonal communication.

In the case of axonal conduction, elevated extracellular potassium concentrations are known to reduce action potential amplitude, depress presynaptic potentials and affect axonal signalling (Hablitz & Lundervold 1981; Meeks & Mennerick 2004; Meeks et al. 2005; Shin et al. 2007). Additionally, potassium levels sufficient to produce changes in axonal and somatic activity have been recorded using potassium selective microelectrodes (KSMs) in the presence of electrical stimulation under a number of pathological and physiological conditions (figure 8a,b; Garcia et al. 2003; Jensen & Durand 2007). These stimulus-induced changes in extracellular potassium have been correlated with block of axonal conduction (figure 8c; Garcia et al. 2003; Jensen & Durand 2007). Recent computer modelling studies show a clear role for potassium dynamics in HFS-induced conduction block during electrical stimulation (Bellinger et al. 2008a; Liu et al. 2008). Also, elevated potassium concentrations in the bath within the ranges observed during stimulus-induced conduction block, are sufficient to depress action potential amplitude and can affect axonal signalling (Hablitz & Lundervold 1981; Kocsis et al. 1983; Poolos et al. 1987; Peacock & Orchardson 1999; Meeks & Mennerick 2004; Shin et al. 2007). Of particular note, potassium concentrations required for complete conduction block are generally higher than those recorded using potassium sensitive electrodes. These differences are due, in part, to the known underestimation of extracellular potassium concentrations by KSMs (Poolos et al. 1987; Chvatal et al. 1999; Garcia et al. 2003), since these electrodes measure the average potassium concentration around the electrode tip.

Figure 8.

Extracellular potassium increases during stimulation. (a(i)) Low Ca²⁺ epileptiform activity was suppressed by a locally applied suprathreshold AC field. (a(ii)) The stimulation resulted in a transient increase in extracellular potassium (Lian et al. 2004; scale bar, 10 s). (b(i)) Changes in extracelluar potassium occurred during sinusoidal stimulation in a stimulus amplitude dependent manner. Increases in potassium were transient (Jensen & Durand 2007). (b(ii)) Axonal activity was suppressed by a local AC field. Conduction block was achieved in a stimulus amplitude dependent manner (Jensen & Durand 2007). (c) Suppression of axonal activity was correlated with stimulus induced increases in extracellular potassium (Modified from Jensen & Durand 2007).

Finally, elevated potassium concentrations (pathological, stimulus-induced) are associated with changes in voltage gated ion conductances such as I_Nap and I_h (Beurrier et al. 2001; Shin & Carlen 2008). Alternation of gating in the persistent sodium channel produces sustained depolarization, such as potassium-induced failure of inactivation as observed during hyperkalemic periodic paralysis (Cannon et al. 1991). An initial increase in potassium may cause depolarization which opens the persistent sodium channels leading to additional sustained depolarization during stimulation even as extracellular potassium concentration decreases. Elevations in extracellular potassium have been shown to increase the persistent sodium current amplitude in isolated cells as well as hippocampal slices (Somjen & Mueller 2000). Sustained enhancement of persistent sodium conductances could lead to prolonged depolarization-induced failure of inactivation.

(b). Sources of potassium during electrical stimulation of axons

The source of extracellular potassium concentration increases during repetitive stimulation is unclear, and could be axonal, cellular and/or glial in origin. Somata are known to release ions and neurotransmitters in response to electrical stimulation (Poolos et al. 1987; Mitchell et al. 1993; Sakatani et al. 1994; Garcia et al. 2003). While glial cells help maintain potassium homeostasis through spatial buffering (Amedee et al. 1997; Chvatal et al. 1999; Zhou & Kimelberg 2000), alterations in their ability to remove and redirect potassium could generate elevations in extracellular concentrations. The role of axons in potassium homeostasis has been analysed from computational studies (Bellinger et al. 2008a,b; Liu et al. 2008), and is difficult to assess experimentally.

(c). Role of glia cells

In the CNS, myelinating oligodendrocytes and surrounding glia express voltage-gated potassium conductances (I_Kdr, I_Ka, I_Kir) involved in maintaining [K⁺]_o homeostasis (Barres et al. 1990; Ritchie 1992; Tse et al. 1992; Sontheimer & Waxman 1993; Amedee et al. 1997; D'Ambrosio et al. 1998; Chvatal et al. 1999). In addition, potassium channels are distributed not only in the dendrites and soma of CA1 pyramidal cells, but also are present along the axon (juxtaparanodal regions, Kv1.1, Kv1.2) and in its terminals (Mongilner et al. 2001; Pedraza et al. 2001; Devaux et al. 2003). Therefore, electrical stimulation may impair the ability of glia and/or axons to modulate potassium, leading to an excess build up of potassium in the extracellular and submyelin space. Prior research indicates that glia are not able to handle potassium buffering in the presence of electrical fields, specifically, the clearance of excess extracellular potassium (Chvatal et al. 1999; Bikson et al. 2001). However, it is not known whether HFS acts to modulate potassium dynamics through (i) voltage gated conductances (influx, efflux) or (ii) uptake via electrogenic pumps. The literature indicates that although glutamate release is enhanced during pulse train HFS (Lee et al. 2004), electrogenic pumps are not adversely affected, maintaining glutamate and potassium clearance during stimulation (Diamond & Jahr 2000).

6. Conclusions

Diffusive coupling has been studied extensively in the literature but its effect on neural tissue had not been identified. Both computer simulations and experiments confirm the fact that potassium diffusion can be a coupling mechanism in neural tissue affecting the activity in both cell bodies and axons within neural networks. In particular, experiments suggest that the synchronization of the neuronal activity within neural networks in the hippocampus can be increased or decreased by potassium diffusion. Moreover, potassium diffusion seems to be responsible for generating synchronized and periodic neural activity in the absence of synaptic transmission. Therefore diffusion alone can modulate the activity within the neural network. This effect of potassium is strongly enhanced by electrical stimulation. Although short pulse trains can be sufficient to generate a significant increase in potassium concentrations, HFS leads to strong depolarization of membrane in axons and cell bodies leading to depolarization block of neural activity. This effect must be reconciled with the fact that neurons can fire at high rates (at least for short periods of time) such as those used in deep brain stimulation (approx. 130 Hz). Synchronized activation of axons and cells by an applied electric field or epileptiform activity is known to produce a large increase in potassium concentration that can alter neural activity in the network. This diffusive coupling effect is observed only when the potassium concentration is higher than normal, suggesting that its importance may be limited to pathological conditions whereby many elements are firing simultaneously, such as in epilepsy. However, a high level of activity in neural networks whereby the extracellular space is limited could be sufficient to induce this effect of diffusive potassium coupling and alter the normal activity of a neural network. Lateral potassium diffusion in neuronal networks could therefore be a physiological realization of the well-studied theoretical model system known as diffusive coupling.