Abstract
Quantifying kill rates and sources of variation in kill rates remains an important challenge in linking predators to their prey. We address current approaches to using global positioning system (GPS)-based movement data for quantifying key predation components of large carnivores. We review approaches to identify kill sites from GPS movement data as a means to estimate kill rates and address advantages of using GPS-based data over past approaches. Despite considerable progress, modelling the probability that a cluster of GPS points is a kill site is no substitute for field visits, but can guide our field efforts. Once kill sites are identified, time spent at a kill site (handling time) and time between kills (killing time) can be determined. We show how statistical models can be used to investigate the influence of factors such as animal characteristics (e.g. age, sex, group size) and landscape features on either handling time or killing efficiency. If we know the prey densities along paths to a kill, we can quantify the ‘attack success’ parameter in functional response models directly. Problems remain in incorporating the behavioural complexity derived from GPS movement paths into functional response models, particularly in multi-prey systems, but we believe that exploring the details of GPS movement data has put us on the right path.
Keywords: carnivores, functional response, handling time, kill rates, movement, predation
1. Introduction
The direct effects of predation on prey populations have been studied by understanding the numerical and functional responses (i.e. changes in predator density and kill rates as a function of prey density; Solomon 1949). Quantifying kill rates for estimating functional response curves remains an important challenge in linking predators to their prey. High variation around empirically derived functional response models constrains our ability to specify model form (sensu Holling 1959) and, therefore, limits our ability to model population-level interactions (Dale et al. 1994; Marshal & Boutin 1999; Vucetich et al. 2002). More mechanistic rather than statistical curve-fitting perspectives of predation processes are needed to resolve the current debates about the nature of functional responses (Abrams & Ginzburg 2000). Progress towards understanding the functional response of large carnivores has lagged behind that for large herbivores (Spalinger & Hobbs 1992). This may be, in part, because of their secretive nature and wide-ranging movements, but also the relatively long temporal scale over which observations are needed to obtain kill rates. The advent of global positioning system (GPS) technology in wildlife studies has enhanced opportunities to examine movement behaviours of carnivores that reflect spatial processes in predation. The use of GPS technology can provide not only cost-efficient and often more precise estimates of kill rates, but can lead to a better understanding of how variation in kill rates is related to both prey densities and landscape features that may influence predator search rate, prey detection and prey vulnerability in naturally heterogeneous environments.
In this paper, we address current approaches to using GPS-based movement data for quantifying kill rates and indicate how GPS data can be used to improve estimates of kill rates and their variances. Next, we briefly review Holling's disc equation (Holling 1959), which gives a simple conceptual approach to viewing allocation of time along a GPS movement path to key components of predation: handling time and killing time. We review approaches to identify kill sites from GPS movement data and illustrate new approaches to determine what environmental (e.g. habitat features) or animal (e.g. age, sex or group sizes) factors influence killing efficiency. Finally, we show how to estimate attack rates when prey densities are known and discuss further issues for linking these measures to functional responses. Our paper focuses on terrestrial large carnivores, in particular wolves (Canis lupus) and cougars (Puma concolour), because availability of GPS data are most abundant for these species owing to their size and the demands of the initial generation of GPS collars. Technological advances in GPS units design will make these approaches accessible to a wider range of carnivore species in the near future (Tomkiewicz et al. 2010), but the potential usefulness of GPS data may depend on the spatio-temporal dynamics in their predatory behaviours.
2. Gps-based movement analysis to estimate kill rates
To date, the most common approach to estimating kill rates of carnivores has been to identify kill sites based on a variety of methods (see below) over an extended monitoring period (Peterson 1977; Dale et al. 1994; Hayes et al. 2000; Garrott et al. 2007). Counts of kills (Pk) are divided by total observation time (T), and kill rates are expressed based on an individual, pack or population-level basis, and a ratio estimator of the variation in Pk/T is derived (Hebblewhite et al. 2005). In the past, ecologists have used radiotelemetry techniques in combination with snow tracking, either from an aeroplane or on the ground, to estimate kill rates of carnivores (Haglund 1966; Peterson 1977; Fuller 1989; Okarma et al. 1997; Jobin et al. 2000; Jedrzejewski et al. 2002). These methods demand extensive field efforts (i.e. highly frequent and accurate telemetry locations, or long ground-tracking sequences by foot, especially for large predators; Jedrzejewski et al. 2002). In snow-free periods, predators cannot be tracked readily back to kills. With aerial approaches only snapshots of their daily position during daylight is usually possible. Unfavourable weather or dense vegetation may limit or preclude aerial observation of radio-collared predators, their tracks, or remains of killed prey even during winter, introducing the potential for substantial bias. When working with species such as wolves, these approaches frequently have been the only methods available to produce estimates of kill rate for large-sized prey (Peterson 1977; Fuller & Keith 1980; Huggard 1993; Dale et al. 1994; Okarma et al. 1997; Jobin et al. 2000; Bergman et al. 2006; Nilsen et al. 2009). Despite the potential biases, the estimates have been considered reliable owing to the assumed habit of some carnivore species to stay close to the killed carcasses of large prey species, such as ungulates (Peterson et al. 1984; Ballard et al. 1987; Hayes et al. 2000; Smith et al. 2004). For small and mid-sized prey species these approaches have probably resulted in gross under-estimates of kill rate (Fuller 1989; Sand et al. 2005). Consequently, as GPS technology became available, it was clear that quantitative data on movement behaviour could be useful for identifying kill sites of prey made at any time of the day, season and year, with low manpower input (Rodgers et al. 1996; Hulbert & French 2001) resulting in increased availability and reliability of information on kill rates (Sand et al. 2005).
Because GPS movement data provide more consistent and continual sequences for monitoring animals (Cagnacci et al. 2010; Frair et al. 2010), these data may minimize several past limitations. For example, when there are differences in the time carnivores spend handling prey, the number of days they are re-located using aerial telemetry will influence the probability of locating them on a kill (Mech 1977; Fuller & Keith 1980). In contrast, GPS data provide regular sampling intervals. Previous field-based methods were often able to sample only 10 to 30 per cent of the winter to estimate wolf kill rates. Because GPS collars can provide data from a greater proportion of the period of interest, they will provide more precise estimates of kill-rates because the variance in ratio-based estimators depends on the proportion of the sampling period (e.g. winter) during which kills are located (Hebblewhite et al. 2003). Several different approaches have been used to truncate the ‘predation period’ (sensu Hayes et al. 2000) that defines the start and finish of the ground tracking period (see Hebblewhite et al. 2003 for review). Although sampling rates may still differ when using GPS data, use of long, continuous sequences of GPS data probably will reduce the influence of these differences and may lead to standardization among approaches. Finally, with more consistent monitoring over time, heterogeneity in kill rates is more easily identified and leads to stratification that can improve the precision of the estimate.
Despite these advantages, GPS data bring their own problems. Re-locations of animals based on GPS collars may miss re-locations owing to habitat bias (Frair et al. 2004, 2010), and they may fail to identify kill sites by not identifying clusters of re-locations or as a result of the uncertainty from statistical models that identify clusters as kill sites (e.g. Webb et al. 2008). As GPS data are used more commonly for defining kill rates, more thought about how to incorporate the error into predictions of kill rates will be required. Regardless, improved estimates of kill rates will be possible simply because of the vast improvement in our ability to estimate kill rates over longer periods compared with most traditional methods.
3. Gps-movement behaviour: components of predation revisited
From the perspective of time budgets, the total time measured in estimating kill rates can be viewed as two key behaviours that potentially can be distinguished in movement patterns: (i) time allocated to searching, capturing and killing prey (Tk); and (ii) time devoted to handling prey (Th) at a kill site. Allocation of time to this simple dichotomy of behaviours was described by Holling (1959) by the ‘disc equation’, where blindfolded human subjects (predators) tried to find and pick up small discs of sandpaper (prey) on a flat surface at different densities. This assumes that the number of prey captured and killed (Pk) over the duration of experiment (T) decreases with prey density (N) and increases with the available time searching (Ts) and the efficiency of searching or attack rate (a) of the predator as
| 3.1 |
Because Ts = T−ThPk, where Th is the handling time per prey, by substituting this into equation (3.1) and rearranging, we have the number of prey killed over a period,
| 3.2 |
where Pk/T is considered the kill rate.
In large carnivores, sources of variation in handling times per prey (Th) have been related to prey size and biomass consumed, number of predators and age or sex composition of a feeding group, specialized handling behaviour like caching, digestive constraints, other large carnivores stealing their kill, and disturbance by humans (Hayes et al. 2000; Packard 2003; Zimmerman et al. 2007; MacNulty et al. 2009). On the other hand, search efficiency (s) is the time necessary to find a prey and is a function of movement rate and the perceptual range of the animal, which is expressed as area searched per unit time (s =As/t). Encounter rate with prey depends not only on search rate but on the density of prey (N) and the ability of the predator to detect the prey (δ). If a predator spends Ts searching, the number of prey encountered is sδNTs. Beyond encountering a prey, a predator must decide to attack the prey (selection) and be efficient at killing the prey. The time devoted to these behaviours combined with search time we call killing time (Tk) or time to kill. Most importantly, we distinguish Tk from the conventional estimate of kill rates (Pk/T). Killing time, therefore, depends on s, probability of attack or prey selection (α) and prey vulnerability or kill success (ν), such that killing efficiency, or ‘attack success’, now becomes a = sδαν. Thus, the number of prey killed is Pk = aNTk. It follows that the inverse in time to find and kill one prey (Pk = 1) is linearly related to the prey density and the attack success (a) as
| 3.3 |
(McKenzie et al. 2009). If density of the prey is known for several Tk, then one can regress 1/Tk against density and the slope (a) is an estimate of attack efficiency over the range of conditions in which the measurements were taken (figure 1).
Figure 1.
The relationship between time to kill (Tk), defined as the time between the first GPS location after leaving a kill site and the first GPS location at the next kill site. Note the y-axis units have been inverted to reflect inverse of time to kill, 1/Tk = aN, in this simple form.
With GPS movement data, if kill sites can be identified, the time along a movement path can be partitioned into times at kill sites, Th, and time along paths between kills, Tk, where T = ∑Th + ∑Tk when killing and handling are exclusive. Mutual exclusion of killing and handling times may not hold for some carnivores or for herbivores that can process (e.g. chew) small prey as they continue to search (Spalinger & Hobbs 1992), but this is a reasonable assumption for large carnivores whose primary prey are also so large that their consumption requires the predator to be in one place to process at least a portion of prey (figure 2).
Figure 2.
Illustration of the time to kill (Tk) derived from GPS-based location data where clusters of locations indicate time spent at a kill site (the handling time, Th) and the dashed line is the path of the animal between kills (the kill path). Tk is defined as the time between the last GPS location at a kill site or first location after leaving a kill site and the first location at the kill site.
Prior to having GPS data, it was possible to locate kill sites by aerial or ground surveys and snow tracking and to obtain general kill rates, Pk, over periods of time (e.g. Pk/T, Peterson 1977; Fuller 1989; Huggard 1993; Dale et al. 1994), but it was difficult or impossible to partition T into Th and Tk directly. The value of partitioning movements into handling and killing behaviour using GPS data is that it can (i) indicate when a prey is killed, (ii) provide an estimate of killing efficiency (1/Tk) and, when prey density is known, an estimate of attack success (a) for developing functional responses, and (iii) permit us to examine factors influencing each process separately without confounding effects of the other behaviour. We submit that this will provide a clearer understanding of the variation in the observed relationships between kill rates and prey densities (Messier 1994; Marshal & Boutin 1999; Hayes et al. 2000) and lead to better models and predictions of the effects of predators on their prey among different areas. In the next sections, we review the state of the art in approaches to identifying kill sites and present new approaches to considering what influences killing time (time to kill) and, when prey density is known, attack success for parameterizing functional responses.
4. Identifying kill events with gps data: state of the art
The link between GPS positions and kill site detection is the analysis of the predator movement pattern: while the predator is handling the kill, it will stay at the same location over a longer time period than for most non-foraging movements. High sampling frequency will result in a more distinct pattern of either consecutive, single positions that indicate movement or ‘clusters’ of positions indicating non-movement. Several studies have shown that the majority of predation events occur during the night (Anderson & Lindzey 2003; Sand et al. 2005; Zimmerman et al. 2007), and this type of information can be extracted from GPS positions given that they are sampled with adequate frequency.
Several approaches have been used to identify clusters of locations along movement paths that represent the time spent handling prey at a kill site. Anderson & Lindzey (2003) used a rule of greater than two locations within 200 m within 6 days for cougars feeding on multiple prey types. Knopff et al. (2009) used the criterion of Anderson & Lindzey (2003) to define a cluster of cougar locations, but automated the process using an algorithm that is available from the authors of that paper. Sand et al. (2005) and Zimmerman et al. (2007) created circles defined by fixed radii (called ‘buffers’) around winter positions of wolves feeding primarily on moose (Alces alces), and defined locations with overlapping buffers as clusters, which were visited in the field. Webb et al. (2008) used a space–time permutation scan statistic (STPSS) originally developed to detect clusters of disease cases to identify clusters of GPS locations of wolves in winter.
Sampling frequency and fix rate bias are both important in identifying potential kill sites. Most approaches are based on randomly selecting a sequence of GPS positions of the predator obtained at relatively short fix intervals (e.g. less than or equal to 1 h) to ensure that all or the vast majority of kills made during the study period are found. Selection of a GPS fix interval is a trade-off between battery capacity (lifetime) of the GPS collar and the ability to identify kill sites successfully. A fix interval needed to identify a certain proportion of the true number of kill sites can be assessed by rarifying the data (i.e. successively removing GPS positions from the dataset; Sand et al. 2005; Webb et al. 2008; Knopff et al. 2009). A detection of smaller-bodied prey is crucial to avoid biases in kill rate estimates towards larger prey and may require high-position frequency (Sand et al. 2005; Webb et al. 2008; Knopff et al. 2009). Small prey such as rodents or neonate ungulates may, however, be consumed too quickly to be detected with a reasonable GPS location schedule. Further, optimal fix rate may need to be shorter for social carnivores than solitary (e.g. wolves versus cougars), because many individuals may feed on the prey. Where fix rate bias exists (Hebblewhite et al. 2007), sampling rate should be evaluated with this error in mind (Knopff et al. 2009).
Once a potential kill cluster is identified, it can be verified by a field visit. Coordinates of the positions or the centres of the clusters may be loaded into a hand-held GPS. Because GPS locations are somewhat inaccurate (e.g. 5% of positions outside 114 m of true location; Webb et al. 2008; see also Frair et al. 2010), and because kill remains may be scattered around actual positions, a sufficiently large area in proximity to the selected positions should be searched thoroughly. Webb et al. (2008) showed that the geometric centres of selected clusters associated with kill sites were found within 200 m of actual kill locations. Investigation of single positions and tracking on snow revealed 9 out of 68 large-sized kills (13.2%) were outside clusters created by 100 m radii around hourly positions (Sand et al. 2005). During snow-free periods, detection of prey remains is even more difficult.
The time span between the kill event and researcher visit to the kill site is critical to detect a carcass, correctly verify the cause of death, and determine information such as prey species, sex and age. To date, average time spans have ranged from approximately 8–9 days (Zimmerman et al. 2007; Sand et al. 2008) to 200 days (Anderson & Lindzey 2003). The latter project used ‘store-on-board’ collars on cougars that allowed access to data only upon retrieval of the collar. GPS collars with remote data download via VHF, UHF, GSM or satellite link allow visitation of sites before decomposition and scavenging make field verification less reliable (Webb et al. 2008). The time span should be long enough that field personnel will not interfere with the predator. Studies using GPS-based locations of wolves, for example, showed they rarely spent more than 3–4 days on any type of kill (Sand et al. 2005; Webb et al. 2008), whereas cougars exhibited a much longer handling of prey (Knopff et al. 2009). The cheaper and less energy-consuming store-on-board collars may be used to provide estimates of kill rates retrospectively provided that models have been developed for a particular predator–prey system and their accuracy evaluated.
Field efforts for visiting kill sites can be reduced or potentially even dropped if models based on movement can reliably predict the presence of a kill. A successful model should be able to distinguish kill sites from non-kill sites and preferably even distinguish between different prey sizes (e.g. Webb et al. 2008). Model building should include a minimum of three steps: (i) inspection of GPS data at known kill and non-kill sites to identify spatial, temporal or location features that might differentiate between such sites; (ii) comparisons of alternative statistical models to predict kill locations following model selection procedures; and (iii) validation of the best model by applying it to new or withheld datasets for which the true number of kill sites is known. A full discussion of statistical models with GPS sequence data is beyond the scope of this paper. We highlight models used for kill rate estimation to date and refer the reader to other contributions in this volume (Fieberg et al. 2010; Smouse et al. 2010).
Modelling approaches have included binomial logistic regression to predict the presence or absence of large kills at GPS location clusters (Anderson & Lindzey 2003; Zimmerman et al. 2007), two-step binomial and multinomial logistic regression to estimate the chances of a site to contain a large- or small-bodied kill, or no kill (Webb et al. 2008; Knopff et al. 2009), and hidden Markov models to distinguish among kill, bed and transit locations (Franke et al. 2006). Variables included in these models ranged from cluster dimensions (including the number of continuous or discontinuous locations at the cluster and geometric cluster dimensions), time of day, individual and pack characteristics (such as sex, age and number of associated animals), characteristics of movements (such as distance travelled, turn angles and travel rates), and environmental variables such as metrics of terrain ruggedness, human disturbance and vegetation cover (Franke et al. 2006; Zimmerman et al. 2007; Webb et al. 2008; Knopff et al. 2009). Random effects models also may include variation among individuals, study periods and/or study areas (Zimmerman et al. 2007).
Validation of the predictions of the models, based on either independent datasets or k-fold cross-validation approaches (Zimmerman et al. 2007; Webb et al. 2008; Knopff et al. 2009), showed that a range of error existed depending on particulars of the clustering rules, sampling frequency, prey composition and sizes, and hunting behaviours of the species under study. Specification of omission error (identifying a kill site as a non-kill site) and commission error (identifying a non-kill site as a kill site; Webb et al. 2008; Knopff et al. 2009) will further help to evaluate model performance. As recommended by a number of authors, an understanding of these errors may help guide field efforts needed to obtain kill rates with a certain precision and accuracy. For example, in the case of a multi-prey system in Alberta, the greatest effort would be required to distinguish wolf kill sites of deer (Odocoileus hemionus, O. virginianus) from non-kill sites (Webb et al. 2008), whereas in Scandinavia differentiating between sites containing wolf-killed moose and non-kill sites or sites with small prey other than moose will be important.
Initial models have suggested that variability in factors influencing predator behaviour at kill sites are likely to be species- and system-specific because of differences in prey items, the types of other predators present and amount of human disturbance. For example, solitary-living cougars seem to express high site fidelity and relatively long handling times of prey, resulting in a high detection rate of killed prey (Anderson & Lindzey 2003; Knopff et al. 2009). In contrast, group-living wolves tend to have shorter handling times, because large packs consume prey rapidly, and show a less distinct behaviour at kill sites, ultimately resulting in lower detection rates of prey killed (Sand et al. 2005; Zimmerman et al. 2007; Webb et al. 2008). Similarly, prey and predator population density, habitat type/quality, and stochastic events such as disturbance by humans or other predator species may influence variance in the behaviour of predators at kill sites. Very high local prey densities may result in excessive killing of individuals that may not be completely consumed (i.e. partial prey consumption). Zimmerman et al. (2007) observed large variation in the time wolves spent handling moose carcasses and discussed human disturbance, scavenging and social organization of the re-colonizing wolf population as possible reasons. At the same time, emerging patterns suggest it may be too difficult to identify some smaller prey (e.g. deer) because of the short handling duration. For example, Webb et al. (2008) could identify 100 per cent of the large-bodied prey, but only 40 per cent of the smaller prey, and the same pattern emerged from the hidden Markov modelling technique (Franke et al. 2006). In contrast, other studies on wolves did not find any differences in the time for handling large and mid-sized/small prey, as exemplified by adult and juvenile moose during both winter (Sand et al. 2005) and summer (Sand et al. 2008).
5. Time to kill: new approaches for gps movements
Once clusters of GPS-based locations have been identified as kill sites along a movement path, the time between kills (Tk) can be determined (figure 2). Delineating Tk depends on a decision rule for when Tk is initiated and when it ends. One approach is to define Tk as beginning at the time of the first recorded GPS location away from the kill site and ending at the first location at the next kill site. Different approaches for allocating GPS fixes near a kill site to handling or killing behaviours may be developed, and frequency of sampling fixes is an important consideration in refining these rules, but no evaluations have been made to date. Once delineated, hypothesized mechanisms for what influences killing time, Tk, such as age, sex or social group size, prey density, or environmental characteristics along paths leading up to the kill, can be evaluated using several modelling approaches that provide somewhat different information and require meeting different assumptions. Further, where the density of prey is known, an estimate of attack success (a) is obtainable for the conditions under study.
We illustrate the modelling approaches using data from one GPS-collared wolf whose movements have been monitored for 19 kills in west central Alberta, Canada in the winter of 2005–2006. The wolf inhabited mountainous areas that were heavily forested (approx. 60%) with clearcuts and open areas (approx. 20%) dispersed through the area (see Webb et al. 2008 for details). Major ungulate prey included deer, elk (Cervus elaphus), moose and wild horse (Equus caballus). Kill sites of the wolf were identified using 2-h locations as described by Webb et al. (2008), with 60 per cent of the potential clusters identified statistically visited in the field to verify the presence of a kill. Time between kills (Tk) was defined as in figure 2 based on the decision rule described above and averaged 7.0 ± 4.9 (mean ± s.d.) days (range 10 h to 15 days). Kill paths (the path between kill sites) were delineated using straight lines that connected sequential 2-h GPS fixes between kill sites. Along each of the 19 kill paths, the following environmental covariates were estimated within a 500-m buffer around each 2-h path segment (and averaged across segments for the entire kill path): density of ungulate prey, mean proportion of area that was forest, open meadow or clearcut, mean elevation (m), terrain ruggedness (s.d. of elevation), distance to forest edge (km), density of roads (km km−2), and density of other linear features (km km−2) such as seismic lines and pipelines (McPhee 2009). Density of ungulate prey was derived from interpolated pellet group densities (based on counts along 372 1-km transects) that we converted to animal numbers, first based on the ratio of aerial moose counts to pellet counts, and for other prey based on the body-weight ratios of moose to other prey assuming similar defecation rates in winter (Webb 2009). Because prey encounter rates also may be altered by prey aggregation (Fryxell et al. 2007; McLellan et al. 2010), a spatial index of prey patchiness based on the coefficient of variation in prey density across a 2-h path segment was also derived. Finally, the average distance travelled between 2-h GPS locations was recorded to indicate rate of search. We related the inverse of Tk to the above covariates using backward stepwise linear regression, and adjusted standard errors for autocorrelation using a Huber-White sandwich estimator in STATA (StataCorp LP, College Station, TX, USA).
We found 1/Tk was related only to prey density (β = 0.0055 ± 0.0820, p = 0.003) and the extent of forest along the paths leading to the kill (β = −0.1427 ± 0.0086, p < 0.001), indicating that it took longer to find prey in areas of low prey density and high forest cover (r2model = 0.92, p < 0.001). Forest extent and prey density were not closely related (r = 0.35, p > 0.15), and a log(time) model did not improve model fit (r2model = 0.70, p = 0.01). These are reasonable results because it is has been reported that prey detection is low in forested habitats (Mech et al. 1998; MacNulty et al. 2007). In fact, only after accounting for prey detectability (i.e. forest extent) did we find a relationship between 1/Tk and prey density. The relatively weak effect of prey density on 1/Tk compared with landscape condition (i.e. forest cover) may result from the generally high deer density in this area or selection by wolves to hunt primarily in areas of high prey density (McPhee 2009). Further, we found no evidence for an interaction between prey density and forest extent, revealing that detecting prey in forest cover did not depend on prey density. Recall that the value of a is the slope of the line between N and 1/Tk. Here, we estimated a = 0.0165 ± 0.0078, but the value varied with extent of forest cover along the path, which we have interpreted to be primarily an effect of prey detection.
Although a simple linear regression illustrates the relationship between 1/Tk and prey density or landscape conditions, other approaches may offer more appropriate means of analysing events in time because ordinary least squares regression assumes normally distributed errors (Cleves et al. 2002). Semi-parametric and parametric time-to-event models provide improved approaches. The Cox proportional hazard (CPH) model, and to a lesser extent, parametric proportional hazard (PPH) or accelerated failure time (AFT) models, are familiar to users of telemetry data for survival analyses (DelGiudice et al. 2002; Murray 2006; Fieberg & DelGiudice 2009). We refer readers to more extensive treatises on these methods (Hosmer & Lemeshow 1999; Therneau & Grambsch 2000; Cleves et al. 2002; Kalbfleisch & Prentice 2002), and briefly illustrate here how they might be applied to analysing Tk.
Both semi-parametric and parametric models can be used to explore the influence of covariates on times to events (i.e. kills). However, they make different assumptions about the baseline hazard functions, which may suit different predator–prey systems differently, and provide different information for a particular question. The CPH model provides a relative assessment of covariate effects on the hazard of a failure (kill) at time t. Using this approach assumes the hazard ratio is constant across subjects (but see ‘frailty’ options below), without making any assumption about the shape of the baseline hazard—it can be constant, increasing or decreasing. With CPH, the cumulative hazard curve can be visually inspected to reveal temporal patterns in Tk as we illustrate below. Further, it has the flexibility of including single or multiple segments (e.g. corresponding to 2-h segments) along one kill path, and a shared frailty term, which is similar to including a random effect that accounts for variation among individuals (Cleves et al. 2002). Continuing with our example, we modelled Tk using CPH and found similar support for models including forest cover both with and without total prey density (ΔAICc < 2.1), although prey density was no longer statistically significant (table 1). Data fitted the proportional hazard model based on a test of the Schoenfeld residuals (χ2 = 0.53, p = 0.76). Plotting the cumulative baseline hazard indicated that the risk of killing increased slowly 3–5 days post-kill, increased moderately from 5 to 12 days post-kill, and increased dramatically thereafter (figure 3). Figure 3 does not depict the effects of covariates; however, the probability of a kill at time t was lower as forest cover in the animal's kill path increased and higher as the density of prey increased (table 1).
Table 1.
Hazard ratio and β coefficients of time-to-event models for the extent of forest cover (proportion of area) and total ungulate prey (no. per km2) along 2-h GPS paths of a wolf (n = 19) that were related to time to kill (Tk). Time to kill was defined as the time between the first GPS location after leaving a kill site and the first GPS location at a kill site. Total prey include only ungulate prey.
| model | β or HR | s.e. | p |
|---|---|---|---|
|
Cox proportional hazard: hazard ratio | |||
| forest extent (hectares per km2) | 0.000022 | 0.000092 | 0.008 |
| total prey (no. per km2) | 1.3500 | 0.4530 | 0.37 |
|
parametric proportional hazard, Weibull: hazard ratio | |||
| forest extent (hectares per km2) | 0.000023 | 0.000058 | <0.001 |
| total prey (no. per km2) | 1.3260 | 0.4038 | 0.35 |
|
parametric proportional hazard, Weibull: β coefficients | |||
| forest extent (hectares per km2) | −10.6730 | 2.5110 | <0.001 |
| total prey (no. per km2) | 0.2826 | 0.3043 | 0.30 |
| intercept | −5.4480 | 1.6713 | 0.001 |
|
accelerated failure time, Weibull: β coefficients | |||
| forest extent (hectares per km2) | 5.0960 | 0.6678 | <0.001 |
| total prey (no. per km2) | −0.1349 | 0.1444 | 0.35 |
| intercept | 2.6016 | 0.6530 | <0.001 |
Figure 3.
Cumulative baseline hazard for time to kill prey along a wolf hunting path based on a Cox proportional hazard model using data from 19 wolf kill events during winter 2005–2006 in west central Alberta, Canada.
Unlike the CPH, parametric time-to-event models specify a priori a distribution for the baseline hazard. The most common distributions include exponential, Weibull, lognormal, log-logistic and gamma failure rates, all of which are log(time) parameterizations (Hosmer & Lemeshow 1999; Cleves et al. 2002). PPH and AFT models provide estimates of baseline hazard rates and coefficient effects that have different interpretations. AFT models directly describe the expected change in the time to event for every unit change in xi, rather than describing the change in the likelihood or relative likelihood of an event occurring at time t, as is the case with the PPH and CPH models (Therneau & Grambsch 2000; Cleves et al. 2002).
Based on the shape of the cumulative hazard curve in figure 3, we fitted parametric models assuming a Weibull distribution to our data. Because regressions based on the Weibull distribution have both a proportional hazard and AFT (table 1) formulation, it is also useful for our illustration. The Weibull baseline hazard is given as
| 5.1 |
and it has two parameters, s and β0, where s is the shape parameter and β0 is the intercept. When s = 1, the hazard rate is constant over time. Adding the effects of covariates, PPH takes the form
| 5.2 |
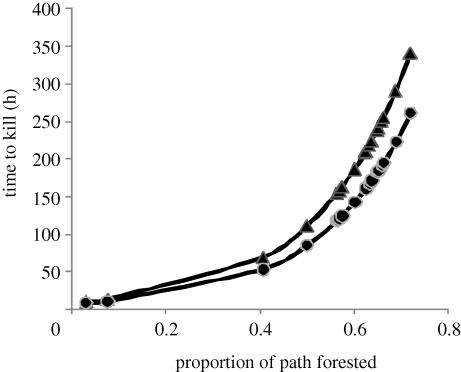
For our example, s = 2.094, which was significantly different from one (Wald test, z = 4.02, p < 0.001; coefficient estimates given in table 1). Thus, our visual interpretation based on the CPH was supported. We also found that hazard ratios of the CPH (table 1) and PPH (table 1) were similar, indicating a good fit to the assumed underlying baseline hazard (Cleves et al. 2002). Under a Weibull distribution, the AFT formulation provided different coefficients because of their interpretation, but they are related to the hazard ratio of the PPH by exp(−sβAFT). In our example, Tk increased rapidly as forest cover exceeded 40 per cent over the path and low prey density augmented the delay in time to kill a prey (figure 4).
Figure 4.
Predicted mean time to kill of a wolf in areas of various forest extent at high (4 km−2, circles) and low (2 km−2, triangles) total prey densities in west central Alberta. Estimates are based on accelerated failure time models assuming a baseline hazard following a Weibull distribution.
Time-to-event models offer both opportunities and challenges to exploring predation processes. The CPH models are flexible in that the shape of the curve and the effect of covariates can be explored without making restrictive assumptions about the distributions of failure times. When enough is known to make reasonable assumptions about the baseline hazard, quantifiable estimates of time to kill under different combinations of covariates can be estimated along with measures of uncertainty. This may permit comparisons in the efficiencies of killing among different wolves or in different landscapes. When movement data from more than one individual are available, frailty models, which accommodate heterogeneity among individual responses similar to random effects, can be employed for population-level assessments. Further, in multi-prey systems, when more than one prey type is killed, and type of prey at each kill is known, a competing-risk analysis (Lunn & McNeil 1995) might be used to determine whether Tk varies across prey species and is influenced similarly by covariates.
However, as with studying most ecological processes, issues of selecting the scale of observation influence our view of the process. For our illustration, we measured covariates at the scale of the entire path leading to a kill, but alternatively we could have used 2-h segments along the path. Our interpretation that forest cover influenced time to encountering a prey by altering prey detection is reasonable at this scale, but characteristics of a 2-h segment might be more informative on what specifically influenced the act of killing. For example, where a kill is located may differ in associated characteristics from those associated with where the predator encounters the prey because certain characteristics influence the act of killing more than encountering a prey (Hebblewhite et al. 2005). Time-to-event models developed on multiple records per path (e.g. each 2-h segment along the path leading to a kill) may allow a better assessment of short-term processes. For example, using CPH models, McPhee (2009) measured path features along each 2-h segment of the path leading to a kill and found that hunting near oil and gas well sites influenced Tk, which was corroborated by kill site locations tending to occur further from well sites. Although sampling segments of movement paths can improve our understanding, sampling at too fine a movement scale also may degrade the signal. Multiscale approaches to measuring covariates back in time along movement paths may be necessary when the processes of predation (sensu Hebblewhite et al. 2005) work at different time scales. Further, if covariates are measured as varying in time along the path, prediction of the mean time to kill as illustrated in figure 3 becomes problematic because the expected Tk most commonly assumes fixed covariates in time. While obtaining estimates of time to kill is still possible, it remains mathematically difficult (Therneau & Grambsch 2000; Cleves et al. 2002), and methods of obtaining these estimates are not readily available in most statistical software packages.
6. Summary and conclusions
Carnivore biologists who address how predators influence prey populations have focused predominately on understanding whether kill rates are most related to prey density alone (prey-dependent) or to the ratio of the number of prey to the number of predators (ratio-dependent), using statistical curve-fitting approaches to develop functional responses. Yet empirical observations show high variation around both these relationships with little advancement gained in understanding the true nature of the interactions (Boutin 1992). Because of the size and weights of the first generation of GPS collars, large-carnivore biologists are among the first to apply this technology to study movement behaviour of carnivores, which has led to a greater understanding of what movements reflect and for quantifying the processes of predation. For these far-ranging animals in particular, GPS technology has opened the door to obtaining sequences of animal locations at temporal extents and resolutions that previously were impossible or extremely difficult even with intensive field efforts. This has led to improved precision in estimating kill rates.
At the same time, movement behaviour of large carnivores lends itself to encapsulating basic predation processes. When predominance of biomass consumed by carnivores comes in relatively large, discrete packages, it results in clustered movements patterns owing to lengthy handling of prey. The large prey typically are dispersed and non-apparent (sensu Spalinger & Hobbs 1992) such that carnivores move relatively far in search of the next prey. This typically results in handling time at a kill site being exclusive of periods of searching and killing. As a result, movement patterns, particularly of large carnivores, lend themselves to a dichotomy of simplified movement modes that can be distinguished with GPS locations and have relevance to key processes in the functional responses of predators—handling time and killing time.
To date, analyses of GPS-based movement patterns of large carnivores have focused on identifying periods of handling time that identify kill sites and the factors influencing handling time. Methods for identifying kill sites based on spatio-temporal patterns in the sequence of movement positions are evolving. As the approach is applied in more studies with a variety of species we will gain a better appreciation of how data sampling protocols and animal behaviour influence our ability to correctly distinguish a GPS-based kill site. At present, modelling the probability of a cluster being a kill site is no substitute for field visits, but can guide our field efforts (Sand et al. 2005; Webb et al. 2008; Knopff et al. 2009). In the process, however, we have found we can identify factors related to handling time, such as prey size, size of predator social groups, environmental site factors (e.g. snow) and disturbance by humans (Zimmerman et al. 2007; Webb et al. 2008).
Once kill sites are identified, the time to kill one prey (Tk) can be determined as the time between kills. Similarly, we can identify animal characteristics and landscape factors along the movement path that influence Tk using time-to-event models. The most appropriate type of model is limited by the model's assumptions, but also depends on whether a probability of the event occurring at a specific time is of interest or the interest lies in how much the factor changes the actual time to event. Plotting the relative hazards owing to variables that influence Tk on a map has the potential to be used as a metric of predation risk. Tk also is equivalent to 1/aN from the typical functional response formulation (Holling 1959), and where prey densities are known an estimate of a is possible to derive. In this context a reflects not only searching for prey but detecting, attacking and killing the prey, which together reflect killing efficiency. Most functional response models have assumed a to be constant and unaffected by landscape factors, and these assumptions can now be tested. However, incorporating changes in social groupings that influence a and obtaining prey densities at relevant scales in both space and time are problematic. While we are not yet at the point of being able to incorporate the complexity derived from GPS movement paths into functional response models, particularly in multi-prey systems, exploring the details of GPS movement data has put us on the right path.
Acknowledgements
We thank the Edmund Mach Foundation for bringing us together to share insights into the utility of GPS technologies for studying animal behaviour. We thank Francesca Cagnacci for her efforts at all stages of bringing these ideas together, Luigi Boitani for his guidance and manuscript comments, and four anonymous reviewers for specific comments on the paper.
Footnotes
One contribution of 15 to a Theme Issue ‘Challenges and opportunities of using GPS-based location data in animal ecology’.
References
- Abrams P. A., Ginzburg L. R.2000The nature of predation: prey dependent, ratio dependent, or neither? Trends Ecol. Evol. 15, 337–341 (doi:10.1016/S0169-5347(00)01908-X) [DOI] [PubMed] [Google Scholar]
- Anderson C. R., Lindzey F. G.2003Estimating cougar predation rates from GPS location clusters. J. Wildl. Manage. 67, 307–316 [Google Scholar]
- Ballard W. B., Whitman J. S., Gardner C. L.1987Ecology of an exploited wolf population in South-Central Alaska. Wildl. Monogr. 98, 1–54 [Google Scholar]
- Bergman E. J., Garrott R. A., Creel S., Borkowski J. J., Jaffe R., Watson F. G. R.2006Assessment of prey vulnerability through analysis of wolf movements and kill sites. Ecol. Appl. 16, 273–284 (doi:10.1890/04-1532) [DOI] [PubMed] [Google Scholar]
- Boutin S.1992Predation and moose population dynamics: a critique. J. Wildl. Manage. 56, 116–127 [Google Scholar]
- Cagnacci F., Boitani L., Powell R. A., Boyce M. S.2010Animal ecology meets GPS-based radiotelemetry: a perfect storm of opportunities and challenges. Phil. Trans. R. Soc. B 365, 2279–2288 (doi:10.1098/rstb.2010.0077) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleves M. A., Gould W. W., Gutierrez R. G.2002An introduction to survival analysis using Stata College Station, Texas: Stata Press [Google Scholar]
- Dale B. W., Adams L. G., Bowyer T. R.1994Functional response of wolves preying on barren-ground caribou in a multiple-prey ecosystem. J. Anim. Ecol. 63, 644–652 [Google Scholar]
- DelGiudice G. D., Riggs M. R., Joly P., Pan W.2002Winter severity, survival, and cause-specific mortality of female white-tailed deer in north-central Minnesota. J. Wildl. Manage. 66, 698–717 [Google Scholar]
- Fieberg J., DelGiudice G. D.2009What time is it? Choice of time origin and scale in extended proportional hazards models. Ecology 90, 1687–1697 (doi:10.1890/08-0724.1) [DOI] [PubMed] [Google Scholar]
- Fieberg J., Matthiopoulos J., Hebblewhite M., Boyce M. S., Frair J. L.2010Correlation and studies of habitat selection: problem, red herring, or opportunity? Phil. Trans. R. Soc. B 365, 2233–2244 (doi:10.1098/rstb.2010.0079) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frair J. L., Nielsen S. E., Merrill E. H., Lele S. R., Boyce M. S., Munro R. H. M., Stenhouse G. B.2004Removing GPS collar bias in habitat selection studies. J. Appl. Ecol. 41, 201–212 (doi:10.1111/j.0021-8901.2004.00902.x) [Google Scholar]
- Frair J. L., Fieberg J., Hebblewhite M., Cagnacci F., DeCesare N. J., Pedrotti L.2010Resolving issues of imprecise and habitat-biased locations in ecological analyses using GPS telemetry data. Phil. Trans. R. Soc. B 365, 2187–2200 (doi:10.1098/rstb.2010.0084) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke K. A., Caelli T., Kuzyk G., Hudson R. J.2006Prediction of wolf (Canis lupus) kill sites using hidden Markov models. Ecol. Model. 197, 237–246 (doi:10.1016/j.ecolmodel.2006.02.043) [Google Scholar]
- Fryxell J. M., Mosser A., Sinclair A. R. E., Packer G.2007Group formation stabilizes predator–prey dynamics. Nature 449, 1041–1044 (doi:10.1038/nature06177) [DOI] [PubMed] [Google Scholar]
- Fuller T. K.1989Population dynamics of wolves in north-central Minnesota. Wildl. Monogr. 105, 1–41 [Google Scholar]
- Fuller T. K., Keith L. B.1980Wolf population dynamics and prey relationships in northeastern Alberta. J. Wildl. Manage. 44, 583–602 (doi:10.2307/3808006) [Google Scholar]
- Garrott R. A., Bruggeman J. E., Becker M. S., Kalinowski S. T., White P. J.2007Evaluating prey switching in wolf–ungulate systems. Ecol. Appl. 17, 1588–1597 (doi:10.1890/06-1439.1) [DOI] [PubMed] [Google Scholar]
- Haglund B.1966Winter habits of the large carnivores as revealed by tracking in the snow. Viltrevy 4, 1–301 [Google Scholar]
- Hayes R. D., Baer A. M., Wotschikowsky U., Harestad A. S.2000Kill rate by wolves on moose in the Yukon. Can. J. Zool. 78, 49–59 (doi:10.1139/cjz-78-1-49) [Google Scholar]
- Hebblewhite M., Paquet P. C., Pletscher D. H., Lessard R. B., Callaghan C. J.2003Development and application of a ratio estimator to estimate wolf kill rates and variance in a multiple-prey system. Wildl. Soc. Bull. 31, 933–946 [Google Scholar]
- Hebblewhite M., Merrill E. H., MacDonald T. L.2005Spatial decomposition of predation risk using resource selection functions: an example in a wolf–elk predator–prey system. Oikos 111, 101–111 (doi:10.1111/j.0030-1299.2005.13858.x) [Google Scholar]
- Hebblewhite M., Percy M., Merrill E. H.2007Are all global positioning system collars created equal? Correcting habitat-induced bias using three brands in the Central Canadian Rockies. J. Wildl. Manage. 71, 2026–2033 (doi:10.2193/2006-238) [Google Scholar]
- Holling C. S.1959The components of predation as revealed by a study of small-mammal predation of the European sawfly. Can. Entomol. 91, 293–320 (doi:10.4039/Ent91293-5) [Google Scholar]
- Hosmer, D. W., Jr, Lemeshow S.1999Applied survival analysis: regression modeling of time to event data. New York, NY: John Wiley [Google Scholar]
- Huggard J.1993Effect of snow depth on predation and scavenging by gray wolves. J. Wildl. Manage. 57, 382–389 [Google Scholar]
- Hulbert I. A. R., French J.2001The accuracy of GPS for wildlife telemetry and habitat mapping. J. Appl. Ecol. 38, 869–878 (doi:10.1046/j.1365-2664.2001.00624.x) [Google Scholar]
- Jedrzejewski W., Schmidt K., Theuerkauf J., Jedrzejewska B., Selva N., Zub K.2002Kill rates and predation by wolves on ungulate populations in Bialowieza primeval forest (Poland). Ecology 83, 1341–1356 [Google Scholar]
- Jobin A., Molinari P., Breitenmoser U.2000Prey spectrum, prey preference and consumption rates of Eurasian lynx in the Swiss Jura Mountains. Acta Theriol. 45, 243–252 [Google Scholar]
- Kalbfleisch J. D., Prentice R. L.2002Statistical analysis of failure time data. New York, NY: John Wiley [Google Scholar]
- Knopff K. H., Knopff A. A., Warren M. B., Boyce M. S.2009Evaluating global positioning system telemetry techniques for estimating cougar predation parameters. J. Wildl. Manage. 73, 586–597 (doi:10.2193/2008-294) [Google Scholar]
- Lunn M., McNeil D. R.1995Applying Cox regression to competing risks. Biometrics 51, 524–532 (doi:10.2307/2532940) [PubMed] [Google Scholar]
- MacNulty D. R., Mech D. L., Smith D. W.2007A proposed ethogram of large-carnivore predatory behaviour exemplified by the wolf. J. Mammal. 88, 595–603 (doi:10.1644/06-MAMM-A-119R1.1) [Google Scholar]
- MacNulty D. R., Smith D. W., Mech L. D., Eberly L. E.2009Body size and predatory performance in wolves: is bigger better? J. Anim. Ecol. 78, 532–539 (doi:10.1111/j.1365-2656.2008.01517.x) [DOI] [PubMed] [Google Scholar]
- Marshal J. P., Boutin S.1999Power analysis of wolf–moose functional response. J. Wildl. Manage. 63, 396–402 [Google Scholar]
- McKenzie H. W., Jerde C. L., Visscher D. R., Merrill E. H., Lewis M. A.2009Inferring linear feature use in the presence of GPS measurement error. Environ. Ecol. Stat. 16, 531–546 (doi:10.1007/s10651-008-0095-7) [Google Scholar]
- McLellan B. N., Serrouya R., Wittmer H. U., Boutin S.2010Predator-mediated Allee effects in multi-prey systems. Ecology 19, 286–292 [DOI] [PubMed] [Google Scholar]
- McPhee H.2009Kill site selection and attack rates of wolves in heterogeneous environments in west central Alberta, Canada. Edmonton, AB: University of Alberta [Google Scholar]
- Mech L. D.1977Population trend and winter deer consumption in a Minnesota wolf pack. In Proc. of the 1975 Predator Symp. Bulletin of the Montana Forest and Conservation Experiment Station Missoula, MT: University of Montana [Google Scholar]
- Mech L. D., Adams L. G., Meier T. J., Burch J. W., Dale B. W.1998The wolves of Denali. Minneapolis, MN: University of Minnesota [Google Scholar]
- Messier F.1994Ungulate population models with predation: a case study with the American moose. Ecology 75, 478–488 (doi:10.2307/1939551) [Google Scholar]
- Murray D. L.2006On improving telemetry-based survival estimation. J. Wildl. Manage. 70, 1530–1543 (doi:10.2193/0022-541X(2006)70[1530:OITSE]2.0.CO;2) [Google Scholar]
- Nilsen E. B., Linnell J. D. C., Odden J., Andersen R.2009Climate, season, and social status modulate the functional response of an efficient stalking predator: the Eurasian lynx. J. Anim. Ecol. 78, 741–751 (doi:10.1111/j.1365-2656.2009.01547.x) [DOI] [PubMed] [Google Scholar]
- Okarma H., Jedrzejewski W., Schmidt K., Kowalczk R., Jedrzejewska B.1997Predation of Eurasian lynx on roe deer and red deer in Bialowieza Primeval Forest, Poland. Acta Theriol 43, 203–224 [Google Scholar]
- Packard J. M.2003Wolf behaviour: reproductive, social, and intelligent. In Wolves: behaviour, ecology, and conservation (eds Mech L. D., Boitani L.). Chicago, IL: University of Chicago Press [Google Scholar]
- Peterson R. O.1977Wolf ecology and prey relationships on Isle Royale. United States National Park Service Sci. Monogr. Ser. 11, 1–210 [Google Scholar]
- Peterson R. O., Woolington J. D., Bailey T. N.1984Wolves of the Kenai Peninsula, Alaska. Wildl. Monogr. 88, 1–52 [Google Scholar]
- Rodgers A. R., Rempel R. S., Abraham K. F.1996A GPS-based telemetry system. Wildl. Soc. Bull. 24, 559–566 [Google Scholar]
- Sand H., Zimmermann B., Wabakken P., Andren H., Pedersen H. C.2005Using GPS technology and GIS cluster analyses to estimate kill rates in wolf–ungulate ecosystems. Wildl. Soc. Bull. 33, 914–925 (doi:10.2193/0091-7648(2005)33[914:UGTAGC]2.0.CO;2) [Google Scholar]
- Sand H., Wabakken P., Zimmermann B., Johansson O., Pedersen H. C., Liberg O.2008Summer kill rates and predation pattern in a wolf–moose system: can we rely on winter estimates? Oecologia 156, 53–64 (doi:10.1007/s00442-008-0969-2) [DOI] [PubMed] [Google Scholar]
- Smith D. W., Drummer T. D., Murphy K. M., Guernsey D. S., Evans S. B.2004Winter prey selection and estimation of wolf kill rates in Yellowstone National Park, 1995–2000. J. Wildl. Manage. 68, 153–166 (doi:10.2193/0022-541X(2004)068[0153:WPSAEO]2.0.CO;2) [Google Scholar]
- Smouse P. E., Focardi S., Moorcroft P. R., Kie J. G., Forester J. D., Morales J. M.2010Stochastic modelling of animal movement. Phil. Trans. R. Soc. B 365, 2201–2211 (doi:10.1098/rstb.2010.0078) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solomon M. E.1949The natural control of animal populations. J. Anim. Ecol. 18, 1–35 [Google Scholar]
- Spalinger D. E., Hobbs T. N.1992Mechanisms of foraging in mammalian herbivores: new models of functional response. Am. Nat. 140, 325–348 (doi:10.1086/285415) [DOI] [PubMed] [Google Scholar]
- Therneau T. M., Grambsch P. M.2000Statistics for biology and health. New York, NY: Springer [Google Scholar]
- Tomkiewicz S. M., Fuller M. R., Kie J. G., Bates K. K.2010Global positioning system and associated technologies in animal behaviour and ecological research. Phil. Trans. R. Soc. B 365, 2163–2176 (doi:10.1098/rstb.2010.0090) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vucetich J. A., Peterson R. O., Schaefer C. L.2002The effect of prey and predator densities on wolf predation. Ecology 11, 3003–3013 [Google Scholar]
- Webb N. F.2009Density, demography, and functional response of a harvested wolf population in west-central Alberta, Canada. PhD thesis, University of Alberta, Edmonton, Alberta, Canada [Google Scholar]
- Webb N. F., Hebblewhite M., Merrill E. H.2008Statistical methods for identifying wolf kill sites using GPS locations. J. Wildl. Manage. 72, 798–807 (doi:10.2193/2006-566) [Google Scholar]
- Zimmerman B., Wabakken P., Sand H., Pederson H. C., Liberg O.2007Wolf movement patterns: a key estimation of kill rate? J. Wildl. Manage. 71, 1177–1182 (doi:10.2193/2006-306) [Google Scholar]