Dynamic interactions between microbubbles in water

Abstract

The interaction between moving bubbles, vapor voids in liquid, can arguably represent the simplest dynamical system in continuum mechanics as only a liquid and its vapor phase are involved. Surprisingly, and perhaps because of the ephemeral nature of bubbles, there has been no direct measurement of the time-dependent force between colliding bubbles which probes the effects of surface deformations and hydrodynamic flow on length scales down to nanometers. Using ultrasonically generated microbubbles (∼100 μm size) that have been accurately positioned in an atomic force microscope, we have made direct measurements of the force between two bubbles in water under controlled collision conditions that are similar to Brownian particles in solution. The experimental results together with detailed modeling reveal the nature of hydrodynamic boundary conditions at the air/water interface, the importance of the coupling of hydrodynamic flow, attractive van der Waals–Lifshitz forces, and bubble deformation in determining the conditions and mechanisms that lead to bubble coalescence. The observed behavior differs from intuitions gained from previous studies conducted using rigid particles. These direct force measurements reveal no specific ion effects at high ionic strengths or any special role of thermal fluctuations in film thickness in triggering the onset of bubble coalescence.

Bubble dynamics has attracted scientific interest since the time of Leonardo da Vinci (1), yet the observation that some simple salts can prevent bubble coalescence at high concentrations whereas others cannot remains unexplained even after over a decade of systematic study (2). In themselves, bubble–bubble interactions are very important because they feature in diverse situations, from the basis of the bends in deep-sea divers, to the development of effective ultrasonic imaging contrast agents, through to enhancing the quality of champagne. However, the delicate and ephemeral nature of bubbles poses significant technical challenges to the precise quantification of the force-displacement characteristics of bubble collisions.

As a vapor phase in a liquid, the interaction between bubbles should be amenable to a simple explanation in terms of basic physical and chemical principles. A detailed understanding of the interaction between moving bubbles can provide the foundation on which to study the fundamental coupling between forces and deformations that defines the dynamic interaction on the nanoscale between soft-matter materials, such as bubbles, drops, emulsions, biological cells, soft tissues, and gels. Here we report direct measurements of the dynamic force between two deformable microbubbles in water under a variety of accurately controlled collision protocols. The typical collision velocities are in the regime of Brownian particles of comparable dimensions. The experimental conditions are such that only attractive van der Waals–Lifshitz forces and hydrodynamic interactions together with bubble deformations are expected to determine whether each collision event will result in bubble stability or coalescence.

The fundamental quantity that we measured was the force as a function of time between the two bubbles during different types of controlled collision events. Well-characterized experimental conditions have permitted precise theoretical modeling to elucidate the complex time dependence and coupling between forces, geometric deformations, and separation between the bubbles in the nanometer range. The questions we sought to answer were the following: To what extent is a collision event that results in bubble coalescence or bubble rebound controlled by attractive surface forces, by hydrodynamic interactions, and by the dynamic collision protocol? What are the hydrodynamic boundary conditions that hold at the air/water interface of nanometer-thick water films? Do structural forces or ion-specific effects at the air/water interface play a role? In our bubble collision experiments, how relevant is the often-invoked paradigm that bubble coalescence is triggered by thermally excited surface wave fluctuations whose amplitudes are then amplified by van der Waals–Lifshitz attraction (3)?

Thin liquid films formed in the Scheludko cell (4) had, for some time, been used as a model to study interaction between bubbles of millimeter radii. For instance, the equilibrium repulsive pressure due to electrical double-layer interactions between charged surfactants used to stabilize such films had been measured as a function of film thickness (4). The time-dependent approach of submillimeter size bubbles, under the influence of buoyancy force in aqueous glycerol solutions and polyglycol oils toward a deformable air-solution interface, had been quantified in terms of the rate of approach and coalescence times (5). The time evolution of the thickness profile of the water film trapped between a bubble emerging from a thin capillary and a flat quartz (6, 7) or mica (8) surface had been studied but the corresponding variations in the force between the bubble and the surface had not been measured. Recently, the dynamics of the encounter between small bubbles (diameter ≤ 100 μm) in ultraclean water rising under buoyancy toward a charged smooth titania plate has been measured (9) and modeled (10) in detail.

Results

An atomic force microscope (AFM) was used to produce precisely controlled single collision events between two ultrasonically generated microbubbles in the 100-μm-size range in aqueous salt solutions (11) (SI Text). One bubble was positioned on a smooth planar substrate and the other anchored at one end of a custom-fabricated rectangular microcantilever (Fig. 1 A–D). The bubble radii, contact areas, and contact angles were determined by optical microscopy. After careful alignment, head-on collisions between the bubbles were initiated by first moving the base end of the cantilever toward (“approach”) and then away (“retract”) from the planar substrate by a piezo-electric transducer whose displacement X(t) (Fig. 1E) was varied accurately with time, t, by a linear variable differential transformer. The maximum piezo-electric motor displacement was in the range 1.5–6 μm with motor speeds up to 50 μm/s. The time-dependent force between the colliding bubbles was obtained from recording the deflection of the cantilever that has a known spring constant.

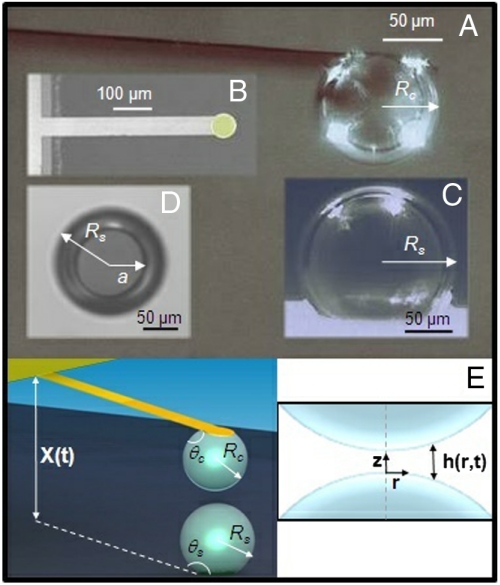
Fig. 1.

Microscopy photographs of bubbles in the AFM with schematics of the two interacting bubbles and the water film between them. (A) Side view of the bubble anchored on the tip of the cantilever. (B) Plan view of the custom-made cantilever with the hydrophobized circular anchor pad for the bubble. (C) Side perspective of the bubble on the substrate. (D) Bottom view of the bubble showing the dark circular contact zone of radius, a (in focus) on the substrate and the bubble of radius, R_s. (E) Schematic of the bubble geometry in the AFM and the axisymmetric coordinate system and water film thickness, h(r,t), between the bubbles.

Bubbles in water are known to develop a surface charge at the air–water interface, though the value is quite variable (8). Therefore we chose to work at a salt concentration of 0.5 M sodium nitrate (NaNO₃), which is close to that of seawater or hypertonic saline, that would effectively suppress all electrical double-layer repulsion between the bubbles. Also, it has been reported in light scattering studies of bubble swarms in aqueous electrolytes (12) that NaNO₃ retards bubble coalescence when present at concentrations above 0.1 M. This behavior at high salt is contrary to predictions of the classical Deryaguin–Landau–Verwey–Overbeek (DLVO) theory of colloidal stability (13) and so this experiment offered the possibility of detecting an ion-specific interaction force. Otherwise, the expected physical forces that can control bubble coalescence are as follows: (i) A surface tension force that minimizes the surface area of the bubbles and the way this affects bubble deformations is well described by the Young–Laplace theory (13); (ii) an attractive van der Waals–Lifshitz force between the bubbles for which accurate methods of calculating its magnitude from dielectric data, including effects due to electromagnetic retardation, is well known (13, 14); and (iii) a hydrodynamic force generated by relative bubble motion and the associated flow of water; where Reynolds lubrication theory (15) for flow in thin films gives a good description. A theoretical model (16) that encompasses all these features, (i–iii), was used to analyze our measurements.

Examples of different characteristic collision outcomes selected from about 100 collision experiments are given in Fig. 2 and compared to predictions of the theoretical model (solid lines). In all cases, the bubbles were initially stationary and undeformed at a distance of closest approach, h_o, in the range 1–6 μm. The cantilever-substrate separation, X(t), was then decreased by a prescribed amount that would ensure the bubbles were driven together beyond the point where they would have come into contact if they had not deformed. (see SI Text for the exact form of X(t)).

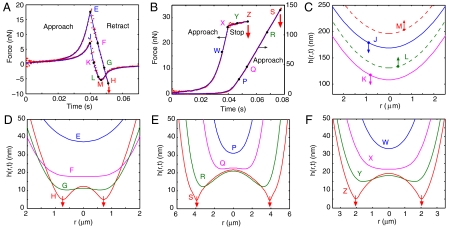
Fig. 2.

Measured and calculated time-dependent forces between interacting bubbles and the corresponding calculated water film thicknesses in the interaction zone. (A) Forces between the two identical bubbles (radii 74 μm) colliding during an approach-retract cycle at nominal speed 50 μm/s. Curve JKLM is first measured with initial separation h_o = 2.45 μm and then curve EFGH with h_o = 2.05 μm. Coalescence is indicated by the arrow at time H. Points are measurements and continuous lines are theoretical predictions. (B) Forces between two bubbles prior to coalescence under the continual approach protocol (right axis, bubble radii 62 and 86 μm, h_o = 5.50 μm, nominal speed 50 μm/s) or the approach-stop protocol (left axis, bubble radii 67 and 85 μm, h_o = 1.65 μm, nominal speed 50 μm/s). (C) Calculated water film thickness h(r,t) of the stable collision (curve JKLM of A) during the retraction phase with solid (broken) lines indicating decreasing (increasing) film thickness. (D) Calculated water film thickness during separation in the retraction phase (curve EFGH of A) leading up to coalescence indicated by arrows. (E) Calculated water film thickness during continual approach (curve PQRS of B) leading up to coalescence indicated by arrows. (F) Calculated water film thickness during approach-stop (curve WXYZ of B) leading up to coalescence indicated by arrows.

In Fig 2A, we show the time-dependent force F(t) during two consecutive measurements with the same bubble pair with identical radii 74 μm, colliding under identical approach–retract protocols at a nominal speed of 50 μm/s. The two measurements only differed in their initial separation, h_o. Because the van der Waals–Lifshitz force in this system was attractive at all separations, the observed repulsion on approach was due solely to hydrodynamic interaction, as water between the approaching bubbles had to be displaced. For the same distance traversed by the piezo-electric drive, the magnitude of the repulsive force maximum was determined by h_o. The continuous lines are predictions of the theoretical model with a fitted value of h_o that is within the expected experimental range. At h_o = 2.45 μm (curve JKLM), the force became attractive during the retraction phase but the bubbles did not coalesce and ultimately separated. This attraction was again of hydrodynamic origin as water has to be drawn into the gap between the separating bubbles. Similar behavior has also been observed between colliding emulsion oil drops in water (17).

Then for a repeat run with the same bubble pair under identical conditions but starting closer at h_o = 2.05 μm (curve EFGH), the magnitude of the repulsion on approach became higher because the bubbles were closer together initially, and so the same piezo-electric drive displacement resulted in larger deformations and larger forces. But as the bubbles were being separated, coalescence occurred instead of the appearance of an attractive force minimum (point H marked by the downward arrow in Fig. 2A). The coalescence time coincided with that predicted by theory. Furthermore, if we take a stable run using the same parameters as for curve JKLM but lower the nominal speed from 50 to 30 μm/s, coalescence could also occur as the bubbles are being separated. This counterintuitive “coalescence on separation” phenomenon has been observed between interacting polymer drops in silicon oil in elongational flowfields created in a four-roll mill (18) and between moving water drops in hexadecane in a microfluidic cell (19) but the forces involved were not measured.

The value of the initial separation, h_o, between the bubbles lies within the expected experimental range, and the predicted results matched all key features of the force curve, namely, the magnitude and location of the repulsive force maximum on approach, the depth and location of the attractive force minimum, or the location and force magnitude at the point of coalescence on retraction. In this way, the value of h_o can be determined to within ± 0.01 μm (see SI Text for a discussion of the sensitivity of h_o in fitting the force data).

In Fig. 2B, we show the force between two bubbles driven under two different collision protocols. In one collision event (curve PQRS, bubble radii 62 and 86 μm, h_o = 5.50 μm), the bubbles were driven together continually at a nominal speed of 50 μm/s to give a force that is about 8 times larger than the maximum at point E of Fig. 2A. This “approach only” collision resulted in bubble coalescence at point S. In the other collision event in Fig. 2B (curve WXYZ, bubble radii 67 and 85 μm, h_o = 1.65 μm, nominal approach speed of 50 μm/s), the bubbles were driven together to a moderate repulsive force of about twice that at the maximum in Fig. 2A (point E) then the piezo-electric drive was stopped rather than retracted to create an “approach-stop” collision. From this point on, the force between the bubbles remained approximately constant (curve XYZ) while the water film between the bubbles continued to thin, and coalescence occurred spontaneously in this constant force region at point Z (Fig 2B), some time after the piezo-electric drive had stopped. This approach-stop protocol mimics the situation in drainage experiments of foam films (3). The time interval from when the piezo-electric drive stopped and the point of coalescence is sometimes referred to as the induction time in the context of bubble attachment or coalescence.

In contrast to intuitions gained from studying the interactions between solid colloidal particles (13), in which coagulation will result whenever the driving force is sufficiently high to overcome the so-called primary maximum, the stability vs coalescence behavior between colliding bubbles is more complex because of surface deformations. The results in Fig. 2 A and B demonstrate the unexpected observation that lower forces are required to achieve coalescence by either an “approach-retract” or approach-stop motion than the approach-only collision. For instance, the magnitude of the force required to bring about coalescence by the approach-only protocol (curve PQRS) is about 8 times larger than the approach-retract collision (curve EFGH).

The excellent agreement between experiment and theory seen here and in all other comparisons required the use of the no-slip or immobile interface hydrodynamic boundary condition at the bubble surface. In other words, the air–water interface behaved like a solid surface in so far as its hydrodynamic response is concerned. On the other hand, using the fully mobile or no tangential stress boundary condition, normally assumed to be valid at the air–water interface, will underestimate the magnitude of the dynamic force by over four orders of magnitude, and the predicted coalescence times will be too short because hydrodynamic effects under this boundary condition are much weaker (20). Although measurements of the terminal velocities of rising bubbles (21, 22) show that the fully mobile boundary condition is applicable in ultraclean water, such degree of cleanliness is impractical to achieve in our experiments. Quantitative estimates suggest that a surface concentration of surface-active species that reduces the interfacial tension by ∼1 mN/m would be sufficient to cause bubbles to exhibit the no-slip boundary condition (23).

Discussion

Given the quantitative success of the model, it can be used with confidence to predict the spatial and temporal variations of the thickness of the water film, h(r,t), between the bubbles (see Fig. 1E for definition) even though the separation between the bubbles is not a quantity that is directly accessible from our force measurements. Furthermore, detailed consideration of our predicted results allows us to quantify the mechanism of bubble coalescence. First, we consider the space-time variations of the water film thickness between the bubbles during stable collisions and during coalescence events under various collision protocols. This will reveal the distinct stages of bubble deformation that leads up to coalescence. We also see that the coalescence times can be predicted quite accurately under different collision protocols. The model we used assumed that bubble deformations were always axisymmetric. The good agreement in the time-dependent force and the coalescence times of different collision modes suggests that this is a reasonable assumption for our well-controlled bubble collision experiments. However, a variety of nonaxisymmetric drainage patterns that precede bubble coalescence have also been observed (24), but the precise circumstances and reasons of when and how such asymmetric patterns arise had not been fully explored. Nonetheless, our comparison between theory and experiment has also allowed us to ascertain whether structural forces or specific ion effects have a role in these bubble coalescence studies.

Stable Collisions.

Because there is excellent agreement between theory and experiment for the force between colliding bubbles, we can use the same theory to calculate the thickness of the central portion (∼a 5 μm region) of the water film between the two bubbles (∼60–90 μm radius) where bubble–bubble interaction takes place. Results for the approach and retract experiment without coalescence (Fig. 2A, curve JKLM) are shown in Fig. 2C. When the film is at its thinnest for this stable case (curve K in Fig. 2C) with minimum thickness ∼110 nm, the flattening of each bubble is estimated to be 35 nm at the center of the film around r = 0. At the attractive force minimum (point M in Fig. 2A), the film profile is given by curve M in Fig. 2C. Although the interaction force is the most attractive at this point, the film is actually increasing in thickness. As the film thickness at this point is in excess of 200 nm, the effect of the attractive van der Waals–Lifshitz surface force is negligible. Thus, in stable collisions under the “approach and retract” protocol, the measured collision forces arise solely from long-ranged hydrodynamic effects and only the no-slip or immobile boundary condition at the bubble surface is capable of giving rise to forces of the observed magnitude.

Different Coalescence Behavior.

The space-time variations of the water film thickness, h(r,t), between the bubbles are similar for all three coalescence cases corresponding to curve EFGH in Fig. 2A and both curves in Fig. 2B. For instance, the evolution of the central portion of the film shown in Fig. 2D corresponds to the force curve EFGH in Fig. 2A. Note the characteristic sequence of film deformations between the bubble surfaces in Fig. 2D: First, the film thins (curve E) while the bubbles remain essentially undeformed. Then the central portion of the bubble surface flattens (curve F) due to repulsive hydrodynamic forces. As this occurs at a separation of around 18 nm, the effect of attractive van der Waals–Lifshitz force is still negligible. When the hydrodynamic pressure starts to exceed the Laplace pressure of the bubbles, their surfaces dimple (curve G). Finally, the bubbles coalesce (curve H) when the thinnest portion of the film located at the dimple radius becomes sufficiently thin (∼5 nm) for the attractive van der Waals–Lifshitz force to destabilize the film (indicated by arrows). A similar sequence is also observed in the film profiles in Fig. 2 E and F.

What differentiates the three coalescence cases (curve EFGH in Fig. 2A and both curves in Fig. 2B) is the time at which the water film flattens and forms the dimple in relation to the approach and retract timing of the piezo-electric drive. For the coalescence on separation case (curve EFGH in Fig. 2 A and D), interfacial flattening first occurs well into the retraction phase (F) and dimple formation (G) occurs close to the coalescence point (H). In contrast, for the “continual approach” case (curve PQRS, Fig. 2B), the water film between the bubbles forms a hydrodynamic dimple during the approach phase (Fig. 2E) and then coalescence occurs while the bubbles are still being driven together. On the other hand, in the approach-stop case (curve WXYZ, Fig. 2B), the water film begins to form a dimple (curve X in Fig. 2F) corresponding to point X of Fig. 2B, just as the piezo-electric drive has stopped in the constant force region, and then the bubbles coalesce later at point Z. However, in all cases, coalescence occurs at the dimple rim that is also the thinnest part of the water film. Thus when the local minimum in film thickness falls below about 5 nm and thus within the range of the attractive van der Waals–Lifshitz force, the film ruptures very quickly on the timescale of the experiment. In all cases, the local minimum in film thickness occurs at the dimple rim. Just prior to coalescence, the thickness of the water film is not constant, but can vary by up to a factor of 4 across the interaction region in the examples shown.

In the approach-stop case (curve WXYZ, Fig. 2B), during the induction phase between when the piezo-electric drive has stopped (point X) and when the bubbles coalesce (point Z), the film thickness at the dimple rim decreases while the central portion of the film around r = 0 actually increases in thickness, between points Y and Z. Again, coalescence only occurs when the local film thickness at the dimple rim drains to below about 5 nm and falls within the range of the attractive van der Waals–Lifshitz force.

The theoretical film profiles in Fig. 2 C–F are calculated from an axisymmetric model. At the point of the film rupture, which is a very rapid process compared to the observed approach and drainage timescales, axial symmetry is unlikely to be preserved. The axisymmetric behavior we observed in this study is due in part to the careful alignment of the interacting bubbles in the force measurement experiment to ensure head-on collisions and in part to the simplicity of the bubbles-in-water system in which water behaves like a Newtonian liquid. In similar film thinning studies using the Surface Force Apparatus, complex drainage film patterns are observed when non-Newtonian fluids are involved (25).

As two bubbles approach each other, the hydrodynamic pressure between the bubbles will increase and, in response, the bubbles will flatten. When this pressure around the region of closest approach between the bubbles starts to exceed the Laplace pressure of the bubble, the curvature of the bubble surface will change sign and a dimple will form. Thus, dimple formation prior to coalescence in our experiments was due to the hydrodynamic pressure that built up around the point of closest approach. However, if the bubbles are brought together very slowly, much slower than the drive speeds used in the present experiments, the attractive van der Waals–Lifshitz interaction between bubbles will in fact pull the portion of the bubbles that are in close proximity toward each other to form a pimple and coalescence will take place around the axis of symmetry between the bubbles rather than at the dimple rim. A detailed exposition of these modes of coalescence and other transient responses of interacting deformable interfaces has been given recently based on the present theoretical framework (26).

The physical origin of the coalescence on separation phenomenon observed in Fig. 2A (curve EFGH) has been investigated by perturbation analysis of the governing equations for the approach-retract collision in the AFM geometry (27) and in the Hele–Shaw cell geometry of microfluidic cell experiments (28). During approach, the deformable bubble surfaces respond to the repulsive hydrodynamic pressure by flattening so that the distance of closest approach decreases slower than would be for nondeforming bubbles. Similarly, during retraction, the resulting attractive hydrodynamic pressure causes the bubble surfaces to deform toward each other so that distance of closest approach increases more slowly than nondeforming bubbles. However, if the retraction speed is fast enough, this will bring the surfaces of the two bubbles sufficiently close together for them to be destabilized by the attractive van der Waals–Lifshitz interaction.

Coalescence Times.

We analyze each set of collision force data to determine the value of the initial separation, h_o to within ± 0.01 μm. This will produce agreement between theory and experiment for the force as a function of time to the degree shown in Fig. 2 A and B. For cases in which the collision leads to coalescence, we can determine the theoretically predicted coalescence times and compare them to experimentally observed values. The theoretical coalescence time is taken to be the time when the minimum separation between the bubbles falls below a cutoff value of 1 nm. Under the influence of van der Waals attraction, the minimum separation decreases very rapidly when it is less than 5 nm, so setting the cutoff separation between 0 and 2 nm would give essentially the same coalescence times.

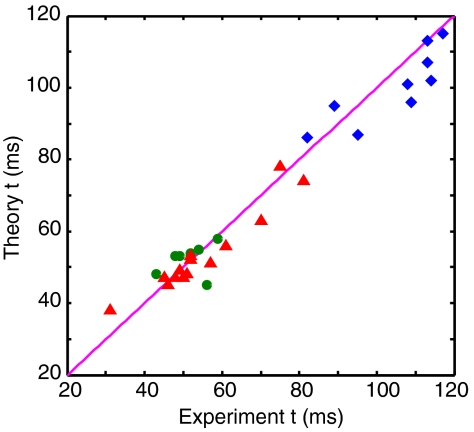
The results in Fig. 3 demonstrate the excellent agreement between the observed and predicted coalescence times for the two different drive modes of dynamic bubble interaction: approach-retract and approach-stop, collected from 30 coalescence experiments. This is very strong evidence that the coalescence time can be predicted accurately with the present model and that coalescence occurs when the local film thickness at the dimple rim becomes thin enough to fall within the range of attractive surface forces to destabilize the film. This mechanism operates irrespective of whether the bubbles are approaching or separating. Whereas the same drive mode gives rise to a range of coalescence times due to slight variations in the initial separation, the good agreement between experiments and the model indicates that the coalescence process is a deterministic process with coalescence times governed by physical parameters of the collision rather than triggered by instabilities due to random surface fluctuations as commonly thought (3).

Fig. 3.

A comparison of experimental and theoretical coalescence times measured from the start of the approach phase for coalescence-on-separation (▵), coalescence-on-approach (◊), and coalescence on stopping of the piezo-electric drive after approach (○) from 30 measurements.

Surface Fluctuations.

What then is the role of thermally excited surface fluctuations that have been postulated as a precursor that triggers coalescence? A linear stability analysis of a quiescent infinite parallel water film of thickness h_o and with immobile hydrodynamic boundary condition at the air–water interface concluded that fluctuations of the interface with wavelengths that exceed a critical value λ_c will be unstable and will lead to coalescence (29, 30). With a Hamaker form 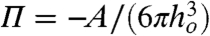for the van der Waals–Lifshitz disjoining pressure, the critical wavelength is 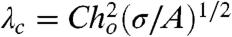, where C = 2π^3/2 or (128π)^1/2, depending on the approximation used. Taking h_o ∼ 20 nm (see Fig. 2 D–F) and A = 5.01 × 10^-20 J (see SI Text), λ_c is comparable to the dimension of the bubbles and is much larger than the flattened portions of the bubbles. Thus, surface fluctuations would not be expected to play a role in the coalescence mechanism in our experiments.

Structural Forces and Specific Ion Effects.

If we apply the DLVO theory of colloid stability to colliding bubbles, they would be expected to be stable at low electrolyte concentrations because long-ranged electrical double-layer repulsion would prevent the bubbles from approaching close enough for attractive van der Waals–Lifshitz interaction to have any effect. However, at high salt concentration, such repulsion will be screened out and coalescence will occur due to van der Waals–Lifshitz attraction. Recent light scattering studies of coalescence in bubble swarms in various aqueous inorganic electrolytes (2, 12) reported that some ion pairs have no effect on bubble coalescence, whereas others inhibit bubble coalescence when present at high concentrations, typically above 0.1 M. For example, sodium perchlorate (NaClO₄) was found not to inhibit bubble coalescence at any concentration, whereas sodium nitrate (NaNO₃), used in our experiments, inhibited bubble coalescence at concentrations above 0.1 M (12).

Our collision studies show that bubbles in aqueous electrolytes of 0.5 M NaNO₃ do coalesce and the behavior is indistinguishable from that in electrolytes of NaClO₄ at the same concentration (see SI Text for detailed results). Furthermore, bubbles are totally stable at a much lower concentration 0.02 M of NaNO₃. Thus, the concentration effect of NaNO₃ in our bubble coalescence studies follows the general trend predicted by the DLVO theory with no evidence of ion-specific stability behavior. Our dynamic force measurements correspond to bubble–bubble collisions at low speeds or low Reynolds numbers, whereas some evidence of ion-specific effects on binary bubble collisions at high Reynolds numbers have been observed (31). Ion partitioning has recently been proposed (32) as the link to the extensive correlations between ions pairs and their ability or otherwise to prevent coalescence at high concentrations. However, a detailed physical mechanism to relate this to collision dynamics remains elusive.

Through detailed measurements and accurate modeling, we demonstrate unambiguously that, under dynamic conditions, when hydrodynamic effects and bubble deformations are both important, there exist two dynamic modes of bubble coalescence: as the bubbles approach or counterintuitively, as they separate. Coalescence on separation is the mechanism that requires less driving force to induce coalescence. Basically, coalescence will occur when the local separation between two bubbles becomes close enough for attractive van der Waals–Lifshitz forces to destabilize the intervening water film. In our head-on collision experiments, the thinnest portion of the film, which is located around the dimple ring, can become small enough when the bubbles are approaching or when they are separating, depending on the mode of collision. There is no need to invoke the mechanism of thermal fluctuations in film thickness to trigger coalescence. Indeed, knowing the collision conditions, the coalescence time can be predicted accurately. However, the final details of the film rupture process occur on too short a timescale to be monitored using the AFM. Whereas structural forces or specific ion forces at high salt concentrations may be present at the air–water interface, they do not appear to have any detectable influence on the bubble coalescence or film rupture processes in our experiments. Indeed, we found that the effects of electrolyte concentration on the coalescence of bubbles follow the general expectation from the classical DLVO theory of colloid stability.

Methods

Experimental.

The bubble colloidal probe technique developed earlier (11) for the Asylum MPF-3D AFM was used in the present dynamic coalescence experiments. The substrates were circular glass slides (35 mm liquid cell substrates, Asylum Research) mildly hydrophobized to give water contact angles in the range of 20–60°. Bubbles on the glass substrate were generated by ultrasonication with an ELAC Nautik ultrasonic device with radio frequency generator type LVG 60-10.

The rectangular silicon cantilevers were custom-made with a circular end platform (Fig. 1B) to facilitate easy bubble pickup and precise, secure anchoring. The cantilever dimensions were 450 × 50 × 2 μm and the circular platform had a diameter of 65 μm with a 20-nm-thick gold coating. The gold-coated platform was hydrophobized by immersing the cantilevers for several hours in 10 mM n-decanethiol solution in ethanol. The cantilever spring constant was measured using the Hutter and Bechhoefer (33) thermal tune function of the Asylum MFP-3D software.

A chosen bubble was picked from the glass surface and anchored on the hydrophobized circular platform of the cantilever to form a bubble colloidal probe (Fig. 1A). Before each bubble collision measurement, microscopy photographs of the cantilever and substrate bubble were taken using the inverted microscope optical system attached to the AFM (Fig. 1C), from which the radius of the cantilever bubble, R_c, and the surface bubble, R_s, as well as bubble-substrate contact zone radius, a, could be measured. The contact angles θ_c, θ_s (Fig. 1E) deduced from these measurements were in the range of 130–160°.

For further details of the experimental method see SI Text.

Theory.

The governing equations we use had been developed previously to describe dynamic interactions between deformable drops and bubbles in liquid at separations that are small compared to their size (34). Although dynamic interaction under a constant external force in the absence (35) and presence (36, 37) of surface-active species has been studied by extensive numerical modeling, there has been no detailed comparisons with relevant experiments. In the absence of added surface-active species, the interface between fluid phases was generally assumed to be fully mobile and therefore could not sustain any shear stress. However, this assumption would lead to predicted forces between bubbles (38, 39) that are smaller than the dynamic forces that we measured by orders of magnitude. In fact, we observed that our experimental results were consistent with bubble surfaces that are immobile as described by the no-slip hydrodynamic boundary condition. To facilitate comparisons with our collision experiments on the AFM, an appropriate description of the collision protocol between two incompressible but deformable bubbles also had to be developed to provide the correct boundary condition to augment the governing equations (16, 40).

Hydrodynamic interaction between the bubbles was modeled with the Reynolds lubrication theory for the movement of water with dynamic viscosity, μ, in the thin film between the bubbles. With the no-slip or immobile boundary condition at the bubble surface and assuming axial symmetry is maintained during head-on bubble-bubble collisions, the film thickness, h(r,t), and the hydrodynamic pressure, p(r,t), were related by

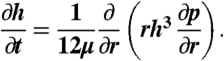The Young–Laplace equation

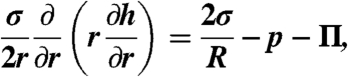where 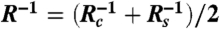, was used to describe deformations of the bubbles (assumed to have constant interfacial tension, σ) due to the hydrodynamic pressure, p(r,t), and the disjoining pressure, Π[h(r,t)], that accounted for the surface force per unit area between the bubbles. The contribution from van der Waals–Lifshitz attraction to the vapor–water–vapor disjoining pressure was calculated using the complete Lifshitz formula (14) with full account of electromagnetic retardation effects. The most recent dielectric data for water were used which, at small separations (< 1 nm), gave a Hamaker constant of 5.61 × 10^-20 J or 5.01 × 10^-20 J if the zero frequency term was omitted (41).

The piezo-electric drive displacement X(t) enters via the boundary condition

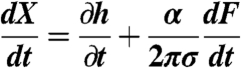imposed outside the interaction zone of the water film between the interacting bubbles at r = r_max, where the solution domain is 0 < r < r_max.

The quantity α is a known function of the radii (R_c,R_s) and contact angles (θ_c,θ_s) of the bubbles (16). This boundary condition follows from a constant volume constraint on the bubbles and is a key and crucial difference between our model for AFM experiments (16) and previous work. The governing equations can be solved numerically by the method of lines (42). Implicit in this model is the assumption that all deformations and separations are small compared to the radii of the bubbles, a condition well satisfied in the present experiments.

For further details of the theoretical model see SI Text.

All parameters of the model were taken from independent measurements and used without adjustment. During interaction, we assumed the three-phase contact line at the base of the bubble on the cantilever and on the surface were pinned and did not move during bubble collision. This was a reasonable assumption for the bubble on the cantilever as it was anchored on the circular hydrophobic platform at the tip of the cantilever. An alternative to the pinned three-phase contact line condition on the surface is the assumption of a constant contact angle condition, while the three-phase line is free to slide along the surface. This boundary condition provides equally good agreement with experimental data as the deformations of the bubbles are small compared to the bubble radii.