Space observations of cold-cloud phase change

Abstract

This study examines the vertically resolved cloud measurements from the cloud-aerosol lidar with orthogonal polarization instrument on Aqua satellite from June 2006 through May 2007 to estimate the extent to which the mixed cloud-phase composition can vary according to the ambient temperature, an important concern for the uncertainty in calculating cloud radiative effects. At -20 °C, the global average fraction of supercooled clouds in the total cloud population is found to be about 50% in the data period. Between -10 and -40 °C, the fraction is smaller at lower temperatures. However, there are appreciable regional and temporal deviations from the global mean (>  ± 20%) at the isotherm. In the analysis with coincident dust aerosol data from the same instrument, it appears that the variation in the supercooled cloud fraction is negatively correlated with the frequencies of dust aerosols at the -20 °C isotherm. This result suggests a possibility that dust particles lifted to the cold cloud layer effectively glaciate supercooled clouds. Observations of radiative flux from the clouds and earth’s radiant energy system instrument aboard Terra satellite, as well as radiative transfer model simulations, show that the 20% variation in the supercooled cloud fraction is quantitatively important in cloud radiative effects, especially in shortwave, which are 10 - 20 W m^-2 for regions of mixed-phase clouds affected by dust. In particular, our results demonstrate that dust, by glaciating supercooled water, can decrease albedo, thus compensating for the increase in albedo due to the dust aerosols themselves. This has important implications for the determination of climate sensitivity.

Cold clouds that consist of mixed-phase particles, are ubiquitous in the Earth’s upper and middle troposphere. Changes in the liquid/ice-phase composition in such clouds may significantly affect the radiative balance of the earth atmosphere system because the cloud radiative properties for both the shortwave (SW) and longwave (LW) such as cloud optical depth, single-scattering albedo, and emissivity vary according to the phase of cloud particles (1–3). It is therefore of fundamental importance to examine the variation in the cloud-phase composition for accurate calculations of cloud radiative effects.

In fact, the cloud-phase composition in mixed-phase clouds is complicatedly affected by several factors other than temperature; e.g., ice nuclei (IN) aerosols. Most of climate models, however, have calculated the cloud-phase composition with limited sophistication, simply as a function of grid-mean temperature (4). For example, it has been typically assumed that clouds are composed entirely of ice and liquid particles below -40 °C and above 0 °C, respectively, of a mixture of ice and liquid phases between -40 and 0 °C. The fraction of supercooled liquid particles within mixed-phase clouds is represented as a linear function of temperatures in general. Because such an oversimplified cloud-phase partitioning method can lead to errors in calculating cloud radiative effects within a climate model, several ice nucleation processes based on theoretical and empirical studies have been developed recently for a more physical treatment of the nucleation processes in climate models (4–7). These works, however, are only partially successful because the microphysical processes involved in ice nucleation are not yet fully understood (8), and that the exact number concentrations and size distributions of IN cannot be calculated during the course of model integrations. Here, we examine the cold-cloud phase composition associated with dust that can act as IN in natural atmospheric conditions. As we will discuss in this paper, retrievals of cloud and aerosol properties from currently available remote sensors are very useful for this purpose.

This study analyzes the vertically resolved observations of clouds and dust aerosols from the National Aeronautics and Space Administration’s (NASA) spaceborne lidar instrument, cloud-aerosol lidar with orthogonal polarization (CALIOP) (9) to examine the global distribution of the supercooled cloud fraction (SCF), defined as the fraction of supercooled clouds within a total cloud population (see Materials and Methods). The capability of the CALIOP algorithm to retrieve vertical profiles of clouds and dust aerosols simultaneously over the globe is especially advantageous for this purpose because it allows us to focus on cloud properties associated with a particular isotherm and to permit isolating factors other than temperature. The role of the SCF values in calculating the mixed-phase cloud optical thickness receives special attention here. It is followed by discussions of the radiative effects of SCF change using the observed radiative flux data from the clouds and the earth’s radiant energy system (CERES) and radiative transfer model simulations.

1. Results

1.1. Observed Supercooled Clouds and the Relations with Temperatures and Various Types of Dust.

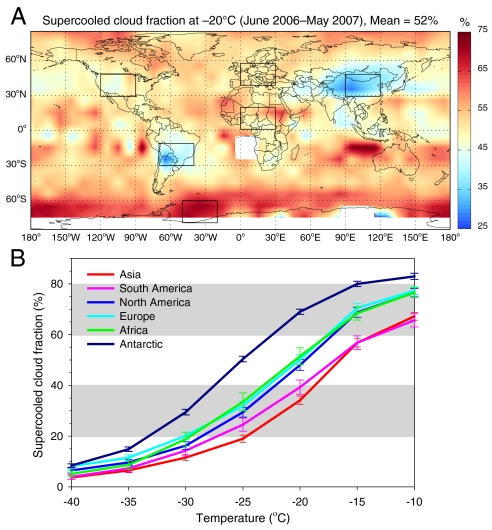
At -20 °C, the global annual average SCF as determined from CALIOP retrievals is 52% (Fig. 1A). The nearly equal probability of liquid- and ice-phase particles occurring at -20 °C is consistent with estimates from many previous cloud chamber experiments that showed homogeneous ice nucleation at -40 °C (10), and is also expected in the improved CALIOP algorithm (11). It is suggestive that the annual mean SCF undergoes substantial regional variations. Smaller SCF values (< 30%) are dominant in Asia and South America, whereas higher SCF values (> 70%) are dominant in the high latitudes (60–90°). SCF is larger in the southern-hemispheric high latitudes than in the northern-hemispheric high latitudes. Over the tropical oceans, the SCF is variable on smaller spatial scales.

Fig. 1.

(A) Annual mean (June 2006–May 2007) SCF at -20 °C isotherm. The fraction is lowest over the Asian continents and South America, but highest over the Southern Hemisphere high latitudes. (B) Annual mean supercooled cloud fraction with respect to temperature over the selected regions in (A): Asia, South America, North America, Europe, Africa, and the Antarctic. The error bar corresponds to a standard error of ± 3.

The change in the SCF occurs at all subfreezing (< 0 C°) temperatures. The SCF values averaged for six regional divisions in Fig. 1A are directly related with temperatures (Fig. 1B). The regional difference in SCF is conspicuous between -40 and -10 °C. The SCF in Asia and South America is lower than that in the Antarctic; the difference is generally > 20% above the -30 °C level and < 20% below the level. The SCF value at -40 °C may be used as an indicator of substantial uncertainty level in our data (about 10%); this may originate from horizontally oriented ice particles (11) and/or quasispherical ice particles (12). However, it is noted that the concentration of these particles is very small at temperatures warmer than -20 °C (11, 12), and the uncertainty should be much smaller than 10% in that temperature range. Given a 10% measurement error, the observed largest regional difference of 30% in an annual average is unlikely to be an artifact. The SCF for North America, Europe, and Africa is in between those in Asia and the Antarctic. Thus, factors other than temperature should be considered in determining SCF.

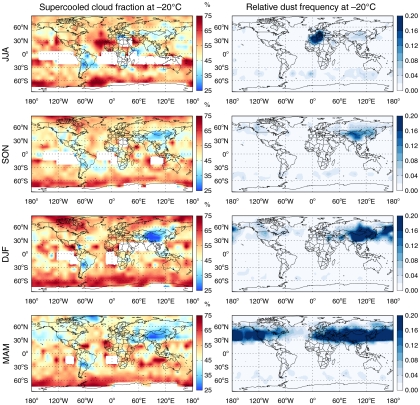
One clear possibility is that the regional difference of the SCF is due to dust aerosols that can serve as IN. There is a theoretical basis for the hypothesis that an increase in IN aerosols decreases SCF by promoting heterogeneous nucleation (10, 13). The SCF and the relative dust frequency (see Materials and Methods) are calculated for the -20 °C isotherm (Fig. 2). Significant correspondence between the SCF and the dust frequency can be found, especially in the Northern Hemisphere. In particular, the decrease in SCF over Asia from June-July-August (JJA) to March-April-May (MAM) is highly correlated with the increase in the dust frequency during the same period (correlation coefficient ≈-0.8). In MAM, the Asian dusts that reach the -20 °C level (about 5 km altitude) appear to have been transported into all of the midlatitude regions; correspondingly, SCF is low over the entire midlatitude regions, including North America and Europe. The total-column optical depth of aerosols over the Saharan dust region is known to be the highest in the world. The vertically resolved CALIOP data show, however, that Saharan dust aerosols mostly reside within the boundary layer and do not rise above the freezing level (Fig. 2). The negligible dust frequency and moderate SCF at the -20 °C level in this region imply that the reduction in SCF occurs only when a sufficient amount of dust is supplied to mixed-phase cloud layers.

Fig. 2.

Seasonal variation in SCF and relative dust frequency (to the highest dust frequency), both at the -20 °C isotherm. Pattern correlation coefficients between SCF and dust frequency for the Northern Hemisphere are negative for all seasons: -0.1, -0.5, -0.5, and -0.6 for JJA, September-October-November (SON), December-January-February (DJF), and MAM, respectively.

In the Southern Hemisphere, very small SCF values occur over the South American continent. A majority of aerosols in this region originate from biomass burning in the Amazon region (14). The IN potential of these aerosols has been observed in many field experiments (15, 16–19). Andreae et al. (19), for example, reported that the reduction in the size of cloud droplets and the delay in the onset of precipitation within smoky warm clouds in the Amazon region allow more aerosols and moisture to reach higher altitudes by means of updrafts. This may also be enhanced by the high terrain of the Andes where the very small SCF values appear. However, neither dust nor biomass-burning aerosols have been detected by CALIOP in this region during the period, and could not be explicitly related to ice nucleation in this study.

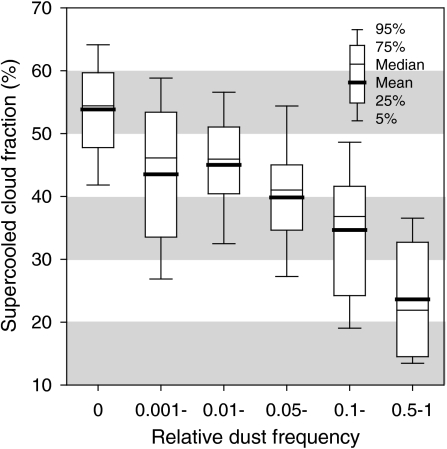
Fig. 3 shows the dependence of SCF on the relative dust frequency at the -20 °C level. The box plots summarizing the distribution, mean, median, and variability are based on the monthly means of the SCF and the relative frequency of dust. To minimize sampling errors, the monthly means are taken only from the regions where their temporal correlation is significant at the 95% confidence level (such regions take about 5% of the globe). Note that the relative frequency of dust is binned in logarithmic intervals, indicating a semilogarithmic relationship between SCF and the relative frequency of dust. For relatively clean air without dust aerosols, the SCF at the -20 °C level is about 50–60%; this can be reduced to 15% in the presence of dust aerosols. Based on our synthetic results (Figs. 1, 2, and 3), it appears that the difference between the maximum and minimum SCF can be as large as 40%. Thus a 20% reduction in SCF, to be discussed next, is a reasonable assumption for dusty regions.

Fig. 3.

Dependence of SCF on relative dust frequency (to the maximum dust frequency) at the -20 °C isotherm. Plots are monthly means taken from the regions where the correlation is significant at the 95% confidence level.

1.2. Radiative Effect of Supercooled Clouds.

Radiative transfer theory indicates that SCF is a dominant factor in determining the mixed-phase cloud radiative effect (CRE; also called cloud radiative forcing) because the fundamental optical properties (i.e., extinction optical thickness, single-scattering albedo, and asymmetry factor) of mixed-phase clouds are calculated in terms of SCF-weighted averages of the liquid and ice cloud paths. In particular, the cloud optical thickness that governs cloud albedo is strongly dependent on SCF. Note that a smaller SCF implies a smaller liquid portion and a greater ice portion. Because liquid cloud particles generally have a larger extinction optical thickness than ice particles, the optical thickness of mixed-phase clouds is expected to decrease in proportion to the reduction in SCF. Radiative-transfer model simulations (see Materials and Methods) show that a 20% decrease in the liquid water path (i.e., a 20% increase in the ice water path) may result in a reduction in cloud optical thickness of approximately 25% (Table 1).

Table 1.

Simulated change in cloud optical thickness when the liquid water path decreases by 20% and the ice water path increases by 20%

	CWP, g m-2
	10	50	100	200	300	400	500
Case 1	−0.25 (27)	−1.26 (27)	−2.52 (27)	−5.05 (27)	−7.57 (27)	−10.09 (27)	−12.61 (27)
Case 2	−0.17 (22)	−0.84 (22)	−1.68 (22)	−3.36 (22)	−5.03 (22)	−6.71 (22)	−8.39 (22)

Case 1 is for r_e,liq = 11 μm and r_e,liq = 100 μm. Case 2 is for r_e,liq = 14 μm and r_e,ice = 60 μm. The percentage of the change in the total optical depth is in parentheses.

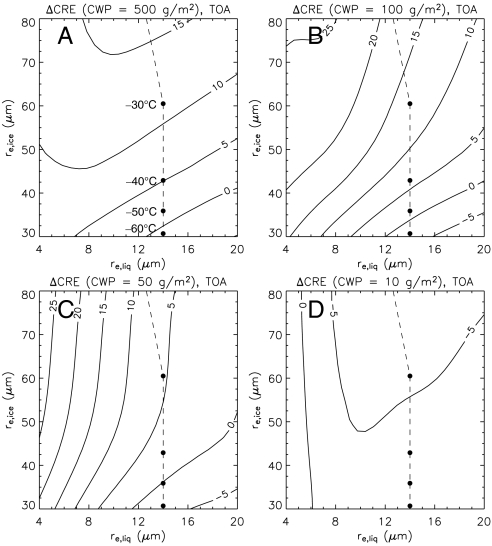
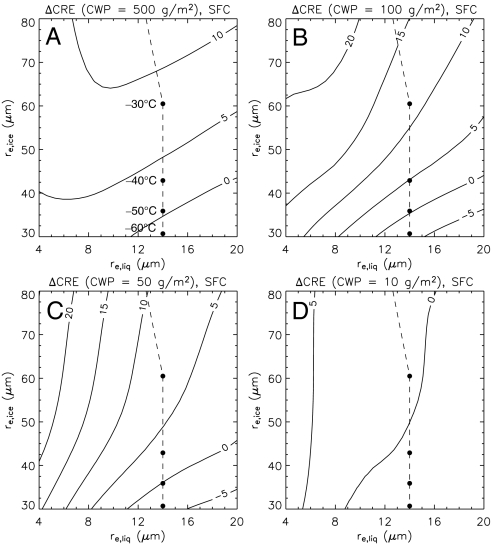
Figs. 4 and 5 show the sensitivity of the CRE difference to the effective radii for a given cloud water path (CWP) when liquid (ice) water content decreases (increases) by 20%; Figs. 4 and 5 are for the top of the atmosphere (TOA) and the surface, respectively. The difference in net CRE is generally positive (i.e., warming), although it depends on r_e,liq, r_e,ice, and CWP in a complicated way. The dashed line indicates the empirical relationship between the effective radii and the cloud temperature by Kristjánsson and Kristiansen (20), one of the most frequently used schemes in climate models. Under this particular constraint, the climate models also simulate the warming.

Fig. 4.

Change in CRE of mixed-phase clouds at TOA when liquid (ice) water content decreases (increases) by 20%. Warming is positive, and cooling is negative. The dashed line indicates the effective radii of cloud particles over land, as diagnosed by temperature in most global climate models.

Fig. 5.

The same as Fig. 4, but for the earth’s surface.

Boundary-layer warm (or nonprecipitating) clouds have CWP close to 50 g m^-2, and cirrus clouds have a CWP of 10 g m^-2 or less. The CRE difference at the TOA and the surface is < 10 W m^-2 for clouds with a CWP < 50 g m^-2 (Fig. 4). In this case, the CRE difference is more sensitive to the effective radii of liquid particles than to those of ice particles (Figs. 4 and 5); the smaller the particles, the larger the CRE difference. For clouds with a CWP < 10 g m^-2, slight cooling (approximately -5 W m^-2) occurs for the TOA and the atmosphere; this is because of the dominant decrease in LW CRE instead of in SW CRE. This cooling increases with lower cloud-top temperatures, but the entire impact of these unusual cases on climate is expected to be minor because they are so rare.

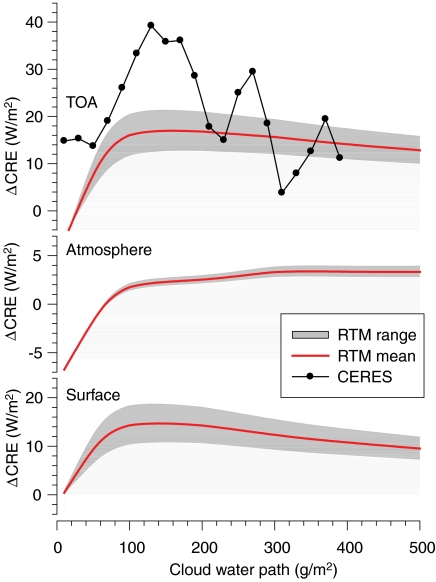
The corresponding difference in the net CRE (the sum of SW CRE and LW CRE) in response to a 20% reduction in SCF is summarized in Fig. 6. Overall, the difference in the net CRE is generally positive except for very small total CWP (< 20 g m^-2). The warming in common mixed-phase clouds (clouds with CWP = 100–500 g m^-2, which take > 80% of the total mixed-phase clouds based on recent satellite retrievals) (21–23) could be up to 25 W m^-2 at TOA.

Fig. 6.

Observed and simulated CRE differences at TOA, the atmosphere, and the earth’s surface, in response to a 20% reduction in SCF with respect to total cloud water path. The observations are from CERES SFC data obtained during 2004, with values statistically significant at a 95% confidence level. Possible ranges of the simulated values are shaded, and the means are indicated by red lines.

At the earth’s surface, the CRE difference is generally positive, but with a smaller intensity compared to that at the TOA (Fig. 4). CRE at the TOA is equal to the sum of the atmospheric CRE and the surface CRE. Therefore, with the exception of very small CWP cases, warming occurs in both the atmosphere and at the surface due to the decrease in the visible optical thickness (or the planetary albedo). It should be noted that when the optical thickness is fixed, the other two optical properties, single-scattering albedo and asymmetry factor, are known to counteract each other in the Earth energy budget (24). With a decrease in SCF, the combination of these two effects may result in atmospheric warming; conversely, it may result in global mean surface cooling (24).

The uncertainty range of the values (shaded area in Fig. 6) is due to the change in the effective radii of ice particles, particularly within the range 60–100 μm; the effective radius follows the Kristjánsson and Kristiansen relationship with cloud temperatures between -20 and -30 °C. In the present simulation, the uncertainty range is < 10 W m^-2 at TOA and the surface, whereas it is < 1 W m^-2 for the atmosphere (Fig. 4). Note that the simulation without the Kristjánsson and Kristiansen relationship allows ΔCRE with larger uncertainty range (i.e., -5–25 W m^-2).

This simulated range is compared with the one-year (2004) CERES/Terra gridded TOA and the surface fluxes and clouds data (25). An average of CRE differences between SCF = 60% and SCF = 40% is calculated in terms of CWP using the CERES upper midcloud (top height = 300–500 hPa) parameters and the coincident hourly single satellite fluxes (see ref. 26, Methods). SW flux is scaled to be suitable for the solar insolation used in the simulation. The observed CRE difference at the TOA is in a range corresponding to that used in the simulation. The bias compared to the simulation may be due to the uncertainties related to retrieved cloud properties, as well as to total-sky fluxes and clear-sky fluxes. This suggests that the simulated magnitude of atmospheric warming is reasonable.

2. Discussion

Recent microphysics modeling studies show that SCF is highly variable in a wide range 0–100% even at the same subzero temperature (7). This study shows observationally the extent of the change in SCF can be > 20% even at the same temperature, depending on regions and seasons. The 20% change in SCF, in turn, results in the change in cloud optical thickness of about 25%, and local cloud radiative forcing of about 10–20 W m^-2.

The contamination of cloud-phase classification due to horizontally oriented ice particles in the present data (11) may not affect the major conclusion. Even in the data with the reduced contamination, the global average of SCF in terms of temperature is clearly found to be comparable with the results in this study (11). The variation in SCF must also exist without the contamination effect because these particles are zonally symmetric and relatively less distributed over our focus regions (11).

This study also shows that there exist statistically significant correlations between the variations in SCF and the occurrences of dust aerosols (that are major component of IN in the atmosphere). The implication is that the presence of substantial compensation processes for the cooling effect via aerosol direct scattering and indirect cloud albedo increment at least for dusty regions (27). Theoretically, the presence of IN allows ice crystals to form at higher temperatures (10, 13). Consistent with the theory, a significant reduction in the SCF (up to 30% relative to the global average at -20 °C, as averaged annually) occurs over the regions where dust aerosols are advected to mixed-phase cloud layers. Such regions are particularly concentrated over Asia, but they could cover all of the midlatitudes in boreal summer. From recent observational estimates, dust aerosols over Asia have a cooling effect of approximately -5 to -20 W m^-2 at the TOA (28). Combining the observed and simulated CRE change caused by a 20% reduction in SCF, we find that the dust cooling effect would be greatly compensated by the cloud warming at the TOA (10–20 W m^-2). Also, this process would counteract the increase in cloud albedo caused by the other aerosols influencing warm clouds at lower altitudes (27). This is somewhat consistent with the results of recent modeling work by Storelvmo et al. (4), who included detailed aerosol processes in both warm and cold clouds in a climate model to show an overall warming of the earth-atmosphere system.

In addition, in calculating the CRE, one should take into account the observed result that the SCF over high-latitude regions is about 20% larger than the global average. If this finding is true, the model parameterizations that assume the SCF to be equal to the global average at -20 °C might significantly underestimate cloud albedo at high latitudes. From the analysis used in this study, this bias should be meridionally asymmetric; i.e., with the values for the Southern Hemisphere being greater than those for the Northern Hemisphere. The consequences of this meridional asymmetry, in addition to the consequences of the difference between high and midlatitudes, must be studied further.

Our study provides a regional distribution showing where the effects of dust aerosols on cold clouds might be dominant. This finding can serve to resolve many contradictions related to interactions between aerosols, clouds, and precipitation. For example, an increase in precipitation caused by an increase in aerosol concentrations is particularly dominant over China (29) and the Amazon region (19), whereas the opposite is true over other regions; the former process is known as the so-called “cold rain process by IN particles,” whereas the latter is known as the “warm rain process by cloud condensation nuclei particles.” In this respect, the observed regional distribution of SCF shown in Fig. 2 is consistent with that reported in many previous studies.

The detailed processes of ice nucleation (5, 10, 16–18, 30) whereby aerosols operate, however, require one to make direct observations of individual dusty, mixed-phase clouds, and then apply a comprehensive analysis of aerosol chemistry and cloud microphysics. Such efforts have the potential to significantly improve our determination of the radiation budget of the earth-atmosphere system. In particular, current climate models generally overpredict current warming, and assume that the excessive warming is cancelled by aerosols (31). As noted by Kiehl et al. (32), the adjustments are different for each model. According to the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment (33), both the primary and secondary (via the effects of aerosols on clouds) are highly uncertain, but the IPCC expects each effect to act to cool. The present paper offers a potentially important example of where the secondary effect is to warm, thus reducing the ability of aerosols to compensate for excessive warming in current models.

3. Materials and Methods

3.1. Calculating the SCF and Dust Frequency from CALIOP Data.

We used the vertical profiles of the cloud phase from the CALIOP level 2 vertical feature mask (version 2.01) with data compiled for the one-year period June 2006–May 2007. The retrievals currently include two categories of cloud phase, liquid and ice. The cloud-phase algorithm uses a layer-integrated particle-depolarization ratio at 532 nm, as well as the cloud top and bottom temperatures (34). In particular, the depolarization ratio at 532 nm can effectively distinguish spherical liquid particles from nonspherical ice particles (34)*. The present CALIOP cloud-phase algorithm has been evaluated against ground lidar measurements, confirming the value of an active remote sensing for the study of subvisible cold clouds (35).

The phase composition within cold clouds is primarily a function of temperature, although affected by various factors (10). Because our focus here is on the cloud-phase composition at a certain temperature, the SCF values at each isotherm are calculated as the ratio of the number of liquid-phase footprints to the number of the total (liquid- and ice-phase) footprints measured by CALIOP in a 10° × 10° latitude-longitude grid. The quality of the SCF data may be guaranteed only if the total number of footprints is sufficient (≥30 in this study). The cloud temperatures are calculated from the CALIOP-measured geometrical cloud heights and the temperature-height relationship in the National Centers for Environmental Prediction–National Center for Atmospheric Research (NCEP–NCAR) reanalysis-2 data (36). Note that the cloud temperatures are essentially determined by the CALIOP-measured cloud heights. Therefore, the use of reanalysis data in determining cloud temperatures would not lead to an artifact of unresolved micrometeorology in this study. The SCF values are calculated only for tropospheric clouds. In addition, isotherms of temperatures higher than -10 °C are excluded because strong lidar return-signal attenuation for these clouds can lead to significant measurement errors.

The CALIOP algorithm first distinguishes aerosol scenes from cloud scenes by using the mean attenuated backscatter values at 532 and 1064 nm, as well as their ratios. From the surface type, depolarization ratio, and mean attenuated backscatter, CALIOP then obtains six aerosol types^†. In this study, we focus on the desert-dust type (mostly mineral soil) because of its dominant impact as IN (37, 15).

Because the intensity of CALIOP dust signals does not depend simply on the number density of the particles, it is hard to quantify the amount of dust. Instead, this study utilizes the frequency of dust events defined as the ratio of the number of the dust footprints to the total measured footprints in the same grid and at the same isotherm used to compute SCF. To ensure statistical significance, the analysis includes only the dust frequency obtained from the grids where a sufficient number of the samples is available (≥30 in this study). Finally, the relative dust frequency with respect to the highest dust frequency is calculated. At the -20 °C level, the highest dust frequency occurs in the midlatitudes during spring. The relative dust frequency is indicative of temporal and spatial variability of the occurrence of dust-laden air in comparison with the highest occurrence. The occurrence is not always proportional to the number or mass concentrations. However, it is also obvious that the occurrence is a major factor controlling the annual/seasonal average of the cloud property. As presented in the results, the occurrence appears to be strongly associated with the mean SCF value. Note that the horizontal and vertical resolutions of the CALIOP data are, respectively, 333 and 30 m from the surface to an altitude of 8.2 km. For higher altitudes (from 8.2–20.2 km), the resolutions are coarser (1000 m horizontally and 60 m vertically). Considering the resolution and the path width (5 km), the calculation of the SCF as well as the dust frequency is more reliable for periods longer than 1 d.

3.2. Radiative Transfer Modeling of Mixed-Phase Clouds.

To simulate the radiative effects of mixed-phase clouds, we employed the discrete-ordinate radiative transfer model “Streamer” (38). In Streamer, the optical properties of liquid cloud particles at all wavelengths are parameterized in terms of the effective radius (r_e) and the cloud water path (CWP) as

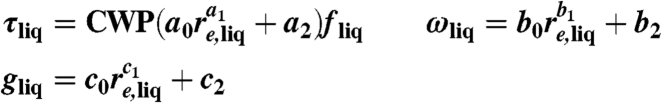[1]

where τ is the extinction optical thickness, ω is the single-scattering albedo, g is the asymmetry parameter, and f_liq is the mass fraction of liquid particles (CWP multiplied by f_liq indicates the liquid water path). We note that the changes in f_liq are essentially the same as the changes in SCF. The coefficients (a₀, a₁, a₂, b₀, b₁, b₂, c₀, c₁, and c₂) dependent on wavelength and r_e are taken from ref. 39, which are commonly used for current cloud radiative transfer modeling.

The optical properties of nonspherical (i.e., ice) cloud particles are calculated by the formulation of ref. 40,

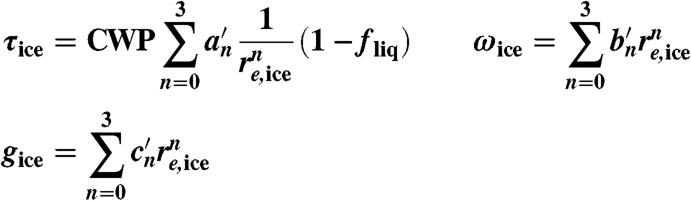[2]

where 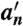, , 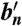and 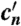are the coefficients, r_e,ice is defined in terms of the maximum dimension of an ice crystal, which is different from that of r_e,liq in Eq. 1. CWP multiplied by (1 - f_liq) indicates the ice water path. We used this parameterization only for the SW case; for the LW case, we used the spherical particle model; i.e., Eq. 1. This limited parameterization may be flawed, but it is known that the effects of LW scattering are secondary to those of absorption (41). The final optical properties of mixed-phase clouds are calculated by weighted averaging the liquid and ice portions (42) as in Eq. 3:

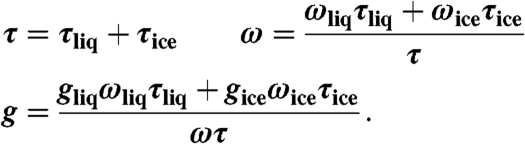[3]

These equations indicate that f_liq is one of major factors in determining mixed-phase cloud radiative effects. This factor is also important in most climate models, which have parameterizations similar to those in Eqs. 1, 2, and 3.

In this study, the effects of single-layer mixed-phase clouds are calculated by using the following parameters: top temperature = -20 °C, effective radii of liquid particles = 11–14 μm, effective radii of ice particles = 60–100 μm, and CWP = 10–500 g m^-2. Here, cloud-top temperature is important in the LW case only for cirrus clouds (CWP = 10 g m^-2). We assume ice particles are aggregates. The global and annual mean solar radiation value, 340 W m^-2, has been used so that the simulated SW CRE corresponds to the averaged magnitude. To gauge the influence of f_liq, we reduced the value of f_liq from 60–40%, and then calculated the corresponding change in cloud optical properties and CRE.