Probing static disorder in Arrhenius kinetics by single-molecule force spectroscopy

Abstract

The widely used Arrhenius equation describes the kinetics of simple two-state reactions, with the implicit assumption of a single transition state with a well-defined activation energy barrier ΔE, as the rate-limiting step. However, it has become increasingly clear that the saddle point of the free-energy surface in most reactions is populated by ensembles of conformations, leading to nonexponential kinetics. Here we present a theory that generalizes the Arrhenius equation to include static disorder of conformational degrees of freedom as a function of an external perturbation to fully account for a diverse set of transition states. The effect of a perturbation on static disorder is best examined at the single-molecule level. Here we use force-clamp spectroscopy to study the nonexponential kinetics of single ubiquitin proteins unfolding under force. We find that the measured variance in ΔE shows both force-dependent and independent components, where the force-dependent component scales with F², in excellent agreement with our theory. Our study illustrates a novel adaptation of the classical Arrhenius equation that accounts for the microscopic origins of nonexponential kinetics, which are essential in understanding the rapidly growing body of single-molecule data.

In 1889 Svante Arrhenius proposed a simple equation for the temperature dependency of the rate of a chemical reaction , where A is a preexponential factor, k_B is the Boltzmann constant, T is the absolute temperature and ΔE is the height of the activation energy barrier (1). This widely accepted description of a single barrier crossing reaction can be readily expanded to include the effect of perturbations that alter the height of the free-energy barrier. For example, when a mechanical force, F, is applied to a molecule, the free-energy barrier height is reduced by an amount equal to FΔx, where Δx represents the actual distance from the native conformation to the transition state conformation along the reaction coordinate. As pointed out by Bell (2), the corresponding Arrhenius law then becomes , where ΔG is the height of the free-energy barrier of reaction in the absence of force. This simple description of the kinetics of a reaction under force has proven useful in a wide variety of single-molecule studies such as bond rupture events (3, 4), protein unfolding (5, 6), and chemical reactions (7, 8). In this work we will focus our investigation on proteins unfolding under a stretching force. However, our conclusions can be readily generalized to other reaction schemes. Assuming a negligible refolding rate, the survival probability, S(t), that a protein remains folded for a time t while under a force, F, satisfies the first-order rate equation, . The resulting survival probability is thus a single exponential. Recent generalizations of the Arrhenius description also lead to a single-exponential survival probability (9, 10). The advent of force-clamp techniques have allowed the direct measurement of the survival probability of protein unfolding under a constant force. The survival probability is expected to follow single-exponential time dependence while assuming each protein in the ensemble has a single native conformation and follows the same unfolding pathway. In sharp contrast with this simple assumption, thousands of ubiquitin unfolding events observed at a constant force of 110 pN revealed a nonexponential survival probability (11, 12). Further, many other biological reactions, including ligand binding to heme proteins (13–18), enzyme catalysis (19–25), and ion channel openings (26, 27), also exhibit nonexponential kinetics. These results are not surprising given that proteins and their solvent environment form complex systems with many degrees of freedom. Indeed, proteins exhibit a large number of conformational substates (28, 29). The transition state of a reaction is more generally described as the saddle point of the multidimensional free-energy landscape for the reaction. Moreover, multiple molecular conformations typically populate a saddle point, allowing the reaction to proceed through a number of pathways with comparable energy barriers, but different transition state structures (30). Thus, we need to develop a generalized Arrhenius equation, k(F), that takes into account reactions that proceed through transition state ensembles, resulting in a nonexponential survival probability.

In a seminal study, Zwanzig investigated the origin of nonexponential kinetics and defined two different kinds of molecular scenarios: dynamic disorder and static disorder (31, 32). Dynamic disorder refers to fluctuations of the reaction rate as a single molecule explores its conformational free-energy landscape (31, 32). If the reaction rate changes rapidly, the value of the reaction rate is an ensemble average, leading to single-exponential kinetics. By contrast, in the case of static disorder, the interconversion rates among different conformations are much slower than the reaction rate, such that individual molecules are “frozen” in distinct conformations during their barrier crossing reactions. In this case, nonexponential kinetics results from the diversity of reaction rates among individual molecules, reflecting the broad distribution of free-energy barrier heights associated with different conformers of the native states and their distinct reaction pathways. Here, we utilize Zwanzig’s approach (31, 32) to develop a generalized Arrhenius term in the presence of static disorder.

Model

Static Disorder Model

For proteins, conformational heterogeneity of the native-state ensemble (33, 34) as well as variations in the structure of the transition state ensemble (6) are likely to contribute to a diverse set of unfolding pathways, implying disorder in the free-energy barrier heights ΔE = ΔG - FΔx under a constant force. Extending from Zwanzig’s approach (31, 32), we consider both ΔG and Δx as functions of independent disorder parameters, which characterize conformational degrees of freedom,

[1]

where ΔG_avgu is the amount of disorder in ΔG respective to the average value, ΔG_avg, and Δx_avgv is the amount of disorder in Δx respective to the average value, Δx_avg. In general, the disorder parameters of u and v fluctuate in time as the protein fluctuates between different conformers. Therefore, the survival probability 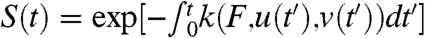is dependent on the dynamics of the two disorder parameters, u and v. We assume that the dynamics of both u and v are governed by the Langevin equation, 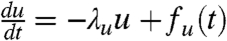, , where λ_u, λ_v are the relaxation rate constants of u and v, and f_u(t), f_v(t) are the Gaussian white noise for u and v, respectively. It is important to note that, if the interconversion rates among different conformational substates are much faster than the reaction rate (λ_u and λ_v are large, ≫k), the time-averaged reaction rate will show single-exponential kinetics. This situation is a special case of dynamic disorder. By contrast, static disorder corresponds to slow interconversion rates among different molecular conformations (λ_u and λ_v are very small, ≪ k), resulting in nonexponential kinetics. Interestingly, in the intermediate cases, the kinetics is initially nonexponential and changes to exponential at long time scales, as discussed by Zwanzig (32). Here, we assume conditions of static disorder throughout.

The Arrhenius/Bell equation for a molecule under force now becomes

[2]

We define r = ΔG_avgu - FΔx_avgv and then Eq. 2 becomes

[3]

where is the rate of crossing the average barrier height (a nondisordered part) and r is the amount of disorder in the barrier heights with respect to the average value, ΔG_avg - FΔx_avg. We assume that the disorder parameters u and v are both normally distributed, centered at zero with a standard deviation of σ_u and σ_v, respectively. Given that u and v are independent variables, it can be shown that the parameter r obeys a Gaussian distribution with a mean of zero and a variance given by

[4]

where σ_ΔG = ΔG_avgσ_u and σ_Δx = Δx_avgσ_v (35). We can now derive the generalized Arrhenius equation for the mean rate of a reaction:

[5]

where f(r) is the probability density of r. This generalized Arrhenius equation for a reaction under a constant force readily reverts back to the simple two-state expression, in the case where there is a single transition state and no disorder (σ = 0). However, in the presence of disorder, the actual mean rate of the reaction becomes different from the rate of crossing the average barrier height, k_F. Owing to the fact that σ² increases rapidly with force (Eq. 4), this difference becomes larger as the pulling force is increased.

Here, what is measured in the force-clamp spectroscopy is the ensemble-averaged survival probability, rather than the mean rate of a reaction. The survival probability for any specific reaction pathway, as parameterized by r, is now given by

[6]

The ensemble-averaged survival probability is given by the superposition of the survival probability for each unfolding pathway, weighted by the probability of the corresponding pathway. Then, the ensemble-averaged survival probability 〈S(t,F)〉 for any Arrhenius type reaction in the presence of static disorder becomes

[7]

It is clear that in the absence of disorder (σ → 0; f(r) → δ(r)), the ensemble-averaged survival probability becomes a single exponential, in good agreement with the standard usage of the Arrhenius equation. However, in the presence of disorder (σ > 0), the survival probability becomes nonexponential. Notably, in the special case where the disorder in the barrier heights is small (σ is small compared to k_BT), the survival probability has an analytical form, clearly showing nonexponential time dependence (SI Text). Our model predicts that in the presence of static disorder, the survival probability will be nonexponential and the measured variance of the barrier heights will show a quadratic dependency on the applied force. Here we test these predictions using force-clamp spectroscopy to measure the survival probability of single ubiquitin proteins unfolding under a stretching force.

Results and Discussion

Pulling a single polyubiquitin protein (nine repeats) at a constant force of 110 pN (Fig. 1A) gives rise to a series of stepwise increments of ∼20 nm in the length of the polyprotein, corresponding to the unfolding of each ubiquitin to a fully extended state (Fig. 1B). The step size of 20 nm marks an extension that is tightly correlated with the number of amino acids released by the unfolding of a ubiquitin protein, providing a well-established mechanical fingerprint. The step size, which can be directly calculated from the worm-like chain model of polymer elasticity (36, 37), varies very slowly in the region between 90 pN and 200 pN. Each step increase in the length marks the unfolding dwell time for an individual ubiquitin in the chain (indicated as t_i in Fig. 1B). Ubiquitin unfolding in a polyprotein was shown previously to be Markovian and not affected by the status of its neighbors (12, 38). Hence, for a given force F, a histogram of the measured dwell times corresponds to the probability density of unfolding, p(t) (Fig. 1C, F = 110 pN). The nonexponential nature of the unfolding reaction is readily observed in such a histogram where a single-exponential fit (Fig. 1C, solid trace) fails to account for the large deviations observed at short dwell times. From the dwell-time histogram, we can measure the ensemble-averaged survival probability, defined as . A clear demonstration of nonexponential behavior of survival probability can be obtained by plotting ln[- ln 〈S(t)〉] versus ln t (Fig. 2). We note that in these coordinates a phenomenological stretched-exponential function, 〈S(t)〉 = exp[-(t/τ)^β], would appear as a straight line whose slope is equal to β, which serves as an indication of nonexponentiality. Using single-molecule force-clamp techniques, the measured survival probabilities over a range of forces were found to be nonexponential (Fig. 2, symbols; 90 pN, 110 pN, 130 pN, 150 pN, 170 pN, 190 pN). We then fit the static disorder model (Eq. 7) to the survival probability measured at each force, with the fit variables k_F and σ², using the Levenberg-Marquardt least-squares algorithm (39) (Fig. 2, solid lines). The measured values of k_F and σ² are listed in Table 1. The errors in the fit parameters were estimated using the bootstrap method (40).

Fig. 1.

Measuring the survival probability of ubiquitin proteins unfolding under a stretching force. (A) A single polyubiquitin molecule is picked up from the surface by the cantilever tip and stretched under a constant force. (B) Stretching a ubiquitin polyprotein at a constant force of 110 pN results in a series of 20 nm stepwise increments in the polyprotein length, marking the unfolding of individual ubiquitins in the chain. We measure the dwell time to unfolding, t_i, for each unfolding event. (C) A histogram of 2799 unfolding events measures the probability density of unfolding p(t) at 110 pN. At short dwell times the distribution deviates significantly from a single exponential (black trace).

Fig. 2.

Survival probability for ubiquitin unfolding under force is well described by static disorder theory. Plot of ln[- ln 〈S(t)〉] versus ln t at 90 pN (filled circles), 110 pN (open circles), 130 pN (filled squares), 150 pN (open squares), 170 pN (filled triangles), and 190 pN (open triangles), respectively. The slopes of all the curves are less than 1, indicating the nonexponential survival probability measured at all forces. The solid lines represent the fits of the static disorder survival probability (Eq. 7) to the data at each force, with the unfolding rate of crossing the average barrier height k_F and the variance of the barrier heights σ² as fit parameters. The values of these parameters are compiled in Table 1. The errors in the fit parameters were estimated using the bootstrap method.

Table 1.

Kinetic parameters for ubiquitin unfolding from the static disorder model fit

Force [pN]	kF [s-1]	σ2 [(pN nm)2]
90	0.13 ± 0.02	9.07 ± 3.48
110	0.73 ± 0.03	12.01 ± 1.35
130	1.28 ± 0.15	17.23 ± 3.40
150	3.11 ± 0.16	18.54 ± 1.47
170	16.28 ± 2.82	22.89 ± 4.35
190	36.81 ± 2.86	12.42 ± 2.26

The unfolding rate of crossing the average barrier height, k_F, and the variance of the barrier heights, σ², were obtained by the static disorder model fit to the data. The errors of k_F and σ² were estimated using the bootstrap method.

From the measured values of k_F we observed a linear relationship between ln k_F and the applied force (Fig. 3), demonstrating that the most probable unfolding rate k_F, corresponding to the rate of crossing the average barrier height ΔG_avg - FΔx_avg, follows the simple Arrhenius law. Fitting ln k_F with the Arrhenius equation using a preexponential factor of A = 10⁶ s^-1 (41) gives an average barrier height of ΔG_avg = 85.1 pN nm and an average distance to the transition state of Δx_avg = 0.23 nm. The extrapolated value of the most probable unfolding rate at zero force is k_F=0 = 10^-3 s^-1. More strikingly, the measured variance of the barrier heights σ² is linearly dependent on the square of the force, in good agreement with the predictions of our model (Fig. 4). In this plot, the intercept at zero force is equal to and the slope corresponds to , demonstrating that the dispersed kinetics of ubiquitin unfolding results from both the disorder of ΔG and the disorder of Δx. A fit of Eq. 4 to σ² (Fig. 4, solid line) yields the values of and . From these measurements we conclude that the probability distribution of barrier heights in the absence of force is a Gaussian distribution with a mean of 85.1 pNnm and a standard deviation of 2.1 pNnm. Similarly, the probability distribution of distances to the transition state is a Gaussian distribution centered at 0.23 nm with a width of 0.025 nm. While these measurements show consistency with the theory up to 170 pN, the data point at 190 pN shows a significantly reduced variance from that predicted by Eq. 4. However, the kinetics of ubiquitin unfolding at 190 pN (k_F ∼36.8 s^-1) is near the upper limit of the resolution of our instrument which has a feedback response time constant of ∼1–3 ms. Therefore, we are likely to be missing many fast unfolding events with short dwell times. Alternatively, the abrupt decrease in disorder observed at 190 pN could represent an abrupt shift in the dynamics of the transition state ensemble, shifting from static to dynamic disorder, causing the unfolding kinetics to become more single-exponential. Resolution of these questions will have to wait until much faster force-clamp measurements become possible.

Fig. 3.

The unfolding rate of crossing the average barrier height, k_F, depends exponentially on the pulling force. A linear dependence between ln k_F and the applied force reveals the remarkable result that the most probable unfolding rate, k_F, follows the simple Arrhenius law. Fitting ln k_F with the Arrhenius equation (solid line) yields the average barrier height in the absence of force ΔG_avg = 85.1 pN nm and the average distance to the transition state Δx_avg = 0.23 nm.

Fig. 4.

Force dependency of the variance in the barrier heights to unfolding. Plot of the measured variance of the barrier heights, σ², as a function of the square of the pulling force. The solid line corresponds to a fit of the data from 90 pN to 170 pN with 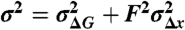(Eq. 4). The fit gives and . The measured values of σ² increase linearly with F² in this range of forces, in agreement with the prediction of our model.

Our theory and experiments support the view that single ubiquitin proteins unfold through different pathways, where both the free-energy barrier height, ΔG, and the distance to the transition state, Δx, vary over a Gaussian distribution of values. In the absence of force, only the variance of the barrier heights at zero force is of consequence for determining the distribution of unfolding rates (see Eq. 4). The standard deviation of the barrier heights in the absence of force is 0.5 k_BT and thus plays only a minor role in the dispersed kinetics, consistent with the bulk probes of ubiquitin unfolding, which show mostly single-exponential kinetics (42). Indeed, using our generalized Arrhenius mean rate equation (Eq. 5) and the measured values of σ² (Fig. 4) we calculate that at zero force the mean rate of the reaction is only 13% bigger than the value estimated if one assumes a simple two-state reaction: 〈k〉 = k_F=0 × 1.13. On the other hand, at 170 pN, the mean rate doubles: 〈k〉 = k_F × 2. These observations resolve the paradox of observing nonexponential kinetics for single proteins unfolding under force (11), while observing single-exponential kinetics for the same proteins under bulk conditions at zero force (42).

We conclude that the dominant factor in the nonexponential kinetics of ubiquitin unfolding under force is a dispersion in the values of Δx. Lattice model simulations of mechanical unfolding have predicted variations in Δx (43). Recent experiments have shown that the value of Δx measured for proteins unfolding under force is determined by the bridging length of solvent molecules at the transition state structure of the reaction (6). We propose that variations in the way that solvent molecules populate the transition state structure may explain the distribution of values of Δx. Here, we performed forced unfolding of ubiquitin using steered molecular dynamics (SMD) simulations to examine this possibility. Previous SMD simulations of ubiquitin showed that the key event in mechanical unfolding is the simultaneous breaking of the four backbone hydrogen bonds bridging the β1 and β5 strands of the protein (44) (Fig. S1A). Therefore, in our studies we defined the reaction coordinate for ubiquitin unfolding as the distance between the first residue of the β1 strand (Q2) and the last residue of the β5 strand (L69). A total of 100 SMD simulations show that water molecules can bridge the breaking backbone hydrogen bonds in many different ways, resulting in varying elongations along the reaction coordinate when reaching the transition state of the reaction (Fig. S1B). While the values of Δx measured in the SMD simulations are smaller than those observed experimentally, they follow a similar distribution (Fig. S1C), supporting the view that a diversity of bridging water conformations could explain the dispersion in the values of Δx measured experimentally. These observations predict that the degree of disorder in Δx will be dependent on the type of solvent surrounding the protein. Furthermore, it is likely that the degree of disorder in Δx varies from protein to protein following the particular architecture of each transition state ensemble. Indeed, in a beautiful study using force-clamp spectroscopy, Li and colleagues showed that protein G unfolds under force following a perfect single-exponential kinetics over the range of 50–120 pN (45), implying either a well-defined transition state structure or much faster interconversion among different configurations at the unfolding transition state of the protein (46). It is well established that proteins fluctuate in a broad range of times scales (19, 22, 29, 46, 47); however, only those motions which interconvert much slower than the unfolding rate will result in the dispersed kinetics reported in our work. Faster interconversions would lead to a single-exponential survival probability, which is not observed in our work. It is also possible that at low pulling forces the unfolding rate may become comparable to the interconversion rate between conformers, reaching a form of dynamic disorder where the kinetics becomes single-exponential.

Our theory provides a direct approach in determining the variance in the height of the activation energy barrier of a reaction and can be readily generalized to any type of perturbation. It is now clear that in the presence of static disorder, the effect of a perturbation is to tease apart transition state conformations with similar energies, such that they can be identified. We have so far considered the effect of a mechanical force on the height of the activation energy barrier, ΔE = ΔG - FΔx. Excitingly, our theory can be applied to other perturbations such as a membrane voltage acting on the gating charges of an ion channel, ΔE = ΔG - Vq (48, 49), or a chemical denaturant triggering unfolding ΔE = ΔG - Dm (50). Then, ion channels kinetics under voltage-clamp conditions will show a variance of the barrier heights equal to , where V is the membrane voltage and q is the equivalent gating charge which shows disorder. Similarly, proteins undergoing chemical denaturation will show a variance of the barrier heights equal to 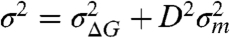, where D is the concentration of the denaturant and the kinetic m-value is the disorder parameter. By replacing the correct expression for the variance of the barrier heights into the generalized Arrhenius mean rate equation (Eq. 5) and the survival probability (Eq. 7) one can predict the kinetics of any type of barrier activated reaction in the presence of static disorder.

Materials and Methods

Protein Engineering and Purification.

The polyproteins consisting of nine tandem repeats of the human ubiquitin were engineered by consecutive subcloning of the monomers using the BamHI and BglII restriction sites, as described previously (44). The DNA molecule containing nine repeats of the ubiquitin cDNA sequence is then subcloned into the pQE80L expression vector and transformed into the BLR(DE3) Escherichia coli expression strain (Novagene). Constructs were purified by histidine metal-affinity chromatography with Talon resin (Clontech) and by gel filtration using a Superdex 200 HR column (GE Biosciences).

Single-Molecule Force Spectroscopy.

The constant-force experiments were performed with the homemade atomic force microscopy (5, 51). The sample is prepared by depositing 3–12 μl of protein in phosphate buffered saline solution onto a freshly gold coverslide. Each cantilever (Olympus, Veeco) was calibrated using the equipartition theorem (52), giving rise to a spring constant of ∼20 pN/nm. Single ubiquitin polyproteins are picked up from the surface by the tip of the cantilever by pushing the cantilever hardly on the surface at 1,500 pN. Then the polyprotein is stretched under a constant force by retracting the piezo actuator, controlled by the analog force feedback system. The force-clamp experiments at 170 pN and 190 pN were performed with a high-speed S-303 piezo (Physik Instrumente, Germany), improving the feedback response time up to 1–3 ms.

Data Analysis.

All data were collected and analyzed using the custom software written in Igor Pro 6 (Wavemetrics). The survival probability is defined as , where p(t)dt corresponds to the probability of unfolding during the period of time between t and t + dt. The survival probability at each force is obtained from the associated probability density histogram of unfolding times, p(t). The integral in the fitting function (Eq. 7) is evaluated by taking a sum of the integrand over the interval [-6σ,6σ], with the interval width of dr = 0.001 pNnm. All the fitting procedures are performed by the Levenberg-Marquardt least-squares algorithm, implemented in the Igor Pro 6 software package. The errors of k_F and σ² are estimated by the bootstrap method (40).

Steered Molecular Dynamics Simulations.

The simulations were carried out with the NAMD2 (for equilibrium) and Gromacs 4.0 (for SMD simulation) simulation suites. The OPLSAA (optimized potentials in liquid simulations all-atom) force field was applied. The complexes were solvated in a 6.0 ∗ 6.0 ∗ 11.0 nm³ box of SPC/E [simple point charge (extended)] water molecules. Simulations were performed in the NPT (isothermal-isobaric) ensemble. The system was energy-minimized (steepest descent, 1,000 steps) before equilibrating the solvent for 1 ns with positional restraints on heavy atoms of ubiquitin. Simulations for 2-ns were performed to equilibrate the whole system, and this was followed by 30-ns simulations to generate various initial configurations for steered molecular dynamics simulations. The C_α-atoms of the terminal residues of the substrate were moved away from each other in the x-direction with a constant force of 400 kJ mol^-1 nm^-1, 667 pN.