Abstract
Along the evolutionary path from single cells to multicellular organisms with a central nervous system are species of intermediate complexity that move in ways suggesting high-level coordination, yet have none. Instead, organisms of this type possess many autonomous cells endowed with programs that have evolved to achieve concerted responses to environmental stimuli. Here experiment and theory are used to develop a quantitative understanding of how cells of such organisms coordinate to achieve phototaxis, by using the colonial alga Volvox carteri as a model. It is shown that the surface somatic cells act as individuals but are orchestrated by their relative position in the spherical extracellular matrix and their common photoresponse function to achieve colony-level coordination. Analysis of models that range from the minimal to the biologically faithful shows that, because the flagellar beating displays an adaptive down-regulation in response to light, the colony needs to spin around its swimming direction and that the response kinetics and natural spinning frequency of the colony appear to be mutually tuned to give the maximum photoresponse. These models further predict that the phototactic ability decreases dramatically when the colony does not spin at its natural frequency, a result confirmed by phototaxis assays in which colony rotation was slowed by increasing the fluid viscosity.
Keywords: adaptation, evolution, flagella, fluid dynamics, multicellularity
The most primitive “eyes” evolved long before brains and even before the simplest forms of nervous system organization appeared on Earth (1, 2). Many organisms are able to sense and respond to light stimuli, an ability essential to the optimization of photosynthesis, the avoidance of photodamage, and the use of light as a regulatory signal. One of the more striking responses is phototaxis, in which motile photosynthetic microorganisms adjust their swimming path with respect to incident light in a finely tuned manner (3, 4). This steering relies on sensory inputs from one or more eyespots (2), primitive photosensors that are among the simplest and most common “eyes” in nature. They consist of photoreceptor proteins and an optical system of varying complexity, which provide information about the intensity and directionality of the incident light (2, 3, 5). This information is then translated into an organism-specific swimming control mechanism that allows orientation to the light with high fidelity.
In most unicellular phototactic organisms, such as the archetypal green alga Chlamydomonas, the presence of a single eyespot implies both a limited vision of the three-dimensional world in which the cell navigates and the impossibility of detecting light directions by measuring light intensity at two different positions in the cell body. To overcome these restrictions, such organisms must compare light intensity measurements from their single eyespot at different moments in time (6). Many species do this by swimming on helical paths along which their eyespot acts as a light antenna continuously searching space for bright spots (3). Higher eukaryotes have a nervous system to integrate visual information from different sources and orchestrate coordinated responses (7, 8).
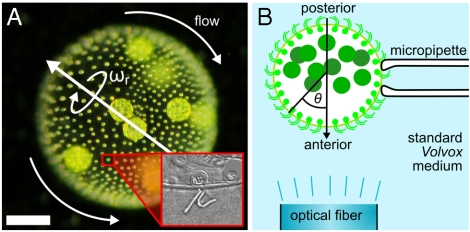
Multicellular organisms of intermediate complexity, such as the colonial alga Volvox and its relatives (9), have evolved a means of high-fidelity phototaxis without a central nervous system and, in many cases, even in the absence of intercellular communication through cytoplasmic connections (10). Volvox carteri consists of thousands of biflagellated Chlamydomonas-like somatic cells sparsely distributed at the surface of a passive spherical extracellular matrix, and a small number of germ cells inside the sphere (Fig. 1A). During development the flagella orient such that Volvox rotates about its swimming direction, the trait that gave Volvox its name (11). Coordination of the somatic cells resembles orchestrating a rowboat with thousands of independent rowers but without a coxswain (9). Nature’s solution is a response program at the single-cell level that produces an accurate steering mechanism, an emergent property at the colonial level. Yet it remains to be understood what form the response program must take to coordinate the cells and to yield high-fidelity phototaxis in the presence of the steering constraints of a viscous environment.
Fig. 1.
Geometry of V. carteri and experimental setup. (A) The beating flagella, two per somatic cell (Inset), create a fluid flow from the anterior to the posterior, with a slight azimuthal component that rotates Volvox about its posterior-anterior axis at angular frequency ωr. (Scale bar: 100 μm.) (B) Studies of the flagellar photoresponse utilize light sent down an optical fiber.
More than a century ago, Holmes (12) proposed that the somatic cells facing a source of light down-regulate their flagellar activity, a hypothesis later confirmed by several investigators (13–16). Although this control principle will initially turn the colony towards the light, the colony might adapt (14, 15) to the light before good alignment with the light direction has been reached. Surprisingly, this observation has not been synthesized into a predictive, quantitative model consistent with the principles of fluid dynamics, nor are there data on Volvox phototaxis that can be compared with such a theory. Here we use a combination of experiment and theory to show that adaptation and colony rotation play key roles in the phototaxis mechanism of V. carteri. By quantifying the flagellar photoresponse of V. carteri in detail, we show that it acts as a band pass filter that allows adaptation to different light environments, minimizes the influence of fast light fluctuations, and maximizes the response to stimuli at frequencies that correspond to the rotation rate of the organism. These measurements suggest that the response kinetics and colony rotation have evolved to be mutually tuned and optimized for phototaxis. Furthermore, we develop a mathematical theory that predicts the phototactic fidelity of Volvox as the rotation rate and other parameters change and confirm experimentally that colony rotation is essential for accurate phototaxis.
Results and Discussion
Temporal Dynamics of the Adaptive Response.
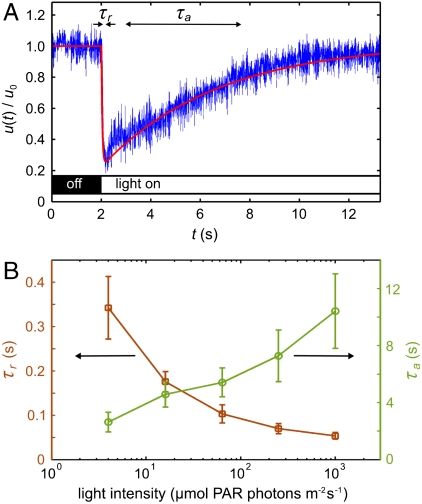
The most elementary photoresponse is the change in flagellar beating accompanying a step up or down in illumination intensity. This response is probed with the experimental setup shown in Fig. 1B. Cyan light from an LED that is coupled to a fiber-optic light guide held in a micropipette is directed toward the anterior of a V. carteri colony held by a second micropipette. Details are given in Materials and Methods and SI Text. High-speed imaging of flagella revealed, in accord with proposals by several investigators (13–15), that the somatic cells change their beating frequency rather than their beating direction (17). Instead of quantifying the average photoresponse by recording the beating frequency of each flagellum of every somatic cell, we measured the fluid motion produced by the flagellar beating by using particle image velocimetry (PIV). This approach implicitly averages over several neighboring flagella, and, by measuring the fluid velocity just above the flagellar tips, we obtain a natural input for the hydrodynamic models of phototactic turning described further below. Because of the low Reynolds number associated with flows generated by V. carteri (18–20), fluid inertia is negligible and the flagella-induced flow is a direct measure of the flagellar activity. Fig. 2A shows a typical time trace of the photoresponse, measured in terms of the flagella-generated flow speed u(t), normalized by the flow speed under time-independent illumination u0, and averaged over ± 30° from the anterior pole. We found that a step up in light intensity elicits a decrease in flagellar activity on a response time scale τr, followed by a recovery to baseline activity on a time scale τa associated with adaptation; there was no change in flagellar activity upon a step down in light intensity. This response underlies the ability of V. carteri to turn toward the light, as explained further below. At very high light intensities and long stimulation, the responses to step up and step down stimuli are reversed (see SI Text), allowing Volvox to avoid photodamage by swimming away from the light. Irrespective of the stimulus light intensity, τr is always a fraction of a second, whereas τa is several seconds (Fig. 2B), consistent with early observations (14, 15).
Fig. 2.
Characteristics of the adaptive photoresponse. (A) The local flagella-generated fluid speed u(t) (Blue), measured with PIV just above the flagella during a step up in light intensity, serves as a measure of flagellar activity. The baseline flow speed in the dark is u0 = 81 μm/s for this dataset. Two time scales are evident: a short response time τr and a longer adaptation time τa. The fitted theoretical curve (Red) is from Eq. 4. (B) The times τr (Squares) and τa (Circles) vary smoothly with the stimulus light intensity, measured in terms of PAR. Error bars are standard deviations.
Although the kinetics and biochemistry of photoreceptor currents have been studied in Chlamydomonas (2, 21) and Volvox (22), their connection to the flagellar photoresponse is unclear. In Volvox, a step stimulus elicits a Ca2+ current whose time scale of 1 ms (22) is too short to account for the measured τr. But the time for Ca2+ to diffuse the length of the flagellum L is τD = L2/D ∼ 0.2 s (for L ∼ 15 μm, D ∼ 10-5 cm2/s), which is similar to τr, suggesting that the photocurrent triggers an influx of Ca2+ at the base of the flagella, consistent with previous hypotheses (22, 23). Although the dependence of τa on light intensity is like that of the H+ current in Volvox, the decay constant of the latter is only ∼75 ms (22); the biochemical origin of τa remains unknown.
The measured adaptive response of the flagella-generated fluid speed just above the colony surface (Fig. 2A) can be described by u(t)/u0 = 1 - βp(t), where p(t) is a dimensionless photoresponse variable that is large when there is a large light-induced decrease in flagellar activity and vanishes when there is no such change in flagellar activity. The empirically determined constant β > 0 quantifies the amplitude of the decrease in u(t)/u0. For a model of p(t) that captures the two time scales τa and τr, we require a second variable h(t), which we define as a dimensionless representation of the hidden internal biochemistry responsible for adaptation (24, 25). A system of coupled equations that is consistent with the measured u(t)/u0 is
| [1] |
| [2] |
where the light stimulus s(t) is a dimensionless measure of the photoreceptor input that incorporates the eyespot directionality. The Heaviside step function H(s - h) is used to ensure that a step down in light stimulus cannot increase u above u0, because it keeps p≥0. In these equations, the values p∗ = 0 and h∗ = s1 are stable and global attractors in the sense that, after a sufficiently long time under constant light stimulus s1, the pair (p, h) relaxes to (p∗, h∗). However, if s increases from s1 for t < 0 to s2 for t≥0, then for t > 0 the solution is
| [3] |
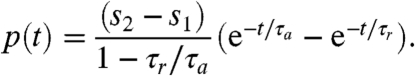 |
[4] |
When τr ≪ τa, as for Volvox, there is a sharp transient increase in p(t) [and decrease in u(t)], peaking at a time t† ∼ τr ln(τa/τr), followed by a slow relaxation back to zero, as in the measured flagellar photoresponse shown in Fig. 2A.
The rotation of Volvox about its axis and the resulting periodic illumination of the photoreceptors suggest an investigation of the dependence of the photoresponse on the frequency of sinusoidal stimulation. For the above model this frequency dependence of the photoresponse is 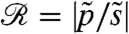 , where
, where 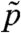 and
and 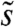 are the Fourier transforms of p and s, respectively.
are the Fourier transforms of p and s, respectively. 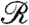 is well-approximated by neglecting the Heaviside function in Eq. 1 (see SI Text) to give
is well-approximated by neglecting the Heaviside function in Eq. 1 (see SI Text) to give
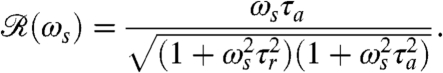 |
[5] |
If the stimulus angular frequency ωs is very low (ωs ≪ 2π/τa), the adaptive process has sufficient time to keep up with the changing light levels and the amplitude of the response vanishes. At very high frequencies, ωs≫2π/τr, the response is limited to short-time behavior and also vanishes.
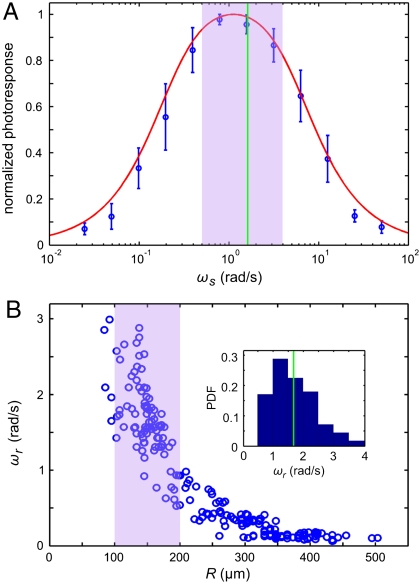
Using the setup in Fig. 1B, we measured the flagellar photoresponse to sinusoidal light stimuli of various temporal frequencies. In Fig. 3A, these measurements are compared with the theoretical 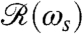 , showing excellent agreement. The maximum response is obtained at stimulus frequencies that correspond to the natural angular rotation frequencies of Volvox about its swimming direction. The frequency dependence of the photoresponse is like a band pass filter that removes high frequency noise, e.g., light fluctuations from ripples on the water surface (26), but retains the key feature of adaptation.
, showing excellent agreement. The maximum response is obtained at stimulus frequencies that correspond to the natural angular rotation frequencies of Volvox about its swimming direction. The frequency dependence of the photoresponse is like a band pass filter that removes high frequency noise, e.g., light fluctuations from ripples on the water surface (26), but retains the key feature of adaptation.
Fig. 3.
Photoresponse frequency dependence and colony rotation. (A) The normalized flagellar photoresponse for different frequencies of sinusoidal stimulation, with minimal and maximal light intensities of 1 and 20 μmol PAR photons m-2 s-1 (Blue Circles). The theoretical response function (Eq. 5, Red Line) shows quantitative agreement, using τr and τa from Fig. 2B for 16 μmol PAR photons m-2 s-1. (B) The rotation frequency ωr of V. carteri as a function of colony radius R. The highly phototactic organisms for which photoresponses were measured fall within the range of R indicated by the purple box, and the distribution of R can be transformed into an approximate probability distribution function (PDF) of ωr (Inset), by using the noisy curve of ωr(R). The purple box in A marks the range of ωr in this PDF (green line indicates the mean), showing that the response time scales and colony rotation frequency are mutually optimized to maximize the photoresponse.
Heuristic Mechanism of Phototaxis.
We proceed to a qualitative discussion of how an adaptive response translates into phototactic turning and the ingredients required for a simple yet realistic mathematical model with predictive power.
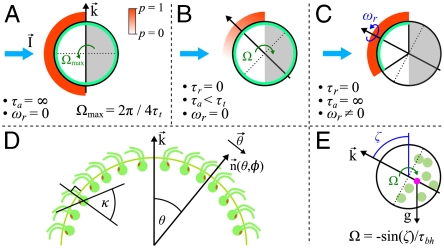
In general, phototactic orientation is due to an asymmetry of the flagellar behavior between the illuminated and shaded sides of the organism. The mechanism that achieves this asymmetry is species-dependent, but it is instructive to consider a hierarchy of ingredients. First, consider a nonspinning spherical organism that can display a nonadaptive photoresponse on its entire surface but will do so only on the illuminated side, as in Fig. 4A. This organism will achieve perfect antialignment of its posterior-anterior axis k with the light direction unit vector 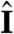 (i.e., face the light) on a turning time scale τt, which is determined by the balance between the torques due to asymmetric flagellar activity and rotational viscous drag. Adaptation to light is a desirable property for such an organism, because it allows a response to light intensities over several orders of magnitude and because it allows the organism to swim at full speed once a good orientation has been reached. If the photoresponse of the above model organism now has the desirable property of being adaptive, it will initially turn towards the light as in Fig. 4A, but adaptation may cause the response to decay before k reaches antialignment with
(i.e., face the light) on a turning time scale τt, which is determined by the balance between the torques due to asymmetric flagellar activity and rotational viscous drag. Adaptation to light is a desirable property for such an organism, because it allows a response to light intensities over several orders of magnitude and because it allows the organism to swim at full speed once a good orientation has been reached. If the photoresponse of the above model organism now has the desirable property of being adaptive, it will initially turn towards the light as in Fig. 4A, but adaptation may cause the response to decay before k reaches antialignment with 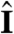 (Fig. 4B), depending on the relative magnitude of τa and τt. If, however, the adaptive organism would spin about k, new surface area would continuously be exposed, thus maintaining an asymmetric photoresponse until perfect antialignment of k with
(Fig. 4B), depending on the relative magnitude of τa and τt. If, however, the adaptive organism would spin about k, new surface area would continuously be exposed, thus maintaining an asymmetric photoresponse until perfect antialignment of k with 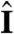 has been reached. For Volvox, which generally have τa ∼ τt, the spinning about the posterior-anterior axis is therefore not just optimized for the photoresponse kinetics, as shown in the previous section, but also essential for high-fidelity phototactic orientation in the presence of adaptation. Spinning may also mitigate the deleterious effects of unsymmetrical colony development and injury (27), and for organisms with a restricted field of view due to a small number of eyespots, such as Chlamydomonas and Platynereis, spinning is also required for detecting the light direction (3, 7).
has been reached. For Volvox, which generally have τa ∼ τt, the spinning about the posterior-anterior axis is therefore not just optimized for the photoresponse kinetics, as shown in the previous section, but also essential for high-fidelity phototactic orientation in the presence of adaptation. Spinning may also mitigate the deleterious effects of unsymmetrical colony development and injury (27), and for organisms with a restricted field of view due to a small number of eyespots, such as Chlamydomonas and Platynereis, spinning is also required for detecting the light direction (3, 7).
Fig. 4.
Heuristic analysis of the phototactic fidelity. A–C illustrate simplified phototaxis models. Photoresponsive regions are colored green, the region that actually displays a photoresponse is in shades of red, and shaded regions are gray. (A) If τa = ∞, ωr = 0, and the responsive region is as drawn, the posterior-anterior axis k will achieve perfect antialignment with the light direction I. The time scale for turning τt ∼ 3.3 s can be estimated by assuming that the fluid velocity on the illuminated side is reduced to 0.7 of its baseline value and using Eq. 8 without bottom-heaviness. (B) If τa < τt, and ωr = 0, the photoresponse may decay before the optimal orientation has been reached. After the initial transient in A has decayed, the largest photoresponse (i.e., flagellar down-regulation) is in the region that just turned into the light. As an illustration, the configuration drawn in this panel surprisingly implies that the organism would turn away from the light, indicating that before this orientation is reached the steering is stopped at a suboptimal orientation of k with I. A remedy against this orientational limitation would be ωr ≠ 0. (C) The best attainable orientation towards the light is drawn, if the photoresponse is localized in a small anterior region, and the eyespots display an all-or-nothing response as they move from the shaded to the illuminated side. (D) Measurements of the eyespot (Orange) placement yield κ = 57° ± 7° (see SI Text). (E) Volvox is bottom-heavy, because the center of mass (Pink) is offset from the geometric center of the colony as indicated.
In Volvox colonies, the flagellar photoresponse is localized near the anterior pole (Fig. 5), yet the importance of spinning outlined above remains. However, having only a small photoresponsive region complicates the heuristic picture: If the eyespots could only direct an all-or-nothing response as they move from the shaded to the illuminated side of the sphere, the best possible phototactic orientation is drawn in Fig. 4C. Such a mechanism may be sufficient for Volvox in natural environments, because it would robustly navigate Volvox closer to the light, even though the organism does not swim directly toward the light. The orientational limit of this response mechanism can be overcome if, as described for several green algae (3, 28, 29), the strength of the photoresponse instead continuously changes with the angle at which the eyespots receive light. Together with an appropriate eyespot placement (Fig. 4D), this directionality leads to the persistence of a response asymmetry between illuminated and shaded regions until perfect orientation toward the light has been achieved.
Fig. 5.
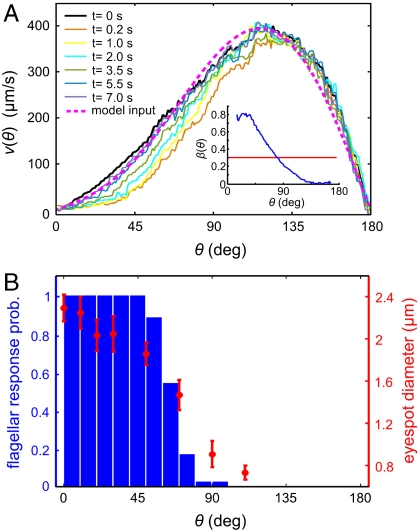
Anterior-posterior asymmetry. (A) The anterior-posterior component of the fluid flow, measured 10 μm above the beating flagella, following a step up in illumination at time t = 0 s. The dashed line indicates the approximation to v0(θ) used in the numerical model. (Inset) β(θ) is blue (with p normalized to unity), and the mean β is red. (B) The probability of flagella to respond to light correlates with the size of the somatic cell eyespots. The light-induced decrease in fluid flow occurs beyond the region of flagellar response because of the nonlocality of fluid dynamics.
Phototactic orientation in natural environments can be opposed by ambient vorticity (30), which may be created by the motion of other nearby organisms, convection, or wind-driven surface waves. A mechanism that can counteract phototaxis even in well-controlled laboratory experiments is due to a property that Volvox shares with its unicellular ancestor Chlamydomonas and other algae: Their center of mass is offset from their center of buoyancy. For Volvox, this bottom-heaviness is due to clustering of germ cells in the posterior (Fig. 4E) and leads to a torque tending to align the swimming direction with the vertical on a time scale τbh ∼ 14 s (20). A faithful theory of phototaxis in Volvox must therefore include at least four features: self-propulsion, bottom-heaviness, photoresponse kinetics, and photoresponse spatial structure.
Hydrodynamic Model of Phototaxis.
In the low Reynolds number regime that Volvox inhabits, the swimming speed and angular velocity Ω of an organism can be calculated if the fluid velocity u on each point of its surface is known (31). Phototactic steering of Volvox can therefore be modeled by specifying the response of u to light stimulation. Rather than solving for the effects of each of the thousands of individual flagella on the colony surface, we adopt a continuum approximation in which there is a temporally and spatially varying surface velocity. If θ and ϕ are the polar and azimuthal angles on a sphere, respectively, the surface velocity u may be decomposed into 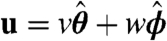 . We interpret u as the velocity at the edge of the flagellar layer (32); for practical reasons experimental measurements of u are made just above that layer. In the absence of a light stimulus, u = u0 and we assume that the ratio v0(θ)/w0(θ) is constant on the colony surface because of the precise orientational order of somatic cells (9). Following step changes in light intensity, measurements of v(θ,ϕ,t) at fixed ϕ show that in each region, the surface velocity displays a photoresponse of the form shown in Fig. 2A but that the overall magnitude varies with θ (Fig. 5A). We thus model u(θ,ϕ,t) by allowing the quantities β, p, and h to depend on position:
. We interpret u as the velocity at the edge of the flagellar layer (32); for practical reasons experimental measurements of u are made just above that layer. In the absence of a light stimulus, u = u0 and we assume that the ratio v0(θ)/w0(θ) is constant on the colony surface because of the precise orientational order of somatic cells (9). Following step changes in light intensity, measurements of v(θ,ϕ,t) at fixed ϕ show that in each region, the surface velocity displays a photoresponse of the form shown in Fig. 2A but that the overall magnitude varies with θ (Fig. 5A). We thus model u(θ,ϕ,t) by allowing the quantities β, p, and h to depend on position:
| [6] |
The measured β(θ) is shown in the inset in Fig. 5A.
To define the stimulus s on the colony surface, we make use of the angle 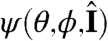 defined through
defined through 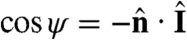 , where
, where  is the unit normal to the surface. When ψ = 0 (π), the light is directly above (behind) a given surface patch. The light-shadow asymmetry in s can therefore be modeled by a factor H(cos ψ). Superimposed on this factor may be another functional dependence on ψ to account for the eyespot sensitivity in the forward direction, with experiments on Chlamydomonas (28) supporting a dependence f(ψ) = cos ψ. The class of models we consider for the dimensionless s is therefore
is the unit normal to the surface. When ψ = 0 (π), the light is directly above (behind) a given surface patch. The light-shadow asymmetry in s can therefore be modeled by a factor H(cos ψ). Superimposed on this factor may be another functional dependence on ψ to account for the eyespot sensitivity in the forward direction, with experiments on Chlamydomonas (28) supporting a dependence f(ψ) = cos ψ. The class of models we consider for the dimensionless s is therefore
| [7] |
With the above specification of the dynamics of the surface velocity, the angular velocity of the colony is (31)
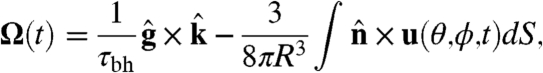 |
[8] |
where 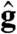 and
and 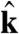 are the directions of gravity and the posterior-anterior axis, respectively. The first term in Eq. 8 arises from bottom-heaviness and represents a balance between the torque that acts when the posterior-anterior axis is not parallel to gravity and the rotational drag of the sphere (20). The second term is responsible for phototactic steering, where the integral is taken over the surface of the sphere of radius R. In a reference frame where the Volvox is at the origin with a fixed orientation, the light direction evolves as
are the directions of gravity and the posterior-anterior axis, respectively. The first term in Eq. 8 arises from bottom-heaviness and represents a balance between the torque that acts when the posterior-anterior axis is not parallel to gravity and the rotational drag of the sphere (20). The second term is responsible for phototactic steering, where the integral is taken over the surface of the sphere of radius R. In a reference frame where the Volvox is at the origin with a fixed orientation, the light direction evolves as 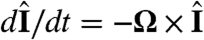 .
.
The above coupled equations can be solved numerically (see SI Text), e.g., to determine the angle α(t) of the organism axis with the light direction. It is interesting to consider two special cases of the model class outlined above. In the biologically faithful “full model,” we use the measured β(θ) and the realistic eyespot directionality f(ψ) = cos ψ. In the “reduced model,” we consider only a light-shadow response asymmetry—i.e., f(ψ) = 1—and use the mean of the measured β(θ)—i.e., β(θ) = 0.3. All other features are shared between the models.
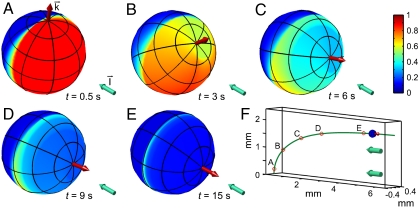
A phototactic turn of a hypothetical non-bottom-heavy Volvox simulated by the reduced model is shown in Fig. 6, indicating an intricate link between organism rotation, adaptation, and steering. In reality, however, Volvox is bottom-heavy, which is particularly important when the light direction is horizontal. In this case, we previously observed (33) that the organisms reach a final angle αf set by the balance of the bottom-heaviness torque and the phototactic torque. We therefore define the “phototactic ability” 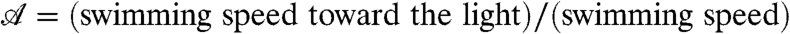 .
.
Fig. 6.
Colony behavior during a phototurn. A–E show the colony axis k (Red Arrow) tipping toward the light direction I (Aqua Arrow). Colors represent the amplitude p(t) of the down-regulation of flagellar beating in a simplified model of phototactic steering. F shows the location of colonies in A–E along the swimming trajectory.
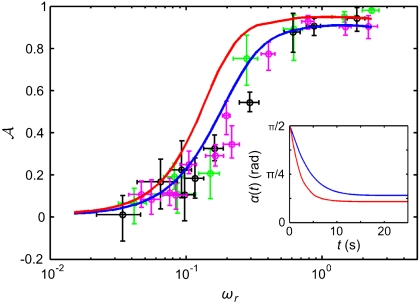
Both models predict that as the viscosity η is increased, while keeping the internal parameters τr and τa fixed, the phototactic ability decreases dramatically (Fig. 7). Qualitatively, an increase in η reduces ωr, which leads to a reduced photoresponse (Fig. 3A) and therefore a reduced phototactic torque. The sharp transition in Fig. 7 occurs when the phototactic torque becomes comparable to the other torques in the system. The simulations neglected torques due to ambient fluid motion and included only the bottom-heaviness torque.
Fig. 7.
The phototactic ability 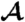 decreases dramatically as ωr is reduced by increasing the viscosity. Results from three representative populations are shown with distinct colors. Each data point represents the average phototactic ability of the population at a given viscosity. Horizontal error bars are standard deviations, whereas vertical error bars indicate the range of population mean values, when it is computed from 100 random selections of 0.1% of the data. A blue continuous line indicates the prediction of the full hydrodynamic model; the red line is obtained from the reduced model. (Inset) α(t) from the full and reduced model at the lowest viscosity.
decreases dramatically as ωr is reduced by increasing the viscosity. Results from three representative populations are shown with distinct colors. Each data point represents the average phototactic ability of the population at a given viscosity. Horizontal error bars are standard deviations, whereas vertical error bars indicate the range of population mean values, when it is computed from 100 random selections of 0.1% of the data. A blue continuous line indicates the prediction of the full hydrodynamic model; the red line is obtained from the reduced model. (Inset) α(t) from the full and reduced model at the lowest viscosity.
We tested the above prediction by measuring the phototactic ability of Volvox at various viscosities in a population assay at low organism concentration and negligible ambient fluid motion. It is important to note that, in the experiment, the phototactic ability is a measure of a slightly different quantity than in the model. In the model, a bottom-heavy Volvox swims in an infinite fluid toward the light at an angle αf with the horizontal. A colony swimming in the same direction in the experiment will collide with the top surface of the sample and change direction. The phototactic ability in the experiments is therefore a measure of the directionality of the population swimming behavior (see SI Text), whereas in the model it is solely a measure of αf. The data from several populations are shown in Fig. 7 and are found to be in quantitative agreement with the full model for realistic parameters (given in SI Text) and in qualitative agreement with the reduced model. The success of the reduced model highlights that spinning and adaptation are the key ingredients for a qualitative understanding of the fidelity of phototaxis in Volvox and that a quantitative understanding can be obtained if a realistic eyespot directionality and anterior-posterior response asymmetry are included. These models further illustrate that if all somatic cells were photoresponsive, the organism would have a higher phototactic ability (Fig. 7). Yet it may be beneficial to keep a high translation speed even during light stimulation, and there may be significant metabolic and developmental costs associated with endowing all cells with a photoresponse, which could make it advantageous to have the photoresponse localized in the anterior.
In additional experiments, we found that very large Volvox (Fig. 3B) have a much lower phototactic ability although they still display the flagellar photoresponse. For such colonies, the hydrodynamic model (Eq. 8) reveals that their lower phototactic ability arises from the increase in R and concomitant decrease in u0, and the reduction in photoresponse p due to the lower ωr (Fig. 3A). The model thus yields insight into which parameters determine the phototactic torque and illustrates the intuitive result that this torque must be significantly larger than competing torques to achieve high-fidelity phototaxis.
Conclusion
We have shown how accurate phototaxis of the alga V. carteri, a colonial organism lacking a central nervous system, is achieved by autonomous cells on its anterior surface endowed with an adaptive flagellar photoresponse. The response and adaptation time scales of this photoresponse determine an optimal frequency for the characteristic spinning of Volvox about its swimming direction. Because the organisms naturally spin at this optimal frequency, the flagellar orientation and photoresponse kinetics seem to have coevolved to maximize the photoresponse. The mathematical model of phototaxis developed here shows that the phototactic fidelity decreases dramatically when the colony does not spin at its natural frequency; the results of a phototaxis assay in which spinning was slowed by increasing the fluid viscosity are in excellent agreement with the model predictions.
This work raises a number of issues for further investigation. Chief among them are the biochemical origin of the adaptive time scale and the reason for displaying a photoresponse only in the anterior part of the organism. Because the rotational frequency of phototactically active V. carteri so closely matches the peak of the frequency response function 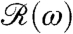 , and Chlamydomonas itself displays a coincidence of its photoresponse and rotation period (34, 35), it is natural to ask whether other species in the same evolutionary lineage, or indeed the larger class of phototactic organisms, can be understood within the present formalism. The allometry of the adaptation time is therefore a key feature for study. It is also of considerable interest to ascertain the dynamics of chemotaxis in Volvox and to determine its relationship to phototaxis, a linkage proposed for Chlamydomonas (36). Whereas larger multicellular organisms like Volvox can rely on an entirely deterministic mechanism for phototaxis, it remains unclear how stochasticity of motion in unicellular organisms like Chlamydomonas, caused by internal biochemical noise (37), affects phototaxis. Finally, the interplay between adaptive flagellar dynamics and the vorticity of natural fluid environments (30) requires further investigation.
, and Chlamydomonas itself displays a coincidence of its photoresponse and rotation period (34, 35), it is natural to ask whether other species in the same evolutionary lineage, or indeed the larger class of phototactic organisms, can be understood within the present formalism. The allometry of the adaptation time is therefore a key feature for study. It is also of considerable interest to ascertain the dynamics of chemotaxis in Volvox and to determine its relationship to phototaxis, a linkage proposed for Chlamydomonas (36). Whereas larger multicellular organisms like Volvox can rely on an entirely deterministic mechanism for phototaxis, it remains unclear how stochasticity of motion in unicellular organisms like Chlamydomonas, caused by internal biochemical noise (37), affects phototaxis. Finally, the interplay between adaptive flagellar dynamics and the vorticity of natural fluid environments (30) requires further investigation.
Materials and Methods
A detailed description of materials, methods, and supplementary measurements is given in SI Text. A brief summary is given below.
Culture Conditions.
V. carteri f. nagariensis EVE strain was grown axenically in standard Volvox medium (SVM) with sterile air bubbling, in a daily cycle of 16 h of cool white light (4,000 lx) at 28 °C and 8 h of darkness at 26 °C.
Measuring the Photoresponse to Various Stimuli.
Volvox colonies were caught on a rotatable micropipette by gentle aspiration and rotated until the posterior-anterior axis was in the focal plane of the microscope and pointing toward an optical fiber at a distance of ∼900 μm. Microscopy was done in red bright-field illumination (λ > 620 nm), to which Volvox is insensitive (15). The flagella-generated flow was visualized with 1-μm polystyrene beads (∼1.4 × 108 beads per mL in SVM) and recorded at 100 fps. Flow speeds were measured by PIV. The PIV data was interpolated and read out 25 μm above the colony surface—i.e., approximately 10 μm above the flagellar layer. To get a single time series that represents the photoresponse of the colony, we averaged the flow speed time series between -30° and +30° as measured from the anterior pole. All stimuli were applied with a cyan LED (500 nm, FWHM 40 nm) coupled into a 550 μm diameter optical fiber. LabVIEW was used to trigger the camera and control the LED light intensity time series. The temperature in the sample chamber was 24.5 ± 0.5 °C.
Measuring the Rotation Rate Dependence of the Phototactic Ability.
We prepared solutions of SVM with various concentrations of methylcellulose (M0512, Sigma-Aldrich UK), up to 0.65% (wt/wt) (38). From a V. carteri culture that just hatched, phototactic organisms were preselected by a simple test and distributed into rectangular Petri dishes with different concentrations of methylcellulose in SVM. A cyan LED (same as for the optical fiber stimuli) was placed on one side of each Petri dish, providing ∼15 μmol photosynthetically active radiation (PAR) photons m-2 s-1. The Volvox were tracked with software written in Matlab, and rotation frequencies were measured manually. The temperature in the Petri dishes was 24 ± 1 °C.
Supplementary Material
Acknowledgments.
We thank J.P. Gollub, J.T. Locsei, C.A. Solari, S. Ganguly, and T.J. Pedley for discussions and D. Page-Croft and J. Milton for technical assistance. This work was supported in part by the Engineering and Physical Sciences Research Council (K.D.), the Engineering and Biological Sciences program of the Biotechnology and Biological Sciences Research Council, the Human Frontier Science Program (I.T.), the US Department of Energy, and the Schlumberger Chair Fund (R.E.G.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1000901107/-/DCSupplemental.
References
- 1.Gehring WJ. New perspectives on eye development and the evolution of eyes and photoreceptors. J Hered. 2005;96:171–184. doi: 10.1093/jhered/esi027. [DOI] [PubMed] [Google Scholar]
- 2.Hegemann P. Algal sensory photoreceptors. Annu Rev Plant Biol. 2008;59:167–189. doi: 10.1146/annurev.arplant.59.032607.092847. [DOI] [PubMed] [Google Scholar]
- 3.Foster KW, Smyth RD. Light antennas in phototactic algae. Microbiol Rev. 1980;4:572–630. doi: 10.1128/mr.44.4.572-630.1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jékely G. Evolution of phototaxis. Philos Trans R Soc B. 2009;364:2795–2808. doi: 10.1098/rstb.2009.0072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kreimer G. Cell biology of phototaxis in algae. Int Rev Cytol. 1994;148:229–310. [Google Scholar]
- 6.Sineshchekov OA, Govorunova EG. Rhodopsin receptors of phototaxis in green flagellate algae. Biochemistry-Moscow. 2001;66:1300–1310. doi: 10.1023/a:1013191504508. [DOI] [PubMed] [Google Scholar]
- 7.Jékely G, et al. Mechanism of phototaxis in marine zooplankton. Nature. 2008;456:395–399. doi: 10.1038/nature07590. [DOI] [PubMed] [Google Scholar]
- 8.Egelhaaf M, Kern R. Vision in flying insects. Curr Opin Neurobiol. 2002;12:699–706. doi: 10.1016/s0959-4388(02)00390-2. [DOI] [PubMed] [Google Scholar]
- 9.Kirk DL. Volvox: Molecular-Genetic Origins of Multicellularity and Cellular Differentiation. Cambridge, UK: Cambridge Univ Press; [DOI] [PubMed] [Google Scholar]
- 10.Hiatt JDF, Hand WG. Do protoplasmic connections function in phototactic coordination of the Volvox colony during light stimulation? J Protozool. 1972;19:488–489. [Google Scholar]
- 11.Linnaeus C. Systema Naturae. 10th Ed. Stockholm: Laurentii Salvii; 1758. p. 820. [Google Scholar]
- 12.Holmes SJ. Phototaxis in Volvox. Biol Bull. 1903;4:319–326. [Google Scholar]
- 13.Hand WG, Haupt W. Flagellar activity of the colony members of Volvox aureus Ehrbg during light stimulation. J Protozool. 1971;18:361–364. [Google Scholar]
- 14.Huth K. Movement and orientation of Volvox aureus Ehrbg (translated from German) Z Pflanzenphysiol. 1970;62:436–450. [Google Scholar]
- 15.Sakaguchi H, Iwasa K. Two photophobic responses in Volvox carteri. Plant Cell Physiol. 1979;20:909–916. [Google Scholar]
- 16.Hoops HJ, Brighton MC, Stickles SM, Clement PR. A test of two possible mechanisms for phototactic steering in Volvox carteri (Chlorophyceae) J Phycol. 1999;35:539–547. [Google Scholar]
- 17.Mast SO. Reactions to light in Volvox, with special reference to the process of orientation. Z Vergl Physiol. 1926;4:637–658. [Google Scholar]
- 18.Solari CA, Ganguly S, Kessler JO, Michod RE, Goldstein RE. Multicellularity and the functional interdependence of motility and molecular transport. Proc Natl Acad Sci USA. 2006;103:1353–1358. doi: 10.1073/pnas.0503810103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Short MB, et al. Flows driven by flagella of multicellular organisms enhance long-range molecular transport. Proc Natl Acad Sci USA. 2006;103:8315–8319. doi: 10.1073/pnas.0600566103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Drescher K, et al. Dancing Volvox: Hydrodynamic bound states of swimming algae. Phys Rev Lett. 2009;102:168101. doi: 10.1103/PhysRevLett.102.168101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Harz H, Hegemann P. Rhodopsin-regulated calcium currents in Chlamydomonas. Nature. 1991;351:489–491. [Google Scholar]
- 22.Braun F-J, Hegemann P. Two light-activated conductances in the eye of the green alga Volvox carteri. Biophys J. 1999;76:1668–1678. doi: 10.1016/S0006-3495(99)77326-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tamm S. Ca2+ channels and signalling in cilia and flagella. Trends Cell Biol. 1994;4:305–310. doi: 10.1016/0962-8924(94)90226-7. [DOI] [PubMed] [Google Scholar]
- 24.Friedrich BM, Jülicher F. Chemotaxis of sperm cells. Proc Natl Acad Sci USA. 2007;104:13256–13261. doi: 10.1073/pnas.0703530104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Spiro PA, Parkinson JS, Othmer HG. A model of excitation and adaptation in bacterial chemotaxis. Proc Natl Acad Sci USA. 1997;94:7263–7268. doi: 10.1073/pnas.94.14.7263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Walsh P, Legendre L. Photosynthesis of natural phytoplankton under high frequency light fluctuations simulating those induced by sea surface waves. Limnol Oceanogr. 1983;28:688–697. [Google Scholar]
- 27.Jennings HS. On the significance of the spiral swimming of organisms. Am Nat. 1901;35:369–378. [Google Scholar]
- 28.Schaller K, David R, Uhl R. How Chlamydomonas keeps track of the light once it has reached the right phototactic orientation. Biophys J. 1997;73:1562–1572. doi: 10.1016/S0006-3495(97)78188-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schaller K, Uhl R. A microspectrophotometric study of the shielding properties of eyespot and cell body in Chlamydomonas. Biophys J. 1997;73:1573–1578. doi: 10.1016/S0006-3495(97)78189-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Durham WM, Kessler JO, Stocker R. Disruption of vertical motility by shear triggers formation of thin phytoplankton layers. Science. 2009;323:1067–1070. doi: 10.1126/science.1167334. [DOI] [PubMed] [Google Scholar]
- 31.Stone HA, Samuel ADT. Propulsion of microorganisms by surface distortions. Phys Rev Lett. 1996;77:4102–4104. doi: 10.1103/PhysRevLett.77.4102. [DOI] [PubMed] [Google Scholar]
- 32.Blake JR. A spherical envelope approach to ciliary propulsion. J Fluid Mech. 1971;46:199–208. [Google Scholar]
- 33.Drescher K, Leptos KC, Goldstein RE. How to track potists in three dimensions. Rev Sci Instrum. 2009;80:014301. doi: 10.1063/1.3053242. [DOI] [PubMed] [Google Scholar]
- 34.Yoshimura K, Kamiya R. The sensitivity of Chlamydomonas photoreceptor is optimized for the frequency of cell body rotation. Plant Cell Physiol. 2001;42:665–672. doi: 10.1093/pcp/pce084. [DOI] [PubMed] [Google Scholar]
- 35.Josef K, Saranak J, Foster KW. Linear systems analysis of the ciliary steering behavior associated with negative-phototaxis in Chlamydomonas reinhardtii. Cell Motil Cytoskeleton. 2006;63:758–777. doi: 10.1002/cm.20158. [DOI] [PubMed] [Google Scholar]
- 36.Ermilova EV, Zalutskaya ZM, Gromov BV, Häder D-P, Purton S. Isolation and characterization of chemotactic mutants of Chlamydomonas reinhardtii obtained by insertional mutagenesis. Protist. 2000;151:127–137. doi: 10.1078/1434-4610-00013. [DOI] [PubMed] [Google Scholar]
- 37.Polin M, Tuval I, Drescher K, Gollub JP, Goldstein RE. Chlamydomonas swims with two ‘gears’ in a eukaryotic version of run-and-tumble locomotion. Science. 2009;325:487–490. doi: 10.1126/science.1172667. [DOI] [PubMed] [Google Scholar]
- 38.Herraez-Dominguez JV, Gil Garcia de Leon F, Diez-Sales O, Herraez-Dominguez M. Rheological characterization of two viscosity grades of methylcellulose: An approach to the modeling of the thixotropic behaviour. Colloid Polym Sci. 2005;284:86–91. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.