Physical–chemical determinants of coil conformations in globular proteins

Abstract

We present a method with the potential to generate a library of coil segments from first principles. Proteins are built from α-helices and/or β-strands interconnected by these coil segments. Here, we investigate the conformational determinants of short coil segments, with particular emphasis on chain turns. Toward this goal, we extracted a comprehensive set of two-, three-, and four-residue turns from X-ray–elucidated proteins and classified them by conformation. A remarkably small number of unique conformers account for most of this experimentally determined set, whereas remaining members span a large number of rare conformers, many occurring only once in the entire protein database. Factors determining conformation were identified via Metropolis Monte Carlo simulations devised to test the effectiveness of various energy terms. Simulated structures were validated by comparison to experimental counterparts. After filtering rare conformers, we found that 98% of the remaining experimentally determined turn population could be reproduced by applying a hydrogen bond energy term to an exhaustively generated ensemble of clash-free conformers in which no backbone polar group lacks a hydrogen-bond partner. Further, at least 90% of longer coil segments, ranging from 5- to 20 residues, were found to be structural composites of these shorter primitives. These results are pertinent to protein structure prediction, where approaches can be divided into either empirical or ab initio methods. Empirical methods use database-derived information; ab initio methods rely on physical–chemical principles exclusively. Replacing the database-derived coil library with one generated from first principles would transform any empirically based method into its corresponding ab initio homologue.

Introduction

During the past several years, fragment assembly has emerged as the most effective strategy for protein structure prediction.¹ This approach is rooted in the assumption that protein structures are mix-and-match assemblies of short peptide fragments drawn from a limited alphabet of distinct structural motifs.^2–8 In practice, the fragment assembly procedure utilizes a comprehensive library of short fragments (<20 residues) selected from proteins of known structure. To predict the structure of a target sequence, fragments are “stitched together” into self-consistent trial structures, which are then evaluated, clustered, and further evaluated, resulting ultimately in a short list of plausible candidates (see e.g.,9,10). The approach is conceptually simple but computationally complex and methodological details vary among investigators and programs.

At present, there is no physical–chemical basis for identifying the fragments that constitute an effective fragment library. Instead, fragments are chosen so as to insure adequate coverage of the observed conformational landscape represented by proteins of known structure. The striking success of fragment assembly methods has nudged the field toward improving practical procedures^11,12 rather than investigating the principles involved in fragment conformation, although not entirely.^13,14 In science, the question of how-to-do-it often precedes the question of why-it-happens, as illustrated vividly by the history of protein secondary structure prediction, which has been directed almost entirely toward methods that can recognize sequence patterns in known structures.

We seek a physical–chemical understanding of fragment structure. An earlier study with similar objectives¹³ focused primarily on α-helices and β-strands, which account for approximately half of all protein structure. The remaining half has been collected in the protein coil library,¹⁵ a repository of non-α-helix, non-β-sheet fragments culled from a database of nonredundant, high-resolution X-ray–elucidated proteins (http://www.roselab.jhu.edu/coil/).

Here, we focus on rationalizing two-, three-, and four-residue turn conformations in the coil library. Conjectures about determinative interactions were tested by simulating structures that can then be compared with their experimentally determined counterparts. In greater detail, simple Monte Carlo simulations were performed in which fragments of interest, flanked by idealized short segments of either α-helix or β-strand, were allowed to explore conformational space freely, subject to an increasingly restrictive regimen of physical–chemical constraints. The major constraints were: (i) Sterics: two atoms were not allowed to occupy the same space at the same time. (ii) Hydrogen bond satisfaction: all backbone polar groups were required to have hydrogen bond partners, provided by either water or another peptide polar group. (iii) Hydrogen bond energy: a scoring function to reward conformers that can form intramolecular hydrogen bonds. A detailed description of constraints and the conditions under which they were imposed is given in Methods.

We find that simulations which impose all three major constraints can successfully capture 98% of the corresponding population in the coil library. Furthermore, over 90% of coil library fragments ranging from 5- to 20-residues are covered by the simulated turn set, evidence that these longer fragments are composites of smaller structural primitives.

Our findings provide criteria that can be used to identify a complete set of fragments from first principles. Additionally, they serve to establish a physical relationship between library fragments and the structural building blocks of earlier studies.

Results

A comprehensive set of 23,185 experimentally determined two-, three-, and four-residue turns was extracted from the PDB.¹⁶ This set was found to be highly degenerate: 72 unique conformers, from a total of 1503, are sufficient to account for approximately two-thirds of the entire population. Throughout this article, it is found repeatedly that a small number of experimentally determined conformers captures most of the observed population, whereas the remaining population spans a large number of rare motifs. We discuss why this might be so.

The PDB turn set was compared with a corresponding set of simulated turns. Specifically, a series of Metropolis Monte Carlo¹⁷ simulations was performed for two-, three-, and four-residue fragments flanked by either α-helices or β-strands, mimicking the layout of these elements in the PDB. Fragments were allowed to sample accessible φ,ψ-space freely, with energy terms included in the Metropolis criteria limited to sterics, hydrogen bond satisfaction, and hydrogen bonding, the three constraints described in the Introduction. Simulated turns were found to cover 98% of the PDB turn set with few false positives. Additionally, 90% of the residues in longer coils—5–20 residues in length—are covered by the simulated turn set, suggesting that longer fragments are structural composites of shorter ones. These results are now described in detail.

Experimentally determined turns

Two-, three-, and four-residue turns bracketed between adjacent segments of repetitive secondary structure (α-helices and β-strands) were extracted from nonredundant, high-resolution X-ray–elucidated crystal structures, as described in Methods. This PDB turn set was subdivided into 12 structural categories based on the four combinations of bracketing secondary structure (helix/strand-turn-helix/strand) and the fragment length (two, three, or four residues). Each category was labeled with an associated three-character code: (H or S)/i/(H or S), where i = 2, 3, or 4. For example, three-residue coil fragments bracketed by an N-terminal helix and a C-terminal strand were labeled H3S.

Turn conformers in each of these 12 structural categories were then grouped into discrete equivalence classes by mapping successive backbone torsion angles into their corresponding φ,ψ-basins (Fig. 1), enabling fragment conformations to be represented by a linear string of basin labels. Fragments with identical strings were considered to have thermodynamically equivalent structures, that is, their conformations were the same to within a spontaneous k_BT-sized fluctuation (where k_B = the Boltzmann constant and T = temperature in K). In effect, this transformation collapses real numbers in three-dimensional space (Euclidian 3-space) to positive integers in one-dimensional space. For example, given the eight basins in Figure 1, there are 8ⁿ possible strings for an n-length fragment. This procedure enables straightforward enumeration of conformers in the 12 structural categories.

Figure 1.

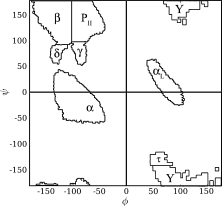
The eight discrete φ,ψ-basins. The Protein Coil Library 15 was contoured and partitioned into disjoint basins, as described in Perskie et al.³³ In total, 98.9% of all φ,ψ-angles in the coil library are subsumed within these eight basins. Basin labels for α, β, PII, and γ were chosen to suggest the most familiar conformer associated with that region of the φ,ψ map. The Y-basin is disfavored for all residues except glycine. Basin boundaries used in this study are given in Supporting Information Table I.

All 12 structural categories exhibit substantial conformational degeneracy. Excluding conformers with glycines (i.e., basin combinations that include Y and τ), the fraction of unique conformations within each category is 0.038 at most, indicating that at least 96% of the observed fragments have redundant conformations (Table I). A global assessment of conformational degeneracy is provided by the histogram in Figure 2. To compile the histogram, the fraction of the turn population subsumed by each unique conformer in every category was calculated, and the conformers were ranked by frequency of occurrence within their respective categories. These individual within-category fractions were summed over all 12 categories, providing a weighted-average of the total turn population subsumed by each rank-ordered step and shown as a bar of the histogram. As rank-order decreases, the subsumed population diminishes exponentially, sinking below 5% beyond the top five conformers, and leveling off to an almost horizontal asymptote after 20 conformers. Below 0.5% of the distribution, remaining conformers are observed only a few times at most in the total population of 23,185 turns (Fig. 3). In our analysis, we ignore conformations that contribute <0.5% of their structural category's total population, hypothesizing that these rare conformations could be minimized into populated ones, as was shown in previous work on β-turns.¹⁸ The distributions in Figures 2 and 3 are a striking illustration that a small number of frequently occurring conformers account for the majority of the total turn population, whereas the remaining population spans a large number of infrequently occurring conformers.

Table I.

Structural Categories, Populations, and Motifs

Structural category	Populationa	Experimentalb	Exhaustivec	% Covered by top sixd
H2S	1402	7	28	99.4
H3S	2947	17	162	84.2
H4S	2343	26	913	74.3
H2H	709	9	32	91.0
H3H	1149	20	183	72.1
H4H	818	32	1053	59.5
S2H	1278	6	27	100.0
S3H	796	30	162	50.5
S4H	1008	37	894	52.9
S2S	2634	5	14	100.0
S3S	1021	17	99	66.2
S4S	2232	23	475	70.2

^aTotal turn population after eliminating those that contributed <0.5% to the population.

^bNumber of experimentally determined unique turns.

^cNumber of conceivable clash-free turns sampling the eight basins.

^dPercentage of the population in col. 2 covered by the top six categories from col. 3.

Figure 2.

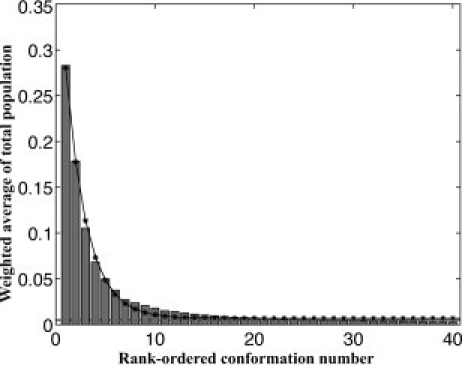
Fraction of the turn the population covered by the top 40 conformers. Every histogram bar represents a weighted-average of the total turn population subsumed by each of the 12 structural categories. Successive bars are rank-ordered by frequency of occurrence. For example, the leftmost bar indicates that the weighted-average of the single-most frequent conformer from each category accounts for over 25% of the total turn population. As rank-order decreases, the subsumed population diminishes exponentially (solid line with asterisks), sinking below 5% beyond the top five conformers, and leveling off to an almost horizontal asymptote after 20 conformers. Conformations contributing less than 0.5% (dashed line) to their respective structural categories were eliminated. The exponential curve fit to these data is given by the equation y = 0.4 × e-0.47 + 0.01.

Figure 3.

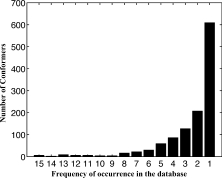
Instances of rare conformers. The absolute number of rare conformers in each structural category was counted, summed, and plotted. Conformer frequencies range from unity to 15, an upper limit set by 0.5% of most populated category. The highest bar, at frequency = 1, indicates that more than 600 unique conformers are found only once in the dataset.

Exhaustive turn sets

Assessment of conformational degeneracy (above) demonstrates that a small subset of the observed conformers comprises the vast majority of two-, three-, and four-residue turns in the PDB. Another measure of degeneracy is the degree to which turns in the PDB exhaust the set of all conceivable turns of corresponding length. In fact, observed PDB conformers represent only a minor fraction of the possible clash-free conformers of equivalent length and matched turn geometry, as described next.

An exhaustive set of nonglycine-containing turns of a given length was generated using a polyalanyl peptide flanked by segments of repetitive secondary structure, either helix or strand. Residues corresponding to the coil fragment were allowed to sample the six nonglycyl basins (Fig. 1, excluding Y and τ) while several adjacent residues from either flanking segment sampled their secondary structure-specific φ,ψ-basin (described in Methods). Clash-free conformers were generated until a statistically significant population was accumulated and an exhaustive set of unique turns was extracted from this population (see Methods).

As shown in Table I, the 12 structural categories generated in this way contain far more allowed conformers than their PDB counterparts, another indication that the PDB population is dominated by a handful of conformations. Depending on the structural category, between 50 and 100% of the observed PDB population is covered by its six most frequent conformations. Yet together, these 72 conformations (six conformations × 12 structural categories) represent only 1.8% of the exhaustive turn set, and even the entire PDB turn set, including all rare conformers, still covers only 5.7% of the exhaustive set.

Simulated turns

Metropolis Monte Carlo simulations were performed to identify energetic factors responsible for limiting the number of observed turn conformations. For comparison, 12 simulated turn sets were generated corresponding to the 12 structural categories of experimentally determined turns. As described in Methods, a reference population of clash-free conformers was generated with turn geometry matching that used to define the PDB turn set. This reference population is, in fact, the exhaustive turn set described above, and it was further refined in simulations using (i) hydrogen bond satisfaction (i.e., requiring that all polar groups have a hydrogen bond partner, provided by either water or another peptide polar group) and (ii) a hydrogen bond energy, introduced via the Metropolis criterion. In all simulations, conformations contributing less than 0.5% of the population were ignored.

Hydrogen bonding constraints (i) and (ii) winnow the exhaustive set by more than an order of magnitude. Unique conformations in the 12 simulated categories cover between 4 and 48% of their corresponding exhaustive populations in each structural class (Tables I and II).

Moving on to the PDB turn set, Table II lists the fraction of each structural category captured by its corresponding simulated counterpart. Fractions range from 49% (for S4S) to 99% (for H2S) and average 79% for simulations that apply both hydrogen bond constraints. Nevertheless, these simulations fail to capture 43% of the unique conformations in the PDB turn set. Almost all of these exceptions (viz. 90%) involve coil fragments with glycines or prolines and/or backbone polar groups hydrogen bonded to a nearby side chain. These structural complexities exceed the scope of our polyalanyl model.

Table II.

Winnowing the Reference Population Using H-Bond Satisfaction and H-Bond Energy^a

Structural category	Reference	H-bond satisfaction	H-bond energy
H2S	11 (99.3)	12 (99.3)	11 (99.3)
H3S	44 (87.5)	51 (95.3)	38 (96.1)
H4S	42 (24.8)	43 (24.8)	49 (93.9)
H2H	12 (76.0)	12 (76.0)	14 (81.8)
H3H	44 (63.3)	45 (63.3)	43 (93.8)
H4H	46 (34.7)	38 (32.8)	42 (74.3)
S2H	13 (94.5)	12 (94.5)	13 (94.5)
S3H	38 (68.8)	38 (63.7)	34 (63.7)
S4H	41 (39.2)	44 (43.4)	39 (74.5)
S2S	7 (74.8)	6 (74.8)	3 (74.8)
S3S	24 (41.4)	25 (51.0)	24 (51.0)
S4S	34 (38.3)	40 (40.5)	20 (48.5)

^aNumber of unique turns in three sets: (col. 2) the reference set (col. 3) H-bond satisfaction applied to col. 2, and (col. 4) H-bond energy applied to col. 3. Numbers in parentheses are the % of the experimentally determined turns captured by this set. The number of unique turns in successive sets can decrease with additional H-bonding constraints when the populations of newly stabilized turns increase, forcing other previously populated turns below the 0.5% threshold. Note that these simulations are for a polyalanyl model.

To simulate such exceptions, an appropriate site-specific glycine, proline, or polar side chain was introduced into the otherwise polyalanyl background in those cases for which the majority of fragments had one or more of these features. Simulations with hydrogen bond constraints were performed as previously, with side chain sampling from distributions in the Penultimate Rotamer Library.¹⁹ Conformations contributing less than 0.5% of the population were discarded.

With these augmentations, the simulated turn set captures 98% of the PDB turn set. It is well known that Pro and Gly are found preferentially in peptide chain turns.²⁰ Consistent with this observation, most of the improvement in the simulations can be attributed to inclusion of Pro and Gly, which reduced the number of false negatives in all 12 categories, especially in categories with longer fragments. The percentage of newly captured unique conformers ranged from 0.6% (H3S) to 38.3% (S3S), with an average of 15.6%. Lesser, but nonetheless significant, improvement resulted on incorporation of side chain hydrogen bonds, which increased the percentage of newly captured conformers in four structural categories, ranging from 4.2% (H4H) to 22.3% (S4S), with an average of 9.8% over the four classes. In sum, after inclusion of site-specific glycine, proline, and polar side chains, remaining exceptions shrink to a small subpopulation of their respective structural categories (Table III).

Table III.

Structural Motifs Captured in Simulations

Structural category	Experimentala	Ala onlyb	Ala + Pro/Glyc	Ala + Pro/Gly + SC:BBd	% Capturede	False negativesf
H2S	7	6	1	0	100.0	0
H3S	17	14	1	0	96.7	2
H4S	26	20	3	0	97.6	3
H2H	9	6	3	0	100.0	0
H3H	20	16	4	0	100.0	0
H4H	32	14	8	1	88.3	9
S2H	6	4	2	0	100.0	0
S3H	30	14	15	0	99.1	1
S4H	37	21	8	4	95.6	4
S2S	5	3	2	0	100.0	0
S3S	17	6	8	1	97.1	2
S4S	23	6	12	3	98.0	2

^aNumber of experimentally determined structural categories in this motif.

^bNumber of categories captured in polyalanyl simulations.

^cNumber of additional categories captured in augmented simulations using Pro and Gly.

^dNumber of additional categories captured in augmented simulations with Pro, Gly, and polar side chains.

^eFraction PDB population captured in all simulations.

^fPDB conformations not captured in simulations.

Longer coils

The simulated turn set was estimated to cover 90.1% of 5- to 20-residue coil fragments found in the PDB (see Methods), indicating that longer fragments are structural composites of shorter ones. This estimate constitutes a lower bound for coverage and the full extent of coverage may, in fact, be considerably higher. To test the significance of this finding, coverage of longer fragments was calculated using randomly generated images of the simulated turn set. A randomly generated image retained the same frequencies of two, three, and four basin labels as the augmented simulated turn set, but with basin labels chosen at random from the eight basins in Figure 1 (See Methods). Randomly generated libraries of two-, three-, and four-residue coil conformations were found to cover only 39.7% of 5- to 20-residue coils in the Protein Coil Library.

Summary and Discussion

A comprehensive set of experimentally determined two-, three-, and four-residue turns was extracted from high-resolution X-ray crystal structures, classified by conformation, and filtered by eliminating conformers contributing less than 0.5% of the population within each class. In all, 98% of the filtered set was reproduced successfully in Monte Carlo simulations. Energy terms were limited to steric exclusion, hydrogen bond satisfaction, and an intrapeptide hydrogen bond potential, pinpointing these three factors as the major conformational determinants. By definition, all coil segments are flanked by elements of repetitive secondary structure—α-helices (H) or β-strands (S)—and their presence imposes an implicit conformational constraint on the intervening coil segment. However, the results reported here do not depend on prior knowledge of specific secondary structure; all four flanking combinations (HH, HS, SH, and SS) were simulated at each fragment length.

Combinations of the simulated two-, three-, and four-residue turns were shown to cover at least 90% of coil library fragments ranging from 5- to 20-residues, indicating that these longer fragments are composites of shorter ones. In previous work, it was shown that native backbone topologies could be reproduced to within a 3.0 Å root-mean-square difference using φ,ψ-angles drawn exclusively from only five basins,²¹ a subset of the eight basins in Figure 1. The realization that longer, ostensibly irregular coil segments are structural composites of well-characterized shorter ones could have practical consequences for ab initio protein structure prediction. In particular, it might be possible to simulate a comprehensive fragment library from physical–chemical principles instead of extracting it blindly from known protein structures.

In the turn simulations reported here, many conceivable conformations are eliminated either by steric clash or because a backbone polar group is sequestered and cannot form a hydrogen bond. Both cases are energetically disfavored, the former by a stiff repulsive potential²² and the latter by as much as ∼ 5 kcal/mol in comparison with hydrogen bond–satisfied alternatives.²³ Elimination of these highly disfavored alternatives—often referred to as negative design—winnows the remaining population to a comparatively small number of viable conformers, at which point intramolecular hydrogen bonding is remarkably effective in identifying those that are observed in experimentally determined structures.

Backbone hydrogen bonding is thought to play a formative role in selecting the protein native state,²⁴ not only in turns but also in general. Even under unfolding conditions, when the protein population has a hydrodynamic radius indicative of the denatured state ensemble, a substantial fraction of intramolecular hydrogen bonds have already formed.^25,26 Conditions that stabilize the native state favor intramolecular hydrogen bonding,²⁷ and in our simulations, intramolecular hydrogen bonding alone is almost always sufficient to select the native turn conformation from the available population of clash-free, hydrogen bond-satisfied possibilities.

Setting aside the details, our simulations are little more than a systematic procedure for interrogating the winnowed population of available backbone possibilities and selecting the most energetically probable remaining hydrogen-bonded survivors. Optimal success required extension of the polyalanyl model to include glycine, proline, and side chain-backbone hydrogen bonding. Glycine enlarges and proline restricts intrinsic backbone conformations, and polar side chains increase the repertoire of available hydrogen bond partners for backbone polar groups. All three extensions underscore the essential role of the hydrogen-bonded backbone.

An anonymous referee asks whether our conclusions would be reinforced if the data were restricted to an ultrahigh resolution subset of the PDB (e.g., resolution ≤ 1 Å). Although we suspect that many rare motifs would be eliminated altogether in this subset, the available data are too sparse to draw statistically meaningful conclusions. Ultrahigh resolution X-ray structures, selected using the criteria described in methods, would represent less than 1% of the data used in our analysis.

Throughout this work, it was found that a conspicuously small number of experimentally determined conformers captures most of the observed population, while the remaining population spans a large number of rare motifs, often singletons. As a practical measure, we eliminated the rare motifs that account for less than 0.5% of their structural category, reasoning that they contribute negligibly to the overall thermodynamic population but cloud the overall structural picture. Practical matters apart, the distributions in Figures 2 and 3 are suggestive of an underlying cause. One possibility is that the large population of rare conformers represents the tail of an authentic Boltzmann-distributed ensemble of conformers.^28,29 Alternatively, rare conformers might arise as an inescapable consequence of microscopic heterogeneity in X-ray structure determination. According to Blundell and coworkers³⁰:

The majority of proteins diffract to resolutions where heterogeneity is difficult to identify and model, and are therefore approximated by a single, average conformation with isotropic variance. Here we show that disregarding structural heterogeneity introduces degeneracy into the structure determination process, as many single, isotropic models exist that explain the diffraction data equally well.

In this latter case, the small number of frequently observed conformers identified here may account for a larger fraction of the experimental data than previously realized.

Methods

PDB fragment selection

High-resolution X-ray crystal structures (resolution ≥ 2.0 Å; R ≤ 0.25), from a nonredundant (sequence similarity < 90%) PISCES list³¹ (June 29, 2009) were extracted from the PDB,¹⁶ and elements of α-helix, β-strand, and coil were identified using PROSS,³² a secondary structure classification method based solely on backbone torsion angles.

Coil conformations

Fragment conformations were reduced to linear strings of basin labels by mapping successive backbone torsion angles onto their corresponding φ,ψ-basins (Fig. 1). Conformers with identical strings were regarded as thermodynamically equivalent, as described in the text. The eight basins are disjoint regions of φ,ψ-space that cover 98.9% of all backbone torsion angles observed in the Protein Coil Library (Fitzkee et al.), a database (www.roselab.jhu.edu/coil) of non-α-helix, non-β-strand protein segments from which the eight basins were derived.³³ Basin boundaries, determined from a contour plot of a high-resolution subset of the Protein Coil Library³³ and extended to include bordering outliers, are listed in Supporting Information Table I. A minor population of fragments (5.6%) with residues adopting φ,ψ-angles outside of these boundaries was not considered in this study, and rare turn conformers that contribute less than 0.5% of their structural category's total turn population were also ignored. Furthermore, strands in SnS conformations were required to have ≤0.83 of their total backbone surface area exposed.

Turn conformations

Coil fragments of identical length and conformation (i.e., identical basin strings) bracketed between identical secondary structure types were grouped together. The fragment was defined as a turn if the crossing angle between their bracketing elements of secondary structure was in the interval [120°, 180°] in at least 50% of the group. The crossing angle interval was based on a histogram derived from coil fragments in the PDB (Supporting Information Fig. 1). As in previous work,³⁴ crossing angles were computed from the principal moments of inertia of each secondary structure element, calculated from its C_α-coordinates; the moment with the smallest eigenvalue is the vector of least-squares best-fit to the long axis of that element.³⁵ The crossing angle between two elements was defined as the scalar angle between their two best-fit vectors, each pointed in the N- to C-terminal direction to avoid ambiguities in sign.

An additional surface area criterion was applied to SnS fragments to eliminate conformations in which the two strands did not hydrogen bond. Specifically, the total accessible surface area of at least 50% of strand segments populating a given motif was required to be ≤83% of the maximum accessible surface area = 1149.2 Å, based on an idealized eight-residue strand with φ,ψ,ω-angles = (−120°,135°,180°). The 83% cutoff was chosen based on the normalized accessible surface area distribution of bracketing polyalanyl strands from all SnS fragments (data not shown).

Turn generation

Turns were generated from idealized models consisting of a coil segment flanked at either end by an element of secondary structure, either helix or strand. Idealized helices were eight-residue segments with torsion angles (φ,ψ,ω) = (−62.5°,−42.5°,180°); idealized strands were four-residue segments with torsion angles (φ,ψ,ω) = (−120°,135°,180°). Coil segments were polyalanine sequences unless otherwise specified. Residue structures were represented at a detailed atomic level, including all heavy atoms plus the backbone amide hydrogen. During simulations, ideal bond lengths and angles (LINUS reference) were maintained, and turn formation was maintained by imposing crossing angles between 120° and 180°, consistent with the PDB turn set.

Turn conformers with glycine, proline, and side chain hydrogen bonds

In instances where a polyalanyl coil model was insufficient to capture a turn structure and in which at least half the observed population included a glycine and/or proline and/or a side chain-backbone hydrogen bond, these site-specific features were introduced into the polyalanyl background at residue positions corresponding to their location in the X-ray structure. Simulations then used this augmented model in lieu of the basic polyalanyl model.

Sampling

During simulations, coil residues randomly and independently sampled backbone torsion angles from uniform φ,ψ-distributions derived from a fine-grained (2° × 2°) contour plot of all residues in the Protein Coil Library; all bins containing 2% or more of the total population were included. All φ,ψ-distributions were generated from the high-resolution (2.0 Å or better, R ≤ 0.25), nonredundant (sequence similarity ≤90%) subset of either the PDB or the Protein Coil Library using a PISCES list (September 3, 2007). Nonglycine, nonproline residues sampled within the six non-Y, non-τ basins in Figure 1, whereas glycine and proline residues sampled within their individual residue-specific φ,ψ-distributions. To avoid forming short β-strands in longer coils, three or more consecutive residues with φ,ψ-angles in the β-basin were disallowed.

If n ≥ 2 consecutive residues of any type simultaneously sampled the α-basin, their φ,ψ-angles were minimized into common combinations of two basins:

To avoid helix continuation, residues directly preceding or succeeding an α-helix were assigned random backbone torsion angles from B₂. If residue 1 did not succeed a helix, it was assigned a random backbone torsion angle from B₁. If residue n did not precede a helix, it was assigned a random backbone torsion angles from either B₁ or B₂ with equal probability. Residues 2 through n − 1 were always independently assigned random backbone torsion angles from B₁.

Sampling was further limited for residues in elements of secondary structure that flank coil segments. Specifically, sampling for the two adjacent flanking residues in strands or the three adjacent flanking residues in helices was confined to secondary structure-specific φ,ψ-basins. Side chain sampling utilized residue-specific distributions from the Penultimate Rotamer Library.¹⁹ Proline sampled endo and exo configurations that preserve ideal bond lengths and angles.³⁶

Simulations

Metropolis Monte Carlo simulations sampled conformational space as described above. Each trial move was evaluated for up to three terms—steric clash, hydrogen bond satisfaction, and hydrogen bond energy—depending on the constraints being evaluated. Atoms were treated as hard spheres (radii given in Scoring) and in all cases, a trial with a steric clash was rejected. In simulations that included hydrogen bond satisfaction, conformers having a completely unsatisfied polar group make only a negligible contribution to the population and the trial was simply rejected. For simulations that included a hydrogen bond energy, the Metropolis criterion, e^−βɛ, was evaluated using a distance-dependent hydrogen bond score, ɛ, (see Scoring) and β = 1.67.

Simulations that included a hydrogen bond energy were run in 10,000-iteration cycles and terminated on reaching convergence, defined as three consecutive cycles (c_i, c_i+1, and c_i+2; i ≥ 2) in which the average energies between all three combinations of cycles deviated by less than a threshold of 0.001, except for SnS conformations, for which the threshold was 0.01. Simulations without a hydrogen bond energy were iterated until a statistically significant population was generated (see Supporting Information Table II).

For consistency with the PDB, the total accessible surface area of the strand segments in SnS fragments was required to be ≤83% of the maximum accessible surface area = 1149.2 Å, based on an idealized eight-residue strand with φ,ψ,ω-angles = (−120°,135°,180°).

Scoring

An H-bond score, S, assigned to intrapeptide hydrogen bonds only, but excluding flanking helices, was calculated as:

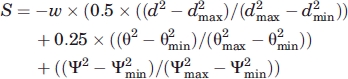where d is the distance between the H-bond donor (H) and acceptor, d_max = 3.0 Å, d_min = 1.5 Å, θ is the N—H—O scalar angle, θ_min = 100° for backbone–backbone and backbone donor-side chain acceptor H-bonds and 45° for side chain donor-backbone acceptor hydrogen bonds, θ_max = 180° for all H-bond types, Ψ is the C—O—H scalar angle, Ψ_min = 90°/Ψ_max = 180° for all H-bond types.³⁷ The weighting coefficient w = 1.5 for backbone–backbone H-bonds four or fewer residues apart (1.0 for SnS fragments) and 3.0 for all other hydrogen bonds (2.0 for SnS fragments). When evaluating H-bond satisfaction, a water probe of radius = 1.25 Å was used (i.e., 1.4 Å scaled to 90%) to test for peptide:water H-bonds to polar groups lacking intrapeptide H-bonds.

Hard sphere radii used throughout, from LINUS¹³, were C (sp³) = 1.64 Å, C (sp²) = 1.5 Å, O (sp²) = 1.35 Å, N (sp²) = 1.35 Å, and H = 1.0 Å. These were scaled to 95% to ensure robustness.

Longer coil segments

The extent to which two-, three-, and four-residue fragments cover longer coil segments was determined as follows. Backbone torsion angles for all 5- to 20-residue coil segments in the Protein Coil Library were transformed into sequences of basin labels as described previously. Sequences were then subdivided into all possible piecewise continuous (i.e., nonoverlapping and complete) combinations of two-, three-, and four-residue fragments, but to avoid trivial coverage, a maximum of only one two-residue fragment was allowed. Every piecewise continuous decomposition was tested in turn by comparing each of the two-, three- or four-residue fragments against the basin sequences of equivalent length in the augmented simulated turn set. A piecewise coil fragment and a simulated turn segment with identical basin sequences constituted a successful match. For any piecewise continuous decomposition, coverage was reckoned as the number of matched residues normalized by the total number of residues in the segment. Coverage for the total segment was given by the decomposition with the highest coverage.

An example will make this clear. Consider a six-residue coil segment (r_1…r₆): it can be decomposed into piecewise continuous fragments in three ways: D₁ = [r₁, r₂, r₃] [r₄, r₅, r₆]; D₂ = [r₁, r₂] [r₃, r₄, r₅, r₆]; and D₃ = [r₁, r₂, r₃, r₄] [r₅, r₆]. Suppose [r₁, r₂, r₃] in D₁ matches a three-residue simulated turn segment but there is no match for [r₄, r₅, r₆]; Coverage₁ = 50%. Further suppose that Coverage₂ = 67% and Coverage₃ = 33%. Then coverage for the six-residue coil segment in question is 67%.

Random libraries were generated as images of the simulated augmented turn library, but with basin labels chosen at random from the eight basins in Figure 1 rather than from turn-based criteria. For a coil segment of given length, the coverage provided by two randomly generated libraries might be expected to differ significantly. To assure convergence, random libraries were generated repeatedly until the average coverage differed by <1% as each new library was added. This procedure resulted in l_i random libraries for each coil segment of length i, where i = 5, 20.