Rank estimation and the multivariate analysis of in vivo fast-scan cyclic voltammetric data

Abstract

Principal component regression has been used in the past to separate current contributions from different neuromodulators measured with in vivo fast-scan cyclic voltammetry. Traditionally, a percent cumulative variance approach has been used to determine the rank of the training set voltammetric matrix during model development, however this approach suffers from several disadvantages including the use of arbitrary percentages and the requirement of extreme precision of training sets. Here we propose that Malinowski’s F-test, a method based on a statistical analysis of the variance contained within the training set, can be used to improve factor selection for the analysis of in vivo fast-scan cyclic voltammetric data. These two methods of rank estimation were compared at all steps in the calibration protocol including the number of principal components retained, overall noise levels, model validation as determined using a residual analysis procedure, and predicted concentration information. By analyzing 119 training sets from two different laboratories amassed over several years, we were able to gain insight into the heterogeneity of in vivo fast-scan cyclic voltammetric data and study how differences in factor selection propagate throughout the entire principal component regression analysis procedure. Visualizing cyclic voltammetric representations of the data contained in the retained and discarded principal components showed that using Malinowski’s F-test for rank estimation of in vivo training sets allowed for noise to be more accurately removed. Malinowski’s F-test also improved the robustness of our criterion for judging multivariate model validity, even though signal-to-noise ratios of the data varied. In addition, pH change was the majority noise carrier of in vivo training sets while dopamine prediction was more sensitive to noise.

INTRODUCTION

Chemometrics has become more prevalent in recent years because of advances in technical computing. Specifically, multivariate calibration represents the fastest growing subdivision of the field.[1] Multivariate calibration is superior to univariate calibration because multivariate calibration can simultaneously improve selectivity, reduce noise, and handle interferences during concentration determination.[2] These reasons have led to the use of multivariate calibration techniques for the analysis of in vivo data.[3, 4, 5]

Principal component regression (PCR) is a multivariate calibration methodology that combines principal component analysis (PCA) with inverse least-squares regression.[6] In this technique, a data set consisting of measured spectra and the corresponding concentrations known as a training set is first assembled. The measured spectra in the training set is broken up into principal components (PCs) which are abstract representations of the information (termed variance) present. Some of the PCs in the data set describe relevant variance and are essential for proper model development and concentration prediction. PCs of this type are termed primary PCs. The rest of the PCs, termed secondary or error PCs, describe only noise and can be discarded.[7] A model is constructed using the relevant primary PCs and a regression matrix is calculated using the concentration data from the training set. Finally, concentration data of an unknown data set is predicted by projecting the unknown data set onto the retained PCs and relating the distance back into concentration using the regression matrix.

Fast-scan cyclic voltammetry (FSCV) is an electroanalytical technique that uses scan rates above 100 V/s to monitor neuromodulator release in biological systems, including freely-moving rats capable of performing behavioral tasks.[8] FSCV offers many advantages including excellent sensitivity, sub-second time resolution, micrometer spatial resolution, and minimal damage from the carbon-fiber microelectrode. Unfortunately, the moderate selectivity obtained using FSCV can complicate the analysis of in vivo data.[9] Incorporating PCR into the analysis of in vivo FSCV spectral data allowed for a more widely acceptable, robust, unbiased multivariate approach to determine the concentration of multiple neuromodulators while simultaneously removing noise.

PCR has been used in conjunction with FSCV to investigate neuromodulator release in cells,[9] brain slices,[9] and in freely-moving rats.[10, 11] PCR has also been used to account for electrode drift, enabling continual FSCV measurements to be made for up to 30 minutes.[12] A residual analysis procedure developed by Jackson and Mudholkar[13] was incorporated to make sure that the primary PCs of the training set describe all relevant sources of variance present in the unknown data set being predicted. Any developed PCR model that fails to meet this requirement is discarded and not used for concentration prediction.[14, 15]

Determining the proper rank (number of primary PCs to retain) of multivariate data is a difficult problem in chemometrics. Although many chemometric texts include a brief overview of some of the more popular methods,[6, 16, 17, 18] a general consensus about which method should be used remains undetermined. Broadly, these approaches can be divided into two categories: methods that require estimation of the error level and methods that require no a priori information on experimental error. Furthermore, some techniques have a statistical basis and significance tests can be developed to determine the proper number of PCs to retain in the PCR model.

In our original work we used the method of cumulative variance to decide the rank of the voltammetric matrix of the training set.[9] In this method, sufficient PCs are retained to describe a specified percentage of the overall variance. A value of 99.5% of the cumulative variance was arbitrarily chosen for factor selection. While the percent cumulative variance method is both extremely simple to comprehend and calculate, this approach has several drawbacks. First, it assumes that all training sets are sufficiently precise to satisfy a specified value of the error present; in our case noise would represent 0.5% of the variance in every training set voltammetric matrix. Differences in experimental variables such as users, equipment, biological variability, and laboratories will most certainly violate this rule.[19] Second, there is not a specific percentage of the variance corresponding to noise that works for all users in all cases so the percentage choice will always have to be arbitrary and inconsistent. Methods exist to determine a distribution of the percentage cumulative variance so more formal procedures could be used.[17] Finally, because of the extreme precision required for widespread usage and the lack of a constant value that works in all cases, the use of the cumulative variance method is not advocated.[16, 18] Therefore, there is a need for the use of a different method of factor selection in the PCR analysis of FSCV data.

There are several requirements in choosing a method of factor selection for the analysis of FSCV data. First, the method should be accepted in chemometrics literature. Second, the method requires robustness sufficient to provide consistent results across laboratories. Third, the method should not require any a priori estimation of error levels. Fourth, a statistical measure should be employed in rank determination to remove any subjectivity and interpretation to make the results more comparable between laboratories. Finally, the method should be simple to understand and calculate.

We have previously used Malinowski’s F-test for factor selection with much success.[12] A thorough evaluation and comparison with the 99.5% cumulative variance method, however, has not been presented. In this work, the two methods of factor selection are compared in several ways beyond estimating rank. Noise removal, model validity, and concentration prediction constructed using the primary PCs retained with each approach are discussed.

THEORY

Malinowski introduced the concept of a reduced eigenvalue (REV) of a data matrix

$${\text{REV}}_j=\frac{{\lambda }_j}{(r-j+1)(c-j+1)}$$ (eq 1)

where λ_j is the eigenvalue corresponding to j^th PC, r is the number of rows in the data matrix, and c is the number of columns in the data matrix.[20] He proposed that REVs of secondary PCs should be statistically equal and REVs of primary PCs would be larger because of contributions due to significant information present in the data matrix. An F-test was developed using REVs to statistically differentiate between primary and secondary PCs, thereby determining the rank of a data matrix.[21, 22] The F-statistic used to test whether the n^th PC is a primary or secondary PC is calculated as

$$F(1,s-n)=\frac{{\displaystyle \sum _{j=n+1}^s}(r-j+1)(c-j+1)}{(r-n+1)(c-n+1)}\frac{{\lambda }_n}{{\displaystyle \sum _{j=n+1}^s}{\lambda }_j^0}$$ (eq 2)

where s is equal to r or c, whichever is smaller, and λ_j⁰ corresponds to the error eigenvalue of the j^th PC. Each PC is orthogonal, capturing variance previous PCs did not, thereby satisfying the requirement of independence necessary for an F-test.[21, 22] These calculations are easy to perform and Matlab command lines are available.[23]

Malinowski’s F-test is conducted as follows. First, the smallest eigenvalue is assumed to represent only noise and is assigned to the null pool. The next smallest eigenvalue is tested for significance using equation 2. If the calculated F-statistic is larger than the tabulated F-statistic at a specific value of α (i.e. 0.05, 0.1, etc.), the null hypothesis is rejected because the n^th PC had a variance statistically larger than the error and the rank of the data matrix is determined. If the calculated F-statistic is smaller than the tabulated F-statistic, the tested eigenvalue is also assigned to the null pool. The test is repeated with the next smallest eigenvalue compared to the pool of eigenvalues until the null hypothesis is rejected. At each iteration of Malinowski’s F-test, there is an α% chance that the n^th PC describes error rather than significant information present in the spectral matrix of the training set. Malinowski determined that an α value of 5% tended to underestimate the rank and an α value of 10% tended to overestimate the rank.[21, 22]

Malinowski originally suggested that REVs would only be constant for uniformly distributed error and normally distributed error could contain one REV that may be significantly larger than the other error REVs, thereby causing Malinowski’s F-test to erroneously overestimate rank.[7] This result was unsubstantiated, however, because uniform, normal, or random sign simulated noise distributions gave identical REVs.[24] Malinowski’s F-test also performed well in the presence of Gaussian error and moderately well in the presence of multiplicative noise.[25] In addition, Malinowski’s F-test takes advantage of the central limit theorem, giving a theoretical basis for the insignificance of the underlying distribution of the noise present in the original data spectrum.[20, 25] Through simulations of random matrices error REVs were determined not to follow a normal distribution when r and c deviated substantially from one another[24] which violate the assumption necessary for an F-test, but Malinowski’s F-test has been used successfully to estimate the rank of these “skinny” matrices in the literature.[25, 26]

One of the assumptions of Malinowski’s F-test is that the noise present in the training set spectral matrix is homoscedastic (has a constant statistical variance) and is uncorrelated between variables.[19, 27] If multiple sources of error are present with significantly different amplitudes or if the data are autocorrelated, Malinowski’s F-test will erroneously overestimate rank.[19] [28] In addition, if the primary PCs contain variance similar to secondary PCs, Malinowski’s F-test is expected to assign those primary PCs to the null pool, thereby underestimating the rank.[26]

One of the criticisms against Malinowski’s F-test is that an incorrect number of degrees of freedom are used in the calculation of the F-statistic.[29] The Faber-Kowalski F-test uses much larger degrees of freedom calculated from the analysis of simulations of random matrices, thus increasing the power of the statistical test and having a much sharper significance level (α ≤ 1%). This method is computationally intensive; however, the authors have supplied command lines for mathematical software programs.[30] However, this adaptation of Malinowski’s F-test has been criticized for being hypersensitive to the requirement of a normal error distribution which many chemical measurements fail to meet.[19, 26]

In sum, there are several assumptions and limitations that we recognize for the use of Malinowski’s F-test. First, we assume the noise to be homoscedastic among the cyclic voltammograms contained in each training set voltammetric matrix. If heteroscedastic noise is present, we recognize noise will be retained in model construction. Second, any PCs that describe variance similar to that of noise will be discarded, even if it is possible that relevant information is buried within noise. We define significant variance as having an amplitude statistically larger than noise variance so any PC that fails to meet this requirement will be discarded. Third, an α value of 5% will be used for Malinowski’s F-test because of the size of the training set voltammetric matrix and we wish to be more confident in the identification of primary PCs.

EXPERIMENTAL

Fast-Scan Cyclic Voltammetry and Animal Experimentation

Carbon-fiber microelectrodes were prepared as described previously using T-650 carbon fibers cut to an exposed length of 25–100 μm.[31] The voltage of the carbon-fiber microelectrode was held at -0.4 V, increased to 1.3 V, and decreased back to -0.4 V at 400 V/s. This triangular excursion was repeated at 10 Hz. All potentials are reported versus a Ag/AgCl reference electrode. Data acquisition was performed as previously described using locally constructed hardware and software.[32] All cyclic voltammograms were low-pass filtered at 2 kHz. The stimulated release and intracranial self stimulation data was also smoothed using a one-pass moving average.

All animal experiments were performed on freely-moving male Sprague Dawley rats weighing approximately 300 g in accordance with the University of North Carolina Animal Care and Use Committee. Surgeries were carried out as described elsewhere.[10, 33, 34] The coordinates used for stimulating and working electrodes varied according to the desired experiment because training sets from multiple users and laboratories were pooled. Generally, the training sets focused on measuring in the dorsal and ventral striatum, with the nucleus accumbens being a region of specific interest. The location in the brain that the cyclic voltammograms in the training set were taken from was irrelevant for the analyses. All training sets used were taken from freely-moving rat experiments so the cyclic voltammograms used in prediction were the best approximation to those recorded in the unknown data sets.[10] In vitro cyclic voltammograms were not included in the training sets because inconsistencies in the shapes of the cyclic voltammograms, peak potentials, and noise levels.

Data Analysis and Principal Component Regression

All chemometric and statistical analyses were carried out in MATLAB (Mathworks, Natick, MA), GraphPad Prism (GraphPad Software Incorporated, La Jolla, CA), Excel (Microsoft Corporation, Redmond, WA) and LabVIEW (National Instruments, Austin, TX). All values are reported as averages ± standard error of the mean (SEM).

Each in vivo training set constructed met specific requirements.[35, 36] First, cyclic voltammograms of all expected analytes were included, generated by electrically stimulating the animal. Second, no more than one cyclic voltammogram for each species was taken per stimulated release event, satisfying the requirement of mutual independence. Third, the training set mimicked the experimental conditions as closely as possible. The same electrode, electronics, and other equipment were used to collect both the training set and the unknown data set. The various cyclic voltammograms in the training set were consistent in shape and representative in noise level to the unknown data set. Cyclic voltammograms of the unknown data set were not used to build the training set. Finally, the training set spanned the concentration range contained in the unknown data set being predicted. Cyclic voltammograms of varying intensity were generated by changing the stimulation parameters (i.e. current, number of pulses, and frequency). Concentrations were estimated using flow injection analysis[37] after the experiment was completed.[34]

In total, 119 training sets were assembled from five users in two different laboratories over the course of several years. These training sets have been used for concentration prediction from a variety of experiments including various behavioral experiments and stimulated release studies. Each training set consisted of five dopamine and five pH change cyclic voltammograms. Any training sets that contained more than five cyclic voltammograms per analyte were truncated to make all training sets consistent in size. However, a uniform distribution of concentration values within the training set was maintained.

PCA was performed using singular value decomposition.[38] PCR using residual analysis was performed as described previously.[14, 15] Cyclic voltammetric representations of the training set consisting of only the primary PCs were calculated as follows. First, the primary PCs of the training set determined by either the 99.5% cumulative variance method or Malinowski’s F-test were organized in a matrix, Vc. The projection of the training set onto the primary PCs, A_proj was calculated,

$${\mathbf{A}}_{\mathbf{proj}}=\mathbf{V}{\mathbf{c}}^{\mathbf{T}}\mathbf{A}$$ (eq 3)

where the superscript T represents the transpose of the matrix and A contains the training set voltammetric matrix. Finally, the training set consisting of only the primary PCs, A_nPC, was reconstructed by multiplying the retained PCs by the projection of the training set onto the primary PCs[13]

$${\mathbf{A}}_{\mathbf{nPC}}=\mathbf{Vc}{\mathbf{A}}_{\mathbf{proj}}$$ (eq 4)

To determine the noise discarded in the secondary PCs of a training set, A_jPC, A_nPC was subtracted from the original training set voltammetric matrix A.

The signal-to-noise ratios of the dopamine cyclic voltammograms were calculated by dividing oxidative peak current by the standard deviation of a flat portion of the cyclic voltammogram, specifically from 0.95 V to 0.25 V on the reductive sweep. Root-mean-square (RMS) noise was calculated from A_jPC. The RMS current, i_RMS, was calculated for each cyclic voltammogram in the training set using the following equation

$$i_{\mathit{RMS}}=\sqrt{\frac{{\displaystyle \sum _{x=1}^w}{(i_x)}^2}{w}}$$ (eq 5)

where i_x is the current at the x^th point of the voltammetric waveform containing w total points taken from the A_jPC matrix. An average i_RMS value for each analyte using each method of factor selection was calculated for each training set.

RESULTS AND DISCUSSION

Principal Component Selection & Training Set Heterogeneity

Table 1 compares how Malinowski’s F-test and the 99.5% cumulative variance method determine the rank of a data matrix. Eigenvalues are given for each PC along with the corresponding cumulative variance percentage as rank increases. From this data, the 99.5% cumulative variance method would estimate the rank of this training set voltammetric matrix to be four. REVs are also given for each PC. For PCs four through ten the REVs are comparable, as evidenced by the small F-statistics. PC ten does not have an F-statistic because its REV is placed in the null pool. Starting from the bottom of the table working upwards, the F-statistic becomes larger than the 5% critical F-values [39] for a rank of three, indicating that three PCs are statistically relevant in model construction for this training set.

Table 1.

Eigenvalue, reduced eigenvalue, calculated F-statistic, critical F-value at 5% significance[39], and PRESS value as a function of PC for an example FSCV training set spectral matrix.

n	λ	% Cum. Var.	REV	FStat	F0.05	PRESS
1	4875.4	85.33	0.4875	26.08	5.12	25.4
2	551.2	94.98	0.0613	7.66	5.32	17.7
3	238.6	99.15	0.0299	17.23	5.59	11.0
4	26.9	99.63	0.0039	3.76	5.99	9.6
5	11.5	99.83	0.0019	2.91	6.61	8.0
6	5.0	99.91	0.0010	2.04	7.71	6.3
7	2.3	99.95	0.0006	1.29	10.13	3.1
8	1.7	99.98	0.0006	1.91	18.51	2.1
9	0.5	99.99	0.0003	0.74	161.45	~ 0
10	0.4	100	0.0004	--	--	--

Leave one out cross validation is also a popular method of rank determination in which the training set concentration matrix is incorporated.[18, 40, 41] Predicted residual error sum-of-squares (PRESS) values are calculated as a function of rank and give the user an idea of the error between the actual concentrations and those predicted using the retained PCs.[40] A minimum or stabilization of PRESS values is indicative of the proper rank of the training set. This test is subjective, but more formal statistical tests are available.[42, 43, 44] Malinowski’s F-test and cross validation have been compared in the past, yielding mixed results.[26, 45, 46, 47] Here, cross validation was not able to estimate rank for all data sets because the rank of many training sets (as in Table 1) was ambiguous using this approach.

When comparing the 99.5% cumulative variance method and Malinowski’s F-test in the number of PCs to retain in the model used for concentration prediction, three outcomes are possible. First, if the number of PCs to retain in the model is fewer for Malinowski’s F-test compared to the 99.5% cumulative variance method (referred to as Case I) then the overall noise level is greater than 0.5% of the cumulative variance and models developed using the 99.5% cumulative variance rule are retaining noise during concentration prediction. Keeping noise should not significantly impact concentration data as long as any noise retained does not significantly alter the factor space generated during PCA deconvolution of a training set. Second, if the number of PCs to retain in the model is greater for Malinowski’s F-test compared to the 99.5% cumulative variance method (referred to as Case II) then the overall noise level is less than 0.5% of the cumulative variance and models developed using the 99.5% cumulative variance rule are discarding significant information in the training set when calculating concentration data. Finally, if the number of PCs to retain in the model is the same for both Malinowski’s F-test and the 99.5% cumulative variance method (referred to as Case III) then the overall noise level is 0.5% of the cumulative variance.

Table 2 compares the 99.5% cumulative variance method to Malinowski’s F-test in the number of PCs to retain in 119 training sets from five different researchers in two different laboratories. Table 2 shows both the heterogeneity of training sets between researchers and failure of the 99.5% cumulative variance method in determining the number of principal components to retain. The vast majority (65.5%) of the evaluated training sets were classified as Case I, a much smaller percentage (10.0%) were classified as Case II, and the rest (24.4%) were classified as Case III.

Table 2.

Inter-researcher comparison of the number of principal components to retain between Malinowski’s F-test and the 99.5% cumulative variance method

	Researcher 1	Researcher 2	Researcher 3	Researcher 4	Researcher 5	Totals
	N = 13	N = 16	N = 20	N = 14	N = 56	N = 119
Case I	2	8	16	8	44	78 (65.5%)
Case II	2	3	0	5	2	12 (10.0%)
Case III	9	5	4	1	10	29 (24.4%)

Table 2 shows how inadequate using a fixed number percentage of the cumulative variance for PC retention was at removing noise from training sets as stated in chemometric texts.[17, 18] The 99.5% cumulative variance rule worked well only for researcher 1 and moderately overall. In fact, if these training sets were analyzed with the 99.5% cumulative variance rule 65.5% of the PCR models constructed would retain noise during PCR prediction and 10% of PCR models constructed would discard significant information used for concentration prediction.

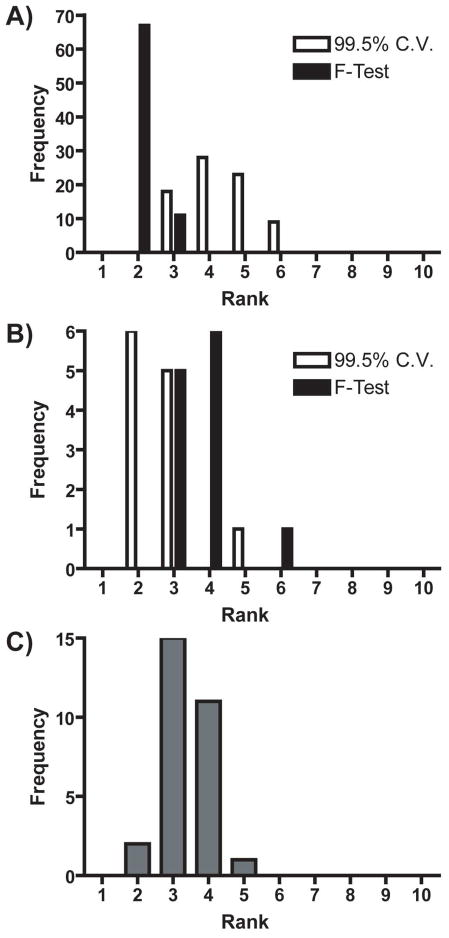
Figure 1 shows the number of PCs retained from the training sets in Table 2 using both the 99.5% cumulative variance method and Malinowski’s F-test. Figure 1A compares both methods for all of the Case I training sets. While the 99.5% cumulative variance method retained a wider distribution of PCs, Malinowski’s F-test retained no more than 3 PCs, with two PCs being the mode of the distribution. On average, Malinowski’s F-test retained two fewer PCs than the 99.5% cumulative variance method for Case I training sets. Figure 1B compares both methods for all of the Case II training sets. The distribution of the number of primary PCs retained by Malinowski’s F-test was shifted higher by approximately one PC on average. Finally, Figure 1C shows the distribution of retained PCs for all of the Case III training sets. For these training sets the average number of primary PCs was three.

Figure 1.

Histograms of the estimated rank of A) Case I and B) Case II training sets. White and black represent rank determined by the 99.5% cumulative variance method and Malinowski’s F-test, respectively. C) Histogram of the estimated rank of Case III training sets.

There were only two analytes in all of these training sets, but one PC does not always necessarily correspond to one analyte.[48] It is possible that any training set voltammetric matrix with a rank higher than two could be due to differences in signal-to-noise ratio, the presence of heteroscedastic noise, or to inconsistencies present in the various cyclic voltammograms of the training set that were larger than noise. In addition, pH change cyclic voltammograms do not have a consistent “correct” shape.[49, 50, 51] This discrepancy makes the process of separating significant information from noise difficult for the pH change cyclic voltammograms of the training set. It is also possible that more than two primary PCs were needed to span significant current contributions to the analytes of interest.

Comparison of Information Contained in Secondary PCs

In PCR, some of the principal components are discarded in an effort to remove noise from the training set before concentration prediction. Visualizing how the training set cyclic voltammograms change as rank is estimated differently should give qualitative information on how noise is removed. This process will also show researchers “effective” cyclic voltammograms of the training set used by PCR for concentration prediction. In addition, visualizing the secondary PCs will determine if any significant information was discarded during factor selection.

Figure 2 shows a representative training set comparing how both methods of factor selection remove noise for a Case I training set. Since there were ten cyclic voltammograms in the training set, ten PCs were calculated. For this training set, the 99.5% cumulative variance method retained five PCs in the model while Malinowski’s F-test retained two PCs. Figures 2A and 2B show the original dopamine and pH change cyclic voltammograms, respectively, in the training set. The noise in the dopamine cyclic voltammograms caused the peak shapes and peak potentials to vary. In addition, there is substantially more noise present in the pH change cyclic voltammograms. By discarding five PCs, the 99.5% cumulative variance method only slightly improved the condition of the cyclic voltammograms as shown in Figures 2C and 2D. Some of the noise in the dopamine cyclic voltammograms was removed and their peak shapes and peak potentials became more consistent. Unfortunately, the pH change cyclic voltammograms showed only a small decrease in noise as evidenced in the similarity between Figures 2B and 2D. Substantial noise remained in the pH change cyclic voltammograms as evidenced by extraneous peaks and inconsistent shapes.

Figure 2.

Comparison of effective cyclic voltammograms in a representative Case I training set. A) Original dopamine cyclic voltammograms containing all PCs before factor selection. B) Original pH change cyclic voltammograms containing all PCs before factor selection. C) Dopamine cyclic voltammograms from A) constructed using only the PCs retained by the 99.5% cumulative variance method (n = 5 PCs). D) pH change cyclic voltammograms from B) constructed using only the PCs retained by the 99.5% cumulative variance method (n = 5 PCs). E) Dopamine cyclic voltammograms from A) constructed using only the PCs retained by Malinowski’s F-test (n = 2 PCs). F) pH change cyclic voltammograms from B) constructed using only the PCs retained by Malinowski’s F-test (n = 2 PCs).

By discarding eight PCs, Malinowski’s F-test was able to remove more noise in the dopamine and pH change cyclic voltammograms as shown in Figures 2E and 2F, respectively. The dopamine cyclic voltammograms were less noisy than those computed using the 99.5% cumulative variance method, specifically at the beginning and end of the cyclic voltammetric sweeps and in the green cyclic voltammogram overall. Some small peaks at -0.1 V and 0.1 V were retained in some of the dopamine cyclic voltammograms. The amplitudes of these peaks were comparable to the noise level in the original dopamine cyclic voltammograms, but since these peaks were conserved in several of the cyclic voltammograms, PCA was able to separate them as a relevant portion of the dopamine cyclic voltammograms. The small peak at the switching potential in some of the dopamine cyclic voltammograms was probably retained for a similar reason. The pH change cyclic voltammograms calculated with Malinowski’s F-test showed a dramatic decrease in the overall noise level. As with the dopamine cyclic voltammograms, the shape of the pH change cyclic voltammograms was conserved as the amplitude of the cyclic voltammograms varied.

Figure 2 showed qualitatively how Malinowski’s F-test could remove more noise than the 99.5% cumulative variance method for Case I training sets, which were the majority of training sets analyzed. It is important to quantify the amount of noise each method removes from Case I training sets rather than relying only on qualitative evaluations. Figure 3 displays the amount of RMS noise removed from dopamine and pH change cyclic voltammograms using both methods of factor selection for all Case I training sets. Overall, Malinowski’s F-test was able to remove significantly more noise than the 99.5% cumulative variance method from dopamine cyclic voltammograms (p < 0.0001, Wilcoxon Signed Rank Test) and from the pH change cyclic voltammograms (p < 0.0001, Wilcoxon Signed Rank Test) proving that the 99.5% cumulative variance method was unsuitable for noise removal in these training sets.

Figure 3.

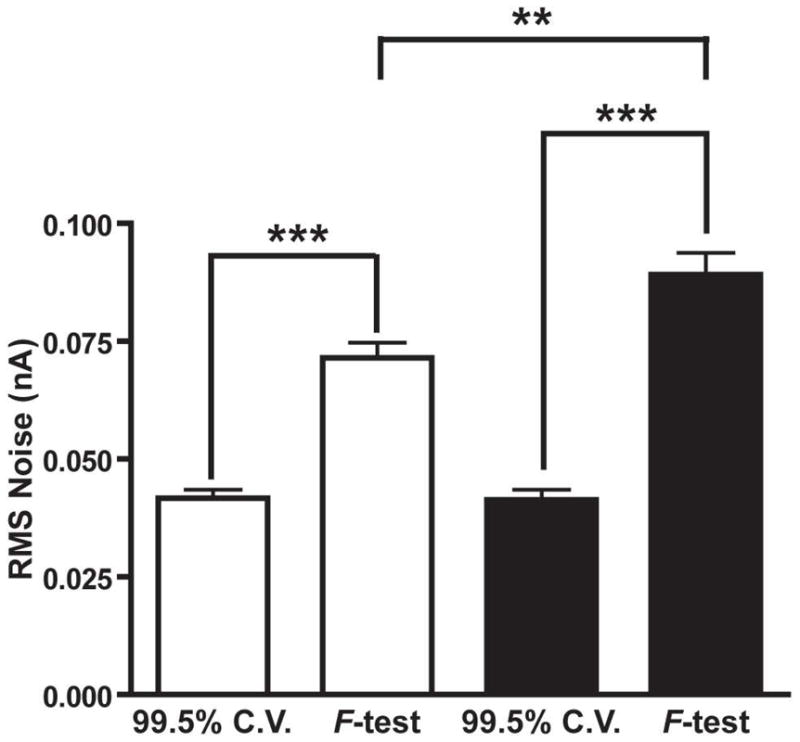
RMS noise removed by the 99.5% cumulative variance method (99.5% C.V.) and Malinowski’s F-test for all of the Case I training sets. Error bars represent SEM. White bars represent noise from dopamine secondary PCs and black bars represent noise from pH change secondary PCs. Two stars and three stars represent P < 0.01 and P < 0.001 significance, respectively.

The noise removed by the 99.5% cumulative variance method was not significantly different between dopamine and pH change (p = 0.3057, Mann-Whitney Test). In addition, significantly more noise was present in the pH change cyclic voltammograms compared to the dopamine cyclic voltammograms (p = 0.0033, Mann-Whitney Test) when Malinowski’s F-test was used for rank estimation. A possible reason for this increased noise could be due to the origin of the pH change cyclic voltammograms used for the in vivo training sets. Background currents that occur when surface functional groups on the electrode are protonated and deprotonated contribute to the shape of the pH change cyclic voltammogram.[52] It is therefore plausible that the pH change cyclic voltammograms are highly dependent on the local environment of the electrode in vivo. Subtle changes in extracellular species could impact the shape of cyclic voltammograms. Changes in the shape of the cyclic voltammograms comparable to noise would be discarded increasing the overall noise level. In addition, the pH change cyclic voltammograms are obtained approximately 2–5 seconds after an electrical stimulation is given to the animal, during which time locomotor activity is increased which can increase electrical noise. Either way, since the signal-to-noise ratio of the cyclic voltammograms used in Figure 3 was low (16 - 61), these differences were not significantly larger than the noise present in the training set cyclic voltammograms and were thus discarded by Malinowski’s F-test.

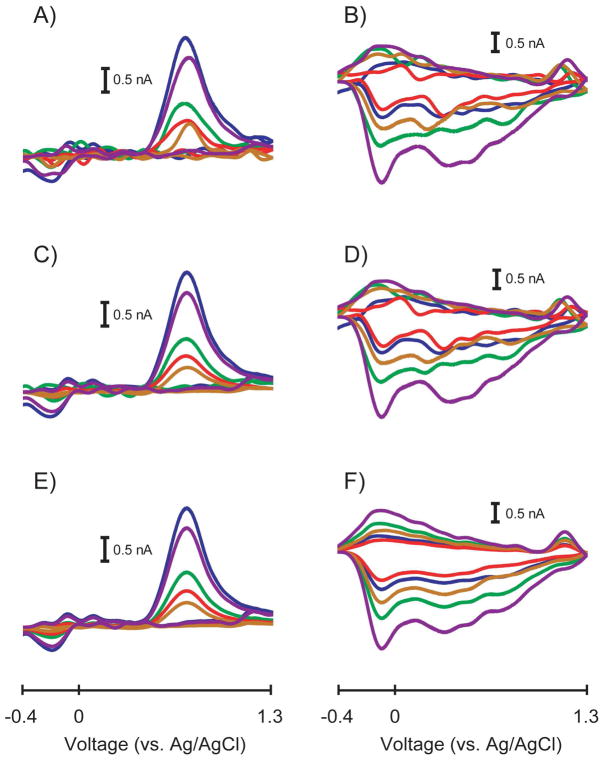
Potentially significant information could be discarded by the 99.5% cumulative variance method for Case II training sets because statistically more PCs should be retained. Figure 4 more clearly illustrates what each method considers error for a representative Case II training set. The 99.5% cumulative variance method estimated rank to be two and Malinowski’s F-test estimated rank to be four for this training set. Figure 4A contains cyclic voltammetric representations of PCs three through ten that were discarded with the 99.5% cumulative variance method for each dopamine sample in the Case II training set. Similarly, Figure 4B contains cyclic voltammetric representations of PCs three through ten for each pH change sample in the training set. Figure 4C and 4D contain cyclic voltammetric representations of PCs five through ten that were discarded with Malinowski’s F-test for dopamine and pH changes, respectively. Figures 4E and 4F contain cyclic voltammetric representations of PCs three and four for both dopamine and pH changes, respectively, in the original training set.

Figure 4.

Cyclic voltammetric representation of the secondary PCs from each method of factor selection for a representative Case II training set. A) Secondary PCs of the dopamine cyclic voltammograms determined by the 99.5% cumulative variance method (PCs 3–10). B) Secondary PCs of the pH change cyclic voltammograms determined by the 99.5% cumulative variance method (PCs 3–10). C) Secondary PCs of the dopamine cyclic voltammograms determined by Malinowski’s F-test (PCs 5–10). D) Secondary PCs of the pH change cyclic voltammograms determined by Malinowski’s F-test (PCs 5–10). E) The difference of secondary PCs between methods for the dopamine cyclic voltammograms (PCs 3–4). F) The difference of secondary PCs between methods for the pH change cyclic voltammograms (PCs 3–4).

Interestingly, a conserved distinct shape emerged in the difference between the secondary PCs discarded between the two methods for the dopamine cyclic voltammograms. Error with such a pattern suggest that PCs three and four represent deterministic variance which was why Malinowski’s F-test retained these PCs. The shapes of the cyclic voltammograms in Figures 4E and 4F show that heteroscedastic noise was not present which could have caused Malinowski’s F-test to overestimate rank. Since the signal-to-noise ratio of the original cyclic voltammograms of this representative Case II training set was high (114 - 307), PCs three and four discarded by the 99.5% cumulative variance rule contained variance that was significantly larger than the variance of the noise present. While discarding these PCs may have helped create more consistently shaped cyclic voltammograms and these PCs may not be necessary for concentration prediction, it is our assertion that it is better and more conservative to retain all statistically significant information present in training sets.

Figures 4E and 4F showed that more than two primary PCs were necessary to describe currents measured at the switching potential and at the end of the voltammetric sweep when signal-to-noise ratios of the cyclic voltammograms in a training set are high. This data, taken with the data presented in Figures 1 and 3 suggest that the number of primary PCs required for in vivo FSCV voltammetric data varies with signal-to-noise ratio. The signal-to-noise ratios of the dopamine cyclic voltammograms for Case I, Case II, and Case III training sets were significantly different (p < 0.0001, Kruskal-Wallis Test) with averages of 74 ± 3 (N = 390), 200 ± 17 (N = 60), and 147 ± 12 (N = 145), respectively, giving evidence for this hypothesis.

Training sets with smaller signal-to-noise ratios will have more room to discard inconsistencies in the cyclic voltammograms with amplitudes similar to that of noise. As signal-to-noise ratio increases, inconsistencies in the shapes of the cyclic voltammograms of the training set become more significant compared to the noise present. In addition, PCs describing only a small amount of the overall variance of the training set become more significant.

Comparison of Model Validity

The most important aspect to our in vivo calibration protocol is PCR model validation. We use a residual analysis method developed by Jackson and Mudholkar to determine if the multivariate model is valid and predicted concentration values can be trusted.[13, 14, 15] This method uses the data contained in the discarded PCs from the training set to determine a threshold for tolerable error (Q_α). Q_α represents a threshold where 1-α% of the sum of squared residuals due to noise would fall below. By convention, we use an α value of 5% for the residual analysis procedure.[14, 15] The sum of the squared residual error present in each cyclic voltammogram at time t of the unknown data file being predicted is calculated as the quantity Q_t, plotted as a function of time, and compared to Q_α. The quantity Q_t is calculated as

$$Q_t=\sum _{x=1}^w{\left(i_x-{\widehat{i}}_x\right)}^2$$ (eq 6)

where i_x is the current at the x^th point of the cyclic voltammogram, î_x is the current predicted using only the relevant PCs of the PCR model, and w is the number of points in the cyclic voltammogram. As long as the Q_t plot falls below Q_α, the retained PCs accurately describe all significant sources of variance present. However, if the Q_t plot crosses Q_α, the retained PCs of the model do not accurately describe all relevant sources of variance in the unknown data set and the model cannot be used for concentration prediction.

Incorrect estimation of the proper noise level would cause an incorrect value of Q_α to be calculated which would impair proper judgment of PCR model validity. Figure 5 shows Q_α distributions for Case I, II, and III training sets shown in Figure 1. Figure 5A shows a histogram of Q_α values calculated for all Case I training sets. First, the Q_α values calculated using the PCs retained with Malinowski’s F-test have a considerably larger distribution, indicating that the amount of error contained in training sets is variable. This variability could be due to low signal-to-noise ratios or to differences in users, electrodes, equipment, or other experimental variables. Second, the Q_α values calculated using the 99.5% cumulative variance method were shifted to lower threshold values because more PCs were retained than necessary. Retaining more primary PCs would decrease the amount of variance contained in the secondary PCs. This difference would render a value of Q_α that would be artificially lower than it rightfully should be, which may lead to possibly rejecting an otherwise valid PCR model.

Figure 5.

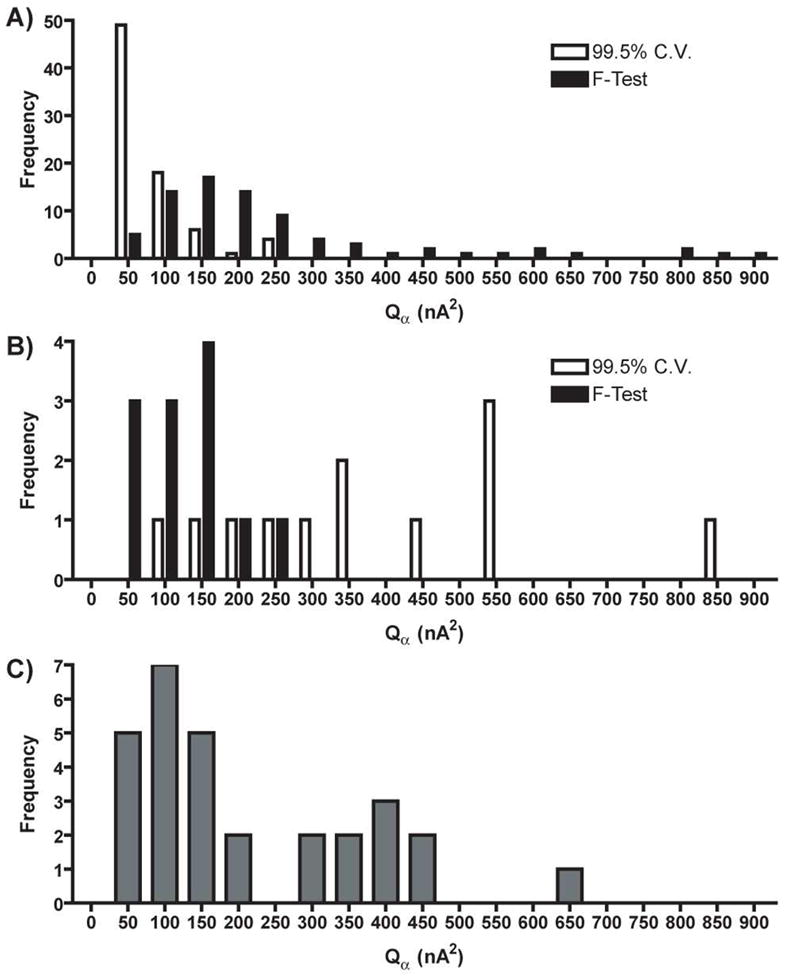
Histograms of Q_α values of A) Case I and B) Case II training sets. White and black represent the rank determined by the 99.5% cumulative variance method and Malinowski’s F-test, respectively. C) Histogram of Q_α values of Case III training sets.

Figure 5B shows a histogram of Q_α values for all Case II training sets. The Q_α values calculated using the PCs retained with Malinowski’s F-test were lower than those calculated using the PCs retained with the 99.5% cumulative variance method. The distribution of Q_α values calculated using the PCs retained with Malinowski’s F-test was also smaller. Retaining too few primary PCs with the 99.5% cumulative variance method would leave more variance in the secondary PCs which would render a value of Q_α that would be artificially higher than it should be, possibly leading to the use of an invalid PCR model for concentration prediction. Figure 5C shows a bimodal distribution of Q_α values existed for all of the Case III training sets.

Table 3 gives average Q_α and values for the data presented in Figure 5. The average Q_α value calculated using the PCs retained with Malinowski’s F-test was approximately four times larger than the average Q_α value calculated using the PCs retained with the 99.5% cumulative variance method for Case I training sets. For Case II training sets the average Q_α value calculated using the PCs retained with Malinowski’s F-test was approximately 3.5-fold lower than the average Q_α value calculated using the PCs retained with the 99.5% cumulative variance method. The average Q_α values from Case III training sets were comparable to the values calculated using the PCs retained with Malinowski’s F-test from Case I training sets.

Table 3.

Comparison of average Q_α values calculated using PCs retained with Malinowski’s F-test and the 99.5% cumulative variance (C.V.) method.

	F-test Qα (nA2)	99.5% C.V. Qα (nA2)
Case I (N = 78)	220 ± 22	58 ± 6
Case II (N = 12)	102 ± 17	364 ± 59

	Qα (nA2)
Case III (N = 29)	186 ± 30

The data in Table 3 suggest that it was possible that the validity of PCR models was improperly assessed. Since Case I training sets were the majority of training sets used, in most instances researchers were being overly cautions, possibly discarding valid PCR models. The analysis of the much smaller number of Case II training sets suggests it was possible that invalid PCR models were used for concentration prediction. However, we do not doubt the validity of our previous results for several reasons. First, Table 2 shows that no more than five of such training sets originated from a specific researcher over several years so any discrepancies were probably averaged out. Second, cyclic voltammograms contained in Case II training sets had such a large signal-to-noise ratio, any errors in concentration prediction using a proper PCR model should be small. Third, it is very unlikely that all of the Case II training sets produced invalid PCR models in the analysis of all experiments. Nevertheless, a statistical-based rank estimation approach that properly distinguishes between information and noise, such as Malinowski’s F-test, should be used with the residual analysis procedure to properly assess multivariate model validity. Because a distribution, rather than one specific value, existed for Q_α suggests that a universal training set does not exist for the analysis of in vivo FSCV data.

Comparison in Concentration Prediction

Ideally, it would be best to assess accuracy of both methods of factor selection in concentration prediction using in vitro training sets, however there are several important features of our in vitro training sets which can limit their applicability to in vivo training sets. First, the shapes of the cyclic voltammograms are more consistent in vitro than in vivo. Second, the shapes of the cyclic voltammograms in vitro are not always consistent with the shapes of the cyclic voltammograms in vivo. Third, the signal-to-noise ratios of the cyclic voltammograms in vitro are different than those in vivo and signal-to-noise ratios are important in determining the type of training set being analyzed (Case I, Case II, or Case III). To guarantee Case I training sets one could artificially add noise through simulations, but the applicability of such data sets could be in question.

In vitro training sets have an independent measure of concentration (i.e. the concentrations we believe we are creating during solution preparation) so accuracy of the prediction can always be determined. However, in vivo training sets have their concentrations determined by dividing measured peak height by sensitivity without an independent measure of concentration. Unfortunately, because the “true” concentration of species in vivo is unknown, we cannot determine whether the extra PCs retained by the 99.5% cumulative variance method were necessary for accurate concentration prediction in vivo. Instead, all that can be inferred is if the extra PCs retained significantly affect the concentration data determined by PCR. We then have to decide which method of factor selection allows us to build the better model, remove noise, and generate the best estimate for in vivo concentration data.

Since the number of Case II training sets is small and no difference in concentration values would be seen for Case III training sets, this section will focus solely on Case I training sets. In every instance that the 99.5% cumulative variance method retains more PCs in the model compared to Malinowski’s F-test, noise will be used in concentration prediction. In theory, concentration information should not be appreciably different between both methods as long as the signal-to-noise ratio of the cyclic voltammograms in the training set is large.

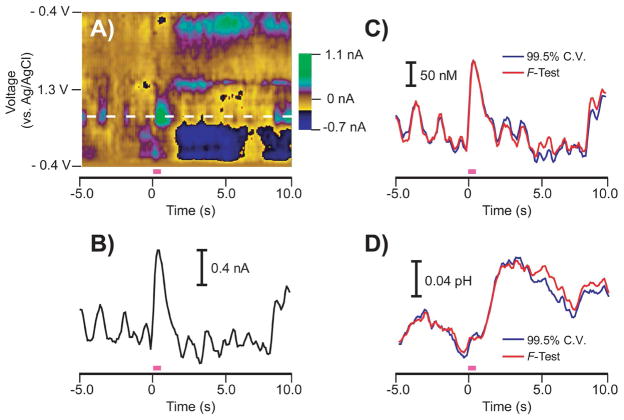
Figure 6 compares the 99.5% cumulative variance method and Malinowski’s F-test in the calculation of both dopamine concentration data and pH changes in vivo. Figure 6A shows a color plot[32] containing stimulated dopamine release, basic pH shifts, and naturally occurring dopamine transients in a freely-moving rat. The white dotted line represents the oxidation potential of dopamine. A current versus time trace at this potential is shown in Figure 6B. As previously reported, a current versus time trace is insufficient in measuring dopamine fluctuations because pH change information is also contained at this potential which convolutes the response.[14, 15] Figures 6C and 6D show dopamine concentration and pH change information, respectively, predicted using both the 99.5% cumulative variance method and Malinowski’s F-test. The 99.5% cumulative variance method retained six PCs while Malinowski’s F-test retained two PCs. Malinowski’s F-test was able to predict virtually identical changes in dopamine and pH levels as the 99.5% cumulative variance method, including dopamine transients at and below 50 nM. Since concentration data was unaffected, these results support the assertion made by Malinowski’s F-test that the extra four PCs retained by the 99.5% cumulative variance method span only noise.

Figure 6.

Comparison of stimulated release predicted by PCR using primary PCs determined with both methods of factor selection for a representative Case I training set. A) Color plot representation of in vivo cyclic voltammograms collected in a freely-moving rat. The pink bar indicates a stimulation given to the animal to evoke dopamine release and pH changes (60 Hz, 24 pulses, 125 μA). The white dashed line indicates the oxidation potential of dopamine. B) Current versus time trace at the oxidation potential of dopamine showing a convoluted response with pH changes. C) Dopamine concentration predicted by PCR using the primary PCs determined by the 99.5% cumulative variance method (blue) and Malinowski’s F-test (red). D) pH change predicted by PCR using the primary PCs determined by the 99.5% cumulative variance method (blue) and Malinowski’s F-test (red).

Figure 6 shows a representative stimulated release example, but more quantitative evidence from a larger data set was needed in the comparison of concentration values. First, changes in dopamine and pH levels were predicted using each method of factor selection using multiple stimulated release events. These stimulated release events were taken from multiple animals from Researcher 5 in Table 2. Accordingly, these multiple stimulated release events used multiple Case I training sets for concentration prediction. Next, coefficients of determination (R²) values were calculated comparing the results obtained with the 99.5% cumulative variance method to those predicted using Malinowski’s F-test from each stimulated release event for both dopamine and pH changes.

Average R² values were 0.963 ± 0.010 for dopamine and 0.992 ± 0.003 for pH change (N = 7 training sets predicting dopamine and pH changes in 18 stimulated release data files). One of two possibilities exists for the average R² value of approximately unity for the pH change data. First, the extra PCs retained by the 99.5% cumulative variance method could be inherently unimportant during concentration prediction. Second, since noise should not have large peaks that substantially deviate from baseline, the broad-shaped pH change information obtained from PCR could be less sensitive to added noise. This second possibility suggests that dopamine cyclic voltammograms, which do not deviate from the baseline for approximately 3/4 of the length of the voltammetric sweep, would be more sensitive to noise, especially if their signal-to-noise ratio is low.

Supporting this theory, five of the eighteen stimulated release files had R² values for dopamine concentrations below 0.95 while all R² values for pH change concentrations were above this value. In the five cases where R² values were below 0.95, the extra noise PCs retained with the 99.5% cumulative variance method led to different dopamine concentration information. One possibility is that noise PCs were retained by the 99.5% cumulative variance method and were included in the factor space during model generation, leading to the calculation of a different regression matrix. In addition, during concentration prediction of the unknown stimulated release data, cyclic voltammograms that contained noise could have had projections onto noise PCs and noise could have been interpreted by PCR as dopamine changes. Training sets with low signal-to-noise ratios would be the most susceptible.

Another possibility for the lower R² values for dopamine is that Malinowski’s F-test discarded significant information necessary for concentration prediction. Qualitative evaluations of the PCs discarded by Malinowski’s F-test (similar to Figure 4) showed no consistent or significant shape distinct from noise, suggesting that the inclusion of noise using the 99.5% cumulative variance method could significantly change concentration information in some instances. Taken together with the data in Figure 3, pH change cyclic voltammograms contained a larger amount of noise, but dopamine concentration data was more sensitive to noise for Case I training sets.

We define the LOD for a significant event as a concentration change larger than five times the standard deviation of the noise in the concentration versus time trace. To provide evidence for the fact that the noise contained in the training set does not impact our LOD, noise levels were estimated by taking the standard deviations of the pre-stimulation dopamine and pH change baselines predicted using both the 99.5% cumulative variance method and Malinowski’s F-test for the data used in the calculation of R² values (N = 7 training sets and 18 stimulated release data files). While Figure 3 showed that Malinowski’s F-test discarded significantly more noise from the training set cyclic voltammograms, the choice of factor selection did not significantly impact noise levels for either dopamine or pH changes in the concentration versus time dimension (data not shown).

We also wanted to provide evidence of how Malinowski’s F-test was able to predict dopamine concentration information during a behavioral experiment. Intracranial self-stimulation (ICSS) is a behavioral model that mimics reward-seeking behavior in animals and we have extensively studied this experimental paradigm previously.[34, 53] We have shown that extracellular dopamine increases following both the presentation of a cue associated with lever presentation and immediately after the stimulation is given.[34]

Figure 7 shows how the 99.5% cumulative variance method and Malinowski’s F-test predicted concentrations during an ICSS experiment where the time between trials was allowed to vary.[34] Each trace represents an average ± SEM of thirty-nine trials. Malinowski’s F-test and the 99.5% cumulative variance method estimated the rank to be two and four, respectively. The concentration values predicted by Malinowski’s F-test were identical within error to those predicted by the 99.5% cumulative variance method, including the approximately 30 nM cue-evoked release. Since the training set for this experiment was classified as a Case I training set and the results were identical for both methods, the extra PCs retained by the cumulative variance method were, in fact, noise.

Figure 7.

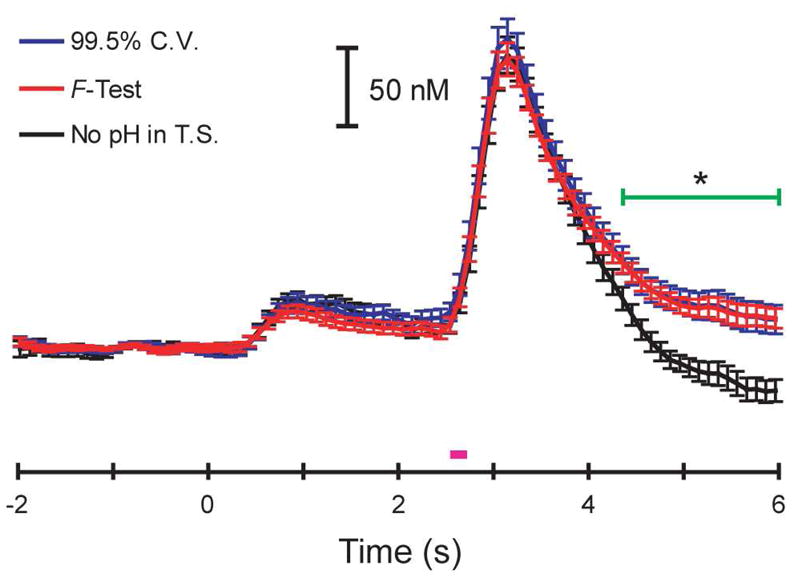
Dopamine release predicted by PCR during an ICSS experiment using primary PCs determined with both methods of factor selection for a Case I training set. Time 0 s represents cue presentation and the pink bar represents the stimulation. The blue and red traces are average (error bars representing SEM) dopamine concentrations predicted using the primary PCs from the 99.5% cumulative variance method (rank = 4) and Malinowski’s F-test (rank = 2), respectively. The black trace is an average dopamine concentration predicted using Malinowski’s F-test without pH in the training set. The green bar represents a significant difference in concentrations predicted when pH was excluded from the training set (one-way ANOVA, p < 0.05).

A calibration set must contain all expected components or the concentration values predicted with PCR may be significantly different.[35] The black trace in Figure 7 shows this effect when pH change was removed from the training set. There was no significant difference in dopamine concentrations during either the cue or stimulation. However, dopamine concentrations were significantly underestimated (p < 0.05, one-way ANOVA) after the stimulation, when basic pH changes occur because basic pH change cyclic voltammograms resemble “anti-dopamine” in a dopamine factor space.

Our residual analysis protocol should notify the user that a specified training set does not contain all significant sources of variation in the unknown data set, however it is not perfect. One limitation to residual analysis is that if a large amount of noise is present in the cyclic voltammograms of the training set, Q_α would be very large and may be unable to inform a user that a training set is invalid. This was the case for the black trace in Figure 7. All of the Q_t values fell below Q_α during concentration prediction indicating a proper model was constructed. During these instances seemingly insignificant sources of variance present in the unknown data set can cause an error in the prediction of concentration changes. Therefore all expected components, no matter how small in amplitude, should be included in the training set to eliminate this type of error from occurring during the validation step. Furthermore, visualizing a residual color plot should aid in determining if other analytes are present, even though residuals are not always directly interpretable.[14, 15]

CONCLUSIONS

Here we have shown that Malinowski’s F-test offered a more accurate, statistical-based approach for the removal of noise from an in vivo FSCV training set. The literature suggested it was possible that the dimensions of our training sets may limit the usage of Malinowski’s F-test[24], but this result was unsubstantiated in this work. Visualizing the discarded PCs in terms of the original data offers an easily interpretable alternative to looking at complicated loading plots or abstract vector transformations of PCs in conventional PCA.

Malinowski’s F-test improved the overall consistency in the shapes of the effective analyte cyclic voltammograms within a particular training set. Malinowski’s F-test was able to remove noise even though its underlying distribution was unknown and the data was already filtered and smoothed before rank estimation. The 99.5% cumulative variance method deteriorated the quality of training sets with large signal-to-noise ratios by discarding potentially important voltammetric information. Interestingly, pH change contributed the majority of error of training sets while dopamine concentrations were more sensitive to error present. Neuromodulator concentration values were not significantly affected for either stimulated release files or an ICCS experiment in most instances using Malinowski’s F-test for factor selection, except when the error PCs retained by the 99.5% cumulative variance method influenced the factor space such that noise from the unknown data set was interpreted as dopamine. Training sets with low signal-to-noise ratios were more susceptible to this type of error.

The specific value of rank for a particular training set was irrelevant because it varied with signal-to-noise ratio, no matter whether the 99.5% cumulative variance method or Malinowski’s F-test was used for factor selection. Even though the number of PCs retained varied depending on the Case, the distributions of the Q_α values calculated using Malinowski’s F-test from all three Cases were similar. The average Q_α value for Case II training sets was significantly lower than the other two Cases, but this could be due to a low number of training sets in the distribution.

The similar overall distributions of Q_α values give new insights into Malinowski’s F-test and the residual analysis validation protocol. Even though the signal-to-noise ratios of the training set cyclic voltammograms varied, on average Malinowski’s F-test was able to remove the similar amounts of noise from all training sets. The residual analysis validation protocol is an excellent measure of quality control and its usage can be improved with using Malinowski’s F-test as a method of rank estimation, even if training sets are heterogeneous. As long as signal-to-noise ratios of training set spectra are moderate (>10)[25] Malinowski’s F-test is robust enough to analyze in vivo data from multiple laboratories with varying signal-to-noise ratios and obtain a comparable standard for validation of multivariate calibration models.