Atlas-based Improved Prediction of Magnetic Field Inhomogeneity for Distortion Correction of EPI data

Abstract

We describe a method for atlas-based segmentation of structural MRI for calculation of magnetic fieldmaps. CT data sets are used to construct a probabilistic atlas of the head and corresponding MR is used to train a classifier that segments soft tissue, air, and bone. Subject-specific fieldmaps are computed from the segmentations using a perturbation field model. Previous work has shown that distortion in echo-planar images can be corrected using predicted fieldmaps. We obtain results that agree well with acquired fieldmaps: 90% of voxel shifts from predicted fieldmaps show subvoxel disagreement with those computed from acquired fieldmaps. In addition, our fieldmap predictions show statistically significant improvement following inclusion of the atlas.

1 Introduction

Echo-planar imaging (EPI) is the standard pulse sequence employed in functional magnetic resonance imaging (FMRI) and diffusion tensor imaging (DTI) studies due to its high temporal resolution. In order to extract meaningful information from EPI data, scientists and clinicians typically register low resolution EPI data to high resolution anatomical images. A major problem in achieving accurate registration is the inherent distortion of EPI data due to B₀ field inhomogeneity.

Field inhomogeneity results in distortion because the MR image reconstruction assumes a one to one relation between spatial location and the frequency produced by known linear gradient fields. In practice, hardware constraints result in inhomogenities in the main field as high as several hundred parts per million (ppm). This can be corrected to within several ppm using shims [1]. Intrinsic magnetic susceptibility of biological materials causes additional perturbations in the field. In neuroimaging studies, soft tissue and bone have similar susceptibilities of (χ_t ≈ −9.1 × 10⁻⁶) [2] and (χ_b ≈ −11.4 × 10⁻⁶) [3] respectively, but differ significantly from the susceptibility of air (χ_a ≈ 0.4 × 10⁻⁶) [2]. This results in large perturbations around the air-filled sinuses and subsequent distortion of EPI data in the frontal and temporal lobes of the brain.

To correct for this, MR systems contain a set of room-temperature shims that are wound to produce fields based on the first and second order spherical harmonics [1]. Imperfect shimming and higher-order perturbations, however, result in residual subject-specific inhomogeneity, and subsequent distortion of the acquired images. Several techniques have been developed to correct for geometric distortion, the majority of which rely on the acquisition of magnetic fieldmaps [4–6]. A fieldmap provides a direct measure of the B₀ inhomogeneity at each point in the image. In EPI, the geometric distortion is a voxel-wise translation restricted predominantly to the phase-encode direction, which can be computed directly from the fieldmap. Fieldmap techniques, however, have several limitations. First, they require additional scan time, which may be difficult to accomodate in clinical settings as well as in DTI studies where many directions need to be acquired in the same session. Second, fieldmaps suffer from low signal-to-noise ratios (SNR) at tissue/air boundaries, which can reduce their reliability in areas where the distortion is most severe. Acquisition of a single fieldmap may also be invalid for unwarping EPI data if there are significant effects due to motion or respiration in the timeseries. Finally, fieldmaps are not available in many retrospective studies.

Given these limitations, there have been several efforts to predict fieldmaps from tissue/air susceptibility distributions of the anatomy using magnetic field models [7, 8, 2]. Jenkinson et al. showed that the perturbing field can be predicted with high accuracy when CT data of the subject is used to obtain a tissue/air segmentation. Since whole-head CT is rarely available, Koch et al. proposed using registered CT from a reference subject to obtain the tissue/air susceptibility model. Both methods were limited by requiring CT to distinguish air from bone, which have similar intensities in structural MR but significant differences in magnetic susceptibility. Second, these models cannot account for the shim fields present in the scanner that partially compensate for B₀ inhomogeneity during EPI acquisition. Without this additional information, applying the fieldmaps for distortion correction is not possible. In [7] it was shown that tissue/air susceptibility models could be derived from structural MRI by using an intensity-based classifier trained with CT. It was also shown that registration of the EPI and structural MR could be used to search over the unknown shim parameters allowing distortion correction of the EPI that agrees well with results obtained using acquired fieldmaps.

Variability in structural MR acquisitions, however, may limit the efficacy of an intensity-based classifier in cases where the MR intensity properties differ significantly from those of the training data. In [7], CT data sets with MR acquired on the same scanner as the subjects of interest could be used to train the classifier, but this may not be possible in many cases. Limited anatomical information below the brain may also prevent accurate estimation of the perturbing field. Therefore, obtaining more reliable susceptibility models from structural MR is critical for retrospective unwarping of EPI data sets that lack acquired fieldmaps. While previous results predicting fieldmaps from structural MR have shown good agreement with acquired fieldmaps, we hypothesized that improved segmentation methods would result in even greater accuracy.

In this paper we describe a method for using anatomical information from a set of 22 whole-head CT data sets to achieve improved, subject-specific segmentation of structural MR. In this approach a tissue/air atlas is constructed from the CT data to obtain priors on the probability of tissue or air at each location in the anatomy. The corresponding structural MR is used to train a classifier that segments the MR of the subject of interest and this is used as input to a first order perturbation field model to compute a subject-specific fieldmap. The method is evaluated by comparison of predicted fieldmaps and acquired fieldmaps. In addition, the MR classifier can be used to obtain probabilistic bone segmentations from structural MR that show promising agreement with segmented CT.

2 Methods

2.1 Atlas Construction

Automatic segmentation of neuroanatomical structures often relies on the use of probabilistic atlases [9–13]. These atlases are usually constructed by co-registering collections of manual segmentations or other training data. The atlas functions as a spatial prior to represent anatomical variability within a population and compensate for missing information in structural MR images [13]. Although atlas-based methods have typically been applied to the segmentation of brain structures, in this work, we construct a probabilistic tissue/air atlas from 22 CT data sets. By incorporating spatial information into the MR segmentation, we expect improved tissue/air classification in regions where bone is often mislabeled as air.

We obtained 22 datasets consisting of CT and MRI from 3 sources: the publicly available Retrospective Image Registration Evaluation (RIRE) database (17 neurosurgery patients), the Radiology department at Brigham and Women's Hospital (BWH) (4 neurosurgery patients) and the Zubal head phantom (1 subject) [14]. In the RIRE data, each CT image has 27 to 34 slices, 4 mm thick, matrix=512×512, voxel size=0.65×0.65mm. The T1-weighted MRI was acquired on a Siemens SP 1.5 Tesla scanner. MRI for 8 of the 17 subjects has 20 to 26 axial slices, 4 mm thick, no gap, matrix=256×256, voxel size= 1.25×1.25mm, TE/TR=15/650ms. T1-weighted MP-RAGE for the other 9 subjects had TE/TR=4/10ms, matrix=128×256×256 and FOV=160×250×250mm. In the BWH dataset, the CT spanned 36 slices with 512×512 in-plane voxels of size 0.46×0.46×4.8mm. 3D-SPGR MRI of these patients was obtained: slice thickness=1mm, TE/TR=3/8ms, matrix=512×512, voxel size=0.5×0.5×1mm. The Zubal data consists of CT of the head and neck: 1.2mm isotropic voxels spanning 230 slices with 256×256 in-plane voxels, and T1-weighted MRI with 90 slices of thickness 0.2cm, matrix=256×256, and 25.6×25.6cm in-plane resolution.

For each subject, the CT data was registered to its corresponding MR using 6 degrees of freedom (DOF) and mutual information as the cost function. The MR was registered to standard space using the MNI152T1 atlas as the reference, 12 DOF and normalized correlation ratio. These transformations were then applied to the co-registered CT. All registrations were carried out using FLIRT [15, 16]. Tissue/air labels were obtained by thresholding the CT data in standard space.

The wide variation in the field of view of the CT data results in highly varying amounts of data at each voxel; in particular only the zubal phantom includes observations in the neck. Probabilistic atlases are frequently constructed by counting the number of occurrences of each tissue class at each voxel and normalizing the result to obtain a probability distribution. In the two class situation, this corresponds to ML estimation of the parameter of a binomial distribution, i.e., if k ∼ Binomial(n, p), then, the ML estimate of p given observed k is p̂ = k/n.

In the case of only one trial (n = 1), or one observation at a given voxel, this will lead to estimates of p that are zero or one, which may be unreasonably certain (i.e. when used as prior probability on tissue class in segmentation, these values would dominate any amount of data in these voxels). One way to avoid this effect, is to put a prior on p; a natural choice is the beta distribution, which is conjugate to the binomial: p ∼ Beta(α, β). (The special case of α = β = 1 corresponds to a flat prior and Laplace's rule of succession). We have chosen to use α = β = ε = 0.05, and in this case, the posterior expected value of the parameter is $\overline{p}=\frac{k+\epsilon }{n+2\epsilon }$, which avoids, by ε, the probability zero and one cases mentioned above. In addition to the tissue/air atlas, a probabilistic atlas of bone was obtained by segmenting bone from CT data and applying the same binomial model and conjugate prior. This was applied to segment bone from MR, which may be useful in other applications such as calculation of attenuation maps for absorption correction in PET or dose calculation in radiotherapy planning.

2.2 Atlas-based Segmentation

Structural MR was segmented using an MR classifier that incorporates spatially dependent prior information from the probabilistic atlas and MR intensity information (from the subject of interest) to obtain a subject-specific susceptibility model. The classifier was trained using the CT/MR training data described in section 2.1, but applied to segment MR data acquired at a separate site. The accuracy of the segmentations was evaluated by comparing fieldmaps predicted from the atlas-based segmenter to acquired fieldmaps. The fieldmaps were also compared to those predicted using intensity information alone (ie. a spatially constant prior).

We obtained T1-weighted MRI and fieldmaps of 5 subjects previously acquired at Massachusetts General Hospital on a 3T Siemens TimTrio scanner as part of the FBIRN multi-center FMRI study. The MP-RAGE spanned 160 slices, with thickness=1.2mm, matrix=256×256, voxel size=0.86×0.86mm, and TE/TR=2.94/2300ms. The gradient echo fieldmaps had 30 slices, thickness=5mm, matrix=64×64, voxel size=3.44×3.44mm, TE1/TE2/TR=3.03/5.49/500ms.

Rigid (6 DOF) registration of the T1 data to the fieldmap magnitude image was carried out using FLIRT [15] so the predicted fieldmaps would be in the same space as the acquired fieldmaps for validation. The MNI152T1 reference image was registered to the fieldmap magnitude image using 12 DOF and the resulting transformation was applied to the atlas-based probability maps.

The prior probabilities of tissue, P(T∣X_n), and air, P(T^C∣X_n), at each voxel were obtained from the co-registered atlas. For each of the 22 T1 images in the training data, the MR was scaled according to the parameter that minimized the Kullback-Leibler Distance to the MR of the subject of interest. The data that showed the minimal distance to the subject of interest was used to compute the likelihood terms, P(I_i∣T) and P(I_i∣T^C), using tissue/air labels from the corresponding CT. The posterior probability of tissue was computed and applied to segment the MR of the subject of interest. Intensity-based segmentation using spatially stationary priors computed from normalized intensity histograms of the training data was also carried out for comparison to the atlas-based approach.

Bone segmentations were obtained in similar fashion and evaluated using a ‘leave-one-out’ framework in which one CT was withheld as ground truth and the remaining CT data sets were used to construct the probabilistic bone atlas. A non-linear direct search was performed to solve for the thresholds that maximized the similarity of the estimated bone segmentations to the ground truth segmentation. The similarity was quantified using the dice score, where a value of 0 indicates the volumes have no overlapping voxels and a value of 1 indicates they are exactly the same.

2.3 Fieldmap Estimation

Fieldmaps are predicted from the atlas and intensity-based segmentations using the perturbation field model described in [2]. In this model, a first order perturbation solution of Maxwell's equations is calculated from a tissue/air susceptibility model, where each pixel takes continuous values between 0 (air) and 1 (tissue). For a single voxel, with the B₀ field along z, the predicted field is given by: $F(\mathbf{\text{x}})=\left(\frac{{\partial }^{2}G}{\partial z^2}\right)\ast \left({\chi }_1{B}_z^{(0)}\right)$, where G(x) = (4πr)⁻¹, $r=\Vert \mathbf{\text{ x }}\Vert =\sqrt{x^2+y^2+z^2}$, $B_z^{(0)}$ is the field strength, and χ₁ = 1 is the susceptibility value of the voxel. Due to the linearity of the perturbing field solution, the total field is given by: $B_z^{(1)}\left(\mathbf{\text{x}}\right)={\sum }_{x\prime }{\chi }_1(\mathbf{\text{x}}\prime )F(\mathbf{\text{x}}-\mathbf{\text{x}}\prime )$ where x′ are the source points (locations of the voxel centers) and x is the field point where the field is evaluated.

Current field modeling techniques, including the one described in [2], do not account for the shim fields that reduce the B₀ inhomogeneity prior to fieldmap acquisition. Therefore, in order to compare an estimated fieldmap to an acquired one, the shim fields must added to the predicted fieldmaps. This is done by modeling the shim fields using the set of first and second order spherical harmonic basis functions. In addition, a global scaling of the predicted fieldmap must be estimated since the model assumes the magnetic susceptibility throughout the brain, (χ_t ≈ −9.1 × 10⁻⁶) [2], is constant, but this may not be accurate near bone interfaces where both partial volume effects and mis-estimation of segmentation values are most likely to occur. Furthermore, the perturbing fieldmaps are calculated assuming a perfectly homogeneous B₀ field, which cannot be achieved in practice due to constraints on the hardware. The fieldmap scaling and shim parameters, θ, can be obtained by least squares fitting to the acquired fieldmap: $\widehat{\theta }=\underset{\theta }{\text{arg min}}{[\mathbf{\text{B}}-\mathbf{\text{A}}\theta ]}^2$ where A = [B̂, S₁, S₂, …, S₈]. The column vectors B, B̂, and S_i, represent the acquired fieldmap, predicted fieldmap, and shim basis functions, respectively. Once these coefficients are known, the predicted fieldmap with shim, B̂_s = Aθ̂, can be compared to the acquired fieldmap.

3 Experimental Results

Results of atlas-based segmentation of structural MR is shown in Fig. 1. Fig. 1a shows T1 of the sinus region. Fig. 1b shows the limitations of using the intensity classifier to segment the MR. While it produces reasonable results for many of the voxels in the sinuses, voxels outside this region which are clearly soft tissue or bone are mislabeled with values close to zero. In contrast, using the atlas-based segmenter (as shown in Fig. 1c) achieves similar results for the highly variable subject-specific anatomy within the sinus region, while producing fewer errors in the surrounding area. The intensity and atlas-based segmentations were used as input to the perturbation field model to obtain predicted fieldmaps. The scaling and shim parameters were fit from the acquired fieldmaps as described in section 2.3. The shim fields could then be added to the predicted fieldmaps for comparison to the acquired fieldmaps as shown in Fig. 2. The first column of Fig. 2 shows fieldmaps computed from the intensity-based segmentations, which show significant differences relative to the acquired fieldmaps shown for each subject in column 3. These are especially noticable in areas that have lower signal in MR, such as in the ventricles and major sulci. Fieldmap results from the atlas-based segmentations are shown in the second column of Fig. 2 and show improved agreement with acquired fieldmaps. Quantitative analysis of the absolute error in the B₀ field between these images is given in the table in Fig. 2. Since the bandwidth/pixel for the EPI data acquired in this study is 22.3 Hz, 90% of the voxels in the atlas-based fieldmaps show subvoxel error. The mean of these statistics across all five subjects is also shown for both the intensity and atlas-based classifiers. The intensity classifier shows a slight improvement over the results reported by Koch et al [8] for a single subject. The atlas-based classifier out performs both the intensity and Koch methods. Paired t-tests comparing the means of the intensity and atlas-based results shows this improvement is statistically significant (all p-values < 0.05). Results of the segmentation of bone from structural MR for a representative subject is shown in Fig. 3. The CT shown in Fig. 3a can be easily thresholded to segment bone from air and soft tissue. Fig. 3b and Fig. 3c show the results of using the intensity and atlas-based classifiers, respectively. While the intensity classifier has some success in segmenting MR into tissue/air classes, it is much less effective in segmenting bone (Fig. 3b). Inspection of the the atlas-based segmentation (Fig. 3c), however, shows good general agreement with the CT, with a dice score of 0.780 for this subject.

Fig. 1.

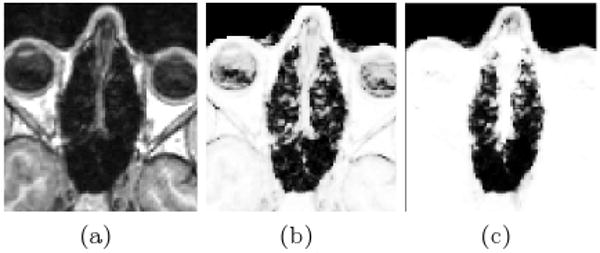
Results of the Segmentation. The T1 MR for a representative subject is shown in (a). The tissue probability map computed using the intensity classifier (b) shows mis-classification of voxels outside the sinus region where intensities are low in MR. Using the atlas-based classifier significantly reduces these errors while adequately resolving much of the subject-specific sinus anatomy (c)

Fig. 2.

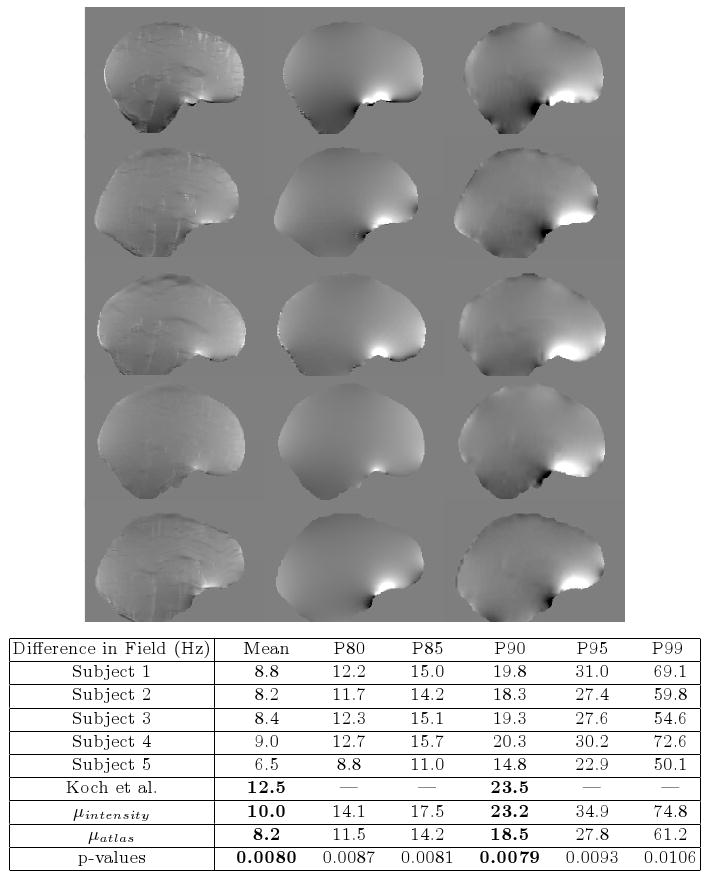
Results of the Fieldmap Estimation. Predicted and acquired fieldmaps for subjects 1-5 are shown in rows 1-5 respectively. Fieldmaps predicted using the intensity classifier (column 1) show significant differences relative to the acquired fieldmaps (column 3), while those computed from the atlas-based segmentation show improved agreement (column 2). The absolute difference between the acquired fieldmaps and the atlas-based fieldmaps are given for each subject in the table above. 90% of voxels show differences that are less than 22.3 Hz, the bandwidth/pixel for the FBIRN EPI data. Results reported by Koch et al. [8] for a single subject are shown, as well as mean statistics across all five subjects for both the intensity classifier and atlas-based classifier. The atlas-based classifier performs better than the Koch and intensity-based methods and the improvement over the intensity method is statistically significant (all p-values < 0.05 for left-sided paired t-test). The scale of the fieldmaps is ±100 Hz.

Fig. 3.

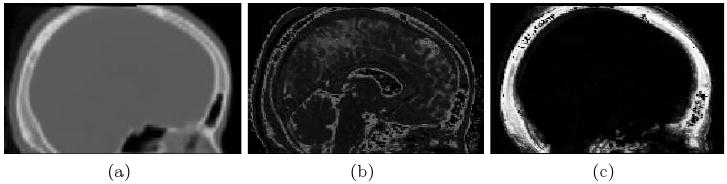
Results of the Bone Segmentation. Segmentation of bone using the intensity classifier (b) results in significant errors when compared with CT (a), while the atlas-based classifier (c) shows good overall agreement