States versus Rewards: Dissociable neural prediction error signals underlying model-based and model-free reinforcement learning

Abstract

Reinforcement learning (RL) uses sequential experience with situations (“states”) and outcomes to assess actions. Whereas model-free RL uses this experience directly, in the form of a reward prediction error (RPE), model-based RL uses it indirectly, building a model of the state transition and outcome structure of the environment, and evaluating actions by searching this model. A state prediction error (SPE) plays a central role, reporting discrepancies between the current model and the observed state transitions. Using functional magnetic resonance imaging in humans solving a probabilistic Markov decision task we found the neural signature of an SPE in the intraparietal sulcus and lateral prefrontal cortex, in addition to the previously well-characterized RPE in the ventral striatum. This finding supports the existence of two unique forms of learning signal in humans, which may form the basis of distinct computational strategies for guiding behavior.

One of the most critical divisions in early-20^th century animal learning psychology was that between behaviorist notions such as Thorndike’s (Thorndike, 1933), that responses are triggered by stimuli through associations strengthened by reinforcement, and Tolman’s proposal (Tolman, 1948) that they are instead planned using an internal representation of environmental contingencies in the form of a “cognitive map”. Although the original debate has relaxed into a compromise position, with evidence at least in rats that both mechanisms exist and adapt simultaneously (Dickinson and Balleine, 2002), a full characterization of their different learning properties and the way that their outputs are integrated to achieve better control is as yet missing. Here, we adopt specific computational definitions that have been proposed to capture the two different structures of learning. We use them to seek evidence of the two strategies in signals measured by functional magnetic resonance imaging (fMRI) in humans learning to solve a probabilistic Markov decision task.

Theoretical work has considered the two strategies to be model-free and model-based, and has suggested how their outputs might be combined depending on their respective certainties (Daw et al., 2005; Doya et al., 2002). In a model-based system, a cognitive map or model of the environment is acquired, which describes how different “states” (or situations) of the world are connected to each other. Action values for different paths through this environment can then be computed by a sort of mental simulation analogous to planning chess moves: searching forwards along future states to evaluate the rewards available there. This is termed a “forward” or “tree-search” strategy. In contrast, a model-free learning system learns action values directly, by trial and error, without building an explicit model of the environment, and thus retains no explicit estimate of the probabilities that govern state transitions (Daw et al., 2005). Because these approaches evaluate actions using different underlying representations, they produce different behaviors in experiments aimed at investigating their psychological counterparts. Most such experiments (Dickinson and Balleine, 2002) study whether animals adapt immediately to changes in the environment. For instance, in classic “latent learning” studies (Tolman and Honzik, 1930), animals are pre-trained on a maze, then rewards are introduced at a particular location to probe whether subjects can plan new routes there taking into account previously learned knowledge of the maze layout. The experiment discussed here, though non-spatial, follows this scheme.

Learning in both model-based and model-free strategies is typically driven by prediction errors, albeit with different meaning and properties in each case. A prediction error is a difference between an actual and an expected outcome and this signal is commonly thought of as the engine of learning, as it is used to update expectations in order to make predictions more accurate.

In the case of model-free learning, this error signal (called the reward prediction error, RPE) amounts to the difference between the actual and expected reward at a particular state. In the context of reinforcement learning (RL), this error signal is used to learn values for action choices that maximize expected future reward (Sutton and Barto, 1998). An abundance of evidence from both single unit recordings in monkeys (Bayer and Glimcher, 2005; Schultz, 1998; Schultz et al., 1997) and human fMRI (D’Ardenne et al., 2008) suggests that dopaminergic neurons in the ventral tegmental area and substantia nigra pars compacta exhibit a response pattern consistent with a model-free appetitive RPE. Furthermore, BOLD signals in the ventral striatum, show response properties consistent with dopaminergic input (Delgado et al., 2008; Delgado et al., 2000; Knutson et al., 2001; Knutson et al., 2005), most notably correlating with RPEs (Haruno and Kawato, 2006; McClure et al., 2003; O’Doherty et al., 2003).

Model-based action valuation requires predicting which state is currently expected, given previous states and/or choices. These expectations can be learned using a different prediction error, called the state prediction error (SPE), which measures the surprise in the new state given the current estimate of the state-action-state transition probabilities. The central questions for the current study are whether the human brain computes the SPE as well as the RPE, and, if so, what the different neural signatures are of these two signals. One indication that the brain may compute SPEs is that neural signals marking gross violations of expectations have long been reported, particularly using both EEG (Courchesne et al., 1975; Fabiani and Friedman, 1995) or in combination with fMRI (Opitz et al., 1999; Strobel et al., 2008). Unlike the prediction error signals associated with dopamine activity, which are largely reward-focused and associated with model-free RL (Holroyd and Coles, 2002), these respond to incorrect prediction of affectively neutral stimuli. Here, we study quantitatively how state predictions are learned, and seek trial-by-trial neural signals that reflect the dynamics of this learning.

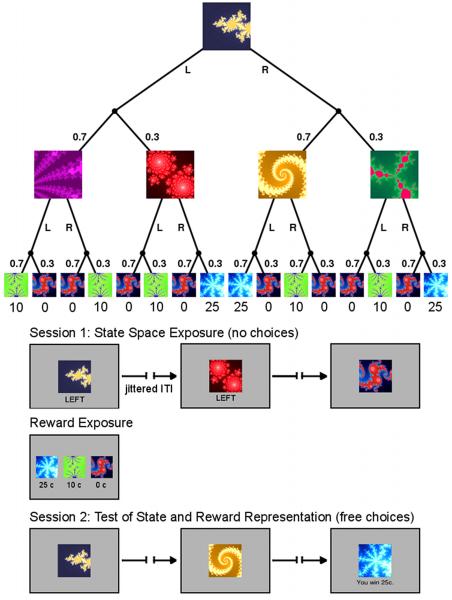
We designed a probabilistic sequential Markov decision task involving choices in two successive internal states, followed by a rewarded outcome state (see Experimental Procedures). The task has the structure of a decision tree, in which each abstract decision state is represented by a fractal image (Figure 1a). In each trial, the participants begin at the same starting state and choose between a left or right button press. Probabilistically, they reach one of two subsequent states, each of which presents another choice between a left or right action. Finally, they reach one of three probabilistic outcome states providing a reward of 0c, 10c or 25c.

Figure 1.

Task Design and Experimental Procedure. (A) The experimental task was a sequential two-choice Markov decision task in which all decision states are represented by fractal images. The task design follows that of a binary decision tree. Each trial begins in the same state. Subject can choose between a left (L) or right (R) button press. With a certain probability (0.7/0.3) they reach one of two subsequent states in which they can choose again between a left or right action. Finally, they reach one of three outcome states associated with different monetary rewards (0c, 10c, and 25c). (B) The experiment proceeded in 2 fMRI scanning sessions of 80 trials each. In the first session, subject choices were fixed and presented to them below the fractal image. However, subjects could still learn the transition probabilities. Between scanning sessions subjects were presented with the reward schedule that maps the outcome states to the monetary pay-offs. This mapping was rehearsed in a short choice task. Finally, in the second scanning session subjects were free to choose left or right actions in each state. In addition, they also received the pay-offs in the outcome states.

In order to dissociate SPEs and RPEs, volunteers were first exposed to just the state space in the absence of any rewards, much as in a latent learning design. This provides a pure assessment of an SPE. Further, to ensure adequate and equivalent experience, all choices in the first scanning session were instructed; subjects only had to register them with the respective button press (Figure 1b). The instructed choices in session 1 were created so as to reflect the underlying transition probabilities of the decision tree exactly, albeit in a randomized order. Next, during a break, the subjects were told the reward contingencies and rehearsed the reward mapping with a simple choice task (see Supplemental Experimental Procedures). Finally, in the second scanning session, they were able to make choices on their own to gain rewards at the outcome states (Figure 1b).

We hypothesized that participants would acquire knowledge about the transition probabilities during session 1, despite of the absence of any rewarding outcomes. This state knowledge can therefore be only acquired through model-based learning, potentially being updated via an SPE. Behaviorally, such knowledge is “latent” during the first session and its presence or absence can only be revealed subsequently when employed to guide choices toward reward. However, we sought neural evidence of state expectation formation during initial training. Specifically, we expected to see correlates of SPEs, perhaps in the lateral prefrontal cortex (latPFC), an area which has previously been suggested to be involved in model-based RL (Samejima and Doya, 2007). We hypothesized that such signals would be distinct from neural RPEs, which are often reported in the ventral striatum (Haruno and Kawato, 2006; McClure et al., 2003; O’Doherty et al., 2003; Seymour et al., 2004).

RESULTS

Behavioral assessment of state-based learning

We first assessed the participants’ performance at the beginning of the free-choice session, as a simple test of whether they were able to make optimal choices by combining the knowledge they acquired about state transitions and reward contingencies. In terms of the two learning approaches described above, this would be possible only with model-based, but not model-free learning, because the latter focuses exclusively on predicting rewards without building a model of the environment and therefore learns nothing during session 1. If, like the model-based theory, the subjects were able to combine their knowledge of the state space with the reward information presented prior to session 2, their first choice in session 2 would be better than chance. Indeed, of all 18 subjects, 13 chose R (the optimal choice) and 5 chose L in state 1 in the very first trial of session 2 (p < 0.05, sign-test, one-tailed), indicating that their choice behavior cannot be completely explained by traditional model-free reward learning theory.

Computational models of model-free and model-based learning

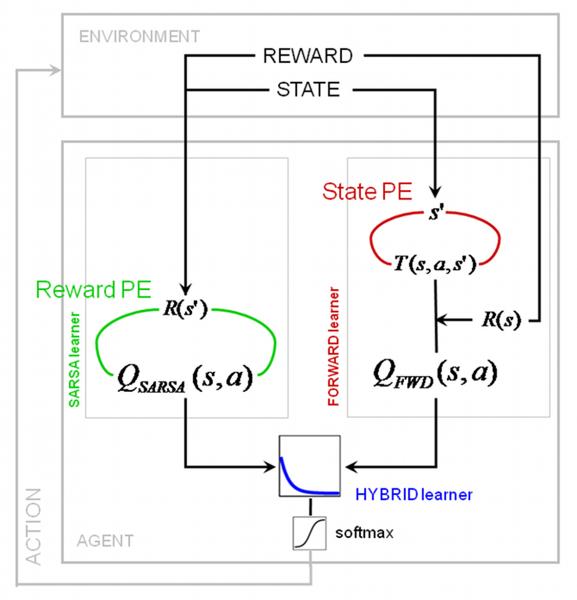
In order to assess the behavioral and neural manifestations of state and reward learning more precisely, we formalized the computational approaches described above as trial-by-trial mathematical models. Based on recent empirical support (Morris et al., 2006), we used a variant of model-free RL, the so-called SARSA learner (state-action-reward-state-action) for implementing value learning via an RPE. By contrast, our model-based FORWARD learner learned a state transition model via an SPE (see Figure 2 and Experimental Procedures), and used this to evaluate actions. In the second session, the mean correlation of these prediction error signals from both models was −0.37 (±0.09 s.d.) across all subjects. (In the first session, the RPE is zero throughout, due to the lack of rewards, and only the SPE is nonzero.) Finally, since previous theoretical proposals suggest that the brain implements both approaches (Daw et al., 2005; Doya, 1999; Doya et al., 2002), we implemented a HYBRID learner that chooses actions by forming a weighted average of the action valuations from the SARSA and FORWARD learners. The relative weighting is expected to change over time; indeed, given suitable prior expectations, there are normative proposals for determining how (Daw et al., 2005) (see also Behrens et al. (2007)). Given the singularity of the transition from non-rewarded to rewared trials, we built three simple models for the change in weighting over time, finding that an exponential decay from FORWARD to SARSA (Camerer and Ho, 1998) (Figure 2) fitted best (see Table S1).

Figure 2.

Theoretical model for data analysis. We used both a model-free SARSA learner and a model-based FORWARD learner to fit the behavioral data. SARSA computes a reward prediction error using cached values from the previous trials to update state-action values. The FORWARD learner on the other hand learns a model of the state space T(s,a,s’) by means of a state prediction error, which is then used to update the state transition matrix. Action values are derived by maximizing over the expected value at each state. In session 2, a HYBRID learner computes a combined action value as an exponentially weighted sum of the action values for the SARSA and FORWARD learner. The combined action value is then submitted to softmax action selection (see Experimental Procedures for details).

Evaluating behavioral model fit

These models not only make different predictions about the first free-choice trial, as examined thus far, but also about how subjects adjust their choice preferences, trial-by-trial, in response to feedback thereafter. In order to test whether either model, or their combination, best accounted for these adjustments, we fitted the free parameters for each model across subjects by minimizing the negative log-likelihood of the obtained choice data over the entire free-choice session. The fit parameters, the resulting model likelihoods and Akaike’s information criteria (AIC) are outlined in Table 1 (actual experiment). Thus fit, the HYBRID learner provided a significantly more accurate explanation of behavior than did SARSA or the FORWARD learner alone even after accounting for the different numbers of free parameters (likelihood ratio tests, HYBRID vs. SARSA: χ²(2) = 21.32, p = 2.35×10⁻⁵; HYBRID vs. FORWARD: χ²(2) = 224.94, p = 0). The expected values and estimated state transition probabilities from all models are visualized in Figure S2 for the optimal choice trajectory. Finally, we also computed the probability of correctly predicted choices by our HYBRID model and a pseudo-R² measure for each participant (Daw et al., 2006) that indicating how much better our HYBRID learner performs compared to a null model of random choices for each subject (Table S2).

Table 1.

Model parameters, negative model likelihoods (Lik), and Akaike’s Information Criterion (AIC), for the actual experiment and for the permutation analysis with random trial sequences. The latter lists the median parameter value from 1000 permutation samples and the interquartile range (25^th – 75^th percentile).

Parameter	actual experiment		random trial sequence
SARSA learning rate	0.20		0.37 (0.19-0.65)
FORWARD learning rate	0.21		0.29 (0.21-0.44)
Offset for exp. decay	0.63		0.40 (0.20-0.64)
Slope of exp. decay	0.09		0.53 (0.20-0.93)
Inverse softmax temperature	4.91		3.75 (2.22-4.82)
	Lik	AIC	Lik	AIC
SARSA	1217.94	2439.88
FORWARD	1319.75	2643.49
HYBRID	1202.28	2414.56	1256.56	2523.12

Further behavioral evidence for model-based learning

We conducted an additional analysis to demonstrate in greate detail how behavioral choices are affected by model-based learning. Although the entirety of all pre-determined trials in session 1 reflected the true transition probabilities exactly, the specific random sequence of these trials in each participant would create different learning trajectories. If participants’ beliefs about the transition probabilities were updated by error-driven model-based learning (with a fixed learning rate, as assumed in FORWARD), this may have left a bias towards the most recently experienced transitions, resulting in particular beliefs at the end of the session. These particular beliefs could in turn lead to subject-specific choice trajectories as session 2 progressed, which would be reflected in the fit of the model to those choices. Conversely, if the subjects did not learn anything about the transition probabilities from their particular transitions using an SPE (with a fixed learning rate), then we would not expect any influence of their particular sequence of trials in session 1 on their choices in session 2. Thus, in the case of no model-based learning in session 1, any sequence of trials (including the actually experienced sequence) should lead to the same quality of model fit to the choices, whereas in the case of state learning with the FORWARD model, we would expect a better model fit under the actual trial sequence compared to any other random sequence.

We tested this by refitting the model 1000 times using randomly permuted session 1 trial sequences and randomly permuted intermediate states (See Supplemental Experimental Procedure for details), and compared the model fit for the session 2 choices against the fit based on the actual trial sequence. The results of this additional analysis are presented in Table 1 (random trial sequence) and confirm that our participants had indeed acquired knowledge about the particular sequence of state transitions during the first session: 99.6 % of permutation samples provided a poorer explanation of choices than the original (p = 0.004).

In conclusion, the behavioral results indicate (a) that the participants successfully acquired knowledge about the state transition probabilities in session 1 through a model-based FORWARD learner and (b) that the participants’ behavior reflects both model-based and model-free learning processes. This invites a search for their neural manifestations in terms of SPEs and RPEs.

Neural signatures of RPE and SPE

We sought neural correlates of the prediction errors from both models. For this, we derived an RPE from the SARSA learner for session 2 and an SPE from the FORWARD learner for both sessions and included them as parametric modulators at the second decision state and the final outcome state in the single subject analyses (see Experimental Procedures). The voxel-wise parameter estimate (beta) for these regressors indicates how strongly a particular brain area covaries with these model-derived prediction errors. These beta images were included in a repeated measures ANOVA at the second level testing for the effect of each error signal across the group (see Experimental Procedures).

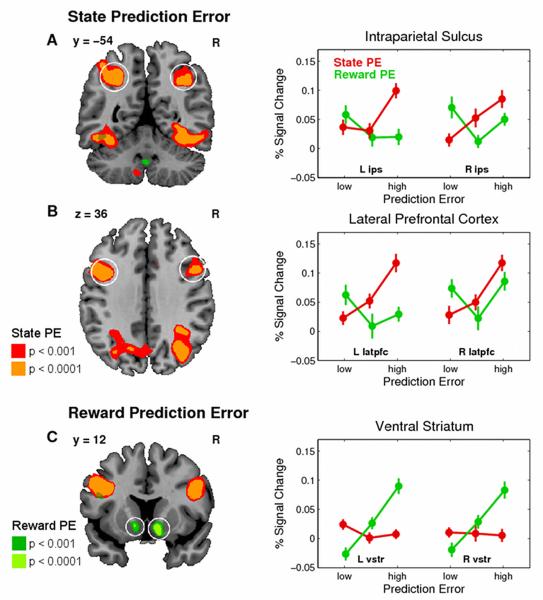
In order to determine those brain areas that covaried with the SPE, we pooled across both sessions and found significant effects bilaterally in the posterior intraparietal sulcus (pIPS) reaching on the left side into the superior parietal lobule and on the right side into the angular gyrus, and in the lateral prefrontal cortex (latPFC) (dorsal bank of the posterior inferior frontal gyrus (pIFG), see circled areas in Figure 3a and 3b and Table 2). Other effects visible in Figure 3a (e.g. inferior temporal gyrus) did not meet our statistical threshold for whole-brain correction and are not further discussed. The graphs show the average percent signal change (PSC) in BOLD activation across subjects for both prediction error signals on trials in which that error signal was either low, medium or high (bins defined at 33^rd, 66^th, and 100^th percentile, see Experimental Procedures for details). This reveals a linear increase in BOLD activation across trials with increasing SPEs, except for the left IPS, in which the increase in BOLD activation occurs only for trials with the highest SPE. In contrast, there is no such systematic relationship between BOLD activation and the RPE.

Figure 3.

Neural representations of state (SPE) and reward prediction errors (RPE). The SPE is pooled across both scanning sessions, whereas the RPE is only available in the rewarded session 2. BOLD activation plots on the right are the average percent signal change (across subjects, error bars: s.e.m.) for those trials in which the prediction error (PE) is low, medium, or high (33^rd, 66^th, and 100^th percentile PE range). Data are extracted using a cross-validation procedure (leave-one-out) from the nearest local maximum from the coordinates listed in the Table 2 (circled areas, see Experimental Procedures for details). red = SPE, green = RPE. (A) and (B) Significant effect for SPE bilaterally in the intraparietal sulcus (ips) and lateral pre-frontal cortex (lpfc). (C) Significant effects for RPE in the ventral striatum (vstr). Color codes in the SPMs correspond to p< 0.001 and p< 0.0001 uncorrected.

Table 2.

Statistical results. All peaks are corrected for the entire brain volume at p < 0.05 unless stated otherwise.

Contrast  Region	Hemi	BA	x	y	z	Z	p
Average SPE in both Sessions
Post IPS/SPL	L	7	−27	−54	45	5.29	0.004
Post IPS/Angular gyrus	R	40	39	−54	39	5.12	0.009
Lat PFC (dorsal pIFG)	L	44	−45	9	33	5.62	< 0.001
Lat PFC (dorsal pIFG)	R	44	45	12	30	4.73	0.049
Reward Prediction Error in Session 2
Ventral striatum	L	25	−12	6	−9	5.18	0.006
SPE signals in session 1 (within sphere (10 mm radius) based on SPE signals in session 2)
Post IPS	L	7					n.s.
Post IPS/Angular Gyrus	R	40	36	−66	39	3.68	0.01*
Lat PFC (dorsal pIFG)	L	44	−39	9	33	4.49	0.001*
Lat PFC (dorsal pIFG)	R	44	48	9	36	3.20	0.039*
		48	45	15	30	3.12	0.049*
Conjunction between SPE signals from both sessions
Lat PFC (dorsal pIFG)	L	44	−39	9	33	4.49	< 0.001 **
Lat PFC (dorsal pIFG)	R	44	48	9	36	3.20	0.001 **
Post IPS/Angular gyrus	R	40	33	−66	39	3.75	< 0.001 **
Post IPS/Angular gyrus	R	40	39	−54	39	3.31	< 0.001 **
SPE in both Session > unsigned Reward Prediction Error (abs(RPE))
Post IPS/Angular gyrus	R	40	36	−66	39	5.49	< 0.001

^*corrected for 10 mm spherical search volume centered on the peak of the SPE contrast in session 2.

^**uncorrected threshold of p < 0.001. IPS intraparietal sulcus, SPL superior parietal lobule, lat PFC lateral prefrontal cortex, pIFG, posterior inferior frontal gyrus, BA Brodmann Area.

Conversely, when we tested for a correlation between BOLD activation and the RPE we found a significant effect in the ventral striatum (vStr) (Figure 3c), consistent with previous accounts (McClure et al., 2003; O’Doherty et al., 2003), but no effects for an SPE even at p < 0.001 uncorrected. The graph of the average PSC across subjects in this region shows the opposite pattern from that in the pIPS and latPFC: a linear increase in BOLD activity across trials with increasing RPE, but no such increase for the SPE.

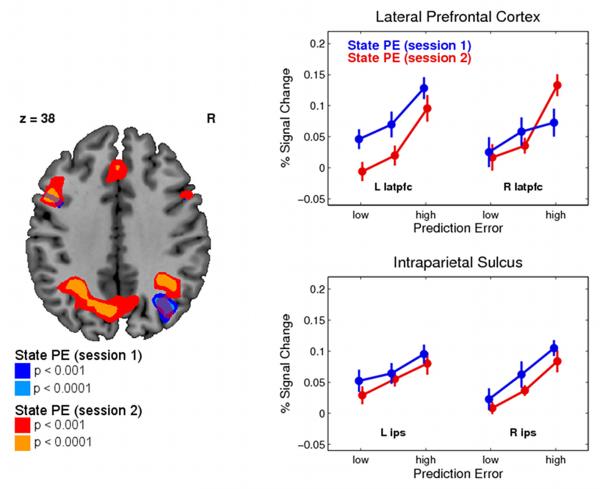
In a follow-up analysis, to investigate the consistency of SPE results between the sessions, we identified the peak voxels for the SPE signal in session 2 only, and then tested for a significant SPE representation in session 1 in a reduced spherical search volume (radius: 10mm, p < 0.05, family-wise error correction for search volume). This procedure ensures that the centers for the search volumes are selected in a way that is independent of the data in session 1. We found significant effects of SPE in session 1 bilaterally in latPFC and in the right pIPS/angular gyrus (Figure 4) confirming that these areas correlate with an SPE even in the absence of any reward information (see Table 2). To test for overlapping voxels with SPE representations in both sessions we employed a conjunction analysis (Nichols et al., 2005) and found evidence that voxels in these regions were activated in both sessions at p < 0.001 uncorrected.

Figure 4.

Neural representations of the state prediction error in pIPS and latPFC separately for both sessions. Data are extracted in the same way as in Figure 3 and plotted according for low, medium, and high SPE (see Experimental Procedures for details). Color codes in the SPMs correspond to p< 0.001 and p< 0.0001 uncorrected.

Relationship between neural SPE signal and behavior

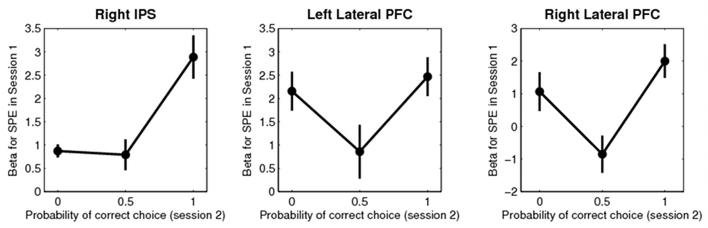
We next considered whether this neural correlate of an SPE is also behaviorally relevant for making better choices at the beginning of the free-choice session. To address this question, we correlated in each participant the parameter estimate for the SPE in those regions possessing a significant SPE representation in session 1 (bilateral latPFC and right pIPS, extracted and averaged from a 10 mm spherical volume centered on the group peak voxel) with the percent correct choices. The latter is a behavioral measure defined as the choice of the action with the highest expected value (reward magnitude × true transition probability) (see Figure S1), and is independent of the computational models employed for the imaging analysis. We observed a significant correlation between the neural and the behavioral data of r = 0.57 (p = 0.013) in the right pIPS, but not in lateral PFC (left: r = 0.28, p = 0.27; right; r = 0.38, p = 0.12). This suggests that the degree to which pIPS encodes an SPE representation across subjects, correlates significantly with the extent to which subjects deploy a forward model in guiding their choices at the beginning of session 2 (see Figure 5).

Figure 5.

Relationship between BOLD correlates of a state prediction error in right pIPS and bilateral latPFC in session 1 and the percent correct choice (3 bins) at the beginning of session 2. A “correct choice” was defined as choosing the action with the highest optimal Q-value in a particular state (see Supplementary Figure 4 for details on the optimal Q-values). Error bars are s.e.m. across subjects.

Differentiating the SPE signal from non-specific attention or salience

A possible explanation for the SPE signal is that it merely reflects a general attentional or salience signal, with subjects deploying greater attention on trials in which a given state was more unexpected, compared to those in which it was less unexpected. However, we might expect that attention would be grabbed equally by the delivery of unexpected rewards or omissions of reward, and certainly more by either of these than the unexpected presentations of the somewhat less behaviorally salient visual stimuli, which denote the different states in our task. Thus, we tested the null hypothesis that the areas identified as correlating with an SPE could be also explained by an unspecific surprise signal by examining the correlations between our fMRI data and the absolute value of our signed RPE signal [abs(RPE)], which exactly captures the unexpectedness of the delivery or omission of reward. This abs(RPE) signal correlated with a number of brain regions including an IPS locus anterior to where we found SPE correlates at p < 0.001 uncorrected (Figure S3). However, a direct comparison between SPE and abs(RPE) revealed a region of both posterior IPS that was significantly better explained by the SPE than by the abs(RPE) signal at p < 0.05 corrected, as well as a region of lateral PFC that showed a difference at p < 0.001 uncorrected (Figure S4). We also tested whether the conjunction of SPE and abs(RPE) showed a significant effect in our target region, in order to assess whether these signals were even partially overlapping. No voxel survived the conjunction contrast, even at an uncorrected threshold. Taken together, these findings suggest that the SPE signal we observe in parietal cortex and lateral PFC is unlikely to reflect a non-specific arousal or attentional signal.

DISCUSSION

We used a probabilistic Markov decision task to investigate the neural signatures of reward and state prediction errors associated with model-free and model-based learning. Our behavioral analysis demonstrated that participants successfully acquired knowledge about the state transition probabilities in the first non-rewarded session, in which only the model-based system could usefully learn. They were able to use that knowledge to make better choices at the beginning of the second, free-choice, session. Subsequent choices were most consistent with a hybrid account, combining model-based and model-free influences. However, we found that the supremacy of the model-based learner in the hybrid declined rapidly over the course of continuing learning. In the imaging data we found trial-by-trial correlations of the model-based SPE in the pIPS and latPFC, whereas a model-free RPE correlated with the BOLD signal in the ventral striatum. The fMRI data, together with the computational modeling, therefore allowed us to assess a trial-by-trial parametric signal of latent expectation formation during the training phase, even though its behavioral consequences on choice are only observable in the rewarded phase of the task.

Our findings of neural correlates of our SPE signal in lateral PFC may relate to studies of human causal learning, which report activity in the region while subjects learn causal relationships between cues and consequences (Fletcher et al., 2001). Prediction errors have been proposed as a putative mechanism for guiding learning of such causal associations (Dickinson, 2001), although to our knowledge, the precise mathematical form of how such a putative causal learning error signal is implemented in the brain has not yet been specified (Fletcher et al., 2001) and previous imaging studies have not examined its trial-by-trial computational dynamics. Furthermore, recent recording studies in monkeys have associated neuronal activity in this area with sequential planning behavior (Mushiake et al., 2006) and with the monkey’s performance during dynamic competitive games (Barraclough et al., 2004; Lee et al., 2004). On these grounds the lateral PFC has been proposed to contribute toward the implementation of model-based RL, possibly in the form of Bayesian belief states (Samejima and Doya, 2007), an account consistent with our proposed role of this area in model-based reinforcement learning. The present results when taken together with these previous findings could suggest a very general role for lateral PFC in learning probabilistic stimulus-stimulus associations.

The finding that BOLD activity in pIPS correlates with an SPE may be interpreted in the context of previous neurophysiological studies into the activity of neurons in the lateral intraparietal area (LIP) during saccadic decision-making. Putative pyramidal cells report expectations about as-yet unknown characteristics about the state of the world (Gold and Shadlen, 2002), possibly coded in terms of the expected values of saccades (Platt and Glimcher, 1999; Sugrue et al., 2004). Other subregions of posterior parietal cortex (PPC) appear to be specialized for different movement modalities (Cui and Andersen, 2007), though less is known about their behavior with respect to decision variables. Under the view that the fMRI BOLD signal reflects in part the input into an area and intrinsic computations within it (Logothetis et al., 2001), it is straightforward to envision the SPE input that we recorded as being necessary for learning the structure of the environment necessary to support these predictions. The finding that SPE signals are present in pIPS while subjects are learning state transitions even in the complete absence of reward (session 1 of our task), suggests that this region is involved also in pure state-learning, and not just in encoding value-based representations. Furthermore, it is interesting to note that SPE signal in right pIPS is predictive of subsequent successful choice behavior, whereas the same signal in the left lateral PFC is not. This underlines the importance of the state space representation that is built in the parietal cortex, and suggests that the lateral prefrontal cortex, despite maintaining a similar representation of the SPE, may be concerned with integrating other learning signals too, and therefore does not exhibit the same clear link to subsequent choice behavior.

Unexpected events are often considered as leading to the deployment of attention, in the form of orienting or executive control. Further, the areas correlated with the SPE signal are thought to be involved in aspects of attention (the PPC with orienting/salience (Yantis et al., 2002) and frontal regions with executive control (Corbetta et al., 2000; MacDonald et al., 2000)) . Thus, it is natural to question whether this correlation is parasitic on some more general forms of attention. Our experimental design does not allow us to rule this out definitively; and indeed some models of associative learning use a signal akin to our SPE to control the assignment of salience for learning to particular stimuli (Pearce and Hall, 1980), according to some accounts via a cholinergic pathway associated with the PPC (Bucci et al., 1998). In this context, the model-based approach used here would provide a computational account of the means by which such attention is allocated on a trial by trial basis, and of how those allocations change as a function of learning and experience. Our findings would then be novel evidence about the mechanisms underlying this form of learning. However, the appeal of this account and other accounts dependent on salience is weakened by the observation that the SPE is only a, possibly minor, but very specific subcomponent of a general surprise signal, which we would expect to be dominated by reward-induced salience signals: unexpected delivery or omission of reward at the end of a trial. Our finding that our model-based SPE provided a significantly better account for the BOLD signal in pIPS and latPFC than an unsigned RPE (Figure S4) provides direct evidence for the distinction between these two signals.

Similarly, we observed that the correlation with the SPE is present in the first session. The subjects’ choices were instructed during this session, which likely requires less engagement of executive control processes compared to the free choice decisions in the second session. Therefore, it seems unlikely executive control is the sole reason for driving the correlation between frontal regions and the SPE.

More recently, neuronal correlates of perceptual learning have been also associated with data recorded from the PPC (Law and Gold, 2008). Because our stimuli (fractal images, see Figure 1) were selected for maximal discriminability in terms of color scheme and shape, low-level perceptual learning resulting in altered activation due to improvement in stimulus detection and discriminability was most likely minimized in our study and cannot account for the SPE signal found in pIPS. However, perceptual learning – in the sense of subtly changed perceptual representations due to reinforcement (Seitz and Dinse, 2007) – may of course be engaged during the task, especially in session 2, although due to the absence of reinforcement in session 1, this explanation is unlikely to account for the state-learning signals observed throughout session 1 and 2.

In addition to the SPE signals we observed in pIPS and latPFC, we also found evidence of RPE signals in the ventral striatum. This is consistent with many previous accounts (McClure et al., 2003; O’Doherty et al., 2003; Seymour et al., 2004). Our findings suggest that the two different types of learning signal are at least partly anatomically dissociable in the brain. Whereas the RPE is present predominantly in sub-cortical structures such as the striatum, appropriate to the rich input into this area from mid-brain dopaminergic neurons (Haber, 2003) known to broadcast this signal (Schultz, 1998; Schultz et al., 1997), the SPE was present instead in dorsal cortical areas, in the parietal and frontal lobes. The distinct neuroanatomical footprints of these signals could reflect the suggestion that they are being used to learn representations in two separate but interacting systems involved in behavioral control: a model-based (goal-directed) system that may involve a number of cortical areas in addition to parts of anterior medial striatum, and a model-free (habitual) system that may be depend predominantly on dopaminergic-striatal pathways (Balleine et al., 2007). However, the data presented here, in particular the weighted combination of both models in the hybrid account, suggests that both learning mechanisms act together to produce effective action selection rather than dualistic processing of two learning modules that exert separate control over choice behavior.

In conclusion, there is an impressive agreement from a wide variety of animal and human paradigms for the involvement of at least two systems in decision-making and control. The simpler of these two, associated with habits and model-free RL, has attracted a huge wealth of work, and there are ample studies (also confirmed here) elucidating its basic learning mechanisms driven by a reward prediction error. By comparison, the more sophisticated, model-based, system, with its rich adaptability and flexibility, has been more sparsely studied. Here, we have pinned down what is perhaps the most critical and basic signal for this system, namely the state prediction error. In particular, we showed that the two error signals are computed in partially distinct brain areas and illustrated how human choice behavior may emerge through the combination of the systems.

EXPERIMENTAL PROCEDURES

Participants

Twenty subjects were tested on the experimental paradigm. All subjects were recruited from the Caltech student population, were free of any neurological or psychiatric diseases, and had normal or corrected-to-normal vision. Informed consent was obtained from every subject and the study was approved by the Caltech Institutional Review Board.

Two subjects were excluded because they did not meet our criterion for minimal learning during the experiment: we compared the total amount of monetary rewards that the subjects obtained at the end of the experiment against a Monte-Carlo simulation of 10000 randomly behaving agents and determined the upper 95^th percentile of this distribution. Two subjects, whose outcome was not greater that this threshold, were excluded from the analyses. The remaining 18 subjects (8 females) had a mean age of 24 years (± 7.57 sd).

Experimental Task

We designed a Markov decision task in which the subjects had to make 2 sequential choices (“LEFT” or “RIGHT”), one in each of two successive decision states in order to obtain a monetary outcome at the end state. Each state was signaled to the subject by a different fractal image (see Figure 1a for an example), which indicated to them that during the first 2 states they had the choice between left or right button press. The states were intersected by a variable temporal interval drawn from a randomly uniform distribution between 3 and 5 sec. The inter-trial interval was also sampled randomly from a uniform distribution between 5 and 7 sec. Upon each state the subjects had 1 sec to make the button press. If they failed to submit their choice in that time window the trials restarted from the beginning.

The layout of the state transitions followed that of a binary tree (see Figure 1a). The first state was always the same. Following the first left/right choice subjects transitioned into 1 of 2 different intermediate states with different state transition probabilities. Following the second left/right choice they transitioned into 1 of 3 different outcome states associated with different amount of monetary wins (0c, 10c, 25c) which were rescaled to 0, 0.4, and 1 for all behavioral modeling. The assignment of fractal images to states was randomized across subjects.

The experiment proceeded in two separate scanning sessions of 80 trials each. During the first session, all decisions were predetermined and the subjects simply had to register them. Subjects also received no rewards at the outcome states during this part of the experiment (see Figure 1b). Taken together all trials in this first session reflected the underlying transition probabilities exactly, but they were presented in a randomized order. Subsequently during a break, subjects were exposed to the reward contingencies (see Supplemental Experimental Procedures). Finally, in the second scanning session, subjects made their own choices and were rewarded at the outcome states.

Data Acquisition

Functional imaging was performed on a 3T Siemens (Erlangen, Germany) Trio scanner. Forty-five contiguous interleaved slices axial slices of echo planar T2*-weighted images were acquired in each volume with a slice thickness of 3 mm and no gap (repetition time 2730 ms, echo time 30 ms, flip angle 80°, field of view 192 mm², matrix size 64×64). Slice orientation was tilted −30° from the line connecting the anterior and posterior commissure to alleviate signal drop out in the orbitofrontal cortex (Deichmann et al., 2003). We discarded the first 4 volumes to compensate for T1 saturation effects.

Image Processing

Image processing and statistical analyses were performed using SPM5 (available at http://www.fil.ion.ucl.ac.uk/spm). All volumes from all sessions were corrected for differences in slice acquisition, realigned to the first volume, spatially normalized to a standard echo planar imaging template included in the SPM software package (Friston et al., 1995) using fourth-degree B-spline interpolation, and finally smoothed with an isotropic 8 mm FWHM Gaussian filter to account for anatomical differences between subjects and to allow for valid statistical inference at the group level. Images contaminated by movement artifacts were identified using a velocity cutoff of 0.2 mm/TR. Furthermore, unphysiological global signal changes were identified using a cutoff for the global image mean of ± 2.5 SD above or below the session-specific mean. Nuisance regressors were created for these scans (with a single 1 for the questionable scan and 0’s elsewhere) to be included as covariates of no interest in the first level design matrices.

Computational Learning Models

We implemented three learning models, which hypothesize different methods by which participants might use experience with states, actions, and rewards to learn choice preferences.

SARSA Learner

We derive a reward prediction error (RPE) by using a model-free SARSA learner, a variant of classic reinforcement learning (Sutton and Barto, 1998) (see also Figure 2). The name refers to the experience tuple <s,a,r,s’,a’>, where s and s’ refer to the current and next state, a and a’ to the current and next action, and r represents the obtained rewards. The learner attempts to estimate a “state-action value” Q_SARSA (s, a), for each state and action. These values are initialized to zero at the start of the experiment, and then at each step of the task the value of the state and action actually experienced, Q_SARSA (s, a), is updated in light of the reward obtained in the next state, r(s’) , and the estimated value Q_SARSA(s’,a’) of the next state and action. In particular, an RPE δ_RPE is computed as:

$${\delta }_{\mathit{RPE}}=r\left(s^{\prime }\right)+\gamma Q_{\mathit{SARSA}}(s^{\prime },a^{\prime })-Q_{\mathit{SARSA}}(s,a)$$

where γ is the temporal discount factor, which we fixed to γ = 1 because the 2-step task does not allow subjects to choose between rewards at different delays.

The RPE is used to update the state-action value as:

$$Q_{\mathit{SARSA}}(s,a)=Q_{\mathit{SARSA}}(s,a)+\alpha {\delta }_{\mathit{RPE}}$$

where α is a free parameter controlling the SARSA learning rate.

FORWARD Learner

We used a Dynamic Programming approach to implement a FORWARD learner, which utilizes experience with state transitions to update an estimated state transition matrix T(s, a, s’) of transition probabilities. Each element of T(s, a, s’) therefore holds the current estimate of the probability of transitioning from state s to s’ given action a. These transitions are initialized to uniform distributions connecting each state and action to those on the next level of the tree. Upon each step, leaving state s and arriving in state s’ having taken action a, the FORWARD learner computes a state prediction error (SPE):

$${\delta }_{\mathit{SPE}}=1-T(s,a,s^{\prime })$$

and updates the probability T(s,a,s’) of the observed transition via:

$$T(s,a,s^{\prime })=T(s,a,s^{\prime })+\eta {\delta }_{\mathit{SPE}}$$

where η is a free parameter controlling the FORWARD learning rate. The estimated probabilities for all states not arrived in (i.e. for all states s” other than s’) are reduced according to T(s,a,s”) = T(s,a,s”) · (1–η), to ensure that the distribution remains normalized.

Estimated transition probabilities are used together with the rewards at the end states, r(s), (which were taken as given since the participants were instructed in them) to compute state-action values Q_FWD as the expectation over the value of the successor state. This is done by dynamic programming, i.e., recursively evaluating the Bellman equation defining the state-action values at each level in terms of those at the next level. Here, Q_FWD(s,a) = 0 for the terminal reward states at the bottom of the tree, and for the other states:

$$Q_{\mathit{FWD}}(s,a)=\sum _{s^{\prime }}T(s,a,s^{\prime })\times \left(r\right(s^{\prime })+\arg \underset{a^{\prime }}{\max }{Q}_{\mathit{FWD}}(s^{\prime },a^{\prime }\left)\right)$$

HYBRID Learner

We considered a third, HYBRID learner, which combines state-action value estimates from both SARSA and FORWARD learners into a single set of value estimates. The model assumes that the two sets of state-action value estimates are combined according to a weighted average. We assume that the relative weight accorded to the two functions in determining the hybrid state-action valuations (and thus choice behavior) can change over the course of the free-choice scanning session (session 2). Following Camerer and Ho (1998), we characterize the form of this change with an exponential function:

$$w_t=l\times e^{-kt}$$

where w_t is the trial-specific weight term for trial number t, and l and k are two free parameters describing the form of the exponential decay (l: offset, k: slope).

Q values for the HYBRID learner are then computed as a weighted sum of the estimates from the two other learners, on trial t:

$$Q_{\mathit{HYB}}(s,a)=w_t\times Q_{\mathit{FWD}}(s,a)+(1-w_t)\times Q_{\mathit{SARSA}}(s,a)$$

Action Selection

Each of the models additionally assumes that participants select actions stochastically according to probabilities determined by their state-action values through a softmax distribution:

$$P(s,a)=\frac{\exp (\tau \times Q(s,a\left)\right)}{\sum _{b=1}^n\exp (\tau \times Q(s,b\left)\right)}$$

where Q is Q_SARSA, Q_FWD, or Q_HYB, depending on the model, and the free “inverse temperature” parameter τ controls how focused the choices are on the highest valued action.

We fit each model’s free parameters to the behavioral data, by minimizing the negative log-likelihood – Σlog(P(s,a)) of the obtained choices a given the previously observed choices and rewards, summed over all subjects and trials. The HYBRID learner has 5 free model parameters (α, η, τ, l, and k); the SARSA and FORWARD learners each have 2 (α or η, and τ). We estimated a single set of parameters for all participants because the unregularized maximum likelihood estimators tend to be very noisy in individual subjects leading to very different and sometimes even outlying parameter estimates. In addition, the resulting regressors for this kind of “model-based fMRI” data analysis tend to perform poorly. A single set of parameters as frequently employed in our recent work (Daw et al., 2006; Gershman et al., 2009; Glascher et al., 2009) imposes a simple, but efficient regularization, which stabilizes the estimated model parameters. Goodness of fit was compared between models taking into account the different numbers of free parameters using likelihood ratio tests and Akaike’s Information Criterion (AIC).

Statistical Analysis of Functional Imaging Data

The analysis of the functional imaging commenced with single subject analyses. We created subject-specific design matrices containing the following regressors: (a) 3 regressors encoding the average BOLD response at each of the 3 states (2 choice states, 1 outcome state), (b) 2 regressors encoding the model-derived prediction error signals (RPE and SPE) modeled at the time of state 2 and the outcome, (c) 2 regressors of model-derived value signals modeled at the time of state 1 and state 2 (not further analyzed in this paper), (d) a nuisance partition containing regressors modeling the individual scans that were identified as contaminated by movement and unphysiological global signal change (see Image Processing above), (e) a nuisance partition containing 6 regressors that encoded the movement displacement as estimated from the affine part of the image realignment procedure. Because subjects did not receive any reward information in session 1, we only included the state prediction error signal; all other model-derived variable were 0 throughout the entire session 1 because of the lacking reward information. Both error signals were enter unorthgonalized into the 1^st level design matrices.

These subject-specific design matrices were estimated and 3 beta images for the prediction error signals (SPE from both sessions, RPE from session 2) were entered into a repeated measures ANOVA with factors error (RPE, SPE) and session (sess1, sess2) correcting for non-spherical distribution of the error term to test for a significant effect across the entire group.

We set our statistical threshold to p < 0.05 family-wise error (FWE) corrected for the entire brain volume. The areas surviving these corrected thresholds are listed in Table 2 and are discussed in the main paper. However, for display purposes we show the statistical maps with the significant correlation with both prediction errors at p < 0.001 and p < 0.0001.

For the analysis about the consistency of SPE signal in pIPS and latPFC we insure independence of voxel selection by first identifying the cluster peaks in these regions for the SPE signal in the rewarded session 2. We then defined a spherical search volume (radius: 10mm) around these peaks and identified significant correlations (p < 0.05, family-wise error for the reduced search volume) between the SPE and the BOLD signal in the independent session 1. For a formal statistical test of identical voxels in session 1 and 2 that exhibit the correlation with the SPE signal we also employed a conjunction analysis (Nichols et al., 2005) at an uncorrected statistical threshold of p < 0.001.

Plots of the data were created using the rfxplot toolbox for SPM5 (Glascher, 2009), which is capable of dividing a parametric modulator into different bins and estimating the average BOLD response for each bin. We extracted the data for the plots of percent signal change in Figures 3 and 4 using a cross-validation leave-one-out procedure: we re-estimated our second level analysis (repeated measures ANOVA, see above) 18 times always leaving out one subject. Starting at the peak voxels for the SPE signal in IPS and PFC and for the RPE in ventral striatum, we selected the nearest maximum in these cross-validation second level analyses. From that new voxel we extracted the data from the left out subject and sorted all trial into a 3 bins according the size of the SPE and defined by the 33^rd, 66^th, and 100^th percentile of the SPE range. Then three new onset regressors containing all trials of each bin were created and estimated for each left-out subject. The parameter estimates of these onset regressors represent the average height of the BOLD response for all trials in each bin. The data plots in Figures 3 and 4 are the average (across all left-out subject in the cross-validation analyses) parameter estimates (betas) converted to percent signal change for these 3 regressors.