Long-Timescale Molecular-Dynamics Simulations of the Major Urinary Protein Provide Atomistic Interpretations of the Unusual Thermodynamics of Ligand Binding

Abstract

The mouse major urinary protein (MUP) has proved to be an intriguing test bed for detailed studies on protein-ligand recognition. NMR, calorimetric, and modeling investigations have revealed that the thermodynamics of ligand binding involve a complex interplay between competing enthalpic and entropic terms. We performed six independent, 1.2 μs molecular-dynamics simulations on MUP—three replicates on the apo-protein, and three on the complex with the pheromone isobutylmethoxypyrazine. Our findings provide the most comprehensive picture to date of the structure and dynamics of MUP, and how they are modulated by ligand binding. The mechanical pathways by which amino acid side chains can transmit information regarding ligand binding to surface loops and either increase or decrease their flexibility (entropy-entropy compensation) are identified. Dewetting of the highly hydrophobic binding cavity is confirmed, and the results reveal an aspect of ligand binding that was not observed in earlier, shorter simulations: bound ligand retains extensive rotational freedom. Both of these features have significant implications for interpretations of the entropic component of binding. More generally, these simulations test the ability of current molecular simulation methods to produce a reliable and reproducible picture of protein dynamics on the microsecond timescale.

Introduction

The mouse major urinary protein (MUP) is a 19 kDa member of the lipocalin family (1). The major features of its structure (2) are a β-barrel of eight strands (a–h) linked by short loops (L1–L7), plus one α-helix toward the C-terminus (see Fig. S1 in the Supporting Material). The barrel is closed at one end, and the other end provides an entrance into the small, deep, and very hydrophobic central cavity. In nature, the protein is proposed to act as a molecular sponge, excreted in the urine to provide a slow-release mechanism for small, volatile mouse pheromone molecules. MUP has provided a fertile test bed for studies of the thermodynamics of ligand-protein recognition. Using isothermal calorimetry, Bingham et al. (3) showed that despite its hydrophobic character, binding of the natural pheromone 2-methoxy-3-iosbutylpyrazine (IBM) to MUP is driven by enthalpy, not entropy. Sharrow et al. (4,5) made the same observation with another ligand, 2-sec-butyl-4,5-dihydrothiazole (SBT). Associated x-ray crystallographic and NMR studies with IBM (6) and other ligands (7–9) suggested that ligand binding restricts protein flexibility in certain regions but increases it in others (a form of entropy-entropy compensation), and it was concluded that binding is driven by enthalpic terms associated with ligand-protein nonbonded interactions. This was something of a puzzle, as it was generally assumed that, in purely enthalpic terms, new interactions that form between the ligand and the protein are almost equi-energetic with those lost between the ligand and the solvent. Subsequent molecular modeling studies (6) suggested an explanation: the binding cavity is so hydrophobic that even in the absence of a ligand, water molecules prefer to avoid it. Simulations predicted an average hydration density of just 0.2–0.3 g/cm³. Binding of the ligand is thus predicted to release very few water molecules from the cavity, which would explain the negligible entropic contribution, and create many new favorable nonbonded interactions, explaining the favorable enthalpic term. In view of the tenet that “nature abhors a vacuum”, this conclusion (10) originally met with some resistance; however, several examples of this process of dewetting have now been observed in a variety of situations (11,12).

Molecular modeling methods have also been used to look at the issue of entropy-entropy compensation. The residue-specific configurational entropies that can be extracted from NMR relaxation data may be directly compared with values obtained from simulations. However, the methodology for doing this is not straightforward, since there are issues regarding how the individual residue motion should be decoupled from overall protein tumbling, and which model should be used to describe the time dependency in the orientations of the selected bond vectors. Macek et al. (13) performed 30-ns simulations on MUP and its complex with SBT. Their results provided qualitative support for the view that ligand binding can increase the mobility of many residues in the protein; however, to complicate matters, there is also NMR evidence that on a much longer timescale (milliseconds), ligand binding appears to reduce MUP's mobility (14).

Modern computational resources make it feasible to perform microsecond-timescale molecular-dynamics (MD) simulations on proteins such as MUP to help resolve or at least clarify some of the issues surrounding ligand binding to this protein. However, conventional all-atom MD simulations of this length are still not well established, and thus must be undertaken with some caution. We must bear in mind that the underlying force fields were parameterized some time ago and have not been rigorously tested in this time regime. An illustration of the problems that can arise was recently provided in the related area of DNA simulation, where the observation of unrealistic and irreversible structural changes when simulation timescales reached beyond 20–30 ns led to a major effort to reparameterize the AMBER force field (15). Building on Duan and Kollman's (16) pioneering simulations of the villin headpiece, a number of studies have conducted microsecond-scale MD simulations of proteins and peptides; however, most of these works employed enhanced sampling methods and/or some level of coarse-graining. As a result, they have not provided an opportunity to answer the simple question: Are current atomistic force fields capable of providing a stable simulation of a small, well-folded globular protein on the microsecond timescale?

To address this issue, we used HECToR, the national supercomputing service of the United Kingdom, to perform six 1.2-μs simulations of MUP—three on the apo-form of the protein, and three on its complex with IBM. The simulations were performed using AMBER9 and the parm03 force field. The three replicate simulations of each system differed only in the initial orientation in space of the protein. The data set therefore provides an unprecedented view (to our knowledge) of the structure, dynamics, and recognition properties of MUP, as well as valuable data for validating the general simulation methodology employed.

Here we report the initial conclusions drawn from this study. We examine general issues pertaining to equilibration, convergence, sampling, stability, and reproducibility, and specific issues regarding MUP-IBM recognition (in particular, how ligand binding affects protein dynamics and hydration), and also identify some surprising behavior in the bound ligand.

Materials and Methods

The starting structures for the protein were taken from the crystal structures of wild-type MUP (2ozq) (17) and wild-type MUP bound to IBM (1qy1) (3). Crystallographically observed solvent molecules were retained. The ionization/tautomeric states of the amino acid side chains were assigned using the web-based WHATIF tools (http://swift.cmbi.ru.nl/servers/html/index.html). The protein parameters were taken from the Amber ff03 force field (18), and parameters for the ligand molecule were generated within the antechamber module of Amber 9 (19) using the General Amber Forcefield (20). Three replicates of each structure were generated by performing random rotations of the original coordinates about the x, y, and z axes. Each replicate was then immersed in a truncated octahedral box containing an additional ∼19,000–21,000 TIP3P water molecules and sufficient Na⁺ ions to neutralize the system. All parameter files and the initial configuration of each system are included in the Supporting Material.

All systems were initially conditioned using our standard multistep energy-minimization and restrained-dynamics protocol (21). The production phase of the simulations consisted of 1.1–1.2 μs of unrestrained MD simulation at constant temperature and pressure (T = 300 K; P = 1 atm) performed using the pmemd module of Amber 9. SHAKE was used to constrain all bonds to hydrogen at equilibrium values, permitting a 2 fs time step. The particle mesh Ewald method was used to treat long-range electrostatic interactions. Coordinates were saved every 1 ps. Trajectory analysis was performed using the ptraj module of Amber 9, plus the pcazip tools for principal component analysis (PCA) (22) distributed by CCPB (http://www.ccpb.ac.uk/software). Cluster analysis was done using the backbone atom root mean-square deviation (RMSD) as the distance metric, and complete linkage as the clustering algorithm. Schlitter configurational entropies were calculated from trajectories after mass-weighted least-squares fitting of all atoms was completed. Further parameters are described in the Discussion. Molecular graphics were produced using the UCSF Chimera package (23) from the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIH P41 RR-01081), and VMD (24).

Results and Discussion

Throughout the text, we refer to the three replicate simulations of the apo-form of MUP as apo1, apo2, and apo3, and to the three replicate simulations on MUP bound to IBM as ibm1, ibm2, and ibm3.

Equilibration and stability

The initial examination of the trajectories revealed that the first 10 residues exhibit highly dynamic and variable behaviors. These residues are not part of any secondary structural element, but in the crystal structures they adopt a random coil conformation and pack closely against the bulk of the protein. Because of the extensive and slow dynamics of this region, and its variability between replicate simulations, it was excluded from most of the analyses of equilibration and sampling.

All simulations eventually reached equilibrated states, with heavy atom RMSDs of 2.5–3 Å from the respective starting structures and 1.5–2 Å from the respective time-averaged structures. However, the RMSD time-course plots (see Fig. S2) clearly show that for the apo replicates, equilibration/relaxation is a process that can take >100 ns. The ligand-bound systems appear to equilibrate much more rapidly, particularly if the RMSD from the time-averaged structure is used to assess this. Despite the variations in the rates of equilibration, the conformational changes involved are consistent between replicate simulations and are dominated by (small) changes in the conformations of the loops linking the β-barrel strands. The most significant motion, that of loop L3 around residue 60, is discussed further below.

For an alternative view of equilibration and stability, we analyzed secondary structure conservation and how well the molecules remained within the favored regions of the Ramachandran map. All simulations remained very close to the crystal structure distributions, with 83–88% of residues in the allowed regions, and never more than 1% in the disallowed regions (the balance being in the generously allowed region). Although secondary structure elements sometimes showed reversible fraying, no general degradation over time was discernible (example data from apo1 are shown in Fig. S3).

We also found that the simulations retained structures in good agreement with NMR data. Using CamShift (25), we calculated the main-chain chemical shifts for 20 equally spaced structures taken from simulation apo1. As shown in Fig. S4, the correlation between the average values of the Cα chemical shifts and the deposited values (BMRB entry 1470) (26) is excellent (R² = 0.91) and the errors are uniformly distributed, with no evidence of, e.g., larger errors in the more apparently mobile regions.

Protein dynamics: sampling and reproducibility

Cluster analysis provides a low-resolution means of examining issues regarding sampling and reproducibility. If the simulations were perfect, we would expect the replicate trajectories to populate the same clusters with the same frequency, and to show frequent hops from cluster to cluster. Clustering the snapshots from all three apo simulations together, we see that this is far from the case (Fig. 1 a; for color version see Fig. S5). Despite the fact that data from all three replicate simulations was pooled before the analysis, clustering redivides the structures broadly along replicate lines. This indicates that even over 1 μs, the simulations retain some memory of their initial state. We also note that most of the jumps between clusters are unidirectional; in other words, these simulations are clearly not completely converged. When applied to the pooled snapshots from the ligand-bound simulations (ibm1–ibm3), the results are somewhat better (Fig. 1 b). In addition to the cluster that contains the starting structures, there is a further cluster populated by snapshots from each of the three replicate simulations, and three more that feature snapshots from two of the three simulations. There are also more cluster transitions, and more of them are bidirectional. Repeating the cluster analysis on the basis of backbone atoms alone gives essentially the same results (results not shown).

Figure 1.

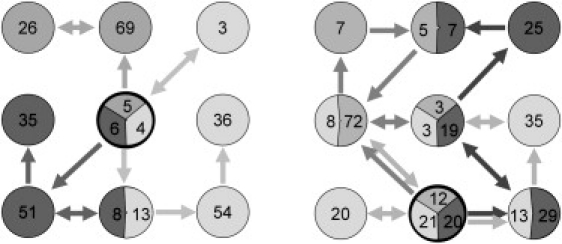
Cluster analysis of apo (left) and ibm (right) simulations. The clusters containing the crystal structures are outlined in black. Numbers in circles give the percentage occupancy of each cluster, and arrows indicate cluster transitions.

PCA allows us to see how well the dynamical behavior of the systems converges between replicates and is conserved or perturbed by ligand binding. As discussed by Rueda et al. (27), one must consider a constant and suitably dimensioned subspace for this analysis. Performing PCA on each trajectory independently, we find that between 48 and 60 eigenvectors are required to capture 90% of the variance. Comparing them pairwise, we find that the apo simulations have an average subspace overlap in the first 48 dimensions of 0.80, whereas for the ibm simulations this is 0.84. Again, as discussed by Rueda et al. (27), one must calculate the Z-scores to assess the significance of these values. To that end, we created 25 random models (by random permutations of the atoms in trajectory apo1) and calculated the subspace overlaps for 300 independent pairwise comparisons of those models. The average subspace overlap had a Z-score of 53.2 for the apo simulations and 55.8 for the ibm simulations. Both are high values, indicating that overall, the replicate simulations show conserved dynamical behavior, and, in line with other observations, this is particularly the case in the ligand-bound state. However, if we look at the actual dot products between eigenvectors from replicate simulations, we see that in general, the individual modes are not well conserved. On average, the highest dot product between any pair of eigenevectors is 0.32 for the apo simulations and 0.35 for the ibm simulations. There is, however, one highly conserved mode, which features correlated motions in loops L2 and L3 (results not shown). When the PCA is performed after pooling replicate trajectories, the subspace overlap between the apo and ibm trajectories is 0.85 (Z-score: 57.2) and the average maximal dot product is 0.35. Thus, we see that ligand binding produces no perturbation to the dynamics of the system that is discernible over interreplicate variation.

The above analysis tells us that all of the simulations occupy the same essential dynamical subspace; however, they do not necessarily sample the same regions of this space. RMS fluctuations (Fig. 2) provide a more detailed view of protein flexibility. As expected, the most mobile regions of the structure are in the loops. We see that the fluctuation profiles are well conserved between replicates, but that some variation exists, particularly (and not unexpectedly) in the most mobile regions. Fig. 2, a and b, also include the RMS fluctuation profiles generated from analysis of the three individual time-averaged structures. This provides a simple test of reproducibility: regions with low RMS fluctuation are those that are very similar in different replicates, whereas high fluctuations identify divergence in the time-averaged structures. Again, not unexpectedly, it is in the most flexible regions of the protein that it is most likely that the time-averaged structures of the replicates will be somewhat divergent, since it is harder to achieve full sampling. Of interest, however, this is not always so; for example, around L2 (residues 43–47) is a dynamic region that appears to have been very similarly sampled in the replicate simulations. We hypothesize that this type of behavior may indicate regions that, though flexible, have relatively simple harmonic motions that can be well sampled over this timescale, whereas in other cases (see, e.g., around L3, residues 57–63) the motion may involve complex “jumping among minima” that make it much harder to sample the motion well.

Figure 2.

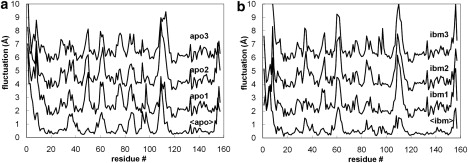
RMS fluctuations of individual amino acids for replicate apo (left) and ibm (right) simulations. In each case the lowest plot is calculated from the fluctuations between the time-averaged structures from each simulation, whereas the plots stacked above are calculated from all snapshots within an individual simulation and are displaced vertically by 1, 3, and 5 Å, respectively, for clarity.

To check the reliability of these observations, we calculated an experimental RMS fluctuation profile for apo-MUP from the 10 structures deposited in PDB entry 1BF3 (28). The profile is in good agreement with that obtained from the simulations (Fig. S6), but there are several discrepancies: 1), the N-terminal region appears more stable in the experimental data than we observe; 2), the variability around loop L4 is greater than the simulations predict; and 3), loops L5 and L6 appear more flexible in the simulations than the NMR data show. However, as we will show below, some of these differences are probably not statistically significant, and in any case we must be aware that in analyzing the NMR data, we are using a small number of structures that have been chosen for deposition by criteria other than that they are representative of an equilibrium distribution.

Fig. 3 shows how RMS fluctuations change on ligand binding. We see that there is no obvious relationship between how close a residue is to the bound ligand and any changes in that residue's dynamics. As noted above, although certain regions of the protein are rigidified, others become more dynamic. At this stage, we have not attempted to make a detailed comparison of our results with those from an S² analysis of NMR experiments, for two reasons: First, as discussed in the Introduction, transforming the MD trajectory data into the NMR observables is nontrivial and requires a detailed study outside the scope of this initial report. Second, there is not always a straightforward interpretation for what the NMR experiment typically measures. For example, we took one random 1-ns section from the equilibrated portions of each trajectory and used a simple model-free approach (29) to calculate backbone amide S² values. We then took the same trajectory sections and calculated the backbone RMS fluctuations. The correlation between the calculated S² values and calculated RMS fluctuations is only modest (R² = 0.23 for the apo data, and R² = 0.24 for the ibm data), and if we try to compare changes in S² with changes in RMS fluctuations as a result of ligand binding, there is effectively no correlation at all (R² = 0.06). This is not necessarily surprising, since the NMR approach only detects changes in the librational motion of the NH vectors, whereas RMS fluctuations are sensitive to translational motions as well.

Figure 3.

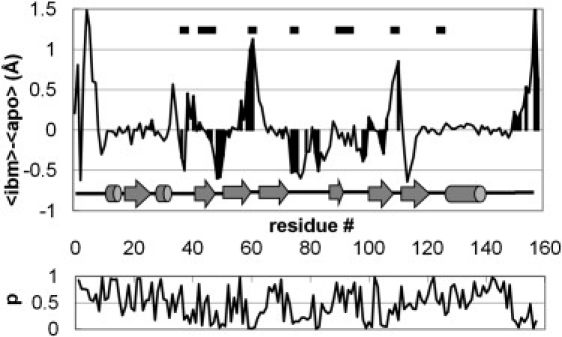
Average change in RMS fluctuation of each amino acid on ligand binding (top), and associated p-values (below). RMS fluctuation changes that have a p-value < 0.2 are highlighted. Black bars at the top of the plot identify amino acids within 5 Å of bound ligand.

Mechanics of ligand-induced changes in protein flexibility

With three replicate simulations, we can use a simple Student's t-test to assess the significance of the various changes in residue dynamics we observe. This reveals that, in fact, only a few of the features seen in Fig. 3 (in particular, the rigidification of the structure in L2 and the loosening of the structure in L3) are statistically significant. Although analyzed in terms of NMR (S²) order parameters rather than RMS fluctuations, these changes were also observed in the shorter (30 ns) simulations of Macek et al. (13). A detailed analysis of the trajectories allows us to provide some insight into how these changes in dynamics come about.

Loop L3 constitutes one of the most flexible regions of the protein, and the initial structural adjustment of this in the dynamics is a large part of the equilibration process described above. In all the trajectories of both the apo- and ligand-bound systems, the loop swings from its crystal structure conformation to one that brings it closer to loop L2 (Fig. 4; color version Fig. S7). This appears to be driven by hydrophobic effects, since there are no clear and consistent hydrogen bonds, salt bridges, or other specific interactions favoring the process. In the apo simulations, this equilibration process is accompanied by a lateral shift in residues 34–38 in L1, such that Phe-38, which forms part of the binding-site cavity, is shifted outward by ∼1.5 Å on average. This shift appears to improve the loop-loop interactions and stabilizes the new conformation of L3. However, in the ligand-bound simulations, the lateral shift of residues 34–38 does not occur, presumably because this would disturb interactions between Phe-38 and the ligand. As a result, the interactions with L3 are not so optimal, and L3 continues to oscillate between the closed position and one more similar to the crystal structure conformation. Plots of the distance between the Cα atoms of residues 35 and 61 show this process clearly (Fig. S8). We note that these observations are not quite the same as those made in the previous study by Macek et al. (13). In that work, only the apo simulations showed the closing of L3 toward L2, and in that case it was diagnosed as being the result of new H-bonds formed between Asn-35 and both Arg-60 and Asp-61. The failure of the ligand-bound systems to undergo this conformational transition was attributed to interactions between Phe-56 and the ligand impeding this motion. In the work presented here, although Asn-35 and Asp-61 are frequently close in the apo simulations, they are rarely in a suitable relative orientation for effective H-bond formation, and although the side chain of Arg-60 does form transient interactions with Asn-35 in the early parts of the simulations, after ∼100 ns it adopts a much more solvent-exposed orientation and never approaches Asn-35 closely again. The role of Phe-56 in this process is also not clear. Though this residue does indeed undergo a small conformational shift on ligand binding, there is no statistically significant alteration in the dynamics of the protein in this region as a result.

Figure 4.

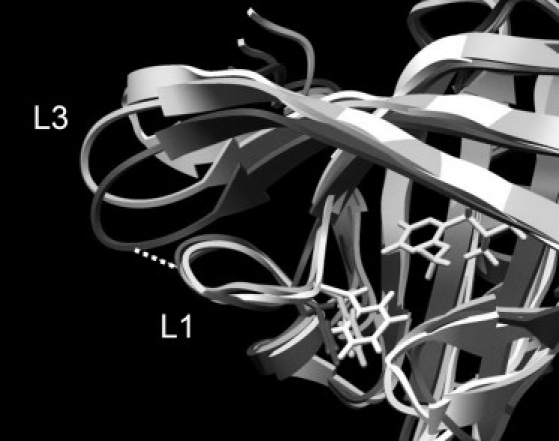
Comparison of the L3 regions of the apo-crystal structure (light gray), time-averaged structure from the three apo simulations (dark gray), and time-averaged structure from the three ibm simulations (medium gray). Phe-38 and the ibm ligand are also shown.

The loop containing residues 48–50 shows the most significant reduction in flexibility on ligand binding. Comparing the time-averaged structures from the apo- and ligand-bound simulations provides a fairly straightforward mechanical explanation for this. Ligand binding results in a reorientation of Phe-90, which forms part of the hydrophobic cavity. This switch results in it packing much more firmly against Tyr-80, reducing its dynamics. This in turn is passed on to the loop via the van der Waals contacts between Tyr-80 and Leu-52 (Fig. 5; color version Fig. S9).

Figure 5.

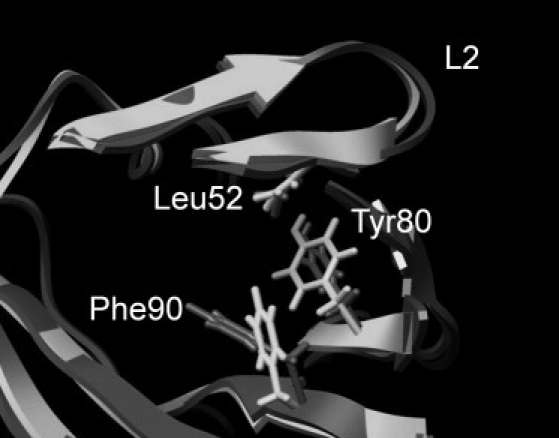
Comparison of the L2 region in the time-averaged structures from the apo (dark gray) and ibm (light gray) simulations. Ligand binding shifts Phe-90, which then packs tighter against Tyr-80, which in turn rigidifies residues 48–50 via the interaction with Leu-52.

Calculations of configurational entropy changes

The observation that the structure of MUP permits the small conformational adjustments that accompany ligand binding to lead to both increases and decreases in protein flexibility in different regions is in agreement with the observations from NMR experiments. Such findings have led to the idea of entropy-entropy compensation as a mechanism to mitigate the reduction in configurational entropy that typically accompanies complex formation. A variety of methods are available to estimate entropy changes from simulation data. Methods based on quasi-harmonic approximation are particularly popular, and the best-known approaches are those developed by Schlitter (31) and Andricioaei and Karplus (30). Though they differ somewhat in philosophy, particularly as regards how they cope with motions that have frequencies beyond the classical limit, in practice they yield very similar results. We used the Schlitter approach to estimate the net effect of all the dynamical changes observed in the simulations on the configurational entropy change. Taking 1000 equally spaced snapshots from the first microsecond of each simulation, the change in the protein configurational entropy that accompanies ligand binding is found to be insignificant (2.0 ± 22 kJ/mol). Since entropy calculations of this type are known to be very sensitive to sampling, it is interesting to see whether the availability of unusually long simulations offers a significant advantage. Repeating the calculations using 1000 equally spaced snapshots taken from the first 100 ns of each simulation, the configurational entropy change is calculated to be −23 ± 25 kJ/mol; i.e., ligand binding tightens the protein structure. However, we recall that for the apo protein in particular, the first 100 ns features a certain amount of relaxation rather than equilibrated sampling, which may affect the result. Repeating the calculation using the second 100 ns of each trajectory, the result is again that the entropy change is insignificant (1.3 ± 20 kJ/mol). Clearly, this result must be reconciled with the NMR observations that ligand binding tends more often to increase backbone S² values than decrease them. In view of our observation (discussed above) of the limited correlations between RMS fluctuations and S² values, we hypothesize that we may be observing another type of entropy-entropy compensation, where a reduction in translational freedom for a residue is offset by an increase in librational motion.

Configurational entropy calculations of this type are sensitive to simulation time and sampling (32). We previously described (33) how estimates for the entropy S(t) calculated over a given simulation time t appear to fit a function of the form:

$$S\left(t\right)=S_{inf}={\mathit{at}}^n$$ (1)

Where S_inf is the entropy for a simulation of infinite length, and a and n are parameters that may be found by curve-fitting. As shown in Fig. S10, the simulation data presented here fit this functional form fairly well; however, in this case the approach does not deliver any significant benefits. The estimates for S_inf calculated from individual replicate trajectories are slightly more divergent than the unextrapolated values, and the values of a and n are also very replicate-dependent.

Analysis of binding-site hydration

Our previous MD simulations on MUP (6) revealed that even in the absence of a ligand, water molecules avoid entering the highly hydrophobic binding cavity, leading to the situation of a partial vacuum within the site. This dewetting process then provides an explanation for the unusual enthalpy-driven nature of the ligand-binding process. The much longer simulations performed here confirm our earlier observation. The cumulative radial distribution function (RDF) for water oxygen atoms around the hydroxyl group of Tyr-120 is shown in Fig. 6. Because of the buried nature of the site, we calibrated the density scale (y axis) of these plots by measuring the RDF for the ligand in the binding site of the ibm simulations, which must integrate to one. In comparison, we can see that the water occupancy of the binding site in the apo protein averages ∼0.4. We also see that a small amount of water (occupancy ∼0.3) remains close to Tyr-120 in the ligand-bound simulations. This appears to be the result of water molecules transiently coming close to this residue via the slightly porous walls of the binding cavity. Hydration density maps confirm these observations (Fig. 7; color version Fig. S11). A very low occupancy of the cavity is evident in the apo-protein (Fig. 7 a), concentrated around the hydroxyl group of Tyr-120. By contouring at a very low level, we can confirm that the cavity still exists—the partial vacuum has not caused it to collapse (Fig. 7 b). Obviously, although the hypothesis of dewetting is attractive in that it helps to explain the experimental data, there is the caveat that these simulations were performed using the TIP3P water model, which is designed to reproduce the behavior of bulk water and may possibly give some artifactual behavior in this rather unusual environment. Further support for this analysis comes from independent modeling studies (34), but in the future it would be useful to investigate this system using alternative water models.

Figure 6.

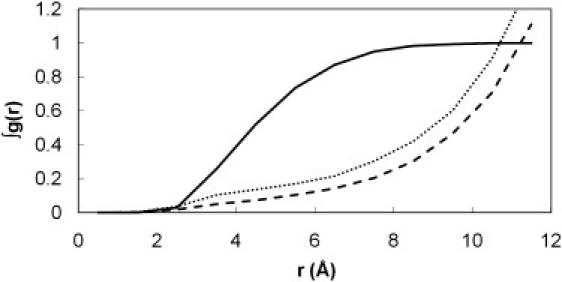
Integrated RDFs for water in the apo simulations (dotted line) compared to the ibm simulations (dashed line). The g(r) values have been scaled so that the equivalent function for the ligand (solid line) integrates to one.

Figure 7.

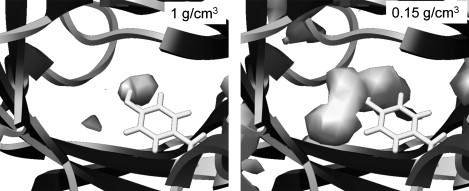
Water density in the ligand-binding site of simulation apo1. The left panel shows the small volume with a normal water density around the hydroxyl group of Tyr-120, whereas the right panel is contoured at a low density to reveal the full extent of the binding pocket.

As discussed by a number of authors (35,36), analyses of the relative contributions of enthalpic and entropic components to recognition processes in solution are complicated by the fact that both ΔH and ΔS terms, as measured experimentally, are likely to feature large contributions from solvent-solvent enthalpy and entropy changes. However, it can be shown that statistically-mechanically, these solvent-solvent terms exactly cancel. Since other terms remain (37), the driving force therefore comes from solute-solvent contributions to ΔH and ΔS. The fact that the binding site is significantly dewetted is nevertheless an important feature. It means that for MUP+IBM, ligand binding is associated with negligible changes in protein-water terms, but significant changes in ligand-water and ligand-protein terms.

Analysis of ligand dynamics

Our simulations reveal a previously unobserved aspect of ligand binding to MUP: the pyrazine is not held rigidly in the cavity, but tumbles extensively. By monitoring the orientation of the pyrazine N1–N4 vector (Fig. 8; stereo color version Fig. S12), we can see a number of broad clusters in its distribution. Two of these correspond to orientations that permit H-bonding between either N1 or N4 and the Tyr-120 hydroxyl group (in the crystal structure the interaction is with N1), but clearly alternative orientations without such an H-bond also occur frequently. Monitoring the orientation of the orthogonal C2-C6 vector also reveals a great deal of motion, though certain orientations are apparently disallowed. The correlation time is 140 ns for the N1–N4 vector and 190 ns for the C2-C6 vector. This observation clearly has significant implications for the free energy of ligand binding. We can use the Schlitter method to estimate this from our simulation data (38). We performed a 1-μs simulation of the free ligand in a box of water, saving coordinates every nanosecond. After removing only translational motion, we calculate the configurational entropy (TΔS, without extrapolation) to be 70 kJ/mol. If we remove rotational motion as well, this drops to 35 kJ/mol. Repeating the calculations for the ligand in the binding site of the protein, we obtain values of 57 ± 1 kJ/mol when just translational motion is removed, and 34 ± 1 kJ/mol if tumbling is removed as well. Using the ideal gas approximation, the translational component is probably on the order of 10 kJ/mol. We predict, therefore, that binding of IBM to MUP actually results in almost no restriction of the internal motion of the side chains, a very modest loss in rotational freedom, and consequently an entropy penalty upon binding of only ∼−22 kJ/mol. In contrast, Bingham et al. (3), who did not consider the possibility of residual rotational freedom for the bound ligand, predicted IBM binding to be accompanied by an entropy penalty (TΔS) of −27 to −78 kJ/mol.

Figure 8.

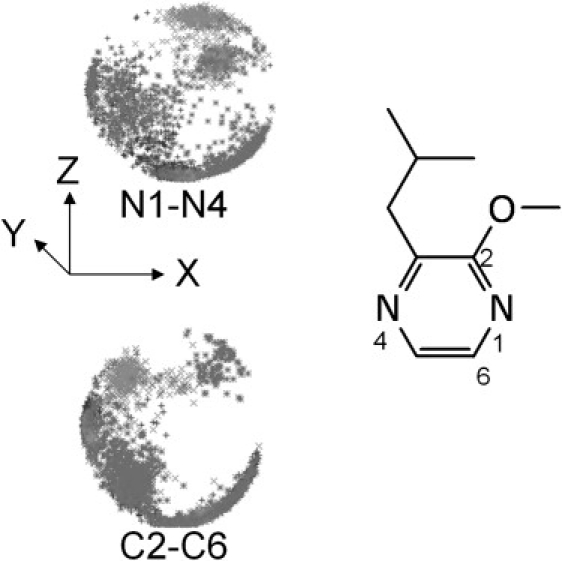
Polar plots to illustrate ligand tumbling. Top: orientation of the N1-N4 vector; bottom: orientation of the C2-C6 vector.

Conclusions

These simulations give rise to valuable new predictions about the dynamics of MUP in the multi-nanosecond regime, and provide valuable insights in general into the reliability and reproducibility of current molecular modeling methods on this timescale. Overall, the results are very encouraging: the simulations are stable and within the general parameters available from experimental data, over timescales that are orders of magnitude greater than those available at the time the original parameters were generated and validated. We see that even for a small, single-domain protein like MUP with a well-defined tertiary structure, elements of the structure may require >100 ns of dynamics simulation to ensure equilibration, and a microsecond is still not long enough to ensure very good sampling. It is possible that some of this slow equilibration is associated with periodicity artifacts introduced by the particle mesh Ewald method (39). However, the fact that this is not observed in all replicate simulations leads us to conclude that this is probably not a major issue. As has been pointed out by others (40), replicate simulations clearly have enormous value for checking sampling and reproducibility, but it is not easy to balance the trade-off between individual simulation times and the number of replicates. Considering the dynamical behavior of MUP revealed in this study, it seems likely that many of the conclusions we have reached through three replicate simulations of a microsecond would also have emerged from thirty replicate simulations of 100 ns; however, some important slow motions (e.g., loop motions and ligand tumbling) would not have been properly characterized. One could also argue that methods such as metadynamics could have been used to ensure better sampling and improved convergence. We chose not to employ such techniques in this study, primarily because our aim was to benchmark the behavior of unenhanced methods, and also because most such approaches require prior identification of the coordinates of interest that define the space one wishes to sample, and we did not want to assume this.

In general, this study supports conclusions drawn from shorter MD simulations on MUP and its ligand complexes, but provides a much more robust analysis of the statistical significance of certain features. The dewetting of the ligand-binding pocket is a robust observation, as are ligand-induced changes in two regions of the protein (loops L2 and L3). Subtle but reproducible networks of amino acid side-chain interactions are identified that couple ligand binding to either the locking down (L2) or release (L3) of surface loops. However, other dynamical changes that were previously thought to be significant may not be. The study also highlights the potential complexities of entropy-entropy compensation mechanisms. Not only do these mechanisms involve relocalization of dynamical hotspots from one region of the protein to another as a ligand binds, it appears they may also involve a more subtle transfer of entropy out of translational modes into librational ones. This is a particular issue as regards the thermodynamic interpretation of S² data generated in NMR experiments. Future work will include a more detailed investigation of how the current simulations relate to NMR observables.

Supporting Material

Representative PDB files for each system, force field parameters for MUP, and additional figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00421-2.