Mechanical Unfolding of Acylphosphatase Studied by Single-Molecule Force Spectroscopy and MD Simulations

Abstract

Single-molecule manipulation methods provide a powerful means to study protein transitions. Here we combined single-molecule force spectroscopy and steered molecular-dynamics simulations to study the mechanical properties and unfolding behavior of the small enzyme acylphosphatase (AcP). We find that mechanical unfolding of AcP occurs at relatively low forces in an all-or-none fashion and is decelerated in the presence of a ligand, as observed in solution measurements. The prominent energy barrier for the transition is separated from the native state by a distance that is unusually long for α/β proteins. Unfolding is initiated at the C-terminal strand (β_T) that lies at one edge of the β-sheet of AcP, followed by unraveling of the strand located at the other. The central strand of the sheet and the two helices in the protein unfold last. Ligand binding counteracts unfolding by stabilizing contacts between an arginine residue (Arg-23) and the catalytic loop, as well as with β_T of AcP, which renders the force-bearing units of the protein resistant to force. This stabilizing effect may also account for the decelerated unfolding of ligand-bound AcP in the absence of force.

Introduction

Understanding the determinants of the native structure of proteins and how this structure is gained or lost during folding and unfolding is a central objective in structural biology. During the past decade, the arsenal of techniques available for studying these issues has been complemented by the use of the atomic force microscope (AFM) and optical tweezers to induce and record the unfolding of single protein molecules through the application of a stretching force, as well as to follow their folding characteristics, in the presence or absence of force (1–8). In comparison with traditional bulk assays of protein folding/unfolding, such pulling experiments have several distinguishing attributes: 1), they provide a direct measure of the molecules' mechanical stability with sufficient sensitivity to detect purely entropic-driven forces; 2), they act solely on the molecules of interest, leaving the environment unaffected; and 3), they are performed at the single-molecule level, and thus provide information that is often masked by ensemble averaging. Furthermore, in contrast to chemical- or thermal-induced denaturation, where the reaction coordinate is generally unknown, the application of mechanical force sets a relatively well-defined reaction coordinate (i.e., the end-to-end distance of the polymer chain). This simplifies data interpretation and allows for direct comparison with results obtained from molecular-dynamics (MD) pulling simulations (steered MD (SMD)) (9,10), enabling the acquisition of a detailed, sometimes atomistic, description of the process investigated.

Small monomeric proteins are difficult to study by force spectroscopy because of spurious interactions between the AFM tip and the substrate-sample surface, and the random nature of the interaction between the AFM tip and the molecules. Earlier studies therefore concentrated on proteins or segments derived from proteins that naturally occur as tandem arrays of globular modules, such as titin (11), tenascin (12), spectrin (13), and fibronectin (14). Such proteins frequently operate under tensile stress, and thus have evolved to withstand mechanical deformations. Because naturally occurring modular proteins usually contain a heterogeneous set of domains that vary in structure and stability, it is generally not possible to assign observable events to individual modules. In addition, the exact three-dimensional structure of the domains present in these proteins is often unknown and mutants are not readily available. The introduction of recombinant (15,16) or chemically linked (17–19) polyproteins (polymeric protein constructs composed of repeated domains derived from, in principle, any protein) extended such studies to individual protein modules and to proteins that have not been selected to resist mechanical forces (although not discussed here, pulling experiments can also be performed on membrane proteins (4)). The availability of polymeric constructs consisting of well-characterized protein domains has enabled the use of mutants and SMD simulations, and has facilitated comparisons between mechanical- and chemical-/thermal-induced unfolding. The results obtained from these experiments and simulations have provided important information about the mechanical stability of proteins and its relation to protein structure and function. They have also provided valuable insights into protein unfolding/refolding dynamics, as well as features of the free-energy landscapes that underlie forced unfolding, and, in some cases, the pathways explored during this process.

Acylphosphatase (AcP; E.C. 3.6.1.7) is a small (∼100 aa) basic protein that catalyzes hydrolysis of the carboxyl-phosphate bond present in a diverse set of biological and synthetic compounds (20). In vertebrates, it is found as two isoforms, known as muscle- (mAcP) and common-type AcP (ctAcP), that share a >50% sequence homology. In both forms, as well as in all other orthologs thus far characterized (including bacterial and archaeal), its structure consists of two parallel α-helices packed against a five-stranded antiparallel β-sheet that follows a 4-1-3-2-5(β_T) strand topology (Fig. 1) (21–28). The small size of AcP, its simple (though rather uncommon) topology, and the fact that it lacks intramolecular disulfide bridges (with the exception of some bacterial homologs) or prosthetic groups make it an attractive candidate for structural and kinetic analyses. Indeed, mAcP and ctAcP and, to a lesser extent, their invertebrate, bacterial, and archaeal homologs, have been the subject of many such analyses, and their folding and unfolding dynamics are extremely well characterized (23,26,29–32). The structure of their transition state ensembles has likewise been thoroughly investigated, both experimentally (31,33–35) and by coarse-grained Monte Carlo sampling (36) and all-atom MD simulations (37), with experimentally determined φ-values used as restraints. The two isoenzymes fold with a two-state kinetics (excluding a cis-trans prolyl isomerization phase) under a wide range of conditions, but typically this occurs unusually slowly. In fact, the human muscular form of AcP (hmAcP) is the slowest autonomous two-state folder known, completing its folding in ∼4 s (32). Notably, under certain destabilizing conditions, hmAcP aggregates and subsequently forms amyloid fibrils similar to those found in protein deposition diseases (38–42). The catalytic activity of AcP has also been studied fairly broadly and is relatively well understood (20,27).

Figure 1.

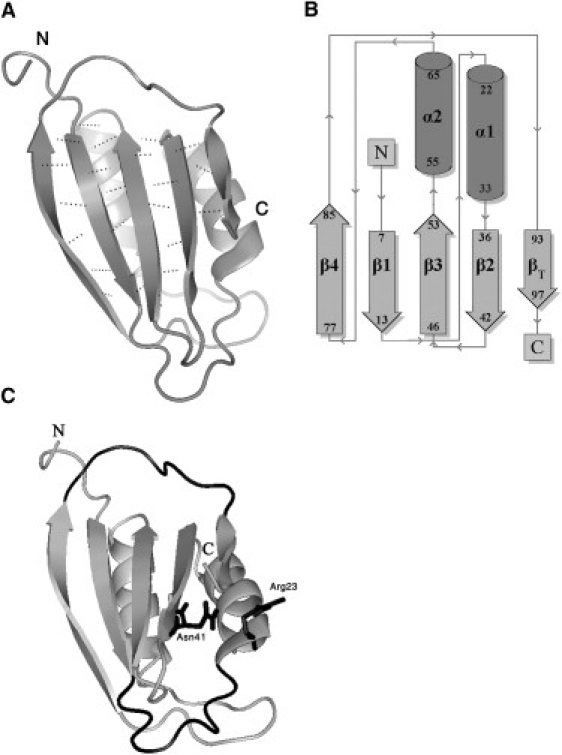
Structure of AcP. (A) Solution structure of horse muscle AcP (PDB code: 1APS (21)). Secondary structures (defined according to DSSP) are represented as ribbons, and backbone hydrogen bonds in the β-sheet are shown as dashed lines. The force-bearing units are the N- and C-terminal strands. (B) Topology diagram. AcP adopts a rather uncommon α/β sandwich fold elaborated by two intercalating βαβ units forming an antiparallel β-sheet with a 4-1-3-2-5(β_T) strand topology. (C) Structural determinants for forced unfolding of AcP. The long loop that follows the N-terminal, force-bearing strand, and the loop that precedes the C-terminal one (β_T) are shown in black (bottom and top, respectively). The former, referred to as the catalytic loop, adopts a cradle-like conformation and constitutes the active site of the enzyme. Also shown are the conserved Arg-23 and Asn-41 residues, which flank the cradle and function in binding the substrate phosphate group and the catalytic water molecule, respectively.

In this work, we combined single-molecule force spectroscopy with Go-type and all-atom SMD simulations to study the mechanical unfolding of the well-characterized form of AcP, hmAcP. The results obtained from the experiments and simulations provide detailed information about the unfolding of AcP under applied force, and the countering of this process by ligand binding. They are also used to address general issues pertaining to the correlation between the mechanical resistance of proteins and secondary structure content and topology, and how well the results obtained from pulling experiments of polyproteins compare with those derived from traditional solution assays of isolated modules.

Materials and Methods

The materials and methods used in this work are described in the Supporting Material.

Results and Discussion

Concatenation of AcP does not lead to changes in structure or activity

To study the mechanical unfolding of AcP, we constructed a polyprotein, [AcP]₄ (Fig. S1 in the Supporting Material), by concatenating the gene encoding for the C21S variant of human muscle AcP (32). This variant is commonly used in studies of hmAcP to eliminate complexities associated with the presence of a free cysteine residue, and is referred to as AcP throughout the text. As observed by others (43), expression of the polymeric construct proved to be difficult. Following various attempts, reasonable amounts could only be obtained by the use of a minimal growth medium before the induction of gene expression. This prevented residual expression of the polyprotein, which is likely toxic to the cells (see Supporting Material).

We then tested whether the modules present in the concatameric construct could preserve the structure and activity of the isolated protein, as these may be altered by interdomain interactions or by constraints imposed by the linkers that separate the modules in the polyprotein. To determine whether the modules constituting [AcP]₄ retained the structure of the native protein, we subjected the innate and oligomeric forms of AcP to far-ultraviolet (UV) circular dichroism (CD) analysis (Fig. 2 A). These and all subsequent measurements described in this work were performed in 50 mM acetate buffer, pH 5.5, which is optimal for AcP activity and is conventionally used in thermodynamic and kinetic analyses of this protein. Isolated AcP exhibited a CD spectrum characterized by a broad, flat trough between 240 and 210 nm, and a positive band centering at 198 nm, primarily reflecting the weighted contributions of its two major secondary structural motifs (∼20% helices and ∼40% β-strands). The spectrum of [AcP]₄ was superimposed on that of the isolated protein over most of the wavelength range, deviating only in the positive CD band, where the amplitude, but not the shape or position of the band, was higher. This increase in amplitude most likely reflects contributions arising from the additional residues present in the three linker regions that separate the individual domains in the polymeric construct.

Figure 2.

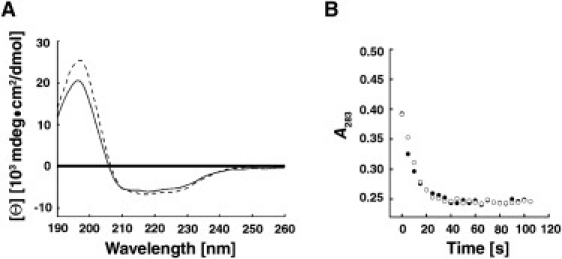
Properties of poly-AcP. Individual modules in the polymeric construct preserve the structure and catalytic activity of the innate, isolated protein at room temperature (25°C), as demonstrated by comparing their far-UV CD spectrum (A, dashed line) and ability to hydrolyze the AcP substrate benzoyl phosphate (B, open circles) to those of monomeric AcP (solid line and solid circles, respectively).

Next, we sought to determine whether the individual domains in the polymer preserved the catalytic activity of the innate protein. This was done by following the change in absorbance of 283-nm light during hydrolysis of benzoyl phosphate (44), an AcP substrate. As shown in Fig. 2 B, the rates of hydrolysis of the substrate by the monomeric and oligomeric forms of the enzyme (used in equal monomer concentrations) were practically identical.

AcP has a relatively low resistance to mechanical force

In addition to the inherent mechanical properties of the molecule under investigation, the measured unfolding forces in force spectroscopy experiments depend on a number of factors. These include the pulling speed, the pulling geometry (the relation between the force vector and breakpoint topology), the number of domains in the polyprotein, and the length and composition of the intervening linkers. Nevertheless, data obtained from different proteins and protein domains, as well as results derived from SMD simulations, enable one to draw some general conclusions about the relationship between protein structure and resistance to applied forces (2,3,5,6,18,45–50). It appears that, for proteins extended by their termini, there exists a hierarchy of resistance to mechanical deformations that is determined predominantly (but not by any means exclusively (51–53)) by the content and pattern of the hydrogen-bond arrays present in the force-bearing regions of the protein. The most resistant are β-sheet-containing proteins in which the terminal strands are parallel, backbone hydrogen-bonded, and oriented orthogonally to the applied force (forming a so-called shear topology), as seen in titin I27 (11), FNIII (14), ubiquitin (54,55), GB1 (56), and protein L (see Table 1 in Brockwell et al. (45)). Also highly stable are β-sheet configurations in which the force-bearing strands are flanked in space by neighboring strands, as exhibited by the designed protein Top7 (48), and which are also present in the aforementioned mechanically stable proteins. In most of these proteins, the flanking strands are connected to the force-bearing strands through β-hairpins, further enhancing their mechanical stability. At the other end of the spectrum lie unstructured and β-spiral proteins (e.g., elastin (57)) and, moderately more stable, all α-helical proteins in which hydrogen bonding is confined to within individual secondary structures. Stability is therefore dominated by hydrophobic contacts between helices, offering lower resistance to mechanical deformations. Proteins that possess other topologies usually exhibit a degree of mechanical stability that lies in between those of the above two classes. As can be seen in Fig. 1, the N- and C-terminal β-strands of AcP, which constitute its force-bearing units, are not hydrogen-bonded to each other, nor are they stabilized by hairpin loops, which are mostly lacking in AcP due to its βαββαβ topology. In addition, one of these strands, the C-terminal strand (β_T), is very short and is connected to the β-sheet core through a few hydrogen bonds (Fig. 1). AcP is therefore expected to have only a moderate resistance to tensile forces.

To test this prediction, we mechanically unfolded [AcP]₄ over a broad range of extension rates, which varied from ∼30 to 10,000 nm/s. Stretching of the polymer gave rise to a characteristic sawtooth pattern (Fig. 3 A) that exhibited more or less regularly spaced force peaks of varying amplitudes. The rising part of the peaks, which corresponds to the entropic elasticity of the unfolded protein domains, fitted well to a worm-like chain model of polymer elasticity, using a persistence length of 0.36 nm. The increment in contour length upon domain unraveling obtained from the fits (which predict this parameter at infinite force) was 33 ± 2 nm (Fig. 3 A, inset). This value is practically identical to that predicted for a fully extended AcP module, and expectedly larger than the observed distances between adjacent peaks in the force-extension curves (30 ± 2), indicating that unfolding occurs before the polypeptide chain is fully stretched. The distributions of the most probable unfolding forces recorded at different pulling speeds are shown in Fig. 3 B. As can be seen, the unfolding force is parameterized by the rate of extension, being shifted to higher values as the latter increases. Such a shift is expected when the loading rate (df/dt) exceeds the characteristic (spontaneous) timescale of the transition (58), which is clearly the case for AcP. Analysis of the force-extension curves and the distributions of the unfolding forces, as well as the observed increments in contour length, indicate that, as observed in solution measurements, AcP unfolds mechanically in an essentially two-state manner with no apparent unfolding intermediates. This conclusion is further supported by the results we obtained from the Go-model simulations (see below).

Figure 3.

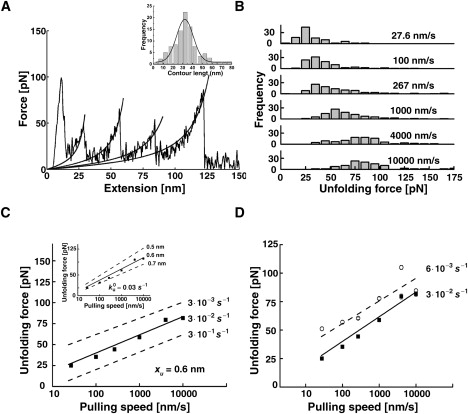
Forced unfolding of poly-AcP. (A) A typical force-extension curve obtained by stretching individual AcP polymers at 100 nm/s. The high force peak seen at the beginning of the extension profile reflects nonspecific interactions between the AFM tip and the mounting surface. The solid lines superimposed on the rising parts of the peaks are fits to a worm-like-chain model. (A, inset) Contour length increments upon domain unraveling obtained from the fitting (v_c = 267 nm/s). (B) Frequency histograms of unfolding forces recorded at different pulling speeds. (C) Dependence of the most probable force for unfolding, taken as the maximum of the unfolding force distributions, on the pulling speed. The best fit to the data from the Monte Carlo simulations (solid lines in the main figure and inset) was obtained using $k_u^0$ = 0.03 s⁻¹ (main figure) and x_u = 0.6 nm (inset). It was previously shown that very high pulling speeds could be associated with distance-dependent drag forces, which may lead to underestimation of the unfolding force at such speeds (67,68). Our analysis reveals that the deviation expected, even for the highest pulling speed used in the experiments described in this work, lies within the thermal noise error. (D) Force spectra obtained for poly-AcP in the absence (solid rectangles, solid line) or presence (open circles, dashed line) of 10 mM P_i. The presence of the ligand stabilizes the native structure of the protein, leading to deceleration of the unfolding reaction. However, the position of the transition state ensemble along the force-set unfolding pathways is not affected by the ligand, as evidenced by the fact that the slope of the force spectrum is unaltered. Albeit not seen in all data points shown, SE bars are included (each data point represents the average of ∼70–250 data points cumulatively acquired in two to three independent experiments).

Consistent with its structural characteristics, AcP unfolds at forces that are significantly smaller (by up to sixfold) than those recorded for mechanically stable proteins or protein domains pulled at similar speeds. Compared with other α/β and all-β proteins that lack force-resistant topologies, AcP exhibits an average mechanical stability. An example of one such protein is the small ribonuclease barnase, which like AcP has an antiparallel, five-stranded β-sheet core. When pulled at 300 nm/s, barnase unfolds at a force of 70 pN (43), compared to the ∼50 pN that is required to unravel individual modules in [AcP]₄ when pulled at a similar speed (267 nm/s). An α/β protein that has a mechanical stability lower than that of AcP is barnase's natural inhibitor, barstar. Compared to barnase and AcP, barstar possesses a smaller β-sheet comprising only three strands. Moreover, the strands exposed directly to the force are located at the edges of the sheet and therefore are connected to it only on one side. As a result, barstar exhibits very poor mechanical stability, unfolding at forces close to or lower than the detection limit of the AFM (∼10 pN) even when pulled at 400 nm/s (48), a rate at which AcP is found to yield to four- to fivefold higher forces. Another relevant example is the first domain of synaptotagmin, C2A, which has a β-sandwich structure consisting of eight antiparallel strands. The terminal strands of this all-β domain are directly hydrogen-bonded, but the bonds are oriented in parallel rather than perpendicular to the direction of the force, allowing for sequential breakage (unzipping) of the bonds (as opposed to shear topologies, where bonds are loaded in parallel). This mechanically feeble topology is partially compensated for by the fact that one of the force-bearing β-strands is stabilized at its outer side by interactions with a neighboring strand (48). Notably, one of the force-bearing strands of AcP, the N-terminal strand, is likewise flanked, at both sides, by neighboring strands to which it is connected by multiple hydrogen bonds (Fig. 1). As a result of this stabilizing effect, both C2A and AcP exhibit a reasonable (and similar) mechanical stability, unfolding at ∼60 pN when pulled at 600 nm/s (2) (Fig. 3 C), although they lack any other topological stabilizing motif in their force-bearing regions. To put this “reasonable” mechanical stability in context, however, we note that the mostly α-helical protein T4 lysozyme (19,59), which derives its stability predominantly from interhelical hydrophobic interactions, unfolds at forces very similar to those needed to unravel AcP.

The unfolding rate of AcP under force does not correlate with its unfolding rate in solution

The mechanical stability of proteins is a kinetic rather than a thermodynamic property. The relevant parameter (if any) for comparing results obtained from single-molecule pulling experiments with those obtained from bulk solution measurements is therefore their thermal unfolding rate. hmAcP unfolds in solution rather slowly, with a rate constant of ∼1 × 10⁻⁴ s⁻¹ (30,32,33). However, the spontaneous (zero force) unfolding rate extracted from the Monte Carlo simulations for the forced unfolding of AcP (Fig. 3 C) was 3 × 10⁻² s⁻¹, more than two orders of magnitude higher. Faster unfolding rates under applied mechanical force were noted previously for other proteins, including barnase (43), ubiquitin (54), and protein L (45). Although the error associated with the estimate of unfolding at zero force could be significant, it is highly unlikely to account for the very large differences in unfolding rates observed for all of these proteins. One possibility is that there exists an outer energy barrier that rate-limits the transition at zero force but is suppressed throughout the range of loading rates used in the pulling experiments. The experimentally accessible dynamics is thus dominated by inner barriers (58,60,61), giving rise to a faulty rate constant for the unloaded protein. However, given that such a barrier is also not seen in solution unfolding or in the MD simulations we performed (see below), we find this possibility unlikely. Another possibility is that the strict exponential decrease of unfolding time with applied force, which is assumed for pulling rates used in the AFM experiments (where unraveling occurs on timescales much longer than those needed for diffusive relaxation), is invalid. Deviation from this Bell-Evans-type behavior is expected if the energy barrier for the transition is not sharp and, hence, not stationary with force. This may result in a more moderate dependence of the unfolding rate on the force at low extension rates (62), giving rise to a slower rate of unfolding when extrapolated to zero force. Finally, the discrepancy may reflect genuine dissimilarities in unfolding pathways under the two sets of conditions.

The barrier for mechanical unfolding of AcP is located 0.6 nm away from the folded state

An important characteristic that can be derived from the force-velocity curves (also called force spectra), such as those shown in Fig. 3, C and D, is the distance between the folded and the transition state along the reaction coordinate set by the force (58,60,63). For AcP, the values we obtained for this parameter, denoted x_u, from the fit of the Monte Carlo simulations to the experimental data and from the Go-model simulations (performed at relatively low pulling rates; see below) were 0.6 and 0.65 nm.

Recently, Li (47) analyzed the correlation between x_u and protein secondary structure and topology for a large set of proteins, using both experimental data and results obtained from pulling simulations employing off-lattice Go-like models. The analysis revealed that all-β or α/β proteins have x_u-values that range from 0.2 to 0.5 nm (barnase, for example, has an x_u-value of 0.33 nm), whereas the more-compliant all-α proteins have larger values, between 0.7 and 1.5 nm. The values we derived in this work for AcP fall in between those derived for the two groups. The aforementioned analysis also revealed that x_u scales linearly with the helix content of the protein. Using the linear regressions derived by Li (47) for the experimental (R = 0.91) or simulated (R = 0.94) data sets, we obtained values for AcP of 0.39 and 0.37 nm, respectively, well below the value we derived from our data. We believe that the significant deviation of x_u of AcP from the expected dependence on helical content, which also accounts for the segregation of this protein from other α/β proteins, is due to the long loop (7 aa) that connects the short C-terminal β-strand (β_T) to strand 4, which is located at the other side of the β-sheet (Fig. 1 C). We propose that this long loop, which is poorly mechanically connected to other structural elements in the protein, substitutes helical structures in the sense that it offers a high compliance to the force and thus attenuates its loading onto strand 4 and, hence, to the β-sheet core of AcP. Indeed, if the amino acids within this loop and within β_T are considered proxy α-helical regions, the corresponding x_u-values generated by the aforementioned linear fits become very close to the 0.6–0.65 nm value we derived from the measurements and Go-model simulations. It thus appears that x_u is determined primarily by structural elements that are the least resistant to mechanical deformation, such as α-helices and loop regions, or poorly connected strands, which likely yield to the applied force first. Next, the major resistors (i.e., significantly hydrogen-bonded β-strands and hairpin loops) submit, leading to unfolding of the protein. This is consistent with the fact that, as opposed to the excellent correlation found in the analysis described above between x_u and helical content, only poor correlations were found between the former and the β-content of proteins in the data set.

Ligand binding to AcP attenuates its forced unfolding to a similar extent as measured in bulk assays

Binding of inorganic phosphate is known to stabilize the native state of AcP. This stabilization results from an attenuated unfolding process; the rate of folding is unaffected by the presence of the anion (33).

Fig. 3 D shows the force spectrum obtained for poly-AcP in the presence of 10 mM phosphate, together with a spectrum obtained in the absence of the anion. As can be seen, the presence of phosphate increased the measured unfolding forces by a more-or-less constant value throughout the entire range of pulling speeds, resulting in a force spectrum that is shifted up relative to that obtained in the absence of the ligand. Because the slope of the force spectrum relates to the position of the transition state along the direction of the force (see inset of Fig. 3 C), this means that the binding of phosphate does not affect this characteristic of the protein. This, in turn, suggests that the bound anion does not change the surface area exposure of the transition state as compared to that of the ligand-free protein. The latter notion is in agreement with results obtained from solution assays, which indicate no significant changes in denaturant folding/unfolding m-values (which report on differences in hydrophobic surface accessible to the solvent between the end states and the transition state) in the presence of phosphate (33). The fit of the simulations to the data yields an apparent unfolding rate that is five times lower than that derived in the absence of phosphate. This is very close to the previously reported 5.8-fold decrease in unfolding rate measured in solution in the presence of 2 mM phosphate dissolved in the same buffer as that used in our studies (33). Thus, the binding of phosphate stabilizes the folded state of AcP relative to the transition state to the same extent whether it is isolated or oligomerized, and regardless of the way unfolding is triggered (i.e., by denaturant or by mechanical force).

Model for forced unfolding of AcP

To gain insight into the sequence of the events associated with the mechanical unfolding of AcP, we performed C_α-Go-type and all-atom SMD simulations. As a model, we used the solution structure of horse muscle AcP (Fig. 1). This protein differs from the human ortholog we used in the experiments in five amino acids.

Go model

Go-model simulations were performed in the overdamped limit (see Supporting Material). This allowed us to study unfolding even at relatively low pulling speeds, with the lowest one being only 2.6 times higher than the maximal speed used in the experiments. Force-extension profiles obtained at (relatively) low pulling speeds revealed a single, stable peak (Fig. 4 A), indicating that, in accordance with the experimental results, mechanical unfolding of AcP proceeds without intermediates in this regime. The x_u-value derived from the corresponding force spectrum (Fig. 4 B) was 0.65 nm, in good agreement with the experimentally determined value (0.6 nm). Plotting the unfolding forces obtained from simulations performed at high pulling speeds yielded another linear regime that has a crossover point with the first at v_c ∼3 × 10⁵ nm/s (Fig. 4 B). Further analysis of trajectories obtained at v_c = 7.3 × 10⁶ nm/s revealed the presence of a second peak in ∼55% of the traces (from a total of 45), indicating that unfolding becomes weakly three-state at these high pulling speeds. This additional peak corresponds to the second, high-force regime in the force spectrum (with the implication that the latter is not the result of a loading-rate-dependent movement of the major energy barrier (first peak) along the reaction coordinate).

Figure 4.

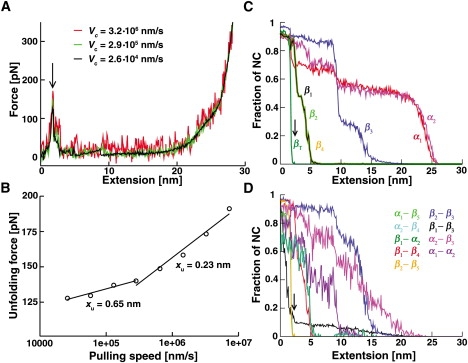
Summary of the results obtained from the Go-model simulations. (A) Representative force-extension profiles. The presence of a single, stable peak in the profiles implies a two-state unfolding process. As expected and as observed experimentally, the height of the peak increases with the pulling speed. (B) Force spectrum derived from simulations conducted at pulling speeds ranging between 2.6 × 10⁴ and 7.3 × 10⁶ nm/s. As discussed in the text, the linear regime observed at pulling speeds higher than ∼3 × 10⁵ nm/s corresponds to the emergence of an additional energy barrier at these high pulling rates. (C and D) Dependence of NCs present in secondary structures of AcP (C) and between nine pair combinations of them (D) on extension (v_c = 2.6 × 10⁴ nm/s). The arrow denotes the position of the peak observed in the force-extension traces.

Fig. 4, C and D, show the dependence of the fraction of native contacts (NCs) present in secondary structures of AcP, as well as between nine pairs of these structures, as a function of extension of the protein. As can be seen, unfolding commences by unraveling of the C-terminal β-strand, β_T, which quickly loses its NCs upon extension. This is swiftly followed by the simultaneous and likewise cooperative unfolding of strands β₁, β₂, and β₄. The remaining strand of the sheet, β₃, survives longer and exhibits a biphasic transition, reflecting loss of contacts with β₁ and β₂. The two helices present in AcP unfold last, in a stepwise manner.

All-atom model

Four trajectories were generated in the all-atom simulations, which were carried out at a pulling speed of 10⁹ nm/s. Here, the process of unfolding was followed by monitoring the number of hydrogen bonds present in secondary structures. The force-extension profiles obtained in the four runs revealed three peaks, the first of which is located at ΔR ≈ 2.5 nm, not far from the position of the peak observed in the profiles generated by the Go-model simulations performed at low pulling speeds (ΔR ≈ 1.8 nm). The other two peaks are likely to be the consequence of the high extension speed employed in the all-atom simulations, in similarity to the one observed in the trajectories of the Go model simulations conducted at high pulling rates. As can be seen in Figs. 5 and 6, unfolding is initiated at β_T after breakage of its hydrogen bonds with β₂. The rest of the protein then unfolds in the following manner: β₄ → (β₁, α₂) → (β₂, β₃, α₁).

Figure 5.

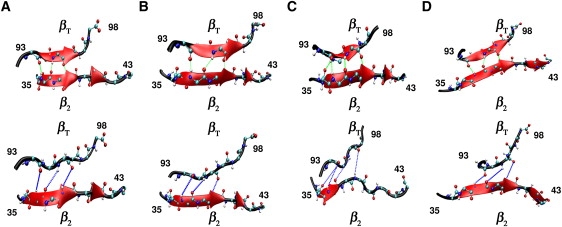
Breakage of hydrogen bonds between β_T and β₂ at the commencement of unfolding, as revealed by snapshots taken from trajectories obtained from four runs (A–D)of SMD simulations using an all-atom model of AcP (v_c = 10⁹ nm/s). The upper and lower panels correspond respectively to structures obtained just before and after the first peak in the corresponding force-extension profiles.

Figure 6.

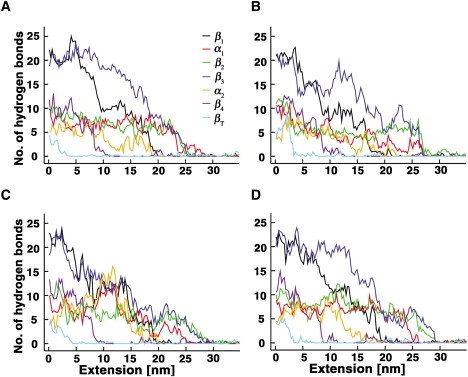
Fraction of hydrogen bonds in secondary structures of AcP as a function of extension, derived from the four runs (A–D) of the all-atom MD simulations.

Although the unfolding pathways predicted by the two methods are not identical, possibly reflecting differences in pulling speeds (64) or models (65), both indicate that unfolding of AcP is initiated at β_T, that β₄ unfolds soon afterward, and that β₃ (and, possibly, β₂) and the two helices persist until the late stages of unfolding. That β_T is the first element of AcP that yields to the force is not surprising, since, as mentioned before, this short, force-bearing strand is positioned at the edge of the β-sheet and is connected to it through a few hydrogen bonds with β₂ (Fig. 1 A). Located in this strand is Phe-94, one of a few residues that determine the folding transition-state architecture of AcP by promoting the establishment of a native-like interaction network (33,36,37). Unraveling of this strand is thus expected to perturb this network, facilitating disruption of the major hydrophobic core of AcP. The poor ability of β₄ to withstand force is likewise expected because, like β_T, it is also located at the edge of the sheet and therefore forms hydrogen bonds with only one strand (β₁). It is also connected, through a loop, to β_T and thus is subjected directly to the force once β_T unravels. Unfolding of β₄, in turn, should destabilize the other force-bearing unit of AcP, β₁, with which it interacts through hydrogen bonds. As discussed above, the transmission of the force from β_T to β₄ is likely to be damped by the long loop that connects them, leading to an unexpectedly large x_u-value. In contrast to β_T and β₄, β₃ lies at the center of the sheet and is hydrogen-bonded to both strands 1 and 2. The mechanical stability of β₃ likely is further increased by the hairpin loop that connects it to β₂ and by the two contacts it makes with Lys-57 and Val-58 in α₂, which, as mentioned above, are maintained through most of the unfolding process (Fig. 4 D). These contacts also contribute to the preservation of α₂ until the very late stages of unfolding. We believe, however, that the strong persistence of this helix, as well as α₁, is mostly a manifestation of the fact that the two helices are topologically segregated from the rest of the protein and therefore are relatively autonomous. This interpretation is consistent with results obtained from MD simulations, which showed that formation of α₁ and α₂ during folding of AcP is distinct from the process of nucleation (37), even though their stabilization can affect both folding and unfolding rates (34,39).

As for the effect produced by phosphate binding on the unfolding rate of AcP, we suggest that it is due to stabilization of the N- and C-terminal strands of AcP. In all AcPs, the phosphate group of the substrate binds to a conserved arginine residue (Arg-23 in hmAcP), which makes contacts with Val-96 in β_T of hmAcP (37), with Thr-100 and Tyr-101 in β_T of AcP of the archaeon Sulfolobus solfataricus (26), and with different residues located in β_T (or its equivalent regions) of all other AcPs whose structure is available (our own observation from an analysis using the contacts structural units program (66)). This residue is located at the N-terminal end of helix 1, adjacent to the C-terminal end of the catalytic loop (Fig. 1 C), which in turn is connected to the N-terminal strand β₁. Analyses of bovine (common-type) (22) and archaeal (27) AcPs crystallized in the presence of sulfate or formate revealed that the anion forms a salt bridge with the guanidinium group of Arg-23, as well as hydrogen bonds to backbone amides of this and several other residues in the catalytic loop. In addition, three structured water molecules, which likely accompany the anion, form hydrogen bonds with the anion and with backbone amide groups in several residues in the catalytic loop. They also form hydrogen bonds with the side chain of a conserved asparagine residue (Asn-41 in hmAcP; Fig. 1 C) located at the C-terminus of the second β-strand, which plays an essential role in catalysis (as it orients the catalytic water molecule that serves as the attacking nucleophile for hydrolysis of the carboxyl-phosphate bond (22)). The result is an extensive interaction network that strongly stabilizes Arg-23 and the catalytic loop. We propose that this stabilization renders β₁ and β_T, which are the force-bearing units of AcP, more resistant to force. Based on the good correspondence we observed in the extent of deceleration of unfolding by phosphate binding in pulling and chemical denaturation experiments, we further suggest that this stabilization also underlies the slower unfolding of phosphate-bound AcP in the absence of external force.

Supporting Material

Methods and one figure are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00435-2.