Using Betweenness Centrality to Identify Manifold Shortcuts

Abstract

High-dimensional data presents a challenge to tasks of pattern recognition and machine learning. Dimensionality reduction (DR) methods remove the unwanted variance and make these tasks tractable. Several nonlinear DR methods, such as the well known ISOMAP algorithm, rely on a neighborhood graph to compute geodesic distances between data points. These graphs can contain unwanted edges which connect disparate regions of one or more manifolds. This topological sensitivity is well known [1], [2], [3], yet handling high-dimensional, noisy data in the absence of a priori manifold knowledge, remains an open and difficult problem. This work introduces a divisive, edge-removal method based on graph betweenness centrality which can robustly identify manifold-shorting edges. The problem of graph construction in high dimension is discussed and the proposed algorithm is fit into the ISOMAP workflow. ROC analysis is performed and the performance is tested on synthetic and real datasets.

I. INTRODUCTION

Meaningful variance in high-dimensional datasets can often be parametrized by comparatively fewer degrees of freedom [4]. Dimensionality reduction (DR) methods transform high-dimensional data X = (x⃗₁, x⃗₂, …, x⃗_N), x⃗_i ∈ ℝ^d, into a Euclidean space of lower dimension, Ψ, ψ⃗_i ∈ ℝ^m, m < d. The data is assumed to inhabit a compact, smooth manifold, , in the Euclidean subspace.

Nonlinear DR methods have been shown to outperform linear techniques on datasets ranging from gene microarrays [5] to images [6]. Graph-based DR methods typically employ a k-nearest-neighbors(kNN) approach with a Euclidean distance metric. Though this work focuses on the kNN graph, the proposed algorithm is applicable provided some transformation is performed to take the inputs, X, from vector space to graph space. Formally, if X ∈ ℝ^d, |X| = N, ∃T such that T(X) ∈ A, where A is the set of N × N adjacency matrices.

The Isometric Mapping algorithm (ISOMAP) [7] relies on a neighborhood graph to construct a geodesic distance matrix. The structure of the geodesic matrix, and thus the ISOMAP embedding, is highly sensitive to the choice of neighbors [1], [2], [3]. Fig. 1 shows the result of improper neighbor choice on the ISOMAP output. Just one shortcut edge is sufficient to distort the geodesic distance matrix of a nonlinear dataset, causing a loss of the global structure of the manifold.

Fig. 1.

Shown here are 2-D embeddings of a 3-D spiral dataset. Manifold shortcuts distort the geodesic distance matrix will prevent ISOMAP from working. (a) 2 edges improperly connect far regions of the graph (b) Principle component analysis is linear and will not properly embed a nonlinear manifold in 2-D. (c) A proper 2-D Embedding is achieved using ISOMAP when the 2 shortcuts are removed. (d) With the shortcuts, ISOMAP embeds regions with a shortcut near each other; the global structure of the manifold is lost.

Prior efforts to address the shortcut problem fall into two classes. The first class attempts to identify and shortcuts from a given graph. Hein and Maier [2] proposed a graph-based diffusion process to denoise high-dimensional manifolds. Nilsson and Anderson [3] proposed a circuit model to estimate the proper geodesic matrix. Choi and Choi [8] proposed the use of a vertex betweenness threshold to identify manifold shortcuts. The second class of methods comprise novel methods of graph construction; they attempt to prevent shortcuts during the graph formation process. For example, Carreira-Perpinan and Zemel [9] introduced a method based on the minimal spanning tree to create graphs robust to noise.

The betweenness measure of [8] has the advantage that it is conceptually simple and requires minimal additional computational effort. In this paper, we propose a betweenness-based shortcut elimination method based on a divisive clustering algorithm introduced by Newman and Girvan [10]. The contribution of this work is the adaptation of the algorithm to shortcut finding and integration into the DR workflow. Additionally, we propose a robust stopping criterion and show that the method can reduce the ISOMAP embedding error in real data.

The paper is organized as follows. Section II discusses the process of graph construction in high dimensional spaces. In Section III, we introduce concept of betweenness and show its specific limitations within the shortcut finding process. Section IV describes the proposed algorithm and the performance results are given in Section V. The datasets mentioned throughout the paper are described in Table IV in the appendix.

II. THE kNN GRAPH IN HIGH DIMENSION

The construction of a graph from data has received new attention with the advent of graph-based DR and clustering algorithms. In the context of manifold learning, a proper graph should have the following qualitative properties:

1. The graph is highly connected within the manifold.

2. The graph leaves distinct manifolds unconnected.

3. The graph does not contain shortcut edges.

k nearest neighbors and the ε-ball are canonical methods to construct a graph. In the ε-ball method, one picks a fixed radius and connects all points within this radius. This approach is sensitive to local scale and causes poor graph connectivity in data with varying density [2]. Without loss of generality, we assume the graph is constructed using k nearest neighbors for the remainder of the paper.

Selection of k is a serious obstacle to graph construction. If k is chosen too large, the resulting graph is over-connected and pairwise geodesic distances are lost. If k is chosen too small, neighbors are disconnected and yield infinite geodesic path lengths. Furthermore, there exists a “discretization error” due to the fact that k is integer valued. A kNN graph has on the order of kN total edges. A unit increase in k thus adds approximately N edges to the graph (in an undirected graph, the number is typically < N since many of the edges are pairwise shared). Depending on the dataset, it is possible that the proper graph requires a number of edges between kN and (k + 1)N. That is, they will be poorly connected with k edges per node and contain shortcuts for k+1 edges per node. An example is shown in the synthetic Step dataset in Fig. 2.

Fig. 2.

Step dataset illustrating the “discretization error” of the kNN graph (edges are overlaid on the 3D data points). Neither k ≤ 6 or k ≥ 7 will give a satisfactory graph.

We now briefly discuss an aside on the unique properties of the kNN graph in high dimension, where ISOMAP is needed most. Sparsity in high dimensional spaces is a barrier to manifold learning, given that the data points must have sufficient density on the manifold¹. Careful attention is especially necessary when constructing a neighborhood graph. A rough measure of density can be obtained by enclosing the x⃗_i ∈ ℝ^d in a hyperrectangle. The density scales inversely with the range of each additional dimension,

$$\rho \equiv N/\text{Volume}=N/\prod _d{\mathit{range}}_d(x_i).$$ (1)

The exponential increase in hypervolume with increasing dimension is a well known piece of the “curse of dimensionality.” It can cause unfeasible sampling requirements and the troubling situation where all points are on or close to the convex hull [12]. A similar problem, which has been called the Theorem of Instability, was formalized by Beyer et al. [13]. Under a wide set of data conditions², the Euclidean distance from a point to its closest neighbor approaches the distance to its farthest neighbor, as dimension approaches infinity³. That is, for any ε > 0, the maximum and minimum interpoint distances are arbitrarily close with probability P = 1,

$$\underset{\mathit{dimension}\to \infty }{lim}P\left(\frac{d_{\mathit{max}}}{d_{\mathit{min}}}-1\le \epsilon \right)=1.$$ (2)

This presents a possible predicament to graph-based DR methods. One must define a neighborhood graph in order to reduce the dimension, but this graph depends on a meaningful distance matrix in ℝ^d.

To elucidate this effect, we define a scale-invariant, global parameter, Δ, which estimates how problematic the effect of Eqn. 2 will be on a dataset. For each data point, we compute the ratio of the distance to its closest and farthest neighbor. The ratios are then averaged over all data points,

$$\mathrm{\Delta }({\overrightarrow{x}}_i)=\frac{1}{N}\sum _i\frac{\underset{j\ne i}{min}\mid {\overrightarrow{x}}_i-{\overrightarrow{x}}_j\mid }{\underset{j\ne i}{max}\mid {\overrightarrow{x}}_i-{\overrightarrow{x}}_j\mid }.$$ (3)

Δ can range between zero and one. It quantifies, albeit crudely, the give-and-take between sample size, dimension, and data distribution. A small value indicates a healthy variance in pairwise distances. The larger the value of Δ, the higher the likelihood the ISOMAP embedding will be insensitive to random permutations of the graph edges. This is highly undesirable. Δ = 1 corresponds to the worst-case scenario, whereby all points are equidistant and any concept of nearest neighbors is meaningless.

It is not helpful to define an absolute cutoff point, but we suggest that a dataset with Δ > 0.5 warrants caution when constructing the neighborhood graph. When Δ = 0.5, each point has, on average, a factor of two difference in the distance between the closest and farthest point. Table I gives the value for several datasets in this paper, as well as datasets consisting of uniform, random noise in [0, 1].

TABLE I.

Delta values (Eqn. 3) for some datasets used in this paper.

Dataset	N	Dimension	Δ
Random	1000	2	0.01
Step	1000	3	0.03
Swiss Roll	1000	3	0.04
FACES	698	4096	0.15
Random	1000	10	0.26
Microarray	273	22283	0.34
MNIST, number 8	5851	784	0.37
Random	1000	100	0.69
Random	1000	1000	0.89

Eqn. 2 does not imply that a kNN graph is meaningless in high dimension. Instead, it suggests the Euclidean distance distribution be examined prior to constructing a graph on the inputs. It is trivial to compute Δ to see if the kNN graph is truly capturing neighborhood relationships. If Δ is large, one may benefit from feature selection, a different distance metric, or an alternate methods of graph construction. Otherwise, the resulting graph may not have the three properties listed in the beginning of this section and methods to find shortcuts are uncalled-for.

III. BETWEENNESS CENTRALITY AS A PREDICTOR OF MANIFOLD SHORTCUTS

We now define notation and formalize concepts used throughout this paper. Let G(V,E) be an undirected, un-weighted graph with a set of edges E = {ε_i}, set of vertices V = {v_i}, and adjacency matrix A,

$$A_{ij}=\{\begin{array}{ll}1\hfill & \text{if}\text{there}\text{is}\text{an}\text{edge}\text{between}i\text{and}j,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (4)

The adjacency matrix is symmetrical and defines an undirected, unweighted representation of the inputs. In practice, the number of neighbors, k, usually satisfies k ≪ N. The adjacency matrix is thus sparse and amenable to fast, polynomial-time manipulation [14].

A manifold metric, d_M(s, t), is defined on as the the length of the shortest arc between s and t. A shortcut is any edge, or set of edges, which connects two points with “large” d_M. The stringency for what is considered large depends on the application. A reasonable choice for uniformly distributed points is to define a shortcut as any edge which connects two points within some fraction of the maximum arc length. For example, if edge ε_i joins s and t,

$$\text{shortcut}({\epsilon }_i)=\{\begin{array}{ll}1\hfill & \text{if}{d}_M(s,t)>\frac{1}{4}\underset{i,j}{max}{d}_M(i,j),\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (5)

A shortcut vertex is any vertex connected to a shortcut edge. We refer to the set of shortcut edges and vertices as E_shortcut and V_shortcut, respectively.

The distance, d_G(s, t), between vertex s and t is the number of edges in the shortest geodesic path between s and t. The geodesic distance matrix, D, is the symmetrical matrix of all pairwise shortest paths, D_st = d_G(s, t).

Let σ_st be the number of shortest paths from s ∈ V to t ∈ V. σ_st(ε_i) is defined as the number of shortest paths from s to t that traverse edge ε_i. The betweenness centrality (which we will shorten to “betweenness”) of an edge is then,

$$b_E({\epsilon }_i)=\sum _{s\ne t\in V}\frac{{\sigma }_{st}({\epsilon }_i)}{{\sigma }_{st}}.$$ (6)

A similar feature is defined on the vertices, with σ_st(v_i) defined as the number of shortest paths from s to t that traverse vertex v_i,

$$b_V(v_i)=\sum _{\begin{array}{c}s,t\\ s\ne t\ne v_i\in V\end{array}}\frac{{\sigma }_{st}(v_i)}{{\sigma }_{st}}.$$ (7)

The eccentricity, ec(v_i), of a vertex is defined as the maximum graph distance to any other vertex in a graph. The eccentricity of an edge, ec(ε_i), is the average of the two vertices it connects. The average eccentricity of a graph is given by,

$${ec}_{\mathit{avg}}(G)={ec}_{\mathit{avg}}(A)=\frac{1}{N}\sum _{v_i\in V}ec(v_i).$$ (8)

Manifold shortcuts are rare compared to the total number of graph edges. If the number of shortcuts is on the order of number of normal edges, either the graph is improperly constructed or the signal-to-noise ratio is too small to overcome. We thus seek an algorithm which favors sensitivity over specificity. In other words, a robust method to identify shortcuts should minimize false negatives at the expense of false positives. Sensitivity is important because one manifold shortcut is sufficient to corrupt geodesic distances. Specificity is less important because the geodesic matrix should be robust to removal of a limited number of its normal edges.

Choi and Choi proposed the use of a vertex betweenness to identify manifold shortcuts [8]. The betweenness of each of the N nodes is computed and the distribution of these flows is then examined for outliers. A threshold is manually determined and nodes with a flow greater than the threshold are eliminated. ISOMAP is then performed on the remaining points.

One intuitively expects vertices with shortcuts to have a high betweenness. Shortcuts are implicated in a large number of shortest geodesic paths. Yet, there are several barriers to using a thresholded vertex betweenness to identify them. In the remainder of this section, we discuss these issues and illustrate them on synthetic datasets, for which the ground-truth manifold is known.

Receiver Operating Characteristic (ROC) curve analysis was performed to determine if vertex betweenness centrality is a suitable feature to identify shortcuts. Several synthetic manifolds were created and isotropic, additive noise was added. kNN graphs were constructed for each dataset by varying k over values where the graph has no shortcut edges to values where the graph is severely over connected. We then compute ROC curves by varying the threshold which determines the betweenness outliers. Representative curves are shown in Fig. 3.

Fig. 3.

Representative ROC curves for the Spiral, Sine, and Step dataset (N = 1000) when using a vertex betweenness centrality threshold. The colorbar shows the number of shortcut edges present in the dataset corresponding to each ROC curve. The performance is dataset-dependent and generally worse when the number of shortcut edges is small.

The ROC analysis illustrates three problems with imposing a threshold on the betweenness histogram. Firstly, 100% sensitivity is reached in a data-dependent way; the error in specificity is a function of dataset properties such as manifold geometry and sampling density. Secondly, the ROC curves are highly variable and have poor area under the curve (AUC) when the number of shortcuts is small. Lastly, the specificity is generally not high enough to ensure the graph remains connected. If too many normal nodes must be deleted to achieve high sensitivity, the graph will split into connected components and the entire dataset cannot be embedded as one manifold by ISOMAP.

The poor specificity achieved in the ROC analysis suggests a one-way relationship between shortcut vertices and the betweenness; while most shortcut vertices have high betweenness, it is not generally true that vertices of high betweenness are shortcuts.

IV. AN IMPROVED BETWEENNESS METHOD

Identifying few shortcuts among many edges is rare-class learning problem. This imbalance inhibits use of traditional classification methods to find the shortcuts. One expects the edges of a graph with |E_shortcut| ≪ kN to have “abnormally” high betweenness centrality. We now justify this claim by examining a subtle difference between the betweenness-centrality distributions of graph with and without shortcuts.

A Kolmogorov-Smirnov test is a standard nonparametric test to determine if two distributions are drawn from the same cumulative probability distribution. Unfortunately, statistical hypothesis testing has limited utility in this context. We are highly interested in a small number of outliers, which may have negligible influence on the test outcome. The test performance will also depend on the number and severity of shortcuts (i.e. how central the shortcut is).

Instead, we characterize the effect of shortcut removal by examining the quantiles of the betweenness distribution with shortcuts and the quantiles of the distribution without shortcuts. The qth quantile of the distribution is defined as the betweenness value where a q fraction of the data is below the value and (1−q) fraction of the data is above it. The quantiles allow for a nonparametric comparison of the distributions and give information about changes in location, scale and outliers.

For each dataset, a kNN graph was constructed and the betweenness histogram computed. The shortcuts are removed and the betweenness recomputed. This was repeated 100 times for each dataset and the change in betweenness was recorded.

Fig. 5 shows the average betweenness change as a function of each quantile for the swiss roll dataset. Similar curves were observed for the other synthetic datasets. Note the interesting behavior in the tail of the distribution. The higher quantiles (about 80–99%) are elevated in the distribution without shortcuts. This indicates that the betweenness histogram is shifting towards its tail as shortcuts are removed. However, there is a dramatic reversal in the most extreme quantiles (near 100%). The greatest quantiles in the distribution with shortcuts are highly elevated. This analysis tells us that, although most of the betweenness distribution remains unchanged, the highest quantiles are lowered when shortcuts are removed. Thus, the histograms in Fig. 4 look qualitatively similar, but have systematic differences in betweenness distributions; the shortcuts really are the edges of highest betweenness.

Fig. 5.

The average betweenness change as a function of each quantile for 100 swiss roll datasets. The vertical coordinate is computed as (betweenness without shortcuts) − (betweenness with shortcuts).

Fig. 4.

By itself, betweenness centrality is not a robust measure of vertices whose edges shortcut manifolds. Vertices with manifold shortcuts tend to be outliers in the histogram. The reverse relationship, in general, does not hold.

We now propose our edge-removal method for identifying manifold shortcuts. Instead of using the graph vertices, the method works on edges. The choice to use edges comes with increased computational costs, but, as shown in the results, is a much more specific approach. The trade-offs are summarized in Table II.

TABLE II.

Trade-offs between graph nodes and edges.

	Vertices, vi	Edges εi
Size	N	typically ≤ kN
Deletion	Removes all edges connected to the vertex	Removes only the edge of interest
Betweenness	A function of all connected edges	Defined on the edge of interest
Typical Rarity	= vshortcut/N < 1	~ εshortcut/kN ≪ 1

Consider a function, f(G), with the following definition,

$$f(G)=arg\underset{i}{max}\{b_E({\epsilon }_i)\}\mid G(E\backslash \{{\epsilon }_i\},V)\text{is}\text{connected}.$$ (9)

This returns the edge with the highest betweenness, subject to the constraint that removal of the edge will not cause the graph to become disconnected. The method we propose is based on a divisive clustering method proposed by Newman and Girvan [10]. We begin with a connected graph and remove the edge returned by f(G). The process is iterated, each time recomputing f(G), until a suitable stopping point is reached (described later in the section). The method is summarized in Alg. 1.

Algorithm 1.

Divisive Algorithm to Identify Shortcuts

Require: High-dimensional inputs, x⃗i ∈ ℝd.
1:	Construct a graph G(V,E) on the inputs
2:	while G is connected do
3:	Construct the geodesic distances
4:	Compute betweenness bE(εi) for all edges
5:	Remove the edge returned by f(G) (Eqn. 9)
6:	E ← E\f(G)
7:	end while
8:	return Estimated G(V,E′) without shortcuts

It is crucial to recompute the betweenness after edge deletion. As illustrated by Fig. 6, deletion of one manifold shortcut may redirect a large number of geodesic shortest paths through a different shortcut edge. This second shortcut edge may or may not have high betweenness prior to the deletion of the first. Without the iterative recomputation of edge betweenness, one misses shortcuts with moderate betweenness values in the original kNN graph. This is the primary reason a threshold of the initial betweenness distribution fails to uncover all shortcuts.

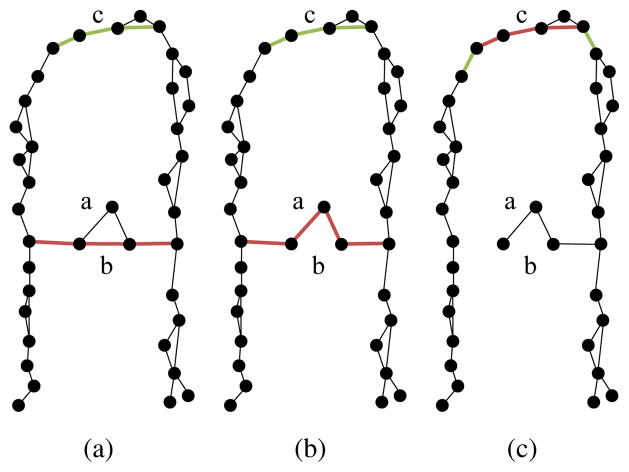
Fig. 6.

Betweenness centrality can significantly change after edge removal. (a) The graph in has high betweenness (indicated by red) in the shortcut edge b, low betweenness in edge a, and moderate betweenness (indicated by green) at the top of the manifold. (b) If edge b is removed, edge a suddenly acquires high betweenness. (c) The betweenness shifts dramatically when the manifold shortcut is broken. Further removal of the edge with highest betweenness, edge c, will split the graph into two connected components.

The connectivity constraint is imposed by f(G) in order to prevent the graph from disconnecting before all shortcuts are removed⁴. For example, if a local patch of the manifold is poorly sampled by the data, removal of an edge will transfer geodesic shortest paths to a nearby edge. Since the region is poorly sampled, there are few edges and removal of the edge with highest betweenness will quickly disconnect the graph. The ROC analysis (Sec. V) shows that this phenomenon is not frequently encountered in practice. That is, the algorithm typically finds all shortcuts before it imposes a connectivity constraint.

Alg. 1 involves computation of the geodesic distance matrix for each candidate shortcut edge. Although the geodesic matrix can be computed in O(kN² logN) using Floyd’s algorithm with Fibonacci heaps [15], it remains a computationally expensive step of the ISOMAP algorithm. With the geodesic matrix precomputed, it is worthwhile to run the second step of ISOMAP (classical Multi-Dimensional Scaling) and find the embedding. Thus, this algorithm is capable of identifying shortcuts but is no less computationally expensive than ISOMAP itself⁵.

A stopping criteria is now presented. Since the geodesic matrix is computed at each iteration, ISOMAP is run and the residual error computed using the cost function from [7]. One computes the fraction of variance in the geodesic distance matrix which is absent in the low-dimensional, Euclidean embedding:

$$\mathit{err}(A)=1-R^2(D_E(A),{\widehat{D}}_G(A)),$$ (10)

where R is the Pearson’s linear correlation coefficient operator, D̂_G(A) the estimated geodesic distance matrix computed on adjacency matrix A, and D_E(A) the Euclidean distance matrix in the low dimensional ISOMAP embedding. This is similar to the scree plot used in Eigenvector methods, where the independent variable is not necessarily the top eigenvalues.

It is noted that the residual variance calculated by Eqn. 10 is computed under the assumption the estimated geodesic distance matrix, D̂_G(A), is ground truth. As shown in Fig. 1, D̂_G(A) is an unreliable representation of true manifold distance when the neighborhood graph is improperly connected. In this case, the cost function will give optimistic error estimates. Since the ground truth is not known a priori, this drawback must be accepted.

We propose that two global changes will happen when shortcut edges are removed. Firstly, we expect a large relative increase in the average graph eccentricity, as defined in Eqn. 8, due to the sudden increase in path lengths (which are no longer short circuited). It is crucial that the eccentricity increase is not gradual; removal of a normal edge will cause a small increase in the mean eccentricity, whereas removal of a shortcut will cause a discontinuous jump. Secondly, we expect the residual error to decrease significantly, since ISOMAP better preserves pairwise distances. One chooses a cutoff point where these two changes happen concurrently.

The ISOMAP embedding must be validated in an independent manner, whether by testing a classifier, visual examination of the embedding, or some other data-dependent criteria. At minimum, the low dimensional embedding should be analyzed before and after the shortcut algorithm is run. If the embedding is better and the above conditions on the error and eccentricity are met, it is likely the graph contained shortcuts.

We conclude by showing an example of how the shortcut removal process fits into the DR workflow. Alg. 2 summarizes a “best practices” usage of the ISOMAP algorithm (or any geodesic-based DR algorithm).

Algorithm 2.

ISOMAP Usage for Manifold Embedding

Require: High-dimensional inputs, x⃗i ∈ ℝd
1:	Check Δ(x⃗i) (Eqn. 3) to ensure the kNN graph defines meaningful neighbors with respect to the chosen distance metric
2:	kmin ← minimum k such that G is connected
3:	kmax ← k such that G is over connected
4:	for k = kmin to kmax do
5:	Construct the kNN graph
6:	Run ISOMAP
7:	Compute err(A) (Eqn. 10)
8:	end for
9:	k ← arg min err(A)
10:	Run Alg. 1 on kNN graph
11:	Examine for the stopping condition
12:	return ISOMAP embedding

V. RESULTS

We begin by validating the method on synthetic data with a known ground truth. We then demonstrate its performance on several real-world datasets. On the real-world data, improvement is quantitatively demonstrated by an improvement in residual error (Eqn. 10) and qualitatively shown by examination of the low-dimensional embedding.

Fig. 7 shows the result of the algorithm on the a step dataset with 15 shortcut edges. The stopping condition is clearly indicated by a significant drop in residual error and a corresponding increase in average eccentricity. The geodesic distance matrix is restored to a state which closely approximates the internal manifold metric.

Fig. 7.

An example of the algorithm applied to the noisy Step dataset with N = 1000, k = 19, and 15 shortcut edges.

The ROC results (Fig. 8) on the four synthetic datasets shows near-ideal sensitivity and specificity. We do not compute the area under the curve because the algorithm terminates when it can no longer remove an edge and maintain graph connectivity⁶. Similarly, the ROC curves do not extend all the way to (1,1) because of this stopping condition.

Fig. 8.

The ROC performance of Alg. 1 on all four synthetic datasets. 187 trials are plotted with the number of shortcuts varying from 2 to 54. The colorbar shows the number of shortcuts in the dataset corresponding to each ROC curve. Since the curves are so close to the vertical, ROC analysis is not useful to see how the performance changes across datasets and varying numbers of shortcuts. The curves do not extend to (1,1) because the algorithm is terminated when no further edges can be removed without breaking connectivity.

It is possible that our method reaches its connectivity limit before achieving 100% sensitivity. This can happen when a shortcut does not have a high betweenness value (by construction, the spiral and sine datasets can possess these minor shortcuts). In Fig. 9, we report the mean sensitivity and specificity at the algorithm termination point as a function of the number of shortcuts. The best performance was achieved on the step and swiss roll datasets, which have shortcuts of approximately uniform length. In the sine and spiral datasets, the shortcuts vary in length and severity. Some of these edges do not have high betweenness, so it is expected the algorithm will not reach 100% sensitivity.

Fig. 9.

The mean sensitivity and specificity reached by the algorithm when no more edges can be removed. Red bars show the variance over the trials. The termination point is the point at which no more edges can be removed without disconnecting the graph.

The sensitivity performance has highest variance (indicated by red bars in Fig 9) when the number of shortcuts is small. This is because the sensitivity penalty for missing an edge is greater when there are fewer shortcuts. It may appear to be a limitation that the number of edges which can be removed according to Eqn. 9 is extremely small compared to the total number of edges in the graph. Fig. 9 shows that the algorithm is not particularly impeded by this limit. More importantly, removal of any significant percentage of edges from the graph will alter the global structure. It may not be worth removing 5% of the normal edges in a graph in order to find one shortcut; deleting too many of the proper edges may damage the global structure more than the shortcut.

We now demonstrate the performance on real-world datasets. The first dataset consists of 2000, 28 × 28 images of handwritten digits of the number 1. The intensity of each image pixel was placed into a vector of length 28*28 = 784. The kNN graph on the dataset was purposely over connected (k = 6) to encourage shortcuts. Fig. 10 shows the 2-D embedding of the images before and after our edge removal procedure. The embedding after the procedure shows better preservation of the dataset variance.

Fig. 10.

2000, 28×28 images of handwritten digits of the number 1 are embedded by ISOMAP in 2-D. (a) Before the application of Alg. 1. (b) After the procedure, the dataset variance is better represented in the low-dimensional space.

The algorithm was also tested on a gene microarray dataset with N = 273 in 22,283 dimensions (Fig. 11). Since the ground truth is unknown, we follow the ISOMAP process described in Alg. 2 and rely on the residual error to show it works. Our algorithm was able to decrease the residual error of the ISOMAP embedding from 0.2 to 0.07. The stopping criterion was clear and the resulting embedding shows class structure.

Fig. 11.

Application of the algorithm to a real colon cancer gene microarray dataset with N = 273 in 22,283 dimensions. Three classes are shown to visualize the embedding quality. Blue points are biopsies of primary colon cancer tissue, green points are polyp tissue, and red points normal colon tissue. The shortcut removal algorithm was able to reduce residual error by over a half.

VI. CONCLUSION

The expenditure to obtain and curate modern datasets is often large compared to the costs of computation. It is thus preferable to extract as much as possible from the data at the expense of increased computation. Shortcut removal restores pairwise geodesic distances to magnitudes that closely approximate the (data-independent) internal manifold metric. With accurate geodesic distances, the ISOMAP algorithm is topologically stable and able to properly embed the data in a lower dimension.

The prevalence of manifold shortcuts in graphs of real, high-dimensional data is a thinly researched topic, largely because it is a nontrivial to determine if the data truly inhabits a manifold. Structure within data is not proof that an underlying manifold exists. As an anecdotal example, consider a dataset in with 20,000 dimensions of noise and samples drawn from 2 classes. Even though the data is random, a subset of the features will correlate well with the 2 classes. This structure is not indicative of a manifold, but rather a fortuitous choice of variables. A parametrization is not a sufficient condition to suggest the data inhabits a meaningful manifold. In addition, a manifold shortcut occurs under the sensitive condition where the graph is not so over-connected that |E_shortcut| ~ |E_normal|, but is connected enough to define a global manifold structure.

Until improved methods are devised to determine when shortcuts are present, it is sensible to examine the data for their presence. This is especially the case when linear methods, or the traditional ISOMAP algorithm, do not produce a satisfactory embedding. If shortcuts are present and the manifold is well sampled, the ROC results indicate the proposed method will find them in a sensitive and specific manner.

TABLE III.

Numerical Results on Four Synthetic Datasets (mean values are reported), N = 1000

Dataset	Sensitivity	Specificity at Maximum Sensitivity	Specificity at Termination
Swiss
Sine
Spiral
Step

TABLE IV.

Datasets

Name	Dimension		Description
Step	3		Step function with narrow gap between its branches.
Swiss Roll	3		The prototypical nonlinear manifold which is prone to shortcuts.
Spiral	3		Like the swiss roll, but has dense core with many manifold shortcuts.
Sine	3		Sine wave which has shortcuts over a broad range of “severity.”
MNIST	784		Large, publicly available dataset of handwritten digits.
Faces	4096		Publicly available face dataset of different poses and lighting conditions.
Microarray	22283		Colon cancer gene microarray dataset.

VII. APPENDIX A: REFERENCED DATASETS

All synthetic datasets are constructed by starting with a basic manifold shape and adding uniformly distributed, isotropic noise. Shortcuts are always created in the construction of the kNN graph and are never artificially imposed.