Functional Anatomy of Incisal Biting in Aplodontia rufa and Sciuromorph Rodents – Part 2: Sciuromorphy Is Efficacious for Production of Force at the Incisors

Abstract

The protrogomorph condition of the rodent masticatory apparatus is thought to be present in only one living species, the mountain beaver Aplodontia rufa. The major anatomical difference between protrogomorphs and sciuromorphs is that the relative size of one part of the masseter muscle, the anterior lateral masseter, is much greater in sciuromorphs than in protrogomorphs. The mechanics of force production at the incisors were compared in A. rufa and six sciuromorph rodents. Is the sciuroid masticatory apparatus more effective for production of forces at the incisors during biting than the primitive, protrogomorph condition? To answer this question, three measures of mechanical ability were employed and three hypotheses were tested: (1) the mechanical advantage of the adductor musculature is greater in sciuromorphs than in A. rufa; (2) the relative force produced at the incisors is greater in sciuromorphs than in A. rufa, and (3) the relative amount of force produced that can be used to drive the incisors into an object, is greater in sciuromorphs than in A. rufa. The results demonstrated that the protrogomorph, A. rufa, is not as efficient at generating bite forces at the incisors as the sciuromorphs.

Introduction

In his seminal paper on grades and clades of rodents, Wood [1965] argued that the sciuromorph, hystricomorph, and myomorph grades represent modifications of the primitive protrogomorph condition that are adaptations for increased efficiency of the incisors. But since its publication little work has been done to test his hypothesis. Satoh [1997, 1998] and Satoh and Iwaku [2004, 2006, 2008] have studied the mechanics of force production at the incisors in several myomorphs and conclude that the anterior masseter muscle fibers are capable of producing large forces at the incisors. Ball and Roth's [1995] and Velhagen and Roth's [1997] comparative studies of the masticatory apparatus in squirrels (and outgroups, including Aplodontia) do not provide a mechanical analysis of incisal biting.

Morphometric analyses of the skull and mandible in marmots by Cardini [2003], Cardini and O’Higgins [2004] and Cardini et al. [2005] provide interesting insights into phylogenetic patterns of shape changes but no evidence for increased ability to produce forces at the incisors. Cardini and Tongiorgi [2003] studied shape changes in the mandible of Marmota flaviventris during growth and development. Their results suggest that as these animals mature, the size (based on attachment area) and the mechanical efficiency of the anterior lateral masseter (ALM) increase dramatically, so that there is a significant allometric increase in the ability to produce biting force at the incisors during ontogeny. Thorington and Darrow [1996] compared the jaw muscles of squirrels (also including Aplodontia as an outgroup). Their mechanical analysis is limited to lever arm/load arm ratios for the mandibular attachment areas of the major masticatory muscles, the load arm being the length from the tip of the mandibular incisor to the condyle. While the ratios tend to be low in Aplodontia, the results do not show a clear improvement in the ability of sciuromorphs to produce forces at the incisors when compared to the protrogomorph Aplodontia.

Today, in spite of lingering questions with regard to the phylogenetics of protrogomorphs [see Druzinsky, 2010, companion paper], there does appear to be a consensus that (1) the protrogomorph condition of the masticatory muscles is the primitive condition for the Rodentia [Wood, 1937, 1965], that (2) Aplodontia rufa is the only extant protrogomorph rodent, and that (3) sciuromorph, hystricomorph and myomorph arrangements of the masticatory muscles are, in some way, mechanical ‘improvements’ over the primitive, protrogomorph, condition.

In the analysis of the mechanics of incisal biting that follows, A. rufa is used to represent the protrogomorph condition of the masticatory apparatus andcompared to 5 sciuroids (Marmota monax, Tamias minimus, Ratufa affinis, Sciurus variagatoides, Cynomys ludovicianus) and one nonsciuroid sciuromorph (Thomomys talpoides). The major anatomical difference between protrogomorphs and sciuromorphs is that the relative size of one part of the masseter muscle, the ALM, is larger in sciuromorphs than in protrogomorphs. Is the sciuroid masticatory apparatus more effective for production of forces at the incisors during biting than the primitive, protrogomorph condition?

To answer this question, three measures of mechanical ability were employed and three hypotheses were tested:

• (1)the mechanical advantage of the adductor musculature, as measured by the length of the MA of the resultant of adductor forces as a percentage of jaw length, is greater in sciuromorphs than in A. rufa;
• (2)the relative force produced at the incisors, as measured by the bite force at the incisors as a percentage of the total force produced by the adductor muscles, is greater in sciuromorphs than in A. rufa, and
• (3)the relative amount of force produced that can be used to drive the incisors into an object, as measured by the bite force projected along the long axis of the incisor as a percentage of total bite force, is greater in sciuromorphs than in A. rufa.

These three measures of mechanical ability are not independent of one another, but each measures a different feature of the mechanics of biting. No single measure of the effectiveness of biting should be relied upon since comparisons of different mechanical measures may yield different results [e.g. Stern, 1974; Gans and De Vree, 1987].

Materials and Methods

Five woodchucks (M. monax) and eight mountain beavers (A. rufa) obtained for the study [Druzinsky, 1989, 1995, 2010] were dissected. Single specimens from 5 sciuromorphous species, from the collections of the Field Museum of Natural History, Chicago, were also dissected [Druzinsky, 2010, table 1]. Skulls and mandibles of each species dissected were studied from the collections of the Department of Oral Anatomy, the FMNH, and the Division of Mammals, American Museum of Natural History, New York [Druzinsky, 2010, table 1].

Table 1.

Adductor muscle masses, PCSs and forces produced by the adductor muscles

Species	Muscle
	SM	ALM	PLM	ZM	PM	T	PI
M. monax (n = 2)
Mass, mean, g	7.24	4.44	5.68	1.27	0.21	9.20	2.82
Mass, SD, g	1.14	1.57	2.57	0.24	0.21	3.04	1.62
Mass, mean, %	24	14	18	4	1	30	9
Mass, SD, %	3	1	3	1	1	1	1
PCS, mean, cm2	4.17	2.25	4.48	1.04	0.15	5.27	5.05
PCS, SD, cm2	0.17	0.43	0.95	0.24	0.15	0.22	0.63
Force, mean, kg	10.42	5.62	11.19	2.60	0.38	13.18	12.62
Force, mean, %	19	10	20	5	1	24	23
Force, SD, %	2	1	3	1	1	3	1
A. rufa (n = 4)
Mass, mean, g	1.78	0.60	2.67	0.92	0.23	3.64	0.84
Mass, SD, g	0.20	0.19	0.61	0.18	0.09	0.83	0.11
Mass, mean, %	17	6	25	9	2	34	8
Mass, SD, %	1	2	2	2	1	4	2
PCS, mean, cm2	1.12	0.44	1.99	0.69	0.25	3.01	2.11
PCS, SD, cm2	0.16	0.21	0.58	0.15	0.14	0.60	0.65
Force, mean, kg	2.79	1.11	4.98	1.73	0.63	7.53	5.27
Force, mean, %	12	5	21	8	3	29	23
Force, SD, %	1	2	4	2	2	3	2
T. thomomys
Mass, mean, g	0.08	0.34	0.11	0.02	0.02	0.20	0.04
Mass, mean, %	10	42	14	2	2	25	5
PCS, mean, cm2	0.10	0.44	0.24	0.05	0.05	0.41	0.09
Force, mean, kg	0.26	1.11	0.59	0.12	0.13	1.02	0.22
Force, mean, %	7	32	17	4	4	30	6
R. affinis
Mass, mean, g	1.41	1.55	1.06	0.04	0.04	1.69	0.61
Mass, mean, %	22	24	17	1	1	26	10
PCS, mean, cm2	1.39	1.45	1.11	0.05	0.06	1.76	1.61
Force, mean, kg	3.47	3.64	2.77	0.11	0.16	4.40	4.03
Force, mean, %	19	20	15	1	1	24	22
S. variagatoides
Mass, mean, g	0.04	0.06	0.05	0.01	0.01	0.06	0.03
Mass, mean, %	15	23	19	4	4	23	12
PCS, mean, cm2	0.04	0.07	0.06	0.03	0.01	0.07	0.04
Force, mean, kg	0.11	0.17	0.16	0.06	0.03	0.18	0.09
Force, mean, %	14	22	19	8	4	23	11
T. eutamias
Mass, mean, g	0.08	0.08	0.05	0.03	0.01	0.08	0.04
Mass, mean, %	22	22	14	8	3	22	11
PCS, mean, cm2	0.14	0.13	0.12	0.05	0.04	0.11	0.11
Force, mean, kg	0.36	0.33	0.29	0.14	0.10	0.28	0.28
Force, mean, %	20	19	16	8	6	16	16
C. cywomys
Mass, mean, g	1.92	0.90	0.73	0.25	0.16	1.53	0.72
Mass, mean, %	31	14	12	4	3	25	12
PCS, mean, cm2	1.38	0.60	0.60	0.25	0.19	1.18	1.22
Force, mean, kg	3.44	1.49	1.51	0.61	0.46	2.96	3.05
Force, mean, %	25	11	11	5	3	22	23

Physiological Cross-Sections

Ten fasciculi were measured for each muscle with a dissecting microscope, and the average length of the fasciculi was used to calculate the physiological cross-sections (PCSs) for each muscle. Fasciculi rather than fibers were measured in the present study since fasciculi are much easier to dissect and provide good estimates of fiber lengths, assuming that the fibers in a muscle are not serially connected [normally a reasonable assumption, but see English, 1985]. There was no indication of serially connected fasciculi in these muscles, but histological staining of the muscles has not been undertaken. Calculations of the PCSs are presented in appendix 1.

Coordinate System and Line of Action

The line of action and magnitude of force was estimated for each of seven adductor muscles in two jaw positions for each osteological specimen. A modified version of the ‘central fiber’ method [Mainland and Hiltz, 1934; Hiiemae, 1971; Bekele, 1983] was employed. In the ‘central fiber’ method, the force produced by a muscle is conceived as acting along a line between the center of the attachment at the origin and the center of attachment at the insertion.

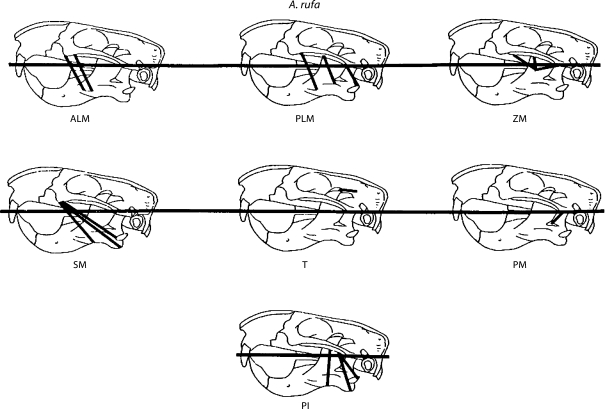
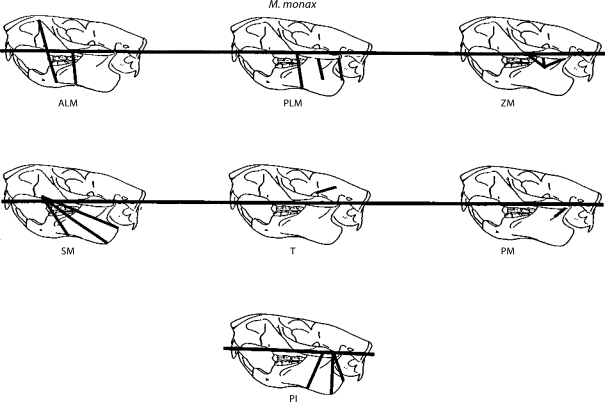
Rather than estimating the center of origin and center of insertion for each muscle, for some of the muscles, the line of action was obtained by estimating lines of action for representative fibers of the muscle (fig. 1, 2) and then performing a vector addition to find the line of action of the whole muscle. The magnitudes of the vectors were determined by dividing the force produced by each muscle (as estimated using the PCSs, see below) equally between the fibers. X, Y, and Z coordinates of each end of the representative fibers defined above from the right side of each skull were recorded. The origin of the coordinate system is the superior end of the mandibular condyle in the right glenoid fossa (fig. 3). The horizontal axis was defined as a line passing between the origin and the superior end of the occlusal wear facet on the right upper incisor, which represents the superior limit of movement of the lower incisor, or 0° gape.

Fig. 1.

Representative fibers used to estimate the line of action of each of seven adductor muscles in A. rufa.

Fig. 2.

Representative fibers used to estimate the line of action of each of seven adductor muscles in M. monax.

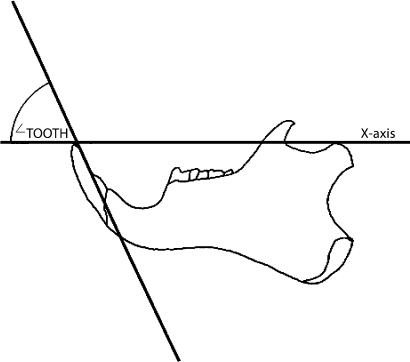
Fig. 3.

The long axis of the lower incisor makes an angle (∠_TOOTH) with the horizontal axis at IO.

The skulls were mounted in a stereotaxic apparatus [Hiiemae, 1971; Druzinsky, 1981; Bekele, 1983] at two gapes: (1) the beginning of incisal occlusion (IO) at which the tips of the upper and lower incisors pass each other (roughly 6–8° gape), and (2) 30° gape, which represents the beginning of a large bite.

Assumptions

Any intraspecific comparison of mechanics requires that the conditions are similar in all of the species studied. In the present study, the following conditions were assumed:

• (1)bilaterally symmetrical muscle activity;
• (2)simple rotation around the mandibular condyle between IO and 30°gape, and
• (3)all of the jaw adductors are active at maximum force.

Study of incisal biting in live A. rufa and M. monax [Druzinsky, 1989, 1995] demonstrates that biting is essentially a behavior that occurs along the midline with bilaterally symmetrical muscle activity, and that during powerful biting all of the adductor muscles are active. Therefore, mechanical analyses utilizing a midline projection that assumes bilaterally symmetrical muscle activity, and estimation of muscular forces from PCSs (an estimate of maximum tetanic tension), should provide reasonable estimates of forces produced during powerful incisal biting. Biting frequently begins at gapes of 30° or more. Therefore, forces produced at IO are compared to forces produced at a gape of 30°. During biting, the condyles translate anteriorly in the glenoid fossa and the jaw rotates open from this anterior position. Although incisal biting has been studied only in A. rufa and M. monax, it is assumed that the mechanics of biting are similar in all of the species considered. There are no features of the masticatory apparatus of any of these species that would suggest that these assumptions are not reasonable.

Any estimate of force based on a PCS is an estimate based on the maximum tetanic tension produced by that muscle. Thus, the present study compares the species at maximum biting force.

Projection

The system is studied in a two-dimensional, lateral projection since incisal biting is an activity that occurs primarily along the midline. Bilaterally symmetrical activity of the adductor muscles is assumed. The magnitudes of the forces produced by the adductor muscles are estimated by determining the PCS for each muscle.

Mechanics

Mechanical calculations are presented in detail in appendix 1.

Statistics

Since the sample sizes were small, nonparametric statistics were employed for most tests because they do not require the assumption that the samples are normally distributed. The Kruskal-Wallis one-way analysis of variance by ranks was used to test for differences among the seven species compared in the mechanical analysis [Siegel, 1956]. Statistical calculations were performed on a microcomputer using the SYSTAT statistical software package.

Results

Mechanics

PCSs and estimated forces produced by the adductor muscles are presented in table 1. For most muscles, the percent contribution to the total PCS of the jaw adductors (or percentage of total force contributed by each individual muscle) is within a few percentage points of the contribution it makes to the total adductor mass. In some muscles, however, the difference is striking. In the masseter muscles, fascicle lengths tend to be relatively long, and contributions to the total PCS are slightly smaller than contributions to the total muscle mass.

The greatest differences between contributions to the total PCS and total adductor mass are found in the internal pterygoid (PI) because it is an extremely complex, multi-pinnate muscle with very short fasciculi in many of these species. The greatest increase is in Aplodontia, in which the PI contributes 8% of the total adductor mass, but 23% of the total PCS. In Thomomys and Sciurus, in which the PI is a fairly simple muscle, the contribution to the total PCS is within 1% of its contribution to the total adductor mass.

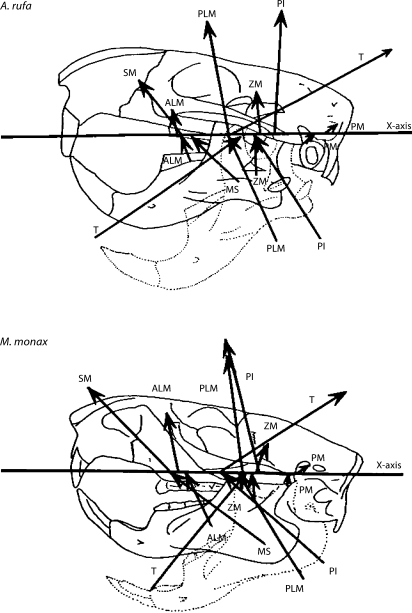
Adductor Muscle Lines of Action

Calculated lines of action of the adductor muscles are presented in figure 4. The superficial masseter (SM) is the most anteriorly directed adductor muscle, especially at gapes of 30°. The SM makes its smallest angle with the horizontal in Tamias, in which the line of action is 34.5° at 30° gape, and it is most vertically oriented in Aplodontia. The moment arm (MA) of the SM is relatively long, reaching 50% of jaw length in Ratufa at IO. It is shortest in Thomomys, in which it is only 24% of jaw length at 30° gape. In all specimens, the MA is greater at IO than at 30° gape.

Fig. 4.

Mean lines of action of the adductor muscles at IO and at 30° gape in A. rufa and M. monax. Lines above the horizontal axis are at IO and lines below the axis are at 30° gape. The length of each arrow represents the relative magnitude of the force.

The ALM is a vertically oriented muscle with a small anterior component. The ALM has its greatest anterior component in Tamias, in which it makes an angle of 61.6° to the horizontal at 30° gape. The ALM has the longest MA of any of the adductor muscles. In all specimens, the MA of the ALM is longer at IO than at 30° gape.

The orientation of the posterior lateral masseter (PLM) is similar to that of the ALM at IO, but in all seven species the mean orientation is directed more anteriorly than in the ALM at 30° gape. In Marmota, Aplodontia, Cynomys, and Thomomys, mean MA lengths are significantly longer at IO than at 30° gape. In each of the other three species (Tamias, Ratufa, and Sciurus) there is one specimen in which the MA of the PLM is longer at 30° gape than at IO.

At IO, the line of action of the zygomaticomandibularis (ZM) is directed slightly posteriorly in all species except Aplodontia, in which the mean is 87.9°. At 30° gape, the mean line of action of the ZM is slightly anterior to the vertical in all species except Thomomys, in which the mean is 90.8°. The line of action of the posterior masseter is directed posteriorly in all seven species at both IO and 30° gape. The line of action of the temporalis has a strong posterior component in all species at both IO and at 30° gape. Clearly, the force produced by the temporalis is capable of producing very large changes in the direction of the bite force [DeMar and Barghusen, 1972; Throckmorton, 1985; Throckmorton and Throckmorton, 1985]. In an animal with a relatively large temporalis such as A. rufa, the large, posteriorly directed force produced by the temporalis shifts the line of action of the adductor muscle resultant posteriorly, producing a large angle between the direction of the bite force and the long axis of the lower incisor. Perhaps rodents are able to exert precise control over the direction of the bite force by changing the relative force exerted by the temporalis during biting.

The line of action of the PI is essentially vertical at IO and has a strong anterior component at 30° gape. In some individuals of all species studied, the line of action of the most posterior fibers of the PI runs behind the craniomandibular joint (CMJ), so that these fibers would tend to open rather than close the jaw. Similar fibers have been reported in a hystricomorph (Cavia porcellus) [Chen and Herring, 1986].

Adductor Muscle Resultants

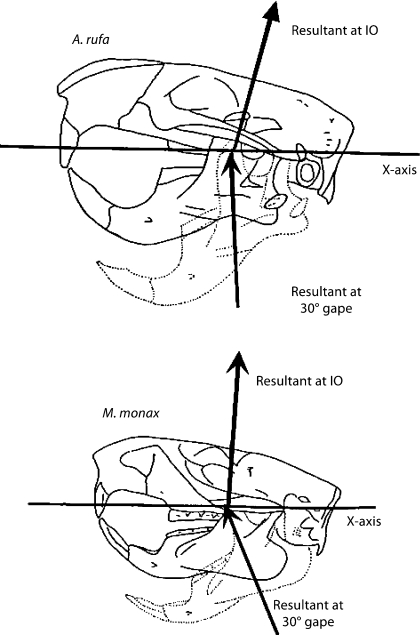
In general, the line of action of the total resultant of muscle forces is close to the vertical at IO and anteriorly directed at a gape of 30° (fig. 5). In all species except Marmota and Tamias, the mean angle to the horizontal is actually greater than 90° (the resultant is directed posteriorly), the greatest mean angle occurring in Aplodontia, in which the angle is 103.5°. The most anteriorly directed resultant at IO is in Tamias, in which the resultant makes an angle of 81.5° to the horizontal. At 30° gape, the mean resultants are all directed anteriorly. At 30° gape, the most vertical resultant is in Aplodontia, in which the mean angle is 88.7° to the horizontal, and the most anteriorly directed resultant is found in Thomomys, in which the angle is 83.4° to the horizontal. Mean actual MA lengths of the muscle resultants at IO range from 26 % of jaw length in Aplodontia to 35% in Ratufa. At 30° gape, MA lengths range from 26% of jaw length in Thomomys to 36% in Ratufa.

Fig. 5.

Mean lines of action of the total resultant of adductor muscle forces at IO and at 30° gape in A. rufa and M. monax. Lines above the horizontal axis are at IO and lines below the axis are at 30° gape. The length of each arrow represents the relative magnitude of the force.

Bite Forces

At IO, mean estimated bite forces range from 14.78 kg in Marmota to 0.25 kg in Sciurus. At 30° gape, forces range from 19.22 kg in Marmota to 0.23 kg in Sciurus. In all specimens of Marmota, Ratufa, Tamias and Cynomys, the bite force is greater at 30° gape than at IO.

Discussion

Is the Mechanical Advantage of the Resultant of Adductor Muscle Forces Greater in Sciuromorphs than in A. rufa?

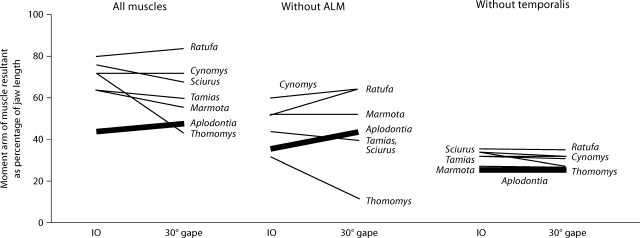
One way in which the sciuromorph masticatory apparatus might be more efficient for incisal biting than that of A. rufa is that the mechanical advantage (the relative length of the MA) of the resultant of adductor muscle forces might be greater in sciuroids than in A. rufa. Comparisons of mechanical advantage in the 7 species are presented in figure 6. At both IO and gapes of 30°, there is a nonrandom distribution of mean values for the 7 species (KW d.f. 6, IO 24.64, p < 0.001, 30° 21.59, p = 0.001). At both gapes, the relative mechanical advantage in A. rufa is lower than in any of the sciuroids, although at 30° gapes the nonsciuroid sciuromorph T. talpoides has a slightly lower mechanical advantage.

Fig. 6.

Mechanical advantage of the resultant of adductor muscle forces at IO and at 30° gape. The mean length of the MA of the resultant (as a percentage of total jaw length) for each species is given at IO and at 30° gape. Left, resultants are calculated with all adductor muscles included. Middle, resultants are calculated with the ALM removed. Right, resultants are calculated with the temporalis muscles removed. Results for A. rufa are highlighted with a heavy black line.

Since the major difference between the protrogomorph, A. rufa, and sciuromorphs is the relative size of the ALM, each of the mechanical comparisons are made with and without the ALM (KW d.f. 6, IO 29.64, p < 0.001, 30° 29.24, p < 0.001). The utility of the ALM is clearly seen when the MA of the total resultant is calculated with and without the ALM (fig. 6). In A. rufa, in which the ALM represents only approximately 5% of the total PCS of the adductor muscles, the relative length of the MA is decreased only slightly. In the other species, the decreases are more dramatic. In T. talpoides, in which the ALM accounts for 32% of the total PCS of the adductor muscles, the relative length of the MA of the resultant at IO drops from 33% of jaw length when the ALM is included to 23% of jaw length when the resultant is calculated with the ALM excluded.

Since the relative width of the skull and mandible differs among the 7 species, and since relative width may be correlated with the relative size of the temporalis muscle (e.g., the relatively widest species have the relatively largest temporalis muscles), the mechanical comparisons are also made with and without the temporalis to evaluate the effect of skull width on the mechanics of incisal biting. When the resultants of adductor muscle forces are compared in the 7 species (fig. 6) with and without the temporalis, once again mechanical advantage is lowest in A. rufa (KW d.f. 6, IO 29.56, p = 0.001, 30° 23.45, p = 0.001). Therefore, the mechanical advantage of the resultant of adductor muscle forces is greater in sciuroids than in A. rufa. Furthermore, the feature of the incisal biting apparatus of A. rufa, which is most prominently correlated with the relatively wide skull (i.e. a relatively large temporalis muscle), does not produce the low mechanical advantage of the adductor muscle resultant in A. rufa. The lower mechanical advantage of the masticatory muscles in A. rufa is due, at least in part, to the fact that A. rufa does not have large anterior sciuromorph extensions of muscle in front of the zygomatic arch.

Is Relative Bite Force at the Incisors Greater in Sciuromorphs than in A. rufa?

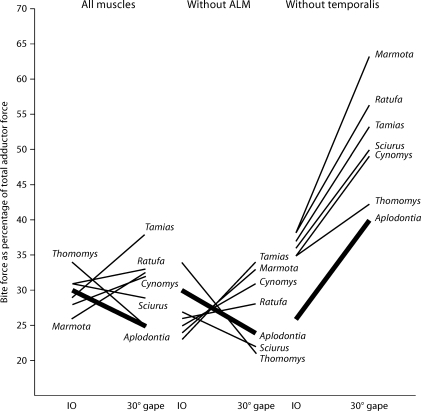
To compare relative force at the incisors, the estimated reaction force at the incisors is expressed as a percentage of the estimated total force produced by the jaw adductor musculature. Thus, for N units of force produced by the total cross-sectional area of the adductor musculature, N′ units of force are produced at the incisors, and relative bite force is equal to N′/N, expressed as a percentage (KW d.f. 6, IO 15.01, p = 0.02, 30° 24.48, p < 0.001). A similar procedure was employed by Baragar and Osborn [1987]. The results of the comparison of relative bite force are presented in figure 7. At IO, mean relative bite force in A. rufa is right in the middle of the values obtained for sciuroids, but at a gape of 30° A. rufa has the lowest mean relative bite force.

Fig. 7.

Bite force as a percentage of the estimated total force produced by the jaw adductor muscles at IO and at 30° gape. Left, bite forces calculated with all adductor muscles included. Middle, bite forces calculated with the ALM removed. Right, bite forces calculated with the temporalis muscles removed. Results for A. rufa are highlighted with a heavy black line.

When the ALM is removed from the calculations (fig. 7), the animals become slightly less efficient, but the effects are quite small (KW d.f. 6, IO 18.66, p = 0.05, 30° 17.24, p = 0.08). Although the decreases in efficiency are statistically significant, in all but one species at IO (Tamias) and one species at 30° gape (Sciurus), the mean decrease is less than 5% (and the species are not significantly different from one another at 30° gape). This suggests that although the ALM has a relatively long MA, its contribution to the efficiency of the masticatory apparatus is small. Even so, the effect of the ALM is clear (table 2). In A. rufa, in which the ALM represents approximately 5% of the total PCS of the adductor muscles, bite force estimated without the ALM is 96 and 99% (at IO and 30° gape, respectively) of the total bite force estimated with the ALM included (KW d.f. 6, IO 27.59, p < 0.001, 30° 29.87, p < 0.001). In the sciuromorphous species, the ALM represents a greater portion of the total PCS of the adductors and, as one would expect, the effect of removing the ALM is greater. For example, in Sciurus, in which the ALM is approximately 22% of the total PCS, bite force estimated without the ALM is only 69% of bite force estimated with the ALM included at IO and drops to 60% at 30° gape. Thus, due to its advantageous position well forward on the jaw, the ALM does indeed account for a relatively large percentage of the bite force.

Table 2.

Bite forces estimated without the ALM as a percentage of total bite force (means ± SD)

Species	Percent of total muscle force	Percent of bite force atlO	Percent of bite force at 30° gape
M. monax (n = 10)	90	75 ± 1	83 ± 2
A. rufa (n = 9)	95	96 ±2	99 ± 19
T. talpoides (n = 10)	68	68 ± 9	55 ± 19
R. affinis (n = 3)	80	67 ± 2	70 ± 2
S. variagatoides (n = 3)	78	69 ± 7	60 ± 3
T. minimis (n = 3)	81	64 ± 3	75 ± 1
C. ludovicianus (n = 3)	89	79 ± 1	86 ± 2

To assess the effects of skull width on the results, relative bite force is calculated without the temporalis muscle (KW d.f. 6, IO 21.24, p = 0.002, 30° 21.85, p = 0.001). At both gapes, mean relative bite force is lowest in A. rufa. If calculation of forces without the temporalis muscle does remove the effects of skull width, then relative bite force at the incisors is clearly greater in sciuromorphs than in A. rufa at IO and at 30° gapes.

Is the Percentage of Bite Force Projected Along the Incisor Axis Greater in Sciuromorphs than in A. rufa?

A third way in which the efficiency of the sciuromorphous masticatory apparatus might be greater than that of A. rufa is that sciuroids might be better than A. rufa at producing forces which would drive the lower incisors into an object being bitten. Let us assume that for the incisors to penetrate an object effectively, bite forces must be produced along the long axis of the incisor [Paphangkorakit and Osborn, 2008]. The angle between the long axis of the lower incisor and the direction of the bite force is measured (fig. 3), and the cosine of the angle, expressed as a percentage, gives the percentage of force projected along the long axis of the incisor. A similar measure is used by Osborn et al. [1986].

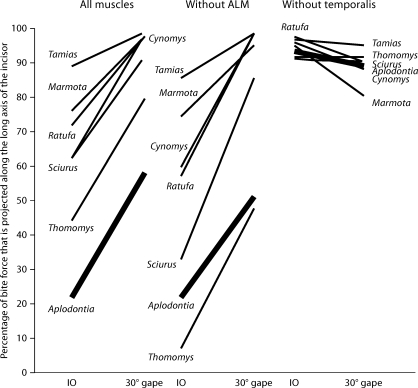
The mean percentage of force projected along the long axis of the lower incisor is given for each of the seven species in figure 8. The distribution of means is nonrandom at IO and at 30° gapes (KW d.f. 6, IO 24.54, p < 0.001, 30° 20.56, p = 0.002). Percentages of force along the incisor are much lower in A. rufa than in any of the other species. These animals, particularly the sciurids, are quite good at producing force along the long axis of the lower incisor. At 30° gapes, all of the sciurids put over 90% of the force along the axis of the incisor (the bite force makes an angle of less than 25° with the incisor axis). Gambarian's [1960; cited in Hildebrand, 1985, pp. 100–101] observation that rodents with procumbent incisors tend to have anteriorly directed masticatory muscles may be correct. There does appear to be a relationship between the orientation of the bite force (which is, of course, dependent on the orientation of the muscle forces) and the orientation of the lower incisor.

Fig. 8.

The percentage of the bite force projected along the long axis of the lower incisor at IO and at 30° gapes. Left, bite forces calculated with all adductor muscles included. Middle, bite forces calculated with the ALM removed. Right, bite forces calculated with the temporalis muscles removed. Results for A. rufa are highlighted with a heavy black line.

Although the percentage of force along the incisor tends to be slightly lower when calculated without the ALM (fig. 8), the effect appears to be similar in most species (KW d.f. 6, IO 22.73, p = 0.001, 30° 24.63, p < 0.001). Among the aplodontoid-sciuroid species, the greatest decrease in efficiency occurs at IO in Sciurus, in which 62% of the bite force is along the axis of the incisor with the ALM, but only 33% is along the incisor when the ALM is removed. In the geomyid Thomomys, the ALM represents 32% of the total PCS. When the ALM is removed from the calculations of bite force, it is not surprising that the direction of the force changes at IO and 30° gape. At IO, 44% of the bite force is along the incisor when the ALM is included but only 7% when the ALM is removed. At 30° gape, 79 % of the bite force is along the incisor when the ALM is included, but that drops to 48% when the ALM is removed.

To correct for skull width, forces are recalculated without the temporalis muscle (fig. 8). At IO, the distribution of mean values is not significantly different from random, but at 30° gapes the distribution of means is nonrandom (KW d.f. 6, IO 6.15, p = 0.406, 30° 15.93, p = 0.014). Without the temporalis muscle, force projected along the lower incisor in A. rufa is well within the mean values of the sciuroid species at both gapes.

Removal of the temporalis from calculations of bite force does, however, have a profound effect on the direction of the bite force. Without the temporalis, mean bite force directions are all within 25° of the orientation of the lower incisor (except for M. monax at 30° gapes, in which the mean angle between the bite force and the tooth axis is about 35°). When the temporalis is included in the calculations, angles between the bite force and the incisor axis are much larger. The mean angle in A. rufa at IO is approximately 78° and only 22% of the force is projected along the long axis of the incisor.

If removal of the temporalis muscle from the calculations does correct for the effects of skull width (and, in a sense, brings all of the animals to the same width), then there is no difference in the percentage of force projected along the lower incisor in A. rufa and sciuroids. Unlike the first two measures, the arrangement of the adductor muscles of sciuroids is not more efficacious for the production of force at the incisors than that of A. rufa.

In conclusion, in two of the three hypotheses tested, the sciuromorphous masticatory apparatus is better able to produce forces at the incisors than the apparatus of A. rufa. If A. rufa does represent the primitive condition for the aplodontoid-sciuroid clade, than the derived sciuromorphous condition may, using these criteria, be considered an ‘improvement’ upon the primitive, protrogomorphous condition.

Abbreviations used in this paper

ALM

Anterior lateral masseter

AZM

Anterior zygomaticomandibularis

CMJ

Craniomandibular joint

IO

Incisal occlusion

MA

Moment arm

PCS

Physiological cross-section

PI

Internal pterygoid

PLM

Posterior lateral masseter

PM

Posterior masseter

PZM

Posterior zygomaticomandibularis

SM

Superficial masseter

T

Temporalis

TA

Anterior temporalis

TP

Posterior temporalis

TZ

Suprazygomatic portion of the temporalis

ZM

Zygomaticomandibularis

Appendix 1

The density of muscle is estimated as 1.0564 g/cm [Mendez and Keys, 1960]. k, the force produced by 1 cm² of muscle, is estimated as 2.5 kg/cm, which is near the average of values measured by Muhl et al. [1978] in the digastric muscle of rabbits and close to values obtained from postcranial muscles in other species [Spector et al., 1980; Powell et al., 1982; Roy et al., 1982]. The PCS is calculated as

$$PCS\left(m^2\right)=\frac{Mass\left(kg\right)}{Fiber\hspace{0.17em}log\left(m\right)\times Density\left(\frac{kg}{m^3}\right)}$$

[after Bodine et al., 1982; Roy et al., 1984]. The force (F) produced by a muscle is estimated by

$$F\left(kg\right)=c\left(\frac{kg}{m^2}\right)cos\hspace{0.17em}P\times PCS\left(m^2\right)$$

[Fick, 1910; Gans and Bock, 1965], where c is an estimate of the force produced by 1 cm² of muscle and P′ is the pinnation angle of the fibers in the muscle.

Pinnation angles were not measured in the present study, so a cosine equal to one (1.0) is used. In most of the adductor muscles, the pinnation angles are small, so their cosines are very close to 1.0. In the most complex muscles, the temporalis and medial pterygoid, the angles are large, so muscular forces are probably overestimated in these muscles. Since pinnation angles decrease as muscles lengthen [Benninghoff and Rollhauser, 1952] force (F) is probably estimated more accurately at 30° gape than at IO.

The moment (MOM) of a muscle is defined as the product of the force (F) produced by the muscle and the length of the moment arm (MA), which is defined as the perpendicular distance between the center of rotation (the joint) and the line of action, or

$$MOM=F\times MA$$

The articulation of the mandibular condyle within the CMJ is defined as the center of rotation (as well as the origin of the coordinate system), the horizontal axis (or X-axis) is defined as a line constructed between the joint and the cranial end of the wear facet on the upper incisor, and the vertical axis (or Y-axis) is an axis perpendicular to the horizontal axis, passing through the origin.

The force produced by each muscle can be divided into a horizontal component (F_H) that acts along the horizontal axis and a vertical component (F_V) that acts parallel to the vertical axis [Throckmorton, 1985; Throckmorton and Throckmorton, 1985]. The vertical components produce rotation around the joint and the horizontal components produce mandibular translation [Bock, 1968; Throckmorton and Throckmorton, 1985]. If the horizontal components of muscle force are considered to act along the horizontal axis, in the plane of the long axis of the CMJ, horizontal components of muscle force can only produce translatory movements of the lower jaw and therefore do not contribute to the turning moments around the joint, because there is no articular eminence.

The X- and Y-coordinates of the origins and insertions of each representative fiber of each muscle are recorded rather than estimating the length of the MA and orientation of each fiber directly. The orientation of each fiber is found by

$${\alpha }_n=arctan\left(\frac{Y_{ORIGIN}-Y_{INSERTION}}{X_{ORIGIN}-X_{INSERTION}}\right)$$

The moment (MOM_n) produced by each representative fiber is found by finding the X-intercept of the line of action (MAL_n)

$$MO{M}_n=F_{n}sin\hspace{0.17em}{\alpha }_n\times MA{L}_n$$

and the moment arm (MA_n) is also found using MAL_n, by substitution

$$M{A}_n=MA{L}_{n}sin\hspace{0.17em}{\alpha }_n$$

so the determination of the length of the MAL for each muscle precedes the determination of the MA for each muscle.

Using the orientation and the force (F_n), the moment arm (MA_n), and the moment (MOM_n) around the CMJ are determined for each of seven adductor muscles considered (SM, ALM, PLM, AZM, PZM, temporalis, PI) for each of the two gapes (IO and 30°) in each specimen. Static equilibrium conditions are assumed, so that

$$\sum MOM=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\sum F_V=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\sum F_H=0$$

Given n muscles, with forces F₁ … F_n, the calculation of moments and the resultant of muscle forces (MUSCLE_F) is as follows: Vertical components of muscle forces are given by

$$\begin{array}{l}{F}_{V_n}=F_{n}sin\hspace{0.17em}{\alpha }_n\\ MUSCL{E}_{F_V}=\sum _{i=0}^n{F}_{V_i}\end{array}$$

horizontal components of muscle forces are given by

$$\begin{array}{l}{F}_{H_n}=F_{n}cos\hspace{0.17em}{\alpha }_n\\ MUSCL{E}_{F_H}=\sum _{i=0}^n{F}_{H_i}\end{array}$$

moments produced by the muscles are given by

$$MUSCL{E}_{MOM}=\sum _{i=0}^{n}MO{M}_i$$

If it is assumed that friction at the jaw joint is negligible so that the mandible is free to translate anteriorly and posteriorly, then horizontal components of muscle forces, even if they are not directed along the axis of the glenoid fossa, do not produce rotation around the jaw joint. Since horizontal components contribute only to translation of the jaw, moments around the CMJ produced by horizontal components of muscle forces equal 0, so horizontal components of force are ignored when computing turning moments around the CMJ.

The magnitude of the total resultant of muscle forces is

$$MUSCL{E}_F={\left(\sum F_V\right)}^2+{\left(\sum F_H\right)}^2$$

and the orientation of the muscle resultant to the X-axis is

$${}^{\angle }MUSCL{E}_F=arctan\left(\frac{\sum F_V}{\sum F_H}\right)$$

The bite force (BITE_F), or reaction force at the incisor, and the reaction force at the CMJ (CMJ_F) are estimated by considering rotational moments around the bite point rather than the CMJ [Bramble, 1978]. This analysis rests on three assumptions:

• (1)Static equilibrium conditions prevail,
• (2)the CMJ resists only vertical forces, and
• (3)the entire horizontal component of the muscle resultant is resisted at the bite point.

The moment produced by the joint reaction force (CMJ_MOM) is equal and opposite to the moment produced by the adductor muscles (MUSCLE_MOM)

$$MUSCL{E}_{MOM}=-CM{J}_{MOM}$$

because the sum of moments is 0,

$$0={\Sigma }_{MOM}=MUSCL{E}_{MOM}+CM{J}_{MOM}$$

The MA (CMJ_MA) of the joint reaction force (CMJ_F) about the bite point is the perpendicular distance between the CMJ and the bite point, and

$$CM{J}_{MOM}=-MUSCL{E}_{MOM}=CM{J}_F\times CM{J}_{MA}$$

so,

$$CM{J}_F=\frac{MUSCL{E}_{MOM}}{CM{J}_{MA}}$$

The vertical component of the bite force (BITE F_V) is found by

$$0=\Sigma {\text{F}}_V=MUSCLE{\text{F}}_V+CM{J}_F+BITE{\text{F}}_V$$

so,

$$\begin{array}{l}-MUSCLE{\text{F}}_V+CM{J}_F+BITE{\text{F}}_V\\ BITE{\text{F}}_V=MUSCLE{\text{F}}_V-CM{J}_F\end{array}$$

The horizontal component of the adductor muscle forces (MUSCLE F_H) is resisted entirely by reaction forces at the bite point, so

$$0=\Sigma {\text{F}}_H=MUSCLE{\text{F}}_H+BITE{\text{F}}_H$$

and MUSCLE F_H is equal and opposite to BITE F_H

$$BITE{\text{F}}_H=-MUSCLE{\text{F}}_H$$

The orientation of the bite force to the horizontal axis (θ_BITE) is found by

$${\theta }_{BITE}=arctan\left(\frac{BIT{E}_{F_V}}{BIT{E}_{F_H}}\right)$$

and the bite force (BITE_F) is given by

$$BIT{E}_F=\sqrt{{\left(BIT{E}_{F_V}\right)}^2+{\left(BIT{E}_{F_H}\right)}^2}$$

To estimate the orientation of the lower incisor relative to the horizontal axis, the following procedure is used:

For each skull measured, a photograph of the left mandible in lateral view was made. The horizontal axis is defined as a line passing through the tip of the incisor and the most superior point on the mandibular condyle (fig. 3). This line corresponds to the horizontal axis of the skull (as defined above) when the mandible is at 0° gape or full occlusion of the upper and lower incisors. A line passing through the straightest portion of the wear facet on the lingual surface of the tooth is constructed, and used to represent the long axis of the lower incisor. The angle formed by the intersection of the horizontal axis and the long axis of the incisor is called angle SPACE_TOOTH (fig. 3). At X^° gape, the orientation of the lower incisor is simply

$${\angle }_{TOOTHx}={\angle }_{TOOTH}-{\text{x}}^0$$

The force produced along the long axis of the incisor (TOOTH_F), or normal to the cross-section of the incisor, is found by projection of the bite force vector (BITE_F) onto the long axis of the incisor using the cosine of the angle between the bite force and the long axis of the incisor (fig. 3):

$$TOOT{H}_F=BIT{E}_{F}cos\left({\theta }_{BITE}-{\angle }_{TOOTHx}\right)$$