Rheology

What is rheology?

Most people are familiar with the basics of rheology from experience with diarrhea or perhaps rheostats. The word rheology was invented in 1929 to name the discipline of a society engaged in the study of how materials deform in response to forces. It was inspired by a quote by Heraclitus: “παντα ρει” translated as “everything flows”. Indeed everything does flow, but to different extents depending on how much force is applied, in what direction, and for how long. For materials more complex than simple springs, where a spring constant relates force to elongation, the goal of rheology is to provide quantitative parameters that define how a material will deform as a function of force, time and spatial orientation.

What are the quantities measured in rheology?

In principle this is very simple — there are only three basic ideas. First: stress, the amount of force applied to a given area of the sample. Second: strain, the degree to which the material deforms. And third: the ratio of stress to strain, which defines the elastic modulus for a solid, and the ratio of stress to rate of strain (or flow rate), which defines the viscosity for a liquid. The big complication is that most materials, and especially all biological materials, have both liquid and solid aspects. Consequently, material properties like elastic moduli and viscosities are not constants but functions of time, force, the direction in which the force is applied, and so on.

What's the difference between stress and strain?

This is important to get straight because these words don't have exactly the same meaning as in everyday speech. Strain is what millions of people feel in their backs, or their relationships, and the cause of it is stress. Stress causes strain, but the amount of strain depends in some sense on how tough one is. Stress in rheology is, as one might expect, related to force. More precisely stress is the ratio of force to the area over which that force is exerted; it has units of force/distance² and, importantly, a direction. In North American engineering, especially bioengineering literature, stress is often given in cgs units of dyne/cm²; in most other studies, stress is given in SI units of N/m², which is the same as a Pascal (1 Pa = 1 N/m² = 10 dyne/cm²). Neither unit is particularly well scaled to cell biology, but 1 Pa = 1 pN/μm². Imagine a single kinesin motor pulling on a 1 μm diameter organelle: with a stall force of, say, 3 pN applied to the area of approximately 3 μm², the motor generates approximately 1 Pa stress. It is important to differentiate stress from force. If you place a 10 kg weight on a carton full of eggs, probably nothing will break. But if you put it on a single egg, things will be different. The weight applies the same amount of force in both cases, but it produces a lot more stress on a single egg than on the array of eggs in a carton.

There are different kinds of stress depending on the direction in which the force is exerted. A shear stress is parallel to the surface. For example, endothelial cells feel a shear stress on their apical surface due to blood flow in an artery, much as a river's edge is subjected to shear stress that depends on how fast a river flows. Elongational and compressive stresses are perpendicular to the surface, and can be generated by the lengthening and shortening of muscles as they pull on the surrounding tissue.

Strain in rheology is somewhat different from its everyday meaning: it's a purely geometrical quantity, a way to quantify the amount of deformation in a given material, and has no units. Much of the complexity of rheology relates to defining or measuring strain. Measurable quantities such as the distance by which some point moves in response to stress requires sometimes complicated formulas to convert them to strains, depending on the shape of the material and the place where the force is applied.

The elastic modulus is the quantity that allows you to predict how much a material will deform elastically when you apply a certain amount of stress, and viscosity is the analogous quantity that tells you how fast the material will flow. The more you stress a tissue, cell or protein network, the more it is strained. But the rate and degree to which it strains is usually a complex function of the magnitude of the stress and how long it is applied.

What's the difference between viscous and elastic?

The ratio of stress to strain is all you need to know the material properties of the material. The difference between elastic and viscous is basically whether the strain reaches a limit or continuously increases in response to a constant stress. An ideal elastic material such as a spring deforms to a given strain in response to a given stress and then sits there forever unless the stress is removed, at which time the material returns to its initial shape. The elastic modulus, the ratio of stress to strain, is a constant in this case. All the work done by the initial stress (remember, work = force × distance) was stored in the material (hence the term storage modulus, see below) and elastically recovered when the stress is removed. Elasticity in this context does not refer to whether a material is `stretchable' or not, but whether it returns to its initial shape when you stop pulling or pushing on it. There are different kinds of elastic moduli depending on the kind of stress. If it's a shear stress, then the ratio of stress to strain is the shear modulus. If it's elongational or compressional stress, then the ratio of stress to strain is generally called the Young's modulus, named for Thomas Young who also identified the cause of astigmatism. If a simple material conserves volume, then shear and Young's moduli are related by a factor of three. An ideal viscous material changes strain in proportion to the time that the stress is applied. In this case, the ratio of stress to the rate of strain defines the viscosity.

Is the relationship between stress and strain for a solid and stress and strain rate for a liquid always linear?

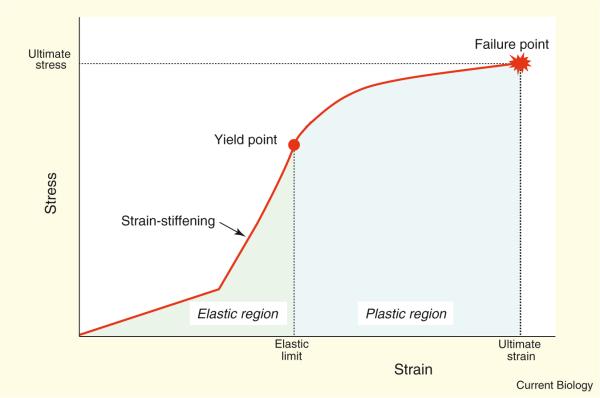
Unsurprisingly: no, and biology offers some good examples. A simple liquid like water has a single viscosity: it might depend on temperature and pressure, but not on how fast it flows. A liquid with constant viscosity is called Newtonian. Cytoplasm, on the other hand, is non-Newtonian — indeed, it was one of the first non-Newtonian liquids to be systematically characterized, partly by botanists studying the sedimentation of beads within cells, who found that under small forces the beads moved hardly at all, but at larger forces they flowed as though in water. Analogously, most soft animal tissues are soft (compliant) under small stresses but much stiffer at larger stresses. Think about pulling on your skin. It's easy to deform it a little, but much harder to deform it a lot. A schematic diagram of the stress–strain relation for a complex non-linear material is shown in Figure 1.

Figure 1. Schematic diagram of a stress-strain curve for a non-linear material.

At small strains, the stress increases linearly, and the elastic modulus is calculated from the slope of the line. Some materials, including many biopolymer gels, are strain-stifffening, and display an increased stress/strain slope at increasing strains. In the purely elastic region, strain will return to zero if stress is removed. At larger strains, this material deforms more easily (strain-weakening) and now, in the plastic region, the strain does not fully recover if the stress is removed. Eventually, the strain can become so large that the material breaks, and flows without limit in the absence of any additional stress (viscous flow). This representation is for some arbitrary rate at which the sample is strained. As the strain rate changes, the magnitudes and shapes of the stress-strain relation will also change.

What's viscoelasticity?

As noted above, most biological materials are both viscous and elastic. The shear moduli and viscosities that define them depend on strain rates as well as strain magnitudes. Differentiating elastic from viscous effects requires measurements at different time scales and is usually done by performing oscillatory deformations at different frequencies. As a result, data are often reported in terms of storage (elastic) or loss (viscous) moduli. The time dependence is important. For example, design of bicycle helmets requires knowing the mechanical response of the brain at very high frequencies that mimic impact. But understanding mechanosensing by neurons requires knowledge of the viscoelasticity of central nervous system tissues at the time scales (which appear to be seconds to minutes) over which the cell probes its mechanical environment.

What has been grotesquely oversimplified and might offend a rheology aficionado?

The main problem is that so far stress and strain have been treated as though they were simple numbers, or maybe vectors for stress, and that materials are uniform and continuous. But really stress and strain are tensors, and the way that forces or deformations distribute in a discrete structure like the heart or the cytoskeleton is often dazzlingly complicated and sometimes incalculable without making iffy assumptions. But don't despair, the situation is no worse than most things in biology. The fact that rheological data cannot completely determine molecular mechanisms is no different from the fact that aspirin or insulin were useful drugs decades before there was a hint of the molecules they affected.

Why should a biologist care about rheology?

Actually, biologists used to care a lot more about rheology than they have lately. A prominent physiology text from the 1950s (An outline of general physiology by L. Heilbrunn) stated that “In any attempt to interpret the machinery of a living cell, it is essential to know something about the mechanical properties of the protoplasm in the cell that is being investigated.” This point of view was largely eclipsed by the emphasis and power of chemical and genetic regulation of cell function. But cells are mechanical as well as chemical and electrical devices, and understanding their biology requires knowledge of all these aspects. Numerous recent studies show that application of external forces or challenging a cell's internal force generation by adhesion to substrates of different stiffnesses generates signals that can augment or override chemical stimuli. Understanding how forces affect cell growth, division, differentiation and activation requires defining the rheological properties of cells in the same way that understanding chemical signaling requires knowledge of rates and affinity constants and signal transduction pathways.