Abstract
Background
Mechanical properties of the foot are responsible for its normal function and play a role in various clinical problems. Specifically, we are interested in quantification of foot mechanical properties to assist the development of computational models for movement analysis and detailed simulations of tissue deformation. Current available data are specific to a foot region and the loading scenarios are limited to a single direction. A data set that incorporates regional response, to quantify individual function of foot components, as well as overall response, to illustrate their combined operation, does not exist. Furthermore, combined three-dimensional loading scenarios while measuring the complete three-dimensional deformation response are lacking. When combined with an anatomical image data set, development of anatomically realistic and mechanically validated models becomes possible. Therefore, the goal of this study was to record and disseminate the mechanical response of a foot specimen, supported by imaging data.
Method of Approach
Robotic testing was conducted at the rear foot, forefoot, metatarsal heads, and the foot as a whole. Complex foot deformations were induced by single mode loading, e.g. compression, and combined loading, e.g. compression and shear. Small and large indenters were used for heel and metatarsal head loading; an elevated platform was utilized to isolate the rear foot and forefoot; and a full platform compressed the whole foot. Three-dimensional tool movements and reaction loads were recorded simultaneously. Computed tomography scans of the same specimen were collected for anatomical reconstruction a-priori.
Results
Three-dimensional mechanical response of the specimen was nonlinear and viscoelastic. A low stiffness region was observed starting with contact between the tool and foot regions, increasing with loading. Loading and unloading response portrayed hysteresis. Loading range ensured capturing the toe and linear regions of the load deformation curves for the dominant loading direction, with the rates approximating those of walking.
Conclusion
A large data set was successfully obtained to characterize the overall as well as regional mechanical response of an intact foot specimen under single and combined loads. Medical imaging complemented the mechanical testing data to establish the potential relationship between the anatomical architecture and mechanical response, and for further development of foot models that are mechanically realistic and anatomically consistent. This combined data set has been documented and disseminated in the public domain to promote future development in foot biomechanics.
Keywords: foot biomechanics, heel, metatarsal heads, tarsometatarsal joint, arch properties, plantar tissue deformation
Introduction
The foot is the interface between the body and ground or footwear during locomotion, and undergoes large loads and deformations. Knowledge of its mechanical response potentially elucidates the causative factors of mechanical dysfunction as a result of abnormal tissue structures and mobility of foot joints. Description of foot mechanics also forms the basis to establish its representation in computational analysis that focus on the investigation of human movement [1]. In a similar manner, predictive exploration of foot disorders [2] and therapeutic or performance related interventions, applied to the foot or its components [3], is possible.
The passive load-deformation behavior of the foot is dictated by plantar tissue properties and the properties of foot joints. Numerous studies have been conducted to investigate the overall stiffness of the foot and the arch [4]. Structural testing studies also quantified stiffness properties of various foot joints [5]. Testing of intact regions of the foot, e.g. heel [6,7], identified regional response due to the underlying plantar tissue. Mechanical loading of tissue samples extracted from the heel [8] or the forefoot [9] aided in reconstruction of material models for plantar tissue [9,10]. The majority of previous studies tested only the region of interest, it being the whole foot [4,11], the heel [12] or forefoot [13], in isolation. Characterization of a foot, including its overall response and the response of its key individual components, is lacking. Loading modes were also limited to a single direction, commonly compressing the tissue [8,9] or the foot [7,11]. While this approach establishes foot response in a dominant loading case of daily activities, three-dimensional representation of foot stiffness and the material properties of its tissues can be critical for predictive purposes [14,15].
Association of the anatomical details of the foot to mechanical data is also important from a modeling perspective. The value of such an association has been recognized [13], yet, a comprehensive testing scheme has not been employed. Anthropometric data, relative joint positions, and regional description of tissue stiffness, for example, are critical to build realistic and validated models of the foot for gait analysis [16] and musculoskeletal simulations [17]. Tissue level geometric detail when supported by mechanical response obtained using the same foot is indispensable to realize accurate models for finite element analysis [18-21]. It is common that in many foot models[2,18-20], the source of structural and/or material properties does not match that of the anatomical reconstruction.
Our goal was to quantify the detailed mechanical response of a foot, supported by medical imaging for anatomical reconstruction. In the spirit of similar studies conducted for musculoskeletal simulations [22-24], this data set is also targeted to become a reference while building foot models representative of its mechanical response. Portrayal of intact response was aimed rather than testing of regions in full isolation, in order to recognize the potential to establish contribution of individual regions to the foot's overall response. Rear foot testing was aimed to record plantar tissue response whereas forefoot testing was targeted at measuring overall deformation characteristics of the arch. Loading of metatarsal head regions provided mechanical response of the individual rays of the foot. Whole foot deformations quantified foot mechanics as a complete entity. The final objective of this work was to disseminate the data set in full detail, with the intent to expedite prospective studies in foot biomechanics.
Methods
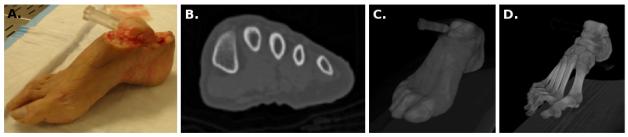
The specimen was a right foot from a male Caucasian donor (Fig. 1-A). At time of death, the age of the donor was 58 years; body weight and height were 79.4 kg and 1.73 m, respectively. Foot length was 0.24 m, measured from the posterior aspect of the heel to the tip of the second toe. Foot width was 0.09 m and its height was 0.08 m. The width of the foot corresponded to the distance between the medial aspect of the first metatarsal head and the lateral aspect of the fifth metatarsal head. Foot height was measured when the foot was resting on its own weight, from resting surface to the superior aspect of the navicular.
Figure 1.
A. The foot specimen used for mechanical testing and anatomical imaging. B. A cross sectional image at the level of mid metatarsals as obtained from computed tomography. C. & D. Volumetric reconstruction of computed tomography scans for the foot boundary and the bones.
Prior to mechanical testing, computed tomography scans were obtained while the foot was resting on its own weight on a flat surface (Fig. 1-B). Before imaging, a registration phantom was screwed in the talus. The phantom was made out of Plexiglas and filled with water with the intent to register anatomical images with coordinate systems of mechanical testing. Axial images (a total of 288) were recorded using a Siemens computed tomography system (SOMATOM Sensation 64, Siemens Medical Solutions USA, Inc., Malven, PA, USA) at a resolution of 512 × 512 pixels. The pixel size was 0.365234 mm and the spacing between the images was 1 mm. In this study, the three-dimensional visualization of computed tomography scans (Fig. 1-C,D) were accomplished with VolSuite (http://www.osc.edu/archive/VolSuite/).
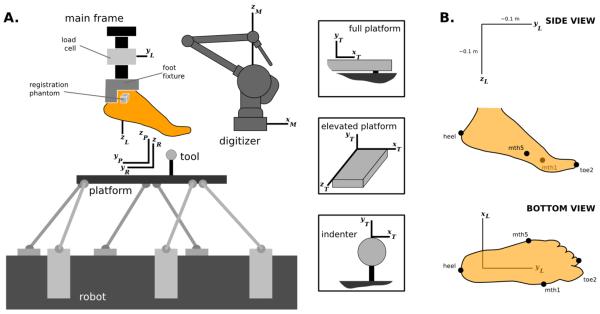
Mechanical testing was conducted on a six degree of freedom parallel robotic system (Rotopod R2000; Parallel Robotic Systems Corp., Hampton, NH, USA) controlled with stepper motors (Fig. 2-A). The robot base contained a stationary coordinate system (R) and the platform of the robot had a moving coordinate system (P) relative to the base (Fig. 2-A). At a zeroed state, approximately at the midpoint of the range of the robot, these coordinate systems were coincident and aligned at the center of the platform. Z-axis pointed upwards, and x- and y-axes defined the plane of the platform. The range of motion of the robot was ±0.1 m in x- and y-axes with a rotation capacity of ±10 degrees. In z-axis the range was ±0.1 m and ±720 degrees. Factory specified movement accuracy of the robot was 50 μm, with a repeatability of 25 μm [25]. The desired robot trajectory (position and orientation) was provided at a sample rate of 50 Hz and recorded.
Figure 2.
A. Experimental setup illustrating assembly of all testing components and the foot, with their associated right-handed coordinate systems (R: robot; P: platform; T: tool; L: load cell; M: Microscribe three-dimensional digitizer, Immersion Corp. San Jose, CA). B. Anatomical landmarks digitized on the foot in relation to load cell coordinate system. This coordinate system was used to report foot loading and tool movement data.
The reaction forces and moments, generated on the specimen during the experiments, were recorded using a spatial load cell (Theta, ATI Industries Corp., Apex, NC, USA). The load cell was attached to the main frame of the experimental setup, with the origin of its coordinate system (L) at the transducer center and orientation was as illustrated in Figure 2 based on the description of the supplier. The load cell had 0.5 N (1.1 N in z-direction) and 0.07 Nm force and moment measurement resolutions, respectively. During experimentation, load cell data was recorded at a sampling rate of 1000 Hz.
For experiments, the foot was first prepared by removing excess tissue around the talus (Fig. 1-A). Talus and calcaneus were fixed relative to each other by passing screws through both. In following, the superior part of the rear foot was firmly attached to an aluminum fixture, using denture base and repair resin (NATURE-CRYL® POUR, GC America, Inc., Alsip, IL, USA). An aluminum support rod attached the fixture to a steel load cell interface component (Fig. 2-A).
Various tools were placed on the robot platform to test desired regions of the foot, or the whole foot (Fig. 2-A). For indentation, large and small steel spheres were used (0.0254 m and 0.0127 m in diameter, respectively). Rear foot and forefoot isolation was accomplished with an elevated platform with the dimensions of 0.086 m × 0.051 m × 0.151 m (width × height × length). A full platform effectively covered the surface of the robot platform to facilitate whole foot testing. For the indenters, y-axis of the tool coordinate system (T) was parallel to the z-axis of the platform coordinate system and the origin was located at the tip of the indenter. For the elevated platform, origin of the tool coordinate system was at the corner of the tool, y-axis in parallel with the z-axis of the platform coordinate system, x-axis along the width and z-axis along the length of the tool. For the whole platform, origin of the tool coordinate system was an arbitrary point and the y-axis was in parallel with the z-axis of the platform coordinate system.
A three-dimensional digitizer (Microscribe G2L; Immersion Corp, San Jose, CA, USA; 130 μm resolution, 430 μm accuracy) was used to establish transformation matrices obtained from the relative position and orientation of stationary coordinate systems [25,26]. For this purpose, points were sampled on the robot, platform, load cell and tools in the digitizer coordinate system (M) [25,26]. As the platform position and orientation was prescribed by the robot, utilization of these transformation matrices allowed tool position and orientation as well as load cell measurements to be represented in any desired coordinate system. The digitizer was also utilized to record points on the anterior, superior and lateral surfaces of the registration phantom for alignment with the computed tomography coordinate system. In addition, four anatomical landmarks were collected on the foot: posterior aspect of the heel approximately at the calcaneal tuberosity, tip of the second toe, medial aspect of the first metatarsal head, and lateral aspect of the fifth metatarsal head (Fig. 2-B). These points establish an anatomically relevant coordinate system and also aid in registration between imaging and mechanical testing data.
Mechanical testing protocols, in particular control of robot trajectory and data collection, were implemented through a custom software written in LabView (National Instruments Corp., Austin, TX, USA) [26]. Mechanical testing was conducted on the rear foot, forefoot, metatarsal heads, and the whole foot, using aforementioned tools (Table 1). Two types of loading scenarios were commonly applied. In a compression dominant test, the tool was pressed against the region of interest along a superior direction. A combined loading test compressed the region with the tool up to a specified point, followed by a shear displacement at that level to induce multimodal loading. Target position of the tool was identified for a desired force accumulation by moving the robot at a slow loading rate (0.01 m/s). Once determined, the tool was moved to that position at a speed of 0.04 m/s to approximate lifelike loading rates [27,12]. Ten cycles were employed, during which the tool was retracted to unload the foot region. This study reports sample data sets extracted for the tenth cycle and presented in the load cell coordinate system (Fig. 2-B). All load cell data are raw, while the tool position and orientation data were resampled at 1000 Hz using Matlab (Mathworks, Inc., Natick, MA, USA).
Table 1.
Mechanical tests conducted on the foot specimen. Mode denotes dominant loading direction induced by tool movement. EP: elevated platform; SI: small indenter; LI: large indenter; FP: full platform. C: compression; CS: compression + shear. Range (min / max) corresponds to the reaction loads measured at the origin of the load cell coordinate system. Whole foot loading data sets involve multiple orientations of the tool relative to the foot. All data were represented in the load cell coordinate system.
| Region | Tool | Mode | Loading Ranges | |||||
|---|---|---|---|---|---|---|---|---|
| Fx (N) | Fy (N) | Fz (N) | Mx (Nm) | My (Nm) | Mz (Nm) | |||
| Forefoot | EP | CS | −24.8 / 2.3 | −7.7 / 33.0 | −3.2 / 147.3 | −0.09 / 20.49 | −3.42 / 0.01 | −0.21 / 3.30 |
| Forefoot | EP | CS | −29.9 / 1.4 | −11.3 / 48.0 | −2.7 / 158.7 | −0.25 / 19.81 | −4.49 / −0.03 | −0.16 / 3.83 |
| Forefoot | EP | CS | −67.2 / 1.8 | −2.8 / 99.4 | −3.5 / 347.3 | −0.11 / 41.03 | −9.25 / −0.03 | −0.16 / 8.62 |
| Forefoot | EP | C | −29.8 / 1.8 | −3.2 / 23.8 | −1.9 / 168.4 | −0.15 / 19.38 | −4.32 / −0.00 | −0.21 / 4.08 |
| Forefoot | EP | C | −79.6 / 1.3 | −2.8 / 95.6 | −2.7 / 396.3 | −0.10 / 35.59 | −11.38 / −0.04 | −0.14 / 10.14 |
| Metatarsal Head 1 | SI | C | −1.3 / 1.9 | −11.5 / 0.6 | −3.1 / 45.1 | −0.11 / 9.14 | −0.78 / −0.01 | −0.31 / 0.25 |
| Metatarsal Head 2 | SI | C | −0.7 / 3.3 | −2.3 / 2.3 | −2.7 / 42.6 | −0.06 / 5.67 | −0.46 / 0.58 | −0.23 / 0.20 |
| Metatarsal Head 3 | SI | C | −2.0 / 2.5 | −6.2 / 1.4 | −4.0 / 40.7 | −0.08 / 7.01 | −0.42 / 0.78 | −0.09 / 0.24 |
| Metatarsal Head 4 | SI | C | −4.1 / 1.7 | −2.6 / 5.9 | −4.1 / 42.8 | −0.15 / 3.48 | −0.52 / 0.10 | −0.14 / 0.42 |
| Metatarsal Head 5 | SI | C | −10.0 / 1.4 | −2.0 / 5.3 | −3.3 / 34.9 | −0.09 / 2.10 | −1.23 / 0.09 | −0.07 / 0.97 |
| Rear foot | EP | CS | −4.1 / 1.2 | −28.7 / 4.3 | −3.4 / 87.4 | −2.00 / 6.89 | −1.11 / 0.07 | −0.24 / 0.15 |
| Rear foot | EP | CS | −10.5 / 0.8 | −69.8 / 3.0 | −1.5 / 273.8 | −4.13 / 15.46 | −3.20 / 0.04 | −0.40 / 0.06 |
| Rear foot | EP | C | −2.7 / 1.2 | −11.3 / 0.8 | −1.4 / 81.6 | −0.12 / 1.87 | −0.95 / 0.06 | −0.13 / 0.18 |
| Rear foot | EP | C | −8.6 / 1.5 | −31.0 / 0.9 | −1.3 / 272.1 | −0.10 / 4.73 | −3.00 / 0.02 | −0.35 / 0.22 |
| Rear foot | EP | C | −16.0 / 2.4 | −54.3 / 0.6 | −0.4 / 514.0 | −0.06 / 7.58 | −5.69 / −0.02 | −0.65 / 0.22 |
| Rear foot | LI | CS | −10.6 / 1.2 | −24.2 / 8.4 | −3.9 / 58.4 | −2.67 / 5.85 | −2.75 / 0.15 | −0.20 / 0.16 |
| Rear foot | LI | CS | −66.7 / 1.3 | −93.7 / 17.3 | −2.1 / 320.2 | −7.29 / 21.11 | −16.25 / 0.03 | −0.55 / 0.19 |
| Rear foot | LI | C | −5.5 / 1.2 | −7.0 / 0.4 | −3.9 / 31.7 | −0.11 / 1.31 | −1.37 / 0.08 | −0.10 / 0.19 |
| Rear foot | LI | C | −21.8 / 0.8 | −24.9 / 0.8 | −2.6 / 110.5 | −0.09 / 4.73 | −5.31 / 0.11 | −0.19 / 0.21 |
| Rear foot | LI | C | −21.8 / 2.9 | −25.3 / 1.5 | −2.2 / 112.1 | −0.09 / 4.88 | −5.37 / 0.06 | −0.18 / 0.21 |
| Rear foot | LI | C | −36.6 / 0.8 | −42.6 / 0.8 | −3.5 / 191.2 | −0.09 / 7.87 | −9.03 / 0.08 | −0.36 / 0.19 |
| Whole foot | FP | C | −8.1 / 1.7 | −1.9 / 33.4 | −2.6 / 549.4 | −1.29 / 12.59 | −1.86 / 0.09 | −0.14 / 1.29 |
| Whole foot | FP | C | −35.4 / 1.3 | −3.3 / 32.7 | −2.0 / 687.4 | −0.99 / 16.42 | −9.33 / 0.06 | −0.11 / 2.50 |
| Whole foot | FP | C | −1.0 / 30.5 | −31.8 / 16.6 | −0.3 / 783.3 | −0.09 / 22.95 | −0.24 / 6.04 | −0.12 / 0.62 |
| Whole foot | FP | C | −35.0 / 1.9 | −2.2 / 95.2 | −1.9 / 668.2 | −0.31 / 12.60 | −8.05 / 0.04 | −0.17 / 4.22 |
| Whole foot | FP | C | −7.1 / 2.5 | −2.0 / 63.8 | −2.2 / 583.3 | −0.14 / 16.88 | −1.24 / 0.02 | −0.13 / 1.91 |
| Whole foot | FP | C | −60.1 / 0.9 | −2.1 / 78.9 | −1.8 / 615.0 | −0.21 / 13.85 | −13.86 / 0.02 | −0.16 / 5.45 |
| Whole foot | FP | C | −124.5 / 1.3 | −1.5 / 419.1 | −0.8 / 765.7 | −14.73 / 6.47 | −25.24 / −0.00 | −0.18 / 13.65 |
Results
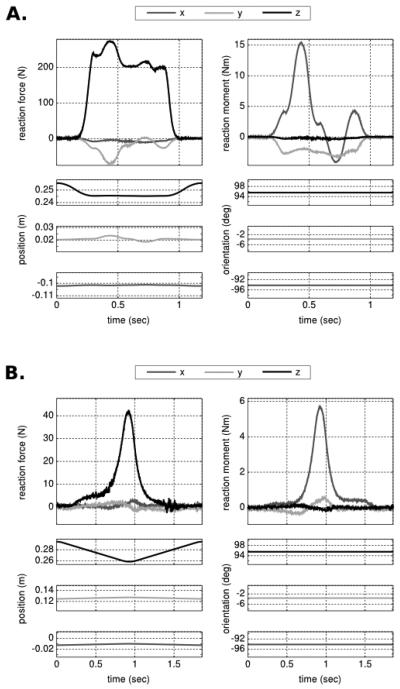
Computed tomography provided a clear differentiation of the soft tissue boundary of the foot (Fig. 1-B) and its bones (Fig 1. D). Rear foot and forefoot were tested under single and combined loading schemes using multiple tools, with forces sometimes exceeding half body weight (Table 1). Metatarsal head testing focused on indentation, whereas whole foot testing included compression up to one body weight (Table 1). The time history of the loading scenarios illustrated the evolution of reaction forces and moments as the tool was positioned to interact with the foot (Fig. 3). In combined load cases, a coupled loading response was apparent as illustrated for rear foot compression and shear (Figs. 3-A & 4). Even in a single loading case, when the tool was moved in a dominant direction, coupling was observed, potentially due to coordinate system selection and the relative alignment of the foot and load transducer (Fig. 3-B). For forefoot regions and the metatarsal heads, the response was a function of tissue deformation and arch stiffness. It is likely that this response was dictated by the tissue at low forces and the tarsometatarsal joint properties at higher forces (Fig. 3-B). In all tests, the mechanical response was nonlinear and exhibited hysteresis (Fig. 4).
Figure 3.
Time history of foot loading and tool movements presented in the load cell coordinate system. Loading corresponds to reaction forces and moments recorded at the origin of the load cell coordinate system. Kinematics describes the position and orientation of the tool coordinate system relative to the load cell coordinate system. A. Rear foot compression and shear using the elevated platform. B. Indentation of the second metatarsal head region using a small indenter (12.7 mm diameter).
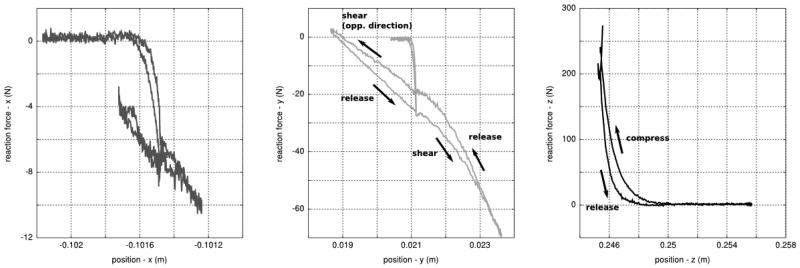
Figure 4.
Reaction forces against tool position. This representation of data from rear foot compression and shear, as applied by the elevated platform, points out the nonlinear nature of foot deformation characteristics. Hysteresis is noticeable as illustrated by the differences in loading and unloading patterns. Tool movement in the shear direction was applied at a fixed tool position in the compression direction. Reaction moments and tool orientation were not shown since tool orientation was kept constant during the test. All data were represented in the load cell coordinate system.
Discussion
The mechanical response of a cadaver foot was documented in detail, which includes the global as well as regional tissue responses for specific regions of the foot. Deformation was induced through single and combined loading modes, using multiple tools, at rates representative of daily locomotion. Regional response was qualitatively similar to those obtained previously, e.g. for the heel [6]. To expedite foot biomechanics research, the data are provided in full, freely accessible through the means described in the Appendix.
An apparent limitation of the study was the constriction of the data to a single specimen. The extent of the viscoelastic response was limited to the loading and unloading cases as we did not conduct standardized tests to adequately characterize such behavior [28]. Yet, the loading rates and scenarios utilized were representative of daily locomotion [27]. Apart from these limitations, the range of mechanical loading and the regions tested for this single foot were extensive. Complementing the mechanical response with anatomical imaging also opens many future possibilities. A certain limitation in previous computational studies [29-31], even those conducted on the foot [32], was the lack of specimen specific mechanical data, from which model parameters, e.g. material coefficients, can be estimated, and by which simulation results are validated. This study overcomes these limitations by providing data from both of these domains to build anatomically realistic and mechanically consistent models of the foot.
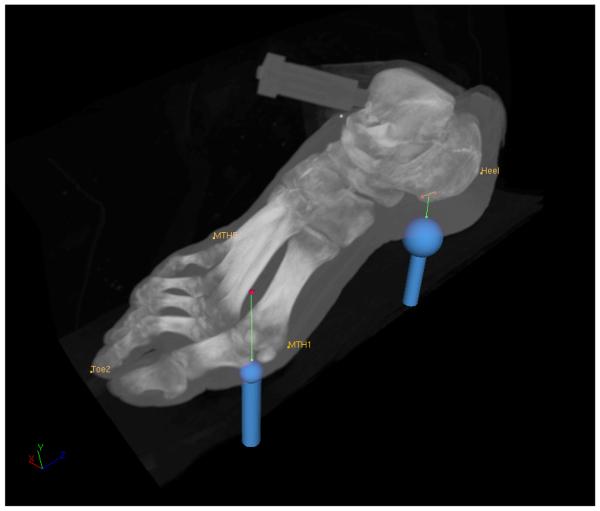
In an attempt to illustrate tool path relative to the computed tomography scan of the foot, a registration between mechanical testing data and the image set was conducted using a rigid body transformation [33]. The process utilized anatomical landmarks of the foot collected during testing and also extracted from the image sets using VolSuite (http://www.osc.edu/archive/VolSuite/). In following, different tool trajectories were overlayed on a volumetric reconstruction of the computed tomography data using VolSuite (Fig. 5). While this process can employ the registration phantom, using foot landmarks accommodates potential differences between relative forefoot and rear foot position in imaging and mechanical testing. With the advent of inverse analysis techniques utilizing anatomically detailed models obtained from such image sets [34], the loading data can be used to estimate plantar tissue properties and deformation characteristics of the joints at the arch of the foot.
Figure 5.
Tool trajectories overlayed on volumetric reconstruction of computed tomography data. Paths of the large indenter (25.4 mm diameter) during rear foot compression and shear and the small indenter (12.7 mm diameter) during compression of the first metatarsal head region are illustrated. Registration between mechanical testing data and computed tomography scans was accomplished using anatomical landmarks measured during robotic testing and extracted from images as well.
Our future work will benefit from this data set to establish comprehensively validated, anatomically detailed, and mechanically representative models of the foot using finite element analysis. The present work was limited to the passive properties of the foot. We envision that muscle function can be represented by additional line elements, in which force is generated by mathematical models of muscle contraction, e.g. [1]. The combination of both techniques will allow musculoskeletal movement simulations and for the investigation of foot tissue and joint deformations [35]. Dissemination of the whole data set will hopefully facilitate investigators in foot biomechanics to take similar paths to accommodate their research needs.
Acknowledgment
The authors are thankful for the efforts of Joshua Polster, MD, of Diagnostic Radiology, Cleveland Clinic, who made computed tomography scanning possible. Robb Colbrunn, MS, of Musculoskeletal Robotics and Mechanical Testing Core in the Department of Biomedical Engineering, Cleveland Clinic, provided expertise on robotic testing. The study was funded by the NIBIB, NIH grant 5R01EB006735, in collaboration with Simbios, NIH Center for Biomedical Computation at Stanford University. The testing facility was partially supported by the NIAMS, NIH Core Center Grant 1P30AR050953.
Appendix
Full data set, including mechanical testing and computed tomography, is freely accessible in the ‘Downloads’ section of the project web site, https://simtk.org/home/multidomain (last accessed March 13, 2009). Alternatively, interested parties can contact the authors to receive a freely available and open copy of the data set.
References
- 1.Wright IC, Neptune RR, van den Bogert AJ, Nigg BM. The influence of foot positioning on ankle sprains. Journal of Biomechanics. 2000 May.33:513–9. doi: 10.1016/s0021-9290(99)00218-3. [DOI] [PubMed] [Google Scholar]
- 2.Budhabhatti SP, Erdemir A, Petre M, Sferra J, Donley B, Cavanagh PR. Finite element modeling of the first ray of the foot: a tool for the design of interventions. Journal of Biomechanical Engineering. 2007 Oct.129:750–6. doi: 10.1115/1.2768108. [DOI] [PubMed] [Google Scholar]
- 3.Cheung JT, Zhang M. Parametric design of pressure-relieving foot orthosis using statistics-based finite element method. Medical Engineering & Physics. 2008 Apr.30:269–77. doi: 10.1016/j.medengphy.2007.05.002. [DOI] [PubMed] [Google Scholar]
- 4.Ker RF, Bennett MB, Bibby SR, Kester RC, Alexander RM. The spring in the arch of the human foot. Nature. 325:147–9. doi: 10.1038/325147a0. [DOI] [PubMed] [Google Scholar]
- 5.Fauth AR, Hamel JA, Sharkey NA. In vitro measurements of first and second tarsometatarsal joint stiffness. Journal of Applied Biomechanics. 2004 Feb.20:14–24. [Google Scholar]
- 6.Aerts P, Ker RF, De Clercq D, Ilsley DW, Alexander RM. The mechanical properties of the human heel pad: a paradox resolved. Journal of Biomechanics. 1995 Nov.28:1299–308. doi: 10.1016/0021-9290(95)00009-7. [DOI] [PubMed] [Google Scholar]
- 7.Challis JH, Murdoch C, Winter SL. Mechanical properties of the human heel pad: a comparison between populations. Journal of Applied Biomechanics. 2008 Nov.24:377–81. doi: 10.1123/jab.24.4.377. [DOI] [PubMed] [Google Scholar]
- 8.Miller-Young JE, Duncan NA, Baroud G. Material properties of the human calcaneal fat pad in compression: experiment and theory. Journal of Biomechanics. 2002 Dec.35:1523–31. doi: 10.1016/s0021-9290(02)00090-8. [DOI] [PubMed] [Google Scholar]
- 9.Ledoux WR, Blevins JJ. The compressive material properties of the plantar soft tissue. Journal of Biomechanics. 2007;40:2975–81. doi: 10.1016/j.jbiomech.2007.02.009. [DOI] [PubMed] [Google Scholar]
- 10.Freed AD, Diethelm K. Fractional calculus in biomechanics: a 3D viscoelastic model using regularized fractional derivative kernels with application to the human calcaneal fat pad. Biomechanics and Modeling in Mechanobiology. 2006 Nov.5:203–15. doi: 10.1007/s10237-005-0011-0. [DOI] [PubMed] [Google Scholar]
- 11.Huang CK, Kitaoka HB, An KN, Chao EY. Biomechanical evaluation of longitudinal arch stability. Foot & Ankle. 14:353–7. doi: 10.1177/107110079301400609. [DOI] [PubMed] [Google Scholar]
- 12.De Clercq D, Aerts P, Kunnen M. The mechanical characteristics of the human heel pad during foot strike in running: an in vivo cineradiographic study. Journal of Biomechanics. 1994 Oct.27:1213–22. doi: 10.1016/0021-9290(94)90275-5. [DOI] [PubMed] [Google Scholar]
- 13.Petre M, Erdemir A, Cavanagh PR. An MRI-compatible foot-loading device for assessment of internal tissue deformation. Journal of Biomechanics. 2008;41:470–4. doi: 10.1016/j.jbiomech.2007.09.018. [DOI] [PubMed] [Google Scholar]
- 14.Yavuz M, Erdemir A, Botek G, Hirschman GB, Bardsley L, Davis BL. Peak plantar pressure and shear locations: relevance to diabetic patients. Diabetes Care. 2007 Oct.30:2643–5. doi: 10.2337/dc07-0862. [DOI] [PubMed] [Google Scholar]
- 15.Zou D, Mueller MJ, Lott DJ. Effect of peak pressure and pressure gradient on subsurface shear stresses in the neuropathic foot. Journal of Biomechanics. 2007;40:883–90. doi: 10.1016/j.jbiomech.2006.03.005. [DOI] [PubMed] [Google Scholar]
- 16.Leardini A, Benedetti MG, Berti L, Bettinelli D, Nativo R, Giannini S. Rear-foot, mid-foot and fore-foot motion during the stance phase of gait. Gait & Posture. 2007 Mar.25:453–62. doi: 10.1016/j.gaitpost.2006.05.017. [DOI] [PubMed] [Google Scholar]
- 17.Erdemir A, Piazza SJ. Changes in foot loading following plantar fasciotomy: a computer modeling study. Journal of Biomechanical Engineering. 2004 Apr.126:237–43. doi: 10.1115/1.1691447. [DOI] [PubMed] [Google Scholar]
- 18.Camacho DLA, Ledoux WR, Rohr ES, Sangeorzan BJ, Ching RP. A three-dimensional, anatomically detailed foot model: a foundation for a finite element simulation and means of quantifying foot-bone position. Journal of Rehabilitation Research and Development. 39:401–10. [PubMed] [Google Scholar]
- 19.Chen WP, Tang FT, Ju CW. Stress distribution of the foot during mid-stance to push-off in barefoot gait: a 3-D finite element analysis. Clinical Biomechanics (Bristol, Avon) 2001 Aug.16:614–20. doi: 10.1016/s0268-0033(01)00047-x. [DOI] [PubMed] [Google Scholar]
- 20.Cheung JT, Zhang M, Leung AK, Fan Y. Three-dimensional finite element analysis of the foot during standing--a material sensitivity study. Journal of Biomechanics. 2005 May.38:1045–54. doi: 10.1016/j.jbiomech.2004.05.035. [DOI] [PubMed] [Google Scholar]
- 21.Gefen A, Megido-Ravid M, Itzchak Y, Arcan M. Biomechanical analysis of the three-dimensional foot structure during gait: a basic tool for clinical applications. Journal of Biomechanical Engineering. 2000 Dec.122:630–9. doi: 10.1115/1.1318904. [DOI] [PubMed] [Google Scholar]
- 22.Janda S, van der Helm FCT, de Blok SB. Measuring morphological parameters of the pelvic floor for finite element modelling purposes. Journal of Biomechanics. 2003 Jun.36:749–57. doi: 10.1016/s0021-9290(03)00008-3. [DOI] [PubMed] [Google Scholar]
- 23.Klein Breteler MD, Spoor CW, Van der Helm FC. Measuring muscle and joint geometry parameters of a shoulder for modeling purposes. Journal of Biomechanics. 1999 Nov.32:1191–7. doi: 10.1016/s0021-9290(99)00122-0. [DOI] [PubMed] [Google Scholar]
- 24.Lachowitzer MR, Ranes A, Yamaguchi GT. Musculotendon parameters and musculoskeletal pathways within the human foot. Journal of Applied Biomechanics. 2007 Feb.23:20–41. doi: 10.1123/jab.23.1.20. [DOI] [PubMed] [Google Scholar]
- 25.Noble LD, Colbrunn RW, Lee DG, van den Bogert AJ, Davis BL. Design and validation of a general purpose robotic testing system for musculoskeletal applications. Journal of Biomechanical Engineering. doi: 10.1115/1.4000851. in review. [DOI] [PubMed] [Google Scholar]
- 26.Sirimamilla PA. Case Western Reserve University; 2008. Elaborate experimentation for mechanical characterization of the human foot using inverse finite element analysis. MSc. [Google Scholar]
- 27.Cavanagh PR. Plantar soft tissue thickness during ground contact in walking. Journal of Biomechanics. 1999 Jun.32:623–8. doi: 10.1016/s0021-9290(99)00028-7. [DOI] [PubMed] [Google Scholar]
- 28.Fung YC. Biomechanics: Mechanical Properties of Living Tissues. Springer; 1993. [Google Scholar]
- 29.Garner BA, Pandy MG. A Kinematic Model of the Upper Limb Based on the Visible Human Project (VHP) Image Dataset. Computer Methods in Biomechanics and Biomedical Engineering. 1999;2:107–124. doi: 10.1080/10255849908907981. [DOI] [PubMed] [Google Scholar]
- 30.Noakes KF, Bissett IP, Pullan AJ, Cheng LK. Anatomically realistic three-dimensional meshes of the pelvic floor & anal canal for finite element analysis. Annals of Biomedical Engineering. 2008 Jun.36:1060–71. doi: 10.1007/s10439-008-9471-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ruan J, El-Jawahri R, Chai L, Barbat S, Prasad P. Prediction and analysis of human thoracic impact responses and injuries in cadaver impacts using a full human body finite element model. Stapp Car Crash Journal. 2003 Oct.47:299–321. doi: 10.4271/2003-22-0014. [DOI] [PubMed] [Google Scholar]
- 32.Wu L. Nonlinear finite element analysis for musculoskeletal biomechanics of medial and lateral plantar longitudinal arch of Virtual Chinese Human after plantar ligamentous structure failures. Clinical Biomechanics (Bristol, Avon) 2007 Feb.22:221–9. doi: 10.1016/j.clinbiomech.2006.09.009. [DOI] [PubMed] [Google Scholar]
- 33.Söderkvist I, Wedin PA. Determining the movements of the skeleton using well-configured markers. Journal of Biomechanics. 1993 Dec.26:1473–7. doi: 10.1016/0021-9290(93)90098-y. [DOI] [PubMed] [Google Scholar]
- 34.Erdemir A, Viveiros ML, Ulbrecht JS, Cavanagh PR. An inverse finite-element model of heel-pad indentation. Journal of Biomechanics. 2006;39:1279–86. doi: 10.1016/j.jbiomech.2005.03.007. [DOI] [PubMed] [Google Scholar]
- 35.Halloran JP, Erdemir A, van den Bogert AJ. Adaptive surrogate modeling for efficient coupling of musculoskeletal control and tissue deformation models. Journal of Biomechanical Engineering. 2009 Feb.131:011014. doi: 10.1115/1.3005333. [DOI] [PMC free article] [PubMed] [Google Scholar]