Sparse Estimation and Inference for Censored Median Regression

Abstract

Censored median regression has proved useful for analyzing survival data in complicated situations, say, when the variance is heteroscedastic or the data contain outliers. In this paper, we study the sparse estimation for censored median regression models, which is an important problem for high dimensional survival data analysis. In particular, a new procedure is proposed to minimize an inverse-censoring-probability weighted least absolute deviation loss subject to the adaptive LASSO penalty and result in a sparse and robust median estimator. We show that, with a proper choice of the tuning parameter, the procedure can identify the underlying sparse model consistently and has desired large-sample properties including root-n consistency and the asymptotic normality. The procedure also enjoys great advantages in computation, since its entire solution path can be obtained efficiently. Furthermore, we propose a resampling method to estimate the variance of the estimator. The performance of the procedure is illustrated by extensive simulations and two real data applications including one microarray gene expression survival data.

1. Introduction

In the last forty years, a variety of semiparametric survival models have been proposed for censored time-to-event data analysis. Among them, the proportional hazards model (Cox, 1972) is perhaps the most popular one and widely used in literature. However, as noted by many authors, the proportional hazards assumption may not be appropriate in some practical applications; for some problems alternative models may be more suitable. One of the attractive alternatives is the accelerated failure time (AFT) model (Kalbfleisch and Prentice, 1980; Cox and Oakes, 1984), which relates the logarithm of the failure time linearly to covariates as

$$\text{log}(T)=\beta \prime Z+\epsilon ,$$ (1)

where T is the failure time of our interest, Z is the p-dimensional vector of covariates and ε is the error term with a completely unspecified distribution that is independent of Z. Due to the linear model structure, the results of the AFT model are easier to interpret (Reid, 1994). Due to these desired properties, the AFT model has been extensively studied in the literature (Prentice, 1978; Buckley and James, 1979; Ritov, 1990; Tsiatis, 1990; Ying, 1993; Jin et al., 2003; among others).

A major assumption of the AFT model is that the error terms are i.i.d., which is often too restrictive in practice (Koenker and Geling, 2001). To handle more complicated problems, say, data with heteroscedastic or heavy-tailed error distributions, censored quantile regression provides a natural remedy. In the context of survival data analysis, Ying et al. (1995), Bang and Tsiatis (2003), and Zhou (2006), among others, considered median regression with random censoring and derived various inverse-censoring-probability weighted methods for parameter estimation; Portnoy (2003) considered a general censored quantile regression by assuming that all conditional quantiles are linear functions of the covariates and developed recursively re-weighted estimators of regression parameters. In general, quantile regression is more robust against outliers and may be more effective for nonstandard data; the regression quantiles may be well estimated even if the mean is not for censored survival data.

In many biomedical studies, a large number of predictors are often collected but not all of them are relevant for the prediction of survival times. In other words, the underlying true model has a sparse model structure in terms of the appearance of covariates in the model. For example, many cancer studies start measuring patients’ genomic information and combine it with traditional risk factors to improve cancer diagnosis and make personalized drugs. Genomic information, often in the form of gene expression patterns, is high dimensional and typically only a small number of genes contains relevant information, so the underlying model is naturally sparse. How to identify this small group of relevant genes is an important yet challenging question. Simultaneous variable selection and parameter estimation then becomes crucial since it helps to produce a parsimonious model with better risk assessment and model interpretation. There is a rich literature for variable selection in standard linear regression and survival data analysis based on the proportional hazards model. Traditional procedures include backward deletion, forward addition and stepwise selection. However, these procedures may suffer from high variability (Breiman, 1996). Recently some shrinkage methods have been proposed based on the penalized likelihood or partial likelihood estimation, including the LASSO (Tibshirani, 1996, 1997), the SCAD (Fan and Li, 2001, 2002) and the adaptive LASSO (Zou 2006, 2008; Zhang and Lu, 2007; Lu and Zhang, 2007). More recently, several authors extend the shrinkage methods to variable selection of the AFT model using the penalized rank estimation or Buckley-James’s estimation (Johnson, 2008; Johnson et al., 2008; Cai et al., 2008).

To the best of our knowledge, the sparse estimation of censored quantile regression has not been studied in the literature. When there is no censoring, Wang et al. (2007) considered the LAD-LASSO estimation for linear median regression assuming i.i.d. error terms. For nonparametric and semiparametric regression quantile models, the total variation penalty has been proposed and studied extensively, including Koenker et al. (1994), He and Shi (1996), He, Ng and Portnoy, S. (1998), He and Ng (1999), and some recent work on penalized triograms by Koenker and Mizera (2004) and on longitudinal models by Koenker (2004). The L₁ nature of the total variation penalty make it work like a model selection process for identifying a small number of spline basis functions. In this paper, we focus on the sparse estimation of censored median regression. Compared with variable selection for standard linear regression models, there are two additional challenges in censored median regression: the error distributions are not i.i.d. and the response is censored. To tackle these issues, we construct the new estimator based on an inverse-censoring-probability weighted least absolute deviation estimation method subject to some shrinkage penalty. To facilitate the selection of variables, we suggest the use of the adaptive LASSO penalty, which is shown to yield an estimator with desired properties both in theory and in computation. The proposed method can be easily extended to arbitrary quantile regression with random censoring. The remainder of the article is organized as follows. In Section 2, we develop the sparse censored median regression (SCMR) estimator for right-censored data and establish its large-sample properties, such as root-n consistency, sparsity, and asymptotic normality. Section 3 discusses the computational algorithm and solution path, and the tuning parameter issue is addressed as well. We also derive a bootstrap method for estimating the variance of the SCMR estimator. Sections 4 is devoted to simulations and real examples. Final remarks are given in Section 5. Major technical derivations are contained in the Appendix.

2. Sparse censored median regression

2.1 The SCMR estimator

Consider a study of n subjects. Let {T_i, C_i, Z_i, i = 1, … , n} denote n triplets of failure times, censoring times, and p-dimensional covariates of interest. Conditional on Z_i, the median regression model assumes

$$\text{log}(T_i)={\theta }_0^{\prime }{X}_i+{\epsilon }_i,i=1,\dots ,n,$$ (2)

where $X_i=\left(1,Z_i^{\prime }\right)\prime ,{\theta }_0=\left({\alpha }_0,{\beta }_0^{\prime }\right)\prime$ is a (p+1)-dimensional vector of regression parameters and ε_i’s are assumed to have a conditional median of 0 given covariates. Here we do not require the i.i.d. assumption for ε_i’s as in Wang et al. (2007). Note that the log transformation in (2) can be replace by any specified monotonic transformation. Define T̃_i = min(T_i, C_i) and δ_i = I(T_i ≤ C_i), then the observed data consist of (T̃_i, δ_i, Z_i, i = 1, … , n). As in Ying et al. (1995) and Zhou (2006), we assume that the censoring time C is independent of T and Z. Let G(·) denote the survival function of censoring times. To estimate the parameters θ₀, Ying et al. (1995) proposed to solve

$${\displaystyle \sum _{i=1}^n{X}_i[\frac{I\{\text{log}({\tilde{T}}_i)-\theta \prime X_i\ge 0\}}{\widehat{G}(\theta \prime X_i)}-\frac{1}{2}]=0,}$$

where Ĝ(·) is the Kaplan-Meier estimator of G(·) based on the data (T̃_i, 1 − δ_i), i = 1, … , n. Note that the above equation is neither continuous nor monotone in θ and thus is difficult to solve especially when the dimension of θ is high. Instead, Bang and Tsiatis (2003) proposed an alternative inverse censoring-probability weighted estimating equation as follows:

$${\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}{X}_i[I\{\text{log}({\tilde{T}}_i)-\theta \prime X_i\ge 0\}-\frac{1}{2}]=0.}$$

As pointed out by Zhou (2006), the solution of the above equation is also a minimizer of

$${\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}}\left|\text{log}({\tilde{T}}_i)-\theta \prime X_i\right|,$$ (3)

which is convex in θ and can be easily solved using an efficient linear programming algorithm of Koenker and D’Orey (1987). In addition, Zhou (2006) showed that the above inverse censoring probability weighted least absolute deviation estimator has better finite sample performance than that of Ying et al. (1995).

To conduct variable selection for censored median regression, we propose to minimize

$${\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}}\left|\text{log}({\tilde{T}}_i)-\theta \prime X_i\right|+n{\displaystyle \sum _{j=1}^p{J}_{\mathrm{\lambda }}(|{\beta }_j|)},$$ (4)

where the penalty J_λ is chosen to achieve simultaneous selection and coefficient estimation. Two popular choices include the LASSO penalty J_λ(|β_j|) = λ|β_j| and the SCAD penalty (Fan and Li, 2001). In this paper, we consider an alternative regularization framework using the adaptive LASSO penalty (Zou, 2006; Zhang and Lu, 2007; Wang et al., 2007; among others). Specifically, let θ̃ ≡ (α̃, β̃′)′ denote the minimizer of (3). Our SCMR estimator is defined as the minimizer of

$${\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}}\left|\text{log}({\tilde{T}}_i)-\theta \prime X_i\right|+n\mathrm{\lambda }{\displaystyle \sum _{j=1}^p\frac{\left|{\beta }_j\right|}{\left|{\tilde{\beta }}_j\right|}},$$ (5)

where λ > 0 is the tuning parameter and β̃ = (β̃₁, … , β̃_p)′. Note the estimators from (3) are used as the weights to leverage the LASSO penalty in (5). The the adaptive LASSO procedure has been shown to achieve consistent variable selection asymptotically in various scenarios when the tuning parameter λ is chosen properly.

2.2 Theoretical properties of SCMR estimator

Suppose that ${\beta }_0=\left({\beta }_{a,0}^{\prime },{\beta }_{b,0}^{\prime }\right)\prime$ and is arranged so that β_a,0 = (β₁₀, … , _βq0)′ ≠ 0 and β_b,0 = (β_(q+1)0, … , β_p0)′ = 0. Here it is assumed that the length of β_a,0 is q. Correspondingly, denote the minimizer of (5) by $\widehat{\theta }={\left(\widehat{\alpha },{\widehat{\beta }}_a^{\prime },{\widehat{\beta }}_b^{\prime }\right)}^{\prime }$. Define ${\theta }_{a,0}=\left({\alpha }_0,{\beta }_{a,0}^{\prime }\right)\prime ,{\widehat{\theta }}_a={\left(\widehat{\alpha },{\widehat{\beta }}_a^{\prime }\right)}^{\prime }\text{and}{b}_1={\left(\frac{\mathit{\text{sign}}\left({\beta }_1\right)}{\left|{\beta }_1\right|},\dots ,\frac{\mathit{\text{sign}}({\beta }_q)}{\left|{\beta }_q\right|}\right)}^{\prime }$. Under the regularity conditions given in the Appendix, we have the following two theorems.

Theorem 1

$\left(\sqrt{n}-\text{Consistency}\right)$ If $\sqrt{n}\mathrm{\lambda }=O_p\left(1\right)$, then $\sqrt{n}\Vert \widehat{\theta }-{\theta }_0\Vert =O_p\left(1\right)$.

Theorem 2

If $\sqrt{n}\mathrm{\lambda }\to {\mathrm{\lambda }}_0\ge 0$ and nλ → ∞, then as n → ∞

1. (Selection-Consistency) P (β̂_b = 0) → 1.

2. (Asymptotic Normality) $\sqrt{n}\left({\widehat{\theta }}_a-{\theta }_{a,0}\right)$ converges in distribution to a normal random vector with mean −Σ_a′λ₀b₁ and variance-covariance matrix ${\mathrm{\Sigma }}_a^{-1}{V}_a{\mathrm{\Sigma }}_a^{-1}$.

The definitions of Σ_a and V_a, and the proofs of Theorems 1 and 2 are given in the Appendix.

3. Computation, parameter tuning and variance estimation

3.1. Computational algorithm using linear programming

Given a fixed tuning parameter λ, we suggest the following algorithm to compute the SCMR estimator. First, we reformulate (5) as a least absolute deviation problem without penalty. To be specific, we define,

$$(X^{*})\prime ={\left(\begin{array}{cccc}\frac{{\delta }_1}{\widehat{G}({\tilde{T}}_1)}& \frac{{\delta }_1}{\widehat{G}({\tilde{T}}_1)}{X}_{11}& \cdots & \frac{{\delta }_1}{\widehat{G}({\tilde{T}}_1)}{X}_{1p}\\ \hfill \mathrm{..............}& \hfill \mathrm{...................}& \hfill \mathrm{........}& \hfill \mathrm{...................}\\ \frac{{\delta }_n}{\widehat{G}({\tilde{T}}_n)}& \frac{{\delta }_n}{\widehat{G}({\tilde{T}}_n)}{X}_{n1}& \cdots & \frac{{\delta }_n}{\widehat{G}({\tilde{T}}_n)}{X}_{np}\\ 0& \frac{n\lambda }{\left|{\tilde{\beta }}_1\right|}& \cdots & 0\\ \hfill \mathrm{..............}& \hfill \mathrm{...................}& \hfill \mathrm{........}& \hfill \mathrm{...................}\\ 0& 0& \cdots & \frac{n\lambda }{\left|{\tilde{\beta }}_p\right|}\end{array}\right)}_{(n+p)\times (p+1)},$$

$$Y^{*}={\left(\frac{{\delta }_1}{\widehat{G}({\tilde{T}}_1)}\text{log}({\tilde{T}}_1),\cdots ,\frac{\delta }{\widehat{G}({\tilde{T}}_n)}\text{log}({\tilde{T}}_n),0,\cdots ,0\right)}_{(n+p)\times 1}^{\prime }.$$

Then, with λ fixed, minimizing (5) is equivalent to minimizing

$${\displaystyle \sum _{i=1}^n\left|Y^{*}-\theta \prime X_i^{*}\right|,}$$

which can be easily computed using any statistical software for linear programming, for example, the rq function in R.

3.2. Solution path

Efron et al. (2004) proposed an efficient path algorithm called LARS to get the entire solution path of LASSO, which can greatly reduce the computation cost of model fitting and tuning. Recently, Li and Zhu (2008) modified the LARS algorithm to get the solution paths of the sparse quantile regression with uncensored data. It turns out that the SCMR estimator also has a solution path linear in λ. In order to compute the entire solution path of SCMR, we first modify the algorithm of Li and Zhu (2008) to compute the solution path of a weighted quantile regression subject to the LASSO penalty

$${\displaystyle \sum _{i=1}^n{w}_i\left|Y_i-\theta \prime X_i\right|+n\mathrm{\lambda }{\displaystyle \sum _{j=1}^p\left|{\beta }_j\right|.}}$$ (6)

In our SCMR estimators, the weight w_i = δ_i/Ĝ(T̃_i). The corresponding R codes are available from the authors.

Next we propose the following algorithm to compute the solution path of the SCMR estimator with the adaptive LASSO penalty.

• Step 1: Create working data $X_i^{**}\equiv \left(1,Z_{i1}^{*},\dots ,Z_{\mathit{\text{ip}}}^{*}\right)\prime$ with $Z_{\mathit{\text{ij}}}^{*}=Z_{\mathit{\text{ij}}}\left|{\tilde{\beta }}_j\right|$ for i = 1, … , n; j = 1, … , p.

• Step 2: Applying the solution path algorithm for (6), solve

  $$\widehat{\gamma }={\text{arg min}}_{\gamma }{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}\left|Y-\gamma \prime X_i^{**}\right|+n\mathrm{\lambda }{\displaystyle \sum _{j=2}^{p+1}\left|{\gamma }_j\right|}.}$$

• Step 3: Define α̂ = γ̂₁ and β̂_j = γ̂_j+1|β̃_j | for _j = 1, … , p

.

Note that the above two computation methods give exactly the same solutions for a common λ. But the solution path method is more effective since it produce the whole solution path, while the first method is more convenient to combine with the bootstrap method to compute the variance of the SCMR estimator for a given λ.

3.3. Parameter tuning

Our estimator makes use of the adaptive LASSO penalty, i.e., a penalty of the form $\mathrm{\lambda }{\displaystyle {\sum }_{j=1}^p\frac{\left|{\beta }_j\right|}{\left|{\tilde{\beta }}_j\right|}}$, where β̃ is the unpenalized LAD estimator. We propose to tune the parameter λ based on a BIC-type criteria. Note that if there is no censoring and the error terms are i.i.d., the least absolute deviation loss is closely related to linear regression with double exponential error. To derive the BIC-type tuning procedure, we make use of this connection. More specifically, assume that the error term ε_i’s are i.i.d. double exponential variables with the scale parameter σ. When there is no censoring, up to a constant the negative log likelihood function can be written as ${\displaystyle {\sum }_{i=1}^n\left|\text{log}\left(T_i\right)-\theta \prime X_i\right|/\sigma }$ and the maximum likelihood estimator of σ is given by $\left(1/n\right){\displaystyle {\sum }_{i=1}^n\left|\text{log}\left(T_i\right)-\tilde{\theta }\prime X_i\right|}$ with θ̃ being the LAD estimator. Motivated by this observation, we propose the following tuning procedure for sparse censored median regression:

$$\mathit{\text{BIC}}(\mathrm{\lambda })=\frac{2}{\tilde{\sigma }}{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}\left|\text{log}({\tilde{T}}_i)-X_i^{\prime }\widehat{\theta }(\mathrm{\lambda })\right|+\text{log}(n)r,}$$

where $\tilde{\sigma }=\left(1/n\right){\displaystyle {\sum }_{i=1}^n\frac{{\delta }_i}{\widehat{G}\left({\tilde{T}}_i\right)}\left|\text{log}\left({\tilde{T}}_i\right)-X_i^{\prime }\tilde{\theta }\right|}$ and r is the number of non-zero elements in β̂(λ). Then we minimize the above criteria over a range of values of λ for choosing the best tuning parameter.

3.4. Variance estimation

Next, we propose a bootstrap method to estimate the variance of our estimator. Specifically, we first take a large number of random samples of size n (with replacement) from the observed data. Then for the kth bootstrapped data $\left({\tilde{T}}_i^{\left(k\right)},{\delta }_i^{\left(k\right)},X_i^{\left(k\right)},i=1,\dots ,n\right)$, we compute the Kaplan-Meier estimator Ĝ^(k)(·) and the inverse censoring probability weighted least absolute deviation estimator θ̃ ^(k). Lastly, we compute the bootstrapped estimate θ̂ ^(k) by minimizing

$${\displaystyle \sum _{i=1}^n\frac{{\delta }_i^{(k)}}{{\widehat{G}}^{(k)}({\tilde{T}}_i^{(k)})}\left|\text{log}({\tilde{T}}_i^{(k)})-\theta \prime X_i^{(k)}\right|+n\mathrm{\lambda }{\displaystyle \sum _{j=1}^p\frac{\left|{\beta }_j\right|}{\left|{\tilde{\beta }}_j^{(k)}\right|}.}}$$

Here for saving the computation cost, we fixed λ at the optimal value chosen by each tuning method based on the original data.

4. Numerical studies

4.1 Simulation studies

In this section, we examine the finite sample performance of the proposed SCMR estimator in terms of variable selection and model estimation. In addition, we conduct a series of sensitivity analyses to check the performance of our estimator when the random censoring assumption is violated.

The failure times are generated from the median regression model (2). Four error distributions are considered: t(5) distribution, double exponential distribution with median 0 and scale parameter 1, standard extreme value distribution, and standard logistic distribution. Since the standard extreme value distribution has median log(log(2)) rather than 0, we subtract its median. We consider eight covariates, which are i.i.d. standard normal random variables. The regression parameter vector is chosen as β₀ = (0.5, 1, 1.5, 2, 0, 0, 0, 0) with the intercept α₀ = 1. The censoring times are generated from a uniform distribution on (0, c), where c is a constant to obtain the desired censoring level. We consider two censoring rates: 15% and 30%. For each censoring rate, we consider samples of sizes 50, 100, and 200. For each setting, we conduct 100 runs of simulations.

For comparisons, we fit six different estimators in our analysis, namely the full model estimator β̃ (called “Full” in the Tables), our SCMR estimators with the adaptive Lasso penalty (“SCMR-A”), the Lasso penalty (“SCMR-L”), and the SCAD penalty (“SCMR-S”), the naive estimator with the adaptive Lasso penalty (“Naive”) in which the censoring information was ignored and all the observed event times were treated as failure times, and the oracle estimator assuming the true model were known (“Oracle”). To obtain the SCMR-S estimator, we use the local linear approximation (LLA) algorithm by Zou and Li (2008). Various estimators are compared with regard to their overall mean absolute deviation (MAD), point estimation accuracy, and the variable selection performance. Here the MAD of an estimator θ̂ is given by

$$\mathit{\text{MAD}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|\widehat{\theta }\prime X_i-{\theta }_0^{\prime }{X}_i\right|}.$$

We summarize the overall model estimation and variable selection results of different estimators in Tables 1 and 3, in terms of the MAD, the selection frequency of each variable, the frequency of selecting the exact true model, and the mean number of incorrect and correct zeros selected over 100 simulation runs. To simplify the presentation, we only present the results for t(5) and double exponential error distributions; the results for other error distributions have similar patterns and hence omitted. In terms of model estimation, the MAD of the SCMR-A and SCMR-S estimators are smaller than those of the SCMR-L and Full estimators in all the settings, and are also close to the oracle estimator when the sample size is large and the censoring proportion is low. With regard to variable selection, compared with the Full and SCMR-L estimators, the SCMR-A and SCMR-S estimators produce more sparse models and select the exact true model more frequently. For example, when n = 200, censoring rate is 15% and the error distribution is t(5), the frequencies of selecting true model (SF) are: Oracle (100), SCMR-A (72), SCMR-L (22), SCMR-S (72), Naive (69), and Full (0). In average, the numbers of correct/incorrect zeros in the estimators are: Oracle (4/0), SCMR-A (3.67/0), SCMR-L (2.59/0), SCMR-S (3.63/0), Naive (3.65/0), and Full (0/0). In summary, the SCMR-A and SCMR-S estimators give comparable performance in both estimation and variable selection, which is not surprising since they are both selection consistenct and have the same asymptotic distribution. In addition, the naive estimator has the biggest MAD in all settings since it is a biased estimator, but it is interesting to note that it selects variables well.

Table 1.

Variable selection results for t(5) error distribution

Prop.	n	Methods	MAD	β1	β2	β3	β4	β5	β6	β7	β8	SF	Inc.	Cor.
15%	100	Full	0.39	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.36	92	100	100	100	13	13	26	10	51	0.08	3.38
		SCMR-L	0.41	98	100	100	100	35	42	46	37	16	0.02	2.40
		SCMR-S	0.35	97	100	100	100	15	14	16	15	57	0.03	3.40
		Naive	0.46	90	100	100	100	5	9	15	14	63	0.10	3.57
		Oracle	0.31	100	100	100	100	0	0	0	0	100	0	4
	200	Full	0.28	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.25	100	100	100	100	9	7	8	9	72	0	3.67
		SCMR-L	0.31	100	100	100	100	40	29	36	36	22	0	2.59
		SCMR-S	0.24	100	100	100	100	9	8	10	10	72	0	3.63
		Naive	0.38	100	100	100	100	5	9	12	9	69	0	3.65
		Oracle	0.23	100	100	100	100	0	0	0	0	100	0	4
30%	100	Full	0.50	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.48	87	100	100	100	17	21	26	12	41	0.13	3.24
		SCMR-L	0.56	93	100	100	100	47	49	52	46	8	0.07	2.06
		SCMR-S	0.47	85	100	100	100	12	14	16	19	50	0.15	3.39
		Naive	0.84	79	100	100	100	10	6	12	21	49	0.21	3.51
		Oracle	0.40	100	100	100	100	0	0	0	0	100	0	4
	200	Full	0.41	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.40	99	100	100	100	13	10	13	13	67	0.01	3.51
		SCMR-L	0.47	100	100	100	100	39	46	36	41	18	0	2.38
		SCMR-S	0.36	95	100	100	100	7	9	17	12	63	0.05	3.55
		Naive	0.78	97	100	100	100	5	8	11	12	69	0.03	3.64
		Oracle	0.36	100	100	100	100	0	0	0	0	100	0	4

Prop.: censoring proportion; MAD: mean absolute deviation across 100 runs; SF: number of times the true model is chosen among 100 runs; Inc. and Cor.: mean number of incorrect and correct 0 selected respectively.

Table 3.

Variable selection results for Double Exponential error distribution

Prop.	n	Methods	MAD	β1	β2	β3	β4	β5	β6	β7	β8	SF	Inc.	Cor.
15%	100	Full	0.36	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.32	94	100	100	100	13	7	9	12	64	0.06	3.59
		SCMR-L	0.39	96	100	100	100	42	37	39	31	17	0.04	2.51
		SCMR-S	0.31	94	100	100	100	16	9	12	11	62	0.06	3.52
		Naive	0.41	94	100	100	100	12	9	11	7	67	0.06	3.61
		Oracle	0.26	100	100	100	100	0	0	0	0	100	0	4
	200	Full	0.24	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.21	100	100	100	100	6	3	8	7	79	0	3.76
		SCMR-L	0.28	100	100	100	100	32	29	31	39	29	0	2.69
		SCMR-S	0.20	100	100	100	100	6	2	5	5	84	0	3.82
		Naive	0.36	100	100	100	100	7	6	10	11	73	0	3.66
		Oracle	0.19	100	100	100	100	0	0	0	0	100	0	4
30%	100	Full	0.47	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.47	88	100	100	100	16	19	8	15	47	0.12	3.42
		SCMR-L	0.53	92	100	100	100	41	44	44	44	16	0.08	2.27
		SCMR-S	0.44	90	100	100	100	12	20	10	12	51	0.10	3.46
		Naive	0.80	72	100	100	100	14	11	10	12	42	0.28	3.53
		Oracle	0.38	100	100	100	100	0	0	0	0	100	0	4
	200	Full	0.36	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.35	99	100	100	100	8	11	15	9	65	0.01	3.57
		SCMR-L	0.43	99	100	100	100	41	34	39	37	17	0.01	2.49
		SCMR-S	0.33	99	100	100	100	8	9	14	8	68	0.01	3.61
		Naive	0.78	96	100	100	100	8	7	11	9	70	0.04	3.65
		Oracle	0.31	100	100	100	100	0	0	0	0	100	0	4

The notations are the same as in Table 1.

The point estimation results of the first three non-zero coefficients are summarized in Tables 2 and 4, including the bias and sample standard deviation of the estimates over 100 runs, and the mean of the estimated standard errors based on 500 bootstraps per run. Based on the results, the naive estimator showed big biases as we expected; the biases of all other estimators are relatively small particularly when the sample size is large and the censoring proportion is low. In addition, the estimated standard errors obtained using the proposed bootstrap method are reasonably close to the sample standard deviations in all scenarios.

Table 2.

Estimation of non-zero coefficients for t(5) error distribution

			β1 = 0.5			β2 = 1			β3 = 1.5
Prop.	n	Methods	Bias	SD	SE	Bias	SD	SE	Bias	SD	SE
15%	100	Full	0.016	0.154	0.195	−0.056	0.158	0.195	−0.069	0.189	0.193
		SCMR-A	−0.052	0.184	0.196	−0.084	0.155	0.193	−0.098	0.186	0.189
		SCMR-L	−0.074	0.160	0.180	−0.144	0.164	0.187	−0.166	0.187	0.188
		SCMR-S	−0.027	0.183	0.217	−0.059	0.165	0.209	−0.074	0.183	0.201
		Naive	−0.126	0.188	0.185	−0.175	0.155	0.184	−0.222	0.174	0.181
		Oracle	0.007	0.151	0.178	−0.062	0.156	0.177	−0.065	0.181	0.177
	200	Full	−0.015	0.109	0.122	−0.038	0.102	0.124	−0.063	0.120	0.120
		SCMR-A	−0.041	0.112	0.127	−0.050	0.104	0.123	−0.078	0.121	0.118
		SCMR-L	−0.065	0.124	0.120	−0.095	0.113	0.122	−0.126	0.130	0.118
		SCMR-S	−0.020	0.116	0.141	−0.037	0.102	0.129	−0.063	0.122	0.131
		Naive	−0.077	0.119	0.117	−0.135	0.098	0.115	−0.193	0.102	0.114
		Oracle	−0.015	0.113	0.116	−0.039	0.098	0.119	−0.065	0.119	0.116
30%	100	Full	−0.054	0.206	0.237	−0.094	0.201	0.232	−0.134	0.220	0.237
		SCMR-A	−0.137	0.222	0.233	−0.137	0.218	0.229	−0.185	0.212	0.231
		SCMR-L	−0.125	0.201	0.214	−0.185	0.224	0.222	−0.254	0.223	0.230
		SCMR-S	−0.102	0.233	0.252	−0.098	0.212	0.261	−0.15	0.205	0.258
		Naive	−0.196	0.206	0.186	−0.33	0.172	0.198	−0.437	0.183	0.196
		Oracle	−0.055	0.190	0.212	−0.09	0.206	0.209	−0.156	0.190	0.214
	200	Full	−0.022	0.134	0.151	−0.092	0.143	0.155	−0.137	0.146	0.145
		SCMR-A	−0.073	0.163	0.156	−0.105	0.144	0.154	−0.15	0.143	0.143
		SCMR-L	−0.081	0.144	0.147	−0.153	0.145	0.151	−0.215	0.154	0.143
		SCMR-S	−0.054	0.169	0.170	−0.083	0.139	0.169	−0.132	0.137	0.170
		Naive	−0.159	0.128	0.128	−0.292	0.117	0.126	−0.435	0.113	0.129
		Oracle	−0.035	0.141	0.140	−0.084	0.141	0.145	−0.133	0.140	0.139

SD: sample standard deviation of estimates; SE: mean of estimated standard errors computed based on 500 bootstraps.

Table 4.

Estimation of non-zero coefficients for Double Exponential error distribution

			β1 = 0.5			β2 = 1			β3 = 1.5
Prop.	n	Methods	Bias	SD	SE	Bias	SD	SE	Bias	SD	SE
15%	100	Full	−0.004	0.144	0.204	−0.043	0.168	0.206	−0.074	0.174	0.204
		SCMR-A	−0.078	0.183	0.206	−0.070	0.169	0.202	−0.083	0.172	0.194
		SCMR-L	−0.091	0.172	0.187	−0.126	0.170	0.196	−0.148	0.187	0.192
		SCMR-S	−0.045	0.193	0.214	−0.047	0.165	0.214	−0.057	0.157	0.199
		Naive	−0.107	0.167	0.176	−0.146	0.146	0.179	−0.184	0.144	0.172
		Oracle	−0.017	0.146	0.180	−0.037	0.150	0.178	−0.053	0.158	0.173
	200	Full	−0.030	0.088	0.118	−0.047	0.094	0.115	−0.063	0.105	0.114
		SCMR-A	−0.057	0.095	0.121	−0.061	0.093	0.112	−0.074	0.104	0.110
		SCMR-L	−0.086	0.093	0.115	−0.109	0.101	0.113	−0.132	0.113	0.110
		SCMR-S	−0.037	0.098	0.141	−0.045	0.091	0.124	−0.064	0.101	0.125
		Naive	−0.083	0.096	0.115	−0.138	0.087	0.108	−0.186	0.095	0.110
		Oracle	−0.027	0.085	0.109	−0.043	0.091	0.105	−0.063	0.100	0.105
30%	100	Full	−0.031	0.168	0.270	−0.078	0.191	0.257	−0.140	0.199	0.271
		SCMR-A	−0.100	0.213	0.265	−0.123	0.190	0.256	−0.192	0.205	0.263
		SCMR-L	−0.109	0.199	0.244	−0.159	0.190	0.245	−0.241	0.217	0.258
		SCMR-S	−0.077	0.215	0.244	−0.076	0.185	0.274	−0.161	0.198	0.272
		Naive	−0.227	0.209	0.176	−0.282	0.17	0.202	−0.415	0.167	0.194
		Oracle	−0.021	0.178	0.237	−0.072	0.184	0.228	−0.143	0.190	0.234
	200	Full	−0.060	0.107	0.152	−0.099	0.111	0.147	−0.112	0.118	0.150
		SCMR-A	−0.095	0.116	0.156	−0.118	0.112	0.144	−0.130	0.125	0.145
		SCMR-L	−0.113	0.116	0.147	−0.165	0.120	0.142	−0.194	0.133	0.144
		SCMR-S	−0.072	0.121	0.173	−0.094	0.111	0.169	−0.115	0.128	0.168
		Naive	−0.170	0.128	0.131	−0.301	0.107	0.127	−0.428	0.118	0.127
		Oracle	−0.054	0.105	0.141	−0.095	0.109	0.135	−0.112	0.123	0.137

The notations are the same as in Table 2.

Next, we conduct a series of sensitivity analyses to check the performance of our estimator when the random censoring assumption is violated. More specifically, the censoring times are now generated as $C_i=e^{\xi X_{1i}}{C}_i^{*}$, i = 1, … , n, where $C_i^{*}’s$ are from a uniform distribution on (0, c) as before. We consider two values of ξ : ξ = 0.1 or 0.2, two censoring rates: 15% and 50%, and two sample sizes: n = 100 or 500. Other settings remain the same as before. The estimation and variable selection results are for ξ = 0.2 with t(5) error distribution are summarized in Tables 5 and 6, respectively. The results for ξ = 0.1 and other error distributions are quite similar, which are omitted here. Based on the results reported in Tables 5 and 6, we observe similar findings as before. The SCMR-A estimator showed much better performance in terms of variable selection compared with the SCMR-L and the Full estimators, although all the methods may produce certain biases in point estimation as expected.

Table 5.

Sensitivity Analysis: variable selection results for t(5) error distribution

Prop.	n	Methods	MAD	β1	β2	β3	β4	β5	β6	β7	β8	SF	Inc.	Cor.
15%	100	Full	0.38	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.33	95	100	100	100	10	15	25	9	56	0.05	3.41
		SCMR-L	0.40	98	100	100	100	41	43	42	39	19	0.02	2.35
		Oracle	0.29	100	100	100	100	0	0	0	0	100	0	4
	500	Full	0.20	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.18	100	100	100	100	5	6	8	9	80	0	3.72
		SCMR-L	0.23	100	100	100	100	27	31	24	28	31	0	2.90
		Oracle	0.17	100	100	100	100	0	0	0	0	100	0	4
50%	100	Full	0.76	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.79	84	98	99	100	20	18	19	26	30	0.19	3.17
		SCMR-L	0.90	90	99	99	100	44	43	42	51	11	0.12	2.20
		Oracle	0.71	100	100	100	100	0	0	0	0	100	0	4
	500	Full	0.60	100	100	100	100	100	100	100	100	0	0	0
		SCMR-A	0.61	100	100	100	100	13	14	8	14	62	0	3.51
		SCMR-L	0.69	100	100	100	100	47	39	50	47	12	0	2.17
		Oracle	0.58	100	100	100	100	0	0	0	0	100	0	4

The notations are the same as in Table 1.

Table 6.

Sensitivity Analysis: estimation of non-zero coefficients for t(5) error distribution

			β1 = 0.5			β2 = 1			β3 = 1.5
Prop.	n	Methods	Bias	SD	SE	Bias	SD	SE	Bias	SD	SE
15%	100	Full	0.017	0.187	0.194	−0.047	0.145	0.196	−0.067	0.142	0.197
		SCMR-A	−0.047	0.195	0.196	−0.076	0.150	0.197	−0.097	0.156	0.193
		SCMR-L	−0.055	0.188	0.182	−0.141	0.156	0.193	−0.148	0.159	0.191
		Oracle	0.003	0.168	0.178	−0.037	0.143	0.182	−0.072	0.146	0.182
	500	Full	0.011	0.076	0.072	−0.035	0.078	0.072	−0.070	0.067	0.073
		SCMR-A	−0.003	0.078	0.073	−0.044	0.079	0.071	−0.074	0.072	0.072
		SCMR-L	−0.027	0.081	0.071	−0.087	0.082	0.072	−0.123	0.075	0.072
		Oracle	0.014	0.077	0.070	−0.034	0.079	0.070	−0.067	0.072	0.071
50%	100	Full	−0.013	0.238	0.342	−0.167	0.216	0.346	−0.261	0.247	0.348
		SCMR-A	−0.058	0.261	0.328	−0.229	0.244	0.344	−0.316	0.281	0.342
		SCMR-L	−0.064	0.234	0.302	−0.272	0.219	0.323	−0.395	0.294	0.326
		Oracle	0.025	0.237	0.324	−0.166	0.230	0.323	−0.284	0.271	0.312
	500	Full	0.020	0.135	0.139	−0.182	0.110	0.141	−0.249	0.131	0.141
		SCMR-A	0.004	0.144	0.142	−0.206	0.128	0.140	−0.275	0.132	0.139
		SCMR-L	−0.010	0.144	0.135	−0.242	0.119	0.138	−0.322	0.141	0.139
		Oracle	0.023	0.136	0.134	−0.181	0.119	0.134	−0.256	0.131	0.136

The notations are the same as in Table 2.

4.2 PBC data

The primary biliary cirrhosis (PBC) data was collected at the Mayo clinic between 1974 and 1984. This data is given in Therneau and Grambsch (2000). In this study, 312 patients from a total of 424 patients who agreed to participate in the randomized trial are eligible for the analysis. Of those, 125 patients died before the end of follow-up. We study the dependence of the survival time on the following selected covariates: (1) continuous variables: age (in years), alb (albumin in g/dl), alk (alkaline phosphatase in U/liter), bil (serum bilirunbin in mg/dl), chol (serum cholesterol in mg/dl), cop (urine copper in µg/day), plat (platelets per cubic ml/1000), prot (prothrombin time in seconds), sgot (liver enzyme in U/ml), trig (triglycerides in mg/dl); (2) categorical variables: asc (0, absence of ascites; 1, presence of ascites), ede (0 no edema; 0.5 untreated or successfully treated; 1 unsuccessfully treated edema), hep (0, absence of hepatomegaly; 1, presence of hepatomegaly), sex (0 male; 1 female), spid (0, absence of spiders; 1, presence of spiders), stage (histological stage of disease, graded 1, 2, 3 or 4), trt (1 control, 2 treatment).

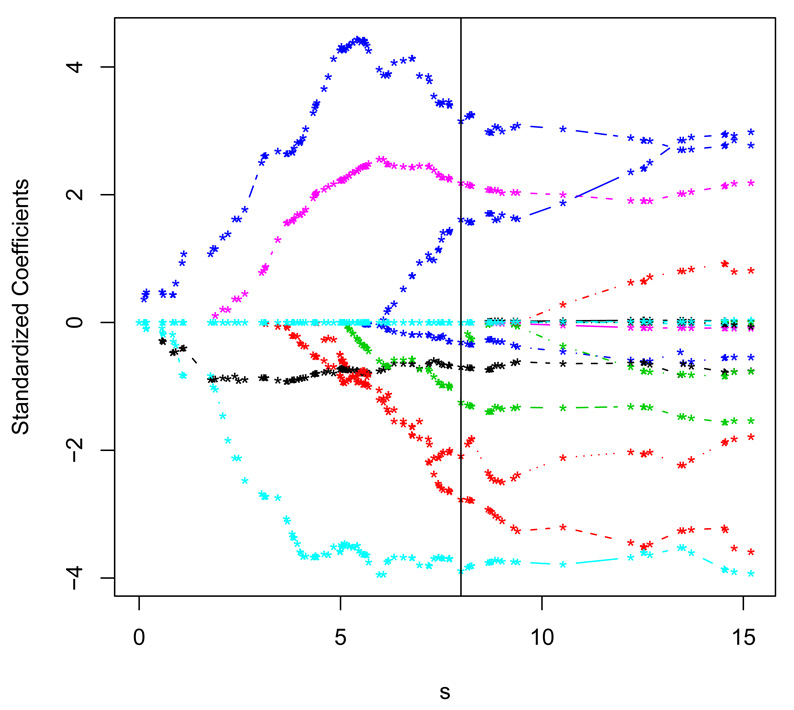
The PBC data has been previously analyzed by a number of authors using various estimation and variable selection methods. For example, Tibshirani (1997) fitted the proportional hazards model with the stepwise selection and with the LASSO penalty. Zhang and Lu (2007) further studied the PBC data using the penalized partial likelihood estimation method with the SCAD and the adaptive Lasso penalty. Here, we apply the proposed SCMR method to the PBC data. As in Tibshirani (1997) and Zhang and Lu (2007), we restrict our attention to the 276 observations without missing values. Among these 276 patients, there are 111 deaths, about 60% of censoring. Table 7 summarizes the estimated coefficients and the standard errors for the Full, the SCMR-L, the SCMR-A and the SCMR-S. We found that the SCMR-A selects 9 variables: age, asc, oed, bil, alb, cop, alk, plat and prot and the SCMR-L selects 13 variables which contain the 9 variables selected by the SCMR-A. Moreover, the 9 variables selected by SCMR-A shared 6 variables out of 8 selected by the penalized partial likelihood estimation method of Zhang and Lu (2007) in the proportional hazards model. We also plot the solution path of the SCMR-A estimator in Figure 1.

Table 7.

Estimation and variable selection for PBC data with censored median regression.

	Full	SCMR-A	SCMR-L	SCMR-S
Intercept	7.62 (0.44)	7.72 (0.40)	7.83 (0.45)	7.71 (0.42)
trt	0.04 (0.14)	0 (−)	0 (−)	0 (−)
age	−3.29 (1.50)	−2.77 (1.36)	−0.93 (0.94)	−2.49 (1.43)
sex	0.03 (0.28)	0 (−)	0.04 (0.24)	0 (−)
asc	−0.57 (0.83)	−0.31 (0.83)	−0.31 (0.81)	0 (−)
hep	−0.05 (0.17)	0 (−)	0.02 (0.17)	0 (−)
spid	−0.09 (0.20)	0 (−)	0 (−)	0 (−)
oed	−0.75 (0.63)	−0.70 (0.61)	−0.70 (0.65)	−0.96 (0.45)
bil	−1.71 (3.24)	−2.09 (3.25)	−1.56 (2.43)	−2.79 (3.68)
chol	−0.87 (3.50)	0 (−)	−0.64 (1.23)	−0.67 (3.07)
alb	2.96 (1.33)	3.16 (1.28)	3.54 (1.17)	2.70 (1.42)
cop	−4.00 (1.97)	−3.89 (1.87)	−2.61 (1.57)	−3.53 (2.02)
alk	2.16 (1.02)	2.19 (0.97)	2.11 (0.87)	2.31 (1.42)
sgot	−0.20 (1.84)	0 (−)	0 (−)	0 (−)
trig	1.16 (2.11)	0 (−)	0 (−)	0.37 (1.74)
plat	−1.61 (1.11)	−1.25 (0.90)	−1.12 (0.67)	−1.48 (0.92)
prot	2.58 (2.31)	1.62 (2.23)	0.93 (1.85)	2.17 (2.72)
stage	0.03 (0.10)	0 (−)	−0.05 (0.09)	0 (−)

Figure 1.

The solution path of our SCMR-A estimator for PBC data. The solid vertical line denotes the resulting estimator tuned with the proposed BIC criterion.

4.3 DLBCL microarray data

Sparse model estimation has wide applications in high dimensional data analysis. In this example, we apply the SCMR method to the high dimensional microarray gene expression data of Rosenwald et al. (2002). The data consists of survival times of 240 diffuse large B-cell lymphoma (DLBCL) patients, and the expressions of 7, 399 genes for each patient. Among them, 138 patients died during the follow-up method. The main goals of the study are to identify the important genes that can predict patients’ survival and to study their effects on survival. This data was analyzed by Li and Luan (2005). To handle such high dimensional data, a common practice is to first conduct a preliminary gene filtering based on some univariate analysis, and then apply a more sophisticated model-based analysis. Following Li and Luan (2005), we concentrate on the top 50 genes selected using the univariate log-rank test. To evaluate the performance of the proposed SCMR method, the data are randomly divided into two sets: the training set (160 patients) and the testing set (80 patients).

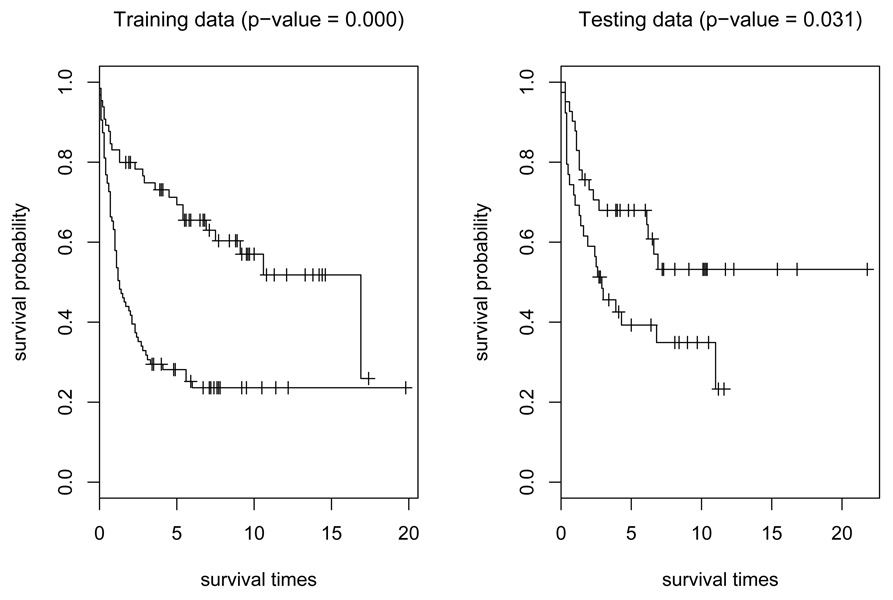
The SCMR-A estimator is then computed based on the training data and the proposed BIC method is used for parameter tuning. Our SCMR-A estimator selects totally 25 genes. To evaluate the prediction performance of the resulting SCMR-A estimator built with the training set, we plot, in Figure 2, the Kaplan-Meier estimates of survival functions for the high-risk and low-risk groups of patients, defined by the estimated conditional medians of failure times. The cut-off value was determined by the median failure time of the baseline group from the training set, and the same cutoff was applied to the testing data. It is seen that the separation of the two-risk groups is reasonably good in both the training and the testing data, suggesting a satisfactory prediction performance of the fitted survival model. The log-rank test of differences between two survival curves gives p-values of 0 and 0.031 for the training and testing data, respectively.

Figure 2.

Kaplan-Meier estimates of survival curves for high-risk and low-risk groups of patients using the selected genes by the SCMR-A.

5. Discussion

We propose the SCMR estimator for model estimation and selection in censored median regression based on the inverse-censoring-probability-weighted method combing with the adaptive LASSO penalty. Theoretical properties, such as variable selection consistency and asymptotic normality, of the SCMR estimator are established. The whole solution path of the SCMR estimator can be obtained and the proposed method for censored median regression can be easily generalized to censored quantile regression.

A key assumption of the proposed method is that the censoring distribution is independent of covariates. However, such a restrictive assumption can be relaxed. For example, Wang and Wang (2009) recently proposed a locally weighted censored quantile regression, in which a local Kaplan-Meier estimator was used to estimate the conditional survival function of censoring times given covariates. We think that the proposed SCMR estimator can be easily generalized to accommodate this case. However, when the dimension of covariates is high, the local Kaplan-Meier estimator may not work due to the curse of dimensionality. Alternatively, Portnoy (2003) and Peng and Huang (2008) studied a class of censored quantile regressions at all quantile levels under the weaker assumption that censoring and survival times are conditionally independent. The model parameters are estimated through a series of estimating equations: the self-consistency equations in Portnoy (2003) and the martingale-based equations in Peng and Huang (2008). The variable selection for such estimating equation based methods becomes more challenging, which needs further investigation.

Appendix: Proof of Theorems

To prove the asymptotic results established in Theorems 1 and 2, we need the following regularity conditions:

1. The error term ε has a continuous conditional density f(·|Z = z) satisfying that f(0|Z = z) ≥ b0 > 0, |ḟ (0|Z = z)| ≤ B₀ and sup_s f(s|Z = z) ≤ B₀ for all possible values z of Z, where (b₀,B₀) are two positive constants and ḟ is the derivative of f.

2. The covariate vector Z are of compact support and the parameter β₀ belongs to the interior of a known compact set ℬ₀.

3. P(t ≤ T ≤ C) ≥ ζ₀ > 0 for any t ∈ [0, τ ], where τ is the maximum follow-up and ζ₀ is a positive constant.

PROOF OF THEOREM 1

To establish the result given in Theorem 1, it is equivalent to show that for any η > 0, there is a constant M such that $P\left(\sqrt{n}\Vert \widehat{\theta }-\theta \Vert \le M\right)\ge 1-\eta$. Let u = (u₀, u₁, … , u_p)′ ∈ ℜ^p+1, and $A_M=\{{\theta }_0+\frac{u}{\sqrt{n}}:\Vert u\Vert \le M\}$ be a ball in ℜ^p+1 centered at θ₀ with the radius $M/\sqrt{n}$. Then we need to show that P(θ̂ ∈ A_M) ≥ 1 −η. Define

$$Q(G,\theta )={\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G({\tilde{T}}_i)}\left|\text{log}({\tilde{T}}_i)-\theta \prime X_i\right|+n\mathrm{\lambda }{\displaystyle \sum _{j=1}^p\frac{\left|{\beta }_j\right|}{\left|{\tilde{\beta }}_j\right|},}}$$

which is a convex function of θ. Thus, to prove P(θ̂ ∈ A_M) ≥ 1 −η for any η > 0, it is sufficient to show

$$P\left\{\underset{\Vert u\Vert =M}{\text{inf}}Q\left(\widehat{G},{\theta }_0+\frac{u}{\sqrt{n}}\right)>Q(\widehat{G},{\theta }_0)\right\}\ge 1-\eta .$$

Let $D_n\left(u\right)=Q\left(\widehat{G},{\theta }_0+\frac{u}{\sqrt{n}}\right)-Q\left(\widehat{G},{\theta }_0\right)$, which can be written as

$$\{Q(G_0,{\theta }_0+\frac{u}{\sqrt{n}}-Q(G_0,{\theta }_0)\}+\{Q(\widehat{G},{\theta }_0+\frac{u}{\sqrt{n}})-Q(G_0,{\theta }_0+\frac{u}{\sqrt{n}})\}-\{Q(\widehat{G},{\theta }_0)-Q(G_0,{\theta }_0)\}.$$ (7)

where G₀(·) is the true survival function of the censoring time.

For the first term in (7), we have

$$\begin{array}{c}Q(G_0,{\theta }_0+\frac{u}{\sqrt{n}})-Q(G_0,{\theta }_0)\hfill \\ ={\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}\left(|{\epsilon }_i-X_i^{\prime }\frac{u}{\sqrt{n}}|-|{\epsilon }_i|\right)+n\mathrm{\lambda }{\displaystyle \sum _{j=1}^p\frac{|{\beta }_{j0}+u_j/\sqrt{n}|-|{\beta }_{j0}|}{|{\tilde{\beta }}_j|}}}\hfill \\ \ge {\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}\left(|{\epsilon }_i-X_i^{\prime }\frac{u}{\sqrt{n}}|-|{\epsilon }_i|\right)+n\mathrm{\lambda }{\displaystyle \sum _{j=1}^q\frac{|{\beta }_{j0}+u_j/\sqrt{n}|-|{\beta }_{j0}|}{|{\tilde{\beta }}_j|}}}\hfill \\ \ge {\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}\left(\left|{\epsilon }_i-X_i^{\prime }\frac{u}{\sqrt{n}}\right|-\left|{\epsilon }_i\right|\right)-\sqrt{n}\mathrm{\lambda }{\displaystyle \sum _{j=1}^q\frac{\left|u_j\right|}{\left|{\tilde{\beta }}_j\right|}}}\hfill \\ \equiv L_n(u)-\sqrt{n}\mathrm{\lambda }{\displaystyle \sum _{j=1}^q\frac{\left|u_j\right|}{\left|{\tilde{\beta }}_j\right|}\ge L_n(u)-{\kappa }_1{Q}_p(\Vert u\Vert ).}\hfill \end{array}$$

where κ₁ is a finite positive constant. The last inequality in the above expression is because that $\sqrt{n}\mathrm{\lambda }=O_p\left(1\right)$ and β̃_j, j = 1, … , q, converges to β_j0 that is bounded away from zero.

In addition, based on the result (Knight, 1998) that for any $x\ne 0,\left|x-y\right|-\left|x\right|=-y\left[I\left(x>0\right)-I\left(x<0\right)\right]+2{\displaystyle {\int }_0^y\left[I\left(x\le s\right)-I\left(x\le 0\right)\right]\mathit{\text{ds}}}$, we have

$$L_n(u)=\frac{u\prime }{\sqrt{n}}{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}{X}_i\{I({\epsilon }_i<0)-I({\epsilon }_i>0)\}}+2{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}{\displaystyle {\int }_0^{u\prime X_i/\sqrt{n}}[I({\epsilon }_i\le s)-I({\epsilon }_i\le 0)]}\mathit{\text{ds}}.}$$

Since ε_i has median zero, it is easy to show that

$$E\left[\frac{{\delta }_i}{G_0({\tilde{T}}_i)}{X}_i\{I({\epsilon }_i<0)-I({\epsilon }_i>0)\}\right]=0.$$

Thus, by the central limit theorem, $\frac{u\prime }{\sqrt{n}}{\displaystyle {\sum }_{i=1}^n\frac{{\delta }_i}{G_0\left({\tilde{T}}_i\right)}{X}_i\{I\left({\epsilon }_i<0\right)-I\left({\epsilon }_i>0\right)\}}$ converges in distribution to u′W₁, where W₁ is a (p + 1)-dimensional normal with mean 0 and variance-covariance matrix ${\mathrm{\Sigma }}_1=E\left(\frac{X_1{X}_1^{\prime }}{G_0\left({\tilde{T}}_1\right)}\right)$. It implies that the first term in L_n(u) can be written as O_p (‖u‖). For the second term in L_n (u), let $A_{\mathit{\text{ni}}}\left(u\right)=\frac{{\delta }_i}{G_0\left({\tilde{T}}_i\right)}{\displaystyle {\int }_0^{u^T{X}_i/\sqrt{n}}\left[I\left({\epsilon }_i\le s\right)-I\left({\epsilon }_i\le 0\right)\right]\mathit{\text{ds}}}$. We will show that ${\displaystyle {\sum }_{i=1}^n{A}_{\mathit{\text{ni}}}\left(u\right)}$ converges in probability to a quadratic function of u. More specifically, for any ψ > 0, write

$$A_{\mathit{\text{ni}}}^2(u)=A_{\mathit{\text{ni}}}^2(u)I\left(\frac{\left|u\prime X_i\right|}{\sqrt{n}}\ge \psi \right)+A_{\mathit{\text{ni}}}^2(u)I\left(\frac{\left|u\prime X_i\right|}{\sqrt{n}}<\psi \right).$$

We have

$$\begin{array}{c}\mathit{\text{\hspace{1em} nE}}\{A_{\mathit{\text{ni}}}^2(u)I(\left|u\prime X_i\right|\ge \psi \sqrt{n})\}\hfill \\ \le \mathit{\text{nE}}\left\{\frac{{\delta }_i}{G_0^2({\tilde{T}}_i)}{({\displaystyle {\int }_0^{u\prime X_i/\sqrt{n}}2\mathit{\text{ds}}})}^{2}I(\left|u^T{X}_i\right|\ge \psi \sqrt{n})\right\}\hfill \\ =\frac{4}{{\varsigma }_0}E\{{\left|u\prime X_i\right|}^{2}I(\left|u\prime X_i\right|\ge \psi \sqrt{n})\}\to 0,\text{as}n\to \mathrm{\infty }.\hfill \end{array}$$

Moreover,

$$\begin{array}{c}\mathit{\text{\hspace{1em} nE}}\{A_{\mathit{\text{ni}}}^2(u)I(\left|u\prime X_i\right|<\psi \sqrt{n})\}\hfill \\ \le \mathit{\text{nE}}(\frac{{\delta }_i}{G_0^2({\tilde{T}}_i)}2{\displaystyle {\int }_0^{|u\prime X_i|/\sqrt{n}}\mathit{\text{ds}}{\displaystyle {\int }_0^{|u\prime X_i|/\sqrt{n}}\{I({\epsilon }_i\le s)-I({\epsilon }_i\le 0)\}\mathit{\text{dsI}}}}(\left|u\prime X_i\right|<\psi \sqrt{n}))\hfill \\ \le \frac{2n\psi }{{\varsigma }_0}{E}_z\left[{\displaystyle {\int }_0^{|u\prime X_i|/\sqrt{n}}\{F(s|Z)-F(0|Z)\}\mathit{\text{dsI}}(\left|u\prime X_i\right|<\psi \sqrt{n})}\right]\hfill \\ \le \frac{2n\psi }{{\varsigma }_0}{E}_z\{{\displaystyle {\int }_0^{|u\prime X_i|/\sqrt{n}}f(s^{*}|Z)\mathit{\text{sdsI}}(\left|u\prime X_i\right|<\psi \sqrt{n}})\}\hfill \\ \le \frac{\psi B_0}{{\varsigma }_0}{E}_z\{{\left|u\prime X_i\right|}^{2}I(\left|u\prime X_i\right|<\psi \sqrt{n})\}\le \frac{\psi B_0}{{\varsigma }_0}{E}_z({\left|u\prime X_i\right|}^2).\hfill \end{array}$$

Since E_Z(|u′ X_i|²) is bounded and ψ can be arbitrary small, it follows that $\frac{\psi B_0}{{\zeta }_0}{E}_Z\left({\left|u\prime X_i\right|}^2\right)\to 0$ as ψ → 0. Thus, we have, as n → ∞,

$$V\mathit{\text{ar}}\{{\displaystyle \sum _{i=1}^n{A}_{\mathit{\text{ni}}}(u)}\}={\displaystyle \sum _{i=1}^{n}V\text{ar}\{A_{\mathit{\text{ni}}}(u)\}}\le \mathit{\text{nE}}\{A_{\mathit{\text{ni}}}^2(u)\}\to 0,$$

which implies ${\displaystyle {\sum }_{i=1}^n\left[A_{\mathit{\text{ni}}}\left(u\right)-E\{A_{\mathit{\text{ni}}}\left(u\right)\}\right]=o_p\left(1\right)}$. Furthermore, we have

$$\begin{array}{cc}{\displaystyle \sum _{i=1}^{n}E\{A_{\mathit{\text{ni}}}(u)\}}\hfill & =\mathit{\text{nE}}\left[\frac{{\delta }_i}{G_0({\tilde{T}}_i)}{\displaystyle {\int }_0^{u\prime X_1/\sqrt{n}}\{I({\epsilon }_1\le s)-I({\epsilon }_1\le 0)\}}\mathit{\text{ds}}\right]\hfill \\ \hfill & ={\mathit{\text{nE}}}_z\left[{\displaystyle {\int }_0^{u\prime X_i/\sqrt{n}}\{F(s|Z)-F(0|Z)\}}\mathit{\text{ds}}\right]\hfill \\ \hfill & ={\mathit{\text{nE}}}_z\{{\displaystyle {\int }_0^{u\prime X_i/\sqrt{n}}\mathit{\text{sf}}(0|Z)}\mathit{\text{ds}}\}+o_p(1)\hfill \\ \hfill & =\frac{1}{2}u\prime \mathrm{\Sigma }u+o_p(1),\hfill \end{array}$$

where Σ = E_Z{f(0|X)XX′}is positive and finite. Thus,

$$Q(G_0,{\theta }_0+\frac{u}{\sqrt{n}})-Q(G_0,{\theta }_0)\ge \frac{1}{2}u\prime \mathrm{\Sigma }u+u\prime W_1-{\kappa }_1{O}_p(\Vert u\Vert )+o_p(1).$$

For the second and third terms in (7), by the Taylor expansion, we have

$$\begin{array}{cc}\sqrt{n}\{\frac{1}{\widehat{G}({\tilde{T}}_i)}-\frac{1}{G_0({\tilde{T}}_i)}\}\hfill & =-\frac{\sqrt{n}\{\widehat{G}({\tilde{T}}_i)-G_0({\tilde{T}}_i)\}}{G_0^2({\tilde{T}}_i)}+o_p(1)\hfill \\ \hfill & =\frac{1}{G_0({\tilde{T}}_i)}\frac{1}{\sqrt{n}}{\displaystyle \sum _{j=1}^n{\displaystyle {\int }_0^{\tau }I({\tilde{T}}_i\ge s)}\frac{{\mathit{\text{dM}}}_j^C(s)}{y(s)}}+o_p(1),\hfill \end{array}$$

where $y\left(s\right)={\text{lim}}_{n\to \mathrm{\infty }}\left(1/n\right){\displaystyle {\sum }_{i=1}^{n}I\left({\tilde{T}}_i\ge s\right),M_i^C\left(t\right)=\left(1-{\delta }_i\right)I\left({\tilde{T}}_i\le t\right)-{\displaystyle {\int }_0^{t}I\left({\tilde{T}}_i\ge s\right)d{\mathrm{\Lambda }}_C\left(s\right)}}$, and Λ_C(·) is the cumulative hazard function of the censoring time C. This leads to

$$\begin{array}{c}Q(\widehat{G},{\theta }_0+\frac{u}{\sqrt{n}})-Q(G_0,{\theta }_0+\frac{u}{\sqrt{n}})\hfill \\ =\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}|{\epsilon }_i-X_i^{\prime }\frac{u}{\sqrt{n}}|{\displaystyle \sum _{j=1}^n{\displaystyle {\int }_0^{\tau }\frac{I({\tilde{T}}_i\ge s)}{y(s)}}{\mathit{\text{dM}}}_j^C(s)+o_p(1).}}\hfill \end{array}$$

Similarly, we have

$$Q(\widehat{G},{\theta }_0)-Q(G_0,{\theta }_0)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}\left|{\epsilon }_i\right|{\displaystyle \sum _{j=1}^n{\displaystyle {\int }_0^{\tau }\frac{I({\tilde{T}}_i\ge s)}{y(s)}}{\mathit{\text{dM}}}_j^C(s)+o_p(1).}}$$

Therefore,

$$\begin{array}{c}Q(\widehat{G},{\theta }_0+\frac{u}{\sqrt{n}})-Q(G_0,{\theta }_0+\frac{u}{\sqrt{n}})-\{Q(\widehat{G},{\theta }_0)-Q(G_0,{\theta }_0)\}\hfill \\ =\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}(|{\epsilon }_i-X_i^{\prime }\frac{u}{\sqrt{n}}|-\left|{\epsilon }_i\right|){\displaystyle {\int }_0^{\tau }{\displaystyle \sum _{j=1}^n\frac{I({\tilde{T}}_i\ge s)}{y(s)}{\mathit{\text{dM}}}_j^C(s)+o_p(1).}}}\hfill \end{array}$$

By the similar techniques used for establishing the lower bound of $Q\left(G_0,{\theta }_0+\frac{u}{\sqrt{n}}\right)-Q\left(G_0,{\theta }_0\right)$, we can show that the right-hand side of the above expression can be represented as

$$\frac{u\prime }{\sqrt{n}}{\displaystyle \sum _{j=1}^n{\displaystyle {\int }_0^{\tau }\frac{h(s)}{y(s)}{\mathit{\text{dM}}}_j^C(s)+o_p(1),}}$$

where $h\left(s\right)={\text{lim}}_{n\to \mathrm{\infty }}\frac{1}{n}{\displaystyle {\sum }_{i=1}^n\frac{{\delta }_{i}I\left({\tilde{T}}_i\ge s\right)}{G_0\left({\tilde{T}}_i\right)}}{X}_i\left\{I\left({\epsilon }_i<0\right)-I\left({\epsilon }_i>0\right)\right\}$ is a bounded function on [0, τ ]. Then by the martingale central limit theorem, we have that $\frac{u\prime }{\sqrt{n}}{\displaystyle {\sum }_{j=1}^n{\displaystyle {\int }_0^{\tau }\frac{h\left(s\right)}{y\left(s\right)}d{M}_j^C\left(s\right)}}$ converges in distribution to u′W₂, where W₂ is a (p + 1)-dimensional normal with mean 0 and variance-covariance matrix ${\mathrm{\Sigma }}_2={\displaystyle {\int }_0^{\tau }\frac{h^2\left(s\right)}{y\left(s\right)}d{\mathrm{\Lambda }}_C(s)}$. In summary, we showed that

$$D_n(u)\ge \frac{1}{2}u\prime \mathrm{\Sigma }u+u\prime (W_1+W_2)-{\kappa }_1{O}_p(\Vert u\Vert )+o_p(1).$$

For the right-hand side in the above expression, the first term dominates the remain terms if M = ‖u‖ is large enough. So for any η > 0, as n gets large, we have

$$P\left\{\underset{\Vert u\Vert =M}{\text{inf}}{D}_n(u)>0\right\}\ge 1-\eta ,$$

which implies that θ̂ is $\sqrt{n}-\text{Consistency}$.

Proof of Theorem 2

(i) Proof of selection-consistency. We will first take the derivative of Q(Ĝ, θ) with respect to β_j for j = q + 1, … , p, at any differentiable point $\theta =\left(\alpha ,{\beta }_a^{\prime },{\beta }_b^{\prime }\right)\prime$. Then we will show that for $\sqrt{n}\Vert \alpha -{\alpha }_0\Vert \le M,\sqrt{n}\Vert {\beta }_a-{\beta }_{a,0}\Vert \le M,\text{and}\Vert {\beta }_b-{\beta }_{b,0}\Vert =\Vert {\beta }_b\Vert \le \frac{M}{\sqrt{n}}\equiv {\epsilon }_n$, when n is large, $\frac{1}{\sqrt{n}}\frac{\delta }{\delta {\beta }_j}Q\left(\widehat{G},\theta \right)$, for j = q + 1, … , p, is negative if −ε_n < β_j < 0 and positive if 0 < β_j < ε_n. Since Q(Ĝ, θ) is a piecewise linear function of θ, it achieve its minimum at some breaking point. Moreover, based on Theorem 1, the minimizer $\widehat{\theta }=(\widehat{\alpha },{\widehat{\beta }}_a^{\prime },{\widehat{\beta }}_b^{\prime })\prime$ of Q(Ĝ, θ) is $\sqrt{n}-\text{Consistency}$. Thus, each component of β̂_b must be contained in the interval (−ε_n, ε_n) for all large n. Then as n → ∞, P(β̂_b = 0) → 1.

To do this, we have, for j = q + 1, … , p,

$$\begin{array}{c}\frac{1}{\sqrt{n}}\frac{\partial }{\partial {\beta }_j}Q(\widehat{G},\theta )\hfill \\ =-\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n{Z}_{\mathit{\text{ij}}}\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}\text{sign}\{\text{log}({\tilde{T}}_i)-X_i^{\prime }\theta \}+\frac{\sqrt{n}\mathrm{\lambda }\text{sign}({\beta }_j)}{\left|{\tilde{\beta }}_j\right|}}\hfill \\ =-\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n{Z}_{\mathit{\text{ij}}}\frac{{\delta }_i}{G_0({\tilde{T}}_i)}\text{sign}\{\text{log}({\tilde{T}}_i)-X_i^{\prime }\theta \}}-\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^n{\displaystyle {\int }_0^{\tau }\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n{Z}_{\mathit{\text{ij}}}\frac{{\delta }_i}{G_0({\tilde{T}}_i)}I({\tilde{T}}_i\ge s)\text{sign}\{\text{log}({\tilde{T}}_i)-X_i^{\prime }\theta \}}\right]\frac{{\mathit{\text{dM}}}_k^C(s)}{y(s)}}}+\sqrt{n}\mathrm{\lambda }\frac{\text{sign}({\beta }_j)}{\left|{\tilde{\beta }}_j\right|}+o_p(1).\hfill \end{array}$$ (8)

Let $\mathrm{\Delta }=\sqrt{n}\left(\theta -{\theta }_0\right)$ and define

$$V_n(\mathrm{\Delta })=\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n{X}_i\frac{{\delta }_i}{G_0({\tilde{T}}_i)}\text{sign}({\epsilon }_i-X_i^{\prime }\mathrm{\Delta }/\sqrt{n})}.$$

Write V_n(Δ) = {V_n,0(Δ), V_n,1(Δ), … , V_n,p(Δ)}′. Then the first term at the right-hand side of (8) can be rewritten as V_n,j(Δ). As shown in Theorem 1, V_n(0) converges in distribution to a (p + 1)-dimensional normal with mean 0 and variance-covariance matrix Σ₁. Furthermore, following the similar derivations of Koenker and Zhao (1996), we can show that sup_{‖Δ‖ ≤M} ‖V_n(Δ)−V_n(0) + Σ₁Δ‖ = o_p(1). This implies that V_n,j(Δ) = O_p(1) since V_n(0) converges in distribution to a normal vector, Σ₁ is finite and Δ is bounded.

Next, since $\sqrt{n}\Vert \theta -{\theta }_0\Vert$ is bounded, by the law of large numbers, we have that $\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{Z}_{\mathit{\text{ij}}}\frac{{\delta }_i}{G_0\left({\tilde{T}}_i\right)}I\left({\tilde{T}}_i\ge s\right)\text{sign}\{\text{log}\left({\tilde{T}}_i\right)-X_i^{\prime }\theta \}}$ converges to $b_j\left(s\right)\equiv E\left\{Z_{\mathit{\text{ij}}}\frac{{\delta }_i}{G_0\left({\tilde{T}}_i\right)}I\left({\tilde{T}}_i\ge s\right)\text{sign}\left({\epsilon }_i\right)\right\}$. Thus, the second term at the right-hand side of (8) can be written as

$$\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^n{\displaystyle {\int }_0^{\tau }\frac{b_j(s)}{y(s)}{\mathit{\text{dM}}}_k^C(s)+o_p(1),}}$$

which is also O_p(1) since it converges to a normal variable with mean 0.

Thus, for j = q + 1, … , p,

$$\frac{1}{\sqrt{n}}\frac{\partial }{\partial {\beta }_j}Q(\widehat{G},\theta )=O_p(1)+\frac{n\mathrm{\lambda }\text{sign}({\beta }_j)}{\sqrt{n}\left|{\tilde{\beta }}_j\right|}.$$

Since the LAD estimator θ̃ is $\sqrt{n}-\text{Consistency}$, we have, for j = q + 1, … , p, $\sqrt{n}\left|{\tilde{\beta }}_j\right|=O_p\left(1\right)$. Then based on the assumption nλ → ∞, when n is large, the sign of $\frac{1}{\sqrt{n}}\frac{\partial }{\partial {\beta }_j}Q\left(\widehat{G},\theta \right)$ is determined by the sign of β_j. So as n gets large, $\frac{1}{\sqrt{n}}\frac{\delta }{\delta {\beta }_j}Q\left(\widehat{G},\theta \right)$, for j = q + 1, … , p, is negative if −ε_n < β_j < 0 and positive if 0 < β_j < ε_n, which implies P(β̂_b = 0) → 1 as n → ∞.

(ii) Proof of asymptotic normality. Based on the results established in Theorem 1 and (i) of Theorem 2, we have the minimizer θ̂ is $\sqrt{n}-\text{consistent}$ and P(β̂_b = 0) → 1 as n → ∞. Thus to derive the asymptotic distribution for the estimators of non-zero coefficients, we only need to establish the asymptotic representation for the following function:

$$\begin{array}{cc}{S}_n(\widehat{G},\upsilon )\hfill & =Q\{\widehat{G},{({\beta }_{a\prime 0}^{\prime }+{\upsilon }^{\prime }/\sqrt{n},0^{\prime })}^{\prime }\}-Q\{\widehat{G},{({\beta }_{a\prime 0}^{\prime },0^{\prime })}^{\prime }\}\hfill \\ \hfill & ={\displaystyle {\sum }_{i=1}^n\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}(\left|{\epsilon }_i-X_{a\prime i}^{\prime }\upsilon /\sqrt{n}\right|-\left|{\epsilon }_i\right|)}+n\lambda {\displaystyle {\sum }_{j=1}^q\frac{\left|{\beta }_{j0}+{\upsilon }_j/\sqrt{n}\right|-\left|{\beta }_{j0}\right|}{\left|{\tilde{\beta }}_j\right|}}\hfill \\ \hfill & ={\displaystyle {\sum }_{i=1}^n\frac{{\delta }_i}{\widehat{G}({\tilde{T}}_i)}(\left|{\epsilon }_i-X_{a\prime i}^{\prime }\upsilon /\sqrt{n}\right|-\left|{\epsilon }_i\right|)}+\sqrt{n}\lambda {\displaystyle {\sum }_{j=1}^q\frac{\mathit{\text{sign}}\left|{\beta }_{j0}\right|{\upsilon }_j}{\left|{\tilde{\beta }}_j\right|},}\hfill \end{array}$$

where ${\beta }_{a\prime 0}=\left({\alpha }_0,{\beta }_{a0}^{\prime }\right)\prime$ and v is a (q + 1)-dimensional vector with bounded norm. Define X_a′i = (1, Z_i1, … , Z_iq)′, i = 1, … , n. Since $\sqrt{n}\mathrm{\lambda }\to {\mathrm{\lambda }}_0$ and β̃_j → β_j0 ≠ 0 and following the similar derivations as those in the proof of Theorem 1, we can show that

$$S_n(\widehat{G},\upsilon )=\frac{1}{2}\upsilon \prime {\mathrm{\Sigma }}_{a\prime }\upsilon +\frac{\upsilon \prime }{\sqrt{n}}{\displaystyle \sum _{i=1}^n\frac{{\delta }_i}{G_0({\tilde{T}}_i)}{X}_{a\prime i}\{I({\epsilon }_i<0)-I({\epsilon }_i>0)\}+}\frac{\upsilon \prime }{\sqrt{n}}{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_0^{\tau }\frac{h_{a\prime }(s)}{y(s)}}{\mathit{\text{dM}}}_i^C(s)+{\lambda }_0\upsilon \prime b_1+o_p(1),}$$ (9)

where ${\mathrm{\Sigma }}_{a\prime }=E\left\{f\left(0|X\right)X_{a\prime }{X}_{a\prime }^{\prime }\right\},h_{a\prime }\left(s\right)={\text{lim}}_{n\to \mathrm{\infty }}\frac{1}{n}{\displaystyle {\sum }_{i=1}^n\frac{{\delta }_{i}I\left({\tilde{T}}_i\ge s\right)}{G_0\left({\tilde{T}}_i\right)}}{X}_{a\prime i}\left\{I\left({\epsilon }_i<0\right)-I\left({\epsilon }_i>0\right)\right\},\text{ and }{b}_1={\left(\frac{\mathit{\text{sign}}\left({\beta }_1\right)}{\left|{\beta }_1\right|},\dots ,\frac{\text{sign}\left({\beta }_q\right)}{\left|{\beta }_q\right|}\right)}^{\prime }$. Define

$$s_i=\frac{{\delta }_i}{G_0({\tilde{T}}_i)}{X}_{a\prime i}\{I({\epsilon }_i<0)-I({\epsilon }_i>0)\}+{\displaystyle {\int }_0^{\tau }\frac{h_{a\prime }(s)}{y(s)}}{\mathit{\text{dM}}}_i^C(s).$$

Then by the central limit theorem, $\left(1/\sqrt{n}\right){\displaystyle {\sum }_{i=1}^n{s}_i}$ converges in distribution to a (q + 1)-dimensional normal vector W_a′ with mean 0 and variance-covariance matrix $V_{a\prime }=E\left(s_1{s}_1^{\prime }\right)$. The minimizer of $\frac{1}{2}\upsilon \prime {\mathrm{\Sigma }}_{a\prime }\upsilon +\upsilon \prime W_{a\prime }+\mathbf{v}\prime {\mathrm{\lambda }}_0{\mathbf{b}}_1$ is given by ${\upsilon }_0=-{\mathrm{\Sigma }}_{a\prime }^{-1}\left(W_{a\prime }+{\mathrm{\lambda }}_0{b}_1\right)$. Moreover, the minimizer of S_n (Ĝ, v) is given by $\sqrt{n}\left({\widehat{\beta }}_{a\prime }-{\beta }_{a\prime 0}\right)$. By the lemma given in Davis et al. (1992), $\sqrt{n}\left({\widehat{\beta }}_{a\prime }-{\beta }_{a\prime 0}\right)$ converges to v₀ in distribution as n → ∞. Therefore we have that $\sqrt{n}\left({\widehat{\beta }}_{a\prime }-{\beta }_{a\prime 0}\right)$ converges in distribution to (q + 1)-dimensional normal vector with mean −Σ_a′λ₀b₁ and variance-covariance matrix ${\mathrm{\Sigma }}_{a\prime }^{-1}{V}_{a\prime }{\mathrm{\Sigma }}_{a\prime }^{-1}$.