Processing Multi-mode Binding Situations in Simulation-based Prediction of Ligand-Macromolecule Affinities

Abstract

The Linear Response (LR) approximation and similar approaches belong to practical methods for estimation of ligand-receptor binding affinities. The approaches correlate experimental binding affinities with the changes upon binding of the ligand electrostatic and van der Waals energies, and of solvation characteristics. These attributes are expressed as ensemble averages that are obtained by conformational sampling of the protein-ligand complex and of the free ligand by molecular dynamics or Monte Carlo simulations. We observed that outliers in the LR correlations occasionally exhibit major conformational changes of the complex during sampling. We treated the situation as a multi-mode binding case, for which the observed association constant is the sum of the partial association constants of individual states/modes. The resulting nonlinear expression for the binding affinities contains all the LR variables for individual modes that are scaled by the same 2–4 adjustable parameters as in the one-mode LR equation. The multi-mode method was applied to inhibitors of a matrix metalloproteinase, where this treatment improved the explained variance in experimental activity from 75% for the uni-mode case to about 85%. The predictive ability scaled accordingly, as verified by extensive cross-validations.

Introduction

Estimation of binding affinities for ligand-receptor complexes is important for several research areas including structure-based drug design. The approaches range from scoring functions^1–9 for quick ranking of large libraries of compounds docked into the binding site to more sophisticated, second-pass methods for examination of the top candidates from the fast docking. The latter category spans from methods utilizing single energy-minimized conformations^10–15 to complex and time consuming Free Energy Perturbation, Thermodynamic Integration, and related approaches based on extensive sampling.^16–19 Fairly accurate binding energy estimates can be obtained by methods of intermediate complexity, requiring only two molecular dynamics (MD) or Monte Carlo (MC) simulations, one with the free solvated ligand and one with the ligand bound to the solvated receptor. The binding free energy is expressed as the sum of several contributions. The methods can be classified based upon various criteria such as (1) the sampling method: MD^20–23 or MC;^24–26 (2) the treatment of solvent: explicit,^20,24–26 continuum,^15,21,27 or in vacuo;^15,22 (3) estimation of the electrostatic component of solvation energies: linearized Poisson-Boltzman equation,^{15,22,23,28,29} the generalized Born model,^21,29,30 or the pair-wise Coulomb relations in the explicit solvent;²⁵ and (4) the parameter optimization: used²⁷ or not used.²³

To illustrate the approaches, let us have a closer look at the Linear Response (LR, a.k.a Linear Interaction Energy) method^20,31–35 and its extension (ELR).^24,36–39 The LR method correlates binding free energies ΔG_i with van der Waals and electrostatics energies between the ligand and its surroundings, to which the ELR method adds the solvent-accessible surface area (SASA) term:

$$\mathrm{\Delta }{G}_i=-RT\text{ln}{K}_i=\alpha \mathrm{\Delta }{\langle E_{vdW}\rangle }_i+\beta \mathrm{\Delta }{\langle E_{el}\rangle }_{\mathrm{i}}+\gamma \mathrm{\Delta }{\langle SASA\rangle }_i+\kappa .$$ (1)

Here, K_i is the association constant, R is the universal gas constant, T is temperature, the subscript i indicates the ith compound, and α, β, γ and κ are adjustable parameters that optimize the agreement between experimental ΔG_b values and calculated energy and SASA terms according to Eq. 1. The angle brackets denote the ensemble averages and Δ indicates the difference between the ensemble averages in the bound and free ligand states. The ensemble averages of the energies and SASA seem to be replaceable by the energies and SASA calculated for the time-averaged structures.^22,39 Usually, conformational sampling leads to better correlations^22,39 than simpler and faster minimization, although the opposite cases have been described.¹⁵

We observed that outliers in the fits of Eq. 1 to experimental data are occasionally associated with larger conformational changes of the bound ligands during the simulation. These changes may happen in spite of careful equilibration, if there are several energetically similar conformation states available. In this communication, we propose a conceptual treatment of such a situation that is based on the multi-mode binding mechanism.

Methods

Reversible 1:1 binding of the ith ligand L_i in m mutually exclusive orientations or conformations (modes) to the receptor site R can be schematically written as

$${\mathrm{L}}_i+\mathrm{R}\{\begin{array}{c}\stackrel{K_{i1}}{\leftrightarrow }{\mathrm{L}\mathrm{R}}_{i1}\hfill \\ \stackrel{K_{i2}}{\leftrightarrow }{\mathrm{L}\mathrm{R}}_{i2}\hfill \\ ⋮\hfill \\ \stackrel{K_{im}}{\leftrightarrow }{\mathrm{L}\mathrm{R}}_{im}\hfill \end{array}.$$ (2)

The ligand is present as a single species in the receptor surroundings. The apparent association constant K_i for this process is, on the concentration basis, defined as

$$K_i={\displaystyle \sum _{j=1}^m}\left[{\mathrm{L}\mathrm{R}}_{ij}\right]/\left(\left[{\mathrm{L}}_i\right]\left[\mathrm{R}\right]\right)={\displaystyle \sum _{j=1}^m}{K}_{ij}.$$ (3)

Each partial association constant K_ij can be expressed using Eq. 1, with the same values of the adjustable parameters α, β, γ, and κ. The apparent association constant can then be correlated with the simulation results by a combination of Eqs. 1 (now with the subscript ij representing the jth binding mode of the ith compound) and 3:

$$\mathrm{\Delta }{G}_i=-RT\text{ln}{K}_i=-RT\text{ln}{\displaystyle \sum _{j=1}^m}\text{exp}\left[-\left(\alpha \mathrm{\Delta }{\langle E_{vdw}\rangle }_{ij}+\beta \mathrm{\Delta }{\langle E_{el}\rangle }_{ij}+\gamma \mathrm{\Delta }{\langle SASA\rangle }_{ij}+\kappa \right)/RT\right].$$ (4)

The simple Eq. 4 is in accordance with published analyses of formally analogous situations: the rigorous statistical thermodynamic⁴⁰ description and equilibrium treatment^41,42 of the multi-mode interactions of ligands with proteins and kinetic analyses of reversible uni-molecular reactions leading to different products⁴³ or isomers⁴⁴. The multi-mode approach represented by Eq. 4 was also implemented in the most frequently used ligand-based method Comparative Molecular Field Analysis (CoMFA).⁴⁵

Notably, Eq. 4 contains the same adjustable parameters α, β, γ and κ as Eq. 4. The multi-mode treatment uses a different correlation equation (Eq. 4) than the classical one-mode approach (Eq. 1) but relies on the same four adjustable parameters. Thus, Eq. 4 has 3×m variables (m is the number of binding modes considered for each ligand) that are equal to the ensemble averages of van der Waals energies, coulombic energies, and SASA terms for individual binding modes. However: (1) all m van der Waals terms are scaled by the parameter α; (2) all m electrostatic terms are scaled by the parameter β; (3) all m SASA terms are scaled by the parameter γ; and (4) there is only one constant parameter κ. In Eq. 4, each mode is represented by one exponential that corresponds to Eq. 1 (for this reason, the separation of the parameter κ from the summation was not made in Eq. 4). Each exponential contains the same adjustable parameters α, β, γ and κ, so there are four optimized parameters in total. After optimization of the parameters by nonlinear regression analysis of experimental data according to Eq. 4, the prevalence of the jth binding mode can be calculated as K_ij/ΣK_ij, where: (1) the partial association constant of the jth mode K_ij is calculated from Eq. 1 with optimized values of adjustable parameters α, β, γ and κ, and the energy and SASA terms for the jth mode; and (2) the sum runs through all m partial association constants K_ij that are calculated in the previous step. The prevalences of individual modes are the outcome of the parameter optimization. No assumptions about the prevalence distribution need to be made before optimization. The prevalences calculated by this approach are in accordance with the Boltzmann distribution.

We applied the multi-mode method to a set of 28 diverse hydroxamate inhibitors of MMP-9,⁴⁶ encompassing the following structural types:

The complete structures of the inhibitors along with the LR terms and the experimental and predicted K_i values are listed in the supporting information. The ligands exhibit ~4000-fold difference in binding affinity, with the association constants K_i ranging from 2.865×10⁶ to 1.25×10¹⁰ M⁻¹.

The crystal structure of MMP-9 complexed with reverse hydroxamate inhibitor (file 1GKC) was downloaded from the Protein Data Bank.⁴⁷ Three-dimensional structures of ligands were constructed using the SYBYL6.91 suite of programs⁴⁸ running under Irix 6.5. The ligands were then docked into the active site of MMP-9 using FlexX.^49,50 Conformations of the ligands in the active site were selected from the top 30 poses generated by FlexX using the distance in the interval 1.5 – 2.5 Å between the hydroxamate oxygens and the zinc atom of the receptor as the primary criterion and the FlexX ranking as the secondary criterion.⁵¹ Protons were added to the heavy atoms of the protein and energy minimization was performed using constraints to relax the added protons using Tripos force field.⁵² All heavy atoms were fixed at the experimental coordinates during energy minimization. The optimized complexes were then subjected MD simulations consisting of 15-ps heating phase, 100-ps equilibration and 200-ps production period. The lengths of the bonds between the hydroxamate groups of inhibitors and the catalytic zinc were constrained to alleviate the deficiencies of the used force field in the description of metal coordination. MD simulations for hydrated ligands were performed under similar conditions. The protocol was described in detail elsewhere.³⁹ The generated ensemble averages are summarized in the supporting information.

Results and Discussion

In our previous study,³⁹ the MD-based LR correlations (Eq. 1) of the hydroxamate inhibitors⁴⁶ of MMP-9 behaved anomalously: the quality of correlations did not improve with increased simulation time and some outliers adopted comparatively different conformations during MD simulations. We decided to examine whether a correlation taking into account multiple binding modes could improve the results.

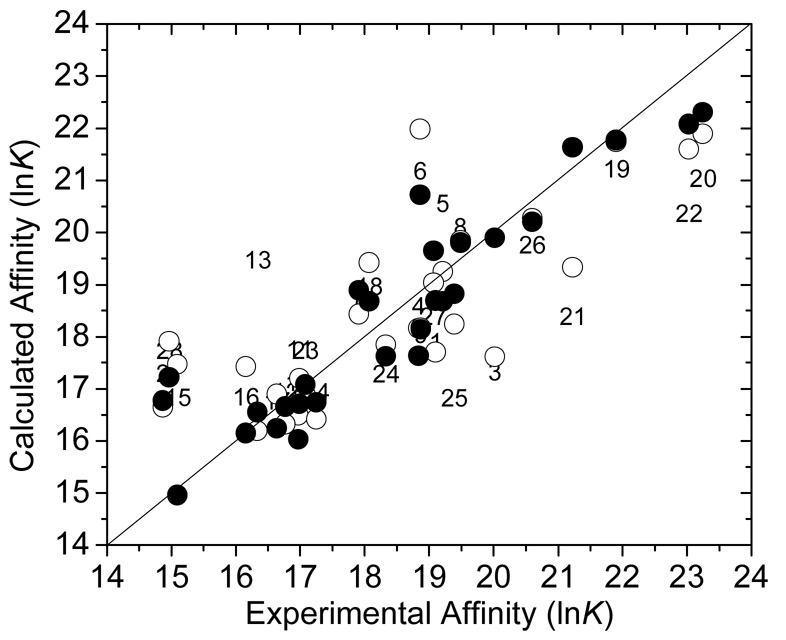
The van der Waals, electrostatic and solvent accessible surface area terms were calculated using the corresponding time-averaged structures of the complex and the free ligand for eight 25-ps intervals of the 200-ps MD simulations. The time-averaged structure for each interval represented a binding mode (0–25 ps: mode 1, 25–50 ps: mode 2, … 175–200 ps: mode 8). No collinearity between the calculated LR terms, used in Eq. 1 and Eq. 4, was observed. The highest mutual correlation was seen between the electrostatic and SASA terms (Eq. 4), with the correlation coefficient r = 0.218. The results of the fit of the data for the classical and multi-mode LR treatment (Eq. 1 and Eq. 4, respectively) are summarized in Table 1. The results for the minimization of the ligands in the binding sites are included for comparison. A plot of experimental vs. calculated activities is shown in Figure 1.

TABLE 1.

Correlations of Inhibitory Potencies with Energy and SASA Terms

Eq.	Sampling	α × 10−2 [mol/kcal]	β × 10−2 [mol/kcal]	γ × 10−2 [Å−2]	κ	SD	r2	RMSE
								LNOb	LOOc	LSOd
1a	minimization	-	-	1.566 ± 0.350	−14.30 ± 0.98	1.128	0.435	1.646	1.785	1.750
1	MD (200 ps)	-	-	1.656 ± 0.251	−11.75 ± 1.04	1.101	0.627	1.338	1.469	1.478
4	MD (8×25 ps)	1.639 ± 0.421	2.231 ± 0.649	1.121 ± 0.235	−5.785 ± 1.588	0.862	0.845	0.931	1.008	1.012

^aNo conformational sampling, just the minimized ligand structures used.

^bNo omission of compounds.

^cLeave-one-out cross-validation.

^dLeave-several-out cross-validation: random selection of a 6-member test set, repeated 200 times.

Figure 1.

Comparison of the experimental versus calculated binding affinity (lnK) for the one-mode model (Eq. 1) with minimization (the compound number, see Supplementary Information for structures) and conformational sampling (○, Eq. 1), and for the multi-mode conformational sampling (●, Eq. 4). The optimized coefficient values are given in Table 1.

For minimization and the one-mode treatment, the van der Waals and electrostatics terms were not significant. For minimization, the parameter errors for the van der Waals and electrostatic terms were higher than the optimized parameter values. Moreover, the parameter for the van der Waals term had a negative value. For the one-mode treatment, the error terms were ~60% of the parameter estimates. Inclusion of the statistically insignificant terms led to negligible improvements in the correlations: for minimization, to r²=0.445, and for the one-mode treatment, to r² = 0.695 (data not shown).

The multi-mode model provides significantly better correlations (Table 1, Figure 1) and explains ~85% (r²=0.845) of the variation in experimental activity with the standard deviation SD = 0.862. All three terms included in Eq. 4 exhibited significant contributions to the correlation. The contributions of the energy terms imply dominant roles of the electrostatic and van der Waals interactions between the inhibitor and the protein. The SASA term indicates that the burying of the ligand, which is exposed to the solvent in the unbound state, is favorable for complex formation. Division of the SASA term into polar and non-polar solvent accessible surface areas did not increase the descriptive and predictive power of the model (data not shown).

The robustness of the regression equations and their predictive abilities were probed by cross-validation. For this purpose, the fits to the potency data are generated leaving out one or more inhibitors from the calibration process. The resulting equation for each fit is used to predict the potencies of the omitted compounds. The leave-one-out (LOO) procedure and especially the leave-several-out (LSO) procedure with a random selection of a 6-member test set that was repeated 200 times provided a thorough evaluation. The RMSE values using LOO (1.008) and LSO (1.012) were only slightly higher than the RMSE value of the whole data set without any omission (0.931).

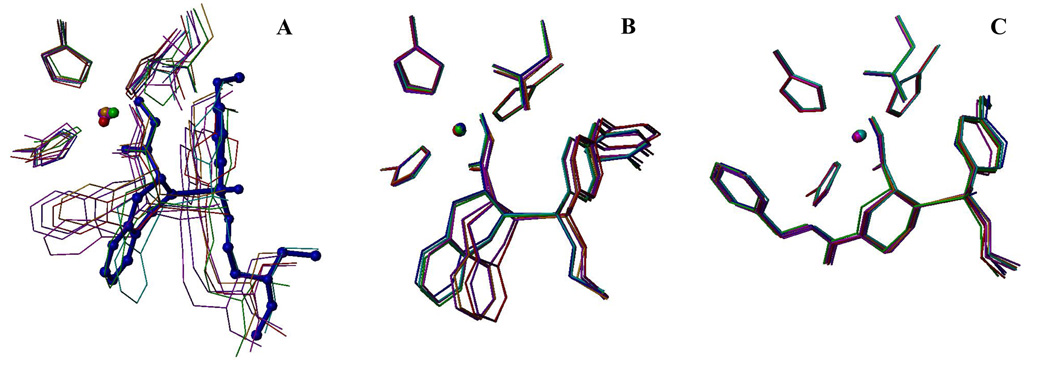
Eq. 4 has an interesting property: it selects the binding modes, which contribute most to the binding. The prevalencies K_ij/ΣK_ij of individual simulation intervals representing the binding modes for the studied ligands are summarized in Supporting Information, along with ligand structures, experimental and predicted affinities, as well as energy and SASA terms. Major outliers in the one-mode treatment (ligands 3, 15, and 21) are predicted accurately by multi-mode treatment (Figure 1). In case of compound 3, the contributions are ~15% for all modes except modes 1 and 7 (4 and 10%, respectively). Compound 15 shows a similar pattern but the minimal contributions are observed for modes 1, 2, and 6. Compound 21 exhibits deviations both positive and negative deviations from the average: mode 2 contributes 26% to overall binding, while modes 1 and 5 represent only 8 and 5%, respectively. Ligands 2, 6, 7, 8, 9, 23, and 24 also have a dominant mode (mode 7, 4, 2, 1, 1, 7, and 8, respectively) representing more than 30% of the total bound ligands. A ligand oscillating around an equilibrium position should exhibit approximately equal contributions to binding for all eight binding modes; i.e. in ideal case, the average prevalence is 12.5% with the standard deviation SD = 0. The SD values of the mode prevalences ranged from 1–4 (compounds 1, 3, 14, 15, 22, 27, 28) to 12–15 (compounds 2, 7, 8). As illustrated in Figure 2, among complexes that substantially change the geometry during simulation, some have one significant binding mode (Figure 2A), while others exhibit an even distribution of binding modes (Figure 2B). As can be expected, well-behaved complexes with similar geometries in each simulation period have approximately equal prevalences of binding modes (Figure 2C).

Figure 2.

Binding modes of compounds 7 (A), 22 (B), and 27 (C). The mode representing 40% or more of the bound ligand is displayed in balls and sticks (A). The time-averaged structures for 25-ps simulation intervals represent individual modes and are color-coded (modes 1 to 8, respectively): cyan - 0–25 ps, blue - 25–50 ps, green - 50–75 ps, magenta - 75–100 ps, orange - 100–125 ps, purple - 125–150 ps, red - 150–175 ps, and violet - 175–200 ps). The structures were superimposed using the α-carbon atoms of the protein.

Conclusions

The developed multi-mode approach to the LR approximation resulted, in the studied case of hydroxamate inhibitors of MMP-9, in correlations with significantly better descriptions and predictions as compared to classical one-mode LR equation. The entire simulation period is divided into time slots called binding modes. The time-averaged structures of bound and free ligands in the binding modes are used to calculate van der Waals, electrostatic, and desolvation contributions to binding. The weights of the contributions are determined by optimization using a multi-mode LR equation. The weights also determine the contributions of individual binding modes to overall binding. Steady ligands, oscillating around the equilibrium positions, exhibit an even distribution of binding modes. Mobile ligands, undergoing substantial geometry changes in the complex during MD simulations, may or may not preferentially bind in selected binding modes. If further studies confirm the findings, the multi-mode LR approach may become a useful tool for prediction of binding affinities.

Supplementary Material

supplement. Supporting Information Available.

Table S1 containing ligand structures, inhibitory potencies (experimental and calculated by all three used approaches). Table S2 listing the energy and SASA terms for individual approaches. Table S3 providing prevalencies of individual binding modes and their structural similarities for the multi-mode approach. This material is available free of charge via the Internet at http://pubs.acs.org.